地震勘探由于外界环境、地表结构、激发与接收条件不同, 接收到的信号中包含有不同类型、不同水平的噪声[1-2]。面波作为一种地震勘探中的相干噪声, 广泛存在于地震记录中, 属于一种能量强、频率低、振动延续时间长的规则干扰波, 在地震记录上比较明显, 严重影响地震数据的分辨率和信噪比, 妨碍解释人员对地震数据进行正确分析, 因此, 对地震信号中的面波进行压制成为了地震数据处理过程中的一个重要环节[3]。根据面波能量强、传播速度低和衰减较慢的特征, 目前国内外常用的面波压制方法主要有频率域滤波、小波变换、FK滤波、Radon变换、径向道变换和极化滤波等[4-8]。频率域滤波和小波变换方法考虑了面波频率低的特点, 但是当有效信号和面波干扰存在频率重叠时, 其压制效果不理想。FK滤波将地震信号转换到频率-波数(f-k)域, 然后将干扰部分的系数置零, 再进行反变换获得去噪结果, 如果有效信号和面波信号混叠, 去噪过程中会对有效信号造成一定的损失。Radon变换方法通过设计Radon域滤波器将面波和有效信号进行分离, 但很难设计合理有效的滤波器将有效信号和面波噪声完全分开。径向道变换将炮检距-双程旅行时(x-t)域中的信号变换到径向道域, 选择合适的滤波参数进行重复多次径向道变换滤波, 但是在去除面波的同时也会损害有效信号的低频分量。极化滤波利用面波的偏振特性进行面波噪声的压制, 但是在非均匀介质中, 由于面波有很强的频散特性, 在时间域或者频率域恢复单独某种波的极化属性较为困难。
深度学习是新近发展起来的一类模拟人脑思维机制的智能、自主学习的机器学习算法[9], 深度学习的实质是构建具有很多隐层的机器学习模型, 并利用海量的训练数据来学习数据特征, 最终提升分类或预测的准确性。卷积神经网络(CNN)算法在计算机视觉领域已经取得了成功, 在学习图像特征和标记图像方面非常有效, JAIN等[10]成功地将CNN应用于图像去噪。其它常用的基于CNN的去噪方法包括堆叠式稀疏去噪自动编码器和可训练的非线性归约扩散模型等[11-12]。ZHANG等[13]提出利用去噪卷积神经网络(DnCNN)进行图像去噪, 使用具有17个卷积层的卷积神经网络, 抛开传统的学习无噪数据的方式, 将噪声作为输出, 即残差学习, 可加快训练过程并改善降噪性能。YU等[14]研究了基于深度学习的地震数据去噪方法, 还将CNN用于面波去噪, 但效果不理想。这些研究主要是针对随机噪声, 而针对地震数据中的面波噪声的深度学习压制方法需要做进一步的研究。
本文研究了去噪卷积神经网络的地震数据面波噪声压制方法, 基于大型训练集的深度神经网络的去噪方法进行训练, 训练完成后, 可以对面波进行自适应智能降噪。
1 方法原理卷积神经网络从大量的训练数据出发, 建立一种针对输入和输出数据之间的隐式映射关系, 该映射关系不需要非常精确的数学表达关系和大量的人为干预, 只需用建立的训练数据库对卷积神经网络模型进行输入、输出训练。地震数据相邻样本高度相关, 卷积神经网络通过利用局部卷积滤波器的相关性, 避免使用大量参数, 在保留数据局部构造的前提下, 充分提取数据的结构特点[15]。面波在地震记录中表现为强能量的低频频散[16], 与有效反射波存在差异, 故通过卷积神经网络可以提取其与有效信号的特征差异进行深度学习压制面波噪声。
1.1 网络结构及特点去噪卷积神经网络模型是基于残差学习[17]和批量标准化处理(batch normalization, BN)[18]的深度卷积神经网络去噪算法。与传统的单层神经网络相比, 卷积神经网络用卷积核代替规则神经元, 用卷积运算代替矩阵的乘法运算, 减少了参数的数量, 优化了数据特征提取的能力, 在此基础上, 同一层卷积核的权值设置相同, 降低了网络的复杂程度, 并能充分利用计算机并行计算技术, 提高计算效率, 为深层网络模型提供计算基础[19]。
为了更好地权衡去噪性能和计算效率, 体系结构设计中的一个重要问题是为DnCNN设置适当的深度。图 1为DnCNN算法的网络结构, 网络的架构是一系列非线性处理层, 网络的输入是包含面波噪声的原始地震数据, 该网络总共包含17层, 第一层采用64个3×3的卷积核进行特征提取, 并采用ReLU激活函数, 卷积滤波器的目的是生成输入地震数据的特征图, ReLU的目的是激活特征图中包含的主要特征。在随后的第2~16层中, 在卷积滤波器和ReLU之间添加批量标准化技术, 用于稳定参数更新和改善学习过程的重新参数化。最后通过一层3×3×1的卷积核输出到残差数据, 输出层是卷积层, 它将上层每个卷积核的输出链接到卷积层的卷积核, 使输出结果包含上层所有卷积核的输出信息。然后, 所建立的神经网络通过求解一系列非线性函数, 将面波噪声衰减过程转化为一个优化问题。
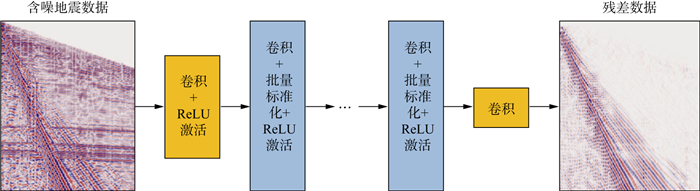
|
图 1 DnCNN网络结构 |
在网络训练过程中存在内部协变量移位(internal covariate shift, ICS)问题, 当遇到多个函数或多个网络层的组合时, 随着函数或网络层数累加增多, 网络模型的深部网络层因低层输入的变化而产生强烈的变化, 这种变化会影响模型对信号特征的学习能力, 也会降低模型的学习效率。残差学习的方式能够解决性能下降的问题, 在假设残差数据比无噪数据容易学习的前提下, 残差学习网络学习各个网络层的残差特征提取信息。DnCNN的优化目标从针对无噪数据与输出数据之间的均方误差转移到真实残差数据与网络输出之间的均方误差, 将噪声压制视为普通的判别式学习问题, 即通过网络从含噪数据中分离出噪声, 通过隐藏层中的操作隐式删除潜在的有效信号。
获得不含面波噪声数据的直接方法是令f(y)=x, 其中y为含面波噪声的地震数据, f(·)为处理函数, x为不含面波噪声的数据。然而在实际生产过程中很难实现上述方法, 只能达到f(y)≈x。DnCNN网络采用残差学习, 面波噪声可以通过R(y)≈q得到, 进而得到不含面波噪声的数据x=y-R(y)。其中, R(y)代表输入y的预测过程; q为预测结果, 即面波。利用网络计算得到估计噪声, 求得其与期望噪声之间的均方误差作为网络算法的损失函数:
| $ L(\mathit{\Theta})=\frac{1}{2 n} \sum\limits_{i=1}^{n}\left\|R\left(y_{i} ; \mathit{\Theta}\right)-\left(y_{i}-x_{i}\right)\right\|_{F}^{2} $ | (1) |
式中: Θ为要学习的参数, 也就是训练参数; n代表输入数据切分的数据块的数量。实验证明, 残差学习的方式可以应用于层数较深的卷积神经网络, 并且可以提高数据分类和数据检测的准确性。
批量标准化方法实质上是一种重参数的数据预处理方法, 通过一些自适应标准化方式, 将每层的输入数据控制在一个统一的范围内, 使数据分布达到标准正态分布模式。上一层输出值先经过批量标准化处理, 再经过激活函数[20], 进行非线性拟合, 最后与神经元进行卷积处理, 输出数据。在输入数据的控制范围内, 激活函数对数据的变化比较敏感, 微小的数值变化会引起激活函数输出值较为强烈的变化, 将数据梯度变大, 避免了反向传播过程中梯度消失的问题, 加快收敛速度, 提升网络训练的效率[21]。常用的激活函数有Sigmoid函数、双曲正切函数、MaxOut函数、ReLU函数等。Sigmoid函数计算量较大, 并且会导致梯度消失问题; 双曲正切函数解决了Sigmoid函数不以0为中心的问题但未能解决梯度消失的问题; ReLU函数和MaxOut函数解决了梯度消失的问题。ReLU激活函数具有更加优异的稀疏表示能力, 经过该函数处理后的数据能够提升梯度下降的速度, 并且简单的运算过程提升了网络的计算效率, 能够更好地挖掘地震数据的特征, 更加准确地拟合训练数据。一般在ReLU效果较差时再考虑Maxout函数。本文方法选用ReLU函数, 其具体形式如下所示:
| $ f(x)=\max (0, x)= \begin{cases}0 & x \leqslant 0 \\ x & x>0\end{cases} $ | (2) |
DnCNN将残差学习和批量标准化相结合, 既能保证模型的去噪效果, 又可以提高网络模型的运算效率[22-24]。
1.2 网络训练过程训练数据包括正演地震数据和实际地震数据两部分。数据库中90%为实际地震数据, 10%为合成地震数据。图 2为面波正演合成地震记录, 图 3为实际地震记录。对含面波噪声数据先采用广义S变换进行时频域面波压制, 再采用局部带宽正交方法恢复被去除的有效信号, 筛选出处理结果中去噪效果较好的数据, 并对其采用平移、镜像、折叠等操作进行扩充, 得到训练数据。如果将实际单炮道集直接用于训练数据, 数据量过大且其中无用信息过多, 会影响训练效果, 因此, 本文方法只将含有面波噪声的数据部分加入训练库, 去除无用信息(如图 2b上方残留的直达横波部分), 对加入数据库的数据进行分块, 统一数据块大小, 数据块本身存在重叠部分, 可以充分保留面波噪声的全部信息。图 3a为部分原始数据, 数据中有大量的面波干扰, 大部分的有效反射被面波所覆盖, 此外反射波振幅在整个记录中变化明显。在模型训练时选择含有面波噪声的原始数据作为输入, 将获得的面波噪声部分作为输出。利用正演模型数据和实际数据建立训练数据库, 通过训练网络得到去噪模型。用3000组数据作为训练库, 500组数据作为验证库, 单个数据大小为200×200。在网络训练的反向传播过程中, 针对实际数据中面波的特点, 不断修正卷积核和权重系数, 得到较好的去噪模型网络。
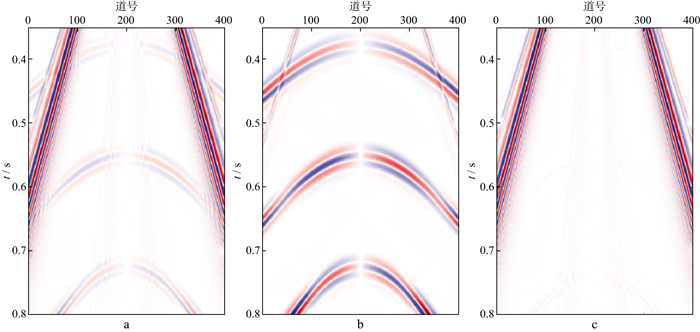
|
图 2 面波正演合成地震记录 a 含面波数据; b 去噪结果; c 去除的面波数据 |
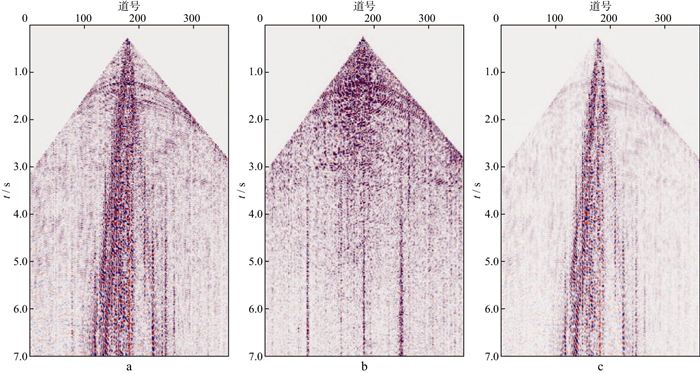
|
图 3 实际地震记录 a 原始地震数据; b 去噪结果; c 噪声部分 |
图 4为模型训练过程中损失函数随着训练迭代次数增加的变化曲线(每进行1000次迭代取其平均值进行绘图)。从图 4中可以看出, 在迭代次数达到3000次之前, 损失函数值快速下降, 在迭代次数达到35000次之前, 损失函数值下降较快且不稳定, 在迭代次数达到35000次之后, 损失函数值达到最小值, 且趋于稳定, 说明此时训练的去噪模型能够稳定进行面波去噪。
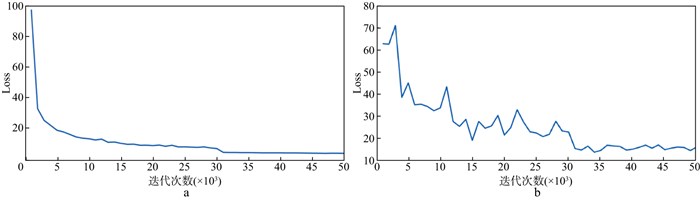
|
图 4 数据训练损失曲线 a 训练数据损失曲线; b 验证数据损失曲线 |
本文进行模型训练所用的计算机CPU型号为Intel(R) Core(TM) i5-4210H CPU@2.90GHz, 运行内存为8.00GB, GPU型号为NVIDIA GeForce GTX 960M, 运行环境为Matlab(R2016a)。训练本文所建训练数据库需要62h, 而利用训练好的模型进行面波去噪处理时, 根据处理数据的大小, 处理时间仅为几秒到十几秒, 处理效率较高。
2 实际数据处理利用本文方法对某单点高密度地震数据进行面波压制实验。如图 5a所示, 共有592道数据, 采样间隔为0.001s, 采样时长为3.0s, 数据中干扰波主要为低频面波, 在面波干扰发育的区域, 很难提取有效信号, 严重降低了地震资料的信噪比。利用本文方法对实际单点高密度地震数据进行面波压制处理, 结果如图 5b所示, 可以看出, 面波被很好地去除, 有效信号也被完好保留, 能够有效地压制面波信号, 改善地震数据的信噪比。而去除的面波数据(图 5c)中仅含少量有效信号, 说明该方法去除面波效果明显, 地震记录的整体质量得到了大幅度改善。由于训练样本只采用图 3中含面波部分数据, 故不会去除随机噪声干扰。
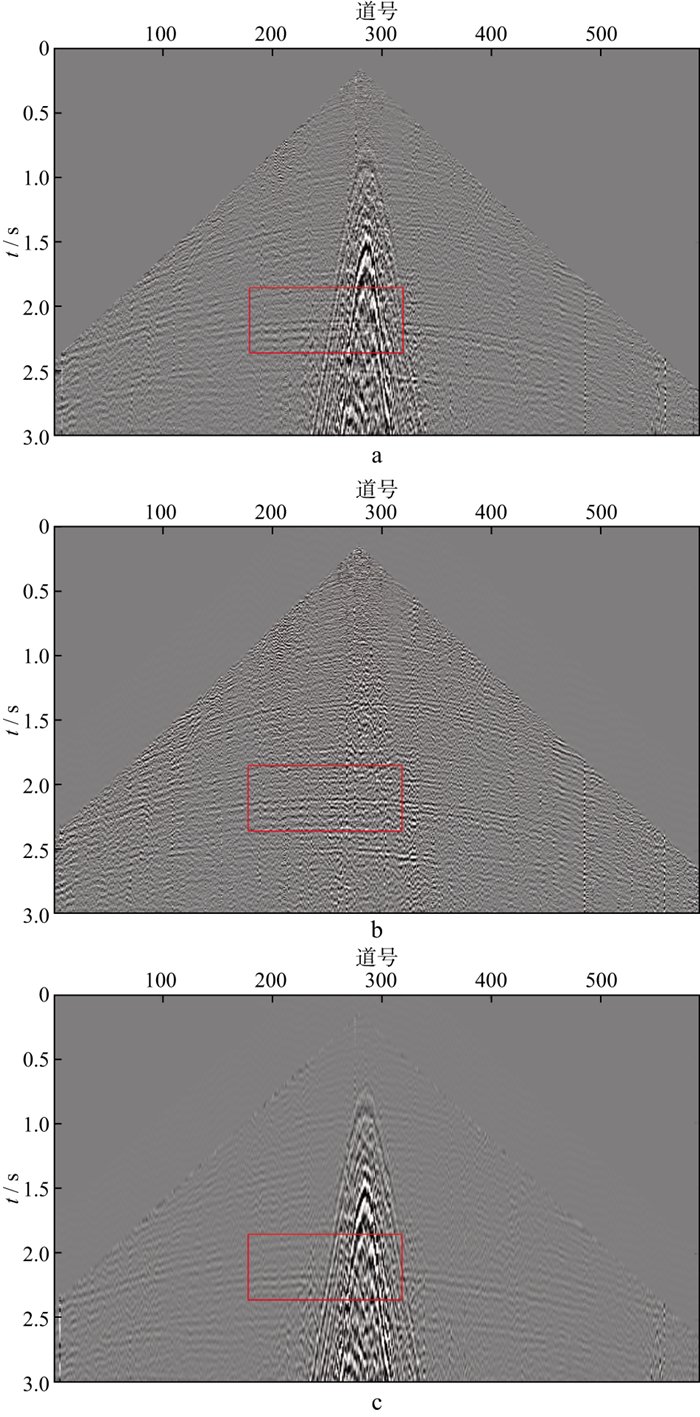
|
图 5 实际地震数据面波压制结果 a 含面波数据; b 去除面波后的数据; c 去除的面波数据 |
图 6为图 5a和图 5b中典型区域(红框区域)的局部放大显示, 可以看出, 采用本文方法可以在不影响有效反射波的情况下消除大部分面波噪声, 深层反射信息也有了更好的体现。由于去噪卷积神经网络方法是提取面波特征进行学习, 且图 2所示正演数据占比较小, 除面波外异常噪声样本较少, 与面波特征相似的噪声也被去除。

|
图 6 局部放大显示 a 含面波数据; b 去除面波后的数据 |
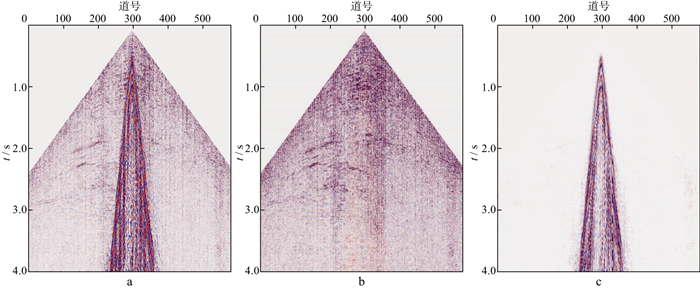
图 7a和图 7b分别为该单点高密度地震资料去除面波前、后的频率-波数(f-k)谱, 对比可以看出, 去除面波前, 面波的频率较低, 约为3~10Hz, 能量较强, 去除面波后, 低频段面波信号得到有效压制, 10~30Hz的有效信号得以凸显。

|
图 7 去除面波前(a)、后(b)的f-k谱 |
分别采用常规带通滤波(23~200Hz)和f-x域经验模式分解方法压制面波噪声, 结果如图 8所示。采用带通滤波耗时约7s, 采用f-x域经验模式分解方法耗时约14s, 采用本文方法耗时约12s。对比图 5b、图 8a和图 8c可以看出, 采用带通滤波压制面波效果较好, 但是低频信息中包含的部分有效信号也被压制; 采用f-x域经验模式分解滤波在压制面波噪声的同时对有效信号造成了较大损伤; 而采用本文方法能够在压制面波噪声的同时保护有效信号。
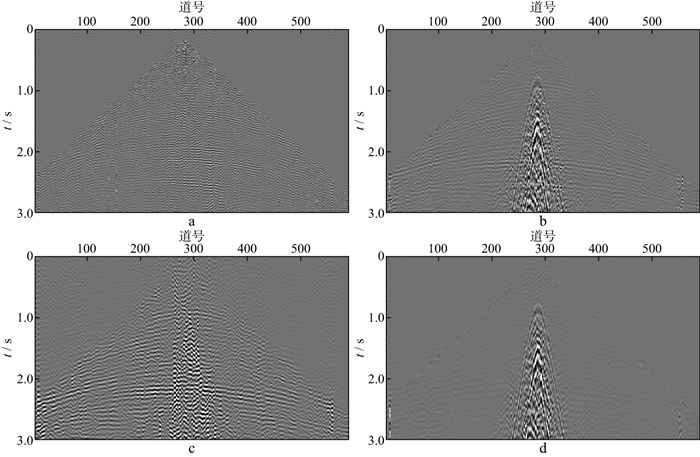
|
图 8 采用常规带通滤波(3~200Hz)和f-x域经验模式分解方法压制面波的效果 a 带通滤波去除面波的数据; b 带通滤波去除的噪声; c 经验模式分解去除面波的数据; d 经验模式分解去除的噪声 |
图 9a为另一地区的地震数据, 图 9b为采用本文方法去除面波后的结果, 图 9c为去除的面波数据。对含面波的地震数据和去除面波后的地震数据进行f-k谱分析, 结果如图 10所示, 可以看出, 去除面波后有效信息得以凸显, 再次验证了本文方法的有效性。
|
图 9 采用本文方法去除面波的结果 a 含面波数据; b 去除面波后的数据; c 去除的面波数据 |

|
图 10 去除面波前(a)、后(b)的f-k谱分析结果 |
1) 深度学习能够模拟人脑思维机制自主学习进行地震记录去噪。卷积神经网络从大量的训练数据出发, 建立了一种针对输入和输出数据之间的隐式映射关系, 该映射关系不需要非常精确的数学表达关系和大量的人为干预, 只要用建立的训练数据库对卷积神经网络模型进行输入输出训练, 就能得到这种映射关系。
2) 去噪卷积神经网络模型基于残差学习和批量标准化处理, 通过网络从含噪数据中分离出噪声, 采用ReLU激活函数激活特征图中包含的主要特征, 提升梯度下降的速度, 并提升网络的计算效率, 能够更好地挖掘面波噪声的特征, 更加准确地拟合训练数据, 更好地权衡去噪性能并提高计算效率。
3) 在进行地震资料面波噪声压制时, 传统面波去噪方法对有效信号造成损失, 本文方法将去噪卷积神经网络引入到面波去噪中, 在保证去噪效果的同时, 又能很好地保持数据的细节特征, 提高地震记录的信噪比。去噪卷积神经网络在面波去噪中能够较好地保护有效信号, 但是由于训练库中无法完全分离有效信号和面波噪声, 所以对面波的去除仍有部分残留, 因此, 改进训练库构建方法及采用优化的深度学习算法对面波去噪具有重要意义。
| [1] |
尹晓菲, 胥鸿睿, 郝晓菡, 等. 水平层状模型中多模式瑞雷波和拉夫波相速度频散曲线的灵敏度分析[J]. 石油地球物理勘探, 2020, 55(1): 136-146. YIN X F, XU H R, HAO X H, et al. Sensitivity analysis of multi-mode Rayleigh and Love wave phase-velocity dispersion curves in horizontal layered models[J]. Oil Geophysical Prospecting, 2020, 55(1): 136-146. |
| [2] |
唐杰, 张文征, 梁雨薇, 等. 自适应数据驱动的紧框架微地震数据随机噪声压制[J]. 石油地球物理勘探, 2019, 54(5): 954-961. TANG J, ZHANG W Z, LIANG Y W, et al. A random-noise suppression approach with self-adaptive data-driven tight frame for microseismic data[J]. Oil Geophysical Prospecting, 2019, 54(5): 954-961. |
| [3] |
王志农, 孙成禹, 伍敦仕, 等. 利用区域自适应极化滤波压制多分量面波干扰[J]. 石油地球物理勘探, 2019, 54(6): 1206-1216. WANG Z N, SUN C Y, WU D S, et al. A surface wave suppression method based on area adaptive polarization filtering[J]. Oil Geophysical Prospecting, 2019, 54(6): 1206-1216. |
| [4] |
李继伟, 刘晓兵, 周俊骅, 等. 基于能量比的Curvelet阈值迭代面波压制[J]. 石油地球物理勘探, 2019, 54(5): 997-1004. LI J W, LIU X B, ZHOU J H, et al. A Curvelet threshold iteration method based on energy ratio for surface-wave suppression[J]. Oil Geophysical Prospecting, 2019, 54(5): 997-1004. |
| [5] |
马见青, 李庆春. 利用时频域极化滤波压制地震面波[J]. 石油地球物理勘探, 2015, 50(6): 1089-1097. MA J Q, LI Q C. Seismic surface wave suppression with polarization filtering method in time-frequency domain[J]. Oil Geophysical Prospecting, 2015, 50(6): 1089-1097. |
| [6] |
刘晗, 张建中, 黄忠来. 应用同步挤压小波变换去除面波[J]. 石油地球物理勘探, 2016, 51(1): 71-79. LIU H, ZHANG J Z, HUANG Z L. Surface wave removal with synchrosqueezing wavelet transform[J]. Oil Geophysical Prospecting, 2016, 51(1): 71-79. |
| [7] |
董烈乾, 张慕刚, 张翊孟. 预测自适应相减面波压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1089-1093. DONG L Q, ZHANG M G, ZHANG Y M. A ground roll suppression method based on predictive and adaptive subtraction[J]. Oil Geophysical Prospecting, 2016, 51(6): 1089-1093. |
| [8] |
AL-HUSSEINI M I, GLOVER J B, BARLEY B J. Dispersion patterns of the ground roll in eastern Saudi Arabia[J]. Geophysics, 1981, 46(2): 121-137. DOI:10.1190/1.1441183 |
| [9] |
LECUN Y, BOTTOU L, ORR G B, et al.Efficient backprop: Neural networks tricks of the trade[EB/OL].[2020-12-01].https://www.doc88.com/p-3465943343870.html?r=1
|
| [10] |
JAIN V, SEUNG H S. Natural image denoising with convolutional networks[J]. Proceedings of the 21st International Conference on Neural Information Processing Systems, 2008, 769-776. |
| [11] |
WU H, ZHANG B, LIN T F, et al. White noise attenuation of seismic data by integrating variational mode decomposition with convolutional neural network[J]. Geophysics, 2019, 84(5): V307-V317. DOI:10.1190/geo2018-0635.1 |
| [12] |
DONG C, LOY C C, HE K, et al. Learning a deep convolutional network for image super-resolution[J]. European Conference on Computer Vision, 2014, 184-199. |
| [13] |
ZHANG K, CHEN Y, CHEN Y, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26: 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [14] |
YU S W, MA J W, WANG W L. Deep learning for denoising[J]. Geophysics, 2019, 84(6): V333-V350. DOI:10.1190/geo2018-0668.1 |
| [15] |
JIA Y, MA J. What can machine learning do for seismic data processing? An interpolation application[J]. Geophysics, 2017, 82(3): V163-V177. DOI:10.1190/geo2016-0300.1 |
| [16] |
BERESFORD-SMITH G, RANGO R. Suppression of ground roll by windowing in two domains[J]. First Break, 1989, 7(1): 55-63. |
| [17] |
KIKU D, MONNO Y, TANAKA M, et al. Residual interpolation for color image demosaicking[J]. IEEE International Conference on Image Processing, 2013, 2304-2308. |
| [18] |
IOFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. International Conference on Machine Learning, 2015, 448-456. |
| [19] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. Advances in Neural Information processing Systems, 2012, 1097-1105. |
| [20] |
TASSANO M, DELON J, VEIT T.An analysis and implementation of the FFDNet image denoising method[OL/J].Image Processing On Line, 2019, 9: 1-25.https://doi.org/10.5201/ipol.2019.231
|
| [21] |
VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. The Journal of Machine Learning research, 2010, 11: 3371-3408. |
| [22] |
WU X, SHI Y, FOMEL S, et al. Convolutional neural networks for fault interpretation in seismic images[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 1946-1950. |
| [23] |
YOSINSKI J, CLUNE J, BENGIO Y, et al. How transferable are features in deep neural networks[J]. Advances in Neural Information Processing Systems, 2014, 3320-3328. |
| [24] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[J]. IEEE Conference on Computer Vision and Pattern Recognition, 2016, 770-778. |



