2. 中国地质调查局广州海洋地质调查局, 广东广州 510075;
3. 北京多分量地震技术研究院, 北京 100029
2. Guangzhou Marine Geological Survey, China Geological Survey, Guangzhou 510075, China;
3. Institute of Multi-Component Seismic Technology Beijing, Beijing 100029, China
天然气水合物(gas hydrate)是烷类气体(主要为甲烷)分子被包裹在水分子内, 在相对高压低温的自然条件下形成的“笼状”结晶复合物。天然气水合物矿藏最早发现于20世纪60年代, 因其可分解释放甲烷气体, 故被看作化石能源的潜在替代品之一[1]。按照成藏地理环境的不同, 天然气水合物主要分为陆地天然气水合物和海洋天然气水合物, 分别分布于陆上永久冻土带和海上近海大陆坡沉积层中。目前, 天然气水合物的研究与勘探调查已经在30多个国家和地区展开, 其中, 以海洋天然气水合物研究居多。总体上看, 少数国家和地区的天然气水合物开发已进入探索试验开采阶段, 水合物勘查识别和实验测试技术相对成熟。
海洋天然气水合物(以下简称水合物)储层的形成机理在学术上尚不明确, 但气源是形成水合物储层的必要条件之一[2]。以我国南海北部水合物的形成机制为例, 由于神狐海域新生代沉积盆地生物气含量丰富, 水合物的形成以生物气作为主要气源; 而在东沙群岛的东南部, 在深部生成了大量热解气, 与较浅部产生的生物气合并, 共同作为水合物生成的气源[3]。气体可沿活动断裂或底辟构造体运移至适合天然气水合物析出的低温高压区域——即天然气水合物稳定带(gas hydrate stability zone, GHSZ), 在此转化为固态水合物, 以扩散状、脉状、块状或结核状形式赋存。
海洋地震作为水合物的主要勘查方法, 利用了地层中含水合物时地震剖面上所呈现的异常地震反射特征, 包括似海底反射(bottom simulating reflectors, BSR)、地震空白带(seismic blanking zone, SBZ)、速度倒转、速度-振幅异常结构等。BSR是见于地震剖面上的一组具有与海底反射极性相反、强振幅、形状大致与海底平行等特征的反射层[4], 常指示GHSZ与其下伏游离气层的分界面[5-6]; SBZ一般存在于BSR上覆区域, 呈弱反射能量特征[3, 7-8], 往往与BSR相伴相生, 共同指示水合物储层。
地震技术除了用于识别水合物储层外, 还可用来估算水合物与游离气的空间分布和储量。一般常用的方法是地震数据全波形反演、走时层析成像、波阻抗反演、AVO属性反演、地震属性综合分析等, 得到相关的成像数据来对水合物空间分布进行预测。其中全波形反演与走时成像技术可以进一步得到弹性波速度, 结合岩石物理模型, 可对储层的水合物饱和度进行评价和估计。波阻抗反演也可以结合钻井曲线数据, 基于Archie公式对地层孔隙中的水合物饱和度进行估算[9]。随着各国对海洋天然气水合物调查研究的重视, 海洋地震技术得到更充分的发展。因其勘探范围较广、施工成本低、成像分辨率较高等特点, 在海洋天然气水合物调查研究中愈来愈发挥着不可替代的作用。因此, 本文重点介绍海洋天然气水合物的地震识别探测技术的发展及存在的问题。
1 水合物储层地震反射特征随着水合物调查与研究的持续开展, 水合物成藏模式的研究也不断深入。但由于水合物成藏气体疏导体系、运移方式和来源的不同, 国内外存在多种以不同标准划分的水合物成藏模型。根据气体疏导方式的不同, 划分为扩散型和渗漏型[10], 扩散型与渗漏型水合物储层在地震剖面上的指示特征不尽相同, 需要分开讨论。
1.1 BSR与SBZ对于扩散型水合物储层, 最明显的地震反射特征为纵波剖面上的BSR与SBZ。目前, BSR被公认为海洋天然气水合物最有可能存在的标志之一, 同时在地震剖面上较易识别, 因而地震勘探是水合物勘探前期必不可少的调查与研究方法。
20世纪70年代, 在Blake海台及其附近海域的一系列地震剖面上发现了强反射现象, SHIPLEY等[4]将这种强反射定名为BSR。他们对美国东海岸、墨西哥湾西部、哥伦比亚北部和巴拿马北部海岸以及从巴拿马到墨西哥阿卡贝科附近的中美洲太平洋一侧的地震成像中出现的异常反射进行了总结, 再综合BSR的空间几何关系、反射系数、反射极性和压力-温度关系, 认为此异常反射可以作为水合物储层存在的标志。随后DILLON等[2]针对美国东海岸地震剖面上的BSR作了进一步说明:水合物使所在地层的纵横波速度均有较大幅度提高; 而下伏地层无论是否含游离气, 都会出现纵波速度的大幅下降, 形成负极性的强反射。我国南海北部被动大陆边缘区存在的水合物储层, 广泛分布于水深350~3000m海域的海底沉积内, 由于该区域通常呈水平沉积, BSR一般与沉积层理反射大致平行[3]。
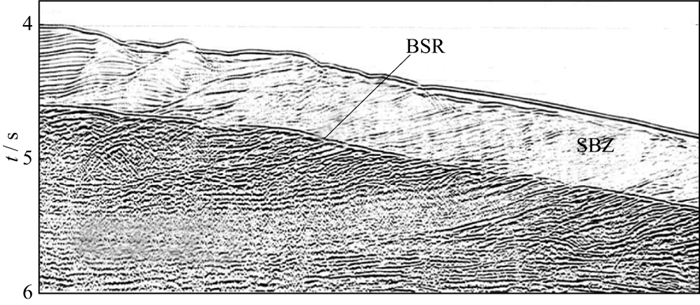
在Blake外海台和巴拿马西部的地震资料中, 异常反射层BSR上方同时出现了SBZ[4], 见图 1。DILLON等[2]推测是GHSZ内地层的孔隙中填充了水合物, 其胶结作用使地层之间的阻抗差减小, 他们根据测井数据建立储层模型, 通过改变水合物含量及胶结程度, 正演模拟得到的合成记录很好地还原了SBZ现象。但HOLBROOK等[8]提出了不同的看法, 认为尽管在研究区内对应SBZ的地层中发现了水合物储层, 但由于钻探结果显示该地区的沉积物几乎全部由绿灰色超微化石粘土组成, 且从海底以下150m开始往深部的岩性变化不大, 所以更相信SBZ是因沉积物的相对均质性而产生的自然低背景反射, 而不是水合物胶结的结果。
|
图 1 Blake外海台顶部和东侧的多道地震反射剖面[4] |
经历了早期仅仅依靠BSR特征在地震剖面上直接识别水合物阶段, 人们开始对水合物储层进行地震属性研究, 即通过地震反射强度、三瞬属性、相对波阻抗和能量半衰时等属性来凸显BSR特征。例如强瞬时振幅可指示BSR的水平和垂向分布特征, 而低瞬时频率可指示水合物储层下伏游离气的富集[11], 瞬时相位则可以实现BSR的追踪, 相对波阻抗有利于更清晰地反映BSR的负极性特征[12]。另外, 近年来随着人工智能和机器学习等技术的兴起, 地层中水合物的存在导致地震反射波形发生了变化, 基于水合物发育区和BSR处的地震道波形特征进行分类和识别的神经网络技术成为当前的研究热点。
尽管BSR与其上部的SBZ联合作为水合物在近海浅层沉积存在的标志已被学术界认可, 但其产生的机制以及与水合物存在的更深层次的相关关系仍存在诸多争议。不论是BSR还是SBZ, 与海底沉积物中是否存在水合物并不是严格的对应关系[8, 13-15]。例如, 在没有游离气的情况下, 即使存在水合物, BSR也可能不发育; 对于BSR上方SBZ形成的原因, 目前尚未形成统一的认识, 通常认为其振幅减弱的程度与水合物的成藏模式、饱和度以及岩石孔隙度有关[16-17]。我国神狐海域钻探揭示地震剖面上SBZ现象产生的原因并非水合物存在, 而是由于浅部地层为未固结的含黏土粉砂和粉砂质泥, 沉积地层岩性较为单一、阻抗差异小所引起。由此可见, 我们依然需要对水合物储层的标志特征BSR及其上的SBZ开展进一步的研究, 以促进对水合物沉积模式的正确认识, 减少地震预测的多解性。
1.2 速度异常速度异常是水合物存在的另一个重要特征, 不论是哪种水合物的成藏模式, 由于纯水合物的纵波速度范围为3.2~3.7km/s[18], 如果地层的沉积物中出现了固态的水合物, 纵波速度很可能会增加, 从而出现速度异常。20世纪90年代后, 基于多次覆盖的人工地震技术迅速发展且在海洋领域获得了应用, 其中层速度反演方法的应用促进了水合物储层垂向速度结构的研究[11], 确定了水合物储层的速度异常识别标志, 即含水合物储层声波速度异常增大, 而上覆地层和下伏地层速度较低, 整体表现为上下低、中间高的高速异常层。
1.3 海底冷泉与甲烷泄露当较深部的烃类气体沿断裂或裂缝等通道运移至海底较浅部, 在合适的温压条件下, 可直接在海底较浅部甚至海底表面聚集形成水合物, 这就是被称作渗漏型水合物成藏系统。当渗漏型水合物储层的温压条件不稳定时, 地层中的水合物可能会分解, 释放出甲烷等气体以喷涌或渗漏的方式注入海洋中, 形成一种以水合物分解为成因的海底冷泉[19]; 如果冷泉气体的通量足够大, 气体会在海水中上升时形成气泡羽状流。世界许多地区都探测到了气泡羽状流, 这些区域常伴有丰富的水合物, 且可被地震成像发现[20-22], 故海底冷泉和气泡羽状流也已被看作是渗漏型水合物的标志。
另外, 渗漏型水合物也可以引起似海底反射(BSR)、地层速度异常等指示扩散型水合物的地震异常特征, 但目前研究表明[23], 由渗漏型水合物引起的这类异常不如扩散型水合物典型, 且由于埋藏更浅, 更难于在地震剖面上发现。
2 水合物储层岩石物理模型岩石物理模型是连接地层物性参数和弹性参数的桥梁, 也是目前利用地震技术估算海洋水合物储层饱和度的主要手段。通过合适的岩石物理模型计算水合物储层的弹性波速度, 将利用地震技术得到的弹性波速度剖面与计算结果进行匹配, 从而反演得到估算的水合物饱和度。目前主要研究基于以下3类针对扩散型水合物储层提出的岩石物理模型。
2.1 等效介质理论模型HELGERUD等[24]针对海底未固结、高孔隙的水合物储层, 提出了一种等效介质理论模型来计算储层的弹性参数。该模型是基于DVORKIN等[25]针对海洋沉积物所提出的岩石物理模型发展而来, 综合考虑了孔隙中水合物和游离气的影响。在该模型下, 水合物储层的等效弹性模量和弹性波速度由Gassmann方程计算得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{{\rm{sat }}}} = {K_{{\rm{s }}}}\frac{{\varphi {K_{{\rm{dry }}}} - \frac{{(1 - \varphi ){K_{\rm{f}}}{K_{{\rm{dry }}}}}}{{{K_s}}} + {K_{\rm{f}}}}}{{(1 - \varphi ){K_{\rm{f}}} + \varphi {K_{\rm{s}}} - \frac{{{K_{\rm{f}}}{K_{{\rm{dr}}y}}}}{{{K_{\rm{s}}}}}}}}\\ {{G_{{\rm{sat }}}} = {G_{{\rm{dry}}}}}\\ {{v_{\rm{P}}} = \sqrt {\frac{{{K_{{\rm{sat }}}} + \frac{4}{3}{G_{{\rm{sat }}}}}}{\rho }} \quad {v_{\rm{S}}} = \sqrt {\frac{{{G_{{\rm{sat}}}}}}{\rho }} } \end{array}} \right. $ | (1) |
式中:Ksat和Gsat分别对应饱和孔隙流体的水合物储层的体积模量和剪切模量; Kdry和Gdry分别表示水合物储层的固体骨架在干燥时的体积模量和剪切模量; Ks和Kf分别表示固相矿物和孔隙流体的等效体积模量; φ是储层的孔隙度; ρ是储层的体密度, 为各相密度的加权平均; vP和vS分别为水合物储层等效的纵波速度与横波速度。
HELGERUD等[24]利用DVORKIN等[25]提出的Hashin-Shtrikman-Hertz-Mindlin(以下简称HSHM)理论模型来计算干燥固体骨架的弹性模量。这里需要介绍一个临界孔隙度的概念, NUR等[26]在岩石物理实验中发现:当多孔岩石的孔隙度小于某一数值时, 矿物颗粒是固结的, 且孔隙度越小固结程度越高; 而孔隙度大于这一数值后, 岩石矿物呈分散状悬浮在孔隙流体当中, 矿物颗粒之间几乎不接触; 这一孔隙度值被定义为临界孔隙度(φc), 一般为36%~40%, 取决于岩石矿物的种类。HSHM理论假设岩石的孔隙度在临界孔隙度时, 干燥的固体骨架可看作是数个完全相同的致密小球随机接触堆积的集合体, 其等效弹性模量由Hertz-Mindlin理论[27]计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{{\rm{HM}}}} = {{\left[ {\frac{{G_{\rm{s}}^2{a^2}{{\left( {1 - {\varphi _{\rm{c}}}} \right)}^2}}}{{18{{\rm{ \mathsf{ π} }}^2}{{(1 - \sigma )}^2}}}P} \right]}^{\frac{1}{3}}}}\\ {{G_{{\rm{HM}}}} = \frac{{5 - 4\sigma }}{{5(2 - \sigma )}}{{\left[ {\frac{{3G_{\rm{s}}^2{a^2}{{\left( {1 - {\varphi _{\rm{c}}}} \right)}^2}}}{{2{{\rm{ \mathsf{ π} }}^2}{{(1 - \sigma )}^2}}}P} \right]}^{\frac{1}{3}}}} \end{array}} \right. $ | (2) |
式中:Gs为固相矿物的等效剪切模量; σ为固相矿物的泊松比; P为一定深度处沉积岩层的有效压强; a为集合体中每个小球的平均接触次数(取值为8.0~9.5);KHM和GHM分别为集合体等效的体积模量和剪切模量。(1)式和(2)式中固相矿物的等效体积模量Ks与等效剪切模量Gs均利用HILL的平均方程[28]计算得到; 孔隙流体的等效体积模量Kf为各流体组分等应力下的平均。
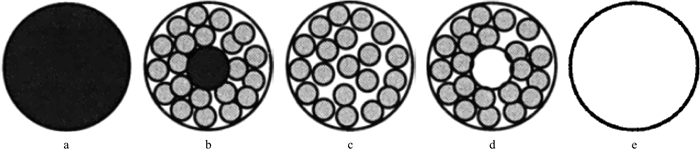
计算多组分混合物的等效弹性模量时, 当已知各组分的体积分数和弹性模量, 我们可以预测混合物弹性模量的上下限。在HSHM理论中, 储层的干燥骨架是两个组分的混合。当水合物储层的孔隙度小于φc时, 看作是孔隙度为φc的致密小球集合体包围在孔隙度为0的固相矿物组分(图 2a)的周围(图 2b), 其等效弹性参数由Hashin-Shtrikman理论[29]的下限来计算; 当水合物储层的孔隙度大于或等于φc时, 看作是孔隙度为φc的致密小球集合体(图 2c)包围在孔隙度为1的零刚度组分(图 2e)的周围(图 2d), 其等效弹性参数由Hashin-Shtrikman理论的上限来计算。因此, 水合物储层的干燥固体骨架的弹性模量由公式(3)计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{{\rm{dry}}}} = {{\left( {\frac{{\varphi /{\varphi _{\rm{c}}}}}{{{K_{{\rm{HM}}}} + \frac{4}{3}{G_{{\rm{HM}}}}}} + \frac{{1 - \varphi /{\varphi _{\rm{c}}}}}{{{K_{\rm{s}}} + \frac{4}{3}{G_{{\rm{HM}}}}}}} \right)}^{ - 1}} - \frac{4}{3}{G_{{\rm{HM}}}}}\\ {{G_{{\rm{dry}}}} = {{\left( {\frac{{\varphi /{\varphi _{\rm{c}}}}}{{{G_{{\rm{HM}}}} + Z}} + \frac{{1 + \varphi /{\varphi _{\rm{c}}}}}{{{G_{\rm{s}}} + Z}}} \right)}^{ - 1}} - Z} \end{array}} \right.\varphi < {\varphi _{\rm{c}}} $ | (3a) |
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{{\rm{dry}}}} = {{\left[ {\frac{{(1 - \varphi )/\left( {1 - {\varphi _{\rm{c}}}} \right)}}{{{K_{{\rm{HM}}}} + \frac{4}{3}{G_{{\rm{HM}}}}}} + \frac{{\left( {\varphi - {\varphi _{\rm{c}}}} \right)/\left( {1 - {\varphi _{\rm{c}}}} \right)}}{{\frac{4}{3}{G_{{\rm{HM}}}}}}} \right]}^{ - 1}} - \frac{4}{3}{G_{{\rm{HM}}}}}\\ {{G_{{\rm{dry}}}} = {{\left[ {\frac{{(1 - \varphi )/\left( {1 - {\varphi _{\rm{c}}}} \right)}}{{{G_{{\rm{HM}}}} + Z}} + \frac{{\left( {\varphi - {\varphi _{\rm{c}}}} \right)/\left( {1 - {\varphi _{\rm{c}}}} \right)}}{Z}} \right]}^{ - 1}} - Z} \end{array}} \right.\varphi \ge {\varphi _{\rm{c}}} $ | (3b) |
| $ Z = \frac{{{G_{{\rm{HM}}}}}}{6}\left( {\frac{{9{K_{{\rm{HM}}}} + 8{G_{{\rm{HM}}}}}}{{{K_{{\rm{HM}}}} + 2{G_{{\rm{HM}}}}}}} \right) $ | (3c) |
|
图 2 HSHM理论下的干岩石骨架微观模型, 孔隙度从左至右增大[25] a φ=0; b φ<φc; c φ=φc; d φ>φc; e φ=1 |
式中:Z为简化算式的代数符, 无实际物理意义。
另外, 该模型考虑了水合物在岩石孔隙中的两种极端赋存形态[30]:“胶结”和“非胶结”, 针对这两种形态, 公式中Kdry和Gdry的计算方式有所不同。胶结模型将水合物作为颗粒接触基质(接触胶结)或包裹基质(包裹胶结)的形式, 此时水合物被视为固相矿物的一部分, 改变了水合物储层固相的弹性参数, 并降低了储层的孔隙度; 非胶结模型认为水合物是孔隙流体的一部分, 不会影响沉积物固体框架的强度。
2.2 三相Biot理论模型CARCIONE等[31]基于Biot的多孔弹性理论[32], 模拟了含水饱和的水合物沉积物的弹性特征, 在LECLAIRE等[33]研究部分冻结多孔介质的方法(LCA模型)基础上提出了一种理论模型。该模型将含水、水合物和固体骨架三相的水合物储层, 设想成两个孔隙含水饱和的骨架——即固体沉积物骨架和水合物骨架, 每个骨架都表现出其特征弹性模量, 这些模量体现在刚度矩阵和剪切矩阵(Rij和μij, i, j=1, 2, 3)中, 矩阵Rij和μij中的元素是关于地层孔隙度、孔隙流体黏度、地震波角频率, 以及流体、固体颗粒和水合物的密度、体积模量和剪切模量, 还有水合物骨架和沉积物骨架的等效体积模量和等效剪切模量的函数。由于LCA模型下的矩阵Rij和μij公式表达过于复杂, 我们在此不展开讨论, CARCIONE等[31]利用此模型推导了水合物储层的3个纵波速度(一个快纵波和两个慢纵波)和2个横波速度(一个快横波和一个慢横波)的方程。
在此基础上, CARCIONE等[34]考虑到在低频假设下, 波的频散可以忽略, 固体颗粒、水和水合物等处于应变状态, 这样形成了一个封闭系统, 此时的三相Biot理论方程可以有一个简化形式, 水合物储层的纵波和横波速度由以下方程计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{v_{\rm{p}}} = \sqrt {\frac{{{K_{\rm{e}}} + \frac{{4{G_{\rm{e}}}}}{3}}}{\rho }} \;\;\;\;\;{v_{\rm{S}}} = \sqrt {\frac{{{G_{\rm{e}}}}}{\rho }} }\\ {\rho = {\varphi _{\rm{s}}}{\rho _{\rm{s}}} + {\varphi _{\rm{w}}}{\rho _{\rm{w}}} + {\varphi _{\rm{h}}}{\rho _{\rm{h}}}}\\ {{K_{\rm{e}}} = {K_{{\rm{sm}}}} + {K_{{\rm{hm}}}} + {{\left( {1 - \frac{{{K_{{\rm{sm}}}}}}{{{K_{\rm{s}}}}} - \frac{{{K_{{\rm{hm}}}}}}{{{K_{\rm{h}}}}}} \right)}^2}M}\\ {M = {{\left[ {\left( {{\varphi _{\rm{s}}} - \frac{{{K_{{\rm{sm}}}}}}{{{K_{\rm{s}}}}}} \right)\frac{1}{{{K_{\rm{s}}}}} + \frac{{{\varphi _{\rm{w}}}}}{{{K_{\rm{w}}}}} + \left( {{\varphi _{\rm{h}}} - \frac{{{K_{{\rm{hm}}}}}}{{{K_{\rm{h}}}}}} \right)\frac{1}{{{K_{\rm{h}}}}}} \right]}^{ - 1}}}\\ {{G_{\rm{e}}} = {G_{{\rm{sm}}}} + {G_{{\rm{hm}}}}} \end{array}} \right. $ | (4) |
式中:K, G, ρ和φ分别表示体积模量、剪切模量、密度和体积分数; 下标“s”、“w”、“h”分别表示固体颗粒、水和水合物; 下标“sm”和“hm”分别表示固体骨架和水合物骨架; Ke和Ge分别表示水合物储层的等效体积模量和剪切模量; ρ为储层的密度。其中各个分量的计算方式详见文献[34]。
GEI等[35]完善了CARCIONE等[31]提出的三相Biot理论方程, 考虑了游离气、孔隙中的等效压力和地震波衰减的影响, 推广了该理论的适应范围, 但可能因其完善后的方程计算过于复杂, 并未得到广泛应用。
LEE等[36]则针对CARCIONE等[31]提出的三相Biot理论方程, 同样在低频假设下从另一个角度进行了简化, 于是含水合物沉积地层的快纵波可通过下式计算:
| $ \left\{ \begin{array}{l} {v_{\rm{P}}} = \sqrt {\frac{{\sum\limits_{i, j}^3 {{\mathit{\boldsymbol{R}}_{ij}}} }}{\rho }} \\ {v_{\rm{S}}} = \sqrt {\frac{{\sum\limits_{i, j}^3 {{\mathit{\boldsymbol{\mu }}_{ij}}} }}{\rho }} \\ \rho = {\varphi _{\rm{s}}}{\rho _{\rm{s}}} + {\varphi _{\rm{w}}}{\rho _{\rm{w}}} + {\varphi _{\rm{h}}}{\rho _{\rm{h}}} \end{array} \right. $ | (5) |
式中:Rij和μij两个矩阵中各个元素的计算也同样得到了简化。与之前的理论模型不同, 在计算水合物骨架和固体骨架的体积模量与剪切模量时, LEE等[36]并没有使用CARCIONE等[31]所用的Kuster-Toksöz模型[37], 而是使用PRIDE等[38]所提出的表达式:
| $ {K_{\rm{d}}} = \frac{{{K_{\rm{s}}}\left( {1 - {\varphi _n}} \right)}}{{1 + \alpha {\varphi _n}}}\quad {\mu _{\rm{d}}} = \frac{{{\mu _{\rm{s}}}\left( {1 - {\varphi _n}} \right)}}{{1 + \gamma \alpha {\varphi _n}}}\quad \gamma = \frac{{1 + 2\alpha }}{{1 + \alpha }} $ | (6) |
式中:Kd为水合物骨架或固体沉积物骨架的体积模量(即Khm或Ksm), μd为水合物骨架或固体沉积物骨架的剪切模量(即μhm或μsm); Ks和Gs分别表示沉积物颗粒的体积模量和剪切模量; α被称为固结参数, 它表征固结引起的沉积物硬化程度, 往往依靠测井所得的P波速度来拟合得到; φn表示非骨架部分的体积分数。水合物在孔隙中与沉积物颗粒的胶结程度对整个沉积物骨架的弹性模量有重大的影响, 所以在计算沉积物骨架的弹性模量时, LEE等[36]给出了视孔隙度φas的概念, 用来替换φn进行计算, 即:φas=φw+εφh, 其中φw和φh分别表示孔隙水和水合物的体积分数。若经验参数ε=1, 则水合物悬浮在孔隙空间中, 不起承载作用; 若ε=0, 则水合物被认为是矿物框架的一部分, 在沉积物颗粒之间形成胶结接触。
2.3 微分等效介质理论模型JAKOBSEN等[39]在HORNBY等[40]和SHE-NG等[41]研究的基础上, 将富含粘土的水合物储层的地震特性与其孔隙度、矿物组分、微观结构、粘土颗粒排列和水合物饱和度联系起来, 提出了一个各向异性的微分等效介质理论模型。该理论基于自洽近似(self-consistent approximation, SCA)[42]与微分等效介质(differential effective medium, DEM)理论[43]结合后的一阶平滑近似[44]。水合物储层在微观上被等效成一组完全相同的块状子复合物, 每个子复合物又由形状相同的椭球体颗粒定向排列构成; 子复合物单元的等效弹性静力学参数可以用张量Kijkl来表示, 它将施加的应力与每个内含物中的平均应变联系起来[45]。
在SCA理论模型中, 子复合物由背景基质与相对无穷小体积的内含物构成, 有待确定的等效介质置于背景基质中; 通过改变背景基质的弹性参数, 即张量Kijkl, 可使背景基质的弹性参数逼近于所求等效介质的弹性参数。这种利用自洽近似法创建的双相连通介质模型是各向异性的, 并考虑了各组分之间的相互关系, 但仅适用于介质孔隙度为40%~60%的情况, 在其它孔隙度下无法保证双相连通性[46], 此时需要与DEM模型结合起来。DEM理论是通过逐渐将内含物替换至背景基质中, 直到该组分的体积分数达到期望值时, 得到多相介质的等效弹性模量。JAKOBSEN等[39]同样考虑了2种情况:在水合物被当作是储层中起承载作用的组分时, 先用SCA理论计算粘土和水合物(各占50%)构成的骨架的等效弹性模量, 再用DEM理论将水以孤立的内含物的形式替换到骨架中, 最终得到子复合物单元的等效弹性模量; 在水合物被认为不起承载作用时, 连通骨架为粘土和水(各占50%), 而之后替换进来的内含物为水合物。如需在储层矿物中加入其它矿物组分(如石英等), 同样利用DEM理论将其当作内含物替换进来。接着, 根据水合物储层实际取样岩心分析, 得到子复合物在统计学上的定向分布规律, 然后运用一阶平滑近似算法最终得到水合物储层的等效弹性参数。受重力影响, 板状粘土颗粒倾向于水平层状排列, 所以该模型下的储层认为是横向各向同性的。
2.4 岩石物理模型适应性分析以上的岩石物理模型是运用最为广泛的3类基础模型, 其后发展的模型大多都是在此基础上进行的改进和拓展[47]。发展至今, 更早的权重方程[48]由于具有一定经验公式的性质, 没有物理实验基础支持, 近年来的研究已经基本不再使用。目前使用最多的是等效介质理论模型和三相Biot理论模型。等效介质理论模型是唯一直接体现地层有效压力的模型, 并针对水合物与沉积物基质骨架胶结和悬浮于孔隙水中的水合物给出了不同的模型考虑, 更适用于未固结的泥质含量更高的松散海底沉积介质的描述。三相Biot理论模型基于水合物占据孔隙空间且相互连通的假设[34], 但由于Biot理论假设孔隙水不依附沉积物颗粒, 因此更适用于模拟泥质含量较少的砂岩储层中的水合物[49]。该模型最初通过赋值经验参数为0或1来表示水合物是否影响了固体框架的弹性参数, 但之后的研究发现, 将经验参数设为常数0.12能更好地拟合实际测井测量的纵、横波速度[36]。此外, 其固结参数的选择在很大程度上影响了该模型的精确度, 因固结参数取决于有效压力和地层的胶结程度, 目前多由研究区其它不含水合物的井位所得到的速度结合Mindlin理论公式拟合计算得到[50], 故对于不同研究区, 其值不同。后来出于模型简化需要, 更多的研究采用了LEE等[36]对其简化而推导的简化三相Biot理论, 可以更快地计算出水合物储层的等效弹性波速度, 但由于其原理只考虑了固相基质、水和水合物三相, 所以当考虑到地层孔隙中游离气与水合物共存的情况时, 无法使用该模型直接进行数值模拟。
这些模型提出时, 科学家还未对渗漏型水合物开展系统的研究调查, 仅仅是用来对扩散型水合物进行等效模拟。针对渗漏型水合物储层, LEE等[51]推导出一个层状介质模型来研究裂缝填充型水合物的各向异性, 对于其它类型的渗漏型水合物储层, 尤其是块状水合物储层, 目前并没有可引用的岩石物理模型, 导致使水合物储层的等效弹性模量计算存在困难。另外, 合适的温压条件是水合物结晶析出的前提, 而现有的模型均未考虑温度参数, 这可以说是水合物储层研究面临的致命之处。
3 天然气水合物地震探测技术 3.1 地震探测技术的发展国外对于水合物的地震勘探起步较早, 当地震勘探还是单道采集时就已经开始在海洋上布置测线进行水合物储层的探测[4]。到后来逐步发展为二维、三维地震勘探。目前, 水合物探测主要依赖高分辨率地震技术, 包括拖缆和海底高频地震仪(high frequency ocean bottom seismometer, HF-OBS)等多种技术。我国对海洋天然气水合物的研究起步较晚, 20世纪八九十年代, 国内学者开始对海洋天然气水合物进行研究, 并对国外的相关调查研究展开了跟踪。直到1999年, 广州海洋地质调查局采用高分辨率地震探测技术率先在我国南海北部西沙海槽区域进行了水合物的调查, 发现了可能指示水合物存在的地震标志——BSR现象, 之后我国开始加大水合物资源调查力度, 对南海北部多处海域进行了大量的高分辨率二维地震探测[5, 7, 52-54]; 随着调查研究的深入, 相继展开一系列配套的钻探工作和海底高频地震仪(HF-OBS)的布设工作[55-62]。
地震探测技术除了用来探测水合物储层外, 对其饱和度的预测结果则直接决定了该储层是否具备开发价值。在OBS技术被广泛应用于水合物探测之前, 通常利用海上拖缆接收的纵波速度信息与测井数据, 结合岩石物理模型或经验公式来对储层的水合物饱和度进行估算, 但利用单纯纵波存在多解性[63]; 且海上拖缆接收地震信号导致了较短的偏移距, 增加了走时反演的不确定性[64], 使纵波速度估计不准, 直接增大了水合物饱和度的估计误差。故由单纯纵波向多波探测发展成为水合物研究的必然趋势。
不同于以往利用海上拖缆在水中接收单分量纵波地震波信号, HF-OBS布设在海底, 能同时接收到P波、S波、SP波与PS波等多波信号, 提供了更多的地震响应信息。其优势可以归纳为以下几点:
1) 由于纯水合物的横波速度可以达到1.8km/s[18], 而一般海底浅部松散沉积的横波速度在0.6km/s以下, 且不同水合物的微观赋存模式(悬浮式、接触式和胶结式[65])下, 水合物储层的横波速度表现不同[66], 所以对海底沉积进行横波速度分析有助于判别水合物的微观赋存状态, 进一步确定所选用的岩石物理模型是否合适;
2) 横波对水合物储层含气构造具有较好的成像效果, 当游离气与水合物共存时, 会降低纵波速度, 对仅用纵波速度进行水合物饱和度的估计存在干扰; 而横波速度受游离气影响较小, 对水合物存在更为敏感[63], 可以更精确地刻画游离气与水合物共存条件下的水合物饱和度, 同时对BSR下方游离气的含量估计有积极作用[60];
3) HF-OBS系统提供了长偏移距的数据, 且横波速度信息提供了附加的约束条件, 使弹性波速度估算结果更可信;
4) 从实际观测情况来看, 在浅层勘探中横波勘探的分辨率要高于纵波[67], 而水合物的赋存环境恰好是近海大陆坡埋深较浅的沉积层。故近年来, 国内外将高分辨率三维探测技术与HF-OBS技术联合运用, 发展了较为系统的海洋天然气水合物多波探测技术[68-71], 可用来进行波形反演、走时反演、多波联合反演等研究, 以提高横向分辨率, 获得更精确的纵、横波速度、地层波阻抗变化等[57]。
3.2 水合物多波探测现状MIENERT等[68]对布设在挪威中部Ormen Lange地区近海已知存在水合物储层的OBS地震数据进行了速度分析, 得到了海底沉积层垂向的纵、横波速度, 并分别利用权重方程和等效介质理论模型对地层中的水合物饱和度进行了估算。
欧盟天然气水合物计划项目在挪威外海Svalbard海域采用三维和二维地震与四分量OBS联合勘探方法, 记录了该天然气水合物区的多波地震响应; WESTBROOK等[69]利用该套数据通过三维走时层析成像、二维射线追踪反演和一维波形反演, 反演了P波和S波的速度, 并分别利用DEM理论模型与三相Biot理论模型估算了BSR上方地层的水合物饱和度。采用DEM理论模型进行估算时, 作者通过不断改变每个深度处的水合物饱和度来达到与反演得到的纵、横波速度的最小二乘匹配; 而采用三相Biot理论模型时, 由反演得到的纵波速度与理论模型计算的背景值(假设地层中不含水合物时)之间的差值得到水合物的饱和度。值得注意的是, 在上述研究中, 水合物饱和度变化的垂向分辨率大约为20m, 即受储层厚度的影响, 这意味着远小于这个厚度的饱和度突变无法被识别。
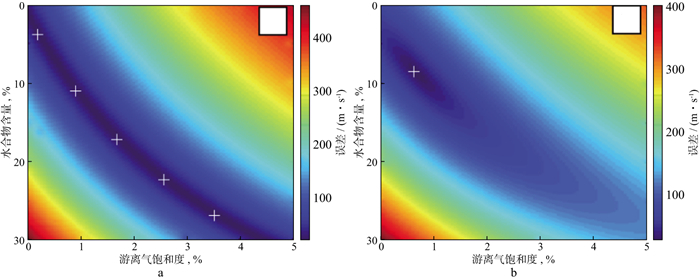
KUMAR等[63]利用美国俄勒冈州近海水合物脊的海上拖缆与OBS联合探测试验地震数据, 对该海域水合物储层中的水合物饱和度进行了估算。纵、横波速度剖面先由四分量OBS数据经走时反演得到, 接着结合Wood平均方程和等效介质模型的思想提出了一个更符合该地区水合物赋存形式的岩石物理模型来拟合P波速度, 而S波速度由一个纵、横波速度的经验关系得到。由于该地区的钻井资料已经证实在GHSZ内水合物和游离气共存, 游离气使水合物带来的P波速度增加被削弱, 这时仅用P波速度进行水合物饱和度的预测存在多解性(图 3), 而S波速度受游离气影响较小, 加入S波速度进行约束, 提高了水合物饱和度估算的精确度。
|
图 3 反演速度与模型计算速度之间的误差与水合物含量和游离气饱和度的变化关系[63](图 3a中的“+”表现了仅用纵波速度时最小误差下的多解性, 而在图 3b中这一点得到了更好的约束) a 仅用纵波速度计算的误差; b 联合使用纵、横波速度计算的误差 |
2005年, 加拿大在温哥华岛外海大陆坡北Cascadia海域的水合物富集区进行了二维拖缆地震与OBS联合探测, DASH等[64]将单道拖缆地震数据与OBS数据相结合进行走时反演, 得到了海底面以下约250m深的BSR处的P波速度结构模型; 近偏移距与远偏移距数据的结合既保证了海底介质层位的刻画, 也提高了速度反演的精度; 随后作者利用P波速度模型和等效介质理论模型对该地层的天然气水合物饱和度进行了估计; 转换横波的速度是通过OBS水平分量的数据进行射线追踪正演估算的, 结果表明BSR上方的水合物赋存区表现出较一般海底沉积中明显的横波速度正异常, 指示水合物在沉积层中胶结了矿物颗粒而作为承载物存在。由于纵波对游离气的存在很敏感, 导致BSR下方的反射纵波急剧衰减, 从而无法得到BSR下方地层可靠的纵波速度; 而横波则能够很好的成像, 这对研究BSR下方的地层结构很有利。
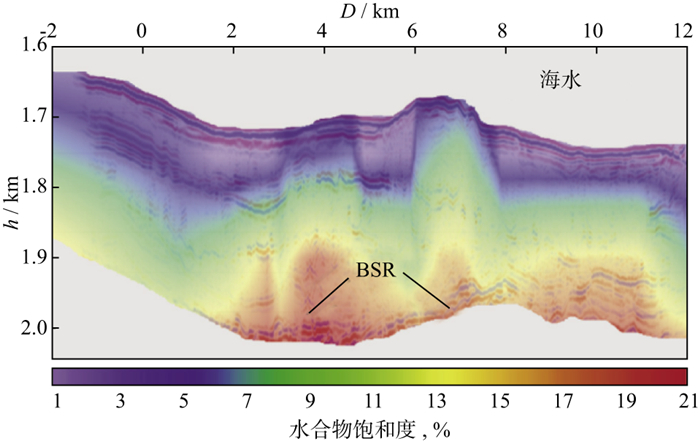
2010年, 印度国家地球物理研究所在Krishna-Godavari海盆区进行了二维地震与OBS联合采集。SATYAVANI等[72]利用多道地震数据和OBS多分量数据通过走时反演得到了纵波与横波速度模型, 随后基于等效介质理论模型分别利用纵波和横波速度进行了水合物饱和度的计算, 最终结果取这两种饱和度的平均值(图 4)。其主要意义是利用OBS的转换横波信息对反射纵波的约束, 提高了纵、横波反演结果的精度。
|
图 4 地震叠加剖面与水合物饱和度空间分布叠合显示[72] |
此外, 杨佳佳等[58]利用岩石物理模型构建3种水合物微观赋存模型(悬浮式、接触式和胶结式)建立了海底水平层状模型, 采用有限差分方法正演了由海面激发、海底OBS接收的合成地震剖面, 结果表明:当水合物作为流体悬浮在孔隙中时, 横波剖面上的BSR不会出现, 验证了该模型下水合物储层的横波速度对水合物存在并不敏感。
以上研究结果表明, 现有的方法大多仍是依靠海上拖缆地震数据, 附加测井数据和OBS数据的约束, 通过各种算法处理得到纵、横波速度剖面, 再匹配某种岩石物理模型来估计水合物在地层中的含量。利用这种方法估计水合物饱和度时的精度主要受两方面的影响:一方面是速度模型的精度, 另外一方面是岩石物理模型的精度。引入宽角度反射的OBS多波信息进行联合反演后, 转换横波信息的约束使速度模型的精度有一定的提高; 但提高岩石物理模型的精度仍很困难, 水合物可以悬浮在孔隙流体当中, 也可以与矿物颗粒胶结, 或者充填在裂缝中, 不同的水合物赋存状态会带来不同的多波地震响应, 且随着水合物饱和度的变化, 这几种赋存状态可能同时出现或只出现其中一种, 然而不同赋存状态的水合物颗粒的比例又是未知的, 造成了饱和度估计时较大的误差与多解性。此外, 水合物饱和度估计的分辨率也值得我们考虑, 这可能主要取决于速度模型分辨率的高低。
4 问题与展望 4.1 面临的问题水合物储层在地震剖面上的特征及识别标志, 目前公认的4大地震特征(BSR、SBZ、速度倒转和速度-振幅异常)已被广泛应用于地震探测中。但BSR及SBZ形成的原因和具体产生机制依然没有确定的解释, 对其判定也没有形成统一的标准。
由于OBS能提供横波信息, 因此近年来得到了大量应用, 但相对于海面拖缆数据, OBS相关处理和反演技术还不成熟。首先是OBS投放数量有限, 且回收率无法达到百分之百, 所以单靠OBS数据, 成像范围有限, 分辨率不高, 与常规拖缆数据成像相比还不具备优势; 其次OBS与海面拖缆数据联合成像精度受限于空间采样严重不足, 采集成本过高[60]; 深海OBS处理技术的不成熟也是限制该技术发挥更大效益的关键因素之一[73]。
在OBS技术之前, 由于水合物及下部游离气藏易引起AVO异常, 学者们往往通过对海上拖缆的纵波地震数据进行AVO分析来研究水合物的分布及储量预测[31, 74], 但随着研究的推进, 问题也随之而来。总结全球已被钻探证实的水合物储层的属性特征, 含水合物地层的厚度多为薄层, 且可与不含水合物常规沉积地层间隔出现, 表现为薄互层沉积, 再加上水合物在横向上分布的不均匀性, 这种情况在我国南海的水合物赋存区表现得十分典型, 因此基于单阻抗差界面的AVO异常分析会受到薄(互)层调谐干涉效应和水平方向的非均匀性的影响。但在现有的研究中, 无论是建立岩石物理模型进行速度拟合来估算水合物储层的水合物饱和度, 还是估算BSR下伏气层的游离气饱和度, 都是将赋存水合物的多个间断薄层当做大套厚层处理, 使用单阻抗差界面来进行地震波场模拟。如何利用薄互层弹性波传播理论[75], 针对水合物储层建立更符合客观实际的水合物薄(互)层模型, 基于OBS技术的多波信息, 将单阻抗差界面反射的AVO分析拓展到频率依赖的薄(互)层多波AVO分析上, 或利用薄(互)层理论进行速度、各向异性等研究, 为研究水合物地震标志的产生机理和水合物储层饱和度估算提供新的思路和方法。
4.2 展望自从海洋水合物被发现, 人类对这一具有广阔前景的新能源的探索就没有停止过。从最初单纯的地震反射剖面上的几何特征研究和标定, 到含水合物地层及其上覆、下伏地层的岩石物性研究, 以及利用地震波衰减吸收特征来识别水合物储层, 再到利用水合物储层的多波响应预测水合物和游离气在地层中的空间分布和体积含量, 海洋地球物理领域对水合物地震技术的研究从宏观描述、定性分析, 逐渐发展到基于微观结构特征和岩石物理理论的定量弹性参数反演与储量估算。
关于水合物储层地震标志的研究, 随着OBS的出现, 单纯纵波方法的局限性有望得以克服。尽管国内外已大量采用高分辨率三维拖缆与四分量OBS联合进行水合物调查, 但水合物储层的多波反射信息的发掘利用仍存在很大的探索空间。即如何充分发挥横波对海底浅表沉积物的高分辨率优势[62], 进而利用纵、横波联合的方式对BSR与SBZ现象进行深入探讨, 降低现有纵波BSR与SBZ标志指示水合物储层的多解性是未来技术发展的重要方向之一。
对于各类型水合物储层综合考虑孔隙中液、气、固混合的多相岩石物理模型的研究, 兼顾温度与压力参数对储层的宏观影响, 发展岩石物理模型理论是当务之急。在此基础上利用含水合物地层和含游离气地层的地震波吸收衰减特征差异, 提取品质因子, 进而进行基于黏弹性介质的AVO反演和全波形反演也是值得尝试的方向。而建立水合物储层的薄(互)层模型, 在此基础上开展弹性波响应特征研究, 实现水合物储层弹性参数及其各向异性的反演预测是未来海洋多波地震技术的主要任务之一。
随着各国水合物试采工作的进行, 出现了很多新问题。比如对水合物储层进行开采时, 多采取对地层升温或减压的方法让固体水合物分解释放甲烷气, 这一过程可能造成地层塌陷、甲烷泄露、水合物二次生成堵塞管道等问题, 然而目前对于水合物开发过程的实时监控局限在生产井和观测井内布设仪器, 对于大范围的储层监控并没有一个完整的方案[76]。在地震技术方面, 何涛等[76]提出在海底布设三维全光纤四分量海底电缆(4-Component Ocean Bottom Cable), 在开发过程中对水合物储层进行时移地震监控, 可能对整个水合物储层的评价和开发风险管控都有着积极作用。故海洋地震技术也需要从探测走向开发, 例如实现对水合物的结晶与析出、动态的空间分布以及饱和度的变化等量化评价, 从而可以间接监测储层温度、压力的变化。
5 结束语综合调研发现, 地震技术在水合物储层探测应用中起到了十分重要的作用, 虽仍存在许多待解决的问题, 但如下的结论得到了业界的广泛认可。
1) 纵波地震剖面上识别水合物储层的四大特征——BSR、SBZ、速度倒转、速度-振幅异常已是业界共识。虽然BSR不一定指示水合物的存在, 但它已成为地震技术探测水合物储层的首选方法。
2) BSR振幅的强弱优先取决于其下伏地层中是否含游离气, 而不是上覆地层中存在水合物; 若BSR下伏地层含游离气, 则会在纵波地震剖面上出现速度倒转现象。
3) 地层含水合物在绝大多数情况下会导致纵波速度的增加, 横波速度是否增加则取决于地层孔隙中水合物的赋存形式, 即存在水合物颗粒胶结固相矿物颗粒而作为承载骨架时, 地层的横波速度才会增加。
4) 产生SBZ可能存在多种原因, 是否为水合物储层的指示标志, 值得进一步深究。
5) 水合物储层的地震波衰减具有频率依赖性, 在高频下呈高衰减异常; 在较低的地震勘探频段下则呈现不明显的衰减。
6) 单纯利用纵波技术预测水合物的饱和度存在较大误差, 采用OBS的横波信息对弹性波速度模型反演附加约束可以提高一定的精度。
| [1] |
宋广喜, 雷怀玉, 王柏苍, 等. 国内外天然气水合物发展现状与思考[J]. 国际石油经济, 2013(11): 69-76. SONG G X, LEI H Y, WANG B C, et al. Present situation and consideration of gas hydrate development at home and abroad[J]. International Petroleum Economics, 2013(11): 69-76. DOI:10.3969/j.issn.1004-7298.2013.11.014 |
| [2] |
DILLON W P, FEHLHABER K, COLEMAN D F, et al. Gas hydrates on the Atlantic continental margin of the United States-Controls on concentration[J]. The Future of Energy Gases, 1993, 1570(9): 313-330. |
| [3] |
WU S, ZHANG G, HUANG Y, et al. Gas hydrate occurrence on the continental slope of the northern South China Sea[J]. Marine and Petroleum Geology, 2005, 22(3): 403-412. DOI:10.1016/j.marpetgeo.2004.11.006 |
| [4] |
SHIPLEY T H, HOUSTON M H, BUFFLER R T, et al. Seismic evidence for widespread possible gas hydrate horizons on continental slopes and rises[J]. AAPG Bulletin, 1979, 63(12): 2204-2213. |
| [5] |
宋海斌, 吴时国, 江为为. 南海东北部973剖面BSR及其热流特征[J]. 地球物理学报, 2007, 50(5): 1508-1517. SONG H B, WU S G, JIANG W W. The characteristics of BSRs and their derived heat flow on the profile 973 in the northeastern South China Sea[J]. Chinese Journal of Geophysics, 2007, 50(5): 1508-1517. DOI:10.3321/j.issn:0001-5733.2007.05.027 |
| [6] |
宋海斌, 张岭, 江为为, 等. 海洋天然气水合物的地球物理研究(Ⅲ):似海底反射[J]. 地球物理学进展, 2003, 18(2): 182-187. SONG H B, ZHANG L, JIANG W W, et al. Geophysical researches on marine gas hydrates(Ⅲ):bottom simulating reflections[J]. Progress in Geophysics, 2003, 18(2): 182-187. DOI:10.3969/j.issn.1004-2903.2003.02.002 |
| [7] |
宋海斌, 耿建华, WANG How-King, 等. 南海北部东沙海域天然气水合物的初步研究[J]. 地球物理学报, 2001, 44(5): 687-695. SONG H B, GENG J H, WANG H-K, et al. A preliminary study of gas hydrates in Dongsha region north of South China Sea[J]. Chinese Journal of Geophysics, 2001, 44(5): 687-695. DOI:10.3321/j.issn:0001-5733.2001.05.012 |
| [8] |
HOLBROOK W S, HOSKINS H, WOOD W T, et al. Methane hydrate and free gas on the Blake Ridge from vertical seismic profiling[J]. Science, 1996, 273(5283): 1840-1843. DOI:10.1126/science.273.5283.1840 |
| [9] |
王秀娟, 吴时国, 刘学伟, 等. 东沙海域天然气水合物特征分析及饱和度估算[J]. 石油物探, 2009, 48(5): 445-452. WANG X J, WU S G, LIU X W, et al. Characteristic analysis and saturation estimation of gas hyrate in Dongsha sea area[J]. Geophysical Prospecting for Petroleum, 2009, 48(5): 445-452. DOI:10.3969/j.issn.1000-1441.2009.05.003 |
| [10] |
梁金强, 张光学, 陆敬安, 等. 南海东北部陆坡天然气水合物富集特征及成因模式[J]. 天然气工业, 2016, 36(10): 157-162. LIANG J Q, ZHANG G X, LU J A, et al. Accumulation characteristics and genetic models of natural gas hydrate reservoirs in the NE slope of the South China Sea[J]. Natural Gas Industry, 2016, 36(10): 157-162. DOI:10.3787/j.issn.1000-0976.2016.10.020 |
| [11] |
勾丽敏, 张金华, 王嘉玮. 海洋天然气水合物地震识别方法研究进展[J]. 地球物理学进展, 2017, 32(6): 2626-2635. GOU L M, ZHANG J H, WANG J W. Progress in seismic identification approach of marine gas hydrate[J]. Progress in Geophysics, 2017, 32(6): 2626-2635. |
| [12] |
张光学, 张明, 杨胜雄, 等. 海洋天然气水合物地震检测技术及其应用[J]. 海洋地质与第四纪地质, 2011, 31(4): 51-58. ZHANG G X, ZHANG M, YANG S X, et al. Application of seismic detecting technique to marine gas hydrate survey[J]. Marine Geology & Quaternary Geology, 2011, 31(4): 51-58. |
| [13] |
吴能友, 陈弘, 蔡秋蓉, 等. 科学大洋钻探与天然气水合物[J]. 地球科学进展, 2003, 18(5): 753-758. WU N Y, CHEN H, CAI Q R, et al. Scientific ocean drilling and gas-hyrates[J]. Advance in Earth Sciences, 2003, 18(5): 753-758. DOI:10.3321/j.issn:1001-8166.2003.05.016 |
| [14] |
SINGH S C, MINSHULL T A. Velocity structure of a gas hydrate reflector at ocean drilling program site 889 from a global seismic waveform inversion[J]. Journal of Geophysical Research:Solid Earth, 1994, 99(B12): 24221-24233. DOI:10.1029/94JB02168 |
| [15] |
JOHN J M, MYUNG W L, ROLAND V H. An analysis of a seismic reflection from the base of a gas hydrate zone, offshore Peru1[J]. AAPG Bulletin, 1991, 75(5): 910-924. |
| [16] |
尤加春, 冯凯, 王成, 等. 含天然气水合物介质地震空白带成因研究[J]. 石油物探, 2014, 53(2): 216-222. YOU J C, FENG K, WANG C, et al. The cause of seismic blanking zone for gas hydrate[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 216-222. DOI:10.3969/j.issn.1000-1441.2014.02.012 |
| [17] |
孙春岩, 章明昱, 牛滨华, 等. 天然气水合物地震空白带现象正演模型研究[J]. 地学前缘, 2003, 10(1): 199-204. SUN C Y, ZHANG M Y, NIU B H, et al. Modeling of seismic blanking zone for gas hydrate[J]. Earth Science Frontiers, 2003, 10(1): 199-204. DOI:10.3321/j.issn:1005-2321.2003.01.023 |
| [18] |
宋海斌, 松林修, 吴能友, 等. 海洋天然气水合物的地球物理研究(Ⅰ):岩石物性[J]. 地球物理学进展, 2001, 16(2): 118-126. SONG H B, SONG L X, WU N Y, et al. Geophysical researches on marine gas hydrates(Ⅰ):Physical properties[J]. Progress in Geophysics, 2001, 16(2): 118-126. DOI:10.3969/j.issn.1004-2903.2001.02.015 |
| [19] |
栾锡武, 刘鸿, 岳保静, 等. 海底冷泉在旁扫声纳图像上的识别[J]. 现代地质, 2010, 24(3): 474-480. LUAN X W, LIU H, YUE B J, et al. Characteristics of cold seepage on side scan sonar sonogram[J]. Geoscience, 2010, 24(3): 474-480. DOI:10.3969/j.issn.1000-8527.2010.03.009 |
| [20] |
SASSEN R, LOSH S L, CATHLES L, et al. Massive vein-filling gas hydrate:relation to ongoing gas migration from the deep subsurface in the Gulf of Mexico[J]. Marine and Petroleum Geology, 2001, 18(5): 551-560. DOI:10.1016/S0264-8172(01)00014-9 |
| [21] |
GREINERT J, ARTEMOV Y, EGOROV V, et al. 1300m-high rising bubbles from mud volcanoes at 2080m in the Black Sea:Hydroacoustic characteristics and temporal variability[J]. Earth and Planetary Science Letters, 2006, 244(1): 1-15. |
| [22] |
SAUTER E J, MUYAKSHIN S I, CHARLOU J-L, et al. Methane discharge from a deep-sea submarine mud volcano into the upper water column by gas hydrate-coated methane bubbles[J]. Earth and Planetary Science Letters, 2006, 243(3): 354-365. |
| [23] |
张光学. 海洋天然气水合物地震联合探测[M]. 北京: 地质出版社, 2014: 1-218. ZHANG G X. Joint seismic detection of marine gas hydrate[M]. Beijing: Geology Press, 2014: 1-218. |
| [24] |
HELGERUD M B, DVORKIN J, NUR A, et al. Elastic-wave velocity in marine sediments with gas hydrates:Effective medium modeling[J]. Geophysical Research Letters, 1999, 26(13): 2021-2024. DOI:10.1029/1999GL900421 |
| [25] |
DVORKIN J, MANIKA P, AKIO S, et al. Elasticity of marine sediments:Rock physics modeling[J]. Geophysical Research Letters, 1999, 26(12): 1781-1784. DOI:10.1029/1999GL900332 |
| [26] |
NUR A, MAVKOG, DVORKIN J, et al. Critical porosity:A key to relating physical properties to porosity in rocks[J]. The Leading Edge, 1998, 17(3): 357-362. DOI:10.1190/1.1437977 |
| [27] |
MINDLIN R D. Compliance of elastic bodies in contact[J]. Japplmech, 1949, 16(3): 259-268. |
| [28] |
HILL R. The elastic behaviour of a crystalline aggregate[J]. Proceedings of the Physical Society, 1952, 65(5): 349-354. DOI:10.1088/0370-1298/65/5/307 |
| [29] |
HASHIN Z, SHTRIKMAN S. A variational approach to the theory of the elastic behaviour of multiphase materials[J]. Journal of the Mechanics & Physics of Solids, 1963, 11(2): 127-140. |
| [30] |
CHAND S, MINSHULL T A, GEI D, et al. Elastic velocity models for gas-hydrate-bearing sediments -A comparison[J]. Geophysical Journal International, 2004, 159(2): 573-590. DOI:10.1111/j.1365-246X.2004.02387.x |
| [31] |
CARCIONE J M, TINIVELLA U. Bottom-simulating reflectors:Seismic velocities and AVO effects[J]. Geophysics, 2000, 65(1): 54-67. DOI:10.1190/1.1444725 |
| [32] |
BIOT M A. Generalized theory of acoustic propagation in porous dissipative media[J]. The Journal of the Acoustical Society of America, 1962, 34(9A): 1254-1264. DOI:10.1121/1.1918315 |
| [33] |
LECLAIRE P, COHEN-TÉNOUDJI F, AGUIRRE-PUENTE J. Observation of two longitudinal and two transverse waves in a frozen porous medium[J]. Journal of the Acoustical Society of America, 1995, 97(4): 2052-2055. DOI:10.1121/1.411997 |
| [34] |
CARCIONE J M, GEI D. Gas-hydrate concentration estimated from P-and S-wave velocities at the Mallik 2L-38 research well, Mackenzie Delta, Canada[J]. Journal of Applied Geophysics, 2004, 56(1): 73-78. DOI:10.1016/j.jappgeo.2004.04.001 |
| [35] |
GEI D, CARCIONEJOSé M. Acoustic properties of sediments saturated with gas hydrate, free gas and water[J]. Geophysical Prospecting, 2003, 51(2): 141-158. DOI:10.1046/j.1365-2478.2003.00359.x |
| [36] |
LEE M W, WAITE W F. Estimating pore-space gas hydrate saturations from well log acoustic data[J]. Geochemistry, Geophysics, Geosystems, 2008, 9(7): 1-8. |
| [37] |
KUSTER G T, TOKSOZ M N. Velocity and attenuation of seismic waves in two-phase media; Part I, Theoretical formulations[J]. Geophysics, 1974, 39(5): 587-606. DOI:10.1190/1.1440450 |
| [38] |
PRIDE S R, BERRYMAN J G, HARRIS J M. Seismic attenuation due to wave-induced flow[J]. Journal of Geophysical Research:Solid Earth, 2004, 109(B1): 1-19. |
| [39] |
JAKOBSEN M, HUDSON J A, MINSHULL T A, et al. Elastic properties of hydrate-bearing sediments using effective medium theory[J]. Journal of Geophysical Research:Solid Earth, 2000, 105(B1): 561-577. DOI:10.1029/1999JB900190 |
| [40] |
HORNBY B E, SCHWARTZ L M, HUDSON J A. Anisotropic effective-medium modeling of the elastic properties of shales[J]. Geophysics, 1994, 59(10): 1570-1583. DOI:10.1190/1.1443546 |
| [41] |
SHENG P, CALLEGARI A J. Differential effective medium theory of sedimentary rocks[J]. Applied Physics Letters, 1984, 44(8): 738-740. DOI:10.1063/1.94900 |
| [42] |
WILLIS J R. Bounds and self-consistent estimates for the overall properties of anisotropic composites[J]. Journal of the Mechanics and Physics of Solids, 1977, 25(3): 185-202. DOI:10.1016/0022-5096(77)90022-9 |
| [43] |
NORRIS A N. A differential scheme for the effective moduli of composites[J]. Mechanics of Materials, 1985, 4(1): 1-16. DOI:10.1016/0167-6636(85)90002-X |
| [44] |
BONILLA L L, KELLER J B. Acoustoelastic effect and wave propagation in heterogeneous weakly anisotropic materials[J]. Journal of the Mechanics and Physics of Solids, 1985, 33(3): 241-261. DOI:10.1016/0022-5096(85)90014-6 |
| [45] |
HUDSON J A. Overall properties of heterogeneous material[J]. Geophysical Journal International, 1991, 107(3): 505-511. DOI:10.1111/j.1365-246X.1991.tb01411.x |
| [46] |
刘子淳, 郝贺晨. 包裹体理论在富有机质页岩岩石物理建模中的依据因素应用[J]. 地球物理学进展, 2017, 32(6): 2505-2513. LIU Z C, HAO H C. Basis application for the theory of inclusion in organic shale physics modelin[J]. Progress in Geophysics, 2017, 32(6): 2505-2513. |
| [47] |
杨凤英, 印兴耀, 刘博. 可变干岩石骨架等效模型研究[J]. 石油物探, 2014, 53(3): 280-286. YANG F Y, YIN X Y, LIU B. The research of variable dry rock matrix equivalent model[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 280-286. DOI:10.3969/j.issn.1000-1441.2014.03.005 |
| [48] |
LEE M W, HUTCHINSON D R, COLLETT T S, et al. Seismic velocities for hydrate-bearing sediments using weighted equation[J]. Journal of Geophysical Research:Solid Earth, 1996, 101(B9): 20347-20358. DOI:10.1029/96JB01886 |
| [49] |
王秀娟, 吴时国, 王吉亮, 等. 南海北部神狐海域天然气水合物分解的测井异常[J]. 地球物理学报, 2013, 56(8): 2799-2807. WANG X J, WU S G, WANG J L, et al. Anomalous wireline logging data caused by gas hydrate dissociation in Shenhu area, northen slope of South China Sea[J]. Chinese Journal of Geophysics, 2013, 56(8): 2799-2807. |
| [50] |
张磊.改进的三相Biot模型在水合物地球物理测井评价中的研究[D].北京: 中国地质大学(北京), 2015: 1-64 ZHANG L.Research on the geophysical well-logging evaluation of the gas hydrate bearing sediment using the modified three-phase Biotequation[D].Beijing: China University of Geosciences(Beijing), 2015: 1-64 |
| [51] |
LEE M W, COLLETT T S. Gas hydrate saturations estimated from fractured reservoir at Site NGHP-01-10, Krishna-Godavari Basin, India[J]. Journal of Geophysical Research, 2009, 114(B7): 1-13. |
| [52] |
吴能友, 张海啟, 杨胜雄, 等. 南海神狐海域天然气水合物成藏系统初探[J]. 天然气工业, 2007, 27(9): 1-6. WU N Y, ZHANG H Q, YANG S X, et al. Preliminary discussion on natural gas hydrate(NGH) reservoir system of Shenhu area, north slop of South China Sea[J]. Natural Gas Industry, 2007, 27(9): 1-6. DOI:10.3321/j.issn:1000-0976.2007.09.001 |
| [53] |
张光学, 梁金强, 陆敬安, 等. 南海东北部陆坡天然气水合物藏特征[J]. 天然气工业, 2014, 34(11): 1-10. ZHANG G X, LIANG J Q, LU J A, et al. Characteristics of natural gas hydrate reservoirs on the northeastern slope of the South China Sea[J]. Natural Gas Industry, 2014, 34(11): 1-10. DOI:10.3787/j.issn.1000-0976.2014.11.001 |
| [54] |
王秀娟, 吴时国, 郭璇, 等. 南海陆坡天然气水合物饱和度估计[J]. 海洋地质与第四纪地质, 2005, 25(3): 89-95. WANG X J, WU S G, GUO X, et al. Estimation of gas hydrate saturation in the continental slope, the South China Sea[J]. Marine Geology & Quaternary Geology, 2005, 25(3): 89-95. |
| [55] |
卫小冬, 赵明辉, 阮爱国, 等. 南海中北部OBS2006-3地震剖面中横波的识别与应用[J]. 热带海洋学报, 2010, 29(5): 72-80. WEI X D, ZHAO M H, RUAN A G, et al. Identification and application of shear waves along the profile OBS2006-3 in the mid-northern South China Sea[J]. Journal of Tropical Oceanography, 2010, 29(5): 72-80. DOI:10.3969/j.issn.1009-5470.2010.05.011 |
| [56] |
伍忠良. 海洋天然气水合物三维地震与海底地震勘探中的震源技术研究[J]. 热带海洋学报, 2011, 30(1): 49-60. WU Z L. Study of source in 3-D seismic and OBS exploration for marine gas hydrate[J]. Journal of Tropical Oceanography, 2011, 30(1): 49-60. DOI:10.3969/j.issn.1009-5470.2011.01.007 |
| [57] |
沙志彬, 郑涛, 张光学, 等. 海底高频地震仪观测系统优化设计及其在南海天然气水合物勘探中的应用[J]. 天然气工业, 2014, 34(7): 136-142. SHA Z B, ZHENG T, ZHANG G X, et al. An optimal design of a high-frequency ocean bottom seismometer(HF-OBS) and its application to the natural gas hydrate exploration in the South China Sea[J]. Natural Gas Industry, 2014, 34(7): 136-142. |
| [58] |
YANG J J, HE B S, ZHANG J Z. Multicomponent seismic forward modeling of gas hydrates beneath the seafloor[J]. Applied Geophysics, 2014, 11(4): 418-428. DOI:10.1007/s11770-014-0465-x |
| [59] |
张光学, 徐华宁, 刘学伟, 等. 海底高频地震仪在南海北部天然气水合物探测中的应用[J]. 海洋地质与第四纪地质, 2015, 35(1): 185-192. ZHANG G X, XU H N, LIU X W, et al. The application of ocean bottom seismometer to gas hydrate exploration on the northern margin of South China Sea[J]. Marine Geology & Quaternary Geology, 2015, 35(1): 185-192. |
| [60] |
易锋, 徐军, 刘斌. 海底地震仪在天然气水合物勘探中的应用综述[J]. 海洋技术学报, 2019, 38(1): 92-101. YI F, XU J, LIU B. An Overview of the application of OBS in the exploration of gas hydrates[J]. Journal of Ocean Technology, 2019, 38(1): 92-101. |
| [61] |
SHA Z B, ZHANG M, ZHANG G X, et al. Using 4C OBS to reveal the distribution and velocity attributes of gas hydrates at the northern continental slope of South China Sea[J]. Applied Geophysics, 2015, 12(4): 555-563. DOI:10.1007/s11770-015-0515-z |
| [62] |
王伟巍, 谢城亮, 赵庆献, 等. 横波勘探在海洋天然气水合物调查中的应用[J]. 海洋技术学报, 2015, 34(2): 111-117. WANG W W, XIE C L, ZHAO Q X, et al. Application of seismic shear wave detection in marine natural-gas-hydrate exploration[J]. Journal of Ocean Technology, 2015, 34(2): 111-117. |
| [63] |
KUMAR D, SEN M K, BANGS N L. Gas hydrate concentration and characteristics within Hydrate Ridge inferred from multicomponent seismic reflection data[J]. Journal of Geophysical Research:Solid Earth, 2007, 112(B12): 1-11. |
| [64] |
DASH R, SPENCE G. P-wave and S-wave velocity structure of northern Cascadia margin gas hydrates[J]. Geophysical Journal International, 2011, 187(3): 1363-1377. DOI:10.1111/j.1365-246X.2011.05215.x |
| [65] |
张聿文, 刘学伟, 李海鸥. 基于单相与双相介质拟海底反射的AVO研究[J]. 石油物探, 2004, 43(3): 209-216. ZHANG Y W, LIU X W, LI H O. A study of AVO responses of bottom simulating reflection in single and two-phase media[J]. Geophysical Prospecting for Petroleum, 2004, 43(3): 209-216. DOI:10.3969/j.issn.1000-1441.2004.03.001 |
| [66] |
ECKER C, NUR A, DVORKIN J. Sediments with gas hydrates; internal structure from seismic AVO[J]. Geophysics, 1998, 63(5): 1659-1669. DOI:10.1190/1.1444462 |
| [67] |
方斌, 徐波, 周立军. 纵、横波联合勘探方法初探[J]. 工程地球物理学报, 2007, 4(5): 411-416. FANG B, XU B, ZHOU L J. Method of combining P-wave exploration with S-wave exploration[J]. Chinese Journal of Engineering Geophysics, 2007, 4(5): 411-416. DOI:10.3969/j.issn.1672-7940.2007.05.004 |
| [68] |
MIENERT J, BVNZ S, GUIDARD S, et al. Ocean bottom seismometer investigations in the Ormen Lange area offshore mid-Norway provide evidence for shallow gas layers in subsurface sediments[J]. Marine and Petroleum Geology, 2005, 22(1/2): 287-297. |
| [69] |
WESTBROOK G K, CHAND S, ROSSI G, et al. Estimation of gas hydrate concentration from multi-component seismic data at sites on the continental margins of NW Svalbard and the Storegga region of Norway[J]. Marine and Petroleum Geology, 2008, 25(8): 744-758. DOI:10.1016/j.marpetgeo.2008.02.003 |
| [70] |
EXLEY R J K, WESTBROOK G K, HAACKE R R, et al. Detection of seismic anisotropy using ocean bottom seismometers:A case study from the northern headwall of the Storegga Slide[J]. Geophysical Journal International, 2010, 183(1): 188-210. DOI:10.1111/j.1365-246X.2010.04730.x |
| [71] |
CHENG W B, SHIH T Y, LIN W Y, et al. Imaging seismic velocities for hydrate-bearing sediments using converted waves near Yuan-An Ridge, off southwest Taiwan[J]. Journal of Asian Earth Sciences, 2014, 92: 215-223. DOI:10.1016/j.jseaes.2013.10.013 |
| [72] |
SATYAVANI N, SAIN K, GUPTA H K. Ocean bottom seismometer data modeling to infer gas hydrate saturation in Krishna-Godavari(KG) basin[J]. Journal of Natural Gas Science and Engineering, 2016, 33: 908-917. DOI:10.1016/j.jngse.2016.06.037 |
| [73] |
张光学, 徐华宁, 刘学伟, 等. 三维地震与OBS联合勘探揭示的神狐海域含水合物地层声波速度特征[J]. 地球物理学报, 2014, 57(4): 1169-1176. ZHANG G X, XU H N, LIU X W, et al. The acoustic velocity characteristics of sediment with gas hydrate revealed by integrated exploration of 3D seismic and OBS data in Shenhu area[J]. Chinese Journal of Geophysics, 2014, 57(4): 1169-1176. |
| [74] |
宋海斌, OSAMU M, 杨胜雄, 等. 含天然气水合物沉积物的岩石物性模型与似海底反射层的AVA特征[J]. 地球物理学报, 2002, 45(4): 546-556. SONG H B, OSAMU M, YANG S X, et al. Physical property models of gas hydrate-bearing sediments and AVA character of bottom simulating reflector[J]. Chinese Journal of Geophysics, 2002, 45(4): 546-556. DOI:10.3321/j.issn:0001-5733.2002.04.012 |
| [75] |
王赟, 杨春. 薄互层弹性波传播理论[M]. 北京: 科学出版社, 2019: 1-180. WANG Y, YANG C. Theory of elastic wave propagation in thin interbed[M]. Beijing: Science Press, 2019: 1-180. |
| [76] |
何涛, 卢海龙, 林进清, 等. 海域天然气水合物开发的地球物理监测[J]. 地学前缘, 2017, 24(5): 368-382. HE T, LU H L, LIN J Q, et al. Geophysical techniques of reservoir monitoring for marine gas hydrate exploitation[J]. Earth Science Frontiers, 2017, 24(5): 368-382. |




