2. 油气资源与勘探技术教育部重点实验室(长江大学), 湖北武汉 430100;
3. 中国石油天然气股份有限公司勘探开发研究院, 北京 100083;
4. 中国石油集团东方地球物理勘探有限责任公司研究院大港分院, 天津 300280
2. Key Laboratory of Exploration Technologies for Oil and Gas Resources, Yangtze University, Wuhan 430100, China;
3. PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China;
4. Dagang Branch of Geophysical Research Institute of BGP, CNPC, Tianjin 300280, China
页岩气作为目前世界上新兴的清洁能源之一, 备受瞩目, 具有良好的发展前景。页岩厚度、有机质丰富度以及热成熟度等相关参数常被用于评价页岩气产能, 即所谓的“甜点预测”技术, 以此找出更有开发前景的页岩储层, 提高页岩气开采的成功率[1]。但页岩储层具有低孔隙度、低渗透性、低连通性等储层物性特征, 一般需要采用水力压裂等技术对页岩储层进行改造, 利用人造裂缝网络作为油气运移的通道, 从而提高页岩气的采收率[2]。
对于压裂后的产能预测分析目前主要使用储层压裂改造体积(stimulated reservoir volume, SRV)作为评判标准。在页岩储层压裂改造过程中, 会形成复杂的裂缝网络结构, 该裂缝网络的空间范围即为SRV, 并可近似为微地震事件云的体积[3-4]。但仅使用SRV作为页岩气产量预测的标准存在明显的不足, 一是没有考虑压裂改造后储层内部缝网结构的变化差异, 二是该评价标准与实际生产存在一定的出入, 即位于同一区域的不同页岩气开发井, 其SRV值接近, 页岩气产能却有很大差别, 或者出现估算的SRV较大, 但页岩气产能却较小的情况。因此, 需要在SRV基础上, 加入更多的信息作为约束条件, 进一步提升页岩气产能的预测准确性。
近年来大量生产资料证明, 页岩储层通过水力压裂改造后, 内部缝网结构越复杂, 产能效果越好。李亚龙等[5]对页岩气藏的赋存特征与渗流运输机制进行了研究, 认为储层内部的缝网表征研究是页岩气井产能预测的关键; 杜悦等[6]对多级裂缝模型进行了分析, 认为裂缝密度与页岩气产能具有明显的相关性; 康凯等[7]对目前裂缝气藏产能评价方法进行了改进研究, 得出裂缝密度越大, 单位长度储层中的裂缝越多, 储层流动能力越强, 气井产能越高的结论; 张德良等[8]对多级压裂水平井产能模型进行了研究, 认为裂缝长度与低渗透气藏的产能有着密切的联系。但是这些研究只是验证压裂改造的效果, 没有考虑如何更好地描述或预测页岩压裂改造形成SRV范围内缝网的复杂性对于页岩气采收率的影响。在相同压裂改造体积下, 不同页岩储层的产能表现存在较大的差异, 储层岩石的破裂程度, 即裂缝网络的密度, 是导致产能差异的主要原因之一, 因此, 亟需研究储层压裂改造后的裂缝密度, 并建立相应数学模型。关于压裂改造后储层内部裂缝密度差异的变化与页岩气产量是否相关, 是本文研究的主要内容。SRV是将计算压裂改造体积的范围大小作为产能预测的评价标准, 具有一定的理论指导意义。为了更好地对页岩气产能进行合理评价, 本文提出裂缝体积与SRV的比值即裂缝体积密度作为压裂效果评价的指标, 在SRV评价基础上进行改进, 引入裂缝体积密度概念对页岩气产能评价方法进行完善。最后将本文方法用于同一地区相邻5口页岩气井数据的分析, 以验证本文方法的有效性与准确性。
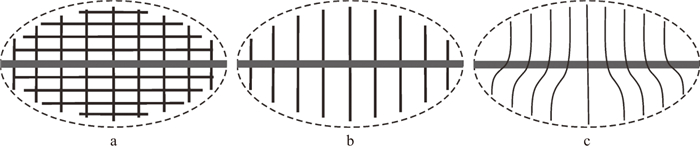
1 方法原理 1.1 裂缝体积密度分析在水力压裂作业过程中, 通过注入压裂液使天然裂缝在应力作用下打开, 形成压裂主裂缝, 产生的压裂裂缝与页岩储层内天然裂缝相互连通, 形成交错复杂的裂缝网络[9]。图 1展示了储层压裂后内部常见的主要缝网形态, 其横向对称的粗实线表示主裂缝形态, 其余细实线表示连接主裂缝的次生裂缝, 外围的椭圆形虚线示意其改造范围。由于储层特征和压裂施工参数差异的影响, 次生裂缝的空间展布形态多样, 例如图 1中的“田”字型、“十”字型和“喇叭”型。
|
图 1 裂缝网络的空间展布特征 a “田”字型; b “十”字型; c “喇叭”型 |
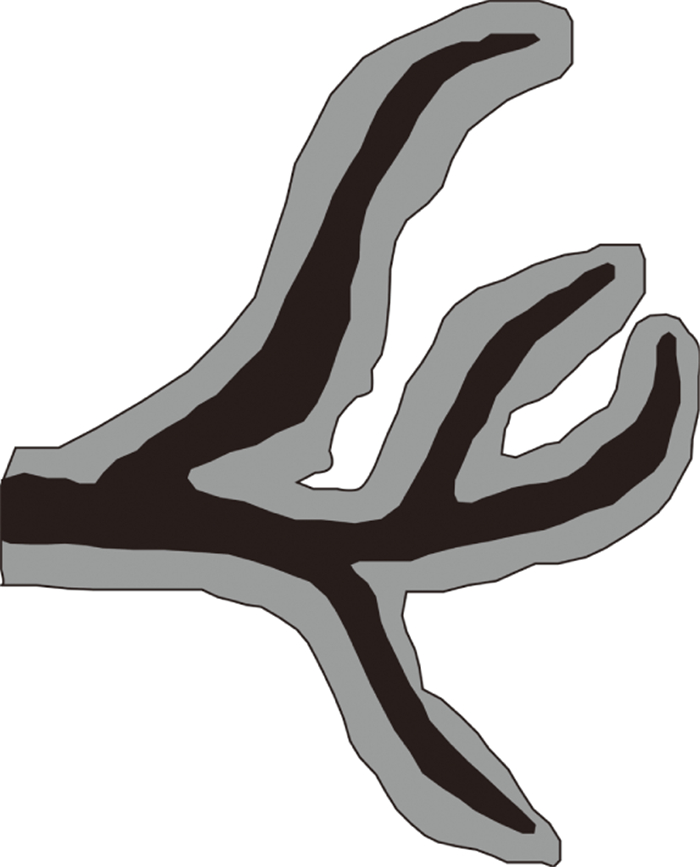
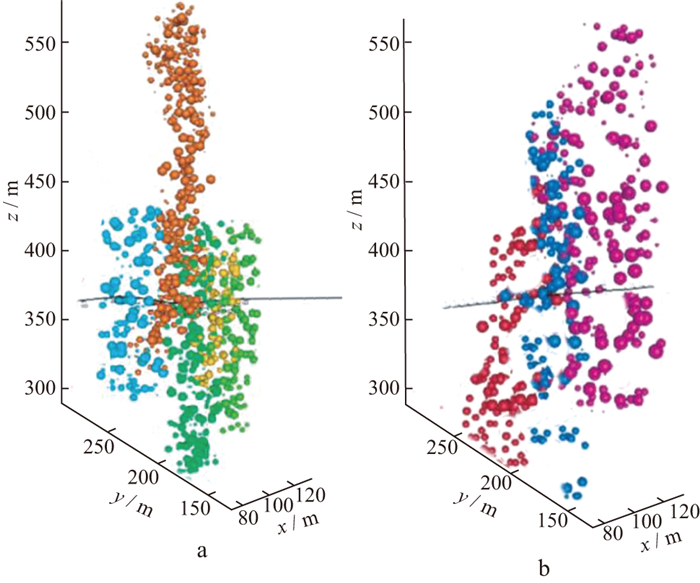
图 2展示了压裂后储层内部缝网的局部特征, 其中黑色阴影区域表示储层内部裂缝走势分布状态, 浅色阴影区域为裂缝扩展影响区域, 空白区域表示此区域未受水力压裂影响。观察图 1与图 2可知, 压裂后储层内部的缝网形态不仅范围大小不同, 其内部的缝网结构也存在较大差异, 储层内部不仅包含水力压裂改造区域, 即传输页岩气的天然裂缝与次生裂缝区域, 也存在未受水力压裂影响区域。假设在压裂改造区域大小相同的情况下, 储层内部的裂缝产生区域占比越大, 推测页岩气的传输效率与采收率相对就越好。给出某压裂工区相邻两口页岩气井, 分别对两口井的某区块压裂储层进行分析, 提取其紧邻压裂段的微震监测结果, 并给出两口井在同等地质条件下压裂改造微震事件点展布(图 3)。三维xyz坐标轴展示了该压裂区域的空间展布大小, 并非实际深度。不同压裂段的微震监测结果用不同颜色加以区别。井1在压裂储层范围内包含了4段压裂段, 井2在压裂储层范围内包含了3段压裂段。
|
图 2 压裂后储层内部缝网局部特征 |
|
图 3 多压裂井段微震事件空间展布形态 a井1四段压裂微震事件空间分布; b井2三段压裂微震事件空间分布 |
在开采环境等条件一致的情况下, 井1与井2的SRV值差别不大, 依照SRV的评价标准, 则这两口井的页岩气产能效果应该相近, 压裂改造效果一致。但实际页岩气采收结果表明, 井1的产能效果明显大于井2, 与SRV预测的结果存在差异。除去SRV的影响因素, 对储层内部的缝网结构差异进行分析, 经过直观观察可知, 两口井的微震事件点数量与分布状态皆不同, 分布状态的差异可以通过提高SRV的计算精度, 以SRV值差异进行比较, 因此分布状态的差异不是两口井产能差异影响因素, 两口井的微震事件的数量差别是影响页岩气井产能效果的主要原因。图 3中井1的压裂区域微震事件点分布更为集中, 而井2的微震事件点分散, 分布范围较大, 压裂段内部呈现明显的空洞。分别计算井1与井2单位区域的微震事件数量, 发现井1的单位区域微震事件密度明显大于井2。比对最终页岩气产量可知, 井1的页岩气累计产量较高, 据此可以推测: 微震事件点分布密度较大的储层, 压裂改造效果较好, 页岩气产量也就较高。但这种情况是否可以广泛适用, 需要进行验证。微震事件网络形态错综复杂, 而且大规模的压裂改造产生的数据集非常庞大, 仅通过直观观察是不可行的, 可以结合数学模型方法对储层内部缝网进行体积换算, 求出裂缝体积所占储层压裂改造区域的比重大小, 记为裂缝体积密度作为页岩气产量预测的标准, 后续讨论的内容将围绕SRV与裂缝体积的求取展开。
1.2 SRV计算方法原理Delaunay三角剖分算法作为计算几何中的一项重要研究内容, 在数据可视化、地理信息系统、计算机图形领域等都有着广泛应用[10]。相比规则包络体拟合的SRV计算方法, Delaunay三角剖分通过构建多个四面体将微震事件点包裹进来形成不规则凸包, 即不规则凸多面体, 且形成的包络体封闭且连续。Delaunay三角剖分主要满足两个特性, 即空圆特性与最大化最小角特性, 这两个特性将保证Delaunay形成的四面体网格接近规则性, 且任意4点不共圆[11-12]。但Delaunay三角剖分算法计算出来的凸包形状十分粗糙, 包含了很大部分的非有效区域。为了剔除这些非有效区域, 使得拟合出的不规则包络体更加准确, 引进AlphaShape算法对Delaunay算法进行优化。
AlphaShape算法的定义[13]为: 假设S是一系列点的集合, 对于点集中的任何两个点p与q, 如果满足: 存在一个半径为α的圆, 这个圆经过p和q, 点集S中的点都不在这个圆的内部, 则p, q定义的线段就是AlphaShape中的一条边。在三维空间中, 就是用一个半径为α的球在数据点集周围进行滚动, 如果球不能通过点集的某一区域, 则这一区域的数据点就作为AlphaShape中的边界。具体算法过程如下。
给定三维点集S={p1, p2, …, pn}, 从三维点集S中任意选择一个点p1, 将与点p1距离不大于2α的点集组成一个新的点集, 记为S′, 从点集S′中任意选取两个点p2, p3, 求出经过这2个点且半径为α的球, 并求出球心o, 再求出过点p1且半径为α的球的球心o′。遍历数据集S′, 求出点集内其余点到球心o与o′的距离d, d′。如果d, d′中至少有一个数值不小于半径α, 则可以判断点p1, p2, p3是边界点, 如果d, d′中都存在小于半径α的点, 则可以判断p1, p2, p3不是点集S的边界点。按照以上方法对点集S内的所有数据点进行遍历, 找出所有边界点, 则此方法结束, 输出边界点, 再通过三角剖分构成空间四面体[14]。
空间四面体计算体积公式为:
| $ V=\left|\begin{array}{llll} x_{1} & y_{1} & z_{1} & 1 \\ x_{2} & y_{2} & z_{2} & 1 \\ x_{3} & y_{3} & z_{3} & 1 \\ x_{4} & y_{4} & z_{4} & 1 \end{array}\right| \times \frac{1}{6} $ | (1) |
(x1, y1, z1), (x2, y2, z2), (x3, y3, z3), (x4, y4, z4)分别为四面体4个顶点A, B, C, D的直角坐标。
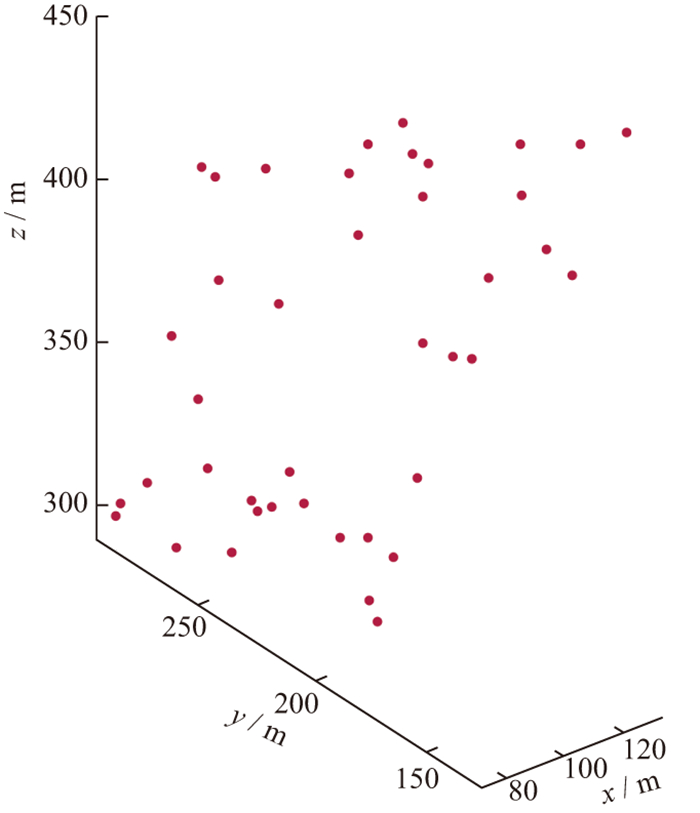
随机拟合出一组三维数据点采用AlphaShape算法进行SRV求取, 拟合的数据点如图 4所示。
|
图 4 三维数据随机拟合结果 |
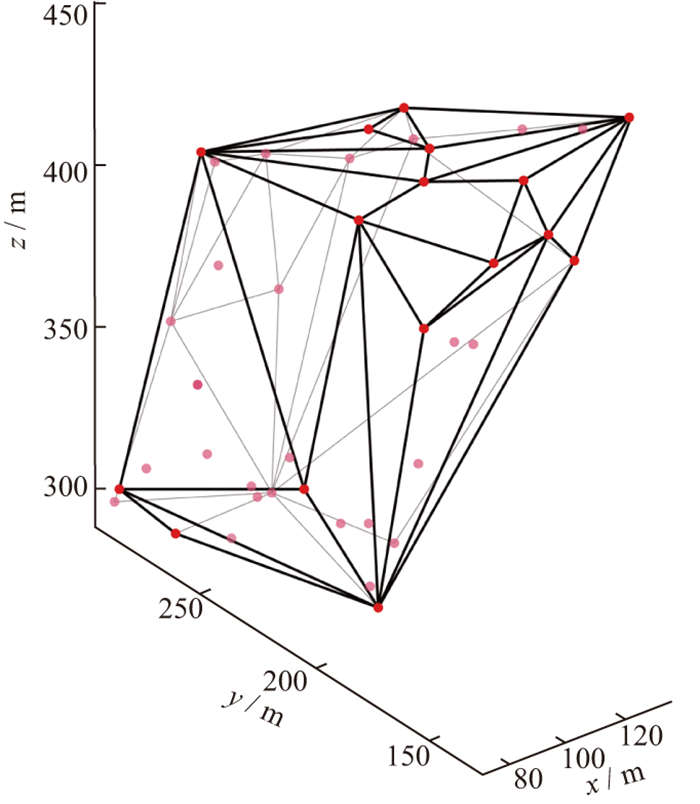
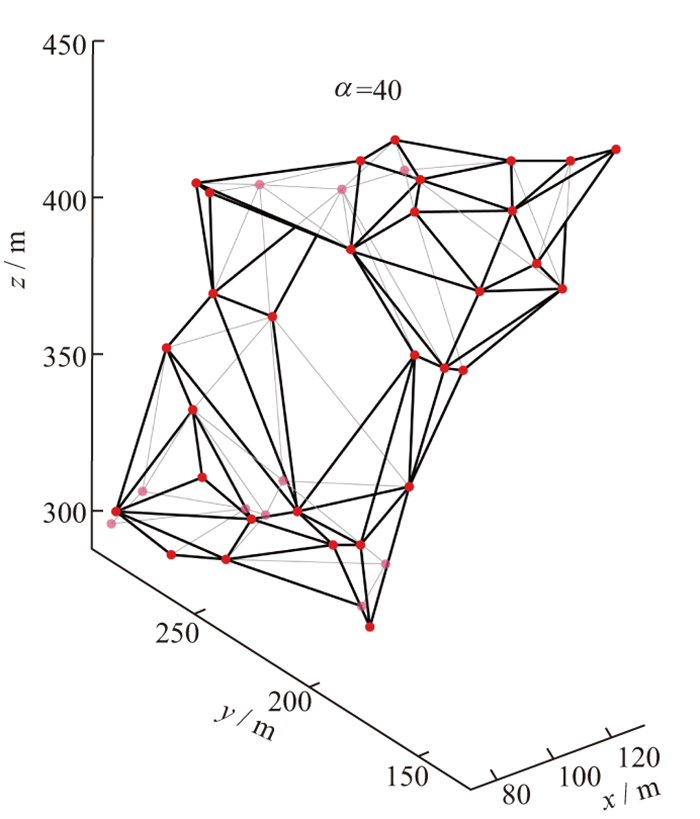
图 5和图 6分别为采用Delaunay三角剖分算法与AlphaShape算法对数据集拟合得到的储层改造范围模型。将AlphaShape算法与Delaunay三角剖分算法计算得到的四面体数据分别代入公式(1)进行计算, 模型包含的所有四面体的体积之和即为所求SRV值。采用Delaunay三角剖分算法得到的SRV值为323×104m3, 采用AlphaShape算法得到的SRV值为255×104m3。虽然这两种方法都可以将事件点进行包裹形成封闭包络进行SRV值求取, 但采用AlphaShape算法得到的SRV值更为精确, 得到的不规则包络体模型与微地震监测的结果具有更好的贴合度, 并且可以剔除非产能区域带来的误差影响, 其计算的包络体还具有一定的收缩性, 根据不同的参数α进行计算, 可以快速得到较为精确的SRV值。
|
图 5 Delaunay三角剖分算法结果 |
|
图 6 AlphaShape算法结果 |
页岩水力压裂改造过程是依靠高压流体在地层岩石中产生裂缝的过程, 这一过程将遵循能量守恒和物质平衡定理, 所以求取裂缝体积可以通过注入压裂液总体积减去滤失体积获得[15]。注入压裂液总体积可知, 需要对滤失体积进行计算。
滤失的定义, 简单来说, 就是由于缝内外存在压力差, 注入压裂液超过了油层的吸收能力而产生的现象[16]。压裂滤失在水力压裂研究中是一个非常关键的参数, 它会影响生成裂缝的几何形状、分布等[17]。目前对滤失量的研究, 一般通过求取滤失系数来求取滤失体积。
滤失系数与压力有关, 一般认为, 整个裂缝压裂闭合期间的滤失系数不变, 且施工过程中滤失系数相同。压裂液的滤失体积Vl的计算公式[18]为:
| $ V_{l}=n \int\limits_{0}^{x} \int\limits_{0}^{t} \frac{2 h c}{\sqrt{t-\tau(t)}} \mathrm{d} t \mathrm{~d} x $ | (2) |
式中: c为液体的滤失系数; h为裂缝高度; n为有效裂缝段数; x为平均裂缝长度; τ(t)为t时刻压裂液到达x处的时间。
由(2)式可知, 滤失体积与有效裂缝段数n、平均裂缝长度x有关。根据能量守恒原理, 在体积压裂过程中注入地层中的能量转化为裂缝内流体的压力能、动能、摩擦产生的消耗能、岩石形变产生的张裂能, 这些能量的转化将遵循最小能量路径[19], 总能量满足的平衡方程为:
| $ Q-x^{\prime} \frac{\partial Q}{\partial x^{\prime}}=C $ | (3) |
式中: x′为裂缝增长率; Q为总能量; C为常数。
将压力能、动能、摩擦产生的消耗能、岩石形变产生的张裂能代入(3)式可以得到:
| $ \left(\frac{\mathrm{d} x}{\mathrm{~d} t}\right)^{2}=\frac{C-\frac{1}{2} p n w h x-\frac{1}{2} \sigma_{h} n w h x+2 e_{s} n h x+V}{2 f n \rho h x^{2}-\frac{1}{2} n \rho w h x} $ | (4) |
式中: V为裂缝总体积; es为比表面能; σh为最小水平地应力; w为缝网内裂缝的平均宽度; p为裂缝内的平均压力; f为范宁摩阻系数。
在压裂过程中的物质平衡方程为:
| $ n h x=\frac{q_{i n j} t-V}{w} $ | (5) |
式中: qinj为注入压裂液量。
裂缝的平均宽度计算公式为:
| $ w=\frac{{\rm{ \mathsf{ π} }}\left(1-\delta^{2}\right)}{4 E}\left(p-\sigma_{h}\right) h $ | (6) |
式中: E为杨氏弹性模量; δ为泊松比。
压裂过程中裂缝的扩展速度等于此时裂缝内流体的流动速度, 在压裂的初始时刻(t=0时), 裂缝的扩展速度等于此时孔眼内流体的流动速度, 由此边界条件求取常数C。
裂缝的扩展速度计算公式为:
| $ \left.\frac{\mathrm{d} x}{\mathrm{~d} t}\right|_{t=0}=\frac{q_{i n j} w\left(3 p-2 p_{i n j}-\sigma_{h}+\frac{4 e_{s}}{w}\right)}{4 f C} $ | (7) |
式中: t为注入时间; pinj为缝口压力。
孔眼流体速度计算公式为:
| $ v_{t=0}=\frac{q_{i n j}}{{\rm{ \mathsf{ π} }} N r^{2}} $ | (8) |
式中: N为射孔孔眼数; r为射孔眼半径。
初始时刻, 裂缝的扩展速度与孔眼内液体的流动速度相等, 可以求出常数C:
| $ C=\frac{{\rm{ \mathsf{ π} }} N r^{2} w\left(3 p_{i n j}-\sigma_{h}+\frac{4 e_{s}}{w}\right)}{4 f} $ | (9) |
联立公式(2)~公式(9), 可得有效裂缝段数n与平均裂缝长度x满足的方程, 即:
| $ \begin{aligned} &x=\frac{\frac{1}{2} w C-p w\left(q_{i n j} t-V\right)+\frac{1}{2} q_{i n j} p_{i n j} t w}{2 q_{i n j} p_{i n j} t f-f\left(q_{i n j} t-V\right)\left(2 p+2 \sigma_{h}-\frac{8 e_{s}}{w}\right)-2 f C-4 p f V} \\ &n=\frac{\left(q_{i n j} t-V\right)\left[2 p_{i n j} q_{i n j} t f-f\left(q_{i n j} t-V\right)\left(2 p+2 \sigma_{h}-\frac{8 e_{s}}{w}\right)-2 f C-4 p f V\right]}{h w^{2}\left[\frac{1}{2} C-p\left(q_{i n j} t-V\right)+\frac{1}{2} p_{i n j} q_{i n j} t\right]} \end{aligned} $ | (10) |
由于压裂改造体积范围内裂缝长度和裂缝段数是关于滤失量的函数, 因而可以采用迭代方法进行计算。首先假设在初始时刻滤失量为0, 计算出该段的平均裂缝长度与有效裂缝段数, 然后增加一个单位Δt的时间, 计算出该时刻平均裂缝长度与有效裂缝段数, 将计算结果代入公式(2)中, 求出新时刻的滤失体积, 按照此方法依次迭代计算, 直到工程施工时间结束为止, 可以计算出最终的滤失体积Vl, 注入压裂液总体积记为VE。
裂缝体积Vc的表达式为:
| $ V_{c}=V_{E}-V_{l} $ | (11) |
裂缝体积密度ρv作为页岩气产能的评价标准, 其表达式为:
| $ \rho_{v}=\frac{V_{c}}{V_{\mathrm{SRV}}} $ | (12) |
页岩气井的产能主要受储层含油度等地质条件和压裂工程改造效果的影响, 为了更真实地反映体积压裂工程改造效果与页岩气产能之间的关系, 我们选取重庆涪陵地区页岩气田的某页岩气储层微地震监测项目作为测试工区, 并挑选相邻5口水平井作为研究对象, 分析了其连续一年的页岩气累积产量。所选取的5口井的井身结构基本相同, 各井的参数如井底压力、温度、岩性、含油性、流体黏度、孔隙度、渗透率等储层地质条件基本一致, 微地震监测结果及初期试采情况均说明各井之间不连通, 并在生产初期排除了各井之间的相互干扰。
5口井的设计压裂段数分别设置为10段、16段、18段、9段和12段。压裂过程主要以低粘度滑溜水作为压裂液。在多级压裂改造过程中, 采用微震监测设备对微地震事件点进行实时定位和采集。对采集到的5口井的微震事件点数据分别采用AlphaShape方法进行SRV值求取, 根据事件点分布分别设置合适的α进行SRV值求取。非压裂改造区域的剔除依据微震事件的分布密度与α的大小设置来计算, 需要根据实测数据的产能效果对α的大小进行校正, 从而得到较为合理的SRV计算结果。α设置越大, SRV值越大; α设置越小, SRV值越小。根据微震检测数据进行调整后, 对于这5口井, 本文将α分别设置为100, 80, 90, 100, 80时可以得到较为合理的SRV值。
5口井的主要相关参数如表 1所示。由表 1可知, 5口井中, 井2的SRV值最小, 井3的SRV值最大, 而裂缝体积密度最小的为井4, 裂缝体积密度最大的为井3, 与最终的页岩气年累计产量进行比对, 井3的SRV值、裂缝体积密度、年累计产量均为5口井中最大, 但是SRV值最小的井2, 其年累计产量却不是5口井中最小的, 而裂缝体积密度最小的井4对应的累计产量也最小, 裂缝体积密度与年累计产量是一一对应的。裂缝体积与页岩气年累计产量之间的关系不足以说明页岩气产能的效果, 因为天然裂缝与压裂裂缝之间的沟通不足时, 也可能出现压裂裂缝体积较大的特点, 但是此时并没有形成复杂的裂缝网络, 对页岩气的产出没有较好的促进作用。因此要更为可靠地对页岩储层压裂改造效果进行评价, 还需考虑其储层改造范围与裂缝体积之间的关系, 从而得出储层内部裂缝的复杂程度, 前人研究成果也表明水力压裂作用形成的压裂主裂缝连通次级裂缝形成复杂的裂缝网络, 通常压裂形成的裂缝越复杂, 储层压裂改造的效果越好, 页岩气产能效果越好[20-21]。
| 表 1 5口井的主要参数数据 |
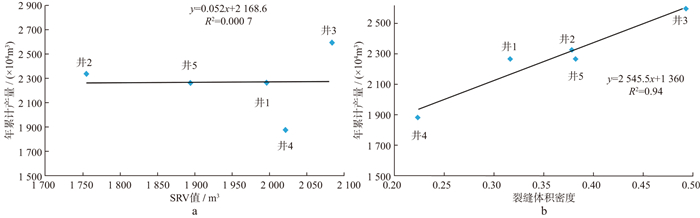
将5口井的SRV值、裂缝体积密度、年累计产量进行相关性分析, 得到的相关性函数与关系曲线如图 7所示。从图 7a可知, 5口井的SRV值与其对应的年累计产量的相关性指数较低, 主要是由井5、井1和井4之间SRV值与累计产量之间相关性较差造成的, 井5、井1和井4的SRV值依次增大, 但是页岩气累计产量却依次减小, 虽然井2、井3的SRV值与累计产量之间的契合度较高, 但在预测页岩气产量时, 会存在一些气井的SRV值与页岩气产量之间没有较好的相关性, 因而对最终的产量预测评价结果产生误导。由图 7b可知, 5口井的裂缝体积密度与其对应的年累计产量之间的相关性较好, 相关系数达到了0.94, 每一口井的裂缝体积密度与其年累计产量之间一一对应, 即认为井的裂缝体积密度越大, 则年累计产量越高。通过这5口井的产量统计分析, 验证了本文方法对于页岩气井的产能效应具有很好的指导预测作用。
|
图 7 相关性分析结果 a SRV值与年累计产量的关系; b 裂缝体积密度与年累计产量的关系 |
对页岩气井压裂后改造的产能效果进行合理有效的评价是目前页岩勘探开发研究的热点问题之一。本文结合水力压裂储层内部缝网结构进行分析, 提出裂缝体积密度概念, 并对地质条件相同的5口井进行页岩气产量分析, 结果表明, 裂缝体积密度与页岩气产量具有很好的相关性, 裂缝体积密度越大, 压裂改造的效果越好。相较于SRV评价参数, 裂缝体积密度不仅解决了SRV在一些情况下对页岩气产能预测不合理的问题, 且基于储层内部真实裂缝形态对压裂改造效果进行评价, 对于裂缝扩展情况监测也具有很好的参考价值。
本文提取的页岩气井的数据较少, 具有一定的局限性, 但是提供了一种新的页岩气产量预测方法, 天然裂缝与压裂裂缝之间的连通是体积压裂的主要目的, 如果可以掌握水力压裂裂缝的动态扩展规律, 将对裂缝的形成机理有更深入的了解, 从而进行更精确的压裂后产能预测。
| [1] |
米华英, 胡明, 冯振东, 等. 我国页岩气资源现状及勘探前景[J]. 复杂页岩气藏, 2010, 3(4): 10-13. MI H Y, HU M, FENG Z D, et al. Current status and exploration prospects of shale gas resources in my country[J]. Complex Oil and Gas Reservoirs, 2010, 3(4): 10-13. |
| [2] |
时贤, 程远方, 蒋恕, 等. 页岩储层裂缝网络延伸模型及其应用[J]. 石油学报, 2014, 35(6): 1130-1137. SHI X, CHENG Y F, JIANG S, et al. Shale reservoir fracture network extension model and its application[J]. Acta Petroleum Sinica, 2014, 35(6): 1130-1137. |
| [3] |
赵金洲, 李勇明, 王松, 等. 天然裂缝影响下的复杂压裂裂缝网络模拟[J]. 天然气工业, 2014, 34(1): 68-73. ZHAO J Z, LI Y M, WANG S, et al. Simulation of complex fracture network under the influence of natural fractures[J]. Natural Gas Industry, 2014, 34(1): 68-73. DOI:10.3787/j.issn.1000-0976.2014.01.010 |
| [4] |
叶泰然, 刘兴艳, 郑荣才, 等. 基于天然裂缝网络的二维裂缝度预测技术及应用研究[J]. 石油物探, 2004, 43(5): 445-449. YE T R, LIU X Y, ZHENG R C, et al. Research on two-dimensional fracture degree prediction technology and application based on natural fracture network[J]. Geophysical Prospecting for Petroleum, 2004, 43(5): 445-449. DOI:10.3969/j.issn.1000-1441.2004.05.007 |
| [5] |
李亚龙, 刘先贵, 胡志明, 等. 页岩气水平井产能预测数值模型综述[J]. 地球科学进展, 2020, 35(4): 350-362. LI Y L, LIU X G, HU Z M, et al. Overview of numerical models for productivity prediction of shale gas horizontal wells[J]. Advances in Earth Science, 2020, 35(4): 350-362. |
| [6] |
杜悦, 崔欢, 袁渊, 等. 天然裂缝对页岩气井产能的影响评价[J]. 天然气工业, 2021, 41(增刊1): 118-123. DU Y, CUI H, YUAN Y, et al. Evaluation of the influence of natural fractures on the productivity of shale gas wells[J]. Natural Gas Industry, 2021, 41(S1): 118-123. |
| [7] |
康凯, 赵林, 罗宪波, 等. 裂缝性潜山气藏产能评价新方法及其应用[J]. 中国海上油气, 2021, 33(3): 100-106. KANG K, ZHAO L, LUO X B, et al. A new method for productivity evaluation of fractured buried hill gas reservoirs and its application[J]. China Offshore Oil and Gas, 2021, 33(3): 100-106. |
| [8] |
张德良, 张烈辉, 赵玉龙, 等. 低渗透气藏多级压裂水平井稳态产能模型[J]. 油气地质与采收率, 2013, 20(3): 107-110. ZHANG D L, ZHANG L H, ZHAO Y L, et al. Steady-state productivity model of multi-level fracturing horizontal wells in low permeability gas reservoirs[J]. Petroleum Geology and Recovery Efficiency, 2013, 20(3): 107-110. DOI:10.3969/j.issn.1009-9603.2013.03.029 |
| [9] |
郑云川, 陶建林, 蒋玲玲, 等. 苏里格气田裸眼水平井分段压裂工艺技术及其应用[J]. 天然气工业, 2010, 30(12): 44-47. ZHENG Y C, TAO J L, JIANG L L, et al. Sequential fracturing technology and application of open hole horizontal well in sulige gas field[J]. Natural Gas Industry, 2010, 30(12): 44-47. |
| [10] |
邵春丽, 胡鹏, 黄承义, 等. Delaunay三角网的算法详述及其应用发展前景[J]. 测绘科学, 2004, 29(6): 68-71. SHAO C L, HU P, HUANG C Y, et al. Detailed description of the algorithm of Delaunay triangulation and its application development prospects[J]. Science of Surveying and Mapping, 2004, 29(6): 68-71. DOI:10.3771/j.issn.1009-2307.2004.06.016 |
| [11] |
郑金华, 王康, 李密青, 等. 基于Delaunay三角剖分的多目标进化算法解集分布度评价指标[J]. 模式识别与人工智能, 2012, 25(6): 885-893. ZHENG J H, WANG K, LI M Q, et al. Multi-objective evolutionary algorithm solution set distribution evaluation index based on Delaunay triangulation[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(6): 885-893. DOI:10.3969/j.issn.1003-6059.2012.06.001 |
| [12] |
余杰, 吕品, 郑昌文. Delaunay三角网构建方法比较研究[J]. 中国图象图形学报, 2010, 15(8): 1158-1167. YU J, LV P, ZHENG C W. Comparative study on the construction methods of Delaunay triangulation[J]. Journal of Image and Graphics, 2010, 15(8): 1158-1167. |
| [13] |
张云银, 刘海宁, 李红梅, 等. 应用微地震监测数据估算储层压裂改造体积[J]. 石油地球物理勘探, 2017, 52(2): 309-314. ZHANG Y Y, LIU H N, LI H M, et al. Application of microseismic monitoring data to estimate reservoir fracture reconstruction volume[J]. Oil Geophysical Prospecting, 2017, 52(2): 309-314. |
| [14] |
何华, 李宗春, 李国俊, 等. 散乱点云的自适应α-shape曲面重建[J]. 计算机应用, 2016, 36(12): 3394-3397. HE H, LI Z C, LI G J, et al. Adaptive α-shape surface reconstruction of scattered point clouds[J]. Computer Applications, 2016, 36(12): 3394-3397. DOI:10.11772/j.issn.1001-9081.2016.12.3394 |
| [15] |
曾晓慧, 郭大立, 王祖文, 等. 压裂液综合滤失系数的计算方法研究[J]. 西南石油学院学报, 2005, 27(5): 53-56. ZENG X H, GUO D L, WANG Z W, et al. Study on the calculation method of comprehensive fluid loss coefficient of fracturing fluid[J]. Journal of Southwest Petroleum University, 2005, 27(5): 53-56. DOI:10.3863/j.issn.1674-5086.2005.05.015 |
| [16] |
任岚, 胡永全, 赵金洲, 等. 高渗透地层压裂液滤失模型研究[J]. 天然气工业, 2006, 26(11): 116-118. REN L, HU Y Q, ZHAO J Z, et al. Research on filtration fluid loss model of high permeability stratum[J]. Natural Gas Industry, 2006, 26(11): 116-118. DOI:10.3321/j.issn:1000-0976.2006.11.036 |
| [17] |
冯福平, 黄芮, 雷扬, 等. 基于能量理论的体积压裂工程改造效果评价模型及应用[J]. 中国石油大学学报: 自然科学版, 2019, 43(1): 86-94. FENG F P, HUANG R, LEI Y, et al. Evaluation model and application of volume fracturing engineering reconstruction effect based on energy theory[J]. Journal of China University of Petroleum: Edition of Natural Science, 2019, 43(1): 86-94. |
| [18] |
夏富国, 郭建春, 刘立宏, 等. 天然裂缝压裂液滤失模型[J]. 油气地质与采收率, 2013, 20(4): 105-110. XIA F G, GUO J C, LIU L H, et al. Natural fracture fracturing fluid fluid loss model[J]. Petroleum Geology and Recovery Efficiency, 2013, 20(4): 105-110. DOI:10.3969/j.issn.1009-9603.2013.04.027 |
| [19] |
ZOU C N, YANG Z, ZHU R K, et al. Progress in China's unconventional oil & gas exploration and development and theoretical technologies[J]. Acta Geologica Sinica(English Edition), 2015, 89(3): 938-971. DOI:10.1111/1755-6724.12491 |
| [20] |
何建华, 丁文龙, 王哲, 等. 页岩储层体积压裂缝网形成的主控因素及评价方法[J]. 地质科技情报, 2015, 34(4): 108-118. HE J H, DING W L, WANG Z, et al. Main controlling factors and evaluation methods for the formation of volumetric pressure fracture network in shale reservoir[J]. Geological Science and Technology Information, 2015, 34(4): 108-118. |
| [21] |
WEI L, HUAN Z, HUI P, et al. Study on the mechanisms of refracturing technology featuring temporary plug for fracturing fluid diversion in tight sandstone reservoirs[J]. Energy Science & Engineering, 2019, 7(1): 88-97. |




