叠加速度分析技术是整个地震波速度建模流程的起点。无论叠前偏移还是速度反演, 高精度的宏观背景速度模型必不可少^[1]。随着宽方位, 宽频带和高密度(“两宽一高”)采集技术的普及, 地震数据量剧增^[2]。面对TB级别甚至PB级别的海量地震数据, 人工速度分析只能通过降低拾取密度来完成处理任务, 导致速度建模精度降低。虽然一些自动化的叠加速度分析方法可以高效地实现密点拾取, 但在低信噪比的实际数据处理中效果仍不理想。此外, 很少有文献讨论如何将处理员的经验认知融入自动化算法当中, 因此, 有必要发展一套全自动化的叠加速度分析处理流程, 并将处理专家的建模经验融入其中, 推动叠加速度分析技术从自动化迈向智能化。

从TANER^[3]提出速度谱概念后, 在很长一段时间里, 人们都致力于提升速度谱的精度, 发展基于CMP道集的自动速度建模方法, 其中包括利用数据的自相关特征^[4-5]、概率统计特征^[6-8], 以及更加精细的模型诸如考虑AVO效应以及非双曲时距关系等^[9-12]提升速度谱的分辨率和信噪比。在机器学习理论框架下也发展了一些自动化速度分析方法, 如采用卷积神经网络(CNN)^[13-16], 循环神经网络(RNN)^[17], 生成对抗网络(GAN)^[18]等监督学习类方法, 实现将速度谱或地震道集作为输入、通过网络模型获得拾取的谱点或速度模型的过程。然而, 该类方法缺乏数据的特征表达, 泛化能力通常较弱, 抗噪能力也仅限于非结构性的高斯噪声。另一方面, 一些无监督的聚类方法主要利用K-均值聚类(K-Means)^[19-20]和密度聚类^[21]及其变种, 将速度谱视作图像进行拾取。此类方法的效果受限于速度谱的精度且抗噪性较差。以上所谓的智能算法仅实现了自动化过程, 其密点拾取方式易导致速度模型中出现“挂面条”现象, 因此, 缺乏横向连续性。真正“智能化”的方法应该保持数据在高维空间的结构特征(即保结构映射), 并将人的处理经验和认识融入自动速度分析的整个过程^[22]。

基于上述认识, 研究思路体现为: 通过合理的引入地震数据体在不同域的特征, 作为选择合理时间-速度对(T-V对)的依据, 进而实现速度模型的建立。若将按照接收时间t和偏移距h, CMP坐标x_cmp所排列的地震数据U(t, h, x_cmp)通过NMO时距关系投影在自激自收旅行时t₀, 叠加速度v_S及CMP坐标x_cmp所构成的空间, 获得变换后的数据(t₀, v_S, x_cmp), 在自激自收旅行时-叠加速度(t₀-v_S)域可以获得地震数据的速度谱信息, 较为直观的体现T-V对信息, 同时引入层速度的约束, 而将数据转换到自激自收旅行时-CMP坐标$ \widetilde U$ (t₀-x_cmp)域, 可以观测到地震数据的结构信息, 利用图像拾取算法, 获得组成层位的结构信息点, 此处获得的t₀可以为后续的密点拾取算法提供T-V对中“T”的趋势。因此, 将结构信息融入到拾取中, 获得具有地质意义的T-V对。在叠加速度-CMP坐标(v_S-x_cmp)域, 观测到的速度横向变化趋势可以控制速度的高频抖动, 修正T-V对的空间形态。经过上述多域处理, 生成最符合地质逻辑的T-V对, 插值实现初始速度模型的建立。

结构信息的提取离不开高质量的地震成像剖面, 而成像剖面依赖于输入的背景速度模型。因此在最初始的背景速度建模过程中, 无法借助于成像剖面等信息。为了解决该问题, 通过引入伪叠加剖面生成结构剖面, 以便实施地质构造的约束。伪叠加剖面是指在生成的速度谱上, 沿时间轴方向取每个时间对应的能量较强速度区间内叠加结果, 用公式可以表示为:

式中: $S\left(t_{0}, x_{\mathrm{cmp}}\right) $为按照CMP排布的伪叠加剖面; $s\left(t_{0}, v_{\mathrm{S}}\right) $为速度谱上位于t₀时间的谱值; v_S为速度谱上叠加速度的取值; $\left[v_{\mathrm{S}}^{\mathrm{inf}}, v_{\mathrm{S}}^{\text {sup }}\right] $为用于叠加的速度范围。速度谱S采用常规的扫描叠加方式实现。而$s\left(t_{0}, v_{\mathrm{S}}\right) $表示为:

式中: u(t, h)为CMP道集, t可以由自激自收时间t₀、偏移距h和叠加速度v_S组成的函数表示, 即t=f(t₀, h, v_S), 在一般情况下, f为双曲时距关系。

伪叠加剖面的生成需要考虑以下关键问题: 首先, 使用常规的扫描叠加方式生成速度谱能够较好地保持地震同相轴的波形特征, 这是在后续拾取结构中利用波峰判别法^[23]所需要的。常规叠加后, 通过希尔伯特变换取包络的形式, 大概率保证每个轴拾取的波峰唯一。此处也可以参照统计相位相关方法中利用波形统计信息叠加生成速度谱的策略^[6]。其次, 依据公式(1)生成伪叠加剖面, 速度谱每个时间上叠加的速度$\left[v_{\mathrm{S}}^{\mathrm{inf}}, v_{\mathrm{S}}^{\mathrm{sup}}\right] $是变化的, 叠加速度范围选择和速度谱谱值相关, 因为双曲Radon变换算子非正交性导致速度谱存在能量泄露, 故此处的范围选择和泄露范围相关。范围过窄, 则会出现同相轴能量太弱的情况, 范围过宽, 则会包含过多的噪声, 这种情况在实际数据中更为严重。若信噪比过低, 则难以获得剖面上有效的结构信息。通常来说, 选择的范围准则为: 选择的范围能够涵盖速度谱上对应时间点能量峰值对应的包络, 同相轴在叠加后才能凸显出来。最后, 获得的剖面在地震数据信噪比较低的情况下, 考虑使用提升图像信噪比和增强图像结构信息的方法^[24-25]对图像进行预处理, 能够一定程度上增强图像的连续性并减少非结构性噪声影响。

基于高精度伪叠加剖面, 进行结构信息的提取。结构信息的提取方法采用VLIET等^[23]和WANG等^[26]提出的方法, 利用方向信息和子波波峰信息, 以及能量信息进行判定。首先, 计算类伪叠加剖面的结构张量, 获得剖面上每个点主方向和垂直主方向的特征值$ \mu_{1}\left(t_{0}, x_{\mathrm{cmp}}\right) $和$ \mu_{2}\left(t_{0}, x_{\mathrm{cmp}}\right)$。由此可以定义伪叠加剖面上每个点线性度$l\left(t_{0}, x_{\mathrm{cmp}}\right) $, 即

l的取值范围为[0, 1], l取值越大, 此处是结构的概率越大, l越趋近于0, 此处为结构的可能性越小。

波峰位置的判断通过计算沿同相轴垂直方向的梯度$ d\left(t_{0}, x_{\mathrm{cmp}}\right)$来获得。

式中: $ I_{x}=\partial S / \partial x $和$ I_{t 0}=\partial S / \partial t_{0} $分别是伪叠加剖面沿着x_cmp和t₀方向的方向梯度。

点(t₀, x_cmp)为波峰的条件为: 在该点前后的d符号相反, 同时波峰点处的|d|小于其前后的|d|, 即:

且波峰点处的振幅值较大, 否则此波峰不对应有效结构部分。因此, 当一个点同时满足线性度要求和波峰条件, 同时幅值较强, 认定该点为对应的结构点(t₀, x_cmp)。

t₀-v_S域的信息是基于CMP道集速度建模中最为常用的信息, 直接对应着待求取的两个参数(t₀, v_S)。通过构建速度谱, 可以展示不同的(t₀, v_S)参数组为潜在T-V对的可能性。许多文献研究和探讨了高精度高分辨率速度谱的制作^[3-12], 这里不讨论速度谱生成问题。利用速度谱可以生成以上所定义的伪叠加剖面, 伪叠加剖面上对应结构的点等同于反射界面对应的位置t₀, 通过结构提取可获得大部分CMP处的t₀信息。将拾取的t₀结果投影到速度谱上, 结合速度谱上拾取点位附近的能量团, 寻找合适的叠加速度v_S便成为一维搜索问题。在t₀处, 寻找对应的能量团的峰值, 即可确定t₀处对应的叠加速度, 衡量最合适的速度通过取窗求和的方式实现。

式中: W为窗函数。遍历搜索所有叠加速度v_S, 即可获得结构约束下满足能量关系的T-V对, 实现对速度谱点的初步筛选。

同时, 在t₀-v_S域中, 还可以施加层速度的信息。根据Dix公式^[27], 将叠加速度与层速度进行变换, 则有:

式中: v_i表示层速度, 可由第i个T-V对和第i-1个T-V对计算获得。为获得层速度, 首先, 必须保证公式(7)根号内的值大于零, 即

定义$ P_{i}=v_{\mathrm{S}, i}^{2} t_{0, i}$, 时刻t_i对应的P_i要大于P_i－1。利用该原则筛选掉的T-V对通常都是出现速度反转较大的位置且t₀间隔过小处, 上述现象来源于速度谱精度导致的拾取误差, 也可能对应真实情况下的薄互层, 此时, 公式(8)不成立, 根号内计算值为负数。即使遇到了真实存在的薄互层现象, 筛选掉薄互层不影响初始建模结果的稳定性。当面对的是大套地层的速度反转现象, 只要叠加速度在合理的范围内, 公式(8)都成立且转换的层速度取值合理。

另外, 速度谱拾取错误导致层速度出现较大异常值, 但公式(8)完全成立。通常来说, 层速度过大产生的原因是由于拾取的两个相邻的谱点在时间上差异较小, 速度差距过大导致。针对上述情况, 当层速度不合理时, 可根据总体趋势回归, 补充将第i个t₀处的v_{S, i}, 从而让异常速度处变得平缓。

基于上述步骤, 选取的T-V对反映了谱点满足地质构造信息以及速度谱的能量聚焦性。但是, 在实际数据处理中仍然会遇到相邻道近似深度位置的速度存在较大偏差问题。横向上较大的偏差会导致速度模型出现“挂面条”现象。因此, 必须考虑控制横向上的缓变情况, 构建更合理的速度模型。在v_S-x_cmp域中, 利用横向的连续性, 修改拾取结果。该原则要求在当前道拾取的谱点中, 在周围道相近的位置也要有相应的能量较强的速度谱点。即:

式中: $ \left(t_{0}^{\prime}, v^{\prime}{ }_{\mathrm{s}}, x_{\mathrm{cmp}}^{\prime}\right)$为对应$ \left(t_{0}, v_{\mathrm{S}}, x_{\mathrm{cmp}}\right)$的邻域点。有$\left|t_{0}-t_{0}^{\prime}\right| <\eta,\left|v_{\mathrm{S}}-v_{\mathrm{s}}^{\prime}\right| <v_{\mathrm{b}},\left|x_{\mathrm{cmp}}-x_{\mathrm{cmp}}^{\prime}\right| <x_{w} $, 其中, η为时间差异阈值, v_b表示叠加速度的差异阈值, x_w表示结构的变化差异阈值, 根据结构的变化快、慢决定其大、小。相邻道速度的变化在百米每秒的量级上有较大差异。为了避免速度谱精度引起的速度误差, 速度差异v_b的取值范围为0~300m/s, t₀和$ t_{0}^{\prime}$之间的差距η在半个子波之内。

公式(9)只能衡量单道差异, 无法衡量多个地震道之间的差异。提出了一种基于多道的差异约束方法, 该方法描述为: 对每一个(t₀, v_S), 定义扰动速度dv_S≤v_b, 扰动时间dt₀ < η, 将扰动结果应用在选定的多道拉平叠加, 取叠加能量最大的值作为最具有稳定性的叠加速度。

式中: $\widetilde U $为变换到(t₀, v_S, x)域的CMP道集, 将其在x方向按照一定范围求和, h为偏移距, 根据速度扰动和时间扰动量, 生成扰动谱, 在谱值最大的位置, 对应的是v_S和t₀最合理的点。由公式(10)可以看出, 得到的(t₀, v_S)未必是对于单个CMP速度谱最优的T-V对, 但保证了整体的速度横向缓变性。

采用大庆二维模型进行算法测试。模型深度为3968m, 模型的宽度为30000m, 获得的有效覆盖次数的CDP号为161~2237, 偏移距为-2800~2800m。模型的层速度为2500~6200m/s。模型的浅部是几层较厚的平层, 但存在速度反转, 而在深层存在断层和岩体侵入。按照建模策略, 生成了速度谱和对应的伪叠加剖面, 如图 1和图 2所示。

图 1(Fig. 1)

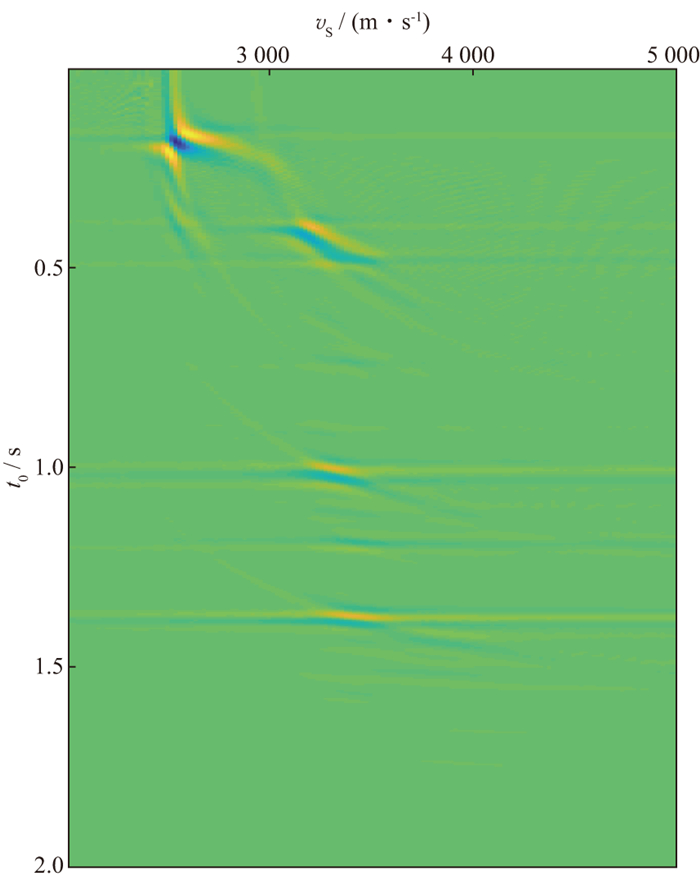
图 1 CDP 500的叠加速度谱(扫描范围为2000~5000m/s, 速度采样点数nv=151, 采样间隔dv=20m/s, 采样时长为2s, 采样间隔为1ms)

图 2(Fig. 2)

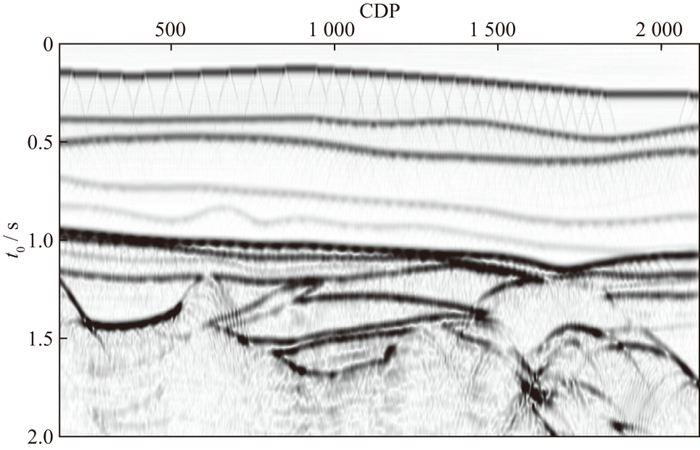
图 2 大庆二维模型的伪叠加剖面(速度积分范围为2000~5000m/s)

为更好地提取波峰, 对伪叠加剖面(图 2)进一步进行预处理。首先, 利用希尔伯特变换求取伪叠加剖面获得包络, 并实施各向异性平滑, 使得剖面上的同相轴只有一个波峰且剖面结构更加连续, 如图 3所示。再基于上述的波峰位置提取方法, 寻找波峰处以及振幅满足要求的点(定义为层位信息), 如图 4所示。

图 3(Fig. 3)

图 3 预处理后的伪叠加剖面

图 4(Fig. 4)

图 4 基于图 3提取的结构剖面

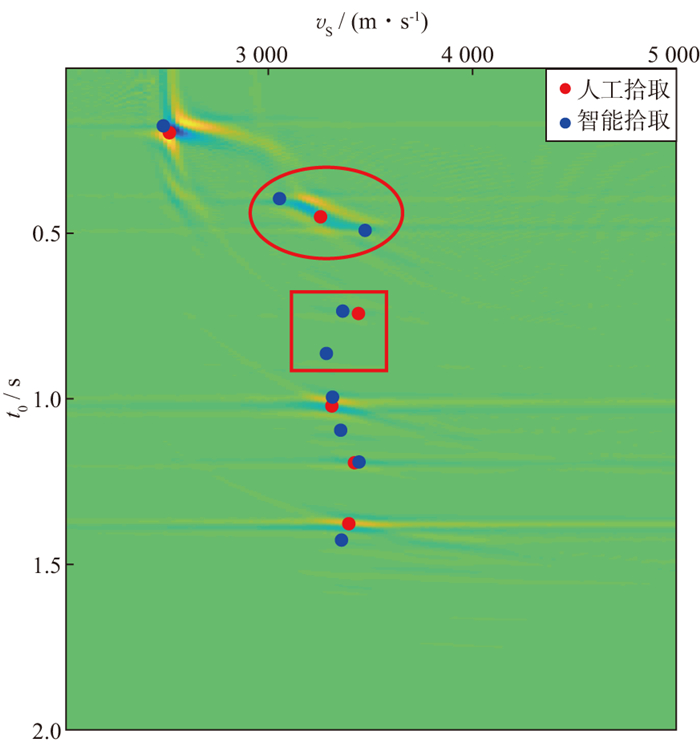
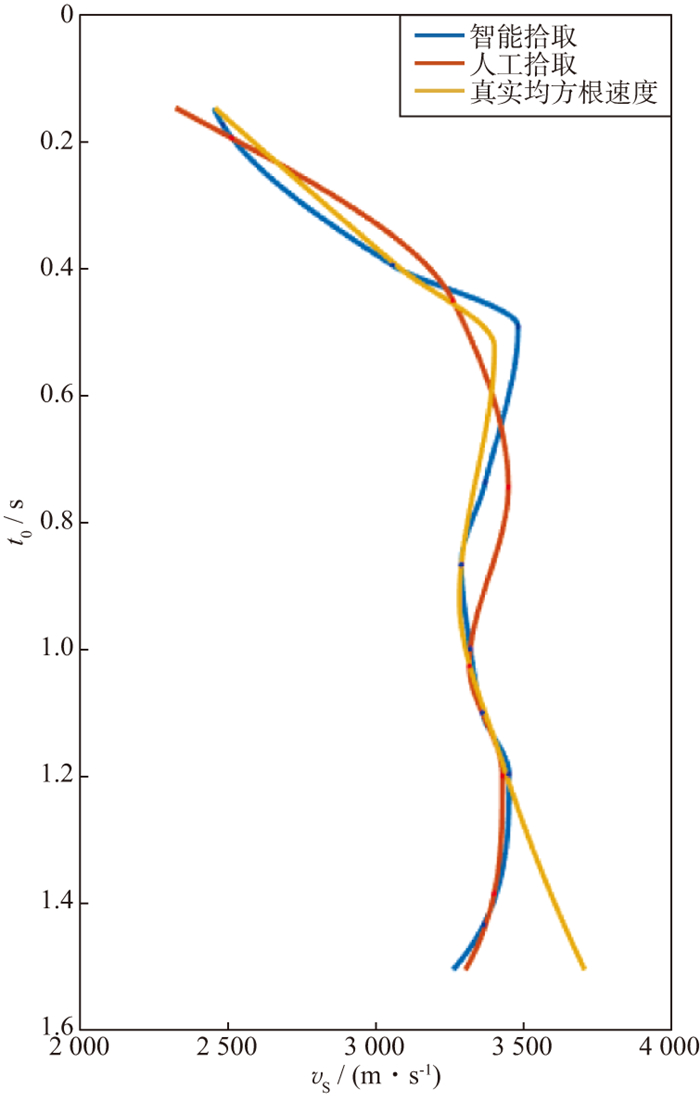
利用提取的结构, 可以找到对应的t₀点, 以此作为约束, 在速度谱上获得拾取的谱点, 如图 5蓝点所示。将单道人工拾取结果(图 5红点)和结构约束智能拾取结果(图 5蓝点)进行对比, 谱点上能量较弱的地方可能无法在单道下被拾取, 进而损失部分有效信息, 如图 5红框中所示。同时, 传统拾取只依靠单道谱点的形态判断, 如图 5红圈位置所示, 对应两个层位的能量团因分辨率较低无法分离, 影响了单道人工拾取结果, 仅勾选了一个谱点。而当引入结构信息拾取谱点, 会分别拾取到对应两个同相轴的谱点, 避免了可能产生的误差。在约束下拾取的谱点生成的叠加速度曲线也更接近真实的均方根速度, 如图 6所示。

图 5(Fig. 5)

图 5 CDP 500拾取的谱点示意

图 6(Fig. 6)

图 6 CDP 500智能拾取速度曲线(蓝)、人工拾取速度曲线(红)和真实均方根速度曲线(黄)

所有的密点拾取结果全部展示如图 7所示, 可以清晰地看到, 拾取点对应的构造信息(对应t₀-x_cmp方向)以及速度的分布趋势(对应v_S-x_cmp方向)。

图 7(Fig. 7)

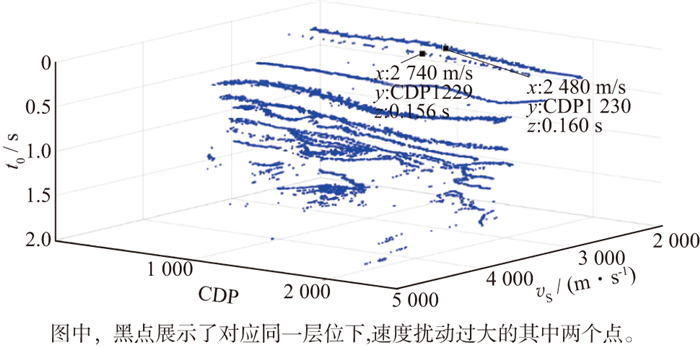
图 7 拾取点的三维散点信息

尽管利用了速度谱和结构信息双重约束进行谱点拾取, 但受限于速度谱的精度, 拾取点仍然存在不合理的现象(图 7中黑点)。在拾取结果中, 较为相邻的两道(第1229个CDP和第1230个CDP)中黑点位置属于同一层位, 叠加速度的差异高达260m/s(两道的叠加速度分别为2480m/s及2740m/s), 考虑到不同道之间的累积效应差异, 相邻两道出现这种差异是不合理的。因此, 针对以上问题, 利用上述定义的横向约束方法, 设定公式(7)中的v_b范围为±300m/s, 扰动速度的间隔为30m/s, 通过动校叠加, 获得可以体现多道叠加能量的扰动速度谱, 如图 8所示。基于扰动速度谱的能量关系, 确定相邻道的最佳速度。经过横向约束后的T-V对, 如图 9所示。对比图 7和图 9可以发现, 利用扰动速度谱施加横向约束后, 不同点间的速度值变化更加合理。

图 8(Fig. 8)

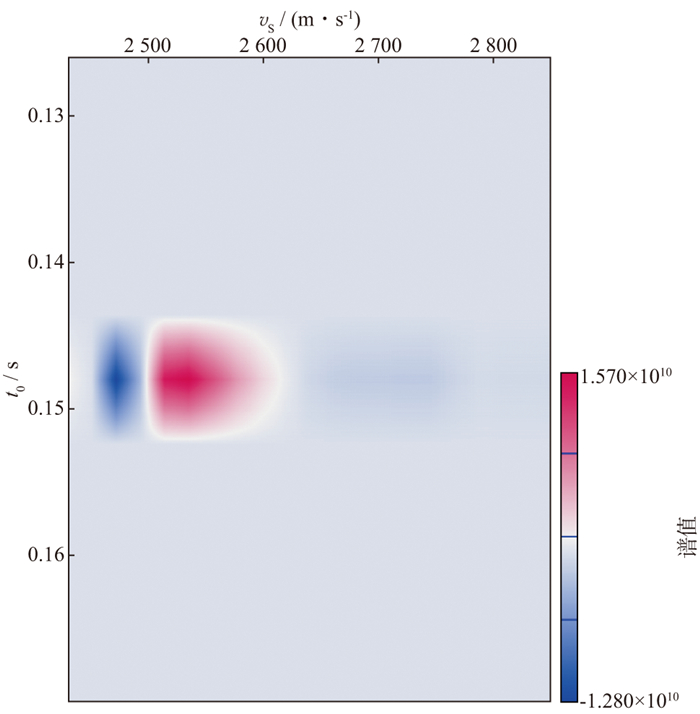
图 8 CDP-1230处及其邻域构成的扰动速度谱

图 9(Fig. 9)

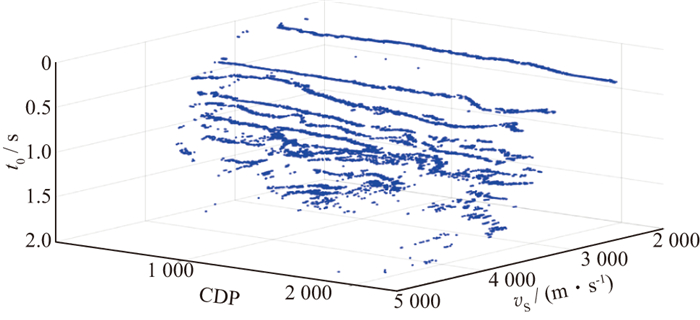
图 9 经过速度横向约束的T-V对散点排列

在横向约束基础上, 施加纵向约束准则, 插值获得完整的叠加速度模型。时深变换后获得深度域层速度模型如图 10所示。其中, 图 10a为深度域层速度模型, 图 10b为常规的不加层位约束建模结果, 图 10c为施加层位约束模型建模结果。可以看到, 智能化叠加速度建模方法建立的层速度范围与理论模型一致, 浅层大套沉积层的速度精度高, 与真实的速度模型有较好的对应关系, 但是, 由于深层存在剧烈的横向变速, 导致深层的速度精度不高, 尽管如此, 建模结果已满足初始建模的基本要求。与不加层位约束结果相比, 该方法能够较好地控制速度模型的主要变化趋势, 得到的结果更具有地质意义, 与真实模型更吻合。

图 10(Fig. 10)

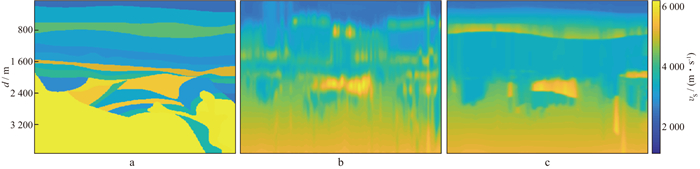
图 10 时深变换后获得深度域层速度模型 a 深度域层速度模型; b 不加层位约束层速度模型; c 施加层位约束模型

利用该方法获得的速度模型在全偏移距下叠加并进行叠后时间偏移, 获得叠加剖面和叠后时间偏移剖面分别如图 11和图 12所示。对比可以看出, 深层很多没有收敛的位置经偏移校正后, 图像的质量明显提高。

图 11(Fig. 11)

图 11 利用大庆叠加速度场所生成的叠加剖面

图 12(Fig. 12)

图 12 大庆叠加剖面对应的叠后时间偏移剖面

实际数据来自中国东部某探区。受限于实际资料的信噪比, 此时不能将$ v_{\mathrm{S}}^{\text {sup }}$和$v_{\mathrm{S}}^{\mathrm{inf}} $设置为和理论资料中一致的速度谱扫描范围。图 13a和图 13b分别展示了两种极端的速度扫描上、下限取值情况的伪叠加剖面。图 13a是取每一个时间叠加速度最大处的值排列而成, 即: $v_{\mathrm{S}}^{\mathrm{inf}}=v_{\mathrm{S}}^{\mathrm{sup}}=s^{\max }\left(t_{0}\right) $, 图 13b则是将速度谱全范围积分而成, $v_{\mathrm{S}}^{\mathrm{inf}}=v^{\min }\left(v_{\mathrm{S}} \in s\right), v_{\mathrm{S}}^{\mathrm{sup}}= $$ v_{\mathrm{S}}^{\max }\left(v_{\mathrm{S}} \in s\right)$。从图 13a可以看出, 浅层表现了更明显的形态特征, 并伴有更强的随机噪声, 而在深层的结构没有得到明显展示。利用速度谱完整扫描范围叠加生成的剖面(图 13b), 却在深层有更清楚的结构。

图 13(Fig. 13)

图 13 两种极端速度扫描上、下限取值情况的伪叠加剖面 a 选取谱上叠加范围最小的情况下得到的伪叠加剖面; b 选取谱上全部范围叠加而成的伪叠加剖面

上述实验结果说明, 当积分范围固定不变时, 浅层和深层分辨率不能同时保证。因此, 针对分辨率差异, 在不同深度设置不同叠加范围, 满足浅部叠加速度范围较小, 深部叠加速度区域较大的原则。将积分范围设置为随深度变化的函数, 如图 14所示, 即{|v_b∝t₀|}。此数据的速度谱展现出, 在浅层时速度谱的能量团更聚焦, 深层更发散, 这也符合大多数CMP道集生成速度谱的情况。当t₀以ms为单位, 速度以m/s为单位时, 设数值上的关系v_b=1000t₀。有: $v_{\mathrm{S}}^{\text {sup }}=s^{\max }\left(t_{0}\right)+0.5 v_{\mathrm{b}}, v_{\mathrm{S}}^{\mathrm{inf}}=s^{\max }\left(t_{0}\right)-0.5 v_{\mathrm{b}} $。调整叠加速度取值范围, 获得的伪叠加剖面如图 15所示, 可见, 浅层和深层的能量信息得到均衡, 以便于后续的结构提取。

图 14(Fig. 14)

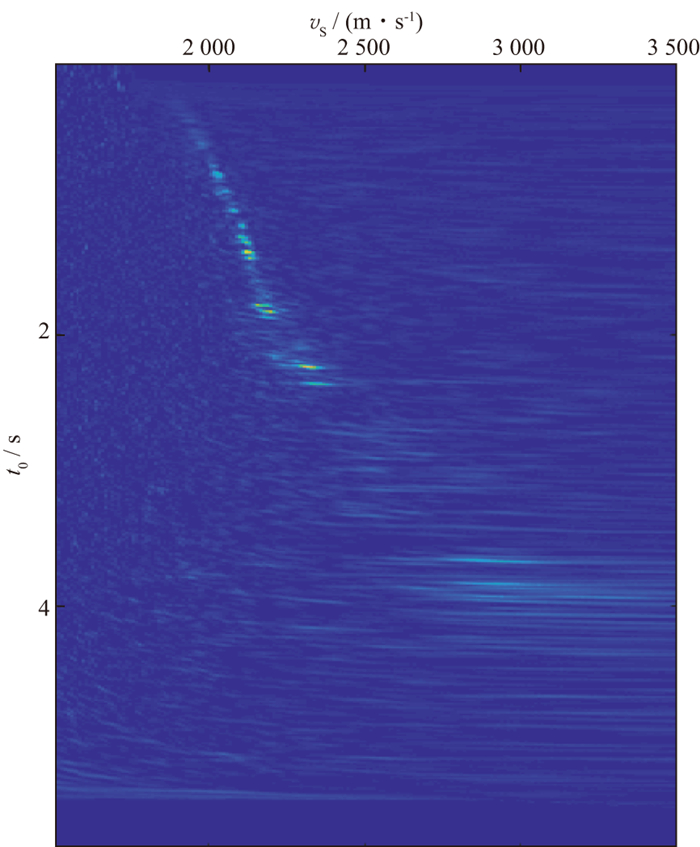
图 14 CDP 800速度谱(能量团随深度增加更发散)

图 15(Fig. 15)

图 15 调整叠加速度范围后的伪叠加剖面

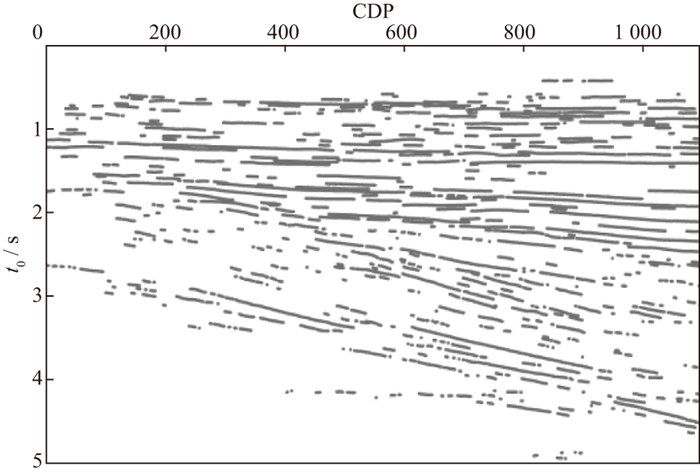
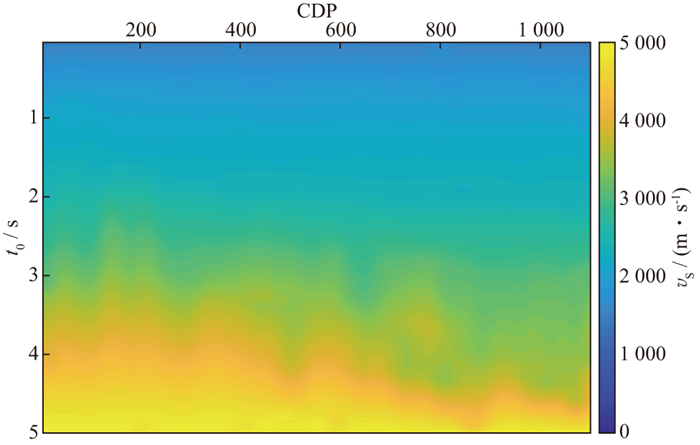
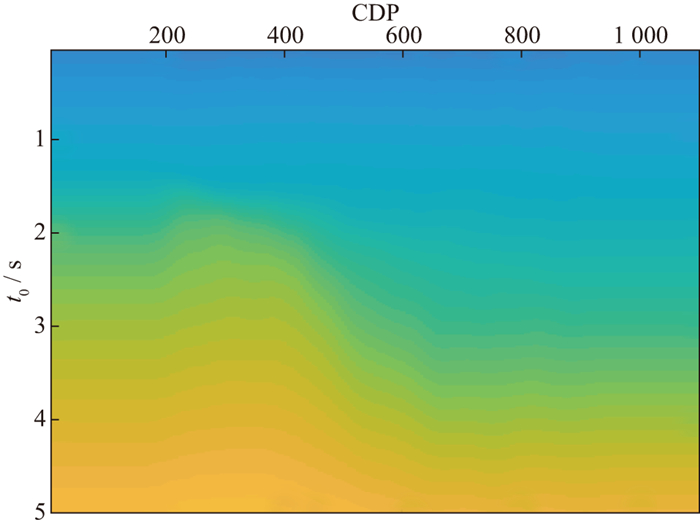
基于上述叠加范围调整后提取的结构信息如图 16所示。采用上述提出的拾取T-V对流程, 获得的叠加速度模型如图 17所示。同时, 针对此数据每隔20个道进行人工拾取, 最后通过插值获得完整的叠加速度模型, 结果如图 18所示。从模型结果上可以看出, 智能化拾取的方式在层位约束下保持了和伪叠加剖面更相似的结构形态, 同时在速度的纵、横向约束下, 速度的变化也更为连续, 而人工拾取生成的速度模型由于拾取密度不足和大尺度的平滑, 出现了“台阶状”的形态。再将智能拾取生成的速度模型和人工拾取生成的速度模型分别生成叠加剖面并将剖面放大对比, 如图 19和图 20所示。相比于图 20, 图 19在多处(红框所示位置)的同相轴更加清晰, 说明高密度智能拾取获得的速度更准确。

图 16(Fig. 16)

图 16 结构点拾取结果

图 17(Fig. 17)

图 17 智能速度建模结果

图 18(Fig. 18)

图 18 人工拾取建模结果

图 19(Fig. 19)

图 19 智能拾取生成的叠加剖面

图 20(Fig. 20)

图 20 人工拾取生成的叠加剖面

通过模拟人工交互速度分析的过程, 提出了一种智能化叠加速度建模方法。基于密点速度分析、横向速度缓变、纵向速度光滑趋势控制及稀疏性要求, 并施加构造特征等约束条件, 保证了“合理的”时间-速度对(T-V对)的智能筛选, 实现了叠加速度建模流程从自动化向智能化过渡。智能建模思想的引入, 使得处理员可以将精力聚焦于质量监控等核心环节, 因此, 有望显著降低人工成本并缩短建模周期。

相比于其它全自动化的建模方法, 智能化叠加速度建模方法有以下优势: ①结构约束下的速度拾取能更好地把握数据的主要特征, 使得模型的构造得到凸显; ②逐点进行速度分析提高了建模精度, 有效保证了局部的信息; ③各种约束的施加保证了拾取结果的合理性, 利用扰动速度谱分析叠加速度对相邻空间的影响作用, 降低了密点拾取引起的横向抖动假象。

在实际资料处理中, 伪叠加剖面结构信息的提取仍然值得进一步优化。下一步将研究如何在极低信噪比情况下, 仍然实现稳健的自动拾取以及结构约束。