2. 中国石油长庆油田公司勘探开发研究院, 陕西西安 710018;
3. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
2. Research Institute of Exploration & Development, PetroChina Changqing Oilfield Company, Xi'an 710018, China;
3. School of Geophysics and Information Technology of China University of Geoscience, Beijing 100083, China
核磁共振(nuclear magnetic resonance, NMR)测井是一种重要的井中地球物理勘探方法, 该方法将探测得到地层中氢质子与外加磁场的相互作用获得观测信息, 而后再进行储层划分、流体识别和参数评价[1-2]。核磁共振测井可以提供地层总孔隙度、有效孔隙度、可动流体与束缚流体等储层参数。为了更好地进行流体识别, 根据核磁共振流体弛豫机理和测量原理, 发展了长短等待时间(双TW)测井和长短回波间隔(双TE)测井等观测方法[3-4]。双TW测井是最有效的流体识别方法之一, 根据流体在不同极化时间内的极化率不同, 即长极化时间里, 水和烃完全极化, 短极化时间里, 只有水完全极化, 通过对比分析不同等待时间的核磁共振测井响应能实现储层流体的定性与定量评价[5-6]。在油气藏勘探开发中, 采用差谱分析和时间域分析(time domain analysis, TDA)实现核磁共振双TW测井数据处理[7-8]。在实际数据处理时, 假定油、气、水的横向、纵向弛豫时间是已知的, 而且整套储层固定不变, 因此对回波串或回波串差采用线性反演方法可实现储层油、气、水体积的计算[9-10]。但新的勘探区块中, 储层流体类型以及流体的弛豫时间等特性参数是未知的, 时间域分析中的反演问题是非线性的, 因此必须探索非线性反演方法[11-12]。谭茂金等[13-14]利用非线性反演遗传算法全局搜索油气的纵向弛豫时间(T1)和横向弛豫时间(T2)值, 再采用阻尼最小二乘法反演标准T2分布和差谱, 实现油气水的准确识别和定量评价。吕婕[15]和ZHU等[16]利用核磁共振测井资料, 结合交会图版、伪毛管压力曲线等方法进行孔隙结构分析和流体识别, 提高了解释符合率。
在实际钻井过程中, 泥浆滤液进入地层驱替孔隙中的流体。若地层含油, 泥浆滤液会冲掉部分可动油与可动水, 但仍存在部分的可动油、可动水以及残余油和束缚水[17]。尽管核磁共振测井的探测范围较浅, 但通过双TW测井计算得到的冲洗带含油体积和含油饱和度也能够反映原状地层的含油性。
本文针对复杂油水层开展了核磁共振双TW观测模式下饱含油水储层的弛豫机理研究, 考虑到水的不完全极化问题, 推导了长短等待时间下回波串差与流体体积及其弛豫性质的理论公式。本文利用遗传算法进行非线性反演[18], 而后得到储层中流体的横向、纵向弛豫时间, 基于反演结果计算得到冲洗带含油体积和含油饱和度。数值模拟和实例应用均表明, 改进后的方法更合理, 流体含量的计算结果比原方法的精度更高。
1 冲洗带核磁共振流体评价方法原理 1.1 方法原理为了对储层进行有效的流体识别, 在核磁共振测井标准T2观测模式基础上发展了双TW观测模式, 也称核磁共振双TW测井。核磁共振测井双TW观测方法的理论基础是基于核磁共振流体的弛豫机理, 即在不同的等待时间里流体的极化率是不同的, 等待时间越长, 流体的极化率越高。由于油、水具有不同的弛豫响应特征, 即在相同的等待时间里, 油、水的极化率存在很大的差别, 因此采用不同的等待时间进行观测, 可反映出油、水在核磁共振测井响应上的差异。在长等待时间(TWL)里, 水信号可以完全恢复, 烃(油、气)信号也可以完全恢复, 在短等待时间(TWS)里, 水信号可以完全恢复, 但烃信号不能恢复。
当储层含油、水两相时, 在水湿条件下, 长等待时间和短等待时间的CPMG序列采集的回波串幅度ML(t), MS(t)分别表示为:
| $ \begin{gathered} M_{\mathrm{L}}(t)=\sum\limits_{j=1}^{n} M_{0 j}\left(1-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_{1 \mathrm{w}}}}\right) \mathrm{e}^{-\frac{t}{T_{2 j}}}+ \\ M_{\mathrm{o}}\left(1-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_\mathrm{1o}}}\right) \mathrm{e}^{-\frac{t}{T_\mathrm{2o}}} \end{gathered} $ | (1) |
| $ \begin{aligned} M_{\mathrm{S}}(t)=& \sum\limits_{j=1}^{n} M_{0 j}\left(1-\mathrm{e}^{-\frac{T_{\mathrm{WS}}}{T_{1 \mathrm{w}}}}\right) \mathrm{e}^{-\frac{t}{T_{2 j}}}+\\ & M_{\mathrm{o}}\left(1-\mathrm{e}^{-\frac{T_{\mathrm{WS}}}{T_\mathrm{1o}}}\right) \mathrm{e}^{-\frac{t}{T_{2 \mathrm{o}}}} \end{aligned} $ | (2) |
式中: M0j为第j种组分的水的磁化强度; Mo为油的磁化强度; T2j为第j种组分的水的横向弛豫时间; T2o为油的横向弛豫时间; T1o为油的纵向弛豫时间; T1w为水的纵向弛豫时间; TWL为长等待时间; TWS为短等待时间; 双TW观测模式中, 不同等待时间磁化矢量差可以反映流体性质。
假设储层岩石饱和流体时, 长短不同等待时间的磁化矢量差ΔM(t)为:
| $ \Delta M(t)=\sum\limits_{j=1}^{n} M_{0 j} \mathrm{e}^{-\frac{t}{T_{2 j}}}+M_{\mathrm{o}} \mathrm{e}^{-\frac{t}{T_\mathrm{2o}}}+\varepsilon $ | (3) |
式中: ε为随机噪声。
假设储层岩石完全饱和油或完全饱和水, 长短不同等待时间的磁化矢量差为:
| $ \begin{gathered} \Delta M(t)=\sum\limits_{j=1}^{n} M_{0 j}\left(\mathrm{e}^{-\frac{T_{\mathrm{wS}}}{T_{1 \mathrm{w}}}}-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_{1 \mathrm{w}}}}\right) \mathrm{e}^{-\frac{t}{T_{2 j}}}+ \\ M_{o}\left(\mathrm{e}^{-\frac{T_{\mathrm{WS}}}{T_\mathrm{1o}}}-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_\mathrm{1o}}}\right) \mathrm{e}^{-\frac{t}{T_\mathrm{2o}}} \end{gathered} $ | (4) |
通常情况下, 假设水完全极化, 那么(4)式的第一项为零, 反演问题变得简单, 因为在原来的数据处理中均是假设该项为零。但是, 通常情况下小孔隙中的水完全极化, 部分大孔隙中的水未完全极化(假定不含天然气)。
核磁共振测井中, 磁化强度与孔隙度具有对应的关系。通过车间刻度, 磁化强度可以转换成孔隙度, 考虑到含氢指数(HI)校正, 则(4)式可转变成:
| $ \begin{gathered} \Delta \varphi(t)=\sum\limits_{j=1}^{n} \varphi_{0 j}\left(\mathrm{e}^{-\frac{T_{\mathrm{WS}}}{T_{1 \mathrm{w}}}}-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_{1 \mathrm{w}}}}\right) \mathrm{e}^{-\frac{t}{T_{2 j}}}+ \\ \varphi_{\circ} H_\mathrm{1o}\left(\mathrm{e}^{-\frac{T_{\mathrm{WS}}}{T_\mathrm{1o}}}-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_\mathrm{1o}}}\right) \mathrm{e}^{-\frac{t}{T_\mathrm{2o}}} \end{gathered} $ | (5) |
式中: Δφ(t)为核磁共振双TW测井数据计算的孔隙度差; φ0j为第j种组分的水的孔隙度; φo为地层冲洗带含油孔隙度; H1o为地层冲洗带含氢指数。
有些地层中尤其是在新的勘探区块中, 油、水的横向、纵向弛豫时间T2o、T1o、T1w往往是未知的, 方程(5)的求解为非线性反演问题, 因此, 必须采用非线性反演方法来求解。遗传算法作为启发式随机搜索的一种全局最优化算法, 可以使目标函数值最小, 从而达到全局优化。
1.2 遗传算法遗传算法是一种模拟自然进化过程搜索最优解的方法, 该方法通过模拟达尔文生物进化论的自然选择, 实现符合遗传学机理的全局寻优搜索。根据遗传学机理, 将流体的弛豫参数的搜索空间映射为遗传空间, 将流体的弛豫参数即油的横向弛豫时间(T2o)、纵向弛豫时间(T1o)、水的纵向弛豫时间(T1w)编码成一个二进制的向量, 称为染色体, 染色体中的每个元素定义为基因。模拟自然界优胜劣汰的进化现象, 根据生存竞争、优胜劣汰的原则, 借助复制、交换、突变等操作, 不断地计算流体弛豫参数的适应值, 即最合适的染色体, 最终得到最优解。图 1为遗传算法流程。

|
图 1 遗传算法流程 |
分析核磁共振长短TW回波串差与流体组分、流体体积及其弛豫特性的关系, 当流体弛豫参数未知时, 流体体积的计算是一个非线性问题, 搜索出最优的流体弛豫参数, 计算得到的流体体积最准确。遗传算法作为一种优化搜索算法, 其目的是寻找流体弛豫参数的最优值, 其搜索过程是从流体弛豫参数搜索空间的一个点集(种群)到另一个点集(种群)进行搜索, 而不是在空间中进行点到点的搜索。遗传算法的适应性强, 除了根据推导的长短回波串差、流体体积及其弛豫性质的理论公式确定目标函数, 即适应度函数外, 几乎不需要其它的条件。核磁共振测井中的回波数据受噪声影响严重, 给反演带来较大困难, 遗传算法能以很大的概率从离散的、多极值的、含有噪声的高维问题中找到全局最优解, 避免了噪声带来的影响。
在利用遗传算法求解上述问题时, 设计目标函数如下:
| $ \begin{aligned} Q_{\min }=& \sum\limits_{i=1}^{m}\left[\mathrm{e}_{\mathrm{cho}, \mathrm{diff}}(i)-\sum\limits_{j=1}^{n} \varphi_{0 j}\left(\mathrm{e}^{-\frac{T_{\mathrm{WS}}}{T_{1 \mathrm{w}}}}-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_{1 \mathrm{w}}}}\right) \mathrm{e}^{-\frac{t}{T_{2 j}}}-\right.\\ &\left.\varphi_{0} H_\mathrm{1o}\left(\mathrm{e}^{-\frac{T_{\mathrm{WS}}}{T_\mathrm{1o}}}-\mathrm{e}^{-\frac{T_{\mathrm{WL}}}{T_\mathrm{1o}}}\right) \mathrm{e}^{-\frac{t}{T_\mathrm{2o}}}\right]^{2} \end{aligned} $ | (6) |
式中: echo, diff(i)为长短不同等待时间下观测到的第i个回波之差; m为回波个数; n为弛豫组分; Qmin为观测到的回波数据与模型理论值的残差平方和。
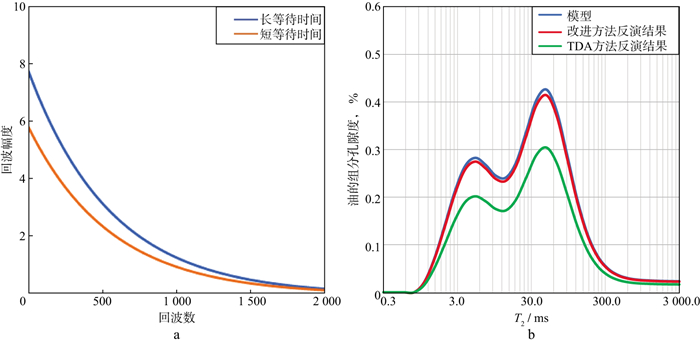
2 数值模拟实验与检验为了验证上述方法的可靠性, 设计了含油饱和度为30%的岩石模型, 设置长等待时间为6s, 短等待时间为2s, 回波间隔为0.9ms, 油水的含氢指数为1。利用预设模型和给定参数以及油水含量, 根据核磁测井双TW响应机理, 通过正演生成双TW观测回波串, 然后, 利用遗传算法对其进行非线性反演。反演时, 种群大小为80, 迭代次数为70, 交叉概率为0.9, 变异概率为0.005, 计算结果如图 2所示。图 2a为长短等待时间下模型的回波串, 图 2b为不同方法的反演结果(横坐标为横向弛豫时间, 纵坐标为油的组分孔隙度)。计算得到的流体弛豫参数、含油、水饱和度及相对误差如表 1所示。相较于原来TDA方法, 改进方法计算的含油饱和度与模型一致, 证明了方法的可靠性, 采用TDA方法计算得到的含油体积与模型差异稍大。通常情况下小孔隙中的水完全极化, 部分大孔隙中的水未完全极化, 利用原来的油水体积计算方法, 选取固定的弛豫参数, 对回波串进行线性反演, 计算结果偏大, 而改进方法消除了水不完全极化的影响, 因此计算的油水体积准确。
|
图 2 理想模型的回波正演与T2分布反演实验结果 a长短等待时间下模型的回波串; b不同方法的反演结果 |
| 表 1 计算结果与模型参数 |
鄂尔多斯盆地长8段致密砂岩储层物性较差, 孔隙结构复杂, 地层水矿化程度变化大, 这些原因导致低对比度油层发育。研究区储层流体弛豫特征不确定, 如果流体弛豫时间参数还采用固定值或者隐含值, 那么计算得到的油水体积不可靠。利用本文提出的处理方法计算出冲洗带含油体积, 进而得到地层中冲洗带含油饱和度。
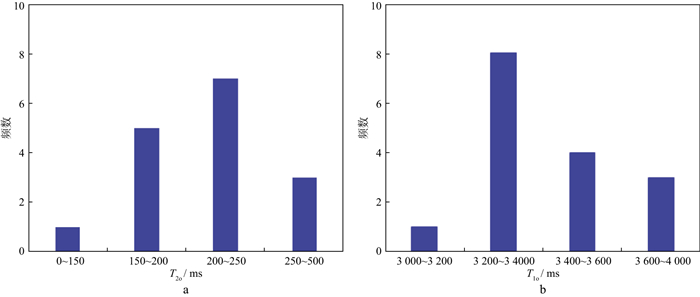
L189井是该研究区的一口评价井, 为了有效识别流体性质, 开展了核磁共振双TW测井。利用本文改进方法对核磁共振测井数据进行处理, 处理和解释结果如图 3所示。图中第3、4道为标准组长、短等待时间T2分布情况, 第5道为差谱, 第6道为孔隙度, 第7道、第8道为饱和度, 第9道为流体分析结果, 其中红色填充部分为计算的含油体积, 蓝色填充部分为计算的含水体积。图 3中2324~2331m目的层段, 油的横向弛豫时间(T2o)为150~250ms, 油的纵向弛豫时间(T1o)为3200~3600ms, 其直方图如图 4所示。采用改进方法计算得到的冲洗带含油饱和度(SONMR)约为40%, 利用中感应电阻率计算得到的冲洗带含油饱和度约为40%, 与采用核磁共振计算方法得到的含油饱和度一致。利用深感应电阻率计算得到的原状地层含油饱和度(So)约为60%, 采用改进方法计算得到的含油饱和度与利用中感应电阻率计算得到的含油饱和度均小于利用深感应电阻率计算原状地层含油饱和度。分析可知, 该目的层段综合解释为油层。该层段试油结果显示: 日产油为11.48t, 日产水为零, 试油结论为油层。该方法为储层流体识别提供了重要信息。

|
图 3 L189井核磁共振双TW测井数据处理与解释结果 |
|
图 4 目标储层油的横向弛豫时间(a)与纵向弛豫时间(b)直方显示 |
利用改进方法对研究区核磁共振测井15口井数据进行重新处理, 共解释30个层, 与试油结果对比发现, 解释符合率达90%, 证明了改进方法的准确性。
4 结论针对复杂致密砂岩储层流体识别的难题, 基于核磁共振双TW观测模式下油水的弛豫机理, 首先对核磁共振测井时间域分析方法进行了改进, 然后提出了计算冲洗带含油体积的新方法, 并利用数值模拟进行了方法检验, 最后利用鄂尔多斯盆地实际测井数据进行了实际应用, 结论如下。
1) 针对水润湿条件下, 基于核磁共振测井双TW观测模式, 考虑小孔隙中的水完全极化, 大孔隙中的水不能完全极化的问题, 推导出宏观磁化矢量与流体体积和弛豫参数的公式, 其核磁共振弛豫机理符合水不完全极化特征。
2) 在流体弛豫时间不确定情况下, 核磁共振长短回波串差与流体体积及其弛豫性质的理论公式是非线性的, 利用遗传算法能够实现非线性反演。
3) 数值模拟表明, 采用遗传算法计算油的横向、纵向弛豫时间以及含油饱和度与模型一致性好, 说明改进方法比TDA方法精度更高。
4) 改进方法在鄂尔多斯盆地延长组地层的应用结果表明, 利用改进方法处理的核磁共振双TW测井解释结果与试油测试结果更一致, 计算得到的含油饱和度也更准确, 为有效识别原状储层流体性质提供了准确信息。
| [1] |
肖立志. 核磁共振成像测井与岩石核磁共振及其应用[M]. 北京: 科学出版社, 1998: 328. XIAO L Z. Nuclear magnetic resonance imaging logging and rock nuclear magnetic resonance and their applications[M]. Beijing: Science Press, 1998: 328. |
| [2] |
谭茂金. 油气藏核磁共振测井理论与应用[M]. 北京: 科学出版社, 2017: 30-32, 35-55. TAN M J. Theory and application of nuclear magnetic resonance logging in oil and gas reservoirs[M]. Beijing: Science Press, 2017: 30-32, 35-55. |
| [3] |
胡亚武, 杨嘉, 王勇军, 等. 核磁共振测井在川中地区上三叠统低孔、低渗储层评价中的应用[J]. 天然气工业, 2012, 32(3): 45-48. HU Y W, YANG J, WANG Y J, et al. Application of NMRL to the evaluation of low-porosity and low-permeability upper Triassic reservoirs in the central Sichuan Basin[J]. Natural Gas Industry, 2012, 32(3): 45-48. DOI:10.3787/j.issn.1000-0976.2012.03.010 |
| [4] |
毕林锐. 核磁共振测井技术的最新若干进展[J]. 工程地球物理学报, 2007, 4(4): 369-374. BI L R. Latest advances in NMR logging technology[J]. Chinese Journal of Engineering Geophysics, 2007, 4(4): 369-374. DOI:10.3969/j.issn.1672-7940.2007.04.021 |
| [5] |
谭茂金, 赵文杰, 范宜仁. 用核磁共振测井双TW观测识别流体性质[J]. 天然气工业, 2006, 26(4): 40-43. TAN M J, ZHAO W J, FAN Y R. Identification of fluid property with NMR dual-TW well logging data[J]. Natural Gas Industry, 2006, 26(4): 40-43. |
| [6] |
翁爱华, 李舟波, 王雪秋. 核磁测井数据弛豫谱反演软件研究[J]. 长春科技大学学报, 2001, 31(4): 395-398. WENG A H, LI Z B, WANG X Q. Study on software design of nuclear magnetic resonance logging data inversion[J]. Journal of Changchun University of Science and Technology, 2001, 31(4): 395-398. DOI:10.3969/j.issn.1671-5888.2001.04.019 |
| [7] |
谢然红, 肖立志, 刘天定. 原油的核磁共振驰豫特性[J]. 西南石油大学学报, 2007, 29(5): 21-24. XIE R H, XIAO L Z, LIU D T. NMR relaxation properties of crude oils[J]. Journal of Southwest Petroleum University, 2007, 29(5): 21-24. DOI:10.3863/j.issn.1674-5086.2007.05.006 |
| [8] |
谢然红, 肖立志, 刘家军. 核磁共振测井时域分析法数值模拟及影响因素分析[J]. 地球物理学报, 2011, 54(8): 2184-2192. XIE R H, XIAO L Z, LIU J J. Time domain analysis numerical simulation and influence factors of NMR logging[J]. Chinese Journal of Geophysics, 2011, 54(8): 2184-2192. DOI:10.3969/j.issn.0001-5733.2011.08.027 |
| [9] |
王忠东, 肖立志, 刘堂宴. 核磁共振弛豫信号多指数反演新方法及其应用[J]. 中国科学(G辑), 2003, 33(8): 323-332. WANG Z D, XIAO L Z, LIU T Y. New multi-exponential inversion method of NMR relaxation and its application[J]. Chinese Science(G), 2003, 33(8): 323-332. |
| [10] |
林振洲, 潘和平. 核磁共振测井进展[J]. 工程地球物理学报, 2006, 3(4): 295-304. LIN Z Z, PAN H P. The progress of nuclear magnetic resonance logging[J]. Chinese Journal of Engineering Geophysics, 2006, 3(4): 295-304. DOI:10.3969/j.issn.1672-7940.2006.04.010 |
| [11] |
陈星, 黄卡玛, 赵翔. 测井中的非线性数据拟合研究[J]. 四川大学学报(自然科学版), 2002, 39(6): 1145-1148. CHEN X, HUANG K M, ZHAO X. A Study of nonlinear data-fitting based on a genetic algorithm in electrical log[J]. Journal of Sichuan University(Natural Science Edition), 2002, 39(6): 1145-1148. DOI:10.3969/j.issn.0490-6756.2002.06.038 |
| [12] |
王为民, 李培, 叶朝辉. 核磁共振弛豫信号的多指数反演[J]. 中国科学(A辑), 2001, 31(8): 730-736. WANG W M, LI P, YE Z H. Multi-exponential inversion of NMR relaxation[J]. Chinese Science(A), 2001, 31(8): 730-736. DOI:10.3321/j.issn:1006-9232.2001.08.009 |
| [13] |
谭茂金, 石耀霖, 赵文杰, 等. 核磁共振双TW测井数据联合反演与流体识别[J]. 地球物理学报, 2008, 51(5): 1582-1590. TAN M J, SHI Y L, ZHAO W J, et al. Joint inversion method for NMR dual-TW logging data and fluid typing[J]. Chinese Journal of Geophysics, 2008, 51(5): 1582-1590. DOI:10.3321/j.issn:0001-5733.2008.05.034 |
| [14] |
运华云, 谭茂金. 核磁共振测井双等待时间观测方式及分析方法[J]. 油气地质与采收率, 2006, 13(4): 96-98. YUN H Y, TAN M J. Analysis on dual waiting time activation of NMR logging[J]. Petroleum Geology and Recovery Efficiency, 2006, 13(4): 96-98. DOI:10.3969/j.issn.1009-9603.2006.04.031 |
| [15] |
吕婕. 核磁测井在阜东斜坡侏罗系头屯河组储层分类及流体识别中的应用[D]. 成都: 西南石油大学, 2014 LV J. The application of nuclear magnetic logging in reservoir classification and fluid identification of Jurassic Toutunhe Formation in the slope of East Funing [D]. Chengdu: Southwest Petroleum University, 2014 |
| [16] |
ZHU L Q, ZHANG C, WEI Y, et al. Permeability prediction of the tight sandstone reservoirs using hybrid intelligent algorithm and nuclear magnetic resonance Logging Data[J]. Arabian Journal for Science and Engineering, 2017, 42(4): 1643-1654. DOI:10.1007/s13369-016-2365-2 |
| [17] |
胡法龙, 周灿灿, 李潮流, 等. 核磁共振测井构建水谱法流体识别技术[J]. 石油勘探与开发, 2016, 43(2): 244-252. HU F L, ZHOU C C, LI C L, et al. Water spectrum method of NMR logging for identifying fluids[J]. Petroleum Exploration and Development, 2016, 43(2): 244-252. DOI:10.11698/PED.2016.02.10 |
| [18] |
阎桂京, 潘葆芝. 遗传算法在估计测井解释参数方面的应用[J]. 物探化探计算技术, 2001, 23(1): 43-46. YAN G J, PAN B Z. The application of genetic algorithm to the parameters in well logging interpretation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2001, 23(1): 43-46. DOI:10.3969/j.issn.1001-1749.2001.01.008 |




