2. 中国石油化工股份有限公司勘探分公司, 四川成都 610041
2. Sinopec Exploration Company, Chengdu 610041, China
四川盆地及周缘页岩气地质资源丰富, 在“二元富集”理论[1]的指导下, 南方海相五峰-龙马溪组页岩气勘探开发取得重大突破, 焦石坝、长宁、威远等页岩气田的发现推动了我国页岩气行业快速发展。勘探地球物理技术贯穿页岩气勘探开发整个过程, 发挥了关键作用[2], 形成了适合我国南方中浅层平稳构造区的海相页岩气“甜点”地震预测与评价技术体系, 包括基于叠前高精度密度反演有机碳含量(TOC)的预测技术[3]、多元回归脆性指数预测技术[4]、压力系数预测技术[5]、二元约束含气量预测技术[6]等, 有效支撑了南方海相页岩气的勘探及开发。目前, 美国页岩气勘探开发由中浅层向深层逐渐拓展, Haynesville、Eagle Ford和CanaWoodford这3个埋深为3500~4100m的深层页岩气藏已实现商业开发, 正在探索更深(埋深4500m左右)的Hilliard-Baxter和Mancos页岩气藏[7-8]。中国深层(埋深≥4000m)页岩气资源量远大于中浅层的页岩气资源量, 2015年以来已取得了系列勘探突破, 单井测试最高产量达137.9×104m3/d, 揭示了良好的勘探前景和巨大勘探潜力[9]。但是, 深层页岩地层温度较高, 页岩塑性增强, 地应力较大且应力差值高, 导致裂缝起裂及延伸困难, 体积压裂改造难度大[10]。工程可压裂性是制约深层页岩气勘探开发的核心问题。
前人针对工程“甜点”的研究形成了一些认识[11-13], 脆性指数及裂缝发育可表征深层页岩地层能否压开, 可结合破裂压力联合分析; 地应力差可以评价能否压裂形成缝网, 可结合压裂G函数或者微地震展开评价。目前, 针对深层页岩气勘探的工程“甜点”地球物理参数不完全明确, 尤其缺少针对性地震预测技术; 常用的矿物脆性指数只能反映页岩气储层静态指标的变化, 不能反映脆性随深度的变化特征; 地应力的理论研究较多, 实际应用仍不完全成熟。本文进一步结合大量岩石力学实验及钻井压裂施工参数, 分析DS地区可表征深层页岩气工程“甜点”的敏感地球物理参数, 建立针对性地震预测模型, 利用OVT域叠前地震资料, 形成脆性指数、裂缝及地应力差地震预测技术, 期望取得良好的应用效果。
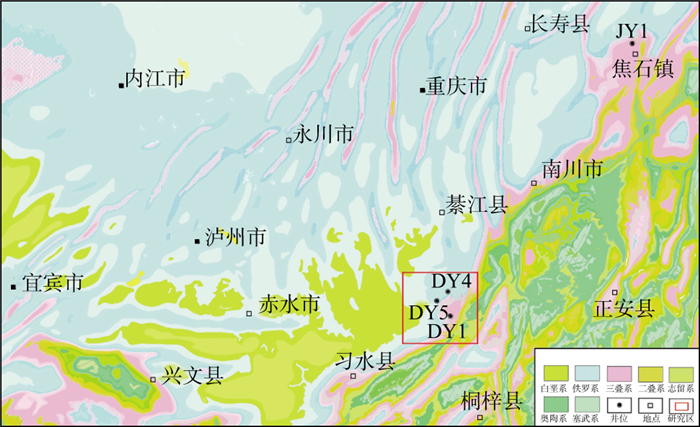
1 研究区概况DS研究区主体位于重庆市綦江县境内, 距离涪陵页岩气田150km, 构造位置位于四川盆地东南部盆缘褶皱带, 形态上表现为一个向盆内延伸的鼻状构造(图 1)。该区五峰组-龙马溪组一段一亚段为典型的深水陆棚沉积环境, 发育了一套黑色碳质泥页岩。共完钻6口重点探井, 早期DY1井及DY3井钻探页岩气层埋深小于3000m, 但保存条件较差, 勘探效果一般, 近期勘探逐步向深层探索, DY4井、DY5井及DYS1井均试获高产页岩气流, 产量分别为20.56×104, 16.33×104, 31.18×104m3/d。研究区页岩整体具有有机碳含量高、有机质类型好、热演化程度适中、脆性矿物含量高等特征; 同时距离齐岳山断裂的远近、埋深、页岩气层顶板特征, 共同决定了该地区保存条件的差异; 随着埋深的增大, 水平扩散影响逐渐减少, 保存条件好, 压力系数高[14-15], 该区深层页岩气具有良好的富集条件。
|
图 1 DS研究区区域构造位置 |
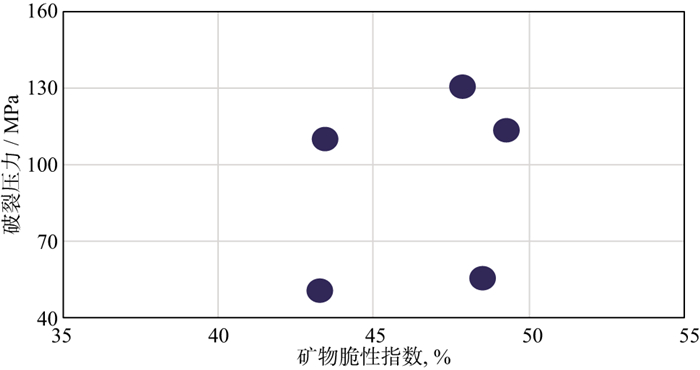
通常利用矿物脆性指数开展页岩地层脆性评价, 目前基于地震资料的脆性指数预测方法主要以基于矿物脆性指数为目标[4, 16], 没有体现埋深变化对脆性的影响。DS地区矿物脆性指数为52%~54%, 差异不大, 但随着埋深、地层围压的增加, 岩石破裂压力及难度显著增大, 矿物脆性指数与破裂压力相关性差, 不能有效评价地层可压性(图 2)。
|
图 2 DS地区矿物脆性指数与破裂压力的交会结果 |
侯振坤等[17]针对龙马溪组页岩脆性特征进行了详细的试验研究, 基于跌落系数、应力降系数、软化模量定义了页岩综合脆性指数:
| $ B_{I}=\alpha B_{1}+\beta B_{2}+\gamma B_{3} $ | (1) |
式中: B1, B2, B3分别为与跌落系数、应力降系数、软化模量相关的岩石力学参数; α, β, γ分别表示B1, B2, B3在脆性评价中的权重, 且α+β+γ=1。
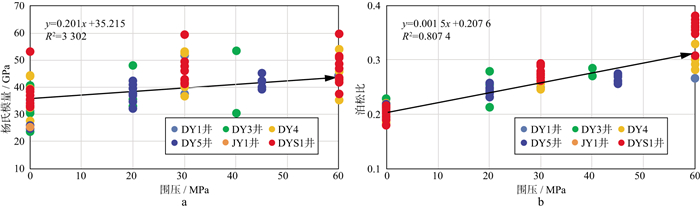
在不同有效围压条件下, 采用相同方法开展DS地区重点探井优质页岩段岩石力学试验。研究结果表明, 随着埋深及有效围压的增大, 页岩会发生脆塑性转换, 围压从0增加至80MPa, 页岩综合脆性指数由0.8696减小到0.6586, 降幅达24.3%(表 1)。同时, 鉴于杨氏模量和泊松比是反映岩石力学性质的两个关键力学参数, 进行了重点对比分析, 结果表明, 杨氏模量与围压相关性差(图 3a), 并不能有效反映脆性随深度变化的脆性特征, 利用杨氏模量的Rickman公式[18]并不适用于DS地区页岩的脆性评价; 同时可以明显看出, 泊松比与有效围压具有较好的相关性, 相关系数达0.81(图 3b), 其线性关系可表示为:
| $ \nu=a P_{\mathrm{eff}}+b $ | (2) |
| 表 1 川东南五峰—龙马溪组页岩脆性综合评价指标统计 |
|
图 3 杨氏模量(a)及泊松比(b)随围压变化的结果 |
式中: ν为泊松比; a, b为回归系数, Peff为有效围压。
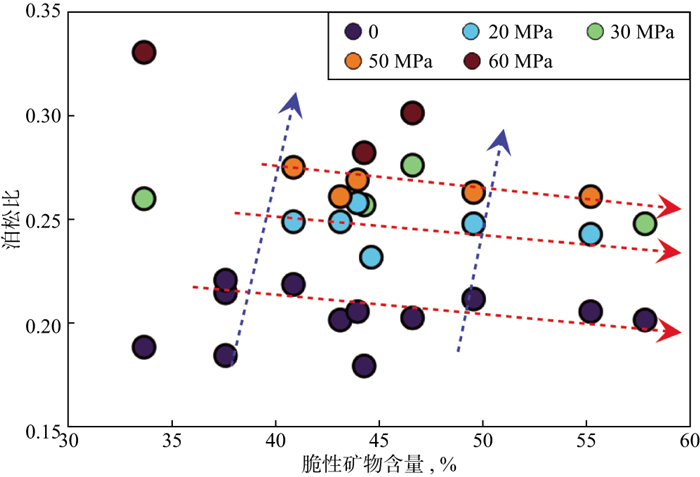
我们对比分析了相同脆性矿物含量下泊松比随围压的变化规律以及相同围压下泊松比随脆性矿物含量的变化规律(图 4), 可以看出, 有效围压相同时, 泊松比随着脆性矿物的增加而缓慢降低(图 4中橙色箭头), 脆性矿物含量由35%增加至60%时, 泊松比由0.22减小至0.20, 相对减少10%;脆性矿物含量相同时, 泊松比随着围压的增加而增加(图 4中蓝色箭头), 表征岩样塑性增强, 脆性降低, 其变化幅度大于泊松比随脆性矿物含量的变化幅度。
|
图 4 泊松比、脆性矿物含量和有效围压的交会结果 |
矿物脆性反映单井纵向上脆性的变化, 不能反映平面上脆性随深度的变化, 而岩石力学参数泊松比反映脆性随围压的变化趋势, 是脆性变化的低频趋势, 将二者结合起来, 基于泊松比引入深层脆塑性转换因子, 构建深层页岩脆性指数, 对矿物脆性指数进行修正:
| $ B_{I_{\mathrm{d}}}=f(\nu) \cdot B_{I_{\mathrm{m}}} $ | (3) |
式中: BIm为矿物脆性指数; BId为深层脆性指数; f(ν)为塑延性转换敏感因子。
泊松比增加表明脆性降低, 为了使f(ν)与脆性的变化趋势一致, 将f(ν)表示为泊松比的倒数形式, 同时为了实现f(ν)对BIm的校正作用, 利用研究区最大有效围压和最小有效围压的泊松比的平均值对其进行归一化处理, 将塑延性转换敏感因子f(ν)表示为:
| $ f(\nu)=\frac{\nu_{\left(P_{\text {effmax }}\right)}+\nu_{\left(P_{\text {effmin }}\right)}}{2 \nu} $ | (4) |
式中: ν(Peffmax), ν(Peffmin)分别为研究区最大和最小有效围压下的泊松比。其中有效围压可以通过埋深和孔隙压力推算得到:
| $ P_{\mathrm{eff}}=\int_{0}^{z} \rho(z) g \mathrm{~d} z-P_{p} $ | (5) |
式中: g是重力加速度; ρ(z)是密度; z是深度; Pp是孔隙压力。
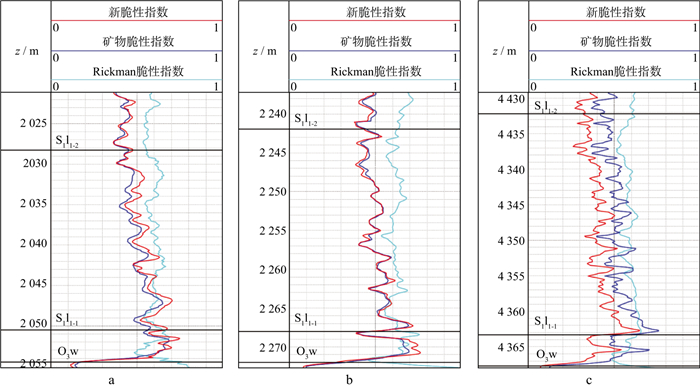
利用公式(3)和公式(4)开展单井计算测试, 由计算结果可知f(ν)在1附近变化, 当f(ν)>1时, 则脆性增强, 当f(ν) < 1时, 则脆性降低。基于Rickman公式计算的DY1井(页岩埋深2054m)、DY3井(页岩埋深2272m)及DY2井(页岩埋深4367m)脆性指数基本相当, 如图 5中浅蓝色曲线, 与深度无明显相关性, 且未体现出自上而下脆性增大的趋势, 其原因为: 杨氏模量影响因素复杂, 不适用于脆性评价; 利用本文方法计算的新脆性指数如图 5中红色曲线所示, 可以明显看出, 自上而下脆性增强, 与石英等脆性矿物含量增加的特征(图 5中蓝色曲线)一致, 同时随着页岩埋深的增加, DY1井和DY2井的脆性指数呈现明显降低趋势, 与岩石力学变化特征一致, DY2井深度超过4300m, 脆性指数基本小于50%, 降低明显。
|
图 5 DY1井(a)、DY3井(b)和DY2井(c)新脆性指数、矿物脆性指数与Rickman脆性指数对比 |
基于上述分析可知, 泊松比是开展深层脆性指数预测的关键参数。为实现泊松比的高精度反演, 基于宗兆云等[19]提出的杨氏模量-泊松比-密度(YPD)弹性阻抗反演方程开展泊松比直接反演, 以减小累计误差, 提高预测精度。YPD弹性阻抗方程为:
| $ I_{\mathrm{E}}(\theta)=A_{0}\left(\frac{E}{E_{0}}\right)^{a(\theta)}\left(\frac{\nu}{\nu_{0}}\right)^{b(\theta)}\left(\frac{\rho}{\rho_{0}}\right)^{c(\theta)} $ | (6) |
式中: E0, ν0和ρ0分别定义为杨氏模量E、泊松比ν和密度ρ的平均值; A0为纵波阻抗的均值, 通过A0的标定, 可以使函数变得更加稳定。
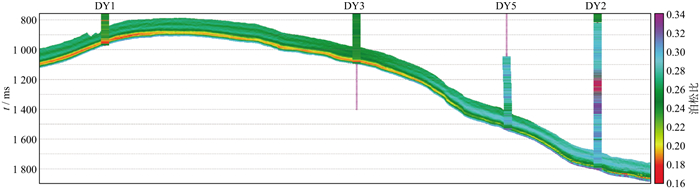
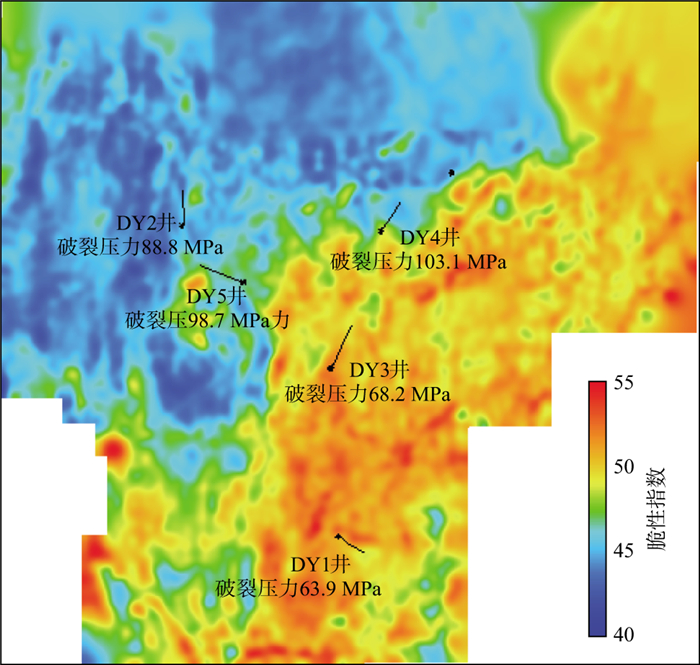
从图 6可以看出, 泊松比反演结果与单井实测结果基本一致, 随着深度的增大, DY1井、DY3井和DY2井的泊松比不断增大, 页岩脆性明显有降低的趋势。基于新建立的深层脆性指数(公式(3))完成了DS地区五峰组—龙马溪组一段优质页岩脆性指数的预测, 结果如图 7所示, 可以看出, 预测结果很好地体现了随埋深增加的塑延性变化趋势特征, 同时由于泊松比的横向变化, 反映出脆性的平面细节变化特征。比较工区内已钻井的脆性预测结果与破裂压力的关系可以看出, 优质页岩脆性与破裂压力有良好相关性, 脆性指数越高, 破裂压力越低, 预测DY5井的脆性指数高于DY4井的脆性指数(表 2), 与实际结果匹配较好。
|
图 6 泊松比反演结果与单井实测结果对比 |
|
图 7 DS地区优质页岩新脆性指数预测平面 |
| 表 2 川东南DS地区探井脆性指数预测对比 |
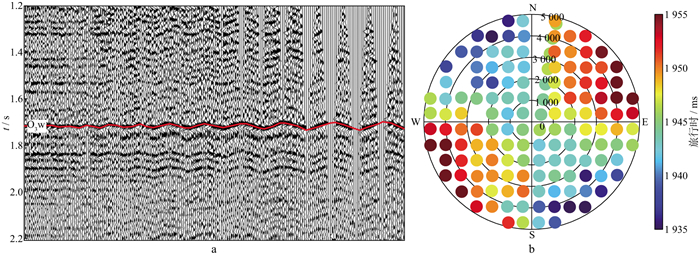
高角度裂缝发育的地层(HTI介质)导致地震波在不同传播方向的振幅、衰减、弹性性质等属性随方位的变化而变化。研究人员提出了多种基于纵波方位各向异性信息识别天然微裂缝的预测方法, 如AVAz技术[20-22]等。但是研究区处于四川盆地盆缘复杂构造区, 地表起伏大、岩性横向变化快, 地震资料振幅能量的保幅性及一致性处理要求极高, 实际资料难以达到上述技术的要求, 未能取得较好的预测效果。HTI介质下地震波传播速度的差异可表现为地震波同相轴旅行时的差异, 固定入射角情形下, 不同方位旅行时可近似为椭圆, 进而可以预测裂缝强度及其走向, 即VVAz技术。本次研究基于DS地区OVT域数据分析旅行时随方位变化的特征, 尽量避免了AVAz技术因能量一致性处理而造成的裂缝预测误差, 形成了方位旅行时椭圆拟合裂缝预测新技术, 尤其是针对五峰组—龙马溪组深层页岩气地震反射层稳定, 旅行时易于自动拾取等特点, 取得了一定效果。
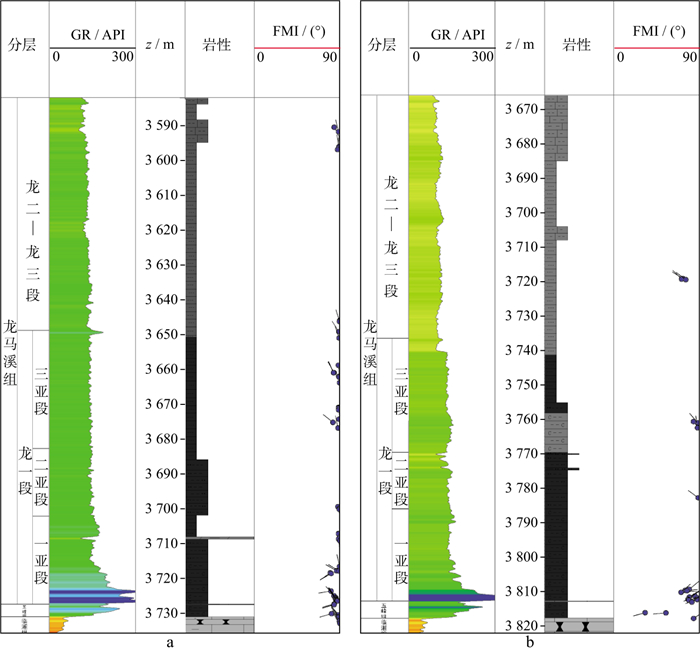
2.2.1 裂缝方位各向异性响应分析通过偏移距向量片(OVT域)单次覆盖地震数据全三维分方位处理, 可充分挖掘宽(全)方位三维地震方位信息和改善成像品质, 为裂缝预测提供丰富的叠前数据信息。单井的岩心裂缝分析结果以及成像测井分析结果均表明, DS地区页岩层内高角度裂缝均较为发育(图 8, 图 9)。抽取了DY4井井旁道OVT域道集, 分析所有方位的五峰组底界反射同相轴的旅行时, 可以看出, 不同的方位存在明显的旅行时差异, 即旅行时各向异性特征(图 10)。
|
图 8 DY4井(a)与DY5井(b)成像测井裂缝发育 |

|
图 9 DY4岩心高角度裂缝发育 |
|
图 10 DY4井区OVT域叠前道集(a)及旅行时随方位变化(b) |
RÜGER[23]研究发现, 纵波的方位各向异性信息可以近似为一个椭圆, 即可以利用最小二乘椭圆拟合法(RÜGER椭圆)或者傅里叶级数展开进行各向异性小尺度裂缝检测。首先求取分方位角的地震同相轴旅行时T与全叠加同相轴旅行时T0的时差, 并将其投影在实际观测三维坐标中, 得到直角坐标系中的x分量与y分量:
| $ \left\{\begin{array}{l} x=\left(T-T_{0}\right) \sin \varphi \\ y=\left(T-T_{0}\right) \cos \varphi \end{array}\right. $ | (7) |
其中, φ是与叠前道集相关的分方位角。
利用坐标旋转原理, 针对方位旅行时间得到的x与y分量进行椭圆拟合, 标准的椭圆方程表示为:
| $ \frac{(x \cos \theta+y \sin \theta)^{2}}{a^{2}}+\frac{(-x \sin \theta+y \cos \theta)^{2}}{b^{2}}=1 $ | (8) |
式中: θ是与裂缝相关的方位角; a, b为确立椭圆的参数。当a>b时, a为椭圆长轴的长度, b为椭圆短轴的长度; 当a=b时, 公式(8)为标准圆, 表明裂缝不发育。
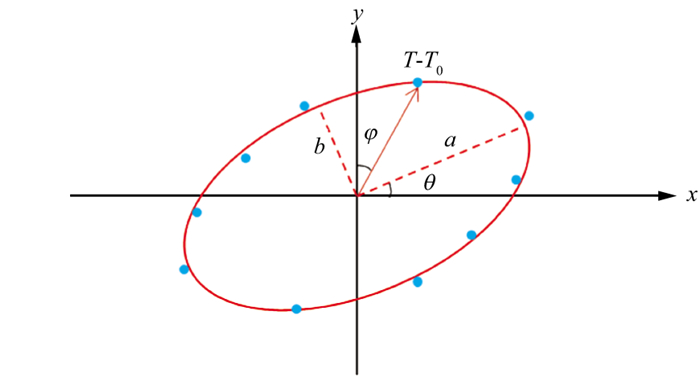
采用最小二乘法求解(8)式, 可以得到椭圆的长、短轴大小以及与裂缝相关的方位角, 椭圆短轴指示裂缝走向, 长短轴之比指示裂缝发育强度(图 11)。
|
图 11 方位旅行时差异椭圆拟合示意 |
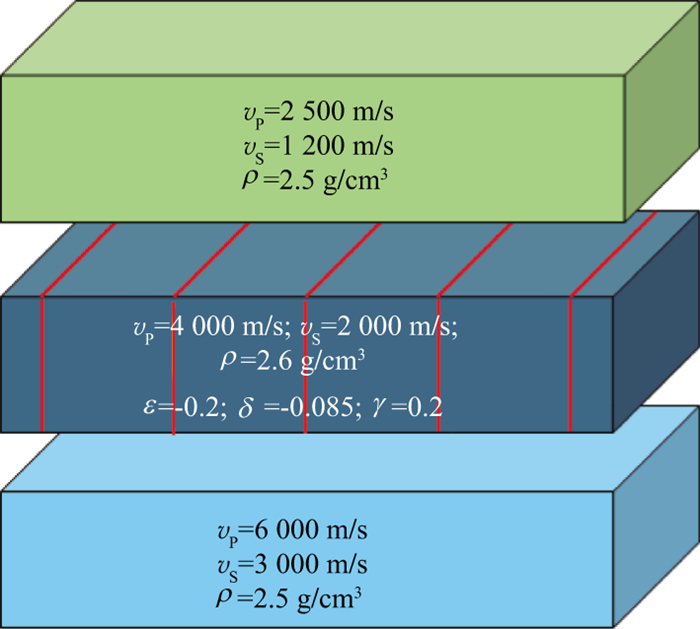
针对该方法采取各向异性正演模拟进行进一步说明。由于HTI介质中的纵波速度随入射角和方位角的变化而变化, 地震同相轴的振幅、旅行时也将随着入射角和方位角的变化而变化, 设计如图 12所示的3层模型开展正演模拟分析。图 12中, 上覆与下伏地层均为各向同性地层, 中间地层为HTI介质, 各地层弹性参数如表 3所示。采用主频35Hz的雷克子波正演的道集如图 13所示, 在入射角相对较大(20°~25°)时, 可以明显看出, 随着方位角的变化, HTI介质地层出现旅行时周期性变化, 据此即可进行裂缝预测。
|
图 12 裂缝介质模型示意 |
| 表 3 裂缝介质模型参数 |

|
图 13 裂缝介质模型正演道集 |
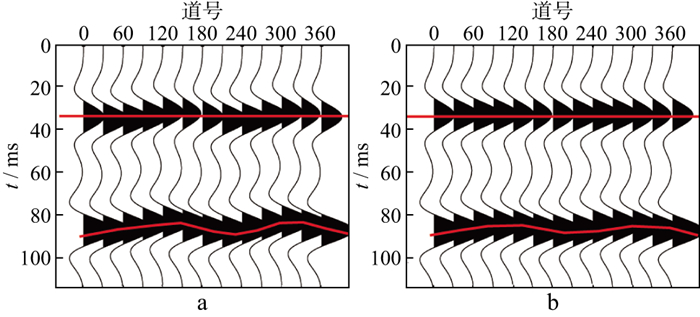
在实际地震预测研究中, 首先需做好OVT域道集预处理, 如未校正目的层上部地层方位旅行时各向异性, 错误地将目的层上部地层的方位旅行时各向异性累积到了目的层, 会影响目的层预测精度。采用的方法是: ①针对目的层顶界面反射波同相轴进行校平处理, 校正后的数据更能真实反映目的层的各向异性特征(图 14); ②针对校平后地震道集数据进行方位角划分与叠加, 获得多个分方位叠加数据, 拾取所述分方位叠加数据的目的层地震同相轴旅行时开展解释, 进而通过椭圆拟合可预测裂缝发育强度和方位。
|
图 14 叠前道集上覆地层各向异性校正前(a)、后(b)对比 |
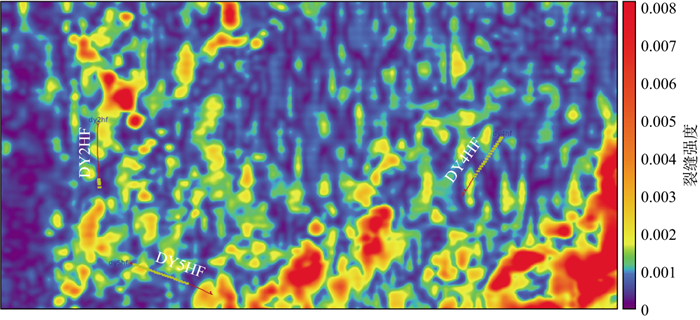
针对五峰组—龙马溪组页岩储层段底界反射开展了椭圆拟合裂缝预测。DY4井、DY5井导眼井处预测的优质页岩段高角度裂缝发育(图 15), 与成像测井解释结果的吻合度较高, 如DY4井深3700~3725m内高角度裂缝发育, DY5井深3800~3825m内高角度裂缝发育。分析预测结果可知, 裂缝的发育程度明显表现出对水平井水力压裂施工有重要影响。DY5HF井各段破裂压力(地面)为93.60~105.73MPa, 大多低于100.00MPa, 平均为98.69MPa; DY4HF井各段破裂压力为97.65~106.47MPa, 大多高于100.00MPa, 平均为103.19MPa。分析后认为, DY5HF井裂缝更为发育, 有效降低了深层页岩破裂压力, 预测结果与工程压裂施工破裂压力相吻合。
|
图 15 DS地区基于方位旅行时差异裂缝强度预测结果的平面展示 |
地应力是决定所生成裂缝的形态、方位以及延伸方向的关键因素, 水平应力差异系数(DHSR)是有效的表征参数[24], 低DHSR值表明其所在区域在水力压裂施工时, 容易被压裂成复杂缝网; 高DHSR值容易被压裂成定向排列的裂缝, 缝网复杂程度较差。马妮等[25]基于地应力的基础理论以及地震各向异性介质地震岩石物理理论, 推导建立了地应力差系数与各种弹性参数、各向异性参数之间的定量关系:
| $ \operatorname{DHSR}=\frac{2 \mu(1+2 \gamma) Z_{\mathrm{N}}}{1+2 \mu(1+2 \gamma) Z_{\mathrm{N}}} $ | (9) |
其中, μ为剪切模量, ZN为裂缝的法向柔度, γ为各向异性参数, 这3个参数均可通过叠前各向异性反演获取。法向柔度(ZN)与法向弱度(ΔN)的关系为:
| $ Z_{\mathrm{N}}=\frac{\varDelta_{\mathrm{N}}}{(\lambda+2 \mu)\left(1-\varDelta_{\mathrm{N}}\right)} $ | (10) |
其中, λ为拉梅参数, μ为剪切模量, ΔN为裂缝的法向弱度。ΔN的表达式为:
| $ \varDelta_{\mathrm{N}}=-\frac{\varepsilon^{(v)}}{2 g(1-g)} $ | (11) |
式中: g为横波速度与纵波速度比的平方; ε(v)为高角度缝各向异性参数, 可以通过叠前各向异性反演获取。
基于方位地震数据的地应力反演方法, 首先要开展方位弹性阻抗反演, 若对不同方位的部分叠加数据分别开展弹性阻抗反演, 则可能导致不同方位的反演结果不具有一致性, 从而造成预测精度降低。对于同一套地层而言, 不同方位、不同入射角的弹性阻抗应具有相同的地层结构, 只是不同方位的弹性阻抗值不同。将同一采样点的不同方位角、不同入射角的反射系数组合, 组内反射系数呈高斯分布, 组与组之间满足修正柯西分布。基于贝叶斯理论框架, 建立组稀疏弹性阻抗反演目标函数(如(12)式), 保证了不同方位弹性阻抗采样点一致性。
| $ \begin{gathered} F(\boldsymbol{m})=(\boldsymbol{G} \boldsymbol{m}-\boldsymbol{d})^{\mathrm{T}} \boldsymbol{X}_{n}^{-1}(\boldsymbol{G} \boldsymbol{m}-\boldsymbol{d})+ \\ \sum\limits_{i=1}^{N} \frac{2\left(\boldsymbol{m}_{g}^{i}\right)^{\mathrm{T}} \boldsymbol{X}_{\boldsymbol{m}_{g}^{i}}^{-1} \boldsymbol{m}_{g}^{i}}{1+\left(\boldsymbol{m}_{g}^{i}\right)^{\mathrm{T}} \boldsymbol{X}_{\boldsymbol{m}_{g}^{i}}^{-1} \boldsymbol{m}_{g}^{i}}+(\boldsymbol{C} \boldsymbol{m}-\boldsymbol{\xi})^{\mathrm{T}} \boldsymbol{\cdot} \\ \boldsymbol{X}_{\boldsymbol{C} \boldsymbol{m}-\boldsymbol{\xi}}^{-1}(\boldsymbol{C} \boldsymbol{m}-\boldsymbol{\xi}) \end{gathered} $ | (12) |
式中: G为正演算子; m为反射系数; d为地震数据; N为采样点数; mgi为同一时间采样点的不同方位、不同入射角的反射系数向量; C为由H×M个(H为方位角个数, M为入射角个数)沿对角线积分算子组成的矩阵; ξ为不同方位、不同入射角相对弹性阻抗组成的列向量。
求解(12)式得到不同方位角、不同入射角的弹性阻抗数据体, 再利用马妮等[25]提出的方法流程, 同时充分考虑测井各向异性岩石物理先验信息, 实现各向异性参数ε(v)的反演, 最后应用(9)式至(11)式, 结合弹性模量的反演, 实现水平地应力差异系数五维地震预测。
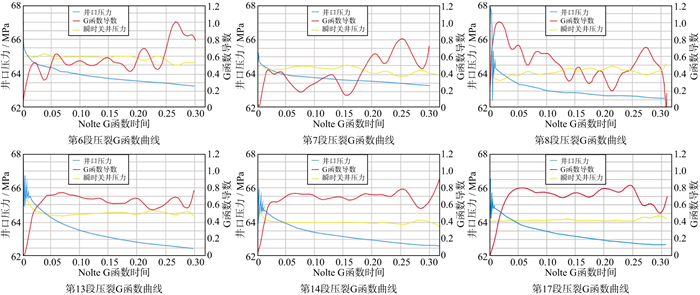
从DY5HF井的DHSR反演预测剖面(图 16)可以明显看出, 在优质泥页岩段具有较低的水平应力差系数, 具备形成缝网的能力。DY5HF井各段压裂G函数显示5~12段压裂裂缝整体复杂程度高(图 17), 形成了复杂网缝, 预测剖面(图 16)中5~12段地应力差系数较低, 与实际压裂效果一致。

|
图 16 DY5HF井的DHSR反演预测剖面 |
|
图 17 DY5HF井压裂施工G函数 |
前文研究结果表明, 脆性指数、裂缝及地应力差是评价本区深层页岩气能否实现体积改造的工程“甜点”, 脆性指数越高, 储层裂缝越发育, 页岩越容易压开, 破裂压力越低; 地应力差越小, 越容易压裂形成复杂缝网, 增加改造体积。我们在此基础上, 利用多属性融合技术, 实现了工程“甜点”的综合预测(图 18), 具体工程甜点预测及评价流程如图 19所示。

|
图 18 DS地区工程“甜点”综合预测 |

|
图 19 工程“甜点”预测及评价流程 |
图 18中, DY4井和DY5井基本处于工程“甜点”区, 基本实现了较好的压裂改造, 测试获工业气流; 从图 18中还可以看出, DY2井区脆性指数高于45%, 储层裂缝更为发育, 地应力差小, 同样为工程“甜点”区, 由于DY2井未实施大规模压裂改造, 所以未获得高产, 评价认为该井区应该是DS地区深层页岩气勘探的有利目标区, 如进一步实施钻探, 有望获得新突破。
4 结论本文以DS地区为例, 分析了深层页岩气工程“甜点”的敏感地球物理参数, 建立了针对性的地震预测模型, 利用OVT域叠前地震资料开展高精度叠前弹性参数反演, 形成了地震预测技术。首先, 结合岩石力学实验, 发现了泊松比对围压变化敏感, 基于此构建了塑延性转换敏感因子及脆性指数地震预测新模型; 其次, 通过各向异性研究, 发现页岩具有明显HTI介质旅行时方位各向异性特征, 通过分方位地震旅行时解释及校正, 利用椭圆拟合技术, 形成了一种有效的裂缝地震预测新技术; 第三, 基于贝叶斯理论推导建立了组稀疏方位弹性阻抗同时反演方法, 保证了不同方位弹性阻抗采样点一致性, 实现了各向异性参数及水平地应力差异系数的预测。
预测结果表明, 脆性指数越高储层裂缝越发育, 页岩越容易压开, 破裂压力越低; 地应力差越小, 越容易压裂形成复杂缝网, 增加改造体积。形成的地震预测技术可有效支撑深层页岩气的勘探部署及评价, 具有较好的推广应用价值。
| [1] |
郭旭升. 南方海相页岩气"二元富集"规律——四川盆地及周缘龙马溪组页岩气勘探实践认识[J]. 地质学报, 2014, 88(7): 1209-1218. GUO X S. Rules of two-factor enrichiment for marine shale gas in Southern China-Understanding from the Longmaxi formation shale gas in Sichuan basin and its surrounding area[J]. Acta Geologica Sinica, 2014, 88(7): 1209-1218. |
| [2] |
陈祖庆, 杨鸿飞, 王静波, 等. 页岩气高精度三维地震勘探技术的应用与探讨——以四川盆地焦石坝大型页岩气田勘探实践为例[J]. 天然气工业, 2016, 36(2): 9-20. CHEN Z Q, YANG H F, WANG J B, et al. Application o f 3D high-preci sion seismic technology to shale gas exploration: A case study of the large Jiaoshiba shale gas field in the Sichuan Basin[J]. Natural Gas Industry, 2016, 36(2): 9-20. |
| [3] |
陈超, 刘韵, 王明飞, 等. 焦石坝地区泥页岩有机碳含量预测技术及对比[J]. 成都理工大学学报(自然科学版), 2016, 43(1): 50-58. CHEN C, LIU Y, WANG M F, et al. Research on shale TOC content prediction techniques and contrast in Jiaoshiba area, Sichuan Basin, China[J]. Journal of Chengdu University of Technology(Science&Technology Edition), 2016, 43(1): 50-58. DOI:10.3969/j.issn.1671-9727.2016.01.05 |
| [4] |
陈祖庆, 郭旭升, 李文成, 等. 基于多元回归的页岩脆性指数预测方法研究[J]. 天然气地球科学, 2016, 27(3): 461-469. CHEN Z Q, GUO X S, LI W C, et al. Study on shale brittleness index prediction based on multivariate regression method[J]. Natural Gas Geoscience, 2016, 27(3): 461-469. |
| [5] |
李金磊. 涪陵焦石坝页岩气层压力预测技术研究[J]. 石油物探, 2017, 56(4): 567-574. LI J L. Pressure prediction of Jiaoshiba shale gas reservoir in the Fuling shale gasfield[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 567-574. DOI:10.3969/j.issn.1000-1441.2017.04.013 |
| [6] |
陈超, 屈大鹏, 王明飞, 等. 川东南焦石坝地区海相泥页岩含气量预测方法探讨[J]. 石油物探, 2016, 55(4): 597-605. CHEN C, QU D P, WANG M F, et al. Prediction method of gas content in marine mud shale at JSB area in south- east Sichuan Basin[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 597-605. DOI:10.3969/j.issn.1000-1441.2016.04.015 |
| [7] |
AMERICAN ASSOCIATION OF PETROLEUM GEOLOGISTS, ENERGY MINERALS DIVISION. Unconventional energy resources: 2017 review[J]. Natural Resources Research, 2018, 28(4): 1661-1751. |
| [8] |
GENTZIS T. A review of the thermal maturity and hydrocarbon potential of the Mancos and Lewis shales in parts of New Mexico, USA[J]. International Journal of Coal Geology, 2013, 113: 64-75. DOI:10.1016/j.coal.2012.09.006 |
| [9] |
郭旭升, 胡东风, 黄仁春, 等. 四川盆地深层—超深层天然气勘探进展与展望[J]. 天然气工业, 2020, 40(5): 1-14. GUO X S, HU D F, HUANG R C, et al. Deep and ultra-deep natural gas exploration in the Sichuan Basin: Progress and prospect[J]. Natural Gas industry, 2020, 40(5): 1-14. |
| [10] |
何治亮, 聂海宽, 胡东风, 等. 深层页岩气有效开发中的地质问题——以四川盆地及其周缘五峰组—龙马溪组为例[J]. 石油学报, 2020, 41(4): 379-391. HE Z L, NIE H K, HU D F, et al. Geological problems in the effective development of deep shale gas: A case study of Upper Ordovician Wufeng- Lower Silurian Longmaxi formations in Sichuan Basin and its periphery[J]. Acta Petrolei Sinica, 2020, 41(4): 379-391. |
| [11] |
陈胜, 赵文智, 欧阳永林, 等. 利用地球物理综合预测方法识别页岩气储层甜点——以四川盆地长宁区块下志留统龙马溪组为例[J]. 天然气工业, 2017, 37(5): 20-30. CHEN S, ZHAO W Z, OUYANG Y L, et al. Comprehensive prediction of shale gas sweet spots based on geophysical properties: A case study of the Lower Silurian Longmaxi Fm in Changning block, Sichuan Basin[J]. Natural Gas industry, 2017, 37(5): 20-30. |
| [12] |
李曙光, 徐天吉, 吕其彪, 等. 深层页岩气双"甜点"参数地震预测技术[J]. 天然气工业, 2019, 39(增刊1): 113-117. LI S G, XU T J, LV Q B, et al. Seismic prediction technology of deep shale gas with double "sweet spot" parameters[J]. Natural Gas industry, 2019, 39(S1): 113-117. |
| [13] |
廖东良, 路保平. 页岩气工程甜点评价方法——以四川盆地焦石坝页岩气田为例[J]. 天然气工业, 2018, 38(2): 43-50. LIAO D L, LU B P. An evaluation method of engineering sweet spots of shale gas reservoir development: A case study from the Jiaoshiba Gas Field, Sichuan Basin[J]. Natural Gas Industury, 2018, 38(2): 43-50. |
| [14] |
黄仁春, 魏祥峰, 王强. 四川盆地东南缘DS地区页岩气成藏富集的关键控制因素[J]. 海相油气地质, 2017, 22(2): 25-30. HUANG R C, WEI X F, WANG Q. Key factors of shale gas accumulation in dingshan area of southeastern Sichuan Basin[J]. Marine Origin Petroleum Geology, 2017, 22(2): 25-30. DOI:10.3969/j.issn.1672-9854.2017.02.004 |
| [15] |
魏祥峰, 赵正宝, 王庆波, 等. 川东南綦江丁山地区上奥陶统五峰组—下志留统龙马溪组页岩气地质条件综合评价[J]. 地质论评, 2017, 63(1): 153-164. WEI X F, ZHAO Z B, LIU Z J, et al. Comprehensive evaluation on geological conditions of the shale gas in Upper Ordovician Wufeng Formation—Lower Silurian Longmaxi Formation in Dingshan Area, Qijiang, Southeastern Sichuan[J]. Geological Review, 2017, 63(1): 153-164. |
| [16] |
YIN X Y, LIU X J, ZONG Z Y. Pre-stack basis pursuit seismic inversion for brittleness of shale[J]. Petroleum Science, 2015, 13(4): 618-627. |
| [17] |
侯振坤, 杨春和, 魏翔, 等. 龙马溪组页岩脆性特征试验研究[J]. 煤炭学报, 2016, 41(5): 1188-1196. HOU Z K, YANG C H, WEI X, et al. Experimental study on the brittle characteristics of Longmaxi formation shale[J]. Journal of China Coal Society, 2016, 41(5): 1188-1196. |
| [18] |
RICKMAN R, MULLEN M J, PETRE J E, et al. A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett shale[J]. SPE Technical Conference and Exhibition, 2008, 2008: 115258. |
| [19] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Z Y, YIN X Y, ZHANG F, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 |
| [20] |
AL-MARZONG A M, NEVES F A, KIM J J, et al. P-wave anisotropy from azimuthal velocity and AVO using wide-azimuthal 3D seismic data[J]. Geophysics, 2006, 71(2): E7-E11. DOI:10.1190/1.2187724 |
| [21] |
曲寿利, 季玉新, 王鑫, 等. 全方位P波属性裂缝检测方法[J]. 石油地球物理勘探, 2001, 36(4): 390-397. QU S L, JI Y X, WANG X. Seis mic method for using full azimuth P wave attribution to deteet fracture[J]. Oil Geophysical Prospecting, 2001, 36(4): 390-397. DOI:10.3321/j.issn:1000-7210.2001.04.002 |
| [22] |
PAN X P, ZHANG G Z, YIN X Y, et al. Azimuthally anisotropic elastic impedance inversion for fluid indicator driven by rock physics[J]. Geophysics, 2017, 82(6): C211-C227. DOI:10.1190/geo2017-0191.1 |
| [23] |
RÜGER A. Reflection coefficients and azimuthal AVO analysis in anisotropic media[D]. Colorado: Colorado School of Mines, 1996
|
| [24] |
GRAY D, ANDERSON P, LOGEL J, et al. Estimation of stress and geomechanical properties using 3D seismic data[J]. First Break, 2012, 30(1): 59-68. |
| [25] |
马妮, 印兴耀, 孙成禹, 等. 基于方位地震数据的地应力反演方法[J]. 地球物理学报, 2018, 61(2): 697-706. MA N, YIN X Y, SUN C Y. Inversion for crustal stress based on azimuthal seismic data[J]. Chinese Journal of Geophysics, 2018, 61(2): 697-706. |



