2. 北京华晖探测科技股份有限公司, 北京 101300
2. Beijing Huahui Test Technology Co.Ltd, Beijing 101300, China
采用瞬变电磁勘探测量瞬态响应波形, 在裸眼井中激发和测量时, 瞬态波形幅度较大; 而在套管井中测量时, 瞬态波形幅度较小, 且波形形状与在裸眼井测量时存在很大差异[1-2]。我们在套管井的套管节箍处发现了套管井的几何因子, 在裸眼井的响应中用相减方法去掉了直接耦合响应[3]。借助于Doll电流环模型得到了井间瞬变电磁涡流激发响应的全空间几何因子, 并进行模型实验, 测量得到不同空间位置的瞬变响应波形[4]。井中空间小, 在其中进行瞬变电磁激发时, 其主要能量均进入了地层。本文进一步研究了在井底用线圈激发, 对超过井底深度的深部地层进行电导率精细勘探的方法。该方法在井底激发, 其瞬变电磁主要能量呈径向偶极子方式沿径向扩散传播并逐渐向上、下扩散, 一部分能量进入深部地层, 一部分能量进入已经钻开的地层。在井底用上、下放置的电极或电偶极子发射时, 主要能量呈纵向偶极子分布的方式沿井轴方向扩散, 即一部分能量沿井轴向深处扩散, 一部分能量沿井轴向浅处扩散[5-8]。由于已钻孔的地层电导率已知, 借助于测井曲线去掉浅层的响应便可获得深部地层的电导率分布。在井底同时移动发射和接收探头进行测量便可直接去除直接耦合响应, 获得深部地层的电导率的分布差异。
在井中、井底激发的瞬变电磁响应与地面激发的瞬变电磁响应有很大区别。因为没有地面激发产生的半无限大空气介质中的瞬变电磁场和地面边界的影响, 井中、井底激发的瞬变电磁响应是全空间的解[9-12]。井中、井底激发的发射和接收探头均直接深入到地层内部, 距离被测的深部地层很近, 不受上部地层影响和地面干扰, 可直接对深部地层的电导率进行测量, 分辨率高, 我们称其为精细勘探方法。
本文在井内激发的瞬变电磁测井响应的基础上, 对井中激发、接收的瞬变电磁深层精细勘探方法需要解决的几个最基本问题: 响应波形的组成、响应波形中直接耦合响应与涡流再次激发响应的耦合方式; 如何去除响应波形中幅度占比很大的直接耦合响应, 突出地层涡流再次激发响应等问题进行了讨论和分析; 借助于电磁感应原理, 设计了去掉直接耦合响应的方法并提出了跨越浅部地层对深层电导率进行精细探测的方法。
1 线圈激发的直接耦合响应线圈作为激发源时, DOLL[2]将地层视为一个个导电的圆环, 与发射线圈同轴。利用空气中线圈激发的交变(正弦激励eiωt)磁场分布计算穿过圆环的磁通量, 获得了单频时导电圆环中的感应电动势[13](产生涡流)和同轴接收线圈的直接耦合感应电动势, 将直接耦合响应乘以正弦激励eiωt后对频率积分(对频谱做Fourier逆变换)得到瞬变电磁响应Vx[1], 该响应与地层电导率σ无关, 幅度大, 占据瞬变电磁响应的主要部分。
| $ {V_x} = \int\limits_{ - \infty }^\infty {\frac{{ - {\rm{i}}\omega \mu }}{{2{\rm{ \mathit{ π} }}{L^2}}}} {{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega $ | (1) |
式中:
DOLL[2]还进一步计算了导电圆环中的单频涡流再次在接收线圈上激发的感应电动势, 将其乘以正弦激励eiωt后对频率积分(对频谱做Fourier逆变换)得到瞬变电磁响应中涡流再次激发响应VR:
| $ {V_R} = - \int\limits_{ - \infty }^\infty {\frac{{{\omega ^2}{\mu ^2}}}{{4{\rm{ \mathit{ π} }}L}}} {{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega \int\limits_0^\infty {\int\limits_{ - \infty }^\infty \sigma } \frac{L}{2}\frac{{{r^2}}}{{\rho _T^3\rho _R^3}}{\rm{d}}r{\rm{d}}z $ | (2) |
式中: r是地层导电环的半径; z是柱坐标系中地层导电环的z坐标; ρT是发射线圈中心到地层导电环任意一点的距离,
由(2)式可见, 由于涡流携带了地层电导率σ, 涡流再次激发响应也携带了地层电导率σ, (2)式最右侧的二重积分描述了空间中各地层环电导率对响应贡献的权重。VR与涡流对时间的导数成正比, 因此, 涡流再次激发响应的相位与直接耦合响应的相位相差π/2, 在频率域中涡流再次激发响应是实部, 而直接耦合响应是虚部, 合在一起做Fourier逆变换后得到总的瞬变电磁响应波形。
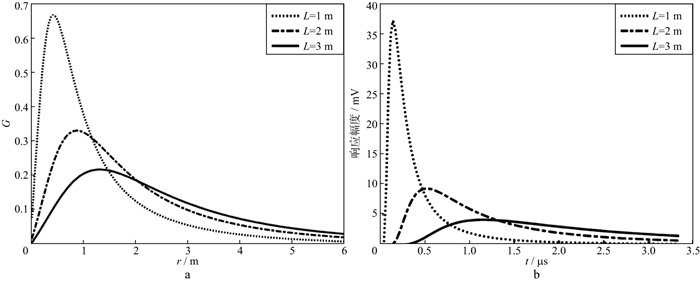
由(1)式可知, 直接耦合响应只与源距L有关, 而涡流再次激发响应不但与地层电导率有关, 还与地层导电环所在的位置(r, z)有关, 即每个地层导电环都对涡流再次激发响应有贡献, 计算时需要对全空间积分。瞬变电磁响应包括所有地层电导率的贡献。图 1a为不同源距接收情况下的Doll径向微分几何因子G的变化曲线, 曲线极大值位置代表涡流再次激发响应径向贡献最大的空间区域。在不同的源距接收, 其径向最大贡献的空间区域不同。全空间的瞬变电磁响应波形是先快速上升、达到极值后再慢速下降。源距不同, 响应波形形状变化大。图 1b是3个源距的响应波形, 其形状与径向微分几何因子具有相似性——上升快、达到极值后下降慢, 两者具有内在的联系。不同的源距或空间位置对应的响应波形快速上升的时刻不一样, 见图 1b中3个不同源距响应波形的上升沿。该上升沿的瞬变电磁响应变化快, 涡流再次激发的响应幅度大。
|
图 1 不同源距下的Doll径向微分几何因子G(a)和其在电导率为1 S/m时的响应波形(b) |
将(1)式和(2)式的绝对值相除得到VR与Vx的比值ωμL。取磁导率为空气磁导率μ=4π×10-7 H/m, 瞬变电磁激发的主要频率小于100 Hz, 取f=100 Hz, 此时VR与Vx的幅度比约为10-3, 两者相差1 000倍, 瞬变电磁响应幅度主要由Vx决定。
将(1)式和(2)式相加得到总响应:
| $ \begin{array}{c} V = {V_R} + {V_x} = \int\limits_{ - \infty }^\infty {\left( {\frac{{{\omega ^2}{\mu ^2}}}{{4{\rm{ \mathit{ π} }}L}}\int\limits_0^\infty {\int\limits_{ - \infty }^\infty \sigma } \frac{L}{2}\frac{{{r^2}}}{{\rho _T^3\rho _R^3}}{\rm{d}}r{\rm{d}}z + } \right.} \\ \left. {\frac{{ - {\rm{i}}\omega \mu }}{{2{\rm{ \mathit{ π} }}{L^2}}}} \right){{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega \end{array} $ | (3) |
其中, VR为总响应实部, Vx为总响应虚部, 两者在相位上相差π/2。所有频率的响应相加后得到瞬变电磁响应波形, 该波形形状主要由Vx决定。VR的作用是移动单个频率响应的相位, 使得相加后的整个波形在每个时刻的相位都有不同的移动。移动量与地层电导率成正比, 以此反映不同深度地层电导率对响应波形的影响。某一深度的地层电导率不同, 对所有频率都产生相位移动, 积分以后对应某个时刻的幅度值会因相位的移动而存在较大的差异。
如果考虑地层环之间的相互作用, 则采用改进型Gianzero几何因子: (L/2)(r2/ρT3ρR3)(1-iγρT)eiγρT, 其中γ= iμωσ是地层的复波数, 该几何因子只考虑了从发射探头到地层环瞬变电磁扩散的时间。地层环涡流在接收线圈上再次激发响应的时间以涡流的速度传播, 比瞬变电磁的扩散速度快得多, 所用的时间很短, 可以被忽略。
2 线圈激发的瞬变电磁响应耦合方式基于Doll地层模型得到的响应是一阶近似响应, 线圈在无限大均匀介质中激发的单频响应V的解析表达式[1]为:
| $ V = - \frac{{{\rm{i}}\omega \mu {n_R}{S_0}M}}{{4{\rm{ \mathit{ π} }}{\rho ^3}}}{{\rm{e}}^{ - {\rm{i}}{\gamma _\rho }}}(1 + {\rm{i}}\gamma \rho ) $ | (4) |
对于瞬变电磁响应, 忽略位移电流, γ=(1-i)/δ是地层的复波数,
| $ V=V_{m} \mathrm{e}^{-P-\mathrm{i} P}(1+P+\mathrm{i} P) $ | (5) |
其中, Vm=(iωμnRS0m)/(4πL3), P=L/δ是源距L与集肤深度δ的比值。对源距以集肤深度为标准归一化, 将(5)式展开为级数并按照实部和虚部分开得到[1]:
| $ V_{R}=-\mathrm{i} V_{m}\left(P^{2}-\frac{2}{3} P^{3}-\frac{2}{15} P^{5}-\cdots\right) $ | (6) |
| $ V_{x}=V_{m}\left(1-\frac{2}{3} P^{3}+\frac{1}{2} P^{4}-\frac{1}{15} P^{5}+\cdots\right) $ | (7) |
对于瞬变电磁井中勘探, P通常很小(当f=1 Hz, σ=1 S/m, L=1 m时, P=0.002), 因此, 可以忽略高阶无穷小, 用级数的最低阶近似, 获得瞬变电磁响应的理论描述。(6)式的第一项-iVmP2是(2)式中σ为常数、几何因子对整个空间积分为1后剩下的被积函数, 即无限大均匀地层的涡流再次激发的响应, 亦即(2)式中的被积函数是(6)式所示精确解的最低阶近似。同样, (1)式的被积函数是直接耦合响应, 是(7)式的第一项, 也是精确解的最低阶近似。精确解描述了瞬变电磁勘探的直接耦合响应和涡流再次激发响应以及两者之间的耦合方式。(1)式、(2)式描述了响应的一阶近似及其耦合关系。
瞬变电磁响应也需要对(6)式、(7)式进行Fourier逆变换, 即类似于(1)式的积分, 得到的波形形状主要由Vx(幅度很大)决定; 涡流再次激发响应VR很小, 能够改变响应波形的相位(延迟), 使波形形状产生微小变化。地层电导率不同相位移动不同。最终使得每一时刻的响应幅度因地层电导率引起的相位移动而产生变化, 该变化直接反映了地层电导率。有用信号在波形中所占据的比例很小, 是小信号测量。
3 电极激发的瞬变电磁响应耦合方式对于电极激发源, 其响应可以用点电极源响应的积分获得。点电极源在空间各点激发的响应等势面是球面, 其单频激发响应可用推迟势描述[1](格林函数):
| $ \begin{aligned} V^{\prime} &=V_{m}^{\prime} \mathrm{e}^{-P-\mathrm{i} P}=V_{m}^{\prime} \mathrm{e}^{-P}(\cos P-\mathrm{i} \sin P) \\ &=V_{R}^{\prime}+V_{x}^{\prime} \end{aligned} $ | (8) |
其中, V′ m是激发的瞬变电磁强度, 与激发电路、点电极周围介质的电导率有关, 在0频率(直流)时:
| $ V_m^\prime = \frac{{{I_0}}}{{4{\rm{ \mathit{ π} }}{L_\sigma }}} $ | (9a) |
| $ \begin{array}{l} V_{x}^{\prime}=V_{m}^{\prime} \mathrm{e}^{-P} \cos P=V_{m}^{\prime}\left(1-P+\frac{P^{2}}{2}-\frac{P^{3}}{3}+\cdots\right) \cdot \\ \ \ \ \ \ \ \ \ \ \ \ \left(1-\frac{P^{2}}{2 !}+\frac{P^{4}}{4 !}-\frac{P^{6}}{6 !}+\cdots\right)= \\ \ \ \ \ \ \ \ \ \ \ \ V_{m}^{\prime}\left(1-P-\frac{P^{3}}{3 !}+\cdots\right) \end{array} $ | (9b) |
| $ \begin{array}{l} V_{R}^{\prime}=\mathrm{i} V_{m}^{\prime} \mathrm{e}^{-P} \sin P=V_{m}^{\prime}\left(1-P+\frac{P^{2}}{2}-\frac{P^{3}}{3}+\cdots\right) \cdot \\ \ \ \ \ \ \ \ \ \ \ \ \left(P-\frac{P^{3}}{3 !}+\frac{P^{5}}{5 !}-\frac{P^{7}}{7 !}+\cdots\right)= \\ \ \ \ \ \ \ \ \ \ \ \ \mathrm{i} V_{m}^{\prime}\left(P-P^{2}+\frac{P^{3}}{3}+\cdots\right) \end{array} $ | (10) |
其中, I0是正弦激发电流的幅度。从(9)式可以看到: 电极激发的单频响应中也有幅度相当大的直接耦合响应V′ m, 它与地层电导率成反比例关系, 在级数展开式中表现为实部。
(10) 式为电极激发的单频响应中地层涡流再次激发响应V′ R, 是级数展开式的虚部。忽略高阶项后, 虚部响应与地层电导率的开平方成反比关系: V′ R=iV′ m(P)∝1/
综上所述, 在瞬变电磁场中无论用何种激发源激发, 其总响应都可分解为实部和虚部的级数展开式。称级数展开式的实部为瞬变电磁响应中的直接耦合响应, 占据了响应主要部分, 级数展开式的虚部为涡流再次激发响应, 幅值较小以相位移动的方式存在于该响应中。在最低阶近似的情况下, 线圈激发的瞬变电磁响应中实部与地层电导率无关, 虚部与地层电导率成正比; 电极激发的瞬变电磁响应中实部和虚部都与地层电导率相关, 实部与地层电导率成反比, 虚部与地层电导率开平方成反比。
4 瞬变电磁响应以上两节讨论的是单频激发的电磁场响应。瞬变电磁响应是个瞬态波形, 具有连续的频谱, 是激发源频谱范围内(一个连续频率段)每个频率成分响应(遵循单频响应)的叠加。不同激发电路所激发出的主频不同, 频率范围(带宽)也不一样, 激发波形形状有差异。每个频率成分从激发源出发, 在地层中经过既衰减又相移的传播过程后构成其单频响应。频率不同, 衰减、相移不同, 所有频率的响应在接收探头处叠加后形成瞬变电磁响应波形。单频响应的衰减和相移量与源距和频率有关。频率越高, 衰减和相移越大; 源距越长, 衰减和相移越大。在不同的接收位置, 这些经过衰减与相移的频率成分叠加, 出现不同的幅度和相位差异, 有些频率成分相位相同, 叠加以后幅度增加, 有些频率成分相位相反, 叠加以后幅度减小, 不同的频率f和观测点到源点距离ρ形成不同的叠加方式, 最终导致不同的响应波形形状V(t), 对于线圈激发源有:
| $ V(t) = - \frac{r}{{2{\rho ^3}}}\int\limits_{{f_0}}^{{f_e}} S (\omega ){\rm{i}}\omega {{\rm{e}}^{{\rm{i}}\left( {{\gamma _\rho } - \omega t} \right)}}\left( {1 + {\rm{i}}{\gamma _\rho }} \right){\rm{d}}f $ | (11) |
观测点设在接收线圈时, 将γ=(1-i)δ, ρ=L代入(11)式得到:
| $ V(t) = {V_m}\int\limits_{{f_0}}^{{f_e}} S (\omega ){{\rm{e}}^{ - P - {\rm{i}}P + {\rm{i}}2{\rm{ \mathit{ π} }}ft}}(1 + P + {\rm{i}}P){\rm{d}}f $ | (12) |
式中: f是频率; 角频率ω=2πf; S(ω)为激发电路响应的激发频谱; f0, fe分别是激发源频谱中的起始频率和终止频率; Vm是与频率无关的仪器常数, 由发射、接收探头的参数确定。响应波形是激发波形经过幅度衰减和相位移动后再叠加的结果: 被积函数中e-P· |1+P+iP|描述每个频率成分的幅度经过距离L传播到达接收探头后的衰减因子; e-iP+iφ描述每个频率成分在此过程中的相位移动, 其中φ是复数(1+P+iP)的相位。
当L较小时, 各个频率的幅度衰减较小, 相位移动较少。叠加以后与原始激发波形形状接近。当源距较大时, 衰减较多, 剩下的高频成分幅度小, 相位移动也较大, 叠加后所得到的波形变化慢, 以低频成分为主。
相移导致响应波形的到达时间出现延迟tf=(-P+φ)/(2πf), 这个延迟随频率改变而改变。当源距固定时, 每个频率成分都有(不同的)延迟。所有这些经过延迟和衰减后的响应加在一起构成了响应波形。其形状与激发波形不再一样并出现明显的延迟和拖尾。频率越低, 延迟越大, 衰减越小; 源距越大, 延迟越多, 衰减越多, 响应波形的起始点、峰值、上升沿等向后移动越明显。相移还与地层的电导率相关, 因此, 波形中的延迟也与地层电导率相关。
对于裸眼井或者无限大均匀介质而言, 其响应的起始位置、上升沿和峰值出现的时间与源距L有关。L确定时, 空间中距离激发源为L的等相位面上各位置的响应波形相同。在点电极激发时等相位和等幅度面为球面, 在线圈激发时为径向偶极子形状。
在接收波形中叠加的涡流激发响应随激发源变化而变化。在电极激发时, 源距为L的响应波形中上升沿位置所接收到的涡流激发响应由接收点所在球面(以发射源为球心, 半径为L)的所有地层电导率贡献(根据接收点与球面之间的空间距离不同对应于不同的因子)。而在线圈激发时, 以发射线圈所在位置为中心, 等势面是径向偶极子形状。源距为L时的响应波形中上升沿位置所接收到的涡流激发响应由接收线圈所在球面的所有地层电导率贡献, 其它位置的因子较小。与该接收波形形状相同的空间各点构成等相位面, 其电导率产生相同的涡流, 都能够再次激发出响应。在不同位置、不同方向用线圈接收, 可以获得不同方向的磁场, 地层中的各点电导率对其响应的贡献与距离和方向有关, 差异很大[14]。
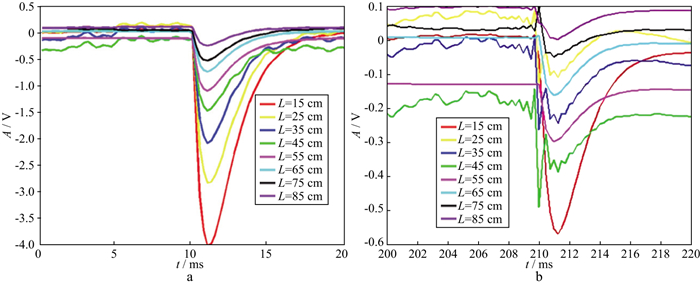
在裸眼井内接收到的响应波形与套管井内接收到的响应波形存在差异。图 2a和图 2b分别为裸眼井与套管井中8个不同源距的线圈在导通时刻所接收到的响应波形, 可以看出, 裸眼井与套管井中响应波形的响应幅度(A)均随源距的增加而减小[3]。井内接收到的响应波形经过了井和地层(裸眼井时)或套管与地层(套管井时)的衰减和相移。在套管井内接收时, 由于套管的电导率高, 响应波形经过套管衰减和相移后, 与裸眼井响应波形相比幅度衰减大、延迟时间长, 响应幅度随源距衰减很快, 只有在近源距才能接收到幅度较大的波形, 其上升沿主要测量发射与接收线圈之间地层的电导率, 波形中的后续波主要反映深部地层的电导率[3]。
|
图 2 不同源距的发射、接收空心线圈在裸眼井(a)与套管井(b)中响应波形 |
源距固定的发射、接收线圈系在井中不同深度位置处测量。直接耦合响应与地层电导率无关, 在源距固定时是确定不变的。涡流再次激发响应受不同深度地层电导率的影响。这两种响应相互耦合组成瞬变电磁总响应, 耦合方式在频谱中表现为实部与虚部的叠加。井中不同深度测量的响应波形频谱相减后, 响应的实部(直接耦合响应)被消除, 剩下响应虚部的差(不同深度地层的涡流再次激发响应差)与不同深度的地层电导率直接相关。
5.1 单频瞬变电磁响应差与电导率的关系依据Fourier变换, 实际测量波形是各个频率响应的叠加, 每个频率成分均对应一个正弦或者余弦波形。瞬变电磁响应实际上是对这些正弦波形的幅度进行衰减, 相位进行移动后得到的波形的叠加。其中, 直接耦合响应的幅度很大, 与电导率有关的地层涡流再次激发响应(导致的相移)幅度很小。对叠加前的单个频率的响应波形进行研究, 以大幅度响应为基准(频谱的实部), 地层电导率的影响(频谱的虚部)表现为: 仅仅引起了很小的相移。在此假设下, 两个不同地层电导率的时域响应波形相减可以简化为: 单个相同频率成分、不同初始相位的三角函数相减, 取其幅度为1。则有:
| $ \begin{array}{c} V_{1}-V_{2}=\cos (\omega t+\beta)-\cos (\omega t)=2 \sin (\omega t+\\ \beta) \sin \beta \approx-2 \beta \sin (2 \omega t+\beta) \end{array} $ | (13) |
其中, β是两个不同地层电导率在响应中引起的相位差, 其值很小, 可用
利用上述结果可以实现瞬变电磁跨越地层测量, 即穿越发射、接收线圈周围的地层, 对外部地层进行探测。在套管井内激发、接收波形可以测量套管外地层的电导率。在井底发射、接收可以穿越井底以下的地层测量深部地层的电导率及其分布。
瞬变电磁能量被激发后, 在地层中边衰减边相移向外扩展传播。频率越低, 衰减越少, 传播的距离越远。传播过程中, 近源距接收到的波形上升快达到峰值以后慢速下降并一直有幅度缓慢地变化。波形中快速上升部分主要测量近源距周围地层的电导率, 缓慢下降部分测量深部地层的电导率。
5.2 瞬变电磁场扩散过程中地层电导率计算方法瞬变电磁能量在地层中扩散传播时, 不同的频率衰减的幅度不一致。频率高的成分衰减多, 频率低的衰减少, 叠加后衰减少的低频成分一直保留在响应波形中。这些低频成分集肤深度大、向外扩展距离远, 随着时间的推移到了深部地层, 此刻其响应包含了瞬变电磁能量所达到的深部地层的电导率信息。低频成分响应包含的深部地层信息以后续波的形式存在于不同源距所测量的波形中。因此, 不论哪个源距接收到的波形, 其后续波均携带了深部地层的电导率信息, 而且时间越晚, 携带的地层电导率的深度越深。
在套管井中进行(激发、接收)测量时, 由于套管的电导率很高, 衰减很强。在瞬变电磁激发初期, 电磁场中的高频成分以电磁波速度传播, 迅速在套管中分布, 在套管的金属内部, 电场强度和磁场强度主要沿着套管的切向方向(圆周、z方向)分布, 通过外边界耦合到地层, 在地层中只有沿套管外壁附近有很小的响应。随着时间的增加, 瞬变电磁场的主要能量在套管内液体和套管金属固体内聚集并沿径向扩散、传播冲出套管外壁进入地层, 在地层中形成椭球形的等势面。设t1时刻瞬变电磁场传播到距激发线圈r1位置处形成等势面, 则与激发线圈距离为L的接收线圈其涡流再次激发响应V(t1)可表示为:
| $ V\left(t_{1}\right)=\sigma_{1} \frac{\partial V\left(t_{1}, r_{1}\right)}{\partial t} \int_{0}^{r_{1}} w_{1}(r) \mathrm{d} r $ | (14) |
式中: σ1代表r1位置等势面的地层电导率; 积分部分∫0r1w1(r)dr是等势面上的几何因子积分以后的w1(r)再次沿径向叠加的结果, 与等势面的形状有关; 微分部分∂V(t1, r1)/∂t刻画了等势面上涡流的变化。对于单个源距而言, 源距L包含在参数w1中。
当时间增加到t2时, 瞬变电磁场传播到r2等势面处, 此时涡流再次激发响应V(t2)由上个时刻t1等势面的涡流再次激发响应与t1到t2时刻所扩展的等势面产生的涡流再次激发响应组成((15)式)。其中w2为t1到t2时刻等势面从r1扩展到r2所扩展区域的几何因子积分组成。由此可得到瞬变电磁场在扩散传播过程中任一时刻tn的涡流再次激发响应V(tn)((16)式), 代入各等势面的几何因子积分wi(r)后便可递推得到各个等势面上的地层电导率σn((17)式)。
| $ \begin{aligned} V\left(t_{2}\right)=\sigma_{1} & \frac{\partial V\left(t_{2}, r_{1}\right)}{\partial t} \int_{0}^{r_{1}} w_{1}(r) \mathrm{d} r+\sigma_{2} \frac{\partial V\left(t_{2}, r_{2}\right)}{\partial t} \cdot\\ & \int_{r_{1}}^{r_{2}} w_{2}(r) \mathrm{d} r \end{aligned} $ | (15) |
| $ V\left(t_{n}\right)=\sum\limits_{i=1}^{n} \sigma_{i} \frac{\partial V\left(t_{i}, r_{i}\right)}{\partial t} \int_{r_{i-1}}^{r_{i}} w_{i}(r) \mathrm{d} r $ | (16) |
| $ \sigma_{n}=\frac{V\left(t_{n}, r_{n}\right)-\sum\limits_{i=1}^{n-1} \sigma_{i} \frac{\partial V\left(t_{n}, r_{i}\right)}{\partial t} \int_{r_{i-1}}^{r_{i}} w_{i}(r) \mathrm{d} r}{\frac{\partial V\left(t_{n}, r_{n}\right)}{\partial t} \int_{r_{n-1}}^{r_{n}} w_{n}(r) \mathrm{d} r} $ | (17) |
上述求解电导率的过程结合了瞬变电磁场在地层中的扩散过程, 按照瞬变电磁场扩散时形成的等势面形状建立有用信号的正演计算公式。从激发源开始由浅入深地逐步计算每一个源距接收线圈的响应。每建立一个时刻的模型, 计算一个深度位置的电导率, 将不同深度的地层电导率计算与响应时间建立了一定的联系。
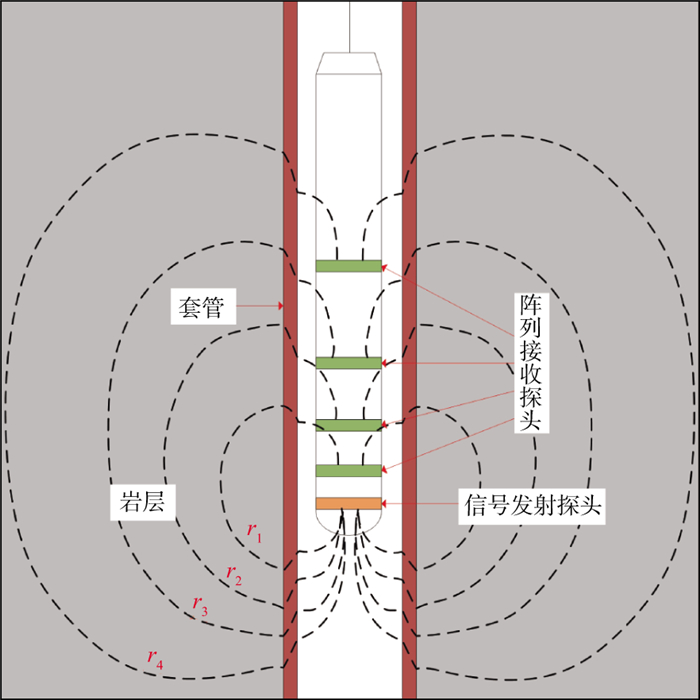
5.3 多源距接收线圈的响应差利用瞬变电磁多源距阵列接收的响应波形差计算不同等势面的地层电导率, 如图 3所示。套管井内放置发射线圈和阵列接收线圈组成的仪器, 上、下移动进行测量。
|
图 3 瞬变电磁发射——多源距接收阵列模型 |
我们将所测量的地层从发射线圈开始沿径向分为4个区域, 每个区域的径向半径依次为r1、r2、r3和r4, 它们分别位于4个等势面上, 裸眼井等势面接近球形, 套管井是椭球形状, 其上的波形与井中对应纵向源距a1、a2、a3和a4的测量波形具有对应关系。4个测量波形的上升沿变化最快的时刻对应接收线圈所在的等势面涡流再次激发响应最大的时刻。这样便将传播过程tx运用于地层电导率计算中, 各个源距的响应差与地层电导率之间的关系可表示为:
| $ \begin{array}{l} \Delta V\left(r_{1}, t_{x}\right)=V_{1}\left(t_{x}, r_{1}\right)-V_{2}\left(t_{x}, r_{1}\right)= \\ \quad\left(\frac{\partial V_{a 1}\left(r, t_{x}\right)}{\partial t} \sigma_{1}-\frac{\partial V_{a 2}\left(r, t_{x}\right)}{\partial t} \sigma_{2}\right) \int_{0}^{r_{1}} w_{1}(r) \mathrm{d} r \end{array} $ | (18) |
| $ \begin{aligned} \Delta V\left(r_{2}, t_{x}\right)=&\left(\frac{\partial V_{a 1}\left(r_{1}, t_{x}\right)}{\partial t} \sigma_{11}-\frac{\partial V_{a 2}\left(r_{1}, t_{x}\right)}{\partial t} \sigma_{21}\right) \cdot\\ & \int_{0}^{r_{1}} w_{2}(r) \mathrm{d} r+\left(\frac{\partial V_{a 1}\left(r_{2}, t_{x}\right)}{\partial t} \sigma_{12}-\right.\\ &\left.\frac{\partial V_{a 2}\left(r_{2}, t_{x}\right)}{\partial t} \sigma_{22}\right) \int_{r_{1}}^{r_{2}} w_{2}(r) \mathrm{d} r \end{aligned} $ | (19) |
| $ \begin{array}{l} \Delta V\left(r_{3}, t_{x}\right)=\left(\frac{\partial V_{a 1}\left(r_{1}, t_{x}\right)}{\partial t} \sigma_{11}-\frac{\partial V_{a 2}\left(r_{1}, t_{x}\right)}{\partial t} \sigma_{21}\right) \cdot\\ \int_{0}^{r_{1}} w_{3}(r) \mathrm{d} r+\left(\frac{\partial V_{a 1}\left(r_{2}, t_{x}\right)}{\partial t} \sigma_{12}-\frac{\partial V_{a 2}\left(r_{2}, t_{x}\right)}{\partial t} \sigma_{22}\right) \cdot\\ \int_{r_{1}}^{r_{2}} w_{3}(r) \mathrm{d} r+\left(\frac{\partial V_{a 1}\left(r_{3}, t_{x}\right)}{\partial t} \sigma_{13}-\frac{\partial V_{a 2}\left(r_{3}, t_{x}\right)}{\partial t} \sigma_{23}\right) \cdot\\ \int_{r_{2}}^{r_{3}} w_{3}(r) \mathrm{d} r \end{array} $ | (20) |
| $ \begin{array}{l} \Delta V\left(r_{4}, t_{x}\right)=\left(\frac{\partial V_{a 1}\left(r_{1}, t_{x}\right)}{\partial t} \sigma_{11}-\frac{\partial V_{a 2}\left(r_{1}, t_{x}\right)}{\partial t} \sigma_{21}\right) \cdot\\ \int_{0}^{r_{1}} w_{4}(r) \mathrm{d} r+\left(\frac{\partial V_{a 1}\left(r_{2}, t_{x}\right)}{\partial t} \sigma_{12}-\frac{\partial V_{a 2}\left(r_{2}, t_{x}\right)}{\partial t} \sigma_{22}\right) \cdot\\ \int_{r_{1}}^{r_{2}} w_{4}(r) \mathrm{d} r+\left(\frac{\partial V_{a 1}\left(r_{3}, t_{x}\right)}{\partial t} \sigma_{13}-\frac{\partial V_{a 2}\left(r_{3}, t_{x}\right)}{\partial t} \sigma_{23}\right) \cdot\\ \int_{r_{2}}^{r_{3}} w_{4}(r) \mathrm{d} r+\left(\frac{\partial V_{a 1}\left(r_{4}, t_{x}\right)}{\partial t} \sigma_{14}-\frac{\partial V_{a 4}\left(r_{4}, t_{x}\right)}{\partial t} \sigma_{24}\right) \cdot\\ \int_{r_{3}}^{r_{4}} w_{4}(r) \mathrm{d} r \end{array} $ | (21) |
式中: Va1(r, tx), Va2(r, tx)分别为发射-接收线圈阵列在两个不同深度a1、a2位置处测量的波形; σ11, σ12, σ13, σ14(σ21, σ22, σ23, σ24)分别为a1(a2)深度处r1, r2, r3, r4位置处等势面的地层电导率。若深度处地层电导率σ11, σ12, σ13, σ14已知, 则根据(18)式至(21)式可求解a2深度处地层电导率σ21, σ22, σ23, σ24。w1(r), w2(r), w3(r)和w4(r)由第1个至第4个接收线圈的几何因子积分得到, 分别沿着每个接收线圈所在的等势面上进行。
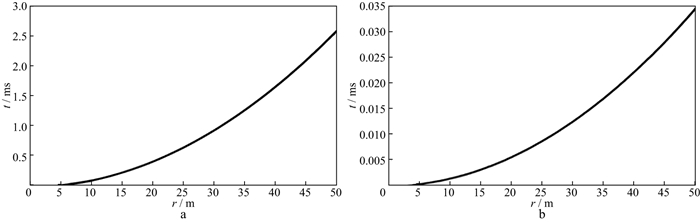
地层中任意一点的响应最大值和响应变化最快的时间与地层深度的对应关系还受地层电导率影响。图 4展示了无限大均匀地层中不同地层电导率的响应峰值到达时间与球半径之间的关系。地层电导率越大, 传播速度越慢、衰减越快, 传播的时间越长, 相同的时间对应的深度越浅。
|
图 4 地层电导率分别为10 S/m(a)、0.1 S/m(b)的响应峰值到达时间与球半径之间的关系 |
在套管井中测量不同深度地层电导率的响应, 两者相减去掉直接耦合响应, 所获得的响应差与地层电导率差呈正比。这个关系在套管井理论计算[15]和实际测量结果中均得以验证。
6 精细勘探方法通过以上对瞬变电磁响应波形的理论分析, 确定了井底发射、接收的瞬变电磁精细勘探方法。
1) 将发射和接收线圈装配在一起, 硬连接构成测量系统, 同时在井中上、下移动进行测量。
2) 在井底连续移动进行测量, 能够获得不同深度位置的瞬变电磁响应波形。
3) 若条件允许, 可加大发射功率, 在邻近井的井底位置放置接收阵列探头接收瞬变电磁响应, 甚至与发射探头同步移动进行瞬变电磁响应波形测量。
4) 将不同深度位置测量的同一源距波形相减, 去除与地层电导率无关的直接耦合响应, 突出在不同深度测量时地层电导率改变带来的响应差。
5) 将响应差波形在不同时刻的幅度用不同颜色表示, 通过时深转换关系转换到深度位置, 借助于瞬变电磁场的传播过程和几何因子建模, 获得径向和纵向不同深度地层的电导率。
6) 在同一深度测量, 用不同源距接收的阵列波形所反映的瞬变电磁场在地层中的扩散过程建模, 将不同深度测量的波形相减, 用波形差构建地层电导率的综合处理方法。
移动测量过程中, 测量系统与地层之间的位置发生改变, 每次测量获得不同空间位置地层的电导率。将同一源距的测量波形相减, 去除幅度较大的直接耦合响应信号和重复测量的地层信号, 仅剩地层不同或者变化时的响应差, 该响应差与地层的电导率差成正比。响应差刻画了不同测量区域内的地层电导率变化——包括地层电导率及其界面。再通过综合处理可获得深部地层的电导率分布。
本文提出的瞬变电磁精细勘探方法是一种直接测量地层电导率差异的方法, 通过响应差突出了不同深度位置处的电导率差异, 再借助几何因子和瞬变电磁响应的扩散过程, 通过积分或者反褶积可获得地层电导率的分布。
在井底和井中激发、接收的瞬变电磁勘探面临的最大问题是测量信号中与地层电导率无关的响应幅度很大。这些响应在线圈激发时来源于直接耦合响应, 这是瞬变电磁勘探无法避开的现实, 也是激发有用信号的基础。DOLL[2]在单井、单频情况下给出了线圈激发和接收时直接耦合信号的近似解。该解从物理上对响应的来源和特点进行了综合描述, 使得我们对瞬变电磁响应的本质有了较深刻的认识。与线圈在无限大均匀介质激发的精确解和推迟势对比后发现, DOLL的解是精确解的最低阶近似。
从瞬变电磁测量波形中提取地层电导率及其分布是深层勘探的目的。为达到该目的, 首要任务是从测量波形中消除直接耦合响应。用不同地层电导率的响应相减是最简单的方法。本文采用单频响应进行推导, 证明了线圈激发情况下可以有效消除直接耦合响应, 获得的响应波形差的幅度与地层电导率成正比。该结果虽然是近似解, 但是, 因为瞬变电磁频率低, 近似条件能够满足。
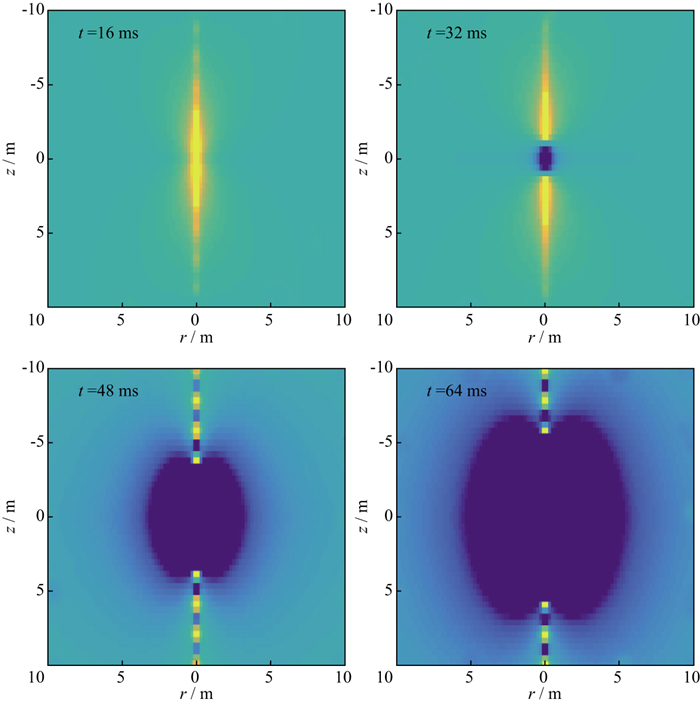
现有的油井通常都有套管, 在套管内激发时, 因套管的磁导率和电导率均很高, 套管本身的磁导率改变了线圈激发磁场的空间分布, 并对瞬变电磁能量有较大的衰减。在套管内接收时, 受套管的衰减影响, 源距大时幅度小。但是, 因为套管很薄, 瞬变电磁场的频率低, 套管的集肤深度(1 Hz、107S/m时为0.700 m)远大于套管厚度(0.009 m)。套管的高电导率和磁导率引起的相位移动很大, 在半径方向等效的传播特征在圆柱形套管也能形成类似于波动的圆周和厚度两种固有频率, 在这些固有频率处透射系数很大, 瞬变电磁能量能够顺利穿过套管壁; 另外, 圆柱形套管使得井内激发的瞬变电磁能量在套管内壁被反射后会再次到达套管内壁, 持续不断地沿径向传播、在套管内壁反射、透射, 这些持续不断的瞬变电磁能量穿过套管进入地层时, 损失并不大。图 5为套管井内线圈激发时套管外地层在不同时刻的瞬变电磁分布图像, 可以看出, 大多数瞬变电磁能量能够进入地层, 在地层中激发出瞬变电磁场, 其形状呈椭圆形状向外扩展。瞬变电磁场所扩散到的区域均是可以测量的。
|
图 5 套管井内线圈激发套管外地层不同时刻的瞬变电磁分布 |
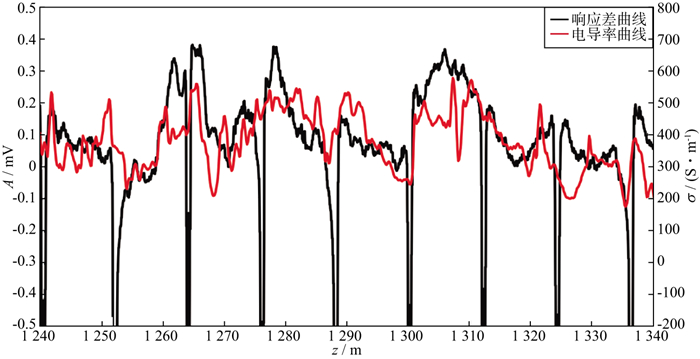
图 6中黑线是用套管井中源距L=0.275 m的接收线圈在时刻t=251 ms时测量的波形减去某个深度的波形后得到的响应差曲线, 红线为裸眼井感应测井电导率曲线。响应差曲线与电导率曲线的变化趋势相近, 响应差曲线幅度随深度改变, 反映了不同深度的地层电导率的差异; 响应幅度随时间改变, 时间越大, 响应幅度越小(衰减引起), 探测的深度越深; 当用不同时刻的响应幅度生成的随深度变化的曲线形状不一致时, 说明地层深部位置的电导率发生了改变。
|
图 6 套管井中源距L=0.275 m的接收线圈在时刻t=251 ms时响应差曲线与裸眼井感应测井电导率曲线随深度变化曲线 |
不同深度地层测量的响应波形相减是一种去除直接耦合响应的有效方法。该方法通过连续移动测量实现(将相同源距不同深度位置测量的波形相减)。在井内移动测量一段距离, 将同一接收探头在不同深度位置测量的波形相减既可以去除直接耦合响应, 又可以突出地层电导率的差异。对相减后的剩余波形建模处理可以获得地层电导率及其分布, 实现对深部地层电导率勘探。
7 结论在井内发射、接收的深层瞬变电磁精细勘探依据全空间的瞬变电磁响应, 在井内测量到的波形是全空间的响应, 有线圈和电极两种激发方式。瞬变电磁响应包含直接耦合响应与涡流再次激发响应。线圈激发情况下直接耦合响应与地层电导率无关; 而在电极激发情况下直接耦合响应与地层电导率有关, 是推迟势的直接响应。线圈发射的响应波形中所包含的地层涡流再次激发响应幅度与地层的电导率成正比, 电极发射的响应波形中的地层涡流再次激发响应幅度与地层的电导率的开平方成反比。直接耦合响应与涡流再次激发响应的相位存在差异, 在频谱中两者以实部、虚部的方式耦合在一起。通过不同地层电导率时同一源距所测量的响应相减可去除直接耦合响应。相减后的波形幅度在线圈激发时与地层电导率差成正比。瞬变电磁深层精细勘探采用移动测量方式, 将不同深度位置测量的波形相减凸显不同位置测量的地层电导率差异。利用瞬变电磁场在地层中的扩散过程和已知的浅层测井曲线对相减以后的波形建模, 实现了浅层电导率信息在探测深部地层电导率中的应用, 套管井测井实例验证了这种方法。
附录A 响应差与地层电导率差成正比的理论推导依据和差化积公式有:
| $ {V_1} - {V_2} = \cos (\omega t + \beta ) - \cos (\omega t) = - 2\sin \left( {\omega t + \frac{\beta }{2}} \right)\sin \frac{\beta }{2} $ | (A1) |
β→0求极限可得:
| $ \mathop {\lim }\limits_{\beta \to 0} \left( {{V_1} - {V_2}} \right) = \mathop {\lim }\limits_{\beta \to 0} \left[ { - 2\sin \left( {\omega t + \frac{\beta }{2}} \right)\sin \frac{\beta }{2}} \right] $ | (A2) |
此时认为sin(ωt+β/2)中ωt为常数且sin(ωt+β/2)极限不为0, 提取非零因子sin(ωt+β/2)后再做等价无穷小替换
| $ \mathop {\lim }\limits_{\beta \to 0} \left[ { - 2\sin \left( {\omega t + \frac{\beta }{2}} \right)\sin \frac{\beta }{2}} \right] = - 2\mathop {\lim }\limits_{\beta \to 0} \sin\left( {\omega t + \frac{\beta }{2}} \right)\mathop {\lim }\limits_{\beta \to 0} \sin\frac{\beta }{2} = - \sin (\omega t)\beta $ | (A3) |
得到单个频率下响应差与地层电导率差成正比。
致谢: 图 2由董凯强同学提供, 在此表示感谢!| [1] |
张庚骥. 电法测井(上)[M]. 北京: 石油工业出版社, 1984: 131-148. ZHANG G Y. Electrical logging (Part Ⅰ)[M]. Beijing: Petroleum Industry Press, 1984: 131-148. |
| [2] |
DOLL H G. Introduction to induction logging and application to logging of wells drilled with oil base mud[J]. Journal of Petroleum Technology, 1949, 1(6): 148-162. DOI:10.2118/949148-G |
| [3] |
沈建国, 舒敦利, 沈永进, 等. 套管井瞬变电磁测井在节箍处的响应与几何因子分析[J]. 石油物探, 2019, 58(4): 613-624. SHEN J G, SHU D L, SHEN Y J, et al. Response of casing hoop and geometry factor to transient electromagnetic logging in cased wells[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 613-624. DOI:10.3969/j.issn.1000-1441.2019.04.016 |
| [4] |
张小康, 沈建国, 李红瑞. 瞬变电磁井间涡流激发响应的实验研究[J]. 石油物探, 2020, 59(2): 317-324. ZHANG X K, SHEN J G, LI H R. Experiment on the transient electromagnetic field induced by eddy currents between wells[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 317-324. DOI:10.3969/j.issn.1000-1441.2020.02.018 |
| [5] |
KAUFMAN A A. The electrical field in a borehole with a casing[J]. Geophysics, 1990, 55(1): 29-38. DOI:10.1190/1.1442769 |
| [6] |
KIM H J, LEE K H. Electromagnetic fields in a non-uniform steel-cased borehole[J]. Geophysical Prospecting, 2006, 54(4): 433-439. DOI:10.1111/j.1365-2478.2006.00545.x |
| [7] |
刘宇, 刘国强. 套管非匀质性对过套管电阻率测井影响的数值模拟与分析[J]. 地球物理学报, 2014, 57(4): 1345-1355. LIU Y, LIU G Q. Numerical simulation and analysis on the influence of casing inhomogeneity on through-casing resistivity logging response[J]. Chinese Journal of Geophysics, 2014, 57(4): 1345-1355. |
| [8] |
MENG Q Y, HU X X, PAN H P, et al. Apparent resistivity for transient electromagnetic induction logging and its correction in radial layer identification[J]. Journal of Applied Geophysics, 2018, 151: 328-342. DOI:10.1016/j.jappgeo.2018.03.001 |
| [9] |
薛国强, 李貅, 底青云. 瞬变电磁法理论与应用研究进展[J]. 地球物理学进展, 2007, 22(4): 1195-1200. XUE G Q, LI X, DI Y Q. The progress of TEM in theory and application[J]. Progress in Geophysics, 2007, 22(4): 1195-1200. DOI:10.3969/j.issn.1004-2903.2007.04.026 |
| [10] |
李建慧, 朱自强, 曾思红. 瞬变电磁法正演计算进展[J]. 地球物理学进展, 2012, 27(4): 1393-1400. LI J H, ZHU Z Q, ZENG S H, et al. Progress in forward calculation of transient electromagnetic method[J]. Progress in Geophysics, 2012, 27(4): 1393-1400. |
| [11] |
MA C G, ZHAO Q, XUAN Y L, et al. Experimental research on transient electromagnetic wave transmission characteristics in single-hole[J]. IEEE International Conference on Electronic Measurement & Instruments, 2013, 92-95. |
| [12] |
王贺元, 薛国强, 郭华, 等. 均匀半空间瞬变电磁场直接时域响应数值分析[J]. 地球物理学报, 2018, 61(2): 750-755. WANG H Y, XUE G Q, GUO H, et al. Numerical analysis of direct time-domain response of transient electromagnetic field in uniform half space[J]. Chinese Journal of Geophysics, 2018, 61(2): 750-755. |
| [13] |
MORAN J H, KUNZ K S. Basic theory of induction logging and application to study of two-coil sondes[J]. Geophysics, 1962, 27(6): 829-858. DOI:10.1190/1.1439108 |
| [14] |
李貅. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社, 2002: 15-24. LI X. Theory and application of transient electron magnetic sounding[M]. Xi'an: Shaanxi Science and Technology Press, 2002: 15-24. |
| [15] |
SHENG X F, SHEN J G, SHEN Y J, et al. Measurement of formation conductivity through-casing using a TEM method[J]. Journal of Geophysics and Engineering, 2019, 16(2): 439-450. DOI:10.1093/jge/gxz022 |



