碳酸盐岩和火成岩油气藏中溶洞发育, 并且溶洞比裂缝具有更强的非均质性, 使得利用常规测井资料评价溶洞型储层非常困难[1-3]。地层溶洞的存在使声波测井的波形发生变化[1, 4], 因此掌握溶洞对井孔声波的影响规律将对溶洞的检测和评价起到重要作用。目前国内外关于裂缝对井中声波传播影响方面的研究成果见诸于许多文献[5-8], 但对溶洞性储层声波测井响应的数值模拟相对不多。BURNS等[9]指出, 地震波在地层传播时遇到裂缝、溶洞等非均匀体会产生散射现象。
偶极子声源向井外辐射的能量以SH横波为主[10-11], 其中S-S散射波为主要成分[12], 黑创等[13]利用偶极子源研究了非均匀地层偶极声波测井的散射效应, 并分析了散射波的衰减特性。李丹等[14]针对井旁不同尺度溶洞的偶极反射声波测井响应进行了数值模拟, 得到了偶极横波的回波信号, 探究了地层横波波长与井旁溶洞尺度之间的关系。赵军等[15]认为溶洞的充填度与纵横波时差之间具有很好的对应关系。根据充填情况的不同, 溶洞可以分为未充填溶洞、砂泥充填溶洞、角砾充填溶洞和方解石充填溶洞4种类型[16]。溶洞的存在使地层的纵波慢度增大, 密度测井值降低, 同时深、浅双侧向电阻率值普遍较低[17]。利用声波测井和电成像测井能全面评价地层溶洞, 斯通利波受到溶洞的影响能量会减弱[1, 4]。
前人研究成果表明, 利用声波测井评价储层中的溶洞是可行的。但其成果多基于实际测井数据, 定性给出了溶洞对纵波等常规测井曲线的影响, 并没有给出溶洞的尺寸、位置和数量对井孔纵波、横波以及散射波的影响规律。我们利用单极子声源的弹性波动方程有限差分方法对储层中不同半径、位置和数量的含水溶洞的全波列测井响应进行了数值模拟, 分析了溶洞对纵、横波首波的影响, 同时研究了由溶洞形成的下行散射波的特征。
在利用弹性波动方程有限差分程序模拟井孔内、外波场的过程中, 矩阵计算占据绝大部分计算量; 与此同时需要划分细小的网格来满足小溶洞的计算需求, 大量增加了数值模拟的时间成本。因此, 我们采用统一计算设备架构(Compute Unified Device Architecture, CUDA)平台的GPU并行计算[18-20]技术来提高计算效率。将程序的CPU串行计算模式转换为GPU并行计算模式, 以减少计算时间。
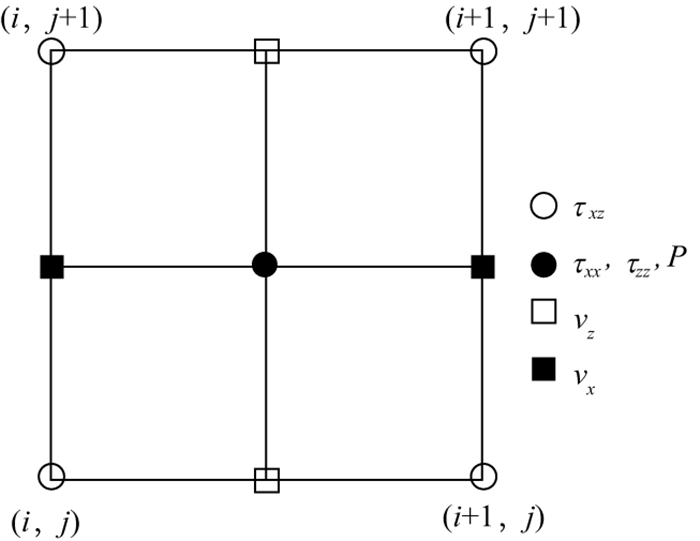
1 方法简介 1.1 弹性波有限差分方程为了研究方便, 数值模拟只考虑二维情况下x和z方向上的波动方程。选用二维直角坐标系, 采用交错网格有限差分法[21-23]模拟弹性波在发育有溶洞的均匀各向同性弹性介质模型中的传播。介质的物性参数和应力、速度分量在交错网格中的位置如图 1所示。
|
图 1 场量和介质参数在交错网格中的位置示意 |
图 1中空心圆表示剪切应力; 实心圆表示正应力和地层参数; 空心方形表示z方向上的速度分量vz; 实心方形表示x方向上的速度分量vx。括号中的参数i和j分别表示x和z方向上的网格点数。在x、z方向上网格步长分别为Δx和Δz, Δx=Δz。二维直角坐标系下, 给出时间上二阶、空间上四阶的弹性波在均匀介质中传播的速度-应力有限差分方程为:
| $ \begin{array}{*{20}{l}} {\left[ {\tau _{xx\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}^{n + 1} - \tau _{xx\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}^n} \right]/\Delta t = \left[ {{\lambda _{\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}} + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {2{\mu _{\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}}} \right]\left[ {L_X^1v_{x\left( {i,j + \frac{1}{2}} \right)}^{\left( {n + \frac{1}{2}} \right)} + L_X^2v_{x\left( {i,j + \frac{1}{2}} \right)}^{n + \frac{1}{2}}} \right] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _{\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}}\left[ {L_Z^1v_{z\left( {i + \frac{1}{2},j} \right)}^{n + \frac{1}{2}} + L_Z^2v_{z\left( {i + \frac{1}{2},j} \right)}^{n + \frac{1}{2}}} \right]} \end{array} $ | (1) |
| $ \begin{array}{l} \left[ {\tau _{zz\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}^{n + 1}\tau _{zz\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}^n} \right]/\Delta t = {\lambda _{\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {L_X^1v_{x\left( {i,j + \frac{1}{2}} \right)}^{\left( {n + \frac{1}{2}} \right)} + L_X^2v_{x\left( {i,j + \frac{1}{2}} \right)}^{n + \frac{1}{2}}} \right] + \left[ {{\lambda _{\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {2{\mu _{\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}}} \right]\left[ {L_Z^1v_{z\left( {i + \frac{1}{2},j} \right)}^{n + \frac{1}{2}} + L_Z^2v_{\left( {i + \frac{1}{2},j} \right)}^{n + \frac{1}{2}}} \right] \end{array} $ | (2) |
| $ \begin{array}{c} \left[ {\tau _{xz(i,j)}^{n + 1} - \tau _{xz(i,j)}^n} \right]/\Delta t = \mu _{\left( {i - \frac{1}{2},j - \frac{1}{2}} \right)}^H\left[ {L_X^1v_{z\left( {i - \frac{1}{2},j} \right)}^{n + \frac{1}{2}} + } \right.\\ \left. {L_X^2v_{z\left( {i - \frac{1}{2},j} \right)}^{n + \frac{1}{2}} + L_Z^1v_{x\left( {i,j - \frac{1}{2}} \right)}^{n + \frac{1}{2}} + L_Z^2v_{x\left( {i,j - \frac{1}{2}} \right)}^{n + \frac{1}{2}}} \right] \end{array} $ | (3) |
| $ \begin{array}{l} {\sigma _i}{\rho _{\left( {i - \frac{1}{2},j + \frac{1}{2}} \right)}}\left[ {{\cal U}_{x\left( {i,j + \frac{1}{2}} \right)}^{n + \frac{1}{2}} - v_{x\left( {i,j + \frac{1}{2}} \right)}^{n - \frac{1}{2}}} \right]/\Delta t = L_X^1 \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\tau _{xx\left( {i - \frac{1}{2},j + \frac{1}{2}} \right)}^n + L_X^2\tau _{xx\left( {i - \frac{1}{2},j + \frac{1}{2}} \right)}^n\quad + L_Z^1\tau _{xz(i,j)}^n + }\\ {L_Z^2\tau _{xz(i,j)}^n} \end{array} \end{array} $ | (4) |
| $ \begin{array}{*{20}{l}} {{\sigma _i}{\rho _{\left( {i + \frac{1}{2},j - \frac{1}{2}} \right)}}\left[ {v_{z\left( {i + \frac{1}{2},j} \right)}^{n + \frac{1}{2}} - v_{z\left( {i + \frac{1}{2},j} \right)}^{n - \frac{1}{2}}} \right]/\Delta t = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L_X^1\tau _{xz(i,j)}^n + L_X^2\tau _{xz(i,j)}^n + L_Z^1\tau _{zz\left( {i + \frac{1}{2},j - \frac{1}{2}} \right)}^n + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L_Z^2\tau _{zz\left( {i + \frac{1}{2},j - \frac{1}{2}} \right)}^n} \end{array} $ | (5) |
式中: λ为拉梅常数; τxx和τzz分别为x、z方向的正应力; τxz为剪切应力; 上标n为时间层数; Δt为时间步长; LX1φ(i, j)和LZ1φ(i, j)为空间二阶差分算子; LX2φ(i, j)和LZ2φ(i, j)为空间四阶差分算子; ρ和μ分别为介质的密度和剪切模量。在介质的分界面上, 分别对ρ和μ取算术平均值和调和平均值; 在固—液分界面上, μ的值为0。σif(i, j)和σjf(i, j)是算数平均算子, 定义为:
| $ {{\sigma _i}{f_{(i,j)}} = 0.5\left[ {{f_{(i + 1,j)}} + {f_{(i,j)}}} \right]} $ | (6) |
| $ {{\sigma _j}{f_{(i,j)}} = 0.5\left[ {{f_{(i,j)}} + {f_{(i,j + 1)}}} \right]} $ | (7) |
μ(i,j)H为调和平均数,定义为:
| $ \begin{array}{c} \mu _{(i,j)}^H = 4/\left[ {1/{\mu _{\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)}} + 1/{\mu _{\left( {i + \frac{1}{2},j - \frac{1}{2}} \right)}} + } \right.\\ \left. {1/{\mu _{\left( {i - \frac{1}{2},j + \frac{1}{2}} \right)}} + 1/{\mu _{\left( {i - \frac{1}{2},j - \frac{1}{2}} \right)}}} \right] \end{array} $ | (8) |
为了减小在计算过程中的数值频散, 纵波速度和声源频率需要满足以下不等式:
| $ {\Delta _{\max }} \le \frac{{{v_{\min }}}}{{10{f_{\max }}}} $ | (9) |
式中: Δmax为模型中最大网格步长; vmin为模型中最小的纵波速度; fmax为声源的最高频率。除此之外弹性波有限差分方程需满足稳定性条件:
| $ {v_{\max }}\Delta t{\left[ {\frac{1}{{\Delta {x^2}}} + \frac{1}{{\Delta {z^2}}}} \right]^{\frac{1}{2}}} < 1 $ | (10) |
式中: vmax为模型中最大的纵波速度。选取中心频率为10 kHz的雷克子波作为声源。
溶洞一般指地层中直径大于2 mm的近似球体的空隙空间。溶洞不一定与井孔相交而可能通过散射波影响井孔声波。为了满足溶洞的计算需求, 网格差分步长Δx=Δz=2 mm。根据稳定性条件可知, Δt=0.2 μs。地层中裂缝的宽度一般小于1 mm, 需要采用变网格差分方法进行模拟。
1.2 模型边界处理考虑到模型边界处可能会形成人工虚假反射波, 故在模型中加入了基于阻抗匹配的完全匹配层分裂吸收边界(PML)[24]。PML的吸收效果主要受吸收层数和衰减因子的影响。本文采用的是COLLINO等[25]提出的一种较为常用的衰减因子:
| $ d(x)=d_{0} \frac{x^{2}}{H} $ | (11) |
| $ d_{0}=\log \left(\frac{1}{R_{\mathrm{c}}}\right) \frac{3 v_{\max }}{2 H} $ | (12) |
式中: x是计算点到内层边界的距离; H表示吸收边界的宽度; d0是与Rc有关的衰减参数, Rc为理论反射系数, 通常取0.001。
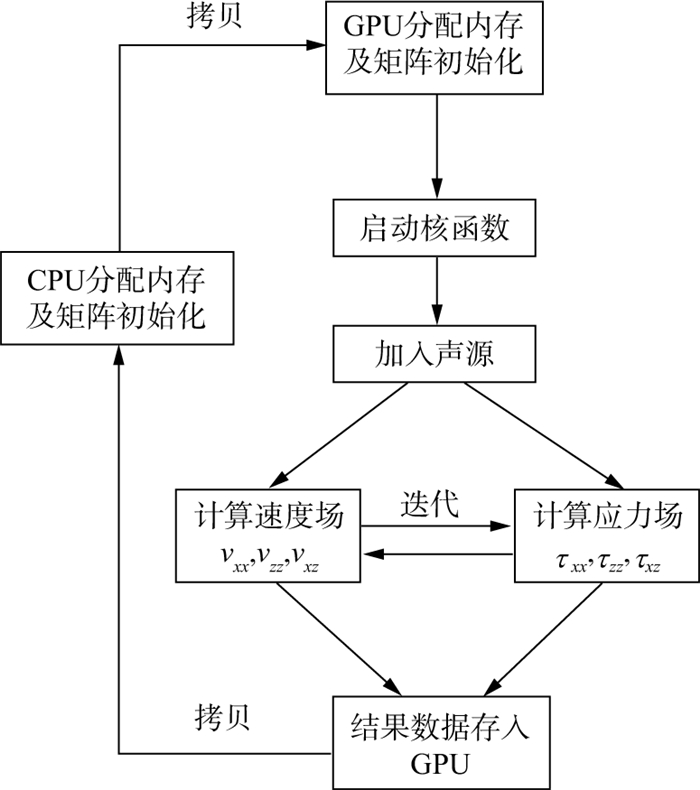
1.3 CUDA并行实现为了满足溶洞的模拟精度, 文中选择的网格差分步长较小, 因而大大增加了波场模拟的时间成本, 我们建立了弹性波动方程有限差分的并行计算模型, 算法实现流程如图 2所示。由弹性波动方程有限差分公式可知, 当前速度场每个网格的变化量由前一时间节点应力场相关网格的数值计算得出, 而当前应力场变化量则由计算后的速度场相关网格的数值计算得出。可见, 在弹性波动方程有限差分计算模型中, 待计算场量仅与已获得的计算结果相关, 而待计算场量各个网格之间在当前计算步骤中没有关联。因此, 并行计算方式可以简单、高效地实现波动方程的有限差分, 而无需考虑计算过程中不同计算结果间的同步问题。在计算模型初始化时, 通过CPU分别为速度场vxx、vzz、vxz和应力场τxx、τzz、τxz以及介质参数在GPU内存中分配二维的存储空间, 对应力场、速度场和声源设计各自的核函数, 通过CPU控制GPU分别完成速度场和应力场的分步计算。利用CUDA并行计算来提高模拟程序的运算速度。模拟实验发现, 对于本文的均匀介质模型, 常规程序的计算时间为8 808.459 s, 并行程序计算时间为584.776 s。CUDA并行计算有效提高了计算效率。
|
图 2 CUDA并行计算流程 |
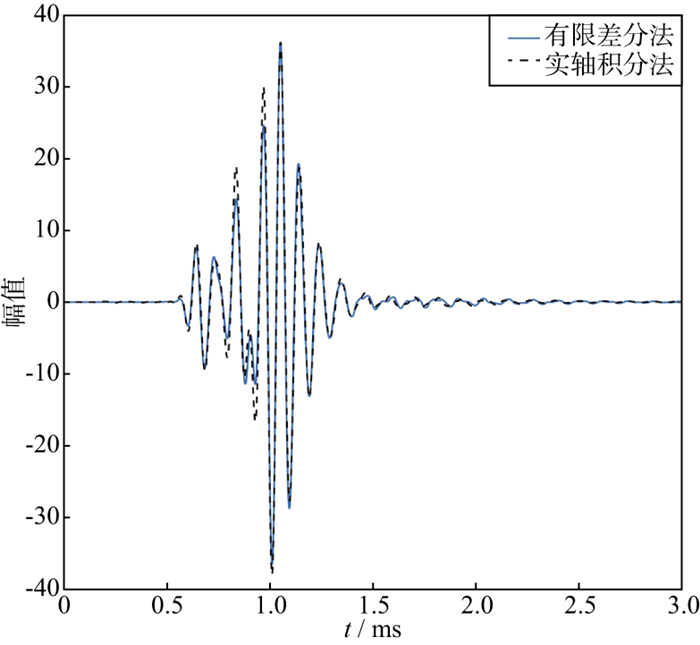
为了验证本文有限差分方法计算结果的正确性, 利用CUDA并行计算有限差分方法和实轴积分法(RAI)模拟了均匀弹性地层中声波的传播[26]。地层参数如表 1所示。声源的中心频率为10 kHz。图 3对比了两种方法的计算结果。由图 3可以看出, 两种方法的波形匹配较好, 说明了二维直角坐标系下的有限差分方法是有效的。这两种方法波形的差异可能是数据离散和归一化引起的。
| 表 1 地层和井孔参数 |
|
图 3 有限差分法和实轴积分法计算结果对比 |
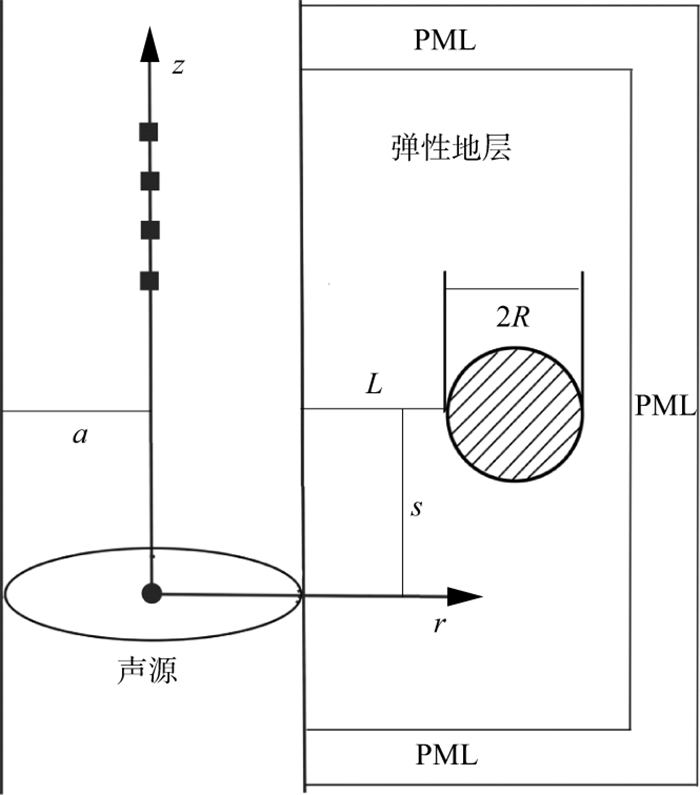
本文设计了如图 4所示的试算模型。模型尺寸为4 m×2 m。井旁有一圆形溶洞, 井孔、溶洞中充满了水, 井孔外为均匀弹性介质, 溶洞半径为R, 溶洞距井壁的距离为L, 井孔的半径a=10 cm。声源和接收器均放置在井孔中。声源距溶洞中心的垂直距离s为2 m。各介质的声学参数如表 1所示。
|
图 4 溶洞地层的井孔模型示意 |
图a和图 5b分别给出了溶洞地层中弹性波在0.90 ms和1.44 ms的波场快照。单极子声源向地层辐射纵波和横波。当溶洞直径小于0.25倍横波波长时, 溶洞可近似为点散射体, 点散射体只能形成一次散射波。直径大于0.25倍横波波长的溶洞自身能形成多次散射波, 散射波的叠加会使散射波前面畸变[27]。声波沿着地层传播到模型的边界PML区域时没有形成人工边界的反射, 说明加入的PML吸收边界是有效的。在0.90 ms时, 只有纵波与溶洞相遇。由于纵波产生的散射波较弱, 在图 5a中不能被观察到, 只能看到声源激发的原始波场。在1.44 ms时, 地层横波与溶洞相遇, 除了声源激发的原始波场外, 在图 5b中能清楚看到横波产生的散射波—S-S波。值得注意的是, 图 5b中横波穿过溶洞后, 幅值明显降低(横波颜色变淡)。
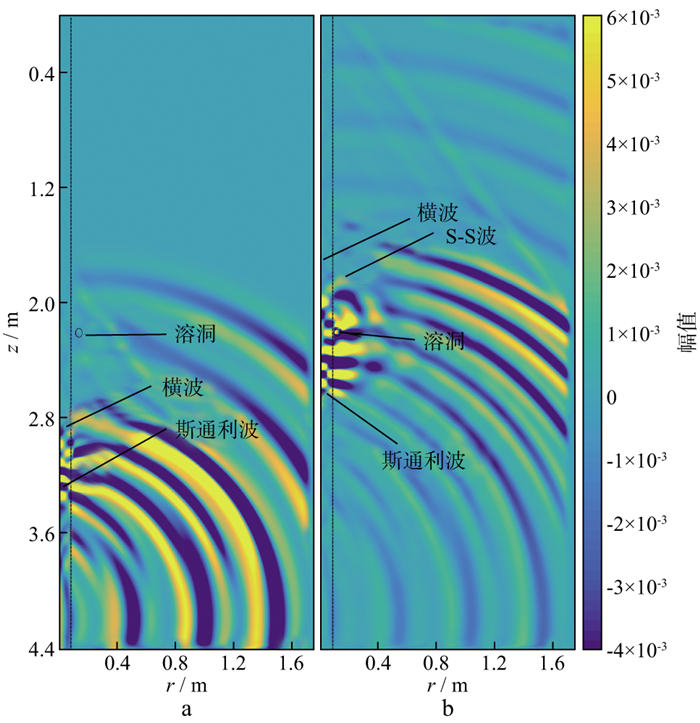
|
图 5 溶洞地层弹性波的波场快照 a 0.90 ms; b 1.44 ms |
图 6展示了位于溶洞上方0.4 m(源距为2.4 m)的接收器所记录的纵波首波波形。其中, R表示溶洞的半径, L表示溶洞距井壁的距离。由图 6可知, 当溶洞半径较小时(R<20 mm), 纵波首波幅值变化很小。当溶洞半径较大时(R>20 mm), 存在一个距离Lp, 当溶洞的井旁距离小于Lp时, 纵波首波的衰减与Lp呈正相关并在Lp处最大; 当溶洞的井旁距离大于Lp时, 纵波首波的衰减与Lp呈负相关。经过观察, 文中模型的Lp为16 cm。当溶洞的井旁距离大于24 cm时, 井旁距离的变化对纵波首波影响很小, 这时溶洞地层与均匀弹性地层的纵波首波比较接近, 说明单极子声波测井存在一个最大探测深度Lmax。在本文的模型中, Lmax约为24 cm。当溶洞的半径较小(R<30 mm)时, 溶洞位置的变化对纵波首波的影响很小。
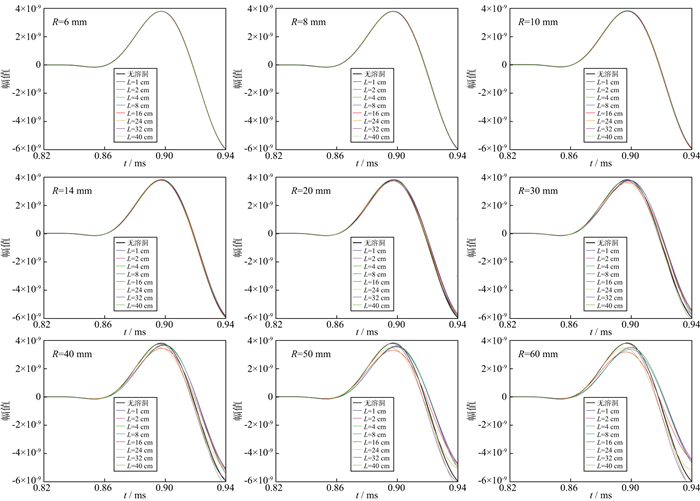
|
图 6 溶洞位置对纵波首波的影响 |
图 7给出了不同半径的溶洞对纵波首波的影响。由图 7可知, 纵波首波的衰减与溶洞半径呈正相关。当溶洞距井壁的距离<24 cm时, 纵波的初至时间与溶洞半径呈正相关。当溶洞距井壁的距离为16 cm时, 纵波首波的衰减最大。
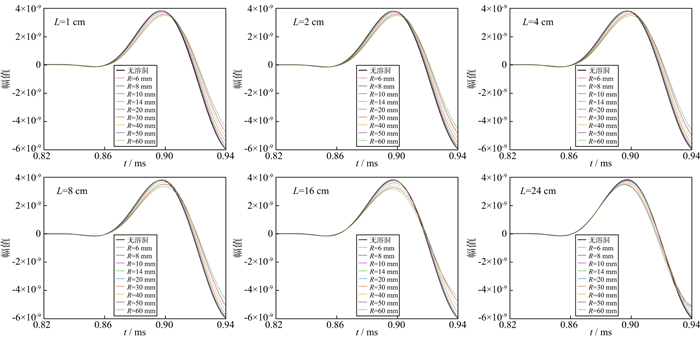
|
图 7 溶洞半径对纵波首波的影响 |
溶洞上方的接收器记录到的纵波是溶洞引起的散射波与井壁滑行纵波的叠加。当溶洞半径较大, 且距井壁的距离不超过声源探测的最大距离时, 不同位置的溶洞形成的散射波与井壁滑行纵波的相位、幅值可能不同, 故纵波首波的衰减也不同。由于溶洞中充满水, 声波在流体中的传播速度小于在地层中的传播速度, 故在地层含有溶洞的情况下, 纵波首波的初至时间后延。溶洞的半径越大, 纵波在流体中的传播时间越长, 纵波初至时间越晚。
2.3.2 溶洞的数量对纵波首波的影响溶洞的数量也会影响声波在井中的传播, 我们模拟了等间隔径向排列的多个溶洞对井孔声波的影响, 最近的溶洞距井壁1 cm, 溶洞的间隔为1 cm。图 8给出了溶洞的数量(N)对纵波首波的影响结果。
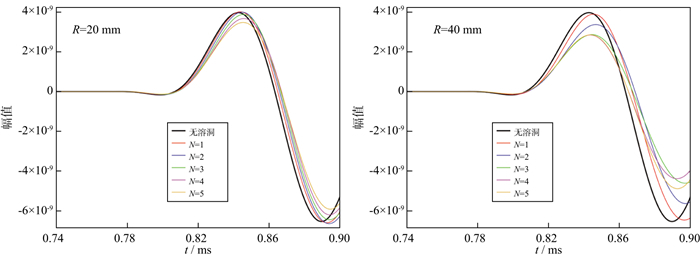
|
图 8 溶洞的数量对纵波首波的影响 |
1) 溶洞的半径为20 mm时, 纵波首波的衰减与溶洞数量呈正相关, 纵波首波的初至时间与溶洞数量呈正相关。
2) 溶洞的半径为40 mm时, 当溶洞数量≤3时, 纵波首波的衰减、初至时间均与溶洞数量呈正相关; 当溶洞数量>3时, 纵波首波的衰减、初至时间几乎保持不变。
由此可知, 若溶洞的井旁距离大于单极子测井的最大探测距离, 溶洞已经较难对井孔声波产生影响。当溶洞的半径R为20 mm时, 横向排列、间隔为1 cm的5个溶洞的最大井旁距离为22 cm, 故此时纵波首波的变化与溶洞数量呈正相关。当溶洞的半径为40 mm时, 由于第4个和第5个溶洞的井旁距离均大于24 cm, 纵波首波的衰减几乎不再受第4个和第5个溶洞的影响, 此时纵波的变化与前3个溶洞的纵波情况非常接近。
2.4 地层溶洞对井孔横波首波的影响 2.4.1 溶洞的位置和半径对横波首波的影响图 9给出了不同位置的溶洞对横波首波的影响。由图 9可知, 同样存在一个井旁距离Ls, 当溶洞的井旁距离小于Ls时, 横波首波衰减与其呈正相关并在Ls处衰减达到最大; 当井旁距离大于Ls时, 横波首波的衰减较弱。当溶洞的井旁距离>24 cm时, 井旁距离的变化对横波首波影响很小; 当溶洞的半径较小(R<20 mm)时, 溶洞位置的变化对横波首波的影响很小。对比纵波可知, 横波对于溶洞井旁距离的变化更敏感。
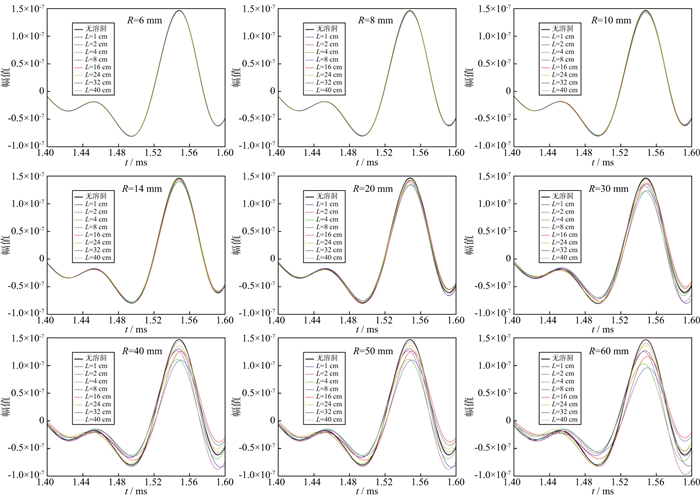
|
图 9 溶洞的位置对横波首波的影响 |
图 10给出了不同半径的溶洞对横波首波的影响。由图 10可知, 溶洞使横波首波明显衰减, 横波首波的衰减与溶洞的半径呈正相关。与纵波对比可知, 横波对地层溶洞半径的变化更敏感。当L=8 cm时, 横波的衰减最大。
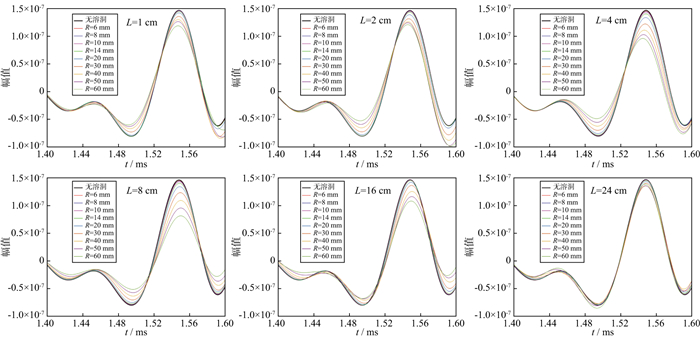
|
图 10 溶洞的半径对横波首波的影响 |
地层溶洞内充满流体, 横波不能在流体中传播。横波遇到含水溶洞时, 溶洞中的流体会抑制横波的传播, 一部分横波能量会转化为流体的压缩能量[28]。这部分流体压缩能量可能又转换成其它模式波的能量, 继续沿地层传播, 最终被接收器接收。因此在溶洞上方的接收器记录到的横波能量会有部分的衰减。溶洞的半径越大, 横波的衰减幅度越大。由于单极子声源的探测距离限制, 当溶洞的井旁距离超过单极子声波测井的最大探测距离时, 溶洞半径对横波首波的影响将会变得很小。
2.4.2 溶洞的数量对横波首波的影响图 11给出了不同的溶洞数量对横波首波的影响。溶洞数量对横波首波的影响与纵波类似。
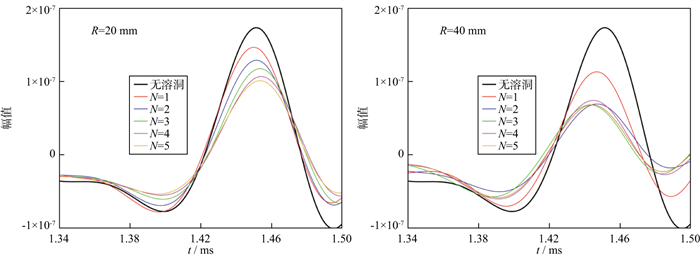
|
图 11 溶洞数量对横波首波的影响 |
1) 溶洞的半径为20 mm时, 横波首波衰减非常明显, 并且与溶洞数量呈正相关。
2) 溶洞的半径为40 mm时, 当溶洞数量≤3时, 横波首波衰减与溶洞数量呈正相关; 当溶洞数量>3时, 横波首波衰减的程度几乎保持不变。
2.4.3 溶洞与横波首波衰减系数的关系本文将横波首波在溶洞作用下的衰减系数A定义为:
| $ A=1-\frac{A_{2}}{A_{1}} $ | (13) |
式中: A1和A2分别为均匀地层和溶洞地层在同一源距横波首波的振幅。图 12a为溶洞半径与横波首波衰减系数的关系, 其中虚线代表拟合的线性方程。由图 12a可知, 横波首波衰减系数与溶洞半径存在正线性相关。特别的, 当溶洞的井旁距离为4 cm时, 不仅横波首波衰减系数最大, 线性方程的斜率也最大。图 12b为溶洞数量与横波首波衰减系数的关系。溶洞数量与横波首波衰减系数之间更像是凸函数, 随着溶洞数量的增加, 衰减系数增加得越来越缓慢。这是因为声波探测距离有限, 一般井旁距离大于24 cm的溶洞很难再对井孔声波产生影响, 故当溶洞在地层中径向等间距排列时, 横波首波衰减系数与有限个溶洞数量呈正相关。图 12a和图 12b中接收器的源距为2.4 m。图 12c为跨过溶洞的不同源距与横波首波衰减系数的关系。溶洞的源距为2.0 m。当接收器位于溶洞下方时, 横波几乎不发生衰减, 此时衰减系数接近0。值得注意的是, 位于溶洞处的接收器接收到的横波衰减仍然很小(源距为2.0 m时)。当接收器逐渐跨越溶洞时, 横波在地层中传播会遇到含水溶洞而形成转换纵波和转换横波, 横波能量的衰减逐渐增强。靠近溶洞上方的接收器所记录到的波形中转换纵波和转换横波叠加在一起, 故横波的波幅较大, 首波衰减系数较小。随着源距的增加, 转换纵波和转换横波逐渐分离, 一部分横波能量就转化为纵波的能量, 明显削弱了横波首波幅值, 首波衰减系数会增加。随着源距的不断增加, 溶洞对横波的影响越来越小, 横波能量衰减也越来越小, 故衰减系数会逐渐减小并趋于稳定。从图 12c中可以看出, 当接收器与溶洞距离为0.4 m时, 转换横波已经与其它模式波分离, 当接收器与溶洞距离>0.9 m时, 衰减系数趋于稳定。
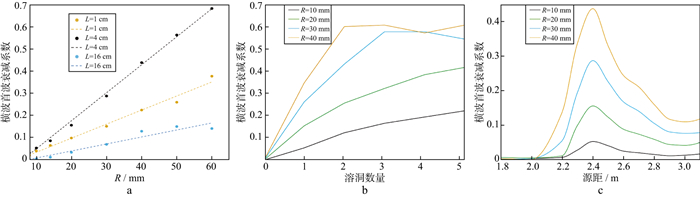
|
图 12 溶洞的半径(a)、数量(b)和源距(c)对横波首波衰减系数的影响 |
图 13a为声波在溶洞地层中的波形。溶洞下方出现了明显的散射波。选取源距为1.6 m处的井孔声波(溶洞下方0.4 m), 我们将均匀地层的波形作为直达波。从图 13a中减去直达波, 分离出散射波, 如图 13b和图 13c所示。由图 13b和图 13c可知, 分离出的波形主要以散射波为主。图 13b中溶洞的半径为10 mm, 幅值较大的波峰以S-S、P-S散射横波为主, 主频约为7.5 kHz, 幅值较小的波峰由其余散射波组成。图 13c中溶洞半径为30 mm, 自身形成多次复杂的散射波场, 其中主频为5~7 kHz的大波峰以横波散射波(S-S波等)为主, 主频为9 kHz的小波峰以纵波散射波(P-P波等)为主。利用傅里叶变换得到散射波的频率谱, 如图 13d和图 13e所示。将每个频率对应数值的平方求和, 得到散射波的能量。
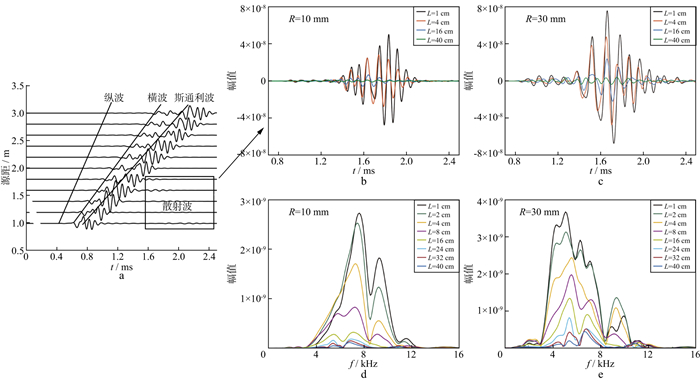
|
图 13 溶洞地层中的声波波形(a)、散射波波形(b, c)以及散射波频率谱(d, e) |
图 14a为散射波能量与溶洞位置的关系曲线。其中半径为6~20 mm的溶洞均可视为点散射体, 此时散射波能量与井旁距离呈负相关; 半径为30~60 mm的溶洞可形成多次散射, 当井旁距离较大时, 散射波能量与井旁距离呈负相关。当溶洞的井旁距离超过单极子声波的最大探测距离时, 任何尺寸的溶洞形成的散射波都可忽略。图 14b为下行散射波能量与溶洞半径的关系曲线。当溶洞半径可视为点散射体时, 形成的下行散射波能量与溶洞半径呈正相关; 当溶洞半径较大可形成自身散射时, 下行散射波能量降低, 井旁距离越小, 降低越明显。随着溶洞半径增大, 下行散射波能量变化不是很剧烈。图 14c展示了溶洞数量对下行散射波能量的影响, 当溶洞在地层中径向等间距排列时, 下行散射波能量与有限个溶洞数量呈正相关。由于单极子声波探测距离的限制, 半径为30 mm和40 mm的溶洞数量达到2时, 下行散射波的能量就不再增加。
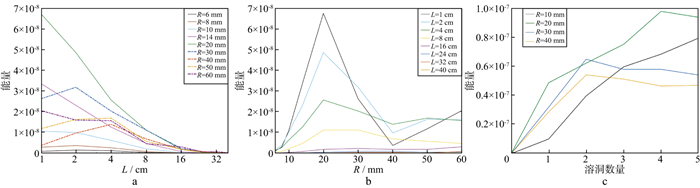
|
图 14 下行散射波能量与溶洞位置(a)、半径(b)和数量(c)的关系曲线 |
通过对溶洞地层的单极子声波有限差分方法的数值模拟, 研究了溶洞对井孔声波的初至和能量的影响规律, 得到以下结论:
1) 单极子声源测井的探测距离是有限的。当接收器源距为2.4 m时, 若溶洞的距离大于单极子声波的探测距离, 很难再对井孔声波产生影响。文中模型声源的最大探测距离约24 cm。
2) 由于散射波的叠加, 纵波的幅度会发生变化。横波的传播机制决定了横波能量总是有所衰减。相对于纵波, 横波对溶洞更敏感, 利用横波能更有效地识别溶洞。随着源距的增加, 横波的衰减系数会先增大后减小。在单极子声波的最大有效探测距离内, 溶洞的数量越多, 对声波的影响越明显。纵波和横波对溶洞的距离没有很好的响应规律。值得注意的是, 当溶洞离井孔的距离为某个值时, 纵波和横波的幅度变化会达到最大。
3) 可视为点散射体的小尺寸溶洞和可形成自身散射的大尺寸溶洞形成的下行散射波的规律明显不同。值得注意的是, 离井壁很近的大尺寸溶洞的散射波与溶洞半径或溶洞的井旁距离没有明显的相关性。
溶洞对纵波、横波的影响与裂缝有些类似, 上述结论能够为利用声波测井评价溶洞地层提供一些理论依据。由于文中的溶洞位于井旁没有与井孔相交, 故不能直接对井孔斯通利波产生影响。本文的理论结果虽然能在一定程度上反映出地层溶洞对井孔声波的影响, 但也存在不足之处。本文模拟的模型是二维的理想简化模型, 但实际地层中的溶洞无论是数量、形状和填充度等方面都十分复杂, 今后需要利用三维复杂地质模型更加系统地研究声波测井的响应特征。
| [1] |
司马立强. 碳酸盐岩缝-洞性储层测井综合评价方法及应用研究[D]. 成都: 西南石油大学, 2005 SI MA L Q.Study on comprehensive evaluation method and application of well logging for fracture-vuggy carbonate reservoir[D].Chengdu: Southwest Petroleum University, 2005 |
| [2] |
余淳梅, 郑建平, 唐勇, 等. 准噶尔盆地五彩湾凹陷基底火山岩储集性能及影响因素[J]. 地球科学, 2004, 29(3): 303-308. YU C M, ZHENG J P, TANG Y, et al. Reservoir properties and effect factors on volcanic rocks of basement beneath Wucaiwan Depression, Junggar Basin[J]. Journal of Earth Science, 2004, 29(3): 303-308. DOI:10.3321/j.issn:1000-2383.2004.03.007 |
| [3] |
王俊杰, 胡勇, 刘义成, 等. 碳酸盐岩储层多尺度孔洞缝的识别与表征——以川西北双鱼石构造中二叠统栖霞组白云岩储层为例[J]. 天然气工业, 2020, 40(3): 48-57. WANG J J, HU Y, LIU Y C, et al. Dentification and characterization of multi-scale pores, vugs and fractures in carbonate reservoirs: A case study of the Middle Permian Qixia dolomite reservoirs in the Shuangyushi Structure of the northwestern Sichuan Basin[J]. Natural Gas Industry, 2020, 40(3): 48-57. |
| [4] |
XU F H, WANG Z W. Numeric simulation of acoustic-logging of cave formations[J]. Energies, 2020, 13(15): 3908. DOI:10.3390/en13153908 |
| [5] |
梁志强. 不同尺度裂缝的叠后地震预测技术研究[J]. 石油物探, 2019, 58(5): 766-772. LIANG Z Q. Poststack seismic prediction techniques for fractures of different scales[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 766-772. DOI:10.3969/j.issn.1000-1441.2019.05.016 |
| [6] |
OU W M, WANG Z W. Simulation of stoneley wave reflection from porous formation in borehole using FDTD method[J]. Geophysical Journal International, 2019, 217(3): 2081-2096. DOI:10.1093/gji/ggz144 |
| [7] |
高利君, 杨建礼, 李俊, 等. 二维随机介质等效裂缝建模及波动方程正演模拟[J]. 石油物探, 2020, 59(3): 404-408. GAO L J, YANG J L, LI J, et al. Building an equivalent fracture model and performing forward modeling of wave equations in a 2D random medium[J]. Geophysical Prospecting for Petroleum, 2020, 59(3): 404-408. DOI:10.3969/j.issn.1000-1441.2020.03.009 |
| [8] |
徐方慧, 王祝文, 刘菁华, 等. 基于EMD的声波测井信息提取与火成岩裂缝地层特征分析[J]. 石油物探, 2018, 57(6): 936-943. XU F H, WANG Z W, LIU J H, et al. Acoustic logging information extraction and fractural volcanic formation characteristics based on empirical mode decomposition[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 936-943. DOI:10.3969/j.issn.1000-1441.2018.06.016 |
| [9] |
BURNS D R, WILLIS M E, TOKSOZ M N, et al. Fracture properties from seismic scattering[J]. The Leading Edge, 2007, 26(9): 1186-1196. DOI:10.1190/1.2780790 |
| [10] |
TANG X M, CAO J J, WEI Z T. Shear-wave radiation, reception, and reciprocity of a borehole dipole source: With application to modeling of shear-wave reflection survey[J]. Geophysics, 2014, 79(2): T43-T50. DOI:10.1190/geo2013-0096.1 |
| [11] |
唐晓明, 魏周拓. 利用井中偶极声源远场辐射特性的远探测测井[J]. 地球物理学报, 2012, 55(8): 2798-2807. TANG X M, WEI Z T. Single-well acoustic reflection imaging using far-field radiation characteristics of a borehole dipole source[J]. Chinese Journal of Geophysics, 2012, 55(8): 2798-2807. |
| [12] |
AKI K, RICHARDS P G.Quantitative seismology: theory and method[M].San Francisco: W.H.Freeman, 1980: 64-119
|
| [13] |
黑创, 唐晓明, 李振, 等. 井孔声场中的弹性波散射效应及其应用[J]. 中国科学: 地球科学, 2016, 46(1): 118-126. HEI C, TANG X M, LI Z, et al. Elastic wave scattering and application in the borehole environment[J]. Science China: Earth Sciences, 2016, 46(1): 118-126. |
| [14] |
李丹, 乔文孝, 车小花, 等. 井旁溶洞的偶极反射声波测井响应研究[J]. 应用声学, 2019, 38(5): 767-773. LI D, QIAO W X, CHE X H, et al. Study on the response of dipole reflected acoustic imaging the near-borehole cave[J]. Applied Acoustics, 2019, 38(5): 767-773. |
| [15] |
赵军, 李宗杰, 虞兵, 等. 洞穴充填程度的声波测井数值模拟与定量评价[J]. 应用基础与工程科学学报, 2013, 21(6): 1070-1077. ZHAO J, LI Z J, YU B, et al. Acoustic logging numerical simulation and quantitative evaluation of cave filling degree[J]. Journal of Basic Science and Engineering, 2013, 21(6): 1070-1077. |
| [16] |
樊政军, 柳建华, 张卫峰. 塔河油田奥陶系碳酸盐岩储层测井识别与评价[J]. 石油与天然气地质, 2008, 29(1): 61-65. FAN Z J, LIU J H, ZHANG W F. Log interpretation and evaluation of the Ordovician carbonate rock reservoirs in Tahe oilfield[J]. Oil & Gas Geology, 2008, 29(1): 61-65. |
| [17] |
王小畅, 张军, 李军, 等. 基于交会图决策树的缝洞体类型常规测井识别方法——以塔河油田奥陶系为例[J]. 石油与天然气地质, 2017, 38(4): 805-812. WANG X C, ZHANG J, LI J, et al. Conventional logging identification of fracture-vug complex types data based on crossplots-decision tree: A case study from the Ordovician in Tahe oilfield, Tarim Basin[J]. Oil & Gas Geology, 2017, 38(4): 805-812. |
| [18] |
STORTI D. CUDA for engineers: An introduction to high-performance parallel computing[M]. New Jersey: Addison-Wesley, 2016: 25-43.
|
| [19] |
宋波, 李威, 廉国选. 基于CUDA的超声二维声场EFIT仿真[J]. 北京航空航天大学学报, 2019, 45(7): 1322-1328. SONG B, LI W, LIAN G X. EFIT simulation of 2D ultrasonic sound field based on CUDA[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(7): 1322-1328. |
| [20] |
HE L L, JIANG Y, OU Y, et al. Revised simplex algorithm for linear programming on GPUs with CUDA[J]. Multimedia Tools and Applications, 2018, 77(22): 30035-30050. DOI:10.1007/s11042-018-5947-z |
| [21] |
张奎涛, 顾汉明, 刘少勇, 等. 基于CPML-RML组合边界条件粘弹TTI介质旋转交错网格有限差分正演模拟[J]. 石油物探, 2019, 58(2): 187-198. ZHANG K T, GU H M, LIU S Y, et al. Rotated staggered grid finite difference forward modeling for wave propagation in viscoelastic TTI media based on CPML-RML combined boundary condition[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 187-198. |
| [22] |
杨怀杰, 潘和平, 孟庆鑫, 等. 导电围岩对井中三维瞬变电磁响应的影响规律研究[J]. 石油物探, 2016, 55(2): 288-293. YANG H J, PAN H P, MENG Q X, et al. Influence laws of conductive host on borehole 3D transient electromagnetic responses[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 288-293. |
| [23] |
欧伟明, 王祝文, 宁琴琴, 等. 基于线性滑动模型的裂缝性地层声波测井响应数值模拟[J]. 中国石油大学学报(自然科学版), 2019, 43(3): 56-64. OU W M, WANG Z W, NING Q Q, et al. Numerical simulation of acoustic logging in fractured formation based on linear-slip model[J]. Journal of China University of Petroleum(Edition of Natural Science), 2019, 43(3): 56-64. |
| [24] |
BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1996, 114(2): 185-200. |
| [25] |
COLLINO F, TSOGKA C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307. |
| [26] |
阎守国, 谢馥励, 龚丹, 等. 含有倾斜薄裂缝孔隙地层中的井孔声场[J]. 地球物理学报, 2015, 58(1): 301-317. YAN S G, XIE F L, GONG D, et al. Borehole acoustic fields in porous formation with tilted thin fracture[J]. Chinese Journal of Geophysics, 2015, 58(1): 307-317. |
| [27] |
牟永光, 裴正林. 三维复杂介质地震数值模拟[M]. 北京: 石油工业出版社, 2005: 136-146. MOU Y G, PEI Z L. Seismic numerical simulation of 3D complex media[M]. Beijing: Petroleum Industry Press, 2005: 136-146. |
| [28] |
PAILLET F L.Acoustic propagetion in the vicinity of fractures which intersect a fluid-filled borehole[J].Expanded Abstracts of SPWLA 21st Annual Logging Symposium, 1980: SPWLA-1980-DD
|




