2. 桂林电子科技大学认知无线电与信息处理教育部重点实验室, 广西桂林 541004
2. Key Laboratory of Cognitive Radio and Information Processing, Ministry of Education, Guilin University of Electronic Technology, Guilin 541004, China
瞬变电磁法是一种重要的地球物理勘探方法。该方法根据电磁感应原理, 利用不接地回线或接地线源向地下发送一次场, 在其激发下, 地下地质体中激励起二次场, 通过分析、处理二次场信号, 达到探测地下地质体的目的[1]。瞬变电磁法具有较高的探测和分辨能力, 已被广泛应用于煤矿、金属矿和油气田等地下目标的勘探工作[2-6]。
在野外作业时, 用瞬变电磁法采集到的信号会受到各种噪声的干扰, 比如: 天电噪声、工频干扰等, 特别是在瞬变电磁信号的晚期, 噪声严重时, 甚至会淹没干净的瞬变电磁信号, 这些噪声严重影响了瞬变电磁信号的后续处理工作。对此, 在瞬变电磁信号处理前期, 人们研究了各种噪声的特性, 提出了多种降噪方法, 大致可分为3类: 传统方法、子空间法和基于深度学习的方法。传统方法主要有小波变换[7-8]、Hilbert-Huang变换[9]和卡尔曼滤波[10]等。利用小波变换来对瞬变电磁信号降噪时, 存在小波选择困难的问题, 也就是缺乏自适应性。Hilbert-Huang变换存在端点效应等问题, 降噪效果不够理想。对于卡尔曼滤波来说, 这种适用于线性系统的降噪方法对于按指数规律下降的非线性瞬变电磁信号的处理能力有限。子空间法主要有奇异值分解[11]等。相比于传统方法, 虽然奇异值分解法降噪效果有所提高, 但一直难以确定有效的奇异值, 其处理步骤也比较复杂。近年来随着深度学习的发展和应用, 基于深度学习的方法在瞬变电磁信号处理领域受到较高的关注, 主要有堆栈式降噪自编码器[12]等。堆栈式降噪自编码器的降噪效果优于传统方法, 但该模型必须建立在特定的地质条件上, 适用范围受到较大限制。一般来说, 基于深度学习的方法都需要大量的数据作支撑, 模型结构复杂, 算法存在难以收敛的风险。
非负矩阵分解(NMF)的有监督算法是一种字典学习方法, 在信源分离和语音增强等方面有着广泛的应用。MOHAMMADIHA等[13]将此法用于估计噪声的功率谱密度, 并与维纳滤波相结合进行语音增强。张龙[14]将较长的房间冲激响应分解为两个较短响应的卷积, 提出了一种两步序贯处理的非负矩阵分解模型的语音增强算法。张星[15]采用对数谱估计方法对时频谱图中的语音存在概率进行估计, 对非负矩阵分解得到的字典进行自适应补偿, 提高了语音增强的性能。本文首次将NMF的有监督算法引入瞬变电磁信号的降噪处理中, 先研究了瞬变电磁信号模型和NMF的有监督算法, 然后介绍了采用该算法对瞬变电磁信号进行降噪处理的技术流程, 最后给出了该算法对模拟信号和实际瞬变电磁信号的实际应用。
1 基本理论 1.1 信号与噪声模型瞬变电磁法中, 采用中心回线法采集时, 接收线圈在时刻t测得的感应电动势表达式为[16]:
| $ v(t) = \frac{{{\mu _0}I{S_r}}}{{4at}}f(z) $ | (1) |
其中核函数为:
| $ {f(z) = \frac{1}{{{z^2}}}\left[ {3{\mathop{\rm erf}\nolimits} (z) - \frac{2}{{\sqrt {\rm{ \mathsf{ π} }} }}z\left( {3 + 2{z^2}} \right){{\rm{e}}^{ - \frac{{{z^2}}}{2}}}} \right]} $ | (2) |
| $ {z = \frac{a}{2}\sqrt {\frac{{{\mu _0}}}{{\rho t}}} } $ | (3) |
式中:
实际采集的瞬变电磁信号混有噪声。本文使用加性噪声模型, 即:
| $ y(t)=v(t)+n(t) $ | (4) |
式中: y(t)为含噪的瞬变电磁信号; v(t)为纯净的瞬变电磁信号; n(t)为加性噪声。
1.2 非负矩阵分解非负矩阵分解(NMF)理论实质上是利用非负约束条件来获取数据表示的一种方法。NMF的理论问题可以描述为: 对于任意给定的一个非负矩阵Y, NMF算法能够找到一个非负矩阵W和一个非负矩阵H, 满足Y≈WH, 从而将一个非负矩阵分解成两个非负矩阵的乘积[17]。
给定一个非负矩阵Y, 分解的算法有很多种[18-22]。本文使用的是基于欧式距离的NMF算法, 其目标函数为:
| $ f(\boldsymbol{W} \mid \boldsymbol{H})=\|\boldsymbol{Y}-\boldsymbol{W} \boldsymbol{H}\|_{F}^{2} $ | (5) |
式中: ‖·‖F为Frobenius范数。
最小化上述目标函数可定义为如下优化问题:
| $ \begin{array}{*{20}{l}} {\mathop {\min }\limits_{W, H} f(\mathit{\boldsymbol{W}}\mid \mathit{\boldsymbol{H}})\quad {\rm{s}}.{\rm{t}}.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {W_{ia}} \ge 0, {H_{bj}} \ge 0\quad \forall i, a, b, j} \end{array} $ | (6) |
式中: Wia和Hbj分别为非负矩阵W和H的元素。
解上述优化问题, 使用如下乘性迭代规则, 可使该算法收敛, W和H达到某个局部最优点。
| $ H_{b j} \leftarrow H_{b j} \frac{\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{Y}\right)_{b j}}{\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{W} \boldsymbol{H}\right)_{b j}} $ | (7) |
| $ W_{i b} \leftarrow W_{i b} \frac{\left(\boldsymbol{Y} \boldsymbol{H}^{\mathrm{T}}\right)_{i b}}{\left(\boldsymbol{W H} \boldsymbol{H}^{\mathrm{T}}\right)_{i b}} $ | (8) |
将非负矩阵分解(NMF)的有监督算法应用于瞬变电磁信号的降噪处理, 该算法可大致分为训练、降噪和求平均3步。
在训练阶段, 得到表示纯净的瞬变电磁信号矩阵Vt和噪声信号矩阵Nt后, 分别对其进行非负矩阵分解, 可通过最小化如下目标函数完成:
| $ f\left(\boldsymbol{W}_{v} \mid \boldsymbol{H}_{v}\right)=\left\|\boldsymbol{V}^{t}-\boldsymbol{W}_{v} \boldsymbol{H}_{v}\right\|_{F}^{2} $ | (9) |
| $ f\left(\boldsymbol{W}_{n} \mid \boldsymbol{H}_{n}\right)=\left\|\boldsymbol{N}^{t}-\boldsymbol{W}_{n} \boldsymbol{H}_{n}\right\|_{F}^{2} $ | (10) |
利用公式(7)和公式(8)求解该优化问题后, 分别得到表示纯净的瞬变电磁信号矩阵Vt和噪声信号矩阵Nt特征的原子字典Wv和Wn。然后, 将Wv和Wn拼接成总字典W=[Wv Wn], 矩阵W包含了表示纯净的瞬变电磁信号矩阵Vt和噪声信号矩阵Nt的特征。
在降噪阶段, 利用在训练阶段得到的总字典W对电磁信号进行处理, 即在固定总字典W的情况下, 将表示含噪的瞬变电磁信号的矩阵Yd进行非负矩阵分解, 公式如下:
| $ {\mathit{\boldsymbol{H}}^d} = \arg \mathop {\min }\limits_{{\mathit{\boldsymbol{H}}^t}} \left\| {{\mathit{\boldsymbol{Y}}^d} - \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}^t}} \right\|_F^2 $ | (11) |
式中: arg表示取(11)式范数最小值的Hd。
求解(11)式后, 得到系数矩阵Hd。系数矩阵Hd可另写为
降噪模型为:
| $ {\mathit{\boldsymbol{Y}}^d} = \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{H}}^d} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{W}}_v}}&{{\mathit{\boldsymbol{W}}_n}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{H}}_v}}\\ {{\mathit{\boldsymbol{H}}_n}} \end{array}} \right] $ | (12) |
则估计的纯净的瞬变电磁信号矩阵
| $ {\mathit{\boldsymbol{\hat V}} = {\mathit{\boldsymbol{W}}_v}{\mathit{\boldsymbol{H}}_v}} $ | (13) |
| $ {\mathit{\boldsymbol{\hat N}} = {\mathit{\boldsymbol{W}}_n}{\mathit{\boldsymbol{H}}_n}} $ | (14) |
实验表明, 由前两步处理得到的降噪后的瞬变电磁信号不够理想。本文通过对前两步进行多次循环, 再求平均来提高降噪效果。显然, 该求平均值的平均次数是一个关键参数。本文对此进行了实验, 实验是在10dB的高斯白噪声环境下进行, 结果如图 1所示。从图 1可以看出, 在平均次数小于50次时, 输出信噪比随着平均次数的增加呈现出上升趋势; 在平均次数大于50次时, 输出信噪比不再随平均次数的增加而增加。因此, 在保证较低的时间、空间复杂度和较高质量的降噪效果的前提下, 本文选择的平均次数为50次。
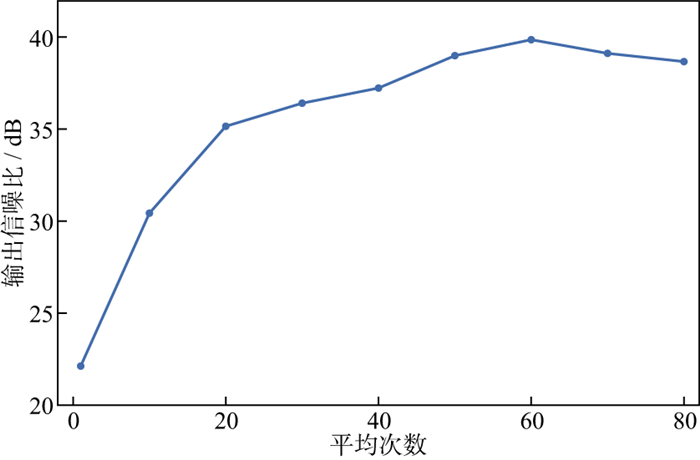
|
图 1 平均次数与输出信噪比的关系曲线 |
NMF的有监督算法的实现步骤(图 2)总结如下:
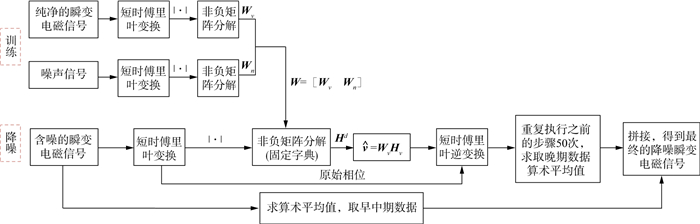
|
图 2 NMF的有监督算法流程 |
1) 取含噪的瞬变电磁信号y, 丢弃晚期数据, 保留早中期数据y, 以备后用;
2) 对含噪的瞬变电磁信号y、纯净的瞬变电磁信号v和噪声信号n分别进行短时傅里叶变换, 得到各自的幅度谱和相位谱, 取其幅度谱, 得到表示相应信号的非负矩阵Y、V和N;
3) 将表示纯净的瞬变电磁信号的非负矩阵V和噪声信号的非负矩阵N进行非负矩阵分解, 分别得到表示各自信号特征的原子字典Wv和Wn, 然后将其拼接成总字典W=[Wv Wn];
4) 在固定总字典W的前提下, 对表示含噪信号的非负矩阵Y进行非负矩阵分解, 得到系数矩阵H;
5) 利用公式(13)估计出表示纯净的瞬变电磁信号矩阵
6) 利用步骤2)得到的含噪信号y的原始相位和步骤5)估计的表示纯净的瞬变电磁信号矩阵
7) 重复执行步骤1)50次, 每次产生不同数值的含噪信号原始早中期数据y, 并求其算术平均值
8) 重复执行步骤2)至步骤6)50次, 求得v的算术平均值并丢弃其早中期数据而保留其晚期数据, 得到初步估计的瞬变电磁信号晚期数据ṽ;
9) 将得到的早中期数据
通过实验仿真及对比的方式来验证非负矩阵分解(NMF)有监督算法的有效性。该方法适用于数据采集后的预处理阶段, 采用的信号模型为加性噪声模型。在本实验中, 加入的噪声为高斯白噪声和天电噪声。天电噪声由Alpha稳定分布[23-24]模拟。纯净的瞬变电磁信号使用公式(1)模拟, 发射天线St的有效面积取10m2, 发射电流I取5A, 接收天线的有效面积Sr取100m2, 视电阻率ρ取大地平均值50Ω·m。另外, 为了与本文采用的实测数据的个数一致(本文的实测数据由重庆地质仪器厂的ATEM-Ⅱ型瞬变电磁仪采集, 密集均匀采样, 样本数为1000个), 模拟信号由采样频率为50kHz的均匀采样获得, 采样时间为20ms, 采样点数为1000个, 取其前40个数据为早中期数据, 后960个数据为晚期数据。为了保证实验的可信度, 噪声训练数据与加在纯净瞬变电磁信号上的噪声为同一类型, 只是数值不同。输入信噪比分别为-5, 0, 5, 10, 15dB。
在对比实验中, 本文选取小波变换、Hilbert-Huang变换(HHT)和奇异值分解(SVD)3种方法与本文方法进行对比。在小波变换中, 本文使用的是sym8小波, 硬阈值函数, 启发式阈值, 5层分解。在HHT中, 本文通过固有模态函数(IMF)分量的能量密度和平均周期的乘积确定有用的IMF分量。在SVD中, 本文采用赵学智等[25]提出的奇异值曲率谱方法确定有效的奇异值。
3.2 对比实验首先, 对加入天电噪声的瞬变电磁信号进行降噪处理。天电噪声是瞬变电磁信号噪声的主要来源之一, 其在波形上表现为突出的毛刺。图 3a是纯净的瞬变电磁时域信号, 图 3b是加入了15dB天电噪声的瞬变电磁信号。图 4是分别使用HHT、SVD、小波变换和本文方法降噪后的信号。
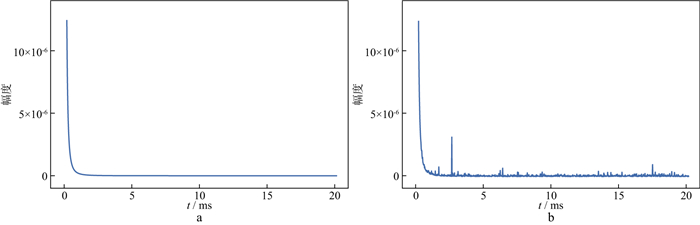
|
图 3 纯净信号与含噪信号 a纯净的瞬变电磁时域信号; b加入了15dB高斯白噪声的瞬变电磁信号 |
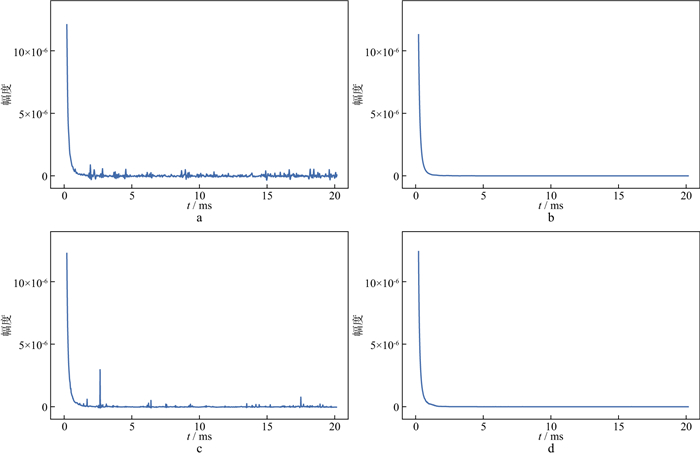
|
图 4 在15dB天电噪声环境下采用不同方法处理后的瞬变电磁信号 a HHT; b SVD; c小波变换; d本文方法 |
由图 4可见, 小波变换对天电噪声的消除基本没有作用, 经HHT处理后仍有较多毛刺, 但经SVD和本文方法降噪处理后, 天电噪声基本被消除, 看不出有明显的毛刺, 降噪效果较好。
对比在不同噪声环境下分别采用HHT、SVD、小波变换和本文方法的输出信噪比, 结果如表 1和表 2所示。一般来说, 输出信噪比越大, 混在信号中的噪声就越小。由表 2可见, 在天电噪声的环境下, 经小波变换处理后, 输出信噪比与输入信噪比基本相同, 这表明了小波变换对天电噪声基本没有抑制能力。HHT对高斯白噪声和天电噪声消除效果大致相同, 但输出信噪比不高。在输入信噪比为10dB和15dB的情况下, 相比于其它噪声环境, 采用SVD的输出信噪比提升幅度不大, 此方法对两种噪声抑制效果相当, 但其输出信噪比要比小波变换和HHT的输出信噪比高, 与本文方法相比, 其输出信噪比相对较低。经本文方法降噪处理后, 无论在何种噪声环境下, 其输出信噪比都有大幅度的提升, 而且要比采用SVD处理的高十几个分贝。
| 表 1 高斯白噪声采用不同方法处理后的输出信噪比 |
| 表 2 天电噪声下采用不同方法处理后的输出信噪比 |
表 3和表 4分别为在高斯白噪声环境下和天电噪声情况下采用4种方法处理后的均方根误差。均方根误差体现了原始信号和降噪之后的估计信号间的差异程度。降噪后的均方根误差越小, 表示原始有效信号和降噪之后的估计信号之间的差异越小, 两者越接近, 表明降噪效果越好。由表 3可以看出, 在高斯白噪声环境下, 采用HHT处理后的均方根误差最大, 采用小波变换、SVD和本文方法基本上依次减小, 说明HHT对高斯白噪声的消除能力最差, 本文方法的降噪能力最高。由表 4可以看出, 在天电噪声的环境下, 小波变换对天电噪声的消除能力最差, 经本文方法降噪处理后的均方根误差依然最小, 降噪效果最好。
| 表 3 高斯白噪声下采用不同方法处理后的均方根误差 |
| 表 4 天电噪声下采用不同方法处理后的均方根误差 |
总之, 从输出信噪比和均方根误差这两个降噪性能评价指标来看, 本文方法都要优于其它3种方法。
需要说明的是, 本文方法不仅对视电阻率为50Ω·m的含噪的瞬变电磁信号有效, 对其它视电阻率的含噪信号同样有降噪效果。另外, 虽然本实验是采用视电阻率为50Ω·m的纯净的瞬变电磁信号进行训练, 得到表征其特征的原子字典, 但利用此原子字典对其它视电阻率的含噪的瞬变电磁信号也起到降噪作用, 换句话说, 本文方法对视电阻率的大小并不敏感。如图 5所示, 对视电阻率为150Ω·m的含噪信号进行降噪, 用视电阻率为50Ω·m的纯净的瞬变电磁信号进行训练, 经本文方法处理后, 降噪后的信号依然与视电阻率为150Ω·m的纯净信号接近。可以预见, 这一重要特性将有利于本文方法的实际应用。
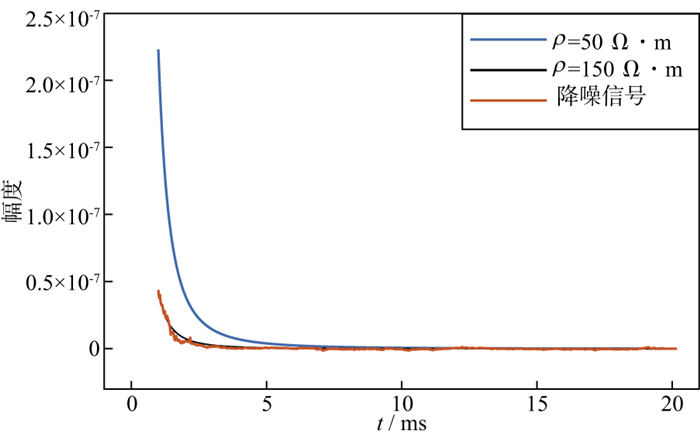
|
图 5 不同视电阻率与降噪信号的对比结果 |
采用本文方法对广东某地区的实测数据进行降噪处理。实验设备为重庆地质仪器厂的ATEM-Ⅱ型瞬变电磁仪, 采用中心回线装置工作, 密集均匀采样, 采样时间为20ms, 测得的数据未经过叠加处理。取10号线第38测点1000道数据中第381~900道作为噪声分析段, 其中第381~400道数据作为早中期数据, 第401~900道数据作为晚期数据, 并使用NMF的有监督算法进行降噪处理。纯净的瞬变电磁信号使用公式(1)仿真得到, 相关参数与仿真实验一致。由于采集数据的最后一部分瞬变电磁信号比较微弱, 噪声占主导地位, 可将这部分数据看作噪声, 则噪声训练数据将由实测数据的最后100道数据组成。另外, 本实验对实测数据进行分段处理, 其中晚期数据为5段, 每100道数据为一段, 早中期数据为单独一小段(早中期数据不需要进行非负矩阵分解处理), 以此来解决训练数据与含噪数据维度不匹配的问题。图 6是在某地测得的瞬变电磁信号, 其噪声分析段信号与降噪后的瞬变电磁信号分别如图 7a和图 7b所示。
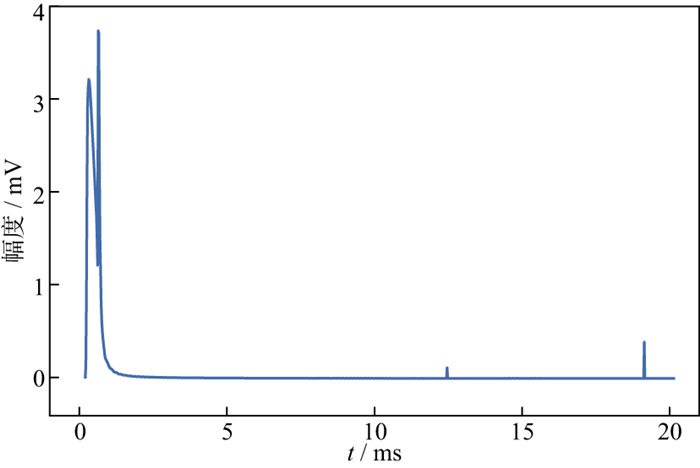
|
图 6 实测信号的时域波形 |
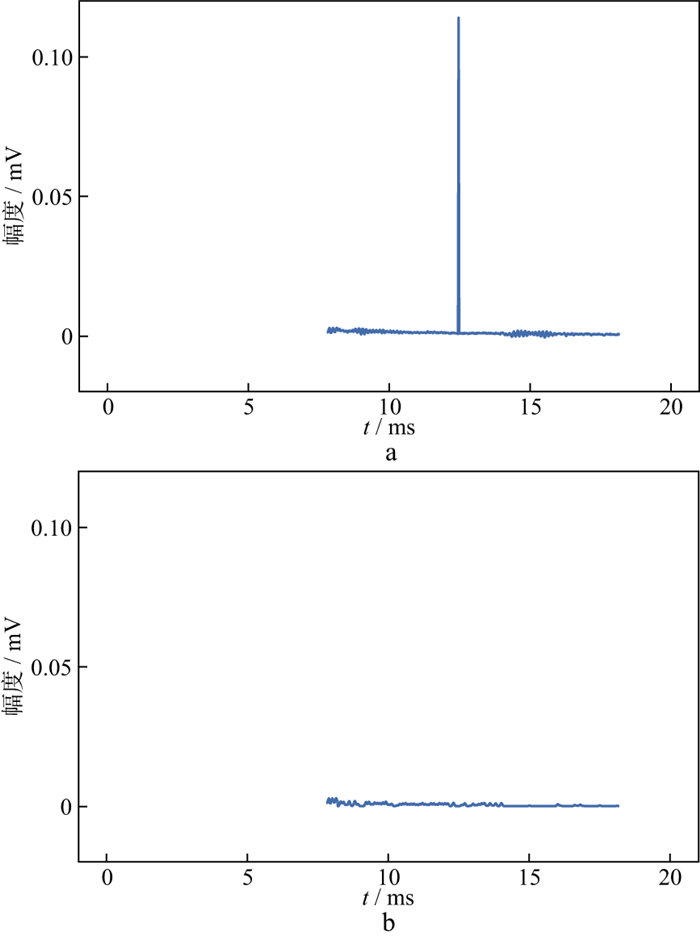
|
图 7 实测数据降噪前、后的对比结果 a噪声分析段; b降噪后的瞬变电磁信号 |
由图 6和图 7a可见, 实测数据存在明显的表现为毛刺的天电噪声和其它噪声。由图 7b可以明显看出, 降噪后的波形无明显的毛刺, 比较平滑, 噪声压制得比较干净, 降噪效果较好。这说明本文方法对实测数据是可行有效的。
5 结论本文对NMF的有监督算法如何应用于瞬变电磁信号降噪进行了研究, 得出如下结论。
1) 将含噪的瞬变电磁信号分为早中期和晚期两部分, 对含噪信号采用NMF的有监督算法处理, 步骤重复多次, 并将处理结果的晚期数据与含噪信号的原始早中期数据分别累加以求算术平均值, 最后拼接出完整的降噪信号。结果表明, 本文方法能有效地抑制高斯白噪声和天电噪声, 处理后的波形比较平滑, 噪声压制得比较干净。另外, 从输出信噪比和均方根误差这两个降噪性能评价指标看, 即使在低信噪比的情况下, 采用本文方法也能较大幅度地提高输出信噪比和降低均方根误差, 能取得较好的降噪效果, 提高了数据的质量, 有利于瞬变电磁信号的后续处理。
2) 相比于传统的降噪方法, 本文方法是一种基于字典学习的降噪算法, 能学习到信号的特征。理论上本文方法能对混有多种噪声的信号进行降噪处理(如非平稳噪声), 局限性较小, 降噪效果也较好。
需要指出的是, 本文方法的收敛速度较慢, 主要是因为非负矩阵分解的速度较慢, 需要几千甚至上万次的迭代计算, 这增加了算法的时间。另外, 本文方法对瞬变电磁信号的早中期数据处理效果不佳, 这一点有待进一步的研究。
| [1] |
牛之琏. 时间域电磁法原理[M]. 长沙: 中南大学出版社, 2007: 18-27. NIU Z L. Principle of time domain electromagnetic method[M]. Changsha: Central South University Press, 2007: 18-27. |
| [2] |
杨毅, 邓晓红, 王丽妍, 等. 地-井TEM典型特征分析与异常解释——以新疆白石泉铜镍矿zk506孔为例[J]. 煤田地质与勘探, 2018, 46(4): 186-190. YANG Y, DENG X H, WANG L Y, et al. Typical characteristics analysis and anomalies interpretation of borehole TEM: Taking Xinjiang Baishiquan Cu-Ni ore zk506 borehole as an example[J]. Coal Geology & Exploration, 2018, 46(4): 186-190. DOI:10.3969/j.issn.1001-1986.2018.04.030 |
| [3] |
刘晓波, 李艳莉, 李磊, 等. 地震属性和瞬变电磁技术在煤田勘探中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 218-223. LIU X B, LI Y L, LI L, et al. Joint application of seismic attributes and transient electromagnetic data in the coalfield exploration[J]. Oil Geophysical Prospecting, 2018, 53(S2): 218-223. |
| [4] |
唐新功, 胡文宝, 严良俊, 等. 瞬变电磁法油藏动态监测模拟[J]. 石油物探, 2004, 43(2): 192-195. TANG X G, HU W B, YAN L J, et al. Modeling of reservoir dynamic performance by TEM method[J]. Geophysical Prospecting for Petroleum, 2004, 43(2): 192-195. DOI:10.3969/j.issn.1000-1441.2004.02.022 |
| [5] |
沈建国, 舒敦利, 沈永进, 等. 套管井瞬变电磁测井在节箍处的响应与几何因子分析[J]. 石油物探, 2019, 58(4): 613-624. SHEN J G, SHU D L, SHEN Y J, et al. Response of casing hoop and geometry factor to transient electromagnetic logging in cased wells[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 613-624. DOI:10.3969/j.issn.1000-1441.2019.04.016 |
| [6] |
王显祥, 底青云, 邓居智. 多通道瞬变电磁法油气藏动态检测[J]. 石油地球物理勘探, 2016, 51(5): 1021-1030. WANG X X, DI Q Y, DENG J Z. Reservoir dynamic detection based on multi-channel transient electromagnetic[J]. Oil Geophysical Prospecting, 2016, 51(5): 1021-1030. |
| [7] |
闫赛, 郭恒庆, 刘树才, 等. 小波变换在瞬变电磁数据去噪中的应用[J]. 工程地球物理学报, 2010, 7(6): 656-660. YAN S, GUO H Q, LIU S C, et al. Application of wavelet transform to de-noising of TEM data[J]. Chinese Journal of Engineering Geophysics, 2010, 7(6): 656-660. DOI:10.3969/j.issn.1672-7940.2010.06.002 |
| [8] |
解海军, 颜羽, 董毅. 混合小波去噪在瞬变电磁资料处理中的应用[J]. 黑龙江科技大学学报, 2016, 26(6): 687-690. XIE H J, YAN Y, DONG Y. Application of mixed wavelet denoising method in TEM data processing[J]. Journal of Heilongjiang University of Science and Technology, 2016, 26(6): 687-690. DOI:10.3969/j.issn.2095-7262.2016.06.020 |
| [9] |
朱通. 基于Hilbert-Huang变换的瞬变电磁噪声压制研究与应用[D]. 西安: 长安大学, 2018 ZHU T. Study on transient electromagnetic method of denoising based on Hilbert-Huang transform[D]. Xi'an: Chang'an University, 2018 |
| [10] |
JI Y J, WU Q, WANG Y, et al. Noise reduction of grounded electrical source airborne transient electromagnetic data using an exponential fitting-adaptive Kalman filter[J]. Exploration Geophysics, 2018, 49(3): 243-252. DOI:10.1071/EG16046 |
| [11] |
张全, 李双田. 改进奇异值分解算法在时间域瞬变电磁信号降噪中的应用[J]. 信号处理, 2015, 31(8): 949-955. ZHANG Q, LI S T. Application of advanced singular value decomposition algorithm to time domain transient electromagnetic signal de-noising[J]. Journal of Signal Processing, 2015, 31(8): 949-955. DOI:10.3969/j.issn.1003-0530.2015.08.010 |
| [12] |
LIN F Q, CHEN K C, WANG X B, et al. A denoising stacked autoencoders for transient electromagnetic signal denoising[J]. Nonlinear Processes in Geophysics, 2019, 26(1): 13-23. DOI:10.5194/npg-26-13-2019 |
| [13] |
MOHAMMADIHA N, GERKMANN T, LEIJON A. A new linear MMSE filter for single channel speech enhancement based on Nonnegative Matrix Factorization[R]. Applications of Signal Processing to Audio and Acoustics(WASPAA), 2011 IEEE Workshop on, New Paltz, 2011
|
| [14] |
张龙. 有监督学习条件下的单通道语音增强算法研究[D]. 合肥: 中国科学技术大学, 2017 ZHANG L. Study on single-channel speech enhancement under supervised learning condition[D]. Hefei: University of Science and Technology of China, 2017 |
| [15] |
张星. 改进NMF单通道语音增强算法[J]. 机械设计与制造, 2019(1): 268-271. ZHANG X. Single-channel speech enhancement algorithm based on improved NMF[J]. Machinery Design & Manufacture, 2019(1): 268-271. DOI:10.3969/j.issn.1001-3997.2019.01.069 |
| [16] |
曾庆宁, 罗瀛, 刘帅, 等. 瞬变电磁全期视电阻率的弦截无限逼近算法[J]. 石油地球物理勘探, 2019, 54(6): 1371-1375. ZENG Q N, LUO Y, LIU S, et al. A secant infinite approximation algorithm for the full-time apparent resistivity in transient electromagnetic method[J]. Oil Geophysical Prospecting, 2019, 54(6): 1371-1375. |
| [17] |
余先川, 胡丹. 盲源分离理论与应用[M]. 北京: 科学出版社, 2011: 247-251. YU X C, HU D. Theory and application of blind source separation[M]. Beijing: Science Press, 2011: 247-251. |
| [18] |
BADEAU R, BERTIN N, VINCENT E. Stability analysis of multiplicative update algorithms and application to nonnegative matrix factorization[J]. IEEE Transactions on Neural Networks, 2010, 21(12): 1869-1881. DOI:10.1109/TNN.2010.2076831 |
| [19] |
LI L X, WU L, ZHANG H S, et al. A fast algorithm for nonnegative matrix factorization and its Convergence[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(10): 1855-1863. DOI:10.1109/TNNLS.2013.2296627 |
| [20] |
LIN C J. Projected gradient methods for non-negative matrix factorization[J]. Neural Computation, 2007, 19(10): 2756-2779. DOI:10.1162/neco.2007.19.10.2756 |
| [21] |
CICHOCKI A, LEE H, KIM Y D, et al. Non-negative matrix factorization with α-divergence[J]. Pattern Recognition Letters, 2008, 29(9): 1433-1440. DOI:10.1016/j.patrec.2008.02.016 |
| [22] |
FÉVOTTE C, BERTIN N, DURRIEU J L. Nonnegative matrix factorization with the itakura-saito divergence: With application to music analysis[J]. Neural Computation, 2009, 21(3): 793-830. DOI:10.1162/neco.2008.04-08-771 |
| [23] |
WERON R. On the Chambers-Mallows-Stuck method for simulating skewed stable random variables[J]. Statistics and Probability Letters, 1996, 28(2): 165-171. DOI:10.1016/0167-7152(95)00113-1 |
| [24] |
马金全, 葛临东. 基于Alpha稳定分布的大气噪声生成算法及其仿真[J]. 信息工程大学学报, 2010, 11(2): 214-217. MA J Q, GE L D. Algorithm and simulation of atmospheric noise generation based on Alpha stable distribution[J]. Journal of Information Engineering University, 2010, 11(2): 214-217. DOI:10.3969/j.issn.1671-0673.2010.02.019 |
| [25] |
赵学智, 叶邦彦, 陈统坚. 基于奇异值曲率谱的有效奇异值选择[J]. 华南理工大学学报(自然科学版), 2010, 38(6): 11-18. ZHAO X Z, YE B Y, CHEN T J. Selection of effective singular values based on curvature spectrum of singular values[J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38(6): 11-18. DOI:10.3969/j.issn.1000-565X.2010.06.003 |




