加拿大阿萨巴斯卡地区油砂资源主要储存于下白垩统Mannville群McMurray组[1-2]。区域内发育有冲积扇、河流相、潮汐三角洲、河口湾等沉积类型[2]。McMurray组自下而上分为3段: Continental为河流相沉积, Asm2和Asm3为河口湾沉积, 埋深在260~460m, 层厚100m左右, 主力层段Asm3段厚度为20~40m。
本地区油砂资源主要使用蒸汽辅助重力泄油(SAGD)技术开发, 影响SAGD技术开采效率的关键地质因素包括连续油层的厚度、泥岩夹层的分布及稳定的盖层等[1]。因此, 对研究区储层的岩性垂向变化和横向分布的精细研究将为后续油砂SAGD开发设计提供有力的参考和决策依据, 降低开发风险和成本[3-6]。
传统的测井岩性识别一般采用图版法、交会图法、本地区经验公式法[7], 或者使用电阻率成像资料识别油砂储层岩性[8], 这些方法应用的参数较少, 人为因素影响较大。神经网络技术在岩性识别方面曾经得到了广泛应用, 但是以BP神经网络为主要技术的识别方法存在收敛速度慢、隐层数以及隐层节点数难以确定、容易陷入局部极小值等缺点[9-10]。近年来以各类支持向量机和深度学习等为代表的机器学习方法越来越多地被用于测井岩性识别中。深度学习方法通过构建具有多个隐层的深度神经网络模型, 并利用大量数据训练模型来学习复杂而有效的信息进而提高预测分类的准确性[11], 在实际应用中取得了良好的效果, 但这类机器学习方法属于有监督学习下的预测方法, 需要规模较大的训练样本作为支撑, 当训练样本不足时模型的泛化能力会受到限制。
主成分分析(principal component analysis, PCA)方法也可以被直接用来识别测井岩性[12]。一般来说主成分分析用于数据预处理, 通过转换将相互关联变量组成的数据集转换为一组互不相关且有序的主变量, 排在前面的几个主变量保留了原始变量中的大部分信息, 从而在数据主要信息没有损失的情况下可以对数据进行降维处理[13]。聚类和判别分析也经常被用来进行测井岩性识别[14]。聚类是利用统计方法根据变量之间的近似程度进行分类, 大多经过反复迭代分类直到样本所属的类稳定为止, K-均值聚类(K-mean clustering)方法是较常用的聚类方法。判别分析是一个学习和预测过程, 一般是利用原有的分类信息得到体现这种分类的判别函数, 利用函数去判断未知样品属于哪一类。常用的判别分析方法有距离判别法、Fisher判别法和Bayes判别法, 在岩性识别中尤以Bayes判别分析法最为常见[15]。有别于机器学习测井岩相分类技术需要建立先验学习模式的方式, 无监督的测井岩相分析依据数据的内在关系, 结果不受人为因素干扰, 客观且可重复[16]。
目前研究区井孔的岩性划分主要依据钻井取心数据[6]。取心数据是非常直观和准确的数据, 但获取取心数据的成本很高, 因此亟需利用常规测井数据准确预测测井储层岩性的技术方法降低开发成本。本文结合Kinosis工区的实际数据, 选用常规测井曲线数据, 首先进行主成分分析, 然后对由数据的内在概率分布混合形成的模型进行聚类分析, 最后运用贝叶斯准则来评估模型, 确定每个样本所属类别及属于该类的概率, 得到井位处的垂向岩相分类。在整个基于贝叶斯概率模型的聚类分析中, 模型的参数和聚类的数量选择使用无监督自主学习的方式, 完全由数据驱动, 避免了人为因素的干预影响。综合应用储层的矿物学特征、岩石力学特征、物性和取心照片对井位处预测的测井岩相进行标定, 确定储层内不同岩相的岩石类型和对应的地质描述, 提出了一套仅利用常规测井曲线预测井孔储层段岩性的技术, 取得了良好的应用效果。
1 方法原理 1.1 主成分分析(PCA)PCA是考察多个变量间相关性的一种多元统计方法, 是研究如何通过少数几个主成分来揭示多个变量间的内部结构, 即从原始变量中导出少数几个主成分, 使它们尽可能多地保留原始变量的信息, 且彼此间互不相关。PCA能够有效提炼数据的信息, 而且在数据主要信息没有损失的情况下对数据降维。PCA的实质是确定一个坐标系统的正交变换, 将一组可能存在相关性的变量转换为一组线性不相关的变量, 在新坐标系统下经变换的数据点的方差沿新的坐标轴得到了最大化, 转换后的这组变量叫主成分(或主组分)。PCA处理过程简述如下。
1) 假设我们有p条测井响应曲线, 每条曲线有n个测量样本, 其样本矩阵为:
| $ \begin{aligned} \boldsymbol{X} &=\left[X_{1}, X_{2}, \cdots, X_{p}\right] \\ &=\left[\begin{array}{cccccc} x_{11} & x_{12} & \cdots & x_{1 j} & \cdots & x_{1 p} \\ x_{21} & x_{22} & \cdots & x_{2 j} & \cdots & x_{2 p} \\ \vdots & \vdots & & \vdots & & \vdots \\ x_{i 1} & x_{i 2} & \cdots & x_{i j} & \cdots & x_{i p} \\ \vdots & \vdots & & \vdots & & \vdots \\ x_{n 1} & x_{n 2} & \cdots & x_{n j} & \cdots & x_{n p} \end{array}\right] \\ i=& 1, 2, \cdots, n ; j=1, 2, \cdots, p ; n>p \end{aligned} $ | (1) |
为了消除实际数据量纲的影响, 对样本矩阵元素进行如下标准化变换:
| $ z_{i j}=\frac{x_{i j}-\overline{x_{j}}}{s_{j}} $ | (2) |
| $ i=1, 2, \cdots, n ; j=1, 2, \cdots, p ; n>p $ |
其中,
2) 求取相关系数矩阵R:
| $ \boldsymbol{R}=\left[r_{i j}\right]_{p \times p}=\frac{\boldsymbol{Z}^{\mathrm{T}} \boldsymbol{Z}}{n-1} $ | (3) |
其中,
3) 解样本相关系数矩阵R的特征方程|R-λIp|=0, 其中, Ip=(A1, A2, …, Ap), 得到按大小排列的p个特征根λ1 > λ2 > … > λp > 0和对应的p个特征向量Ai=(a1i, a2i, …, api), 其中, i=1, 2, …, p。
4) 将标准化后的数据样本变量转换为主成分, 即
| $ \begin{array}{l} \boldsymbol{F}=\boldsymbol{A} \boldsymbol{Z} \text { 或 } F_{i j}=\sum\nolimits_{k=1}^{p} a_{k i} z_{j k} \\ i=1, 2, \cdots, p ; j=1, 2, \cdots, n \end{array} $ | (4) |
定义Fi=(Fi1, Fi2, …, Fin)为主成分, F1为第一主成分, F2为第二主成分, …, Fp为第p主成分。
5) 根据给定的门槛值(一般q=0.85), 当前m个主成分的方差和占全部总方差的比例大于给定门槛值q时, 利用如下特征值累积贡献度确定m值:
| $ \frac{\sum\nolimits_{j=1}^{m} \lambda_{j}}{\sum\nolimits_{j=1}^{p} \lambda_{j}}>q $ | (5) |
此时m < p, 选取前m个主成分表示原样本, 起到降维的作用。
1.2 基于贝叶斯概率模型的聚类分析聚类分析的目标是依据数据本身的分布特征, 将整个数据(空间)划分成不同的类。基本准则是同类数据应该具有某种相似性, 而异类数据应该具有某种差异性。基于无监督学习的测井岩相分析, 不需要地质先验信息, 而是遵循所选用测井曲线特有的岩性、物性或流体特征, 综合运用主成分分析、基于贝叶斯概率模型的聚类分析和判别分析来识别和描述测井岩相类别。BANFIELD等[17]通过分解参数化协方差矩阵的特征值提出了一种基于模型的聚类分析方法, 该方法的核心思想是数据是由内在概率分布混合而成。相较于传统的聚类分析方法, 比如单链聚类(Single-link clustering)或K-mean clustering方法, 该方法可以得到更好的结果。基于模型的另一个优势就是运用贝叶斯准则来评估模型, 这样就提供了无监督的学习方式来选择模型的参数和聚类的数量。整个分析过程完全由数据驱动, 避免了人为因素的干预影响。
该概率模型中, 样本总体由G个不同的聚类组成, 假设第k个聚类的p维观测值x由密度函数fk=(X; θ)产生。给定观测值X=(x1, x2, …, xn), Γ=(γ1, γ2, …, γn)T表示识别标签, 如果xi来自第k个聚类, 则γi=k。最大似然分类法就是选择θ和γ, 使(6)式的似然达到最大。
| $ L(x;\theta , \gamma ) = \prod\nolimits_{i = 1}^n {{f_{{\gamma _i}}}} \left( {{x_i};\theta } \right) $ | (6) |
然而, 最大似然分类法有如下几个限制:
1) 只考虑协方差矩阵在所有聚类中均为常数的限制性模型, 或考虑协方差矩阵是任意且不相等的不相容模型;
2) 只允许高斯分布, 而其它分布在某些情况下可能更合适;
3) 通常不允许存在噪声或不符合当前集群模式的数据点。
(6) 式定义的模型具有普遍性, 可以包含具有非高斯分布的聚类。
为了突破上述限制, 我们使用近似贝叶斯方法来选择聚类的数目。将估计聚类数量的问题视为在相同数据的竞争模型之间进行选择的问题。精确的贝叶斯解包括在给定数据x的情况下, 求出每个聚类G的后验概率p(G|x)。在对模型进行比较时, 这种方法似乎比假设检验的替代方法更具优势, 因为它避免了多重比较、比较非嵌套模型的问题, 并且避免了样本量较大时假设检验选择非简约模型的趋势。
贝叶斯因子(Brs)用来描述一个模型优于另一个模型的相对确定性, 常被用来进行模型比较, 定义Brs为:
| $ $ | (7) |
其中, X为观测到的地震数据, G=r表示r个聚类的模型, G=s表示s个聚类的模型。一般地, p(X|G=k)表示聚类模型G=k成立时观测到X的概率, p(X|G=k)又称为边际似然函数, 其表达式为:
| $ \begin{array}{*{20}{c}} {p(X\mid G = k) = \sum\nolimits_{\gamma \in {\mathit{\Gamma }_k}} {\iint L } (x;\theta , \nu , \gamma ) \cdot }\\ {p(\theta , \nu , \gamma ){\rm{d}}\theta {\rm{d}}\nu } \end{array} $ | (8) |
式中:Γk={0, 1, …, k}n;L(x; θ, ν, γ)为广义似然函数;p(θ, ν, γ)为θ, ν和γ的联合先验密度。
我们集中讨论Br, r+1(r=1, 2, …, n-1)的近似计算, 其直接产生后验概率p(G=r|x), 如(9)式所示。注意到
| $ p(G = r\mid x) = \frac{{{B_{r{s_0}}}p(G = r)}}{{\sum\limits_{t = 1}^{n - 1} {{B_{t{s_0}}}} p(G = t)}} $ | (9) |
其中, p(G=r)是存在r个聚类的先验概率, p(G=t)是存在t个聚类的先验概率。
在聚集层次聚类算法中, 比较G=r+1和G=r的差异大小, 决定是否将两个特定的聚类合并为一个。在p维多元情况下, 这正好是一般线性模型中嵌套假设的标准比较。
在基于模型的贝叶斯概率分布基础上进行判别分析确定样本点的最后类别。
2 实际应用及效果分析Kinosis工区位于阿萨巴斯卡矿区南部, 油砂资源埋深较浅, 原油黏度较大, 发育较厚盖层。McMurray组主力储集层为内河口湾复合点坝沉积, 岩性以中、细砂岩为主, 发育多种类型泥岩隔夹层。该区域由于受到河流和潮汐的共同作用, 发育顺流加积型点坝、泛滥平原、废弃河道、河道底部滞留等沉积微相[2]。油砂资源主要使用SAGD技术进行开发, 大量实际数据和模型研究表明, 除了垂向渗透率、储层厚度、孔隙度、含油饱和度等储层参数[18]和不同类型水层[19]对油砂SAGD开发产生影响外, 储层的岩性特征, 特别是储层内的夹层和隔夹层的空间分布、平面展布及厚度变化等[3-6]对油砂SAGD开发效果影响较大。因此, 精确刻画油砂储层内的侧积砂层和隔夹层的空间分布是该地区储层研究的重要内容。在进行此类研究之前, 一般应先准确地识别储层段内的测井岩相。
本研究中共收集到Kinosis工区内71口井的测井信息, 其中59口井收集到了完整的地质分层数据和常规测井数据(包括自然伽马、密度、声波、电阻率、自然电位等)及测井解释数据(包括泥质含量、孔隙度、含水饱和度、渗透率等曲线), 还收集到了5口井的取心照片, 它们将用于对比标定岩相。考虑数据的客观性, 选择了自然伽马(GR)、密度(RHOB)、电阻率(RT)和自然电位(SP)原始测量数据用于基于贝叶斯概率模型无监督学习的聚类分析。其中GR曲线对岩性敏感, 可识别砂泥岩; SP曲线对岩性敏感, 还反映渗透性, 可识别隔夹层; RHOB对岩性和物性敏感, 可识别砂岩; RT对流体敏感, 可识别油水层。区域内的71口井中有59口井在目的层含有这4种测井曲线, 满足统计分析大样本量需求。同时结合井径曲线(CAL)和声波曲线(AC)对全区59口井的测井曲线进行质量控制检查, 所选择的测井曲线质量可靠, 受井径影响较小。由于井的数量较多, 存在多井的系统误差, 尤其是SP各井基线偏移差异大, 在进行PCA之前首先对多井目标地层测井采集系列曲线进行一致性检查并对SP、RHOB和GR曲线进行标准化处理。
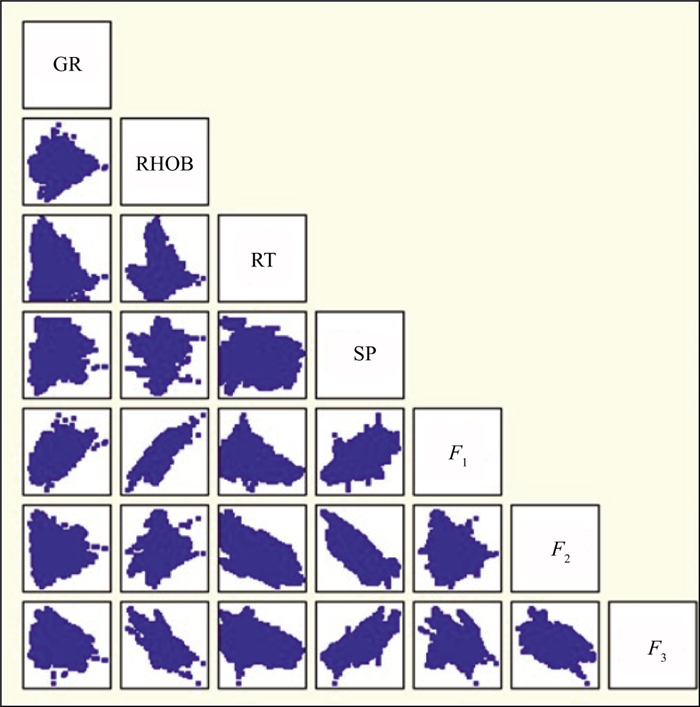
在研究区内, 用前面提到的4种测井曲线(GR、RHOB、RT、SP)在McMurray层段进行了主成分分析。从表 1和表 2可以看出, 主成分F1占总信息的53.5%, 4条曲线与之相关性较接近, 其中, RHOB与GR曲线相关性略大; F2占总信息的23.7%, 与RT高度相关, 其次与SP较相关; F3占总信息的15.4%, 其与4条曲线的相关性较接近, 与SP相关性略大; 前3组占总信息的92.7%。图 1为测井曲线与主成分曲线交会图, 显示了各主成分曲线与测井曲线的关系, 即:
| 表 1 PCA的特征值贡献率 |
| 表 2 样本测井曲线与主成分曲线相关性 |
|
图 1 测井曲线与主成分曲线交会分析结果 |
1) F1与RHOB、GR、SP呈正相关, 与RT呈弱负相关;
2) F2与RT、SP呈负相关, 与GR、RHOB曲线几乎没有相关性;
3) F3与SP呈正相关, 与RT、RHOB、GR呈负相关。
由于F4只含有不足8%的有效信息, 在进行测井岩相分析的时候, 采用了降维处理, 去掉F4曲线, 以期提高测井岩相分析结果的可靠性。
在Kinosis工区使用59口井的主成分曲线(F1、F2、F3)作为样本进行无监督学习的测井岩相分析, 根据对油砂储层的地质认识, 设置岩相类别个数最少为6个, 最多为12个。首先根据数据内在概率分布建立从6类到12类的7个分类概率模型, 然后在每个模型内对所有样本点进行聚类分析和贝叶斯准则判别, 通过迭代计算, 系统自动学习判别模型的优劣, 最后输出认为最优的分类结果。经过基于贝叶斯概率模型无监督学习的测井岩相分析, 得到59口井的8个岩相类别曲线。
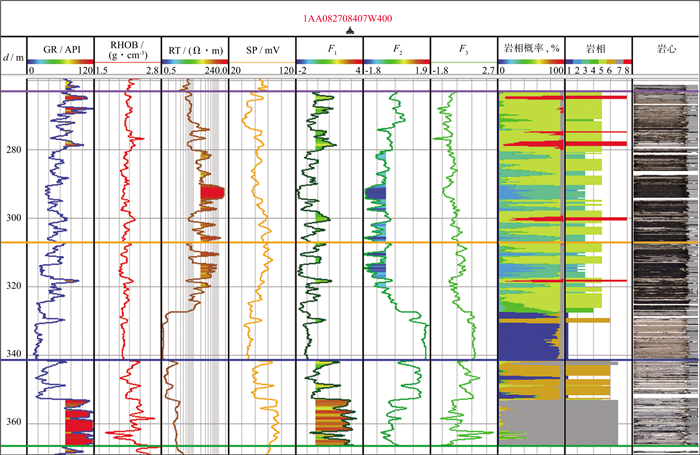
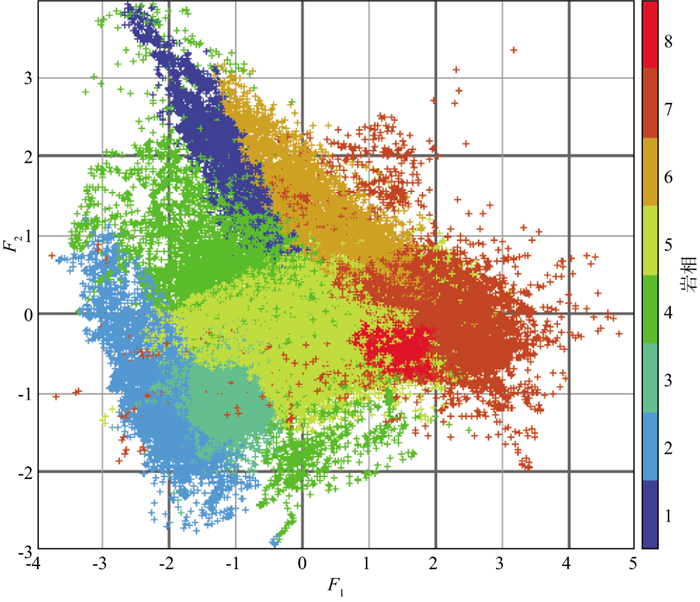
图 2显示了某口岩心井在McMurray层段的岩相分析结果。图 2从左至右分别是用于分相的源曲线(GR、RHOB、RT、SP)、主成分曲线(F1、F2、F3)、样本点归属某类的概率曲线(概率值填充颜色与所属岩相相同)及岩相结果和对应的岩心。主成分F1与GR和RHOB曲线形态相似, 呈正相关, 其高值对应泥质隔夹层或泥岩。主成分F2与RT和SP曲线形态相似, 方向相反, 呈负相关, 其低值表示含油。岩相概率曲线用来判别样本点属于某个岩相的概率, 以最高概率值的岩相作为该样本最终确定的岩相, 从图上可以看出, 某些样本属于岩相4还是岩相5的概率是比较接近的, 也可以说这些样本属于岩相4还是岩相5都是可以接受的。从不同岩相的F1与F2交会分析结果(图 3)也可以看出, 除了岩相4和岩相5有较多重叠外, 其它岩相基本被分开了, 说明基于贝叶斯概率模型无监督学习的测井岩相分析结果与数据内在规律一致。
|
图 2 某口岩心井在McMurray层段的岩相分析结果 |
|
图 3 不同岩相的F1与F2交会分析结果 |
对岩相分类结果使用常规测井曲线(包括自然伽马、电阻率、密度、声波等)、测井解释曲线(包括泥质含量、孔隙度、含水饱和度、渗透率等)以及岩心照片等地质资料, 采用数据交会图、直方图、多井剖面图进行统计分析和标定, 确定每个岩相在储层段的测井电性特征、矿物学特征、物性特征、岩性特征和地质描述。
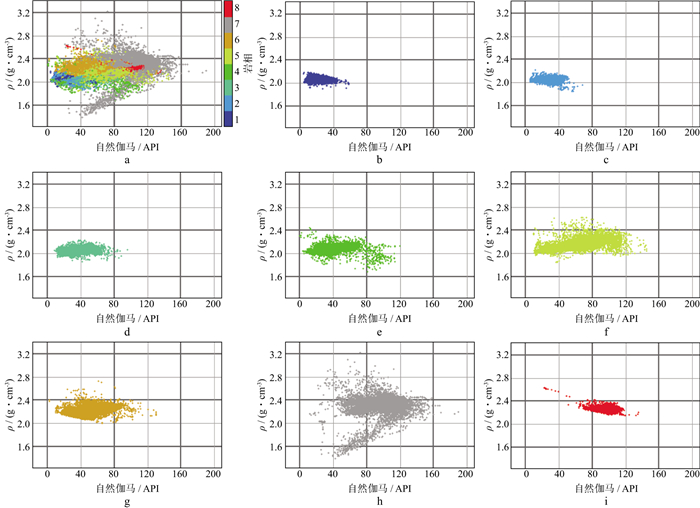
图 4给出了不同岩相的自然伽马与密度交会分析结果。图 4a为59口井目的层段内所有样本点数据的交会分布结果; 图 4b至图 4i分别为每个岩相的自然伽马和密度交会结果。图 4b中岩相1表现为低伽马(大部分值低于40API)、低密度(大部分值低于2.2g/cm3)特征; 图 4c中岩相2表现为低伽马(大部分值低于50API)、低密度(大部分值低于2.1g/cm3)特征; 图 4d中岩相3表现为低伽马(大部分值低于60API)、低密度(大部分值低于2.2g/cm3)特征; 图 4e中岩相4表现为中低伽马(大部分值位于10~80API)、低密度(大部分值低于2.2g/cm3)特征; 图 4f中岩相5表现为中高伽马(大部分值位于30~90API)、中低密度(大部分值位于2.0~2.4g/cm3)特征; 图 4g中岩相6表现为中低伽马(大部分值位于20~90API)、中低密度(大部分值位于2.1~2.4g/cm3)特征; 图 4h中岩相7表现为高伽马(大部分值位于60~160API)、高密度(大部分值高于2.2g/cm3, 少量小于2.0g/cm3)特征; 图 4i中岩相8表现为高伽马(大部分值位于70~120API)、高密度(大部分值位于2.2~2.4g/cm3)特征。同样的, 对任意测井曲线和解释曲线两两组合, 采用交会图方式, 定量研究它们在每个岩相的数值分布范围和特征(表 3)。
|
图 4 不同岩相的自然伽马与密度交会分析结果 a所有样本点交会分析结果; b岩相1交会分析结果; c岩相2交会分析结果; d岩相3交会分析结果; e岩相4交会分析结果; f岩相5交会分析结果; g岩相6交会分析结果; h岩相7交会分析结果; i岩相8交会分析结果 |
| 表 3 无监督测井岩相分析及解释结果 |
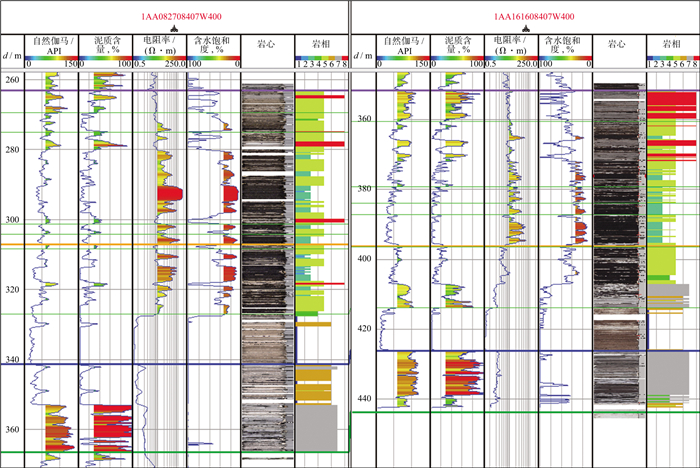
图 5为利用测井曲线、测井解释曲线和岩心照片在垂直剖面上对预测出的岩相进行分析、识别和标定的结果。在分析、统计测井曲线交会图和直方图的基础上, 根据对岩心照片的对比识别, 对岩相结果进行了进一步的解释和标定, 认为在Kinosis工区岩相1、2、3、4为砂岩, 岩相7、8为泥岩, 岩相5和岩相6为砂泥互层。
|
图 5 利用测井曲线、测井解释曲线和岩心照片在垂直剖面上对预测出的岩相进行分析、识别和标定的结果 |
图 6给出了各岩相及其对应的岩性(解释的泥质含量)、岩心、流体性质(解释的含水饱和度)的局部放大结果。根据岩性、含水饱和度和岩心上表现出的岩石地质现象确定各岩相的岩性及地质意义。通过大量的数据比对, 认为岩相1为砂岩(单层厚度 > 10m), 河道沉积, 水层, 主要分布在Asm2底部; 岩相2为砂岩(单层厚度 > 10m), 河道沉积, 油砂(无隔夹层); 岩相3为砂岩(单层厚度 < 10m), 河道沉积, 油砂(有时见单层厚度 < 10cm的薄夹层); 岩相4为砂岩, 河道沉积, 油砂(相对岩相3含油饱和度较低, 发育薄的砂岩隔夹层); 岩相5部分为砂岩/泥质砂岩(Asm3段上部), 河漫沉积, 部分为砂岩, 河道沉积(Asm3段中下部/Asm2段上部), 油砂与夹层互层(单夹层厚度3~30cm); 岩相6为砂岩/泥质砂岩, 河道沉积, 水层, 主要分布在Asm2下部和Continental段; 岩相7为泥岩, 河漫/牛轭湖, 隔夹层(单层厚度 > 2m), 主要分布在Asm2上部和Continental段; 岩相8为泥岩, 河漫沉积, 隔夹层, 主要分布在Asm3上部。

|
图 6 各岩相及其对应的岩性、岩心、流体性质的局部放大结果 |
按照上述流程进行大量的数据交会图、直方图、多井剖面图的统计分析和标定, 确定每一种岩相的自然伽马、电阻率、密度、纵波速度、泥质含量、孔隙度、含水饱和度、渗透率的响应特征和数值范围, 解释出岩相的岩性特征, 并依据井上的所属地质层位和岩心照片进行地质描述。该解释结果与钻井取心解释结果吻合度达到97%, 表 3详细记录了每个岩相的解释结果。
3 结论1) 本文方法在Kinosis工区的实际应用中, 主成分F1与岩性密切相关, 其高值对应泥质隔夹层或泥岩; 而主成分F2与流体关系密切, 其低值表示含油, 高值表示含水。采用PCA方法能有效地从多种测井参数中提取出突出岩性和流体特征的主成分, 实现数据降维, 为岩相分析奠定基础。
2) 在主成分分析的基础上, 利用主成分曲线(F1、F2、F3)作为样本进行基于贝叶斯概率模型无监督学习的测井岩相分析。通过迭代计算, 系统自动学习判别模型的优劣, 从7个分类概率模型中输出认为最优的8类岩相。不同岩相的F1与F2交会分析结果显示, 每个岩相内样本点基本上是分开的, 表明岩相分析结果反映了数据内在规律。由于使用的岩相分析方法无需提供先验的岩性类别模型, 使用无监督自主学习的方式选择模型参数和聚类数量, 完全数据驱动, 避免了人为因素的干预影响, 使得结果更加客观。
3) 对岩相分类结果使用常规测井曲线、测井解释曲线以及岩心照片等地质资料, 采用交会图、直方图、多井剖面图进行统计分析和标定, 确定每个岩相在储层段的测井电性特征、矿物学特征、物性特征、岩性特征和地质描述。认为在Kinosis工区岩相1(含水)、2、3、4为砂岩, 岩相7、8为泥岩, 岩相5和岩相6为砂泥互层。随机抽取研究区内没有参与标定的井的钻井取心资料对解释结果进行检验, 吻合度达到97%, 岩相分类结果稳定可靠, 可用于没有取心数据的井中。
本文方法在Kinosis工区的实际应用, 展示了一种利用常规测井曲线预测井孔油砂储层岩性的较为经济的研究方法。考虑到在阿尔伯塔省和世界其它地方对油砂储层进行表征的重要性, 本文方法具有潜在的广泛应用前景。
| [1] |
刘子玉, 吕明. 加拿大Athabasca地区下白垩统McMurray组沉积特征分析[J]. 四川地质学报, 2012, 32(1): 1-5. LIU Z Y, LV M. Sedimentology of the lower cretaceous McMurray formation in Athabasca, Canada[J]. Acta Geologica Sichuan, 2012, 32(1): 1-5. DOI:10.3969/j.issn.1006-0995.2012.01.001 |
| [2] |
胡光义, 许磊, 王宗俊, 等. 加拿大阿萨巴斯卡Kinosis区域下白垩统McMurray组内河口湾复合点坝砂体构型解剖[J]. 古地理学报, 2018, 20(6): 1001-1012. HU G Y, XU L, WANG Z J, et al. Architectural analysis of compound point-bar sandbody in inner estuary of the lower cretaceous McMurray formation in Kinosis area, Athabasca, Canada[J]. Journal of Palaeogeography, 2018, 20(6): 1001-1012. |
| [3] |
郑强, 田冀, 谭先红, 等. 油砂SAGD合理开发界限与主控因素研究[J]. 中国科学, 2017, 47(2): 204-209. ZHENG Q, TIAN J, TAN X H, et al. Rational development boundaries and main controlling factor of SAGD in oil sand[J]. Scientia Sinica Technologica, 2017, 47(2): 204-209. |
| [4] |
魏绍蕾, 程林松, 张辉登, 等. 夹层对加拿大麦凯河油砂区块双水平井蒸汽辅助重力泄油开发的影响[J]. 油气地质与采收率, 2016, 23(2): 62-69. WEI S L, CHENG L S, ZHANG H D, et al. Physical simulation of the interlayer effect on SAGD production by dual horizontal well in Mackay River oil sands block, Canada[J]. Petroleum Geology and Recovery Efficiency, 2016, 23(2): 62-69. DOI:10.3969/j.issn.1009-9603.2016.02.011 |
| [5] |
孔令晓, 齐梅, 张帅超, 等. 泥质薄夹层不同参数对油砂SAGD开发效果的影响[J]. 现代地质, 2018, 32(3): 538-546. KONG L X, QI M, ZHANG S C, et al. Effects of different parameters in thin muddy interlayer on SAGD production in Oil Sands[J]. Geoscience, 2018, 32(3): 538-546. |
| [6] |
胡元现, CHAN M, BHARATHA S, 等. 西加拿大盆地油砂储层中的泥夹层特征[J]. 地球科学—中国地质大学学报, 2004, 29(5): 550-554. HU Y X, CHAN M, BHARATHA S, et al. Mudstone interbeds in McMurray oil sand reservoirsin Alberta, Canada[J]. Earth Science——Journal of China University of Geosciences, 2004, 29(5): 550-554. |
| [7] |
雍世和, 张超谟. 测井资料处理与综合解释[M]. 北京: 中国石油大学出版社, 2007: 121-133. YONG S H, ZHANG C M. Logging data processing and comprehensive interpretation[M]. Beijing: China University of Petroleum Press, 2007: 121-133. |
| [8] |
李冰, 令狐松, 包鑫, 等. 加拿大油砂储层测井评价关键技术[J]. 测井技术, 2019, 43(4): 391-397. LI B, LINGHU S, BAO X, et al. Key technologies for log evaluation of oil sand reservoirs in Canada[J]. Well Logging Technology, 2019, 43(4): 391-397. |
| [9] |
SAMUEL J R, FANG J H, KARRA C L, et al. Determination of lithology from well logs using a neural network[J]. AAPG Bulletin, 1992, 76(5): 731-739. |
| [10] |
付光明, 严加永, 张昆, 等. 岩性识别技术现状与进展[J]. 地球物理学进展, 2017, 32(1): 26-40. FU G M, YAN J Y, ZHANG K, et al. Current status and progress of lithology identification technology[J]. Progress in Geophysics, 2017, 32(1): 26-40. |
| [11] |
安鹏, 曹丹平. 基于深度学习的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2018, 33(3): 1029-1034. AN P, CAO D P. Research and application of logging lithology identification based on deep learning[J]. Progress in Geophysics, 2018, 33(3): 1029-1034. |
| [12] |
周游, 张广智, 高刚, 等. 核主成分分析法在测井浊积岩岩性识别中的应用[J]. 石油地球物理勘探, 2019, 54(3): 667-675. ZHOU Y, ZHANG G Z, GAO G, et al. Application of kernel principal component analysis in well logging turbidite lithology identification[J]. Oil Geophysical Prospecting, 2019, 54(3): 667-675. |
| [13] |
JOLLIFFO I T. Principal component analysis[M]. USA: Springer, 2002: 30-33.
|
| [14] |
寻知锋, 余继峰. 聚类和判别分析在测井岩性识别中的应用[J]. 山东科技大学学报——自然科学版, 2008, 27(5): 10-13. XUN Z F, YU J F. The application of cluster and discriminant analyses in logging lithology recognition[J]. Journal of Shandong University of Science and Technology, 2008, 27(5): 10-13. |
| [15] |
孙健, 周魁, 冉小丰, 等. Bayes判别分析方法在岩性识别中的应用[J]. 石油天然气学报, 2009, 31(2): 74-77. SUN J, ZHOU K, RAN X F, et al. Application of Bayes discriminant analysis method in lithology identification[J]. Journal of Oil and Gas Technology, 2009, 31(2): 74-77. DOI:10.3969/j.issn.1000-9752.2009.02.017 |
| [16] |
林年添, 付超, 张栋, 等. 无监督与监督学习下的含油气储层预测[J]. 石油物探, 2018, 57(4): 601-610. LIN N T, FU C, ZHANG D, et al. Supervised learning and unsupervised learning for hydrocarbon prediction using multiwave seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 601-610. DOI:10.3969/j.issn.1000-1441.2018.04.015 |
| [17] |
BANFIELD J D, RAFTERY A E. Model-based Gaussian and non-Gaussian clustering[J]. Biometrics, 1993, 49(3): 803-821. DOI:10.2307/2532201 |
| [18] |
李浩哲, 梁琳琳, 潘少杰, 等. 储层参数对蒸汽辅助重力泄油技术开发效果的影响[J]. 非常规油气, 2017, 4(1): 84-87. LI H Z, LIANG L L, PAN S J, et al. Effect of reservoir parameters on development technology with steam assisted gravity drainage[J]. Unconventional Oil & Gas, 2017, 4(1): 84-87. DOI:10.3969/j.issn.2095-8471.2017.01.014 |
| [19] |
皮建, 朱磊, 武静, 等. 不同类型水层对油砂SAGD开发的影响分析[J]. 长江大学学报(自科科学版), 2015, 12(20): 69-72. PI J, ZHU L, WU J, et al. The influence of different water layers on oil sand SAGD development[J]. Journal of Yangtze University(Natural Science Edition), 2015, 12(20): 69-72. |



