2. 中海石油(中国)有限公司湛江分公司, 广东湛江, 524057
2. Zhanjiang Branch of CNOOC Ltd., Zhanjiang 524057, China
随着油气勘探开发的不断深入, 开发井和探井的数量不断增加, 测井解释人员需要结合本区域的地质模式选择测井解释模型和解释参数, 对测井资料进行精细化解释评价[1-2]。目前主流的测井解释系统均未包含区域研究成果及专家经验知识, 因此测井人员在测井解释时, 需要先对区域地质数据进行分析, 再分选模型和确定参数, 这在很大程度上降低了测井解释的效率。不熟悉区域地质情况的测井解释人员往往不能正确地选择测井解释模型及参数, 从而造成了测井解释评价不准确, 其结果无法准确反映真实油气藏情况。包含专家经验的测井知识库可以将专家头脑中的认知转化为测井解释人员实际工作中的理性认知, 使测井解释人员在模型选择和参数确定等测井解释环节中最大限度地减少人为干扰因素, 提高测井解释效率及精度。
目前, 知识库[3-4]的研究和应用在国内外引起广泛关注, 知识库的种类及构建方法[5-6]较多。传统的知识检索和知识智能调用方法主要包括混合推理[7]、最小井距法[8]等, 当知识库中存在不确定性的知识时, 传统方法普遍存在准确度不高的问题。SHARMA[9]提出通过人工智能自适应模式获取知识, 通过增加知识的依赖性进而获取准确的知识, 但这是一种理想状态的知识库系统, 且建立过程复杂。GENE ONTOLOGY CONSORTIUM [10]提出了一种基于本体的知识库构建模式, 该模式通过本体推理获得知识, 但本体构建均针对特定的领域, 无法形成通用的知识模式。尚福华等[11]提出了一种首先利用关联规则查找知识, 然后采用模糊推理对多条规则消除冲突, 最后利用结果分析得到知识的方法, 该方法的不足之处在于对于复杂规则需要人工判别。ZHU等[12]提出了基于KNN算法的知识库查询方法, 该方法利用KNN算法判别和调用知识流, 但KNN算法对于高维数据的判别存在不足之处。
在对测井解释评价流程综合分析以及相关算法研究的基础上, 本文提出了基于KNN-Fisher算法的测井解释知识库构建方法, 该方法在ZHU等[12]提出的KNN算法分类知识调用的基础上, 引入了Fisher判别法对知识降维分类, 同时, 为提高计算精度, 在KNN算法中加入权重及质心点等约束条件, 实现了对知识的自动调用。将该方法应用于南海西部某油田测井解释, 解释成果证明了方法的有效性。
1 KNN-Fisher算法研究考虑到Fisher判别法[13-16]与KNN算法[17-18]各自的优点, 将KNN算法与Fisher判别法相结合建立了KNN-Fisher算法, 该算法既具有KNN算法的稳定性及准确性, 又具有Fisher处理高维数据集及多样本数据集的优势。KNN-Fisher算法原理如下: 首先利用Fisher判别法对样本数据进行降维分类, 求取各类样本的质心, 再利用KNN算法对测试数据进行判别分类, 为了减少样本不均衡对KNN算法准确性的影响, 在KNN判别算法中加入权重约束和Fisher分类后的质心点约束, 最终建立判别函数F。
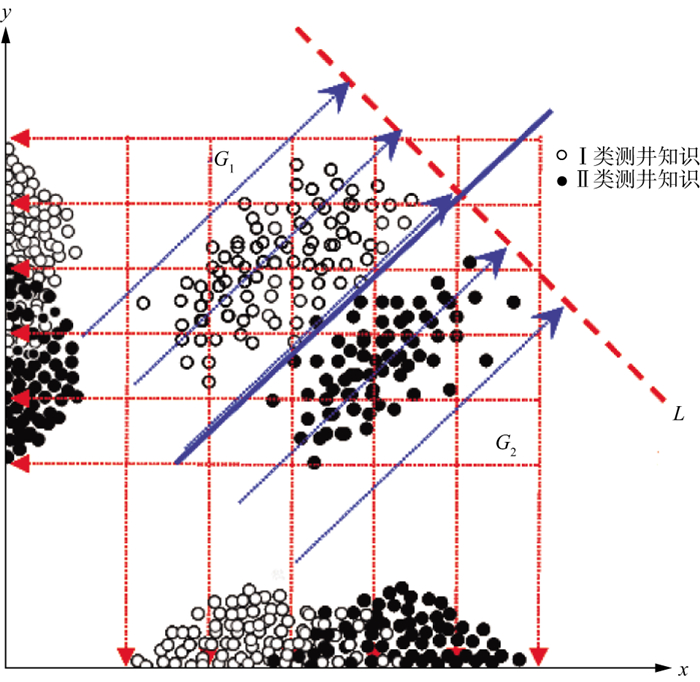
采用Fisher判别法对测井知识进行降维分类, 首先需要选择能反映测井知识特点且尽可能独立的测井资料, 然后建立样品点的观测向量, 再对样品变量进行变换并将其投影于判别向量方向, 最后建立判别函数。利用Fisher判别法对两类测井知识进行判别分析, 图 1通过两类知识的研究数据在x、y方向上的投影展示了Fisher判别法原理, 图 1中箭头为数据投影方向, G1、G2为知识的测井数据, x轴和y轴上的数据点为G1、G2的投影, 从图 1可知, Ⅰ类和Ⅱ类测井知识存在较大程度的重叠, 需要设法找到一个新y轴(直线L), 使得散点投影在新y轴上时, Ⅰ类和Ⅱ类测井知识重叠程度较小, 即两类测井知识的类间离差大, 类内离差小, 以达到提高识别率的目的。
|
图 1 Fisher判别法原理 |
根据两类知识对应的测井资料建立样本数据矩阵集合D, 设D={(X, Y)}, xi是第i类测井资料, xi∈X, yi是第i类知识的标识, yi∈Y, i=1, 2。令最佳投影为W, μi为第i类质心, Ni为第i类的样本数量, μi的计算公式可表示为:
| $ \boldsymbol{\mu}_{i}=\frac{1}{N_{i}} \sum\limits_{i=1}^{2} \boldsymbol{x}_{i} $ | (1) |
两类测井知识的质心点分别为μ1, μ2。两类测井知识的最大类间距离, 即样本间离差J0可表示为:
| $ \boldsymbol{J}_{0}=\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{\mu}_{2}-\boldsymbol{W}^{\mathrm{T}} \boldsymbol{\mu}_{1}\right)^{2}=\boldsymbol{W}^{\mathrm{T}}\left(\boldsymbol{\mu}_{2}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{\mu}_{2}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} \boldsymbol{W} $ | (2) |
类间离散度矩阵S0可表示为:
| $ \boldsymbol{S}_{0}=\left(\boldsymbol{\mu}_{2}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{\mu}_{2}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} $ | (3) |
(2) 式可表示为:
| $ \boldsymbol{J}_{0}=\boldsymbol{W}^{\mathrm{T}} \boldsymbol{S}_{0} \boldsymbol{W} $ | (4) |
两类测井知识的最小类内距离, 即样本内离差为J1可表示为:
| $ \begin{array}{c} \boldsymbol{J}_{1}=\sum\limits_{i=1}^{2}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{x}_{i}-\boldsymbol{W}^{\mathrm{T}} \boldsymbol{\mu}_{i}\right)^{2}=\boldsymbol{W}^{\mathrm{T}}\left(\boldsymbol{x}_{i}-\boldsymbol{\mu}_{i}\right) \cdot \\ \left(\boldsymbol{x}_{i}-\boldsymbol{\mu}_{i}\right)^{\mathrm{T}} \boldsymbol{W} \end{array} $ | (5) |
类内离散矩阵S1:
| $ \boldsymbol{S}_{1}=\sum\limits_{i=1}^{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)\left(\boldsymbol{x}-\boldsymbol{u}_{i}\right)^{\mathrm{T}} $ | (6) |
(5) 式可表示为:
| $ \boldsymbol{J}_{1}=\boldsymbol{W}^{\mathrm{T}} \boldsymbol{S}_{1} \boldsymbol{W} $ | (7) |
要想达到较好的分类效果, 应该使同类样本的投影点尽可能接近, 样本内离差尽可能小, 即J1尽可能小; 同时也要保证不同类样本投影点尽可能远离, 即J0尽可能大。同时考虑两者的关系建立目标函数J:
| $ \boldsymbol{J}=\frac{\boldsymbol{J}_{0}}{\boldsymbol{J}_{1}}=\frac{\boldsymbol{W}^{\mathrm{T}} \boldsymbol{S}_{0} \boldsymbol{W}}{\boldsymbol{W}^{\mathrm{T}} \boldsymbol{S}_{1} \boldsymbol{W}} $ | (8) |
当J最大时, 分类效果最好。因此, 对(8)式求偏导, 即可实现样本数据的降维分类。
样本数据降维分类后, 采用KNN算法对新加入的测试集进行分类, 建立判别函数F, 可实现测井知识的判别调用。假设数据降维后的数据矩阵集合为
| $ L_{2}\left(\overline{\boldsymbol{x}}_{i}, \overline{\boldsymbol{x}}_{j}\right)=\left(\sum\limits_{l=1}^{n}\left|x_{i}^{l}-x_{j}^{l}\right|^{2}\right)^{\frac{1}{2}} $ | (9) |
K值为KNN算法中K个最近邻近数, K值对KNN算法的结果影响重大, K值过大或过小, 均会造成较大误差, 为简化计算和提高判别精度, 令K的计算公式为:
| $ K=\left\{\begin{array}{l} N, \text { 当 } N<20 \\ 19, \text { 当 } N \geqslant 20 \end{array}\right. $ | (10) |
式中: N为样本类数。
利用距离的倒数可以提高特征向量之间相似度计算的准确性以及分类精度。我们采用距离平方倒数对近邻样本的贡献进行加权[19], 以提高分类精度并简化计算过程, 对于测试数据
| $ w_{t(j)}=\frac{1}{\left[d_{t(j)}\right]^{2}}=\frac{1}{\left[L_{2}\left(\bar{\boldsymbol{x}}_{t}, \bar{\boldsymbol{x}}_{j}\right)\right]^{2}} $ | (11) |
| $ j \in K $ |
当测试样本
| $ d_{s(t)}=L_{2}\left(\boldsymbol{u}_{s}, \overline{\boldsymbol{x}}_{t}\right) $ | (12) |
建立加入权系数以及质心点约束条件的F函数:
| $ \begin{aligned} F\left[w_{s(t)}, \boldsymbol{x}_{t}\right]=& \sum\limits_{j=1}^{k} w_{t(j)} I_{t(j)}\left[w_{s(t)}, w_{t(j)}\right]+\\ & \frac{1}{\left[L_{2}\left(\boldsymbol{u}_{s}, \boldsymbol{u}_{t}\right)\right]} \end{aligned} $ | (13) |
式中:
我们利用各种分析方法分区域、分油田、分层组对测井基础资料、岩石物理分析资料以及试油资料进行分析, 再将建立的孔-渗-饱模型及参数、解释图版、模型函数等保存下来, 形成测井知识[7-8]。测井知识包括解释模型和解释参数。
解释模型为针对不同地区、不同类型储层, 应用数理统计的方法分析测井资料和岩心分析资料之间的关系, 建立的地区孔隙度、渗透率、含水饱和度、束缚水饱和度、渗透率解释模型。
解释参数是调用地区地质和试油试水资料、测井曲线资料, 采用交会图版、M-N交会图、Pe-K交会图和Pe-Th/K交会图等, 结合地区地质和解释经验确定的地层水电阻率、岩电参数、岩性、骨架参数以及粘土矿物类型等参数。区域性解释参数的确定需考虑地区性和经验性, 因此上述参数均非常重要。
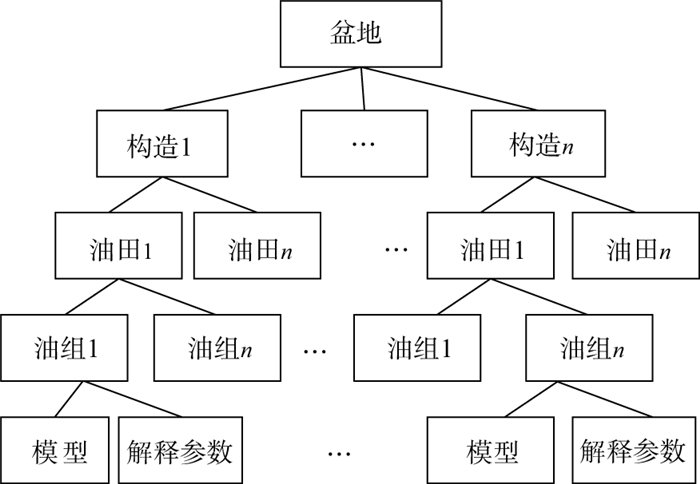
为了方便调用, 我们采用多叉树存储结构, 将知识按照盆地、油田、层组和知识类别分类存储。图 2为知识的存储结构, 按照盆地→构造→油田→油组→模型/参数的层次结构存储知识, 一个盆地包含多个构造, 每个构造包含多个油田, 每个油田包含多个油组, 每个油组包含多个解释参数和模型。
|
图 2 知识存储结构 |
在多叉树知识存储的基础上, 为了进一步提高知识的辨识度, 还需要对知识进行分类标识。进行测井解释时, 需要将测井知识分为下限参数、解释模型等类别, 同时根据不同的研究目的对知识进行细分。因此, 在测井知识库加入了知识类别及知识名称。为了实现KNN-Fisher算法对知识的调用, 我们在测井知识库中引入了知识研究参数。表 1是存储在测井知识库中的知识。
| 表 1 存储在测井知识库中的知识 |
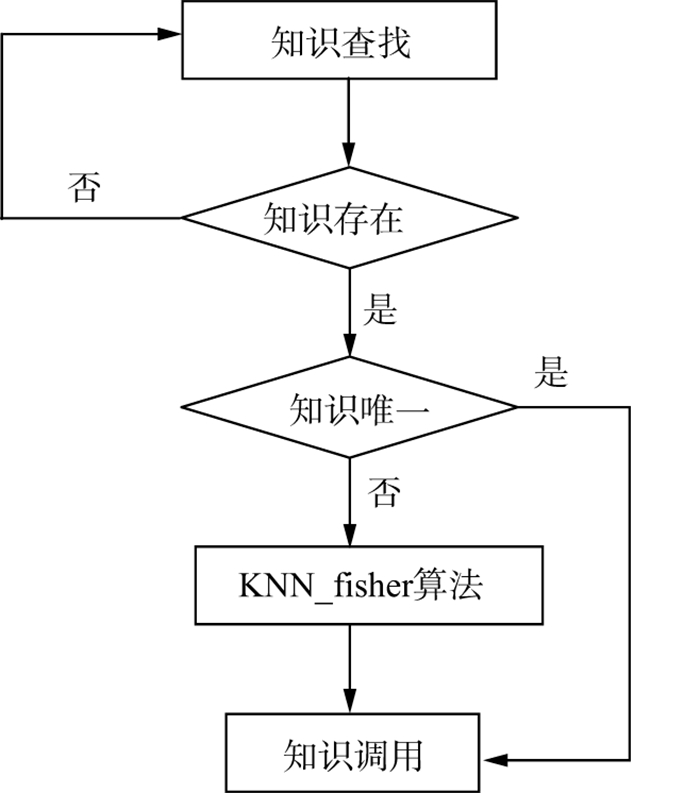
我们基于测井综合处理解释平台建立了测井解释知识库系统, 将研究得到的知识保存在测井综合处理解释平台的知识库中, 实现知识的调用。知识的调用采用混合推理与KNN-Fisher算法相结合的方式, 选用堆栈存放知识查找路径, 依次匹配盆地、构造、油田、层组, 并存入栈中。如果层组匹配且有相关的知识, 则调用; 否则, 返回上一级, 继续匹配, 直到查找结束。当检索到多个知识时, 则采用KNN-Fisher算法进行智能调用。图 3为测井知识库系统的调用流程。以从测井知识库中调用参数为例展开说明, 步骤如下。
|
图 3 测井知识库调用流程 |
1) 判断测井解释是否需要调用测井知识库的参数, 如果是, 则获取盆地P、构造S、油田A、层组C依次入栈, 转步骤2);否则, 转步骤7)。
2) 通过混合推理查找知识, 如果不存在知识或者不存在层组C知识, 则弹出堆栈, 如果堆栈不为空, 重复步骤2);如果存在层组C知识或者存在知识且堆栈为空, 转步骤3), 否则, 转步骤7)。
3) 判断知识是否唯一, 如果唯一, 则转步骤7);否则, 转步骤4)。
4) 查找知识库中知识的研究参数, 并从数据库中获取知识的研究参数, 转步骤5)。
5) 根据研究参数, 提取解释井的资料, 转步骤6)。
6) 利用KNN-Fisher算法对研究资料以及解释井资料进行建模, 优选解释参数, 转步骤7)。
7) 调用知识。
KNN-Fisher算法的实现流程如下: 首先对导入的知识参数集及测试集进行预处理, 去除异常值, 再利用Fisher判别法对预处理后的数据进行降维分类, 计算中心质点, 最后调用改进的KNN算法实现知识判别调用。KNN-Fisher算法的描述如图 4所示。

|
图 4 KNN-Fisher算法的描述 |
采用基于KNN-Fisher算法构建的知识库对南
海西部海域某油气田的20多口井资料进行处理解释, 效果良好。XX井的测井资料有效储层解释流程如下: 首先根据测井曲线的形态特征将测井解释剖面划分为具有相同岩石物理性质和流体类型的小层结构, 然后对这些小层定性解释, 最后给出合理结论。在解释过程中需要调用相关层组的下限参数包括孔隙度(POR)下限、含水饱和度(SW)下限及泥质含量(VSH)下限参数, 对储层流体性质判断, 以识别油气。XX井位于A1气田、S1构造, 从表 2中可知S1构造包括B1、B2、C1共3个目的层组, 知识库中已经存在了A1气田B1、B2层组下限参数以及A2、A3气田C1层组的下限参数。
| 表 2 P1盆地知识 |
XX井距离A2气田21.5km, 距离A3气田30.0km, 包含3个目的层组B1、B2、C1, 其中C1层组在A1油田知识库中无下限参数, 因此为了对C1层组进行有效储层解释, 需要借助构造内同一层组或者同一油田中邻近层组的信息进行解释分析。经过混合推理, 首先查找知识库中A1气田C1层组的知识, 返回结果为无; 接着返回A1气田查找, 存在B1、B2层组知识, 不存在C1层组知识; 然后返回构造继续查找, 存在A2气田C1层组以及A3油田C1层组知识, 查找结束, 一共查找到4个知识, 下一步需要利用KNN-Fisher算法判别调用知识。
我们利用孔隙度、泥质含量、含水饱和度、电阻率以及声波曲线进行知识研究。采用KNN-Fisher算法判别调用知识时, 需要利用A1气田B1、B2层组的孔隙度、泥质含量、含水饱和度、电阻率及声波曲线以及A2、A3气田C1层组的孔隙度、泥质含量、含水饱和度、电阻率及声波曲线建立模型, 并将A1气田C1层组的孔隙度、泥质含量、含水饱和度、电阻率及声波曲线作为测试集。
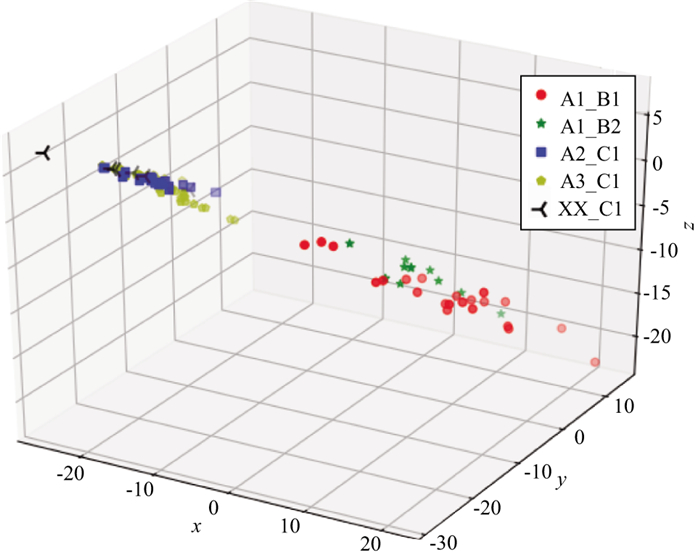
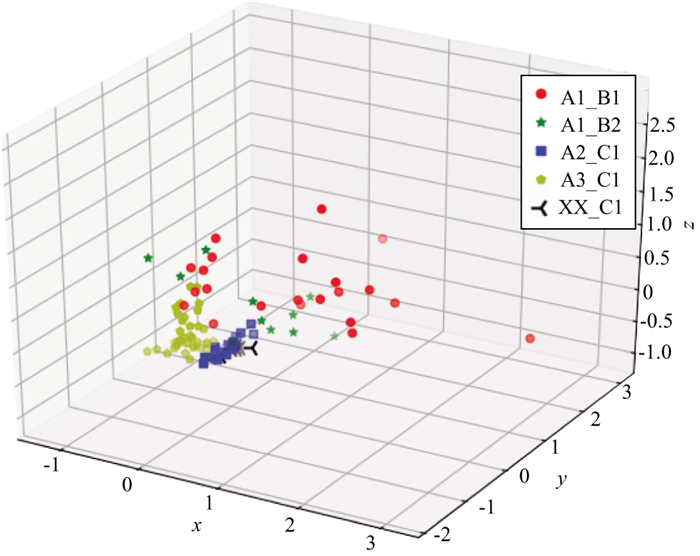
将该油气田相关研究资料与XX井C1层组资料进行预处理后, 再采用KNN-Fisher算法建模, 得到的因子分析结果如图 5所示。将该油气田相关研究资料与XX井C1层组资料进行预处理后, 不调用Fisher判别法, 仅采用KNN算法建模, 得到的因子分析结果如图 6所示。对比图 5和图 6可以发现, 图 5中同一层组的数据更集中, 而图 6中的数据较为分散。从采用KNN-Fisher算法建模可以看出, XX井C1层组与A3气田C1层组最接近, 因此, 我们采用A3气田的C1层组下限参数对XX井C1层组进行有效储层解释。利用ZHU等[12]提出的KNN算法建模得到的XX井C1层组与A2气田C1层组最接近, 因此, 我们调用A2气田C1层组的知识对XX井C1层组进行有效储层解释。
|
图 5 采用KNN-Fisher算法建模得到的因子分析结果(x轴为因子1, y轴为因子2, z轴为因子3) |
|
图 6 采用KNN算法建模得到的因子分析结果(x轴为因子1, y轴为因子2, z轴为因子3) |
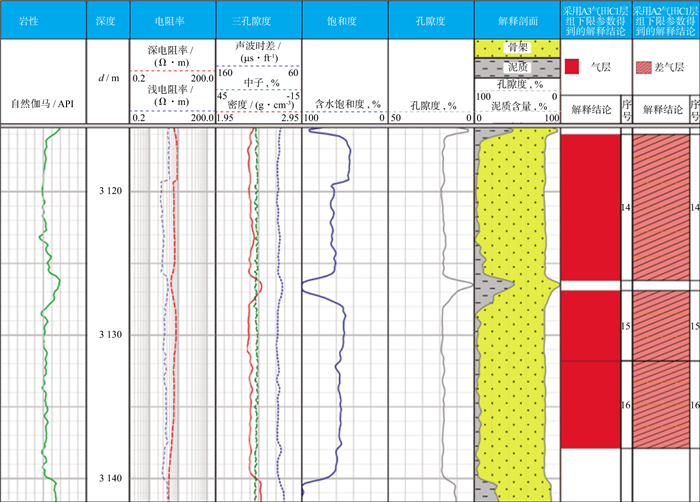
将利用本文方法与ZHU等[12]提出的方法得到的分析结果进行比较研究。图 7是分别利用A3气田C1层组的下限参数及A2气田C1层组的下限参数对XX井C1层组的有效储层解释得到的结果。XX井C1层组被分为3个小层进行有效储层解释, 采用A2气田C1层组的下限参数进行解释, 解释结果为差气层, 而采用A3气田C1层组的下限参数得到的解释结果为气层。在XX井C1层组进行地层测试, 获天然气124935.0m3/d、水9.0m3/d, 证实C1层组为高产气层, 不难发现, 利用A3油田C1层组的下限参数得到的解释结果更符合实际情况。
|
图 7 利用A3气田C1层组和A2气田C1层组的下限参数对XX井C1层组的有效储层解释得到的结果(1 ft≈0.3048 m) |
表 3是KNN-Fisher算法与KNN算法在南海西部海域某油气田的应用统计结果, 从表 3可以看出, KNN-Fisher算法的符合率为80%, KNN算法的符合率为60%, KNN-Fisher算法的符合率较KNN算法的符合率高。KNN-Fisher算法能够实现知识自动、准确调用, 有效克服了混合推理及KNN算法存在的不足。
| 表 3 KNN-Fisher算法与KNN算法在南海西部某油气田的应用统计结果 |
本文结合测井解释知识库的特点, 提出了基于KNN-Fisher算法构建知识库的方法, 研究了知识库调用方法, 并将该方法应用于南海西部海域某油气田的测井解释, 得出以下结论。
1) 该方法在利用Fisher判别法进行降维分类的同时, 对KNN算法加入权重系数以及质心点约束条件, 提高了算法的准确度, 有效克服了混合推理及KNN算法存在的不足。
2) 该方法实现了测井知识库中知识的自动、准确调用, 获取的知识与实际的地层条件吻合, 提高了解释精度和解释效率。
3) 在实际应用中应该注意, 当知识库中不存在知识研究所需的测井资料或者当前处理井的资料与知识库的知识研究参数不符合时, 采用该算法得到的知识将会给测井解释造成较大的误差。
| [1] |
雍世和, 张超谟. 测井数据处理与综合解释[M]. 东营: 中国石油大学出版社, 1996: 1-139. YONG S C, ZHANG C M. Logging data processing and comprehensive interpretation[M]. Dongying: China University of Petroleum Press, 1996: 1-139. |
| [2] |
钟华明, 何胜林, 曾少军, 等. 一种基于多条件约束测井有效储层解释方法[J]. 石油物探, 2015, 54(6): 780-786. ZHONG H M, HE S L, ZENG S J. A multi-constrained log interpretation method for effective reservoirs[J]. Geophysical Prospecting for Petproleum, 2015, 54(6): 780-786. DOI:10.3969/j.issn.1000-1441.2015.06.017 |
| [3] |
张斌, 魏扣, 郝琦. 国内外知识库研究现状述评与比较[J]. 图书情报知识, 2016, 3: 15-25. ZHANG B, WEI K, HAO Q. Review and comparison of research status of knowledge base at home and abroad[J]. Document, Informaiton & Knowledge, 2016, 3: 15-25. |
| [4] |
CUZZOCREA A. Advanced knowledge-based systems[J]. Data & Knowledge Engineering, 2010, 69(7): 661-663. |
| [5] |
RELICH M, ANTONI S', GOLA A. A knowledge-based approach to product concept screening[J]. 12th International Symposium on Distributed Computing and Artificial Intelligence, 2015, 341-348. |
| [6] |
MARTIN L, ROMANOVSKY A. An approach for designing knowledge-based systems for high-integrity applications[J]. 13th Dependable Computing Conference, 2017. DOI:10.1109/EDCC.2017.25 |
| [7] |
钟秀琴, 刘忠, 丁盘苹. 基于混合推理的知识库的构建及其应用研究[J]. 计算机学报, 2012, 35(4): 761-766. ZHONG X Q, LIU Z, DING P P. Construction of knowledge base on hybrid reasoning and its application[J]. Chinese Journal of Computers, 2012, 35(4): 761-766. |
| [8] |
徐文, 刘龙龙, 李小锋. 鄂尔多斯盆地环江油田虎二区块储层地质知识库的构建及应用[J]. 北京师范大学学报(自然科学), 2018, 54(4): 510-515. XU W, LIU L L, LI X F. Construction and application of geological knowledge database for Hu2 Block of Huanjiang oilfield, Ordos Basin[J]. Journal of Beijing Normal University(Natural Science), 2018, 54(4): 510-515. |
| [9] |
SHARMA K. Designing knowledge based systems as complex adaptive systems[J]. 2008 Conference on Artificial General Intelligence: First Agi Conference, 2008, 424-428. |
| [10] |
GENE ONTOLOGY CONSORTIUM. Expansion of the geneontology knowledge base and resources[J]. Nucleic Acids Research, 2016, 45(D1): D331-D338. |
| [11] |
尚福华, 原野, 王才志, 等. 基于知识库的解释模型智能优选测井数据处理方法[J]. 石油学报, 2015, 36(11): 1449-1456. SHANG F H, YUAN Y, WANG C Z. A logging data processing method of intelligent optimization logging interpretation model based on Knowledge-base[J]. Acta Petrolei Sinica, 2015, 36(11): 1449-1456. DOI:10.7623/syxb201511015 |
| [12] |
ZHU L, SONG X, LIU C. Evaluating a stream of relational KNN queries by a knowledge base[J]. International Journal of Cooperative Information Systems, 2015, 24(2): 1550003. DOI:10.1142/S0218843015500033 |
| [13] |
SULEIMANOV B A, GUSEINOVA N I. Analyzing the state of oil field development based on the fisher and shannon information measures[J]. Automation and Remote Control, 2019, 80(5): 882-896. DOI:10.1134/S0005117919050072 |
| [14] |
张润莲, 张昭, 彭小金. 基于Fisher分和支持向量机的特征选择算法[J]. 计算机工程与设计, 2014, 35(12): 4145-4148. ZHANG R L, ZHANG Z, PENG X J. Feature selection algorithm based on Fisher value and support vector machine[J]. Computer Engineering and Design, 2014, 35(12): 4145-4148. DOI:10.3969/j.issn.1000-7024.2014.12.017 |
| [15] |
李峰, 王正群, 徐春林, 等. 基于马氏距离的局部边界Fisher分析降维算法[J]. 计算机应用, 2013, 33(7): 1930-1934. LI F, WANG Z Q, XU C L. Dimensionality reduction algorithm of local marginal Fisher analysis based on Mahalanobis distance[J]. Journal of Computer Applications, 2013, 33(7): 1930-1934. DOI:10.11772/j.issn.1001-9081.2013.07.1930 |
| [16] |
SEBASTIAN RASCHKA. Python machine learning[M]. Beijing: China Machine Press, 2018: 63-113.
|
| [17] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 37-42. LI H. Statistical learning methods[M]. Beijing: Tsinghua University Press, 2012: 37-42. |
| [18] |
肖辉辉, 段艳明. 基于属性值相关距离的KNN算法的改进研究[J]. 计算机科学, 2013, 40(11A): 157-160. XIAO H H, DUAN Y M. Improved the KNN algorithm base on related to the distance of attribute value[J]. Computer Science, 2013, 40(11A): 157-160. |
| [19] |
杨金福, 宋敏, 李明爱. 一种新的基于距离加权的模板约简K近邻算法[J]. 电子与信息学报, 2011, 33(10): 2378-2383. YANG J F, SONG M, LI M A. A novel template reduction k-nearest neighbor classification method base on weighted distance[J]. Journal of Electronics & Information Technology, 2011, 33(10): 2378-2383. |



