2. 自然资源部古地磁与古构造重建重点实验室, 北京 100081;
3. 中国石油集团东方地球物理公司辽河物探处, 辽宁盘锦 124010;
4. 中国科学院地质与地球物理研究所, 北京 100029;
5. 南方科技大学地球与空间科学系, 广东深圳 518055
2. Key Laboratory of Paleomagnetism & Tectonic Reconstruct, Ministry of Natural Resources, Beijing 100081, China;
3. BGP Liaohe division, Panjin 124010, China;
4. Institute of Geology and Geophysics, Chinese Academy of Sciences.Beijing 100029, China;
5. Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen 518055, China
随着油气地震勘探技术的发展, 基于双程波方程的逆时偏移技术(RTM)成为对日益复杂的地质构造进行准确成像的有力工具[1-6]。近年来, 随着多分量采集技术和计算能力的进步, 叠前弹性逆时偏移(ERTM)越来越受到重视。与常规声波成像相比, ERTM在储层监测、油气检测和岩性识别方面具有很大优势, 是近年来地震成像的研究热点[7-11]。
然而, 由于弹性波场中P波和S波在垂直和水平方向的不解耦性和波场分离的不彻底性导致成像过程中往往伴随着串扰噪声等非物理噪声, 使得成像分辨率显著降低[12-15]。近年来, 为了减轻这种噪声的影响, 提高ERTM的成像质量, 许多学者讨论了在倾角域压制噪声的应用。如KLOKOV等[16]提出了在倾角域利用反射波和绕射波在形态上的差异将两者进行分离; XU等[17]直接在倾角域将不平的部分从道集中去掉, 在菲涅尔带内叠加完成反射波成像; ZHANG等[18]在各向异性叠前时间偏移中输出倾角道集, 并在其上解析地近似估计菲涅尔带, 完成最优叠加, 提高成像的信噪比。以上这些应用都是在Kirchhoff型积分偏移中完成的, 在弹性波逆时偏移(ERTM)领域还没有相关研究。
深度学习是一种人工智能(AI)技术, 它可以让计算机像人类一样从经验中学习, 并模拟人类处理数据的方式[19-21]。近年来, 深度学习的应用也成为地震学研究的一个活跃领域。在勘探地球物理领域中, 学者们提出了一些基于深度神经网络的方法, 如层析成像、数据插值、盐丘边界识别等[22-24]。深度学习方法的一个显著特点在于能发现隐藏在高维数据中的特征, 并且具有一定泛化能力, 能够让机器自动大批量地完成很多复杂的工作[25]。前人研究了通过在倾角域生成偏移道集, 并利用手动拾取倾角范围来控制成像叠加的方式压制偏移过程中的噪声, 但这类方法主要是通过手动拾取来实现这一过程[26-27]。本文介绍了在ERTM生成的倾角道集上利用一种深度学习方法——卷积神经网络(CNN)[28-30]实现自动拾取该倾角叠加范围, 从而实现压制偏移噪声的方法, 即, 基于CNN的倾角域弹性波逆时偏移噪声压制方法, 可以节约大规模三维成像的人工拾取工作量。最后给出数值算例, 验证了该方法的可行性和实用性。
1 技术方法本文方法对弹性波矢量逆时偏移成像结果进行噪声压制的思路简要概括为: 在具备准确的速度模型等参数模型前提下, 采用弹性波逆时偏移方法对弹性波数据进行成像, 这一过程中关键技术是利用波印廷矢量进行波场分离并计算角度, 实现弹性波逆时偏移生成多套以地层倾角为索引的成像道集(矢量道集)。在倾角道集上, 可以清楚观察到对成像贡献最大的有效部分和噪声部分, 各自按照倾角范围分布在道集上, 所以可以通过在倾角道集上拾取适当的倾角范围, 即叠加孔径, 然后在叠加孔径内对有效信号进行叠加成像, 从而实现噪声压制。由于成像点处构造情况变化剧烈, 单一参数无法满足去噪要求, 因此逐点进行倾角范围手动拾取的工作量非常大。基于此, 本文应用CNN算法, 将部分道集手动拾取的叠加孔径函数作为目标输出, 即标签数据, 使用CNN来实现自动预测, 从而实现噪声压制的同时节约大量手动拾取的工作量, 该方法适用于大规模的道集倾角范围拾取。
1.1 利用波印廷矢量生成倾角道集| $ \begin{array}{c} \rho \frac{\partial v_{i}}{\partial t}=\frac{\partial \tau_{i j}}{\partial x_{j}} \\ \frac{\partial \tau_{i j}}{\partial t}=\lambda \frac{\partial v_{k}}{\partial x_{k}} \delta_{i j}+\mu\left(\frac{\partial v_{i}}{\partial x_{j}}+\frac{\partial v_{j}}{\partial x_{i}}\right) \end{array} $ | (1) |
式中: i, j, k=1, 2;ρ表示密度; vi表示x方向上的质点速度; vj表示y方向上的质点速度; τij表示应力张量; δij表示Delta函数; λ, μ表示拉梅常数。我们采用了基于非结构网格的格子法求解方程(1)[29], 在输出倾角道集时, 本文使用坡印廷矢量[30-31]计算倾角, 波印廷矢量表示为:
| $ s_{i}=-\tau_{i j} v_{j} $ | (2) |
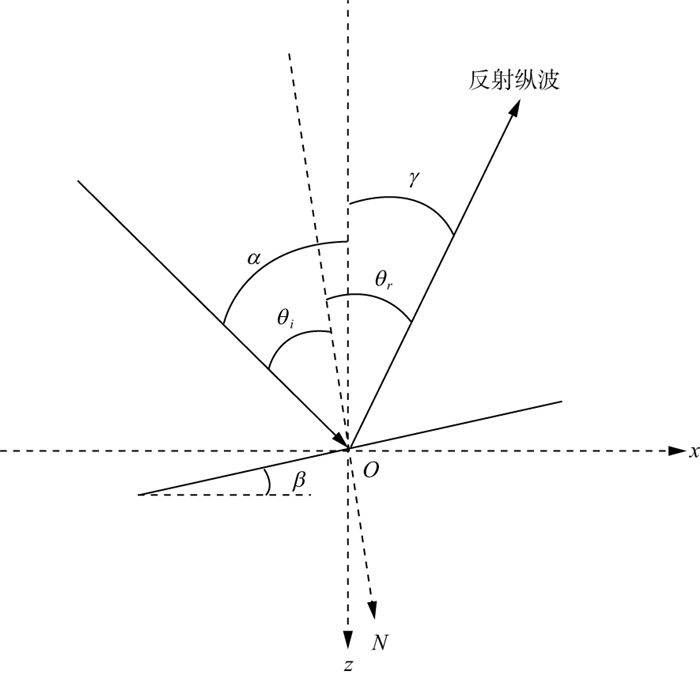
式中: i和j分别表示弹性波波印廷矢量的水平和垂直分量。我们使用波印廷矢量来计算倾角(图 1)[32-33], 公式如下:
|
图 1 利用波印廷矢量计算倾角示意 |
| $ \beta=\alpha-\gamma $ | (3) |
式中: α表示入射波与z方向的夹角; γ表示反射波与z方向之间的夹角; β表示倾角。在波场外推过程中, α可由炮点的波印廷矢量计算得到, γ可由检波点的波印廷矢量计算得到。对于每个成像点, 在每个时间步长内用公式(3)计算倾角。然后, 存储每个成像点每个时间步的倾角总和。在获得每个炮点的倾角后, 在每个成像点处叠加所有炮的结果, 生成倾角道集。这一过程可表示为:
| $ \begin{array}{l} I_{\mathrm{PP}}(x, \beta)=\sum\limits_{n_{\mathrm{shot}}} \sum\limits_{t} P_{\mathrm{src}}(x, t) P_{\mathrm{rec}}(x, t) D_{\mathrm{PP}}\left(p_{\mathrm{s}}, p_{\mathrm{g}}, \beta\right) \\ I_{\mathrm{PS}}(x, \beta)=\sum\limits_{n_{\mathrm{shot}}} \sum\limits_{t} P_{\mathrm{src}}(x, t) S_{\mathrm{rec}}(x, t) D_{\mathrm{PS}}\left(p_{\mathrm{s}}, p_{\mathrm{g}}, \beta\right) \end{array} $ | (4) |
式中: I表示倾角道集; D表示倾角; Psrc, Srec分别表示炮点和检波点的波场, nshot表示参与成像的总炮数。
1.2 基于CNN的倾角道集自动拾取 1.2.1 CNN介绍CNN是一类特殊的人工神经网络, 区别于神经网络的其它模型, 其主要特点是卷积运算操作[19-21]。卷积是一种特殊的线性运算。卷积网络是指那些至少在网络中的一层中使用卷积运算替代一般的矩阵乘法的神经网络。CNN在诸多领域特别是图像相关任务处理的应用中表现优异, 如图像分类、图像语义分割、图像检索、物体检测等计算机视觉问题[25, 28, 30]。此外, 随着CNN研究的深入, 如自然语言处理中的文本分类, 软件工程数据挖掘中的软件缺陷预测等问题都在尝试利用CNN解决, 并取得了相比于传统方法甚至其它深度网络模型更优的预测效果[25]。
1.2.2 用于倾角道集自动拾取的网络结构对于弹性波逆时偏移方法生成的倾角道集, 我们选择拾取每个深度切片的倾角值作为CNN的输入, 范围为-90°~90°, 间隔为3°。因此CNN网络的输入层节点数为61。对于CNN的输出, 采用归一化处理, 使输出在(0, 1)范围内变化。CNN用卷积和汇聚层代替了传统的全连接神经网络。此外, CNN使用共享权值和稀疏连接, 因此可以显著降低需要训练的参数个数。
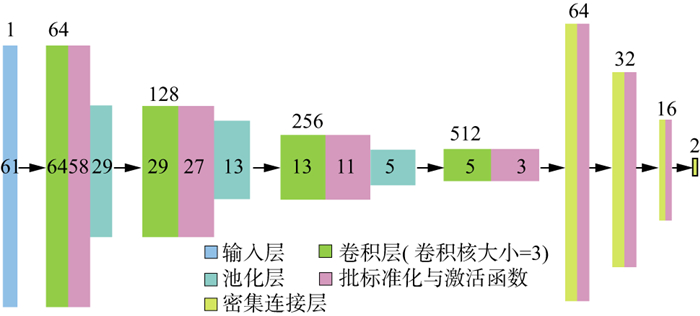
在本文研究中, 倾角拾取可概括为一个一维目标检测问题。考虑到CNN的输出值是连续的, 此处的CNN架构应该是回归型网络。我们遵循Alexnet架构, 构建了一个8层的CNN。该CNN的网络架构如图 2所示。对于前4层, 使用卷积核大小为3的卷积层和大小为2的池化层。卷积层的通道数分别为64, 128, 256, 512。之后, 对最后4层使用全连接输出。致密层的深度分别为64, 32, 16和2。注意, 最后一层深度为2, 输出标准化倾角的预测值。该网络可训练参数为620402, 输出文件大小约7.6MB。
|
图 2 本文采用的CNN结构 |
神经网络可看作一种反演问题求解器, 因此训练神经网络需要定义一个目标函数, 它代表了预测值和真实期望值之间的差异[34-35]。我们认为过切和选取不足的倾角拾取结果是不同的。一方面, 如果拾取的预测孔径过窄(过切), 则会削弱反射波成像的贡献, 降低最终叠加结果的成像分辨率, 甚至丢失成像信息。另一方面, 过大的预测孔径(欠切)会将串扰噪声包括进来。过窄孔径的损失大于过宽孔径估计的损失。因此, 对过切情况进行额外处理, 目标函数可表示为:
| $ \begin{aligned} J(\theta)=& \frac{1}{N_{z}} \sum\limits_{i=1}^{N_{z}}\left\{\left(y_{i}-\hat{y}_{i}\right)^{2}+\alpha^{*}\left[ { \max } \left(0, \hat{y}_{i}^{\text {left }}-\right.\right.\right.\\ &\left.\left.\left.y_{i}^{\text {left }}\right)^{2}+\max \left(0, \hat{y}_{i}^{\text {right }}-y_{i}^{\text {right }}\right)^{2}\right]\right\} \end{aligned} $ | (5) |
式中: Nz表示深度点的个数; yi, ŷi分别表示每一个深度上倾角的预测值与标注值, 并区分左边界和右边界; α表示过切倾角的惩罚因子。右边的第一项表示均方误差; 第二项是对过切的附加惩罚因子, 其程度由超参数α决定。
如果超参数α太大, 基于CNN的方法将给出太宽泛的拾取结果。为了获得合适的参数, 需经过测试选择适当的超参数, 测试结果表明α应该小于1。在本文中, α的值是0.8。
有了目标函数之后, 选择恰当的优化方法对于成功拾取至关重要[36], 我们选用了小批量梯度下降方法(MBGD)[37], 通过一小批训练样本计算梯度。在MBGD方法里选择的批处理量参数值为64。
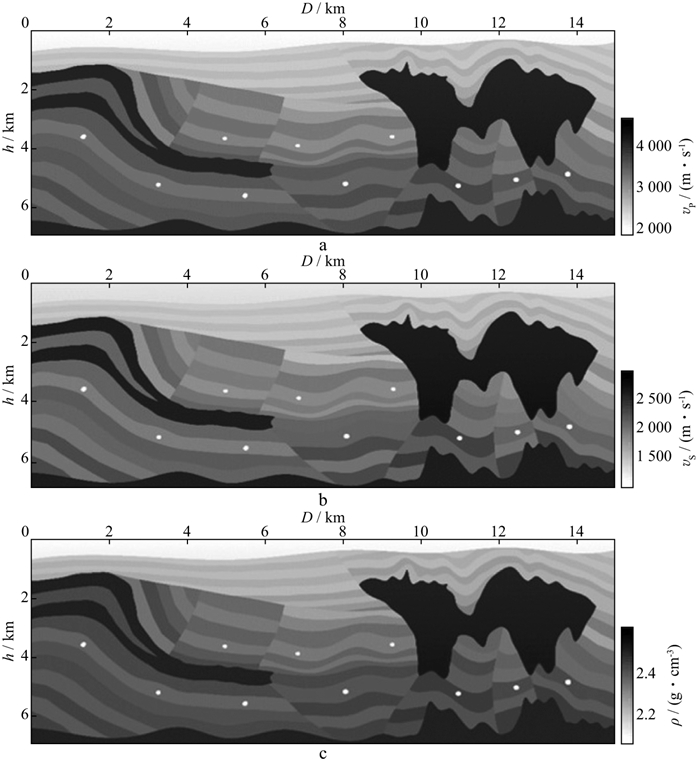
2 数值算例 2.1 BGP盐丘模型数据利用BGP盐丘模型数据来验证基于CNN的倾角域成像孔径自动拾取方法的有效性。图 3为P波速度、S波速度与密度的模型数据。使用准确的速度模型进行偏移输出倾角道集。输出倾角道集后, 使用的带标记的CDP倾角道集的总数为837个。将它们随机地分成训练集、验证集和测试集, 其大小分别为600, 138和99。CDP号的范围为70~1200, 倾角变化范围为-80°~80°, 倾角间隔为1°。每个道集时间方向的采样点数为4051个, 采样间隔为0.002s。首先将训练集输入到搭建好的训练集数据上对网络进行训练, 获得合适的网络权值系数和偏置, 然后输入测试集数据, 输出预测结果, 将由网络预测出的倾角域成像孔径结果与倾角道集叠合显示, 如图 4所示。图中, 白线是手工拾取结果; 绿线是自动拾取结果; 黄线是自动拾取结果平滑后作为CNN自动拾取的最终结果。
|
图 3 BGP盐丘弹性波模型 a P波速度; b S波速度; c密度 |
由图 4可以看出, 经过训练的CNN对倾角叠加范围(孔径)函数具有良好的估计。首先, 对于数据大部分区域, 使用CNN得出的倾角叠加范围比手动选取的倾角叠加范围紧凑, 这表明所设计的损失函数符合初衷。第二, 我们认为CNN拣选和手动拣选之间的差异是由标签的差异引起的。标注工作受人为因素影响较大。第三, 相邻时间片之间的波动较小, 表明CNN预测的结果具有一定的稳定性。最后, 采用CNN方法拾取倾角叠加范围, 对于大数据量特别是三维情况下, 比手动拾取要节约许多时间, 这是该方法最主要的优势。实际操作中, 在没有反射波同相轴等异常情况的道集上做一个很宽松的标注或者不拾取。采用这样的标签数据训练网络后, 一旦验证集数据是没有反射波同相轴的情况, 将不做拾取或者给一个很宽的拾取结果, 相当于全孔径叠加。图 5显示了原始未经倾角叠加范围切除得到的成像结果, 可以观察到明显的串扰噪声等。图 6显示了在经过成像孔径切除后的PP波和PS波逆时偏移叠加成像结果, 与图 5对比可以看出, 有效部分得到了加强, 并且消除了一些成像噪声, 而主要的同相轴没有被损伤。

|
图 4 CNN在弹性波倾角道集上的叠加倾角范围拾取结果 a倾角道集1; b倾角道集2 |

|
图 5 原始未经倾角叠加范围切除得到的成像结果 a PP波; b PS波 |

|
图 6 基于自动拾取倾角叠加范围进行叠加的弹性波成像结果 a PP波; b PS波 |
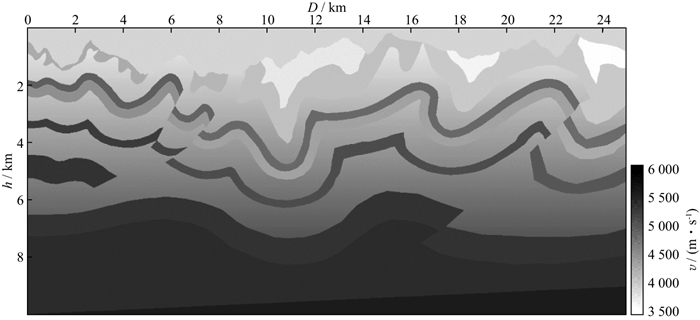
深度学习类方法的一个特点是在一类数据上训练好的网络参数, 可以很快地应用到其它类似的数据上, 即泛化能力。在本节中, 我们使用SEG起伏地表模型来进一步检测本文方法的泛化能力。图 7为SEG起伏地表P波速度模型。该模型在x方向上包含1668个样点, 在z方向上包含1000个样点。网格间距: x方向为15m, z方向为10m, 时间步长为0.5 ms, 记录时间长度为6s, 采用主频20Hz的Ricker子波激发。沿着崎岖的地形表面共设计277炮, 震源间隔为90m。每次激发由480个检波器以15m的间隔进行记录。
|
图 7 SEG起伏地表速度模型 |
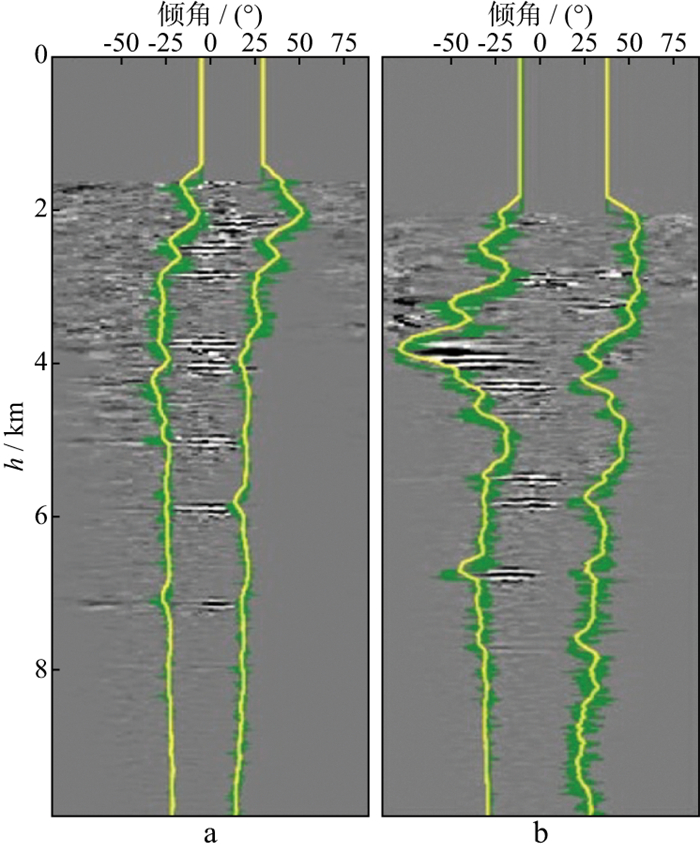
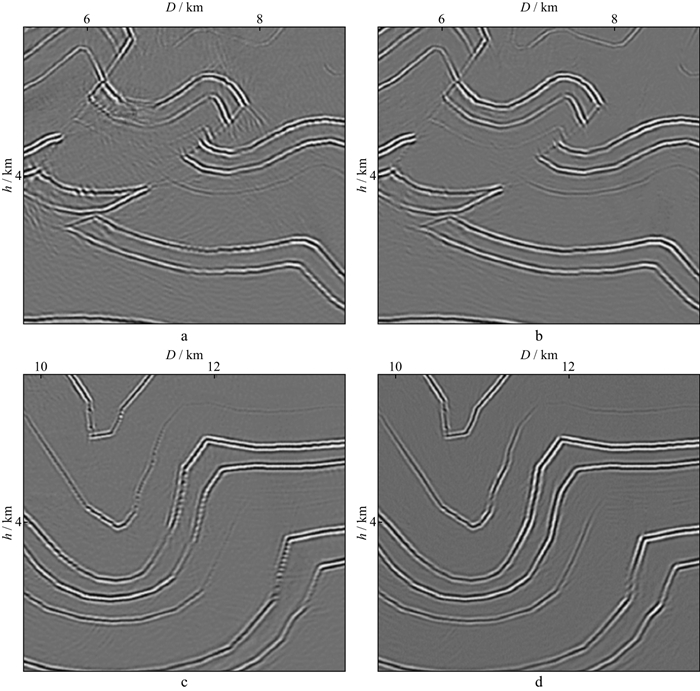
为了获得更高质量的成像结果, 采用前文训练好的网络参数, 对基于CNN自动拾取的倾角域限定函数进行约束。在该数据成像道集上直接使用训练好的CNN网络来预测倾角道集约束函数的左右边界。随机抽取一些倾角道集和网络预测的结果叠加, 结果如图 8所示, 图中绿线是原始自动拾取结果; 黄线是自动拾取结果平滑后的曲线, 将其作为CNN自动拾取最终结果。对比了图 9的成像细节, 图 9a和图 9c是复杂构造不同位置处未加叠加倾角范围成像结果, 可见偏移噪声对成像细节的影响; 图 9b和图 9d是经自动拾取叠加孔径的叠加成像结果, 偏移噪声得到较好压制, 成像质量明显提升。在SEG起伏地表模型上的数值算例表明, 本文方法很容易泛化并推广应用到不同的数据集上。
|
图 8 CNN在SEG起伏地表数据倾角道集上的自动拾取结果 a倾角道集1; b倾角道集2 |
|
图 9 起伏地表模型数据成像结果细节对比 a复杂构造位置1处未加倾角叠加范围成像结果; b位置1处经自动拾取倾角叠加范围叠加成像结果; c复杂构造位置2处未加倾角叠加范围成像结果; d位置2处经自动拾取倾角叠加范围叠加成像结果 |
弹性波逆时偏移(ERTM)是地震成像研究的前沿领域。本文通过偏移输出倾角道集, 在倾角域可以有效地分离反射信号和成像噪声, 进而可对噪声进行压制从而提高成像质量。为了有效地输出倾角道集, 本文采用了在波场外推过程中使用坡印廷矢量的方法实现波场有效分离。然后, 采用一种基于卷积神经网络(CNN)的倾角域自动拾取方法拾取有效倾角叠加范围, 在该范围内实现反射波最优叠加, 从而抑制串扰噪声的影响。数值算例验证结果表明, 该方法可以实现海量道集的自动拾取, 通常从成像道集中随机挑选出约10%的道集进行人工标注, 即可训练出对整体有效的神经网络; 并且该方法除了极大降低手动拾取工作量外, 其拾取质量不受道集信噪比的影响, 而仅仅与人工标注质量与网络训练参数有关, 这对于低信噪比数据很有意义。相比于传统方法, 该方法计算主要集中在使用标签数据对神经网络训练上, 由于目标函数是两个一维的孔径函数, 训练的时间相比于成像运算时间较短。一旦网络模型训练完成, 就可以对数据进行快速预测, 这个特点对于三维情况下海量道集的拾取很有意义, 虽然训练需要花费一部分时间, 但对海量道集进行快速自动拾取, 反而能节约计算时间。最后, 该方法若使用较典型的数据进行训练, 可以用小规模理论数据训练, 对大规模实际数据进行预测, 从而解决同一类型拾取问题, 具有一定的泛化能力, 可较容易应用到其它类似的数据体上。文中数值算例证明了本文方法的有效性和实用性。接下来的工作是将本文方法拓展到散射成像领域。
| [1] |
BAYSAL E, KOSLOFF D, SHERWOOD J. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [2] |
YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 59(1): 102-107. |
| [3] |
ZHANG Y, ZHANG H Z, ZHANG G Q. A stable TTI reverse time migration and its implementation[J]. Geophysics, 2011, 76(3): WA3-WA11. DOI:10.1190/1.3554411 |
| [4] |
周阳, 王华忠. 基于高频近似波传播的实用化保真RTM成像方法[J]. 石油物探, 2019, 58(3): 391-403. ZHOU Y, WANG H Z. On practical implementation of amplitude-preserving reverse time migration based on asymptotic approximation[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 391-403. DOI:10.3969/j.issn.1000-1441.2019.03.008 |
| [5] |
焦叙明, 张明强, 王艳冬, 等. 叠前逆时偏移实用化方法研究[J]. 地球物理学进展, 2019, 34(1): 107-112. JIAO X M, ZHANG M Q, WANG Y D, et al. Research of prestack reverse time migration[J]. Progress in Geophysics (in Chinese), 2019, 34(1): 107-112. |
| [6] |
曲英铭. 起伏地表直接成像技术研究进展[J]. 石油物探, 2019, 58(5): 625-644. QU Y M. Research progress of topographic imaging methods[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 625-644. DOI:10.3969/j.issn.1000-1441.2019.05.001 |
| [7] |
CHANG W F, MCMECHAN G A. Elastic reverse-time migration[J]. Geophysics, 1987, 52(1): 243-256. |
| [8] |
DU Q Z, GUO C F, ZHAO Q, et al. Vector-based elastic reverse time migration based on scalar imaging condition[J]. Geophysics, 2017, 82(2): S111-S127. DOI:10.1190/geo2016-0146.1 |
| [9] |
GU B L, LI Z C, YANG P, et al. Elastic least-squares reverse time migration with hybrid l1/l2 misfit function[J]. Geophysics, 2017, 82(3): S271-S291. DOI:10.1190/geo2016-0235.1 |
| [10] |
LI Y Y, DU Y, DU J Z, et al. Elastic reverse time migration using acoustic propagators[J]. Geophysics, 2018, 83(5): S399-S408. DOI:10.1190/geo2017-0687.1 |
| [11] |
WANG W L, MCMECHAN G A. Vector-based elastic reverse time migration[J]. Geophysics, 2015, 80(6): S245-S258. DOI:10.1190/geo2014-0620.1 |
| [12] |
李闻达, 孟小红, 刘洪, 等. 基于改进余弦组合窗的解耦方程弹性波逆时偏移[J]. 地球物理学报, 2019, 62(11): 4378-4392. LI W D, MENG X H, LIU H, et al. Elastic wave reverse time migration of decoupling equation based on improved cosine combined window function[J]. Chinese Journal of Geophysics, 2019, 62(11): 4378-4392. DOI:10.6038/cjg2019M0694 |
| [13] |
王维红, 张伟, 石颖, 等. 基于波场分离的弹性波逆时偏移[J]. 地球物理学报, 2017, 60(7): 2813-2824. WANG W H, ZHANG W, SHI Y, et al. Elastic reverse time migration based on wave field separation[J]. Chinese Journal of Geophysics, 2017, 60(7): 2813-2824. |
| [14] |
吴潇, 刘洋, 蔡晓慧. 弹性波波场分离方法对比及其在逆时偏移成像中的应用[J]. 石油地球物理勘探, 2018, 53(4): 710-721. WU X, LIU Y, CAI X H. Elastic wavefield separation methods and their applications in reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(4): 710-721. |
| [15] |
张婧, 张文栋, 张铁强, 等. 应用τ-p域矢量旋转的地震数据波场分离[J]. 石油地球物理勘探, 2020, 55(1): 46-56. ZHANG J, ZHANG W D, ZHANG T Q, et al. Wavefield separation of seismic data based on vector rotation in τ-p domain[J]. Oil Geophysical Prospecting, 2020, 55(1): 46-56. |
| [16] |
KLOKOV A, FOMEL S. Separation and imaging of seismic diffractions using migrated dip-angle gathers[J]. Geophysics, 2012, 77(6): S131-S143. DOI:10.1190/geo2012-0017.1 |
| [17] |
XU J C, ZHANG J F. Prestack time migration of nonplanar data: Improving topography prestack time migration with dip-angle domain stationary-phase filtering and effective velocity inversion[J]. Geophysics, 2017, 82(3): S235-S246. DOI:10.1190/geo2016-0087.1 |
| [18] |
ZHANG H, ZHANG J J, LI Z W, et al. Improving the imaging resolution of 3D PSTM in VTI media using optimal summation within the Fresnel zone[J]. Journal of Seismic Exploration, 2017, 26(4): 311-330. |
| [19] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[J]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 770-778. |
| [20] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521: 436-444. DOI:10.1038/nature14539 |
| [21] |
SCHMIDHUBER J. Deep learning in neural networks: An overview[J]. Neural Networks, 2015, 61(1): 85-117. |
| [22] |
ARAYA-POLO M, JENNINGS J, ADLER A, et al. Deep-learning tomography[J]. The Leading Edge, 2017, 37(1): 58-66. |
| [23] |
郑浩, 张兵. 基于卷积神经网络的智能化地震数据插值技术[J]. 地球物理学进展, 2020, 35(2): 721-727. ZHENG H, ZHANG B. Intelligent seismic data interpolation via convolutional neural network[J]. Progress in Geophysics, 2020, 35(2): 721-727. |
| [24] |
张玉玺, 刘洋, 张浩然, 等. 基于深度学习的多属性盐丘自动识别方法[J]. 石油地球物理勘探, 2020, 55(3): 475-483. ZHANG Y X, LIU Y, ZHANG H R, et al. Muiti-attribute salt dome identification method based on deep learning[J]. Oil Geophysical Prospecting, 2020, 55(3): 475-483. |
| [25] |
KRIZHEVSKY A, SUTSKEVER I, GEOFFREY E H. Imagenet classification with deep convolutional neural networks[EB/OL]. [2018-01-18]. https://web.cs.ucdavis.edu/~yjlee/teaching/ecs289g-winter2018/alexnet.pdf
|
| [26] |
CHEN J. Specular ray parameter extraction and stationary-phase migration[J]. Geophysics, 2004, 69(1): 249-256. DOI:10.1190/1.1649392 |
| [27] |
ZHANG J F, LI Z W, LIU L N, et al. High-resolution imaging: An approach by incorporating stationary-phase implementation into deabsorption prestack time migration[J]. Geophysics, 2016, 81(5): S317-S331. DOI:10.1190/geo2015-0543.1 |
| [28] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [29] |
RONNEBERGER O, FISCHER P, BROX T. U-net: Convolutional networks for biomedical image segmentation[EB/OL]. [2015-05-18]. https://arxiv.org/pdf/1505.04597.pdf
|
| [30] |
李章维, 胡安顺, 王晓飞. 基于视觉的目标检测方法综述[J]. 计算机工程与应用, 2020, 56(8): 1-9. LI Z W, HU A S, WANG X F. Survey of vision based object detection methods[J]. Computer Engineering and Applications, 2020, 56(8): 1-9. |
| [31] |
YANG K, ZHANG J F, GAO H W. Unstructured mesh based elastic wave modelling on GPU: A double-mesh grid method[J]. Geophysical Journal International, 2017, 211(2): 741-750. DOI:10.1093/gji/ggx339 |
| [32] |
LIU Q C, ZHANG J F, GAO H W. Reverse-time migration from rugged topography using irregular, unstructured mesh[J]. Geophysical Prospecting, 2017, 65(2): 453-466. DOI:10.1111/1365-2478.12415 |
| [33] |
ZHOU Y, WANG H Z. Efficient wave-mode separation in vertical transversely isotropic media[J]. Geophysics,, 2017, 82(2): C35-C47. DOI:10.1190/geo2016-0191.1 |
| [34] |
BOTTOU L, CURTIS F E, NOCEDAL J. Optimization methods for large-scale machine learning[J]. SIAM Review, 2018, 60(2): 223-311. |
| [35] |
KINGMA D P, BA J. Adam: A method for stochastic optimization[EB/OL]. [2017-01-30]. https://arxiv.org/pdf/1412.6980.pdf
|
| [36] |
RUDER S. An overview of gradient descent optimization algorithms[EB/OL]. [ 2017-06-15]. https://arxiv.org/pdf/1609.04747.pdf
|
| [37] |
IOFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. Proceedings of the 32nd International Conference on International Conference on Machine Learning, 2015, 448-456. |



