速度建模是地震数据处理中的重要步骤之一, 通常需要在叠加速度谱上根据能量团精细拾取时间-速度对, 然后迭代更新均方根速度模型, 并通过时深转换得到深度域的初始层速度, 最后借助层析反演不断提高速度模型的精度。这个过程需要花费大量时间和精力来人工拾取速度谱, 尤其是在地表、地下结构复杂的低信噪比探区, 地震散射噪声、多次波等广泛发育, 速度谱能量团的聚焦性非常差, 速度拾取需要丰富的地震处理经验和地质认识[1]。随着采集数据规模的增加, 速度建模的工作量剧增, 人工拾取速度谱难以跟上实际生产的节奏, 适应复杂低信噪比地区的自动化速度建模尤其是层速度建模变得非常迫切。
近年来, 机器学习方法在自然语言理解、视觉目标识别等许多领域都发挥了巨大作用[2]。地球物理学家也积极探索深度学习技术在噪声压制[3-4]、初至拾取[5]、速度谱拾取与建模、地震数据重建与插值、散射波成像[6-7]等地震数据处理中的应用。其中基于深度学习的速度谱自动拾取与建模方法研究可以分为两个方向: 一是利用深度学习神经网络实现时间-速度对的自动拾取, 然后通过常规方法建立速度模型; 二是借助深度神经网络直接利用观测地震数据建立层速度模型。其中, 从速度谱中自动拾取时间-速度对建立叠加速度模型, 可以看作是对速度谱图像中能量团的识别和定位, 主要思路为通过卷积神经网络(CNN)[8]、递归神经网络模型(RNN)[9]、CNN和长短期记忆(LSTM)混合结构神经网络模型[10]、YOLO(You Only Look Once)和LSTM混合神经网络模型[11]从速度谱中提取时间-速度对或估计均方根速度误差, 并通过含噪数据训练提升神经网络拾取的稳定性, 或者基于全连接神经网络模型自动实现全工区时间-速度对质量控制与速度建模约束, 剔除拾取质量较差的点, 省去人工检査和修改, 提高建模效率, 对于高信噪比模型数据取得了较好的建模效果[12]。神经网络自动化层速度建模, 则直接根据观测地震数据建立层速度模型, 可以看作是通过神经网络建立地震数据与层速度模型的非线性关系, 受地震数据质量影响非常大, 主要思路是基于深层神经网络模型(DNN)[13]、CNN[14]和生成性对抗网络(GANS)[15]建立数据空间与模型空间的映射关系, 直接根据单炮或多炮道集估计背景层速度模型[16], 理论模型的测试结果表明, 深度学习神经网络模型能够从高信噪比模型数据实际炮集中提取有意义的速度信息, 在层速度建模方面具有应用潜力, 不过受资料信噪比的影响比较大。
然而, 上述两类基于深度学习的自动化速度拾取与建模方法, 仍然有两个问题需要进一步解决: 一是自动化时间-速度对拾取方法对低信噪比数据速度谱的拾取适用性不强, 并且拾取时间-速度对的方法没有克服速度分析基于水平层状介质假设的近似, 难以适用于复杂构造情况下的速度建模; 二是自动化层速度建模方法对输入地震数据的波形非常敏感, 通过深度神经网络直接将地震数据映射为速度模型的泛化性不够好, 难以在实际资料应用中取得稳定的效果。
为此, 本文提出了基于卷积神经网络和叠加速度谱的时间域地震层速度自动建模方法, 该方法将速度谱整体作为输入数据, 削弱了地震波形对背景层速度估计的影响, 将时间域层速度作为标签数据, 通过卷积神经网络模型直接估计地震层速度而不是拾取时间-速度对, 能够在一定程度上降低时间-速度对拾取对速度谱信噪比的要求, 同时克服了水平层状假设的限制, 通过一系列随机模型训练实现了速度谱到层速度的自动建模, 最后用理论模型数据和复杂低信噪比资料测试验证了该方法在地震层速度建模中的实用性。
1 方法原理 1.1 卷积神经网络结构卷积神经网络算法近两年来得到了较多应用, 作为一种高效的深度学习算法, 通过多层结构的设计能自动学习不同层次的特征, 提升模型分类能力和泛化能力, 通过卷积核的局部感知和权值共享降低网络模型复杂度, 将数据量庞大的数据体不断降维, 提高训练效率[17]。典型的卷积神经网络通常由卷积层、池化层、全连接层组成。卷积自编码器(CAE)使用卷积层和池化层替代全连接层, 编码过程采用卷积方式将输入数据压缩到一个稀疏表示空间里, 重建过程就是基于该稀疏编码进行重构, 卷积自编码器能很好地保留二维信号的空间信息[18]。
其中, 卷积层可采用下述公式表示:
| $ \boldsymbol{h}^{k}=\sigma\left(\boldsymbol{x} W^{k}+b^{k}\right) $ | (1) |
式中: W为卷积核; k为卷积核的个数, 对应于神经网络的通道数; b是每个卷积核对应的偏置; x为输入矩阵; h为卷积后生成的特征矩阵; σ表示激活函数。卷积层的作用是检测前一相邻层特征的局部连接情况, 相当于一个滤波器, 提取更抽象的特征。
池化层是将语义上相似的特性合并为一个, 提取不变特征, 降低模型维度, 并且在一定程度上增强了网络对于噪声和轻微扰动的鲁棒性。
目标函数是衡量预测值与期望值差异的范数, 深度学习算法进行训练的数学原理实际是对目标函数进行最优化, 通过最小化期望输出与实际输出之间的差异, 不断调整每一层的权重和偏差, 使得目标函数最小化。为了提高训练模型的稳定性和泛化性, 应采用正则化方法。其中, L1正则化指权值向量中各个元素的绝对值之和, L2正则化是指权值向量中各个元素的平方和然后再求平方根, 两者都可以在一定程度上防止过拟合, 提高网络模型的泛化能力。因为L1正则化产生稀疏权值矩阵, 可以用于特征选择, 考虑到地下层速度模型的稀疏性, 建议采用L1正则化。
1.2 卷积神经网络层速度建模的原理思路利用地震道直接建立深度域层速度模型具有挑战性, 首先是因为它涉及到从地震道(t-x)到空间/模型域(z-x)的数据转换, 两者不在同一个数据域, 而本文采取时间域层速度可以很巧妙地解决这个问题。某一时刻处的时间域层速度与该时刻附近速度谱的能量团分布有关, 并且该关系可以被深度学习的卷积神经网络所识别。在水平层状介质情况下, 速度谱的能量团可以直接反映该时刻的叠加速度, 进而通过DIX公式得到该时刻的层速度。然而当地下结构复杂变化时, 速度谱能量团与叠加速度以及层速度之间变成了复杂的非线性对应关系, 此时直接拾取能量团的做法会导致速度建模的误差急剧变大。虽然如此, 目前生产中仍然广泛使用根据速度谱估计背景速度的流程, 这表明速度谱确实包含了确定当前位置处地下速度的有效信息。
将速度谱作为神经网络的输入而不是根据能量团直接拾取速度谱上的时间-速度对, 可以克服复杂构造对速度谱能量团的影响, 同时有效忽略了地震波形对速度估计的影响, 从而克服了实际资料地震波形的极大差异, 保证了基于模拟数据的训练网络模型应用于实际数据的泛化能力。
采用时间域层速度作为标签数据, 首先是因为相对于深度域层速度, 时间域层速度和叠加速度谱之间有更直接的空间对应关系, 有利于卷积核提取对应的局部特征, 其次时间域层速度模型标签与速度谱具有相同的时间长度, 而深度域层速度则往往难以确定具体的深度, 此外时间域层速度模型比均方根速度模型分辨率高, 并且可以方便地转换为均方根速度模型和深度域层速度模型。
卷积神经网络能够自动提取速度谱的多尺度特征信息, 实现速度谱的稀疏、稳定表达, 对随机噪声具有很强的抗干扰性, 同时还能保留速度谱的空间位置信息, 因此本文采用叠加速度谱作为输入, 时间域层速度作为标签, 通过卷积神经网络实现从速度谱到时间域层速度模型的自动建立。
1.3 卷积神经网络模型设计基于卷积自编码器模型, 使用张量流(TensorFlow)的深度学习框架构建了一个28层卷积深度神经网络, 该网络由14个卷积层、7个池化层、7个上采样层和sigmoid激活函数构成。在算法选择上使用了L1正则化和随机梯度下降(SGD)算法来计算损失函数, 采用自适应矩估计(ADAM)优化算法、阶梯型学习率进一步优化计算过程。该方法对应的目标函数为:
| $ J(\theta)=\frac{1}{2 m} \sum\limits_{i=1}^{m}\left|y_{\theta i}(x)-\tilde{y}_{i}\right|^{2}+\lambda \sum\limits_{j=1}^{n}\left|\theta_{k}\right| $ | (2) |
式中: yθi(x)表示卷积自编码器模型实际输出层速度;
图 1为神经网络结构示意图, 图中每一层的数字参数代表图像高度×图像宽度×通道数; upsample代表上采样, 用邻近值插值。该神经网络的基本组件为编码降维层和解码增维层。其中编码降维层由7组二维卷积层(conv)与最大池化层(maxpool)(取2×2小区域中的最大值)组成[19], 解压增维层由7组一维卷积层与上采样层组成, 其中卷积核尺寸均为3×3。输入数据为CMP道集(或反动校后的CRP道集)对应的速度谱, 通过7层卷积+最大池化搭建的编码降维过程, 可以逐步提取速度谱的多尺度特征信息, 并且可以很好地过滤掉随机噪声。通过7层卷积+上采样过程, 逐步恢复数据尺寸, 最后通过sigmoid激活函数输出期望结果。目标输出为CMP道集零偏移距处对应的层速度。要注意的是, 卷积的计算窗口有重叠(卷积核每次只移动一步), 而采样的计算窗口没有重叠。训练开始对所有卷积核权重进行随机初始化, 而对偏置进行全零初始化。
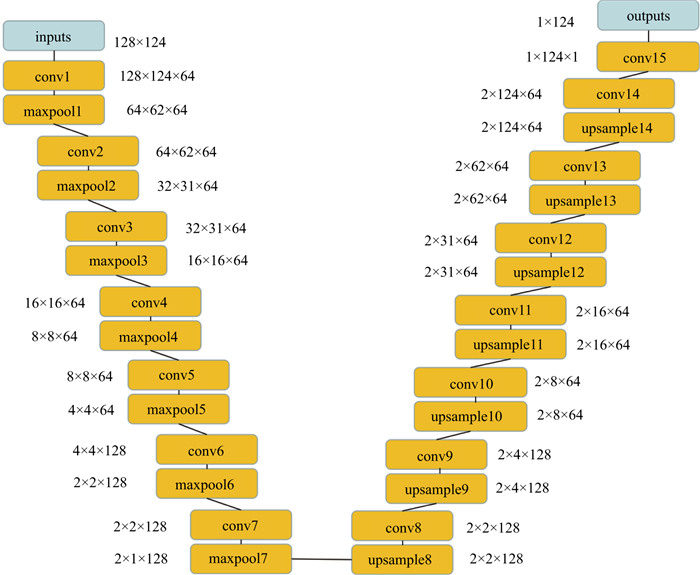
|
图 1 神经网络结构示意 |
与CNN网络一样, 卷积神经网络也需要大量预设样本进行训练。本研究使用的样本数据来源于二维声波模拟CMP道集计算的速度谱, 标签数据是CMP道集零偏移距处对应的时间域层速度。同时, 为了增加训练模型的泛化能力, 获得适用性强的神经网络模型, 训练样本应当多样化、随机性强。
本文采用随机生成速度模型的方式产生11000个速度模型, 速度模型的地层数量、地层倾角、层速度均为随机产生, 其中地层数量为2~15, 地层倾角为-60°~60°, 层速度为1000~6500m/s, 以确保生成样本的随机性。对每个生成的随机速度模型(图 2a), 采用声波正演模拟方法生成对应的CMP道集(图 2b), 然后通过扫描叠加产生叠加速度谱(图 2c)作为训练输入数据。同时为了增强训练集的抗噪性, 在CMP道集中加入不同信噪比的随机噪声, 然后生成对应的速度谱, 共获得55000个训练样本, 我们使用50000个模拟数据进行训练, 剩余5000个作为测试。训练标签数据是每个CMP道集零偏移距处对应的时间域层速度, 此时采用最大速度进行归一化处理, 使所有的速度值变化范围为0~1。
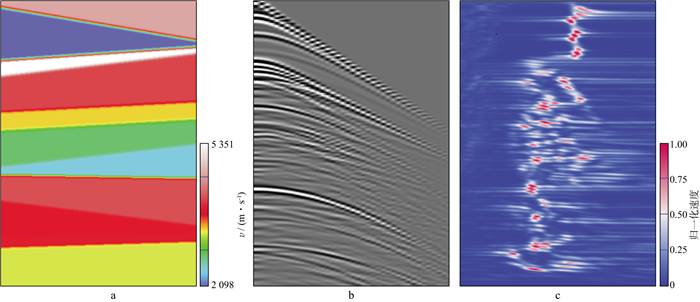
|
图 2 随机训练样本 a速度模型; b CMP道集; c速度谱 |
我们使用TensorFlow构建神经网络, 并在TensorFlow进行训练和测试。训练在一个台式机上进行, 该机配置: 4核CPU, 32G内存, 1块GTX1070Ti显卡, 8G显存。训练的batch大小为128, 采用随机梯度下降法迭代求解, 训练误差迅速减少到4%以内(图 3)。图 4给出了在递增速度模型和倒转速度模型验证集上的测试结果。可以看出, 测试集数据的期望输出(蓝色)与该数据采用训练后的神经网络模型计算得到的速度模型(红色)非常接近, CMP速度反演结果精度高, 即使对于速度模型倒转情况, 也有很好的适用性, 没有出现过拟合现象, 不过对于薄层的分辨率有待进一步提高, 这可能与第7层卷积网络的神经元太少有关。
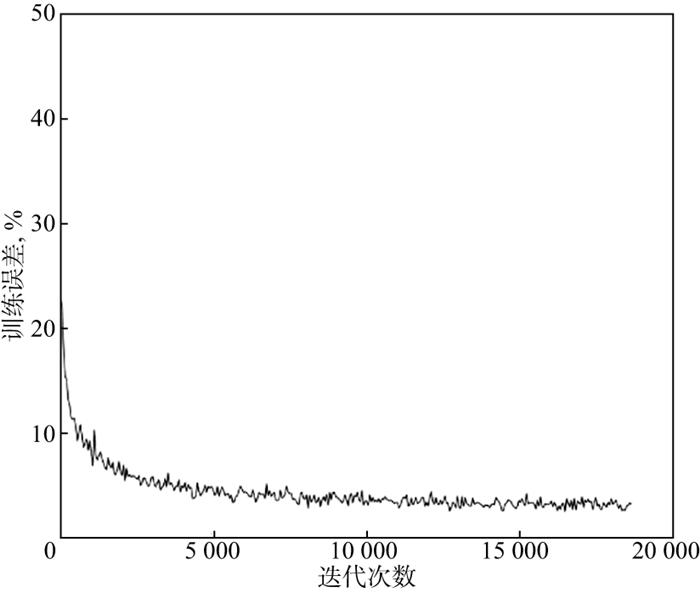
|
图 3 训练误差收敛曲线 |
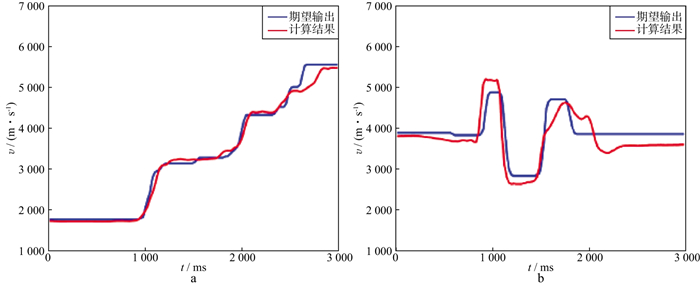
|
图 4 验证集层速度建模测试结果 a递增速度模型测试结果; b倒转速度模型测试结果 |
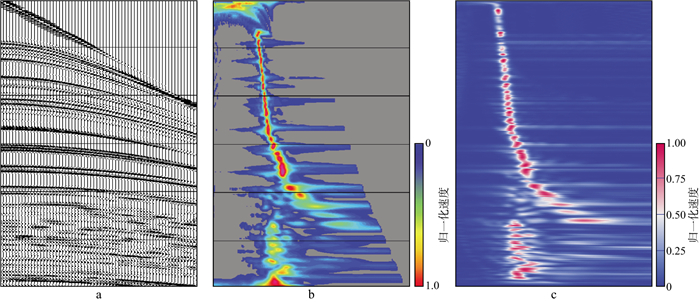
以2D marmousi模型为基础, 并添加一个递增背景速度构建速度模型, 如图 5所示。共正演851炮, 炮距为20m, 每炮128道, 道距40m, 偏移距范围为-2560~2520m, 采样点数为1000, 采样间隔为3ms, 水平地表观测。第一层速度在2500m/s左右, CMP范围为874~2828。基于正演模拟得到的CMP道集(图 6a), 常规方法利用商业软件计算速度谱(图 6b)并人工拾取速度谱时间-速度对建立均方根速度模型; 而本文训练的卷积神经网络模型可以直接输入速度谱(图 6c)自动计算时间域层速度, 然后利用Dix公式得到均方根速度模型。

|
图 5 测试速度模型 |
|
图 6 正演模拟得到的CMP道集(a)及商业软件生成的归一化速度谱(b)和卷积神经网络输入的归一化速度谱(c) |
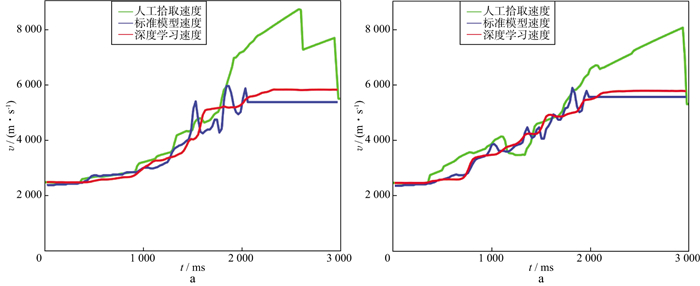
不同CDP处基于人工拾取的速度谱通过Dix公式得到的时间域层速度、深度学习方法得到的时间域层速度以及标准模型时间域层速度的对比如图 7所示。由图 7可以看出, 深度学习方法得到的层速度与人工拾取方法得到的层速度整体趋势一致, 不过深度学习方法得到的层速度与标准模型层速度更加吻合, 速度误差更小, 尤其是在复杂构造地区和中深层区域的速度保持了很好的稳定性。图 8给出了人工拾取时间-速度对建立的均方根速度模型和本文深度学习建立的均方根速度模型。由图 8可以看出, 两者中浅层比较接近, 中下部差别较大, 人工拾取时间-速度对建立的均方根速度模型明显速度偏高。
|
图 7 不同位置处速度曲线对比 a CDP251层速度曲线对比; b CDP421层速度曲线对比 |

|
图 8 均方根速度模型对比 a人工拾取均方根速度模型; b深度学习均方根速度模型 |
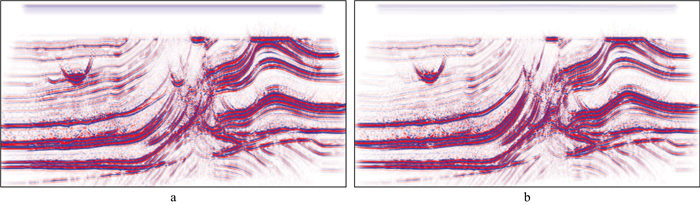
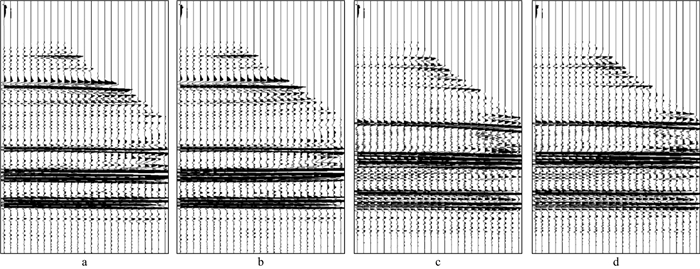
图 9给出了采用图 8所示速度模型进行叠前时间偏移得到的成像剖面。由图 9可以看出, 两种速度模型得到的叠前时间偏移剖面整体面貌比较接近, 不过在复杂断裂发育的模型中部区域, 基于深度学习的神经网络速度模型偏移剖面聚焦性更好, 绕射收敛效果明显。图 10给出了采用图 8所示速度模型进行叠前时间偏移得到的不同位置处的偏移道集。由图 10可以看出, 两种方法得到的道集同相轴的拉平效果相当, 但是在复杂构造区域, 深度学习均方根速度模型对应的成像道集更平。
|
图 9 不同速度模型得到的叠前时间偏移剖面 a人工拾取均方根速度模型得到的叠前时间偏移剖面; b深度学习均方根速度模型得到的叠前时间偏移剖面 |
|
图 10 叠前时间偏移成像道集对比 a人工拾取均方根速度模型CIG251; b深度学习均方根速度模型CIG251; c人工拾取均方根速度模型CIG421; d深度学习均方根速度模型CIG421 |
模型数据测试结果表明, 与人工拾取时间-速度对建模方法相比, 本文基于深度学习的自动化速度建模方法对复杂构造区域的速度模型具有更好的适应性。而且在建模效率方面, 人工拾取用时26220s(每个CDP都拾取速度), 自动化速度建模用时小于3600s, 建模效率提升数百倍以上, 具有非常明显的优势, 初步验证了本文方法的有效性。
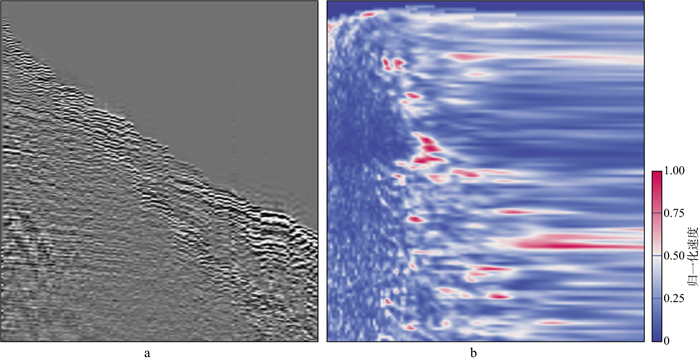
3 实际数据应用选择东部某陆地三维工区的地震数据检验本文方法的应用效果。该工区地形比较平缓, 地下构造复杂, 火成岩广泛发育。数据采集方式: 震源距为200m, 检波点距为50m, 经过处理后的偏移距范围为500~3000m, CDP范围为1342~1782, 共100条线。实际资料的CMP道集和归一化后的速度谱如图 11所示。图中CMP道集信噪比较低, 速度谱的能量团聚焦性差, 浅层覆盖次数太少, 速度谱能量不集中, 中深层受复杂噪声影响能量团非常分散, 给人工拾取带来了很大挑战。
|
图 11 实际资料CMP道集(a)与归一化后的速度谱(b) |
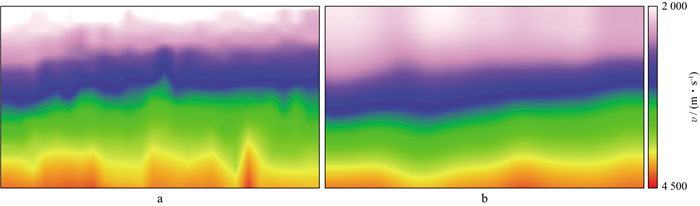
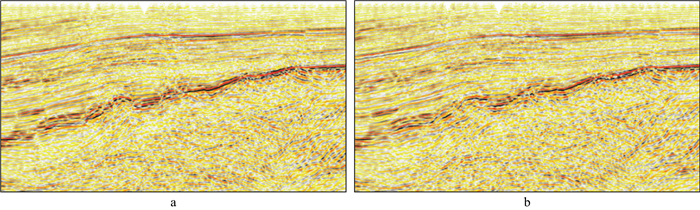
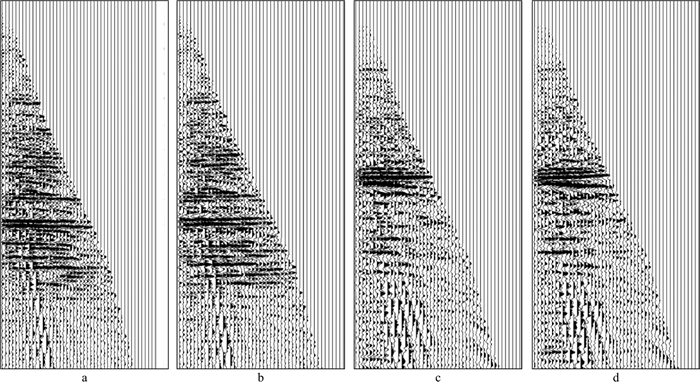
图 12a和图 12b分别给出了人工拾取的均方根速度模型和采用本文方法建立的均方根速度模型; 图 13给出了采用不同均方根速度模型得到的叠前时间偏移剖面。由图 12和图 13可以看出, 两个均方根速度模型的整体速度分布特征一致, 偏移效果整体相当, 但本文方法建立的速度模型与偏移剖面构造形态更加一致。图 14给出了不同建模方法在不同位置处的叠前时间偏移成像道集。由图 14可以看出, 深度学习速度建模与人工拾取速度建模得到的成像道集拉平整体相当。但在建模效率方面, 深度学习速度建模在不到300s的时间内就可以完成三维工区的均方根速度建模, 而人工拾取往往耗费几个小时的时间。
|
图 12 采用人工拾取方法(a)和本文方法(b)建立的均方根速度模型 |
|
图 13 采用不同速度模型得到的叠前时间偏移剖面 a人工拾取方法建立的速度模型; b本文方法建立的速度模型 |
|
图 14 不同建模方法在不同位置处的叠前时间偏移成像道集 a人工拾取速度建模CIG1450; b深度学习速度建模CIG1450; c人工拾取速度建模CIG1700; d深度学习速度建模CIG1700 |
该实际资料的应用结果表明, 在复杂陆上探区, 本文提出的深度学习卷积神经网络自动速度建模技术能够克服复杂构造和地震资料信噪比低的影响, 建立更加符合地质构造特征的时间域层速度模型, 具有一定的应用前景。
4 结论本文介绍了多层卷积神经网络模型, 设计了大规模随机模型训练集, 将速度谱作为输入数据, 将时间域层速度作为标签数据, 形成了能够适应复杂地区低信噪比地震资料的自动化速度建模神经网络。
将速度谱整体作为神经网络的输入数据, 避免了拾取复杂构造地区速度谱能量团的时间-速度对, 克服了常规速度分析水平层状介质假设的限制, 同时消除了地震波形差异对速度估计的影响, 增加了卷积神经网络自动速度建模的泛化能力。
将时间域层速度作为标签数据, 增强了地震数据和速度模型的空间匹配, 更有利于神经网络建立速度谱和层速度之间的映射关系, 加速神经网络模型的收敛速度。
卷积神经网络可以实现数据降维和特征抽取, 克服“维数灾难”, 增加建模的稳定性。然而, 过度压缩往往导致必要建模信息的缺失, 进而引起薄层信息难以恢复。下一步的工作重点是优化网络模型结构, 提高深度学习自动化速度建模的精度并进行大规模的实用化测试。
致谢: 感谢中国石油化工股份有限公司石油物探技术研究院郑浩、张林、宋林在技术试验阶段所做的工作!| [1] |
ZHANG B, ZHAO T, QI J, et al. Horizon-based semiautomated nonhyperbolic velocity analysis[J]. Geophysics, 2014, 79(6): U15-U23. DOI:10.1190/geo2014-0112.1 |
| [2] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [3] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN W X, ZHOU Y T, CHI Y. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [4] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI H S, CHEN D W, WU J, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [5] |
赵明, 陈石, 房立华, 等. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报, 2019, 62(8): 3034-3042. ZHAO M, CHEN S, FANG L H, et al. Earthquake phase arrival auto-picking based on U-shaped convolutional neuralnetwork[J]. Chinese Journal of Geophysics, 2019, 62(8): 3034-3042. |
| [6] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度[J]. 石油地球物理勘探, 2020, 55(3): 484-492. SUN Y H, LIU Y. Prediction of S-wave velocity based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 484-492. |
| [7] |
奚先, 黄江清. 基于卷积神经网络的地震偏移剖面中散射体的定位和成像[J]. 地球物理学报, 2020, 63(2): 687-714. XI X, HUANG J Q. Location and imaging of scatterers in seismic migration profiles based on convolution neural network[J]. Chinese Journal of Geophysics, 2020, 63(2): 687-714. |
| [8] |
MA Y, JI X, FEI T W, et al. Automatic velocity picking with convolutional neural networks[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 2066-2070. |
| [9] |
BISWAS R, VASSILIOU A, STOMBERG R, et al. Stacking velocity estimation using recurrent neural network[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 2241-2245. |
| [10] |
张吴, 朱培民, 顾元, 等. 基于深度学习的地震速度谱自动拾取方法[J]. 石油物探, 2019, 58(5): 724-733. ZHANG W, ZHU P M, GU Y, et al. Velocity auto-picking from seismic velocity spectra based on deep learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 724-733. DOI:10.3969/j.issn.1000-1441.2019.05.011 |
| [11] |
HAO Z, PEI M Z. Automatic velocity picking based on deep learning[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 2604-2608. |
| [12] |
赵改善. 石油物探智能化发展之路: 从自动化到智能化[J]. 石油物探, 2019, 58(6): 791-810. ZHAO G S. Road to intelligent petroleum geophysical exploration: from automatic to intelligent[J]. Geophysical Prospecting for Petroleum, 2019, 58(6): 791-810. DOI:10.3969/j.issn.1000-1441.2019.06.002 |
| [13] |
ARAYA P M, JENNINGS J, ADLER A, et al. Deep-learning tomography[J]. The Leading Edge, 2018, 37(1): 58-66. DOI:10.1190/tle37010058.1 |
| [14] |
WANG W L, YANG F S, MA J W. Velocity model building with a modified fully convolutional network[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 2086-2090. |
| [15] |
DUQUE L, GUTIERREZ G, ARIAS C, et al. Automated velocity estimation by deep learning based seismic-to-velocity mapping[J]. Expanded Abstracts of 81st EAGE Conference & Exhibition, 2019, Th_R04_10. |
| [16] |
YE O K, DAHL E K. Velocity model building from raw shot gathers using machine learning[J]. Expanded Abstracts of 81st EAGE Conference & Exhibition, 2019, Th_R04_09. |
| [17] |
SWIETOJANSKI P, GHOSHAL A, RENALS S. Convolutional neural networks for distant speech recognition[J]. IEEE Signal Processing Letters, 2014, 21(9): 1120-1124. DOI:10.1109/LSP.2014.2325781 |
| [18] |
CHEN S X, ZHANG Y. Deep features learning formedical image analysis with convolutional autoencoder neurnetwork[J]. IEEE Transactions on Big Data. DOI:10.1109/TBDATA.2017.2717439 |
| [19] |
BOUREU Y L, PONCE J, LECUN Y. A theoretical analysis of feature pooling in visual recognition[J]. Expanded Abstracts of the 27th International Conference on Machine Learning, 2010, 111-118. |



