2. 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
2. Key Laboratory of Earth Exploration and Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu 610059, China
深度偏移在复杂地质构造和地质体的高精度成像方面具有突出的优势[1-3]。随着叠前深度偏移处理技术的广泛应用, 业界对系统的真深度域地震反演和解释方法技术提出了日益迫切的需求。深度域地震子波提取是进行深度域地震反演和解释等工作的基础。由于深度域地震子波是与地下介质速度有关的函数[4], 其波形随着介质速度的增加而拉伸、随着介质速度的降低而压缩, 且在不同介质层界面处的波形呈现非对称特征, 因此, “线性时不变”条件在深度域中并不成立, 基于褶积模型的地震子波提取方法对深度域地震数据并不是直接适用的。如何准确提取深度域地震子波, 从而为深度域地震资料反演和解释等工作奠定可靠的基础具有重要意义。
目前, 常规深度域地震反演和解释通常是先将深度域测井数据和地震数据根据时深关系转换至时间域, 完成反演和解释后, 再将结果转换回深度域。这样的流程存在两个主要缺点: 一是在将测井的各物性参数曲线从深度域转换至时间域的过程中, 会损失其中的重要高频特征信息; 二是在不同域之间的转换过程中, 会在有效数据中引入累积误差。因此, 常规深度域地震反演和解释流程, 不能充分利用深度域地震数据中反映储层结构、岩性和流体情况等的有效信息, 不利于挖掘深度域地震数据的应用价值和潜力, 也不利于实现储层的精细描述。为了避免常规深度域地震反演和解释中的深-时和时-深转换, 需要利用好深度域地震子波的特性。如果介质速度是一个常数, 那么在该介质中的地震子波波形就能在不同深度位置处保持不变, 可以满足“线性时不变”条件。因此, 可以采用一定的速度变换方法, 将深度域测井数据和深度域地震数据无损地转换到一个介质速度处处相等的等效介质(即常速度深度域)中[4-7], 从而可以基于褶积模型提取深度域地震子波, 进而充分利用深度域测井数据和深度域地震数据中的有效信息, 实现更高质量和更加精细的深度域地震反演和解释[8-12]。
本文首先对深度域地震子波提取中存在的主要问题进行了分析; 然后, 对目前已有的深度域地震子波提取方法进行了梳理, 并对每种方法的优缺点及适用条件进行了总结; 最后, 对深度域地震子波提取方法的未来发展提出了一些建议。
1 深度域地震子波提取存在的主要问题 1.1 深度域地震子波对介质速度的依赖特性一个波动过程, 既可以用时间域函数表征, 也可以用空间域函数表征。时间域地震子波是在波动延续时间范围内, 某一质点的各时刻振动幅度形成的振动曲线。空间(深度)域地震子波是在某一时刻波动延续空间范围内, 一系列质点的振动幅度形成的波形曲线。地震子波可以被表示为一系列谐波(一组不同振幅、频率和相位的正弦曲线)叠加而成的信号[4, 13], 在时间域和深度域分别表示为:
| $ {w(t) = \sum w (f){{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }}ft}}} $ | (1) |
| $ {w(d) = \sum w (k){{\rm{e}}^{{\rm{i}}kd}}} $ | (2) |
式中: w(t)和w(d)分别表示时间域和深度域的地震子波; t和d分别表示时间和深度; w(f)和w(k)分别表示时间域子波的频谱和深度域子波的波数谱; k和f分别表示波数和频率。波数与频率之间的关系为:
| $ k=\frac{f}{v} $ | (3) |
式中: v是地下介质的速度, 随深度变化。
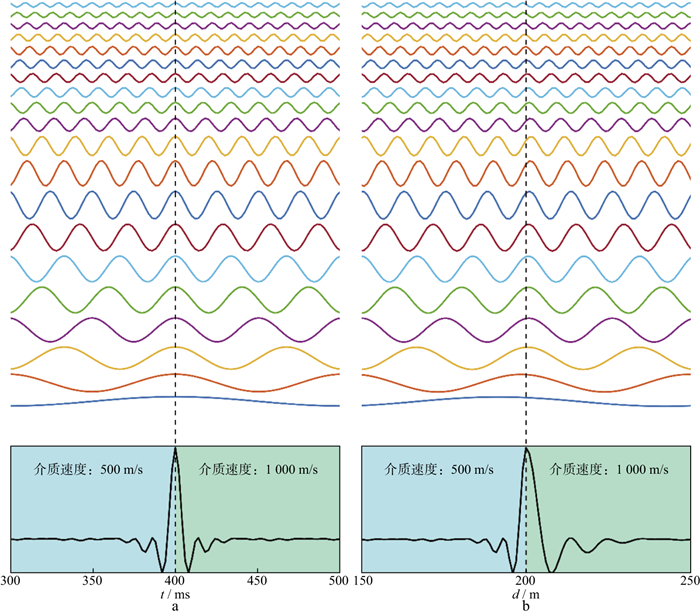
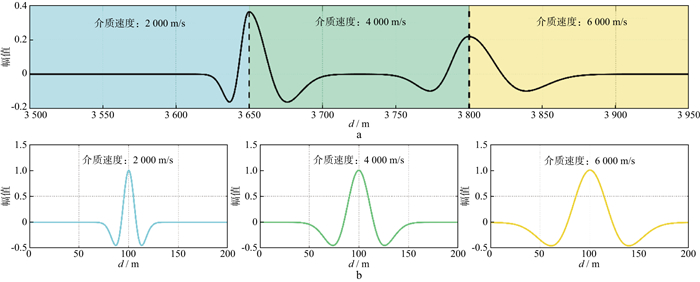
为直观展示时间域地震子波与深度域地震子波的异同, 图 1a和图 1b分别显示了在2层不同介质中的时间域地震子波和深度域地震子波以及各自的前20个主要正弦分量。从图 1可以看出: 零相位的时间域地震子波波形在不同介质的分界面处是对称的, 对应的主要正弦分量在分界面处也是对称的; 深度域地震子波波形在不同介质的分界面处是不对称的, 主要的正弦分量在分界面处也是不对称的, 且各正弦分量之间存在不同的相位差。图 2显示了3层介质模型中的深度域合成地震记录及其在速度为2000, 4000, 6000m/s的常速度介质中的深度域地震子波。图 2通过一个3层水平地质模型和与之对应的深度域合成地震记录, 以及每一层常速度介质中的深度域地震子波, 展示了深度域地震子波波形随介质速度变化的特性。由图 2可以看出, 介质速度越大, 深度域地震子波的波形越宽(对应的波数越小)。图 1和图 2所展示的深度域地震子波对介质速度的依赖特征在盐丘体附近的深度域地震数据中很常见[14]。因此, 与时间域地震子波相比, 深度域地震子波除了受到地震震源特征、地下介质的吸收和频散等因素影响外[15-16], 还受到介质速度的影响。
|
图 1 在2层不同介质中的时间域地震子波和深度域地震子波 a时间域零相位地震子波及构成这条振动曲线的前20个时间域正弦分量; b某一时刻(波形曲线振幅峰值恰好位于介质分界面)的深度域地震子波(由101个质点组成)及构成这条波形曲线的前20个空间域正弦分量 |
|
图 2 3层介质模型中的深度域合成地震记录(a)及其在速度为2000, 4000, 6000m/s的常速度介质中的深度域地震子波(都与主频为30Hz的时间域Ricker子波相对应)(b) |
时间域中常用的褶积运算的假设前提是“线性时不变”。对于一个线性时不变系统, 当输入一个谐波时, 其对应的输出是一个同频率但振幅和相位不同的谐波。而(2)式和(3)式表明, 在深度域中, “线性时不变条件”不成立。因此, 要对深度域地震数据进行反演、属性分析等处理, 需要采用一定的变换方法将数据转换至一个能够满足“线性时不变条件”的转换域中, 目前主要有以下2种途径: ①将深度域地震数据根据时-深关系转换到时间域; ②将深度域地震数据进行速度变换, 转换到一种介质速度处处相等的均匀介质中, 即常速度深度域中。这2种途径的基本思想都是在转换域(时间域或常速度深度域)中完成反演、属性分析等处理之后, 再将处理结果反变换回深度域。
1.2 深度域测井数据与地震数据的采样间隔非一致性通常, 深度域测井数据的深度采样间隔小于深度域地震数据的深度采样间隔。在利用地震数据和测井数据提取地震子波时, 测井数据和地震数据的采样间隔须要保持一致。使测井数据与地震数据的采样间隔保持一致的方法主要有以下3种: ①将深度域测井数据按照时-深关系转换到时间域, 使测井数据与地震数据的时间采样间隔保持一致; ②对深度域测井数据进行降采样, 使其深度采样间隔与深度域地震数据的采样间隔保持一致; ③对深度域地震数据进行插值, 使其深度采样间隔与深度域测井数据的采样间隔保持一致。方法①和方法②都是数据的降采样过程, 常规的降采样处理方法并未考虑地下反射界面的信息, 从而导致有用的层位信息丢失。因此, 在对深度域测井数据进行降采样时, 应使用能够尽可能保留反射界面信息的降采样处理方法[17]。方法③是数据的插值过程, 该过程不会增加深度域地震数据本身的信息, 其缺点是会增加数据量。但目前的计算机软硬件条件足以应对这个缺点, 故我们推荐使用该方法解决深度域测井数据与地震数据的采样间隔非一致性问题。
2 深度域地震子波提取方法若要基于褶积模型进行深度域地震子波提取, 需要先将深度域地震数据和深度域测井数据转换至时间域或常速度深度域。由于将深度域地震数据和测井数据转换到时间域(降采样处理)会丢失数据信息, 所以, 更佳的做法是将数据转换至常速度深度域。具体的常速度深度域转换方法流程可以参考文献[4]和文献[7]。需要说明的是, 深度域转换至常速度深度域是一个数据插值过程, 不会增加深度域地震数据本身的信息。我们对目前已有的深度域地震子波提取方法以及可以借鉴的时间域地震子波提取方法进行了梳理, 并根据在方法中是否用到测井信息, 将方法分为确定性地震子波提取方法和统计性地震子波提取方法2大类。
2.1 确定性地震子波提取方法当线性时不变系统条件得以满足时, 合成地震记录s可由反射系数向量r和地震子波向量w进行褶积运算(线性褶积)再加上噪声项n获得, 其具体形式为:
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{r}}{\rm{ }}*{\rm{ }}\mathit{\boldsymbol{w}} + \mathit{\boldsymbol{n}} $ | (4) |
其中, “*”表示一维褶积运算, 噪声项通常被假设为高斯随机白噪声。从(4)式可以看出, 当已知地震记录和反射系数时, 地震子波成了唯一要确定的量, 这也是确定性地震子波提取方法名称的由来。在时间域或常速度深度域中, 利用测井数据和井旁地震记录进行地震子波提取的方法就属于这一类。基于褶积模型的不同形式, 目前的确定性地震子波提取方法主要有谱除法和最小二乘法。除了最小二乘法已经用于深度域地震子波提取外[12, 18], 其余的确定性方法均还未见到在这方面的应用, 但这些方法的思想是值得借鉴的。
2.1.1 谱除法两个向量的褶积运算在傅里叶变换域(频域或波数域)中是两个向量傅里叶变换结果的乘积运算:
| $ \boldsymbol{s}^{\prime}=\boldsymbol{r}^{\prime} \boldsymbol{w}^{\prime}+\boldsymbol{n}^{\prime} $ | (5) |
式中: s′, r′, w′和n′分别表示合成地震记录、反射系数、地震子波和噪声项的傅里叶变换结果。若忽略噪声项, 地震子波可由地震记录与反射系数的傅里叶变换结果相除获得[15-16, 19]:
| $ {\mathit{\boldsymbol{w}}^\prime } = {\mathop{\rm IFT}\nolimits} \left( {\frac{{{\mathit{\boldsymbol{s}}^\prime }}}{{{\mathit{\boldsymbol{r}}^\prime }}}} \right) $ | (6) |
式中: IFT(·)表示反傅里叶变换。从(6)式可以看出, 反射系数的傅里叶变换结果中若存在零值, 将导致结果异常。可以通过在反射系数的傅里叶变换结果中添加一个非常小的常数以避免这个问题[16]。此外, 由于数量级不同的小数在进行除法运算后会出现异常大值(主要出现在高频或高波数部分), 所以还需要对谱除结果用带通滤波器作进一步的处理。谱除法对噪声非常敏感, 为了减少噪声的影响, 在实际应用中, 更多的是使用反射系数与地震记录的互相关结果和反射系数的自相关结果进行谱除[20-21]。由谱除法得到的结果通常作为迭代优化地震子波提取方法的初始子波模型[22]。
2.1.2 最小二乘法最小二乘法是要使得合成数据与已知数据之间的残差能量达到最小, 具体的目标函数可表示为如下形式:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{w}} \left\{ {\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Rw}}} \right\|_2^2} \right\} $ | (7) |
式中: d为包含M个采样点的已知地震记录向量; R为由反射系数r构成的M阶Toeplitz方阵[23-24]; ‖·‖2表示向量的L2范数。(7)式的解析解形式为:
| $ \mathit{\boldsymbol{\hat w}} = {\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{R}}} \right)^{ - 1}}{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (8) |
式中:
一般而言, 地震子波的延续范围有限[25-26], 所以, 在提取地震子波的过程中, 可以用这一点作为约束, 以便在地震数据信噪比不高的情况下获得合理的结果。已有许多学者提出了不同的地震子波长度确定方法: 梁光河[27]将褶积模型看作一个移动平均(moving average, MA)过程, 从而将子波长度确定问题转换为MA过程的定阶问题; BUNCH等[28]基于合成地震记录与已知地震记录之间的均方根误差, 利用试错法确定子波长度; BULAND等[29]与GUNNING等[30]指出, 可以将子波长度作为一个未知参数包括在子波提取过程中; RIETSCH[31-32]用多道地震记录的自相关和互相关所构建矩阵的零特征值个数作为所提取地震子波的长度。将地震子波长度作为约束与最小二乘法相结合后, (8)式改写为[24]:
| $ \hat{\boldsymbol{w}}=\left(\boldsymbol{R}_{P}^{\mathrm{T}} \boldsymbol{R}_{P}\right)^{-1} \boldsymbol{R}_{P}^{\mathrm{T}} \boldsymbol{d} $ | (9) |
式中: RP=RP, P是根据地震子波长度L(L < M)构建的M×L阶投影矩阵, 其具体形式如下:
| $ \boldsymbol{P}=\left[\begin{array}{l} \boldsymbol{I} \\ 0 \end{array}\right] $ | (10) |
式中: I为L阶单位方阵。由于求解(9)式比较容易且快速, 因此, 可以通过试错法确定最合适的地震子波长度L。通过地震子波长度信息的约束, 不但可以降低过拟合, 还可以降低运算过程中的矩阵维度, 提高计算效率。
在确定性地震子波提取方法的实际应用中, 由于测井资料的深度范围有限, 与之对应的井旁地震记录也只有有限的一段数据, 在这段数据中包含着在此深度范围之外的信息, 相对而言, 这部分信息是要处理的“噪声”, 故还需要考虑在(9)式中加入正则约束项以形成更加稳健的算法。一般而言, 正则约束项多采用L1范数, 但是L1范数不可求导, 对应的目标函数没有解析解, 只能通过迭代求解, 且求解的结果是稀疏的, 因此, 最小二乘法中多用L2范数作为正则约束项[18, 24, 33], 相应的目标函数及其解析解如下:
| $ {\mathop {\min }\limits_\mathit{\boldsymbol{w}} \left\{ {\left\| {\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{R}}_P}\mathit{\boldsymbol{w}}} \right\|_2^2 + \left\| \mathit{\boldsymbol{w}} \right\|_2^2} \right\}} $ | (11) |
| $ {\mathit{\boldsymbol{\hat w}} = {{\left( {\mathit{\boldsymbol{R}}_P^{\rm{T}}{\mathit{\boldsymbol{R}}_P} + \lambda \mathit{\boldsymbol{I}}} \right)}^{ - 1}}\mathit{\boldsymbol{R}}_P^{\rm{T}}\mathit{\boldsymbol{d}}} $ | (12) |
式中: λ(λ > 0)是正则化参数, 可以通过试错法或广义交叉验证(generalized cross-validation, GCV)方法确定[34-35]。由于L1范数对异常值的处理效果优于L2范数[36], 所以还可以进一步考虑将L1范数和L2范数相结合的处理方案, 例如Hybird、Huber、Biweight范数等。张杰等[18]采用Huber范数约束最小二乘法在较短的深度窗中获得了优于L2范数约束最小二乘法的深度域地震子波提取结果。此外, BULAND等[29]基于贝叶斯理论提出了一种贝叶斯最小二乘法。贝叶斯理论重视利用先验信息, 贝叶斯最小二乘法是在(12)式的基础上使用了多层先验, 例如: 不仅假设子波满足高斯分布, 而且还在此基础上, 进一步假设该高斯分布的均值和方差分别满足高斯分布和逆伽马分布(inverse gamma distribution)。贝叶斯最小二乘法的优点是能给出所提取子波结果的不确定性评价, 但是, 由于其没有明确的后验概率分布表达式, 需要通过马尔科夫链蒙特卡洛(Markov chain Monte Carlo, MCMC)算法进行大量抽样, 算法耗时长。
2.1.3 其它确定性地震子波提取方法LIU等[37]使用测井数据作为输入, 井旁地震记录作为输出, 利用误差反向传播(back propagation, BP)神经网络方法来提取地震子波。由于训练好的网络结果是一系列的网络连接权重系数, 并不是一个子波波形, 还需要将训练好的网络作用于单反射界面模型上, 输出的结果才是最终提取的地震子波。该方法的缺点是如果井震之间不匹配会导致算法收敛较慢, 优点是不需要依赖初始子波模型, 也不需要对地震子波和反射系数进行任何假设。
2.2 统计性地震子波提取方法当工区无测井资料可用时, 就无法获取反射系数信息。公式(4)存在两个未知数, 解的多解性是必然的。故想要得到合理的反射系数和地震子波估计, 就需要对二者进行一定的假设[21, 38]: ①反射系数是统计独立的平稳随机过程, 其对应的概率密度函数是对称的非高斯函数; ②地震子波是最小相位或常相位的; ③噪声是统计独立的平稳随机过程, 其均值为0, 满足高斯分布, 且与地震记录和反射系数是相互独立的统计量。常用的统计性地震子波提取方法有同态法、交替迭代法、二阶统计量法和高阶统计量法。目前, 除了二阶统计量法已用于提取深变地震子波外[39-40], 其余的统计性方法均还未见到在深度域地震子波提取中的应用。此外, 在缺少测井速度信息的情况下, 如何进行速度变换也制约着统计性方法在深度域地震子波提取中的应用。
2.2.1 同态法忽略噪声项, 将(5)式两边分别取自然对数, 可以得到如下线性关系:
| $ \ln \left(\boldsymbol{s}^{\prime}\right)=\ln \left(\boldsymbol{r}^{\prime}\right)+\ln \left(\boldsymbol{w}^{\prime}\right) $ | (13) |
对(13)式中各变量进行反傅里叶变换, 可以得到褶积运算在复倒谱域(complex cepstral domain)中[41]的对应形式:
| $ \operatorname{IFT}\left[\ln \left(\boldsymbol{s}^{\prime}\right)\right]=\operatorname{IFT}\left[\ln \left(\boldsymbol{r}^{\prime}\right)\right]+\operatorname{IFT}\left[\ln \left(\boldsymbol{w}^{\prime}\right)\right] $ | (14) |
(13) 式和(14)式构成一个同态系统, 可以将褶积运算转变为加法运算, 基于该思想的统计性地震子波提取方法称为同态法。与反射系数相比, 地震子波波形较为平滑且其延续范围有限, 因此, 同态法假设地震子波的复倒谱通常位于原点附近, 反射系数的复倒谱远离原点, 且二者可分离。通过设计相应的低通滤波器, 可以从地震数据的复倒谱中分离地震子波和反射系数。同态法不需要对地震子波的相位和反射系数的概率分布函数做出假设, 但该方法涉及到相位解缠和移除解缠相位线性趋势等复杂处理。ULRYCH等[42]使用微分复倒谱来避免相位解缠和线性趋势移除, 并采用多道地震数据的复倒谱叠加来突出地震子波的复倒谱。在实际地震数据中, 地震子波和反射系数在复倒谱域并不是完全可分的, 需要用多道地震记录的统计平均[43-44]以及随机时窗来压制反射系数的影响[42, 45]。DE MACEDO等[46]利用测井反射系数的复倒谱信息, 构建了稳健的分离滤波器来提取子波, 但这实际上属于一种确定性地震子波提取方法。
2.2.2 交替松弛迭代法交替松弛迭代法求解两个未知变量的基本思想是: 先给定其中一个变量的初始解, 基于此初始解求解另一个变量; 然后固定求解后的变量, 再求解另一个变量, 如此反复交替求解两个变量, 直至满足停机准则。对于地震子波提取问题而言, 由于有很多成熟的方法(如高阶统计量法)可以仅利用地震数据信息获得一个较为可靠的地震子波估计[47], 所以, 通常先给定子波的初始解。交替松弛迭代法的目标函数为:
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{w}}, \mathit{\boldsymbol{r}}} \left\{ {\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{r}}*\mathit{\boldsymbol{w}}} \right\|_2^2 + {\lambda _1}\left\| {\mathit{\boldsymbol{w}} - {\mathit{\boldsymbol{w}}_0}} \right\|_2^2 + {\lambda _2}{\mathop{\rm Reg}\nolimits} (\mathit{\boldsymbol{r}})} \right\} $ | (15) |
式中: w0是给定的子波初始解; Reg(r)是反射系数约束项; λ1和λ2分别是地震子波约束项和反射系数约束项的正则参数。当固定反射系数求解地震子波时, (15)式退化为(11)式, 可以采用(12)式的解析解形式直接求解子波。交替松弛迭代法的重点是求解反射系数。曹静杰[48]在反射系数满足广义高斯分布的假设前提下, 采用Lp(0 < p < 1)范数作为约束(与反射系数概率密度函数特性相关的约束[49]), 使用迭代加权最小二乘法求解反射系数; KAZEMI[34]采用L1范数作为约束, 使用快速软阈值迭代算法求解反射系数; HAGHSHENAS LARI等[35]采用L1范数和二阶全变分(total variation, TV)正则化作为约束, 使用分裂Bregman迭代算法求解反射系数; HAGHSHENAS LARI等[35]在块褶积运算和窗口重叠法的基础上将交替松弛迭代法用于时变子波提取。交替松弛迭代法属于局部优化方法, 需要充分利用反射系数和地震子波的先验信息, 以给出接近全局最优解的初始解。
2.2.3 二阶统计量法二阶统计量, 即信号的自相关, 其结果并不包含相位信息, 但由于计算简单, 通常主要用于估计地震子波的振幅谱。一个零均值、统计独立的平稳随机过程y(t), 其二阶统计量定义为[50]:
| $ c_{2 y}(\tau)=\frac{1}{N} \sum\limits_{t} y(t) y(t+\tau) $ | (16) |
式中: N是信号的采样点个数; τ是时间延迟量。基于反射系数的非高斯白噪假设, 其自相关是一脉冲函数, 可以近似当作一个常数处理, (4)式所示的褶积模型对应的二阶统计量形式为:
| $ c_{2 s}(\tau)=\sigma c_{2 w}(\tau) $ | (17) |
式中: σ是反射系数自相关的近似; c2s(τ)和c2w(τ)分别为地震记录和子波的自相关。由于自相关的傅里叶变换就是功率谱, 因此, 可以利用地震记录的功率谱估计地震子波的功率谱。ZHANG等[51]利用基于局部属性的时频分解方法对时间域地震数据进行时频分解, 然后基于瞬时振幅谱提取了零相位时变地震子波; ZHANG等[39]利用S变换对叠后深度域地震数据进行深度-波数分解, 然后基于瞬时波数振幅谱提取了零相位深变地震子波; 之后, ZHANG等[40]又将该方法扩展到叠前深度域地震数据, 提取了随深度和入射角度变化的地震子波集。然而, 在对深度域地震数据使用深度-波数分解方法时, 需要考虑深度域地震子波随地下介质速度变化的特征, 否则在利用深度域地震数据的深度-波数分解结果进行衰减频散属性分析时, 就有可能出现误判。此外, ROSA等[52]提出一种谱模拟方法:
| $ |w(f)|=|f|^{n} \mathrm{e}^{H(f)} $ | (18) |
式中: |w(f)|是时间域地震子波的振幅谱; n是大于等于0的实数; H(f)是和频率有关的多项式。利用(18)式, 通过拟合地震记录的功率谱, 可以得到地震子波的振幅谱。与时频分析方法(如S变换)相结合, 谱模拟方法可用于提取时变地震子波的振幅谱。谱模拟方法的前提假设是, 地震子波的振幅谱是一光滑的单峰曲线, 若地震数据的振幅谱是多峰曲线(如短时窗中地震数据的振幅谱), 不建议使用该方法。
2.2.4 高阶统计量法通常, 将二阶以上的统计量称为高阶统计量。常用的高阶统计量主要是三阶统计量和四阶统计量。高阶统计量包含高阶累积量和高阶矩两个概念, 高阶累积量是一阶至高阶矩的和[50]。由于三阶和四阶累积量的维度分别是二维和三维, 在计算过程中意味着将单道一维地震数据扩展到二维和三维, 导致算法复杂、计算量大, 限制了其在实际中的应用。但由于高阶统计量包含了数据的相位信息, 因此多将其用于估计地震子波的相位。高阶统计量法实际上又分为两类: ①利用地震数据的高阶统计量提取子波, 主要是高阶累积量拟合法; ②利用地震数据的高阶统计量提取子波的相位谱(子波的振幅谱通过二阶统计量法获得), 常用方法主要是Kurtosis最大化准则法和高阶累计量谱估算法。
一个零均值、统计独立的平稳随机过程y(t), 其三阶和四阶累积量定义为[50]:
| $ c_{3 y}\left(\tau_{1}, \tau_{2}\right)=\frac{1}{N} \sum\limits_{t} y(t) y\left(t+\tau_{1}\right) y\left(t+\tau_{2}\right) $ | (19) |
| $ \begin{array}{c} c_{4 y}\left(\tau_{1}, \tau_{2}, \tau_{3}\right)=\frac{1}{N} \sum\limits_{t} y(t) y\left(t+\tau_{1}\right) y\left(t+\tau_{2}\right) \cdot\\ y\left(t+\tau_{3}\right)-m_{4 g}\left(\tau_{1}, \tau_{2}, \tau_{3}\right) \end{array} $ | (20) |
式中: m4g(τ1, τ2, τ3)是一个与y(t)有着相同均值和自相关的高斯过程的四阶矩, 其定义为:
| $ \begin{array}{c} m_{4 g}\left(\tau_{1}, \tau_{2}, \tau_{3}\right)=c_{2 y}\left(\tau_{1}\right) c_{2 y}\left(\tau_{3}-\tau_{2}\right)+c_{2 y}\left(\tau_{2}\right) \cdot \\ c_{2 y}\left(\tau_{3}-\tau_{1}\right)+c_{2 y}\left(\tau_{3}\right) c_{2 y}\left(\tau_{2}-\tau_{1}\right) \end{array} $ | (21) |
可以看出, 一个随机过程的概率密度函数若是高斯函数, 那么其三阶和四阶累积量均为0。(4)式中的噪声项通常被假设为满足高斯分布, 故利用高阶累积量可以压制随机白噪声的影响。
2.2.4.1 高阶累积量拟合法(4) 式褶积模型对应的四阶累积量形式为[38]:
| $ c_{4 s}\left(\tau_{1}, \tau_{2}, \tau_{3}\right)=c_{4 r}\left(\tau_{1}, \tau_{2}, \tau_{3}\right) * m_{4 w}\left(\tau_{1}, \tau_{2}, \tau_{3}\right) $ | (22) |
式中: c4s(τ1, τ2, τ3)和c4r(τ1, τ2, τ3)分别为地震记录和反射系数的四阶累积量; m4w(τ1, τ2, τ3)为地震子波的四阶矩。(22)式中的“*”对应三维褶积运算。(4)式褶积模型对应的三阶累积量形式与(22)式类似。由于统计性地震子波提取方法对反射系数的非高斯白噪假设, 其三阶累积量为0, 而其四阶累积量不为0, 因此更常采用四阶累积量[38, 53]。此外, 反射系数序列长度越长, 其四阶累积量就越接近一个脉冲函数(近似于一个非零常数), 因此(22)式进一步改写为:
| $ c_{4 s}\left(\tau_{1}, \tau_{2}, \tau_{3}\right)=\sigma m_{4 w}\left(\tau_{1}, \tau_{2}, \tau_{3}\right) $ | (23) |
式中: σ是反射系数四阶累积量的近似。可以看出, 地震子波的四阶矩与地震记录的四阶累积量之间只相差一个比例系数, 因此, 可利用多道地震记录的四阶累积量叠加提取地震子波, 相应的目标函数为:
| $ \mathop {\min }\limits_{{m_{4w}}} \left\{ {\sum\limits_{\tau 1} {\sum\limits_{\tau 2} {\sum\limits_{\tau 3} {{{\left[ {{c_{4s}}\left( {{\tau _1}, {\tau _2}, {\tau _3}} \right) - \sigma {m_{4w}}\left( {{\tau _1}, {\tau _2}, {\tau _3}} \right)} \right]}^2}} } } } \right\} $ | (24) |
LAZEAR[38]利用最速梯度下降法, 通过拟合地震记录的四阶累积量提取地震子波。该方法的一个缺点是容易陷入初始模型附近的局部最优值。此外, 该方法还受限于地震数据的信噪比和数据量: 所用地震数据的信噪比越高、数据量越大, 反射系数的四阶累积量才会越接近一个非零常数, 该方法才会越有效。HARGREAVES[54]进一步指出, 若是地震数据的带宽太窄, 会导致数据的高阶累积量中没有足够的相位信息, 进而导致该方法失效, 但目前的宽频采集技术已能够避免这个问题。为避免梯度法陷入局部最优, VELIS等[55]使用了混合方法: 先使用模拟退火优化算法找到初始子波, 再用梯度下降法求得最优子波。戴永寿等[56]基于(23)式, 用自回归滑动平均(autoregressive moving average, ARMA)方法对地震子波进行建模, 只需要求解少量模型参数即可提取子波。考虑到实际地震数据中噪声的概率密度函数不一定是高斯函数, 故其四阶累积量不一定为0, 还需要对地震数据的高阶累积量进行加窗平滑, 以压制噪声的影响[55]。
2.2.4.2 峰度(Kurtosis)最大化准则法Kurtosis反映了随机变量概率密度分布曲线的峰部尖度: Kurtosis值越大, 峰的形状就越尖锐。Kurtosis是数据四阶累积量在原点处的值, 归一化的Kurtosis定义为[57]:
| $ \operatorname{kurt}[y(t)]=\frac{\sum\limits_{t} y^{4}(t)}{\left[\sum\limits_{t} y^{2}(t)\right]^{2}}-3 $ | (25) |
对于(25)式, 若忽略等号右边的常数项, 就是最大方差模[58]。反射系数的四阶累积量可以近似为其峰度, 且峰度值越大, 反射系数越稀疏[59]。
陆文凯等[60]先将多道地震数据的平均对数振幅谱作为估计子波的振幅谱, 然后给定常相位扫描范围和步长, 通过常相位扫描, 分别找出使得每一道地震记录的方差模达到最大的常相位, 再将多道地震记录的常相位求平均后作为子波的常相位, 最后基于振幅谱和常相位构建最终的子波提取结果。李鲲鹏等[61]先采用谱模拟方法[52]获得子波的振幅谱, 然后找出使得反褶积结果的Kurtosis值达到最大时的子波Z变换在单位圆内的零点个数, 最后基于单位圆内零点个数和振幅谱构建最终的子波提取结果。VAN DER BAAN[62]基于分段平稳假设, 先利用相互重叠的时窗将地震数据分段, 并将每段时窗中地震数据振幅谱的叠加平均结果作为子波的振幅谱, 然后用该振幅谱的反傅里叶变换结果作为初始子波, 基于Kurtosis最大准则法和常相位扫描, 确定子波的常相位, 进而获得该时窗对应的地震子波。对每个时窗进行相同的操作后, 就得到了时变地震子波。但由于对地震记录的分段数量有限, 故提取的时变地震子波相位是分段(非连续)变化的。VAN DER BAAN等[63]进一步使用负熵(Negentropy, 即广义的Kurtosis)以提高子波相位的估计精度。VAN DER BAAN等[64]将单个时窗内的Kurtosis最大化问题转化为整个地震剖面上的正则化最小二乘优化问题, 以消除分段平稳假设, 使所提取的时变地震子波相位是连续变化的。Kurtosis最大化准则法的优点是计算方便且对高斯噪声不敏感, 其缺点是不适用于当反射系数的概率密度函数是弱非高斯函数以及地震数据量少的情况。
2.2.4.3 高阶累积量谱估算法对(19)式的三阶累积量进行傅里叶变换, 可得到:
| $ \begin{array}{*{20}{c}} {{B_y}\left( {{\omega _1}, {\omega _2}} \right) = \sum\limits_{{\tau _1} = - \infty }^\infty {\sum\limits_{{\tau _2} = - \infty }^\infty {{c_{3y}}} } \left( {{\tau _1}, {\tau _2}} \right){{\rm{e}}^{ - {\rm{i}}\left( {{\omega _1}{\tau _1} + {\omega _2}{\tau _2}} \right)}}}\\ { = \left| {{B_y}\left( {{\omega _1}, {\omega _2}} \right)} \right|\exp \left[ {{\rm{i}}\varphi \left( {{\omega _1}, {\omega _2}} \right)} \right]} \end{array} $ | (26) |
其中, By(ω1, ω2)称为双谱, 其振幅谱|By(ω1, ω2)|和相位谱φ(ω1, ω2)分别为:
| $ {\left| {{B_y}\left( {{\omega _1}, {\omega _2}} \right)} \right| = \left| {y\left( {{\omega _1}} \right)} \right|\left| {y\left( {{\omega _2}} \right)} \right|\left| {y\left( {{\omega _1} + {\omega _2}} \right)} \right|} $ | (27a) |
| $ {\varphi \left( {{\omega _1}, {\omega _2}} \right) = \varphi \left( {{\omega _1}} \right) + \varphi \left( {{\omega _2}} \right) + \varphi \left( {{\omega _1} + {\omega _2}} \right)} $ | (27b) |
式中: |y(ω)|和φ(ω)分别为信号y(t)的振幅谱和相位谱。
同样, 对(20)式的四阶累积量进行傅里叶变换, 可得:
| $ \begin{array}{*{20}{c}} {{B_y}\left( {{\omega _1}, {\omega _2}, {\omega _3}} \right) = \sum\limits_{{\tau _1} = - \infty }^\infty {\sum\limits_{{\tau _2} = - \infty }^\infty {\sum\limits_{{\tau _3} = - \infty }^\infty {{c_{4y}}} } } \left( {{\tau _1}, {\tau _2}, {\tau _3}} \right) \cdot }\\ {{{\rm{e}}^{ - {\rm{i}}\left( {{\omega _1}{\tau _1} + {\omega _2}{\tau _2} + {\omega _3}{\tau _3}} \right)}} = \left| {{B_y}\left( {{\omega _1}, {\omega _2}, {\omega _3}} \right)} \right| \cdot }\\ {\exp \left[ {{\rm{i}}\varphi \left( {{\omega _1}, {\omega _2}, {\omega _3}} \right)} \right]} \end{array} $ | (28) |
其中, By(ω1, ω2, ω3)称为三谱, 其振幅谱|By(ω1, ω2, ω3)|和相位谱φ(ω1, ω2, ω3)分别为:
| $ \begin{array}{l} \left|B_{y}\left(\omega_{1}, \omega_{2}, \omega_{3}\right)\right|=\left|y\left(\omega_{1}\right)\right| \cdot\\ \ \ \ \ \left|y\left(\omega_{2}\right)\right|\left|y\left(\omega_{3}\right)\right|\left|y\left(\omega_{1}+\omega_{2}+\omega_{3}\right)\right| \end{array} $ | (29a) |
| $ \begin{array}{l} \varphi\left(\omega_{1}, \omega_{2}, \omega_{3}\right)=\varphi\left(\omega_{1}\right)+\varphi\left(\omega_{2}\right)+\varphi\left(\omega_{3}\right)+ \\ \ \ \ \ \varphi\left(\omega_{1}+\omega_{2}+\omega_{3}\right) \end{array} $ | (29b) |
由(27b)式和(29b)式可以看出, 双谱和三谱的相位谱具有线性关系, 基于该线性关系估算子波的相位相对容易。
褶积模型的双谱、三谱频域表达式形式与(5)式类似:
| $ B_{\mathrm{s}}\left(\omega_{1}, \omega_{2}\right)=B_{\mathrm{r}}\left(\omega_{1}, \omega_{2}\right) B_{\mathrm{w}}\left(\omega_{1}, \omega_{2}\right) $ | (30) |
| $ B_{\mathrm{s}}\left(\omega_{1}, \omega_{2}, \omega_{3}\right)=B_{\mathrm{r}}\left(\omega_{1}, \omega_{2}, \omega_{3}\right) B_{\mathrm{w}}\left(\omega_{1}, \omega_{2}, \omega_{3}\right) $ | (31) |
由于反射系数的高阶累积量可以近似为高维度的脉冲函数[38], 对应的高阶累积量谱可以近似看作一个常数, 因此(30)式和(31)式可改写为:
| $ B_{\mathrm{s}}\left(\omega_{1}, \omega_{2}\right) =\sigma B_{\mathrm{w}}\left(\omega_{1}, \omega_{2}\right) $ | (32) |
| $ B_{\mathrm{s}}\left(\omega_{1}, \omega_{2}, \omega_{3}\right) =\sigma B_{\mathrm{w}}\left(\omega_{1}, \omega_{2}, \omega_{3}\right) $ | (33) |
可以看出, 地震数据与地震子波之间的双谱和三谱均是成比例的, 因此可利用地震数据的高阶累积量谱信息提取地震子波。此外, 也可以基于高阶累积量相位谱的线性关系, 通过构建对应的矩阵形式, 用最小二乘法求解子波的相位谱[65-69]。但由于存在相位缠绕问题, 因此需要进行相位解缠, 否则会影响子波的相位提取结果。YU等[69]采用保角变换解决相位缠绕问题; 戴永寿等[70]和DAI等[71]将基于三阶累积量相位谱的子波相位提取方法与基于时频分解的谱模拟方法相结合, 提取了时变地震子波。由于地震数据中噪声不一定满足高斯分布, 也不一定与地震数据相互统计独立, 故在使用高阶累积量谱估算法进行地震子波提取时, 需要使用一些窗函数(如Parzen窗)压制噪声的影响[72]。
2.2.5 其它统计性地震子波提取方法RIETSCH[31-32]基于求解2项或2项以上多项式公因式的思想, 提出了一种从多道地震记录中分离反射系数和地震子波的方法。该方法假设这些地震记录含有相同的子波, 但每道的反射系数不同。首先, 利用多道地震记录的Z变换系数构成一个矩阵, 计算该矩阵的特征值, 并将特征值中的零特征值个数作为地震子波的长度; 然后, 用该长度作为约束, 计算矩阵最小特征值对应的特征向量, 该特征向量即为多道地震记录所对应的反射系数拼接而成的向量; 最后, 用提取的反射系数和地震记录采用最小二乘法获得最终的地震子波。该方法不需要对子波的相位和反射系数的概率分布做出假设, 同时对数据量要求较小。但由于地震子波通常是空变的, 不符合该方法的假设, 所以该方法不适用于从构造复杂区域的地震数据中提取地震子波。王德营等[73]基于单输入多输出系统(single input multiple output, SIMO)的假设, 即假设相邻2道或多道地震记录的反射系数相同, 而地震子波不同, 通过计算多道地震记录的二阶统计量(即自相关), 先将反子波计算出来, 再根据反子波求取子波并进行反褶积。该方法的优点也是不需要对子波的相位和反射系数的概率分布做出假设, 对数据量要求也不高; 缺点是该方法并不能直接得到子波结果, 而是得到反子波结果, 需要进一步的计算才能得到地震子波, 且其中涉及到多个大型矩阵的求逆运算。孔德辉等[74]将时变子波提取问题转化为在线字典学习问题, 认为字典中的每个原子(一个固定的子波)代表局部时窗内时变子波的一个分量, 通过原子的线性组合可以实现对时变子波的有效逼近。该方法依赖于对时窗的选取, 对于复杂地震数据, 如何选取合适的窗函数以及窗函数如何随深度变化还需进一步探索。
2.3 对深度域地震子波提取的几点认识1) 目前的深度域地震子波提取方法都需要通过速度转换处理, 将深度域的地震数据和测井数据转换至常速度深度域以完成子波提取。因此, 需要进一步发展不用速度转换处理的深度域地震子波提取方法, 例如: 基于波动方程理论的子波提取方法, 或是基于机器学习的子波提取方法等。此外, 每一种地震子波提取方法都有各自的优缺点和适用条件, 并没有绝对的优劣之分。在具体应用中, 需要结合工区的实际情况, 以确定采用何种地震子波提取方法。
2) 大多数地震子波提取方法基于单道地震数据计算, 不利于体现地震子波随空间变化这一基本特征。LECOMTE[75]指出, 地震子波提取方法需要考虑地震数据采集过程中“照明条件”的影响。虽然基于一维褶积模型的地震子波提取方法运算效率高, 但是无法体现“照明条件”对深度域地震数据的影响, 从而导致后续的地震反演结果出现错误。因此, 一维深度域地震子波提取方法还需要扩展到二维和三维的深度域进行地震子波提取。
3) 如何恢复地震子波相位是地震子波提取中的关键。振幅谱相同的地震子波, 其波形会由于相位谱的不同而不同。YUAN等[76]通过正演模拟指出, 振幅谱相同而波形不同的地震子波, 若以合成地震记录与井旁地震记录的相关性为判断标准, 那么这些子波都是“合格”的; 但实际上只有相位正确的子波才能得到正确的波阻抗反演结果。换言之, 对子波提取结果优劣的评判还应该与测井的阻抗信息关联起来。使用Kurtosis最大化准则法也会出现相似的问题: 由于Kurtosis值越大, 对应的反射系数反演结果越稀疏, 直观上, 就是突出强振幅的反射系数而压制弱振幅的反射系数。若将Kurtosis最大化准则用于迭代方法中, 会导致最终的反褶积结果不一定是最优的[45]。此外, 也应注意到测井数据与地震数据之间的匹配不一定是最优的, 在子波提取过程中需要不断地根据当前子波提取结果调整井-震之间的匹配。ZHANG等[77]考虑到测井数据与地震数据之间的不匹配, 在子波提取过程中用动态时间规整(dynamic time warping, DTW)方法更新与当前提取子波对应的井-震时深关系, 直至基于当前提取子波的阻抗反演结果与测井阻抗达到最佳匹配。故笔者建议使用交互式地震子波提取方法, 并将阻抗反演结果与测井阻抗的相关性纳入到子波提取结果可靠性的评判标准中。
4) 若使用交互式地震子波提取方法, 那么对方法的计算效率方面就有较高要求。对地震子波用较少的参数进行建模是提高方法计算效率的有效途径之一。在基于地震数据拟合的子波提取方法中(如最小二乘法、高阶累积量拟合法、高阶累积量谱估算法等), 子波的每一个采样点都是要求解的未知量, 如果能用含有少量参数的子波模型来替代, 那么就可以减少未知量的计算量, 从而提高计算效率[56, 78-80]。关于地震子波模型, 可以进一步参考ALDRIDGE[81]、RYAN[82]、俞寿朋[83]、张海燕等[84]、WANG[85]、SKAUVOLD等[22]的工作。
3 结束语随着计算机计算性能的不断提升以及叠前深度偏移处理方法的不断改善, 今后深度域地震数据将会越来越丰富。然而, 目前的深度域地震数据反演和解释几乎都是先将深度域地震数据转换至时间域, 在时间域完成反演和解释后, 再将结果转换回深度域。在时-深和深-时转换过程中, 不仅会丢失能够反映储层结构、岩性和流体情况等的有效信息, 还会产生转换累计误差, 这无益于降低油气勘探和开发中的钻探风险和成本, 因此, 对深度域地震数据的反演和解释今后必将是直接在真深度域进行, 发展真深度域的地震反演和属性分析等方法也势在必行。
在不考虑震源特征以及地下介质的吸收频散等因素的影响下, 深度域地震子波由于受到地下介质速度的影响, 其波形在不断发生变化, 且在不同介质分界面处的波形呈现非对称特征。因此, 褶积模型以及基于褶积模型的方法对深度域地震数据并不是直接适用的。如何准确提取深度域地震子波, 对真深度域的地震反演和解释等工作具有重要意义。笔者总结了目前深度域地震子波提取中存在的问题, 整理和概括了现有的深度域地震子波提取方法。虽然目前的深度域地震子波提取方法还比较少, 但是有很多时间域地震子波提取方法值得借鉴, 笔者对这些时间域地震子波提取方法也一并进行了整理和概括。最后, 对深度域地震子波提取方法的未来发展提出以下建议。
1) 统计性深度域地震子波提取方法有待进一步发展。如何利用已知速度信息(如具有地质意义的速度模型), 并在考虑了深度域地震子波随介质速度变化特征的基础上, 直接利用深度域地震数据的统计信息提取深度域地震子波是值得探索的。
2) 对于确定性地震子波提取方法, 合成地震记录与井旁地震记录之间相关性高低仍然是评价确定性地震子波提取结果优劣的主要标准。但是, 最高的相关性并不意味着最优的地震子波提取结果, 还需进一步考虑地震反演结果与测井资料之间的相关性。
3) 使用参数化的地震子波模型, 以减少地震子波提取中需要求解的未知量个数, 提升方法的计算效率。
4) 考虑地震数据采集过程中“照明条件”因素对深度域地震数据的影响, 将一维深度域地震子波提取方法扩展至提取二维和三维深度域地震子波。
5) 利用机器学习的优势, 建立不依赖褶积模型的直接深度域地震子波提取方法, 或是建立可以省去地震子波提取步骤, 直接完成深度域地震反演的方法。
致谢: 感谢中海油田服务股份有限公司对本文研究工作的资助与支持, 同时也感谢中海油田服务股份有限公司物探事业部特普公司的但志伟、肖为等专家对本文研究工作提出的许多有益意见和建议。| [1] |
王喜双, 梁奇, 徐凌, 等. 叠前深度偏移技术应用与进展[J]. 石油地球物理勘探, 2007, 42(6): 727-732. WANG X S, LIANG Q, XU L, et al. Application and progress of prestack depth migration technology[J]. Oil Geophysical Prospecting, 2007, 42(6): 727-732. DOI:10.3321/j.issn:1000-7210.2007.06.021 |
| [2] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. LI Z C. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [3] |
张宇. 从成像到反演: 叠前深度偏移的理论、实践与发展[J]. 石油物探, 2018, 57(1): 1-23. ZHANG Y. From imaging to inversion: Theory, practice, and technological evolution of prestack depth migration[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 1-23. |
| [4] |
林伯香, 胡中平, 薛诗桂. 利用变换深度域速度函数制作深度域合成地震记录[J]. 石油地球物理勘探, 2006, 41(6): 640-643. LIN B X, HU Z P, XUE S G. Using velocity function in transformed depth domain to make synthetic seismograph in depth domain[J]. Oil Geophysical Prospecting, 2006, 41(6): 640-643. DOI:10.3321/j.issn:1000-7210.2006.06.007 |
| [5] |
何惺华. 深度域地震资料若干问题初探[J]. 石油物探, 2004, 43(4): 353-358. HE X H. Discussion on seismic data of depth domain[J]. Geophysical Prospecting for Petroleum, 2004, 43(4): 353-358. DOI:10.3969/j.issn.1000-1441.2004.04.011 |
| [6] |
HU Z P, ZHU H L, LIN B X, et al. Wavelet analysis and convolution in depth domain[J]. Expanded Abstracts of 77th Annual Internat SEG Mtg, 2007, 2733-2737. |
| [7] |
胡中平, 林伯香, 薛诗桂. 深度域子波分析及褶积研究[J]. 石油地球物理勘探, 2009, 44(增刊1): 29-33. HU Z P, LIN B X, XUE S G. Depth domain wavelet analysis and convolution studies[J]. Oil Geophysical Prospecting, 2009, 44(S1): 29-33. |
| [8] |
FLETCHER R P, ARCHER S, NICHOLS D, et al. Inversion after depth imaging[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012, 1-5. |
| [9] |
SINGH Y. Deterministic inversion of seismic data in the depth domain[J]. The Leading Edge, 2012, 31(5): 538-545. DOI:10.1190/tle31050538.1 |
| [10] |
LETKI L, DARKE K, BORGES Y A. A comparison between time-domain and depth-domain inversion to acoustic impedance[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 3376-3380. |
| [11] |
SENGUPTA M, ZHANG H Z, JERVIS M. Direct depth domain elastic inversion[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 506-510. |
| [12] |
JIANG W, CHEN X H, ZHANG J, et al. Impedance inversion of pre-stack seismic data in the depth domain[J]. Applied Geophysics, 2019, 16(4): 427-437. DOI:10.1007/s11770-019-0791-0 |
| [13] |
SIMM R, WHITE R. Tutorial: Phase, polarity and the interpreter's wavelet[J]. First Break, 2002, 20(5): 277-281. |
| [14] |
BANSAL R, MATHENEY M. Wavelet distortion correction due to domain conversion[J]. Geophysics, 2010, 75(6): V77-V87. DOI:10.1190/1.3494081 |
| [15] |
LINES L R, TREITEL S. Wavelets, well logs and Wiener filters[J]. First Break, 1985, 3(9): 9-14. |
| [16] |
BROWN R L, MCELHATTAN W, SANTIAGO D J. Wavelet estimation: An interpretive approach[J]. The Leading Edge, 1988, 7(12): 16-19. DOI:10.1190/1.1439470 |
| [17] |
马劲风. 声波测井与地震数据匹配的新方法[J]. 西北大学学报(自然科学版), 1998, 28(3): 31-39. MA J F. New method of acoustic log and seismic data match[J]. Journal of Northwest University (Natural Science Edition), 1998, 28(3): 229-232. |
| [18] |
张杰, 陈学华, 蒋伟, 等. 基于子空间约束Huber范数的深度域地震子波提取[J]. 石油地球物理勘探, 2020, 55(6): 1231-1236. ZHANG J, CHEN X H, JIANG W, et al. Depth-domain wavelet estimation using the subspace-constrained Huber norm[J]. Oil Geophysical Prospecting, 2020, 55(6): 1231-1236. |
| [19] |
DANIELSEN V, KARLSSONT T V. Extraction of signatures from seismic and well data[J]. First Break, 1984, 2(4): 15-21. |
| [20] |
WALDEN A T, WHITE R E. On errors of fit and accuracy in matching synthetic seismograms and seismic traces[J]. Geophysical Prospecting, 1984, 32(5): 871-891. DOI:10.1111/j.1365-2478.1984.tb00744.x |
| [21] |
WALDEN A T, WHITE R E. Seismic wavelet estimation: a frequency domain solution to a geophysical noisy input-output problem[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(1): 287-297. DOI:10.1109/36.655337 |
| [22] |
SKAUVOLD J, EIDSVIK J, THEUNE U. A parametric model for seismic wavelets—with estimation and uncertainty quantification[J]. Geophysical Journal International, 2016, 205(2): 796-809. DOI:10.1093/gji/ggw029 |
| [23] |
CUI T C, MARGRAVE G F. Seismic wavelet estimation[EB/OL]. [2021-03-06]. https://www.crewes.org/ForOurSponsors/ResearchReports/reports.php?year=2014
|
| [24] |
BIANCO E. Tutorial: Wavelet estimation for well ties[J]. The Leading Edge, 2016, 35(6): 541-543. DOI:10.1190/tle35060541.1 |
| [25] |
BERKHOUT A J. Least-squares inverse filtering and wavelet deconvolution[J]. Geophysics, 1977, 42(7): 1369-1383. DOI:10.1190/1.1440798 |
| [26] |
NEIDELL N S. Could the processed seismic wavelet be simpler than we think?[J]. Geophysics, 1991, 56(5): 681-690. DOI:10.1190/1.1443085 |
| [27] |
梁光河. 地震子波提取方法研究[J]. 石油物探, 1998, 37(1): 31-39. LIANG G H. On the methods of seismic wavelet extraction[J]. Geophysical Prospecting for Petroleum, 1998, 37(1): 31-39. |
| [28] |
BUNCH A W H, WHITE R E. Least-squares filters without transient errors: An examination of the errors in least-squares filter design[J]. Geophysical Prospecting, 1985, 33(5): 657-673. DOI:10.1111/j.1365-2478.1985.tb00771.x |
| [29] |
BULAND A, OMRE H. Bayesian wavelet estimation from seismic and well data[J]. Geophysics, 2003, 68(6): 2000-2009. DOI:10.1190/1.1635053 |
| [30] |
GUNNING J, GLINSKY M E. Wavelet extractor: A Bayesian well-tie and wavelet extraction program[J]. Computers & Geosciences, 2006, 32(5): 681-695. |
| [31] |
RIETSCH E. Euclid and the art of wavelet estimation, Part Ⅰ: Basic algorithm for noise-free data[J]. Geophysics, 1997, 62(6): 1931-1938. DOI:10.1190/1.1444293 |
| [32] |
RIETSCH E. Euclid and the art of wavelet estimation, Part Ⅱ: Robust algorithm and field-data examples[J]. Geophysics, 1997, 62(6): 1939-1946. DOI:10.1190/1.1444294 |
| [33] |
DE MACEDO I A S, DE FIGUEIREDO J J S, DE SOUSA M C, et al. Estimation of the seismic wavelet through homomorphic deconvolution and well log data: Application on well-to-seismic tie procedure[J]. Geophysical Prospecting, 2020, 68(4): 1328-1340. DOI:10.1111/1365-2478.12908 |
| [34] |
KAZEMI N. Automatic blind deconvolution with Toeplitz-structured sparse total least squares[J]. Geophysics, 2018, 83(6): V345-V357. DOI:10.1190/geo2018-0136.1 |
| [35] |
HAGHSHENAS LARI H, GHOLAMI A. Nonstationary blind deconvolution of seismic records[J]. Geophysics, 2019, 84(1): V1-V9. DOI:10.1190/geo2018-0225.1 |
| [36] |
JI J. Robust inversion using biweight norm and its application to seismic inversion[J]. Exploration Geophysics, 2012, 43(2): 70-76. DOI:10.1071/EG12014 |
| [37] |
LIU Z P, CASTAGNA J P. Seismic wavelet estimation constrained by well data using artificial neural networks[J]. Expanded Abstracts of 70th Annual Internat SEG Mtg, 2000, 2460-2463. |
| [38] |
LAZEAR G D. Mixed-phase wavelet estimation using fourth-order cumulants[J]. Geophysics, 1993, 58(7): 1042-1051. DOI:10.1190/1.1443480 |
| [39] |
ZHANG R, DENG Z W. A depth variant seismic wavelet extraction method for inversion of poststack depth-domain seismic data[J]. Geophysics, 2018, 83(6): R569-R579. DOI:10.1190/geo2017-0816.1 |
| [40] |
ZHANG R, DENG Z W. Depth domain pre-stack seismic inversion with depth and angle variant wavelets[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 1843-1847. |
| [41] |
ULRYCH T J. Application of homomorphic deconvolution to seismology[J]. Geophysics, 1971, 36(4): 650-660. DOI:10.1190/1.1440202 |
| [42] |
ULRYCH T J, VELIS D R, SACCHI M D. Wavelet estimation revisited[J]. The Leading Edge, 1995, 14(11): 1139-1143. DOI:10.1190/1.1437089 |
| [43] |
OTIS R M, SMITH R B. Homomorphic deconvolution by log spectral averaging[J]. Geophysics, 1977, 42(6): 1146-1157. DOI:10.1190/1.1440780 |
| [44] |
TRIA M, VAN DER BAAN M, LARUE A, et al. Wavelet estimation and blind deconvolution of realistic synthetic seismic data by log spectral averaging[J]. Expanded Abstracts of 77th Annual Internat SEG Mtg, 2007, 1982-1986. |
| [45] |
郭向宇, 周兴元, 董敏煌. 混合相位子波的相位估算及校正[J]. 石油地球物理勘探, 1998, 33(2): 214-221. GUO X Y, ZHOU X Y, DONG M H. Estimation and correction of mixed-phase wavelet phase[J]. Oil Geophysical Prospecting, 1998, 33(2): 214-221. |
| [46] |
DE MACEDO I A S, DE FIGUEIREDO J J S. On the seismic wavelet estimative and reflectivity recovering based on linear inversion: Well-to-seismic tie on a real data set from Viking Graben, North Sea[J]. Geophysics, 2020, 85(5): D157-D165. DOI:10.1190/geo2019-0183.1 |
| [47] |
EDGAR J, VAN DER BAAN M. How reliable is statistical wavelet estimation?[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 3233-3237. |
| [48] |
曹静杰. 基于广义高斯分布和非凸Lp范数正则化的地震稀疏盲反褶积[J]. 石油地球物理勘探, 2016, 51(3): 428-433. CAO J J. Seismic sparse blind deconvolution based on generalized Gaussian distribution and non-convex Lp norm regularization[J]. Oil Geophysical Prospecting, 2016, 51(3): 428-433. |
| [49] |
CANADAS G. A mathematical framework for blind deconvolution inverse problems[J]. Expanded Abstracts of 72nd Annual Internat SEG Mtg, 2002, 2202-2205. |
| [50] |
MENDEL J M. Tutorial on higher-order statistics (spectra) in signal processing and system theory: Theoretical results and some applications[J]. Proceedings of the IEEE, 1991, 79(3): 278-305. DOI:10.1109/5.75086 |
| [51] |
ZHANG R, FOMEL S. Time-variant wavelet extraction with a local-attribute-based time-frequency decomposition for seismic inversion[J]. Interpretation, 2017, 5(1): SC9-SC16. DOI:10.1190/INT-2016-0060.1 |
| [52] |
ROSA A L R, ULRYCH T J. Processing via spectral modeling[J]. Geophysics, 1991, 56(8): 1244-1251. DOI:10.1190/1.1443144 |
| [53] |
WALDEN A T, HOSKEN J W J. The nature of the non-gaussianity of primary reflection coefficients and its significance for deconvolution[J]. Geophysical Prospecting, 1986, 34(7): 1038-1066. DOI:10.1111/j.1365-2478.1986.tb00512.x |
| [54] |
HARGREAVES N. Wavelet estimation via fourth-order cumulants[J]. Expanded Abstracts of 64th Annual Internat SEG Mtg, 1994, 1588-1590. |
| [55] |
VELIS D R, ULRYCH T J. Simulated annealing wavelet estimation via fourth-order cumulant matching[J]. Geophysics, 1996, 61(6): 1939-1948. DOI:10.1190/1.1444109 |
| [56] |
戴永寿, 郑德玲, 魏磊, 等. 高阶统计量地震子波估计建模[J]. 石油地球物理勘探, 2006, 41(5): 514-518. DAI Y S, ZHENG D L, WEI L, et al. Estimation of high order statistic seismic wavelet[J]. Oil Geophysical Prospecting, 2006, 41(5): 514-518. DOI:10.3321/j.issn:1000-7210.2006.05.006 |
| [57] |
WHITE R E. Maximum kurtosis phase correction[J]. Geophysical Journal International, 1988, 95(2): 371-389. DOI:10.1111/j.1365-246X.1988.tb00475.x |
| [58] |
LEVY S, OLDENBURG D W. Automatic phase correction of common-midpoint stacked data[J]. Geophysics, 1987, 52(1): 51-59. DOI:10.1190/1.1442240 |
| [59] |
WIGGINS R A. Minimum entropy deconvolution[J]. Geoexploration, 1978, 16(1): 21-35. |
| [60] |
陆文凯, 牟永光. 神经网络子波反褶积[J]. 石油地球物理勘探, 1996, 31(增刊2): 107-111. LU W K, MOU Y G. Deconvolution based on Neural Network[J]. Oil Geophysical Prospecting, 1996, 31(S2): 107-111. |
| [61] |
李鲲鹏, 李衍达, 张学工, 等. 基于谱模拟技术混合相位地震子波估计方法[J]. 石油物探, 2001, 40(2): 21-28. LI K P, LI Y D, ZHANG X G, et al. The mixed-phase wavelet estimate method based on spectral modeling[J]. Geophysical Prospecting for Petroleum, 2001, 40(2): 21-28. DOI:10.3969/j.issn.1000-1441.2001.02.003 |
| [62] |
VAN DER BAAN M. Time-varying wavelet estimation and deconvolution by kurtosis maximization[J]. Geophysics, 2008, 73(2): V11-V18. DOI:10.1190/1.2831936 |
| [63] |
VAN DER BAAN M, PHAM D T. Robust wavelet estimation and blind deconvolution of noisy surface seismics[J]. Geophysics, 2008, 73(5): V37-V46. DOI:10.1190/1.2965028 |
| [64] |
VAN DER BAAN M, FOMEL S. Nonstationary phase estimation using regularized local kurtosis maximization[J]. Geophysics, 2009, 74(6): A75-A80. DOI:10.1190/1.3213533 |
| [65] |
SACCHI M D, ULRYCH T J. Nonminimum-phase wavelet estimation using higher order statistics[J]. The Leading Edge, 2000, 19(1): 80-83. DOI:10.1190/1.1438466 |
| [66] |
MATSUOKA T, ULRYCH T J. Phase estimation using the bispectrum[J]. Proceedings of the IEEE, 1984, 72(10): 1403-1411. DOI:10.1109/PROC.1984.13027 |
| [67] |
谢桂生, 石玉梅, 尹成. 高阶累积量法子波估计与处理[J]. 石油物探, 2000, 39(2): 19-25. XIE G S, SHI Y M, YIN C. Wavelet estimation and processing using high-order accumulation method[J]. Geophysical Prospecting for Petroleum, 2000, 39(2): 19-25. |
| [68] |
杨培杰, 印兴耀, 张广智, 等. 三谱混合相位子波估计与最大后验反褶积[J]. 石油地球物理勘探, 2007, 42(4): 396-401. YANG P J, YIN X Y, ZHANG G Z, et al. Trispectrum mixed-phase wavelet estimation and maximum posteriori deconvolution[J]. Oil Geophysical Prospecting, 2007, 42(4): 396-401. DOI:10.3321/j.issn:1000-7210.2007.04.007 |
| [69] |
YU Y C, WANG S X, YUAN S Y, et al. Phase estimation in bispectral domain based on conformal mapping and applications in seismic wavelet estimation[J]. Applied Geophysics, 2011, 8(1): 36-47. DOI:10.1007/s11770-011-0269-1 |
| [70] |
戴永寿, 张漫漫, 张亚南, 等. 基于时频谱模拟的时变混合相位子波提取[J]. 石油地球物理勘探, 2015, 50(5): 830-838. DAI Y S, ZHANG M M, ZHANG Y N, et al. Time-variant mixed-phase seismic wavelet estimation based on spectral modeling in the time-frequency domain[J]. Oil Geophysical Prospecting, 2015, 50(5): 830-838. |
| [71] |
DAI Y S, WANG R R, LI C, et al. A time-varying wavelet extraction using local similarity[J]. Geophysics, 2016, 81(1): V55-V68. DOI:10.1190/geo2015-0317.1 |
| [72] |
崔庆辉, 芮拥军, 尚新民, 等. 混合相位地震子波提取及应用[J]. 石油物探, 2011, 50(5): 481-486. CUI Q H, RUI Y J, SHANG X M, et al. Mixed-phase seismic wavelet extraction and its application[J]. Geophysical Prospecting for Petroleum, 2011, 50(5): 481-486. DOI:10.3969/j.issn.1000-1441.2011.05.009 |
| [73] |
王德营, 李振春, 张丰麒, 等. 基于矢量预测的SIMO系统混合相位地震子波提取方法研究[J]. 地震学报, 2013, 35(4): 561-572. WANG D Y, LI Z C, ZHANG F Q, et al. Mixed-phase seismic wavelet extraction of SIMO system based on vector prediction[J]. ACTA Seismologica Sinica, 2013, 35(4): 561-572. DOI:10.3969/j.issn.0253-3782.2013.04.011 |
| [74] |
孔德辉, 彭真明. 利用改进的在线字典学习估计时变子波[J]. 石油地球物理勘探, 2016, 51(5): 901-908. KONG D H, PENG Z M. Time-varying wavelet estimation based on improved online dictionary learning[J]. Oil Geophysical Prospecting, 2016, 51(5): 901-908. |
| [75] |
LECOMTE I. Resolution and illumination analyses in PSDM: A ray-based approach[J]. The Leading Edge, 2008, 27(5): 650-663. DOI:10.1190/1.2919584 |
| [76] |
YUAN S Y, WANG S X. Influence of inaccurate wavelet phase estimation on seismic inversion[J]. Applied Geophysics, 2011, 8(1): 48-59. DOI:10.1007/s11770-011-0273-5 |
| [77] |
ZHANG B, YANG Y H, PAN Y, et al. Seismic well tie by aligning impedance log with inverted impedance from seismic data[J]. Interpretation, 2020, 8(4): 917-925. DOI:10.1190/INT-2019-0289.1 |
| [78] |
WANG S, YUAN S, MA M, et al. Wavelet phase estimation using ant colony optimization algorithm[J]. Journal of Applied Geophysics, 2015, 122: 159-166. DOI:10.1016/j.jappgeo.2015.09.013 |
| [79] |
MALKIN A, CANNING A. Global multiwell wavelet estimation[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2026-2030. |
| [80] |
姚振岸, 孙成禹, 李红星, 等. 基于基追踪的时变子波提取与地震反射率反演[J]. 石油地球物理勘探, 2019, 54(1): 137-144. YAO Z A, SUN C Y, LI H X, et al. Time-variant wavelet extraction and seismic reflectivity inversion based on basis pursuit[J]. Oil Geophysical Prospecting, 2019, 54(1): 137-144. |
| [81] |
ALDRIDGE D F. The Berlage wavelet[J]. Geophysics, 1990, 55(11): 1508-1511. DOI:10.1190/1.1442799 |
| [82] |
RYAN H. Ricker, Ormsby, Klauder, Butterworth-A choice of wavelets[J]. CSEG Recorder, 1994, 19(7): 8-9. |
| [83] |
俞寿朋. 宽带Ricker子波[J]. 石油地球物理勘探, 1996, 31(5): 605-615. YU S P. Wide-band Ricker wavelet[J]. Oil Geophysical Prospecting, 1996, 31(5): 605-615. |
| [84] |
张海燕, 李庆忠. 几种常用解析子波的特性分析[J]. 石油地球物理勘探, 2007, 42(6): 651-657. ZHANG H Y, LI Q Z. Analysis on feature of common analytic wavelets[J]. Oil Geophysical Prospecting, 2007, 42(6): 651-657. DOI:10.3321/j.issn:1000-7210.2007.06.008 |
| [85] |
WANG Y. Generalized seismic wavelets[J]. Geophysical Journal International, 2015, 203(2): 1172-1178. DOI:10.1093/gji/ggv346 |




