2. 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
2. School of Geosciences, China University of Petroleum(East China), Qingdao 266580, China
波阻抗反演是储层预测的一种重要手段[1-2]。针对波阻抗反演存在分辨率低及多解性等问题, 许多学者通过改进算法、联合利用多种地震资料等方法来提高反演结果的分辨率[3-4]。马劲风等[5]从测井约束反演方法的理论与模型试算结果出发, 对波阻抗反演的多解性问题进行了详细的分析论证。王仲杰等[6]对薄储层地震预测影响因素进行了分析, 提出了采用层序地层学进行薄储层预测的思路。对于如何提高地震波阻抗反演的分辨率, 地球物理工作者进行了大量的研究。敬荣中等[7]对联合反演的现状及实现方法进行了概述, 提出了非线性联合反演方法的发展方向; 罗钏江等[8]采用地质统计学反演方法进行储层预测; 崔炯成等[9]研究了多井约束分频非线性波阻抗反演方法; 王明超等[10]将Geoeast高分辨率反演方法应用于辽河坳陷牛居地区的储层预测; ZHANG[11]、张玉芬等[12]与LI[13]提出了测井与地震联合反演方法; 朱成宏[14]与张繁昌等[15]研究了小波变换地震多尺度反演方法, 这些方法通常都以地面地震资料为主进行波阻抗反演, 旨在提高薄储层的识别能力。还有学者在重震资料结合以及多波地震资料的联合反演等方面进行了尝试[16-18]。由于地面地震资料主频不高、频带有限, 因而反演纵向分辨率较低, 识别薄储层时多解性严重。通过贝叶斯理论, 将地面地震资料、井间地震资料和VSP地震资料融合, 可实现多尺度地震资料的联合反演, 这种反演方法能够充分利用同一地下介质地面地震、井间地震和测井曲线等在不同观测尺度下的多种地球物理响应特征, 提高对反演结果的约束能力[19]。理论上多尺度联合反演比单一尺度的地面地震资料反演更具优越性, 能够降低常规地面地震资料反演的多解性。同时, 由于井间地震资料分辨率较高, 能够为联合反演提供丰富的高频信息, 因此多尺度地震资料联合反演方法可以提高地震反演的垂向分辨率, 弥补常规地面地震资料反演中垂向分辨率不高的不足[20]。
多尺度联合反演中所用的地面地震、VSP地震、井间地震等资料都来自于地下同一地质目标、同一反射系数在不同观测尺度下的地震响应。由于采集方式、震源类型、接收仪器的不同, 使得这些地震资料通常存在较大的数值差异。地面地震资料、井间地震资料和VSP地震资料这3种不同尺度的地震资料采集和处理过程相对独立, 因此它们之间在观测噪声和分辨率方面存在明显的差异。由于这些不同尺度地震资料的数值范围不同, 地下地层的波阻抗和地震资料的度量单位、数值均不同, 将其同时置于一个目标函数表达式中, 将直接影响目标函数值的计算, 使目标函数值不能正确反映不同尺度地震资料的贡献, 导致对不同的工区无法给定合理的反演收敛条件, 此外, 反演控制参数的选择困难致使反演的运算速度慢甚至不收敛, 上述因素共同作用造成了不合理的反演结果。因此, 多尺度地震资料的匹配程度制约了联合反演效果。在自适应反演方面, 高静怀等[21]提出了提高零偏VSP地震资料Q值和速度精度的自适应波形反演方法, 张广智等[22]利用提高叠前纵横波联合收敛速度的自适应马尔科夫链构建协方差矩阵。上述方法均针对单一数据或同期采集的地震数据。本文提出的多尺度地震资料自适应联合反演方法, 通过引入多尺度地震资料标准差实现多尺度地震资料的自适应规范化, 消除了波阻抗和不同观测方式所得地震资料的度量单位、数据大小的影响, 提高了地面地震、VSP地震和井间地震资料联合反演的稳定性。利用二维模型数据和实际地震资料对本文方法进行了测试, 取得了良好的反演结果。
1 联合反演多尺度资料自适应规范方法研究 1.1 贝叶斯理论多尺度联合反演基于贝叶斯理论, 将待反演地层参数的后验概率分解为先验分布和似然函数的乘积。其中, 似然函数反映了实际地震资料与合成地震记录的相似程度。多尺度地震观测数据与反射系数之间的似然函数p(d|r)通过联合概率建立:
| $ p(\mathit{\boldsymbol{d}}\mid \mathit{\boldsymbol{r}}) = p\left( {{\mathit{\boldsymbol{d}}_{\rm{s}}}\mid \mathit{\boldsymbol{r}}} \right)p\left( {{\mathit{\boldsymbol{d}}_{\rm{v}}}\mid \mathit{\boldsymbol{r}}} \right)p\left( {{\mathit{\boldsymbol{d}}_{\rm{w}}}\mid \mathit{\boldsymbol{r}}} \right) $ | (1) |
式中: p(d|r)为反射系数r与所有参与反演的多尺度地震资料d之间的似然函数; p(ds|r)为反射系数r与地面地震资料ds之间的似然函数; p(dv|r)为反射系数r与VSP地震资料dv之间的似然函数; p(dw|r)为反射系数r与井间地震资料dw之间的似然函数。
1.2 基于贝叶斯理论联合反演目标函数建立已知先验信息p(r)和似然函数, 根据贝叶斯公式可以得到地面地震、VSP地震和井间地震资料联合反演的后验分布。对后验分布取对数, 可以得到多尺度联合反演的目标函数, 多尺度地震资料联合反演问题可以转化为求取该目标函数最小的最优化问题。为提高反演精度, 加入波阻抗约束模型约束后的多尺度联合反演目标函数J(r)表示为:
| $ \begin{array}{*{20}{l}} {J(\mathit{\boldsymbol{r}}) = \frac{\alpha }{2}{{\left( {{\mathit{\boldsymbol{d}}_{\rm{s}}} - {\mathit{\boldsymbol{G}}_{\rm{s}}}\mathit{\boldsymbol{\gamma }}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{d}}_{\rm{s}}} - {\mathit{\boldsymbol{G}}_{\rm{s}}}\mathit{\boldsymbol{\gamma }}} \right) + \frac{\beta }{2}\left( {{\mathit{\boldsymbol{d}}_{\rm{w}}} - } \right.}\\ {{{\left. {{\mathit{\boldsymbol{G}}_{\rm{w}}}\mathit{\boldsymbol{\gamma }}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{d}}_{\rm{w}}} - {\mathit{\boldsymbol{G}}_{\rm{w}}}\mathit{\boldsymbol{\gamma }}} \right) + \frac{\chi }{2}{{\left( {{\mathit{\boldsymbol{d}}_{\rm{v}}} - {\mathit{\boldsymbol{G}}_{\rm{v}}}\mathit{\boldsymbol{\gamma }}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{d}}_{\rm{v}}} - {\mathit{\boldsymbol{G}}_{\rm{v}}}\mathit{\boldsymbol{\gamma }}} \right) + }\\ {\frac{\mu }{2}\log \left( {\frac{1}{{1 + {\mathit{\boldsymbol{r}}^{\rm{T}}}\mathit{\boldsymbol{r}}}}} \right) + \frac{\rho }{2}{{\left( {{\mathit{\boldsymbol{C}}_{\rm{r}}} - {\bf{ \pmb{\mathit{ ξ}} }}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{C}}_{\rm{r}}} - {\bf{ \pmb{\mathit{ ξ}} }}} \right)} \end{array} $ | (2) |
式中: ds、dv、dw分别为地面地震、VSP地震及井间地震观测资料; Gs、Gv、Gw分别为地面地震、VSP地震、井间地震子波褶积矩阵; ξ为波阻抗约束模型; Cr为反射系数的积分矩阵; α为地面地震约束系数; β为井间地震约束系数; χ为VSP地震约束系数; μ为反射系数稀疏性约束系数; ρ为波阻抗模型约束系数。
由(2)式可以看出, 不同的权重因子可以对目标函数中地面地震、VSP地震及井间地震资料产生不同的影响。由于对应地下同一地质目标的多尺度地震资料具有相对独立性, 在实际反演过程中易受不同尺度的地震资料的数值范围影响, 因此求取反射系数时, 难以确定各个约束系数的值, 进而影响反演结果的稳定性, 导致反演过程不收敛。
1.3 联合反演目标函数多尺度地震资料自动规范化改进对于(2)式所示的目标函数, 在各种尺度的地震中分别加入不同尺度地震资料的方差项, 可实现不同尺度地震资料的规范化。基于上述原理, 将(2)式改进为:
| $ \begin{array}{*{20}{l}} {J(\mathit{\boldsymbol{r}}) = \frac{\alpha }{2}{{\left( {\frac{{{\mathit{\boldsymbol{d}}_{\rm{s}}} - {\mathit{\boldsymbol{G}}_{\rm{s}}}\mathit{\boldsymbol{r}}}}{{{\sigma _{\rm{s}}}}}} \right)}^{\rm{T}}}\left( {\frac{{{\mathit{\boldsymbol{d}}_{\rm{s}}} - {\mathit{\boldsymbol{G}}_{\rm{s}}}\mathit{\boldsymbol{r}}}}{{{\sigma _{\rm{s}}}}}} \right) + \frac{\beta }{2} \cdot }\\ {{{\left( {\frac{{{\mathit{\boldsymbol{d}}_{\rm{w}}} - {\mathit{\boldsymbol{G}}_{\rm{w}}}\mathit{\boldsymbol{r}}}}{{{\sigma _{\rm{w}}}}}} \right)}^{\rm{T}}}\left( {\frac{{{\mathit{\boldsymbol{d}}_{\rm{w}}} - {\mathit{\boldsymbol{G}}_{\rm{w}}}\mathit{\boldsymbol{r}}}}{{{\sigma _{\rm{w}}}}}} \right) + \frac{\chi }{2}{{\left( {\frac{{{\mathit{\boldsymbol{d}}_{\rm{v}}} - {\mathit{\boldsymbol{G}}_{\rm{v}}}\mathit{\boldsymbol{r}}}}{{{\sigma _{\rm{v}}}}}} \right)}^{\rm{T}}}}\\ {\left( {\frac{{{\mathit{\boldsymbol{d}}_{\rm{v}}} - {\mathit{\boldsymbol{G}}_{\rm{v}}}\mathit{\boldsymbol{r}}}}{{{\sigma _{\rm{v}}}}}} \right) + \frac{\mu }{2}\log \left[ {\frac{1}{{1 + {{\left( {\frac{\mathit{\boldsymbol{r}}}{{{\sigma _{\rm{r}}}}}} \right)}^{\rm{T}}}\left( {\frac{\mathit{\boldsymbol{r}}}{{{\sigma _{\rm{r}}}}}} \right)}}} \right] + }\\ {\frac{\rho }{2}{{\left( {\frac{{{\mathit{\boldsymbol{C}}_{\rm{r}}} - {\bf{ \pmb{\mathit{ ξ}} }}}}{{{\sigma _\xi }}}} \right)}^{\rm{T}}}\left( {\frac{{{\mathit{\boldsymbol{C}}_{\rm{r}}} - \xi }}{{{\sigma _\xi }}}} \right)} \end{array} $ | (3) |
式中: σs、σv、σw、σr、σξ分别为地面地震资料、VSP地震资料、井间地震资料、反射系数、波阻抗模型数据的标准差。不同地震资料的标准差σs、σv、σw由实际地震资料与合成地震记录之间的残差计算得到, σξ、σr分别根据初始波阻抗和对应的反射系数计算得到。
对比(3)式和(2)式可以看出, 改进后的目标函数由于将标准差引入各约束项, 因此有效避免了不同尺度地震资料的数量级不同给反演带来的影响, 使得联合反演过程稳定, 提高了目标函数的收敛速度。对多尺度地震资料进行规范化处理后, 改进的多尺度联合反演目标函数可以自动适应不同尺度地震资料数量级的影响, 反演过程稳定、可控, 且反演收敛速度快。优化后目标函数的意义在于反演过程不受不同尺度地震资料数值范围的影响, 整个联合反演过程稳定收敛, 计算速度快, 即使地面地震、井间地震、VSP地震资料之间的数值范围差别大, 也不会对反演过程造成影响。
1.4 改进后的目标函数梯度解析表达式的推导根据(3)式, 重新推导该目标函数的梯度解析表达式及联合反演迭代求解方程。在贝叶斯反演框架下, 重新推导得到的梯度解析表达式为:
| $ \begin{array}{l} \nabla {J_{\rm{r}}}(\mathit{\boldsymbol{r}}) = \alpha \left( {\mathit{\boldsymbol{G}}_{\rm{s}}^{\rm{T}}{\mathit{\boldsymbol{G}}_{\rm{s}}}\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{G}}_{\rm{s}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{\rm{s}}}} \right) + \chi \left( {\mathit{\boldsymbol{G}}_{\rm{v}}^{\rm{T}}{\mathit{\boldsymbol{G}}_{\rm{v}}}\mathit{\boldsymbol{r}} - } \right.\\ \left. {\mathit{\boldsymbol{G}}_{\rm{v}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{\rm{v}}}} \right) + \beta \left( {\mathit{\boldsymbol{G}}_{\rm{c}}^{\rm{T}}{\mathit{\boldsymbol{G}}_{\rm{c}}}\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{G}}_{\rm{c}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{\rm{c}}}} \right) + \mu Q\mathit{\boldsymbol{r}} + \rho \left( {\mathit{\boldsymbol{C}}_{\rm{r}}^{\rm{T}}{\mathit{\boldsymbol{C}}_{\rm{r}}}\mathit{\boldsymbol{r}} - } \right.\\ \left. {\mathit{\boldsymbol{C}}_{\rm{r}}^{\rm{T}}{\bf{ \pmb{\mathit{ ξ}} }}} \right) \end{array} $ | (4) |
其中, 矩阵Q是对角矩阵, 第i个对角元素为:
| $ Q\left( {r_i^{k - 1}} \right) = \frac{1}{{1 + {{\left( {\frac{{r_i^{k - 1}}}{{{\sigma _{\rm{r}}}}}} \right)}^2}}} $ | (5) |
式中: k表示迭代次数。
重新推导得到的联合反演迭代求解方程为:
| $ \begin{array}{l} \left( {\alpha \mathit{\boldsymbol{G}}_{\rm{s}}^{\rm{T}}{\mathit{\boldsymbol{G}}_{\rm{s}}} + \chi \mathit{\boldsymbol{G}}_{\rm{v}}^{\rm{T}}{\mathit{\boldsymbol{G}}_{\rm{v}}} + \beta \mathit{\boldsymbol{G}}_{\rm{c}}^{\rm{T}}{\mathit{\boldsymbol{G}}_{\rm{c}}} + \mu {\mathit{\boldsymbol{Q}}^{k - 1}} + } \right.\\ \left. {\;\;\;\;\rho \mathit{\boldsymbol{C}}_{\rm{r}}^{\rm{T}}{\mathit{\boldsymbol{C}}_{\rm{r}}}} \right){\mathit{\boldsymbol{r}}^k} = \left( {\alpha \mathit{\boldsymbol{G}}_{\rm{s}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{\rm{s}}} + \chi \mathit{\boldsymbol{G}}_{\rm{v}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{\rm{v}}} + \beta G_{\rm{c}}^{\rm{T}}{\mathit{\boldsymbol{d}}_{\rm{c}}} + } \right.\\ \left. {\;\;\;\;\rho \mathit{\boldsymbol{C}}_{\rm{r}}^{\rm{T}}{\bf{ \pmb{\mathit{ ξ}} }}} \right){\mathit{\boldsymbol{Q}}^{k - 1}} = \mathit{\boldsymbol{Q}}\left( {{\mathit{\boldsymbol{r}}^{k - 1}}} \right) \end{array} $ | (6) |
改进后的多尺度地震资料联合反演方法可根据不同尺度的地震资料自动确定反演参数, 无需人为干预, 反演过程稳健。
2 二维模型试验为验证本文方法的有效性, 建立了如图 1a所示的地震地质模型, 该模型长度为2600m, 深度为800m, 中心区长度400m, 是根据K71地区构造和储层特征建立的典型地质模型。该模型包括2~6m薄互层、断距6~12m断层、岩性尖灭、微幅构造、楔状砂体等地质构造。模型参数来自于该地区岩石物理参数分析结果, 主要参数包括纵波速度、横波速度、密度、纵波品质因子和横波品质因子。我们根据实际地震资料情况进行了井间地震、地面地震等不同尺度地震资料的正演, 地面地震资料主频30Hz, 井间地震资料主频50Hz, 得到的地面地震与井间地震正演剖面分别如图 1b与图 1c所示。与地面地震剖面相比, 井间地震剖面分辨率较高, 薄层、断层等地质现象成像更清楚。反演时首先将地面地震与井间地震资料保持为原量级, 然后将地面地震资料量级设定为原地震资料量级的100倍, 再分别利用原联合反演目标函数(2)以及优化后的联合反演目标函数(3)进行反演, 反演结果分别如图 1d与图 1e所示。

|
图 1 地震地质模型(a)、地面地震剖面(b)、井间地震剖面(c)以及采用原联合反演目标函数(d)和优化后的联合反演目标函数(e)得到的反演结果 |
从图 1e可以看出, 联合反演目标函数优化后, 多尺度地震资料自适应联合反演对不同数量级的地震资料具有良好的适应性。原目标函数反演结果能够反映模型中的大部分厚储层, 0.47s处的薄互层只能作为一套储层得到反映, 而且储层厚度与模型实际储层厚度不吻合, 0.6s处模型底部的一套薄层未能得到反映(图 1d)。联合反演目标函数优化后, 多尺度地震资料自适应联合反演结果与阻抗模型更匹配, 很好地反映了模型中的一些细节, 特别是0.47s处的一些透镜体以及薄互层得到了清楚的刻画, 0.6s处模型底部的一套薄层清晰可见, 储层分辨能力有所提高(图 1e)。
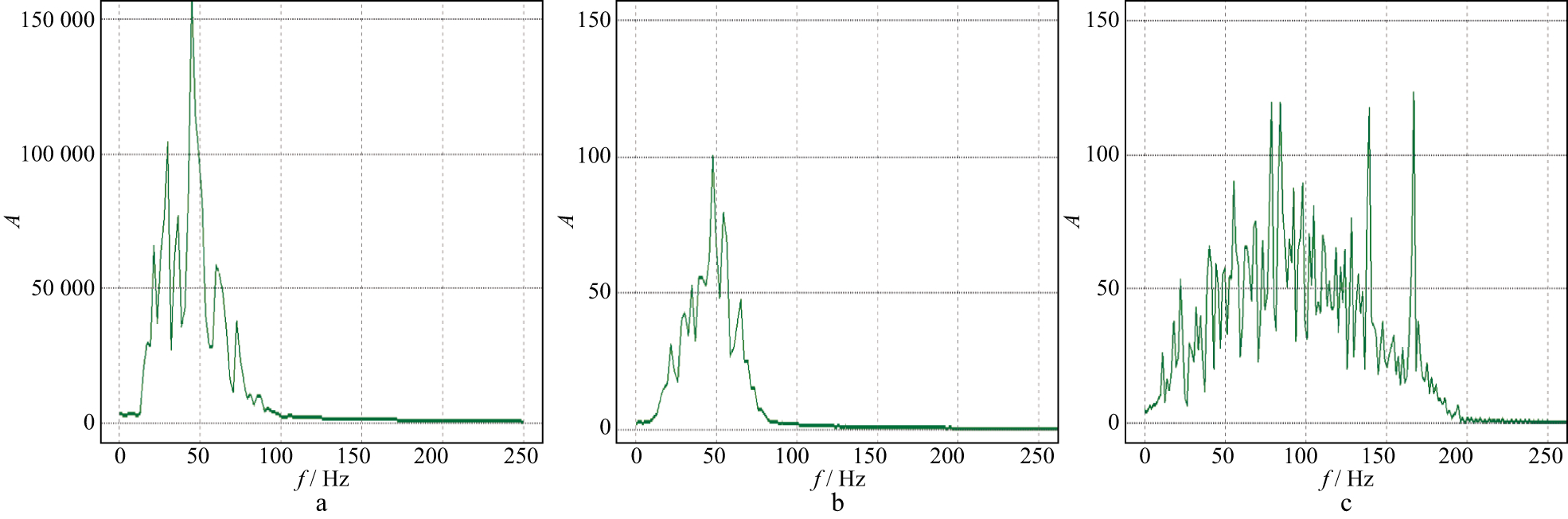
3 实际地震资料应用采用K71地区实际地震资料, 测试本文方法的有效性。该地区目的层馆陶组为河流相沉积, 储层薄, 横向变化快, 难以识别。该地区现有地面地震、VSP地震及井间地震资料。此外, 测井资料齐全, 波阻抗曲线与自然电位曲线对应关系良好, 储层自然电位负异常、低阻抗。K71地区多尺度地震资料联合反演采用的地震资料包括地面三维地震、井间地震、VSP地震以及初始波阻抗模型数据, 地面地震资料共10721道, 时间长度为0~3000ms, 时间采样间隔为2ms。工区目的层地面地震资料主频为30Hz, VSP地震资料主频与地面地震资料主频基本一致, 井间地震资料主频为60Hz。目前地面地震资料不足以识别薄储层, 与地面地震资料相比, VSP地震资料分布范围仅限于井眼附近。井间地震资料虽然分辨率高, 但只能反映两口井之间的变化。初始波阻抗约束模型资料为构造层位约束下测井波阻抗曲线内插后的波阻抗模型数据体。目的层附近3种不同类型的地震资料的振幅范围、平均值和方差如表 1所示, 3种不同类型的地震资料振幅谱如图 2所示。不难发现, 不同类型地震资料的平均值接近0, 但各自的数值范围及方差差别极大, 其中方差的差异达到百万级。
| 表 1 不同类型地震资料统计结果 |
|
图 2 K71地区地面地震(a)、VSP地震(b)与井间地震(c)资料振幅谱 |
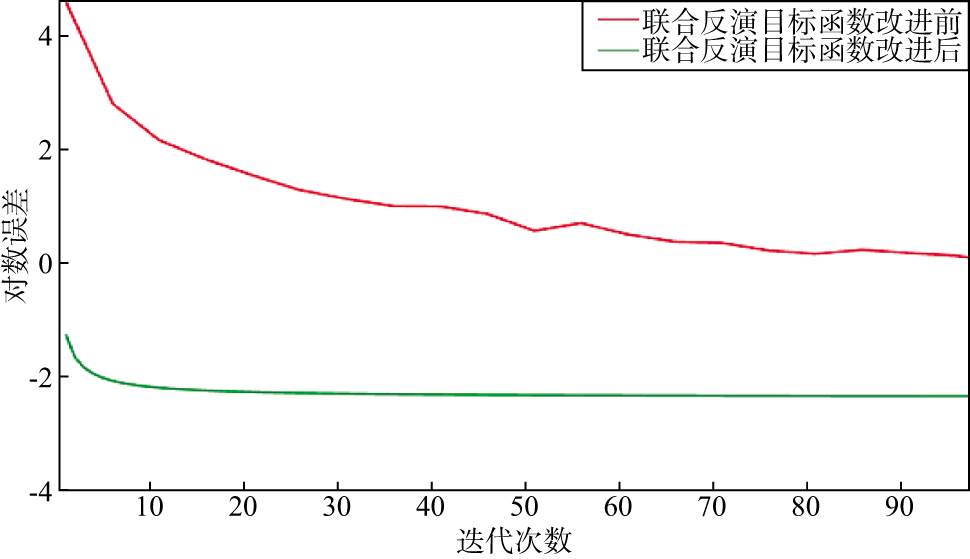
常规反演由于受地面地震资料分辨率的限制, 提高储层识别的能力有限。联合反演通过引入井间地震、VSP地震等多尺度地震资料克服地震反演的多解性, 因此提高了地震反演的分辨率。我们针对K71地区地震资料进行了联合反演计算稳定性及效率测试, 结果如图 3所示。从联合反演目标函数改进前、后的误差曲线可以看出, 目标函数改进后误差曲线收敛较快, 说明利用改进后的目标函数能够较快得到合理的反演结果。改进前用时约56h, 改进后用时仅1.5h, 计算效率提高了36倍, 说明利用改进后的目标函数得到的计算结果稳定性和计算效率均有所提高。
|
图 3 联合反演目标函数改进前、后的误差曲线 |
经参数测试, 设置地震约束系数α为1.0、井间地震约束系数β为0.4、VSP地震约束系数χ为0.03、反射系数稀疏性约束系数μ为0.3, 波阻抗模型约束系数ρ为0.1时, 可以得到较理想的联合反演结果。从图 2可以看出, K71地区VSP地震与地面地震资料频率相当并且在本次反演中作用较小。图 4a和图 4b分别为地面地震剖面和井间地震剖面; 图 4c和图 4d分别为常规测井约束反演结果与采用本文方法得到的反演结果。图 4c和图 4d中井位置插入的是自然电位曲线, 可以看出, 采用本文方法得到的反演结果与常规反演结果整体特征一致, 但后者受地面地震频带的限制, 不能分辨薄砂层特征。本文方法利用多尺度地震资料, 可以清晰地反映常规反演方法无法得到的细分储层组合特征。此外, 本文方法得到的反演结果与自然电位曲线对应较好, 说明其具有更好的反映小尺度地质体的能力。图 4d椭圆位置处的馆陶组4砂组9小层以及馆陶组6砂组2、3小层处2~3m薄层经过多尺度联合反演得以识别。由图 4d中地层与自然电位曲线的良好对应关系可知, 采用本文方法得到的薄层信息可靠。

|
图 4 K71地区过A井和B井地震剖面以及常规测井反演结果与采用本文方法得到的反演结果 a地面地震剖面; b井间地震剖面; c常规测井约束反演结果; d本文方法反演结果 |
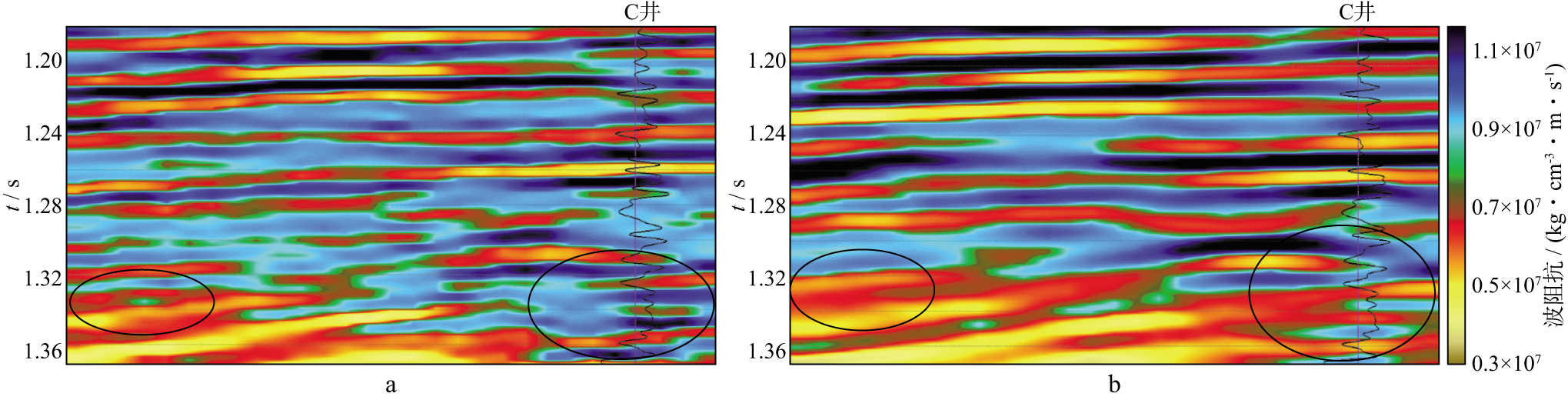
图 5a为过C井多尺度地震资料采用本文方法得到的反演结果, 与常规测井约束反演结果(图 5b)相比, 可以看出, 采用本文方法得到的反演结果分辨率较高。地面地震资料由于受自身频带的限制只能够反映厚度较大的砂层组特征, 在测井资料的约束作用下, 常规测井约束反演结果虽然能够更为合理地反演目的层馆陶组砂层组特征, 但是很难进一步提高反演结果的分辨率(图 5b)。采用本文方法得到的反演结果由于引入了井间地震资料和测井资料, 这些资料具有丰富的、有效的高频成分特征, 弥补了地面地震资料高频成分缺失的不足, 能够在保持地面地震资料整体特征的基础上提高分辨率, 1.32~1.36s处对应该地区馆陶组馆4、馆5小层(图 5a)。多尺度地震资料自适应联合反演结果更有利于该地区的薄储层识别, 为储层分析提供了可靠依据。
|
图 5 过C井多尺度地震资料采用本文方法得到的反演结果(a)与常规测井约束反演结果(b) |
多尺度地震资料联合反演中, 由于所采用的地面地震、VSP地震及井间地震等资料的采集和处理过程相对独立, 因此造成这些不同尺度的地震资料数值范围差别极大。同时, 由于地层波阻抗和地震资料的度量单位和数值范围差异大, 故将不同类型、不同尺度的数据融合在同一个目标函数表达式中, 难以对不同工区的数据进行自适应反演, 更无法确定合理的收敛条件, 选择合适的反演控制参数, 最终会导致反演过程不收敛, 反演结果不合理。
本文提出的多尺度地震资料自适应联合反演方法, 自动计算地面地震、VSP地震和井间地震资料及波阻抗资料的标准差, 实现了多尺度资料的自适应调整。在此基础上, 将不同地震资料的标准差引入联合反演目标函数, 重新定义多尺度联合反演目标函数, 使目标函数不再受波阻抗和不同观测方式所得地震资料的度量单位及数量级的影响, 反演控制参数的选择也不需再考虑地震资料本身的差异, 从而使多尺度地震资料联合反演过程变得稳定、可控, 提高了联合反演的收敛性。由模型数据和实际数据的反演过程可知, 基于改进目标函数的多尺度地震资料自适应联合反演方法可快速收敛, 对地震资料的适应性好。从反演结果看, 该方法分辨率高, 可提高识别薄层的能力, 为研究区馆陶组河流相储层勘探开发提供了重要参考资料。该方法为具有类似地震资料条件的多尺度地震反演提供了很好的借鉴思路。
| [1] |
杨文采. 评地球物理反演的发展趋向[J]. 地学前缘, 2002, 9(4): 389-396. YANG W C. A perspective to development of geophysical inversions[J]. Earth Science Frontiers, 2002, 9(4): 389-396. DOI:10.3321/j.issn:1005-2321.2002.04.019 |
| [2] |
李国发, 王艳仓, 熊金良, 等. 地震波阻抗反演实验分析[J]. 石油地球物理勘探, 2010, 45(6): 868-872. LI G F, WANG Y C, XIONG J L, et al. Experimental analysis on seismic impedance inversion[J]. Oil Geophysical Prospecting, 2010, 45(6): 868-872. |
| [3] |
栾颖, 冯暄, 刘财, 等. 波阻抗反演技术的研究现状及发展[J]. 吉林大学学报(地球科学版), 2008, 38(增刊1): 99-103. LUAN Y, FENG X, LIU C, et al. The research present and future of wave impedance inversion technique[J]. Journal of Jilin Unviersity(Earth Science Edition), 2008, 38(S1): 99-103. |
| [4] |
隋淑玲, 唐军, 蒋宇冰, 等. 常用地震反演方法技术特点与适用条件[J]. 油气地质与采收率, 2012, 19(4): 38-41. SUI S L, TANG J, JIANG Y B, et al. Technical characteristics and applicable conditions analysis on seismic inversion traditional methods[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(4): 38-41. DOI:10.3969/j.issn.1009-9603.2012.04.011 |
| [5] |
马劲风, 王学军. 波阻抗约束反演中的约束方法研究[J]. 石油物探, 2000, 39(2): 52-63. MA J F, WANG X J. Study of constraint methodology in constrained impedance inversion[J]. Geophysical Prospecting for Petroleum, 2000, 39(2): 52-63. DOI:10.3969/j.issn.1000-1441.2000.02.006 |
| [6] |
王仲杰, 张元, 张治民, 等. 薄储层地震预测影响因素分析及研究方向探讨[J]. 长江大学学报(自然科学版), 2017, 14(3): 34-39. WANG Z J, ZHANG Y, ZHANG Z M, et al. Analysis of influencing factors on seismic prediction of thin reservoirs and discussion on its research direction[J]. Journal of Yangtze University(Natural Science Edition), 2017, 14(3): 34-39. DOI:10.3969/j.issn.1673-1409.2017.03.009 |
| [7] |
敬荣中, 鲍光淑, 陈绍裘. 地球物理联合反演研究综述[J]. 地球物理学进展, 2003, 18(3): 535-540. JING R Z, BAO G S, CHEN S Q. A review of the researches for geophysical combinative inversion[J]. Progress in Geophysics, 2003, 18(3): 535-540. DOI:10.3969/j.issn.1004-2903.2003.03.033 |
| [8] |
罗钏江, 罗耀华, 鲁建隆, 等. 基于地质统计学反演方法的洛带气田储层预测[J]. 物探化探计算技术, 2019, 41(2): 200-206. LUO C J, LUO Y H, LU J L, et al. The application for the geostatistical inversion in Luodai gas field[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2019, 41(2): 200-206. |
| [9] |
崔炯成, 吴媚, 李维新, 等. 高分辨率非线性地震波阻抗反演方法和应用[J]. 石油物探, 2007, 46(1): 1-12. CUI J C, WU M, LI W X, et al. Nonlinear high-resolution impedance inversion method and its application[J]. Geophysical Prospecting for Petroleum, 2007, 46(1): 1-12. |
| [10] |
王明超, 刘宝鸿, 张斌, 等. 利用高分辨率波阻抗反演技术预测薄储层—以辽河坳陷牛居地区为例[J]. 石油地球物理勘探, 2018, 53(1): 186-190. WANG M C, LIU B H, ZHANG B, et al. Thin bed prediction with high-resolution impedance inversion: A case study of Niuju Area, Liaohe Basin Oil[J]. Oil Geophysical Prospecting, 2018, 53(1): 186-190. |
| [11] |
ZHANG Y F. A method of improving seismic data resolution: comprehensive inversion of well and seismic data[J]. Journal of China University of Geosciences (in English), 1996(2): 193-196. |
| [12] |
张玉芬, 罗延钟, 凌峰. 井震联合地震道多尺度反演[J]. 地球科学, 2001, 26(5): 533-537. ZHANG Y F, LUO Y Z, LING F. Seismic trace multi-scale inversion using logging data and seismic data[J]. Earth Science, 2001, 26(5): 533-537. DOI:10.3321/j.issn:1000-2383.2001.05.016 |
| [13] |
LI Y F. Joint inversion of seismic data for acoustic impedance[J]. Geophysics, 2004, 69(4): 994-1004. DOI:10.1190/1.1778242 |
| [14] |
朱成宏. 地震资料波阻抗多尺度反演[J]. 石油物探, 1993, 32(2): 20-30. ZHU C H. Multiscale acoustic impedance inversion using poststack seismic data[J]. Geophysical Prospecting for Petroleum, 1993, 32(2): 20-30. |
| [15] |
张繁昌, 代荣获, 刘汉卿, 等. 叠前地震道集AVA多频信息同时反演[J]. 石油物探, 2014, 53(4): 453-460. ZHANG F C, DAI R H, LIU H Q, et al. Multi-frequency AVA simultaneous inversion for prestack seismic gathers[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 453-460. DOI:10.3969/j.issn.1000-1441.2014.04.011 |
| [16] |
邬世英, 王延江, 李莉, 等. 支持向量机在重震联合反演中的应用研究[J]. 地球物理学进展, 2007, 22(5): 1611-1616. WU S Y, WANG Y J, LI L, et al. The application of support vector machine in the joint inversion of gravimetric and seismic data[J]. Progress in Geophysics, 2007, 22(5): 1611-1616. DOI:10.3969/j.issn.1004-2903.2007.05.042 |
| [17] |
HELENE H V, MARTIN L. Simultaneous inversion of PP and PS seismic data[J]. Geophysics, 2006, 71(3): R1-R10. DOI:10.1190/1.2194533 |
| [18] |
ZHANG F C, DAI R H, LIU H Q. Seismic inversion based on L1-norm misfit function and total variation regularization[J]. Journal of Applied Geophysics, 2014, 109(5): 111-118. |
| [19] |
曹丹平, 印兴耀, 张繁昌, 等. 多尺度地震资料联合反演方法研究[J]. 地球物理学报, 2009, 52(4): 1059-1067. CAO D P, YIN X Y, ZHANG F C, et al. A study on the method of joint inversion of multiscale seismic data[J]. Chinese Journal of Geophysics, 2009, 52(4): 1059-1067. DOI:10.3969/j.issn.0001-5733.2009.04.023 |
| [20] |
王延光, 孟宪军, 夏吉庄, 等. 油藏地球物理技术发展与应用实践[J]. 地球物理学进展, 2015, 30(5): 2246-2256. WANG Y G, MENG X J, XIA J Z, et al. Development and practice in reservoir geophysics[J]. Progress in Geophysics, 2015, 30(5): 2246-2256. |
| [21] |
高静怀, 汪超, 赵伟. 用于零偏移距VSP资料的自适应波形反演方法研究[J]. 地球物理学报, 2009, 52(12): 3091-3100. GAO J H, WANG C, ZHAO W. On the method of adaptive waveform inversion with zero-offset VSP data[J]. Chinese Journal of Geophysics, 2009, 52(12): 3091-3100. DOI:10.3969/j.issn.0001-5733.2009.12.018 |
| [22] |
张广智, 潘新朋, 孙昌路, 等. 纵横波联合叠前自适应MCMC反演方法[J]. 石油地球物理勘探, 2016, 51(5): 938-946. ZHANG G Z, PAN X P, SUN C L, et al. PP- & PS-wave prestack nonlinear inversion based on adaptive MCMC algorithm[J]. Oil Geophysical Prospecting, 2016, 51(5): 938-946. |



