目前, 国内外常用的逆时偏移成像算法包括有限差分法和有限元法。有限差分法因实现过程简单且计算高效而被广泛应用, 但是, 当山地地表起伏较大或地质构造复杂时, 难以确保成像精度, 且有限差分逆时偏移的适应性和灵活性较差。有限元法具有良好的边界适应性及模拟精度, 可以适应山地起伏地表等复杂边界问题, 但面对大规模复杂三维问题时, 难以在波场模拟精度和运算效率方面取得平衡。国内外学者从地下介质特征、波场传播算子、吸收边界条件以及并行计算效率等方面对逆时偏移方法进行了大量研究, 逐步提高成像精度及运行效率。冀国强等[1]研究基于粘声介质的逆时偏移方法, 同时考虑因地层吸收而导致振幅衰减与相位频散, 提出一种正则化形式的稳定传播粘声逆时偏移方法, 提升深层构造的分辨率与可信度。曲英铭等[2]提出面向高陡构造的粘声棱柱波逆时偏移方法, 改善了高陡构造的照明和成像效果。巩向博等[3]研究基于稀疏约束的最小二乘逆时偏移方法, 提高小尺度散射体的成像分辨率。李青阳等[4]提出一种新的卷积完全匹配层(NCPML)吸收边界条件, 用于逆时偏移后, 计算效率和内存占用上较常规的完全匹配层(SPML)吸收边界条件更优。段心标[5]提出基于GPU的傅里叶有限差分逆时偏移方法, 保护了低频信息的成像且提高了成像效率。
PATERA[6]在研究Navier-Stokes方程的数值解法时提出谱元法(spectral element method, SEM), 该方法不仅具备有限元法处理复杂构造边界的适应性, 还有伪谱法高阶插值和快速收敛的优势。谱元法的基本思路是: 首先, 将求解域剖分成相互连接互不重叠的有限个单元; 然后, 在每个单元上应用伪谱法, 将单元的近似解表示成不同格式的截断正交多项式展开式; 最后, 采用伽辽金法求解得到整体问题的近似解, 实现求解域内波场传播的模拟[7-8]。谱元法的核心是采用的插值基函数形式, 目前常见的用于谱元法单元插值的基函数有切比雪夫(Chebyshev)正交多项式和勒让德(Legendre)正交多项式。PRIOLO等[9]在研究声波波场传播特性时, 采用切比雪夫正交多项式进行单元插值, 形成了切比雪夫谱元法, 之后该方法逐步被应用于不同情况下的波场模拟中。MADAY等[10]在谱元法单元分析时采用勒让德正交多项式作为单元插值基函数, 同时结合GLL(gauss lobatto legendre)积分, 将积分节点设定为插值节点, 形成了勒让德谱元法。李孝波等[11]采用勒让德谱元法进行局部工程地震的波场模拟研究, 认为谱元法能够较好地反映地形条件和近地表特征及断裂构造样式, 具有较高的精度。林伟军等[12]对复杂非均匀介质下谱元法波场模拟效率进行研究, 通过在单元内引入独立的辅助网格, 在较稀疏的主网格上进行波场求解, 获得较高的精度。
与传统方法相比, 谱元法虽然在理论上有待进一步完善, 但由于结合了有限元法处理复杂构造的几何适应性和伪谱法高精度快速收敛的特性, 目前已成为复杂地表、复杂构造地震模拟与成像的重要工具[13]。随着油气地震勘探的不断深入, 逐步向复杂山地、复杂构造及复杂储层探区发展, 这些探区地表起伏大, 横向速度变化剧烈, 多处地表高速体出露, 地下高速火成岩及低速膏泥岩不规则穿插, 常规的有限差分逆时偏移成像方法不能完全适应起伏地表复杂断裂精确成像, 无法满足勘探开发及井位部署需求, 急需研究适应起伏地表的复杂构造高精度成像方法。本文以起伏地表复杂构造高精度地震成像为目标, 以起伏地表谱元逆时偏移成像方法为研究内容, 推导了波动方程切比雪夫谱元逆时偏移成像算法, 同时为了提高该方法的并行计算效率, 基于自由度凝聚和局部松弛的思想, 推导了切比雪夫谱元逆时偏移方法的多级并行算法(HEP-CSE-RTM), 运行效率大幅度提高, 达到与常规有限差分法逆时偏移相当的计算效率。用加拿大起伏地表逆掩断层二维模型数据进行测试, 验证了本文方法对起伏地表探区复杂构造成像的适应性; 同时利用SEAM三维起伏地表复杂构造模型数据进行了测试, 成像结果表明, 该方法在起伏地表复杂构造区成像精度明显高于常规的有限差分法逆时偏移, 验证了该方法的有效性和科学性。
1 方法原理 1.1 切比雪夫谱元逆时偏移方法(CSE-RTM)采用切比雪夫谱元方法并结合隐式Newmark时间积分方法求解波动方程, 得到波场传播算子, 进行逆时偏移成像, 该解法在空间上具有谱精度, 在时间上达到二阶精度。均匀介质空间Ω中, 时间T内二维波动方程如下:
| $ \frac{\partial^{2} u}{\partial t^{2}}-c_{0}^{2} \nabla^{2} u=f \quad \varOmega \times[0, T] $ | (1) |
式中: Ω为分析空间R2中有界区域, Ω≡Γ为分析域Ω的边界; u(x, z)为声波位移场; c0(x, z)为声波速度场; x, z和t分别为空间和时间坐标; f为震源项。
时间T内, Ω空间边界Γ上Clayton-Engquist吸收边界条件(CE-ABC)[14]:
| $ B_{1} u=\frac{1}{c_{0}} \frac{\partial^{2} u}{\partial x \partial t}+\frac{1}{c_{0}} \frac{\partial^{2} u}{\partial t^{2}}-\frac{c_{0}}{2} \frac{\partial^{2} u}{\partial y^{2}}=0 \quad \varGamma[0, T] $ | (2) |
初始条件:
| $ u(x, y, 0)=u_{0} \quad \dot{u}(x, y, 0)=\dot{u}_{0} \quad \varOmega \times[0, T] $ | (3) |
上述方程中, u0和
| $ \frac{\partial^{2}}{\partial t^{2}} \int_{\varOmega} u v \mathrm{~d} \varOmega+c_{0}^{2} a(u, v)+c_{0} \frac{\partial}{\partial t} \int_{\varGamma} u v \mathrm{~d} s=\int_{\varOmega} v f \mathrm{~d} \varOmega $ | (4) |
式中: s为求解域Ω边界Γ的切线方向; v为H1(Ω)空间中的任意函数。
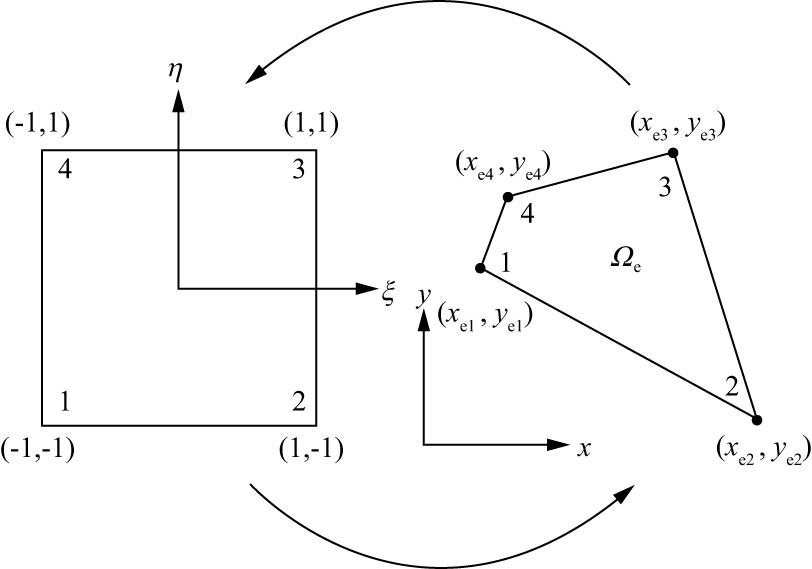
使用谱元方法求解公式(4)。首先, 将求解域分解成Nd=NmNn个互不重叠的子区域Ω=∪i=1NdΩei, Ωe称为单元, 这里, Nm为x方向的单元数; Nn为y方向的单元数; Nd为求解域总单元数。然后, 应用公式(5)将各真实单元转化成标准单元(图 1), 这些任意四边形真实单元具有比三角形单元精度高、比矩形单元适应性强的双重优点, 但在整体坐标下形成满足任意形状单元完备性的试函数很困难, 且不利于计算机的批量运算。为了便于单元分析, 可按单元的几何形状, 在每个单元内建立一个局部坐标系列, 使单元边界上的节点和单元边界都在局部坐标(ξ, η)下具有特定的值, 通过坐标变换, 将整体坐标系(x, y)中形状较复杂的真实单元变换成局部坐标系(ξ, η)中规则的标准单元。
|
图 1 局部坐标与标准坐标的相互转换 |
| $ \left\{\begin{array}{l} \xi=\frac{2}{L_{x}^{i}}\left(x-x_{i}\right)-1 \\ \eta=\frac{2}{L_{y}^{i}}\left(y-y_{i}\right)-1 \end{array}\right. $ | (5) |
式中: Lxi, Lyi为几何形状函数, 表征了单元几何形状的变化。
在一个标准单元内, 选取切比雪夫多项式的极值点(Chebyshev-Gauss-Lobatto点)为插值点, 使用高阶切比雪夫正交多项式对试函数进行逼近, 标准单元内的试函数为:
| $ \left\{\begin{array}{l} u^{i}(\xi, \eta, t)=\sum\limits_{j=0}^{N_{x}^{i}} \sum\limits_{k=0}^{N_{y}^{i}} u_{j k}^{i}(t) h_{j}^{i}(\xi) h_{k}^{i}(\eta) \\ v^{i}(\xi, \eta, t)=\sum\limits_{p=0}^{N_{x}^{i}} \sum\limits_{q=0}^{N_{y}^{i}} v_{p q}^{i}(t) h_{p}^{i}(\xi) h_{q}^{i}(\eta) \end{array}\right. $ | (6) |
插值函数表示为:
| $ \left\{\begin{array}{l} h_{j}^{i}(\xi)=\frac{2}{N_{x}^{i}} \sum\limits_{j=0}^{N_{x}^{i}} \frac{1}{c_{j} c_{m}} T_{m}\left(\xi_{j}^{i}\right) T_{m}(\xi) \\ h_{k}^{i}(\eta)=\frac{2}{N_{y}^{i}} \sum\limits_{k=0}^{N_{y}^{i}} \frac{1}{c_{k} c_{n}} T_{n}\left(\eta_{j}^{i}\right) T_{n}(\eta) \\ h_{p}^{i}(\xi)=\frac{2}{N_{x}^{i}} \sum\limits_{p=0}^{N_{x}^{i}} \frac{1}{c_{p} c_{l}} T_{l}\left(\xi_{p}^{i}\right) T_{l}(\xi) \\ h_{q}^{i}(\eta)=\frac{2}{N_{y}^{i}} \sum\limits_{q=0}^{N_{y}^{i}} \frac{1}{c_{q} c_{r}} T_{r}\left(\eta_{q}^{i}\right) T_{r}(\eta) \end{array}\right. $ | (7) |
式中: Tm, Tn, Tl与Tr为切比雪夫多项式, 其极值点为插值函数的插值点; Nx为x方向的网格数; Ny为y方向的网格数。插值函数hji(ξ), hki(η), hpi(ξ)及hqi(η)在标准单元外为零。在标准单元边界节点上cm=2, 在标准单元内部节点上cm=1。
然后, 在标准单元上对具有吸收边界的波动方程进行离散化, 为了方便介绍, ∂2ue/∂t2及∂ue/∂t分别用ü及
| $ \boldsymbol{M}_{\mathrm{e}} \ddot{u}^{i}(t)+\boldsymbol{C}_{\mathrm{e}} \dot{u}^{i}(t)+\boldsymbol{K}_{\mathrm{e}} u^{i}(t)=\boldsymbol{S}_{\mathrm{e}} $ | (8) |
式中: Me, Ce和Ke分别为单元质量矩阵、单元阻尼矩阵和单元刚度矩阵。通过单元刚度矩阵的合成, 整体平衡方程为:
| $ \boldsymbol{M} \ddot{u}(t)+\boldsymbol{C} \dot{u}(t)+\boldsymbol{K} u(t)=\boldsymbol{S} $ | (9) |
考虑到算法的稳定性, 在时间域处理时, 采用隐式Newmark时间积分方案, 在一个时间步长t~t+Δt内采用下列假设:
| $ \left\{\begin{array}{l} \dot{u}_{t+\Delta t}=\dot{u}_{t}+\left[(1-\delta) \ddot{u}_{t}+\delta \ddot{u}_{t+\Delta t}\right] \Delta t \\ u_{t+\Delta t}=u_{t}+\dot{u}_{t} \Delta t+\left[(1 / 2-\alpha) \ddot{u}_{t}+\alpha \ddot{u}_{t+\Delta t}\right] \Delta t^{2} \end{array}\right. $ | (10) |
式中: α和δ是由数值精度和稳定性要求决定的参数, δ称为Newmark因子, α和δ取不同数值, 代表不同差分方案; 当α≥0.25(0.5+δ)2且δ≥0.5时是绝对稳定的[15-16]。因此, 常微分方程组(9)可以离散为如下形式:
| $ \begin{array}{l} \left(K+\frac{1}{\alpha \Delta t^{2}} M\right) u_{t+\Delta t}= \\ S_{t+\Delta t}+M\left[\frac{1}{\alpha \Delta t^{2}} u_{t}+\frac{1}{\alpha \Delta t} \dot{u}_{t}+\left(\frac{1}{2 \alpha}-1\right) \ddot{u}_{t}\right]+ \\ C\left[\frac{\delta}{\alpha \Delta t} u_{t}+\left(\frac{\delta}{\alpha}-1\right) \dot{u}_{t}+\left(\frac{\delta}{2 \alpha}-1\right) \Delta t \ddot{u}_{t}\right] \end{array} $ | (11) |
其中初始值可以通过如下方程求得:
| $ \ddot{u}_{0}=M^{-1}\left(S_{0}-K u_{0}-C \dot{u}_{0}\right) $ | (12) |
关于Newmark积分方法有两点值得注意: 一是该积分方法有多种表示形式, 限于篇幅, 本文不做赘述; 二是尽管该积分方法是绝对稳定的, 但是时间步长也要足够小, 因为时间步长是波场模拟及成像精度的决定性因素之一。
1.2 谱元逆时偏移多级并行算法(HEP-CSE-RTM)在谱元法波场模拟及成像中, 通过结构网格空间离散及经典Newmark方法时间离散将偏微分方程化成如下代数方程组:
| $ \sum\limits_{j=1}^{n_{d}} \boldsymbol{k}_{i j} \cdot \boldsymbol{d}_{j}=\boldsymbol{s}_{i} \quad i=1,2, \cdots, n_{d} $ | (13) |
对一个超大规模的谱元法波场模拟及成像问题, 假设其中有nd个节点, 每个节点的自由度数(NDOF)是s, 这样整体的自由度数是s·nd, 公式(13)中的kij是整体刚度矩阵, si和dj分别是载荷向量和待求的位移向量。在谱元法波场模拟及成像问题中矩阵kij通常是对称正定的, 这样线性方程组的求解等价于寻找对应泛函极小时的dj, 泛函形式如下:
| $ \varPi=\frac{1}{2} \sum\limits_{i, j=1}^{n_{d}} \boldsymbol{d}_{i} \cdot \boldsymbol{k}_{i j} \cdot \boldsymbol{d}_{j}-\sum\limits_{i=1}^{n_{d}} \boldsymbol{d}_{i} \cdot \boldsymbol{s}_{i} $ | (14) |
根据最小势能原理, 若能设计一种迭代格式使得泛函Π的值不断降低, 那么必然能够得到方程组(13)的解。由此思路出发设计谱元法逆时偏移多级并行迭代算法。
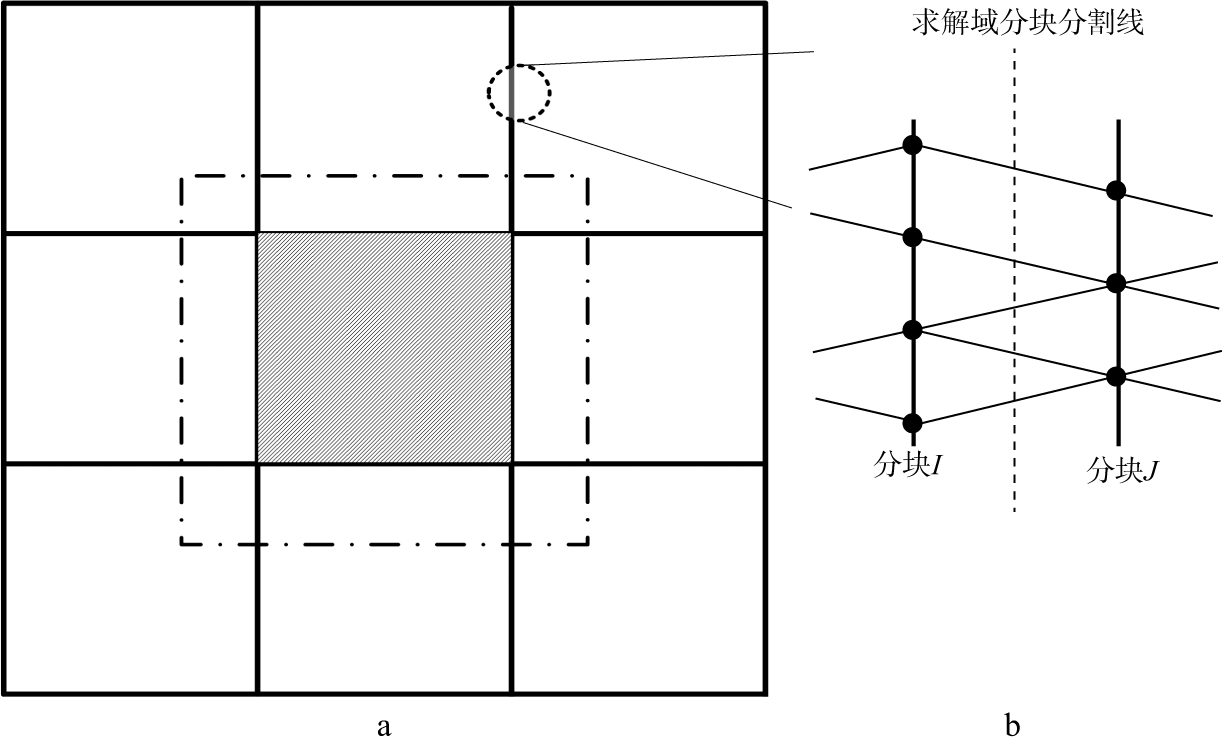
为了进行大规模并行计算, 首先需将求解域划分成块(Set), 把nd个节点按照初始位置分成B个分块(对应B个处理器), 各分块内的自由度约为s·nd/B。拟采取的分割方法与域分解思路不同处是, 将分割面放在单元内, 而不是节点上(图 2)。分割面穿过的单元定义为界面单元, 相邻分块共享界面单元, 以此保证位移连续条件, 该方法与域分解方法的重要不同点是不需要再引入罚函数或拉格朗日乘子, 但方程组迭代求解过程中, 分块需要与相邻分块通信获取界面单元上外部节点的解。
|
图 2 谱元法波场模拟求解域分块方案示意 a求解域分块示意; b求解域分块方案 |
对谱元法多级并行波场模拟及成像算法而言, 分块和网格数量共同决定了计算效率和计算时间, 若分块I内网格(单元)数量明显多于其它分块, 则计算时间将完全由分块I决定, 因此, 在算法中要求使用匹配的分块和网格关系, 将尽量使各分块负载均衡。假设所要研究的深度域模型在x和z轴方向上的长度分别是Lx和Lz, 计算模型面积为S=Lx×Lz, 为便于理解, 先假设整个计算域中x和z方向步长为hx和hz, Lx可以被hx整除, Lz可以被hz整除。x和z方向的网格数分别为nxgrid和nzgrid, 即, 要满足:
| $ \left\{\begin{array}{l} \bmod \left(L_{x}, h_{x}\right)=0 \\ \bmod \left(L_{z}, h_{z}\right)=0 \\ n_{x}^{\text {grid }}=\frac{L_{x}}{h_{x}} \\ n_{z}^{\text {grid }}=\frac{L_{z}}{h_{z}} \end{array}\right. $ | (15) |
在设置分块信息时, 若假设在x和z轴分别划分为nxs和nzs个分块, 为保证并行计算的负载均衡, 要求其必须满足nxgrid可以被nxs整除, nzgrid可以被nzs整除, 即:
| $ \left\{\begin{array}{l} \bmod \left(n_{x}^{\text {grid }}, n_{x}^{s}\right)=0 \\ \bmod \left(n_{z}^{\text {grid }}, n_{z}^{s}\right)=0 \end{array}\right. $ | (16) |
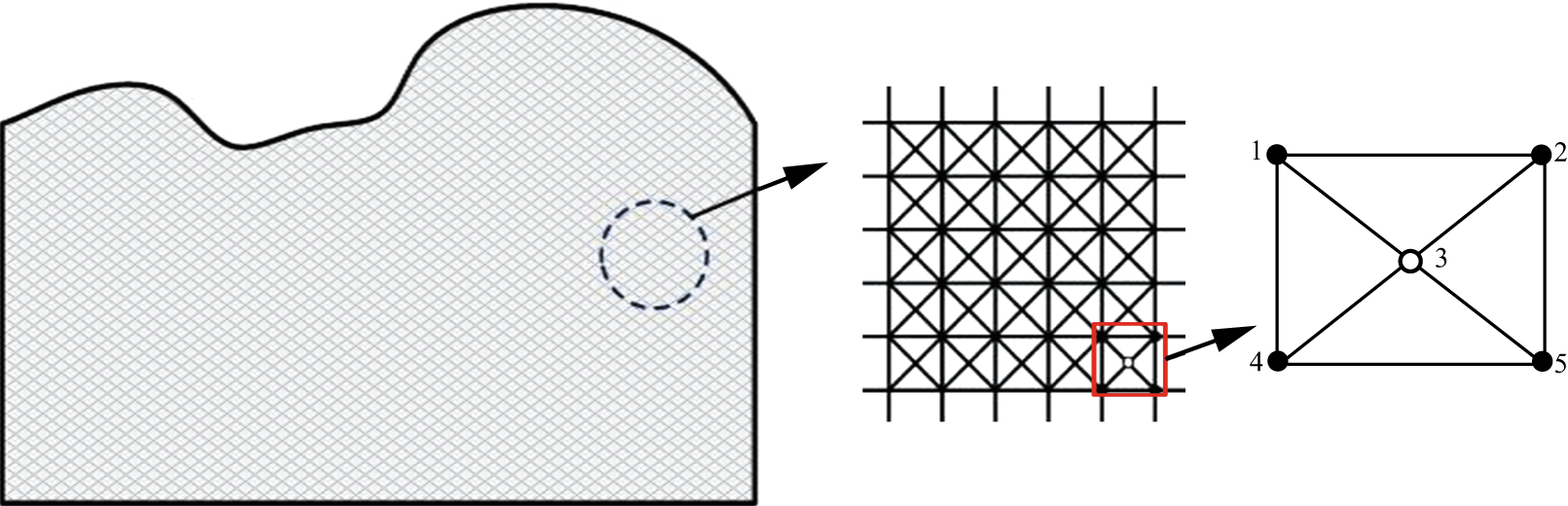
以二维起伏地表模型谱元法波场模拟及成像问题为例, 对于起伏地表而言, 三角形网格具有更好的适应性(图 3), 在形状较为规则的区域, 为保持一致, 我们同样使用三角形网格, 相当于在矩形网格图形中心位置增加一个离散点, 形成1-3-2、2-3-5、5-3-4和4-3-1(平面内按逆时针排列)4个三角形单元, 构建一个满足坐标二次函数的物理量分布, 实现较高的计算精度。
|
图 3 网格与三角形单元对应示意 |
于是, 每个分块内的网格数量为:
| $ N_{s}^{g}=4 \times \frac{n_{x}^{g}}{n_{x}^{s}} \times \frac{n_{z}^{g}}{n_{z}^{s}} $ | (17) |
参照图 3, 分块内的节点总数为:
| $ N_{s}^{n}=\frac{n_{x}^{g}}{n_{x}^{s}} \times \frac{n_{z}^{g}}{n_{z}^{s}}+\left(\frac{n_{x}^{g}}{n_{x}^{s}}-1\right) \times\left(\frac{n_{z}^{g}}{n_{z}^{s}}-1\right) $ | (18) |
根据叠前逆时偏移理论和Newmark时间积分方案, 每个节点只有标量波一个自由度, 因此任务所需计算时间与分块节点数Nsn成正比。
在求解域的每个分块内, 使用位移增量模式的线性组合来表示节点位移值, 如第I分块Set(I)内节点的位移值可写作:
| $ \boldsymbol{d}_{i}=\boldsymbol{d}_{i}^{\text {old }}+\sum\limits_{m=1}^{q} a_{m}^{I} \boldsymbol{r}_{m}^{I} \quad i \in \operatorname{Set}(I) $ | (19) |
式中: diold是上一次迭代所得近似解; q是位移增量模式的数量; rmI和amI分别是第I分块的第m个位移增量模式与系数, 将分块内s·nd/B个精细自由度凝聚成q个高阶自由度, q一般约为10个量级。将公式(19)代入公式(14), 可得到用amI表示的势能形式。根据最小势能原理(泛函极值条件)可得到:
| $ \begin{array}{*{20}{c}} {\frac{\mathit{\Pi }}{{\partial a_m^I}} = \sum\limits_{J = 1}^M {\sum\limits_{\begin{array}{*{20}{c}} {i \in {\mathop{\rm Set}\nolimits} (I)}\\ {j \in {\mathop{\rm Set}\nolimits} (J)} \end{array}} {\mathit{\boldsymbol{r}}_{mi}^I} } \cdot {\mathit{\boldsymbol{k}}_{ij}} \cdot \left( {\mathit{\boldsymbol{d}}_j^{{\rm{old }}} + \sum\limits_{l = 1}^q {a_l^J} \mathit{\boldsymbol{r}}_{lj}^J} \right) - }\\ {\sum\limits_{i \in {\mathop{\rm Set}\nolimits} (I)} {{\mathit{\boldsymbol{s}}_i}} \cdot \mathit{\boldsymbol{r}}_{mi}^I = \sum\limits_{J = 1}^B {\sum\limits_{l = 1}^q {{K_{a_m^Ia_l^J}}} } a_l^J - {P_{a_m^I}} = 0} \end{array} $ | (20) |
其中有:
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{a_m^Ia_l^J}} = \sum\limits_{\begin{array}{*{20}{c}} {i \in {\mathop{\rm Set}\nolimits} (I)}\\ {j \in {\mathop{\rm Set}\nolimits} (J)} \end{array}} {\mathit{\boldsymbol{r}}_{mi}^I} \cdot {\mathit{\boldsymbol{k}}_{ij}} \cdot \mathit{\boldsymbol{r}}_{lj}^J}\\ {{P_{a_m^I}} = \sum\limits_{i \in {\mathop{\rm Set}\nolimits} (I)} {\mathit{\boldsymbol{r}}_{mi}^I} \cdot \left( {{\mathit{\boldsymbol{s}}_i} - \sum\limits_{J = 1}^B {\sum\limits_{j \in {\mathop{\rm Set}\nolimits} (J)} {{\mathit{\boldsymbol{k}}_{ij}}} } \cdot \mathit{\boldsymbol{d}}_j^{{\rm{old }}}} \right)} \end{array}} \right. $ | (21) |
分别是与高阶自由度对应的刚度矩阵和非平衡力向量。得到凝聚自由度的整体平衡方程为:
| $ \begin{array}{*{20}{l}} {\sum\limits_{J = 1}^B {\sum\limits_{l = 1}^q {{K_{a_m^Ia_l^J}}} } a_l^J - {P_{a_m^I}} = 0}\\ {m = 1,2, \cdots ,q\quad I = 1,2, \cdots ,B} \end{array} $ | (22) |
相较于公式(13), 自由度凝聚后的平衡方程的未知数明显减少, 可以在新处理器上进行求解后得到各块位移增量的系数amI。当amI确定后, 使用公式(19)进行更新便可得到各节点在精细自由度下的位移场di, 相较于diold必然对应着较低的泛函值, 因此它是一个较好的近似解。通过一定次数的迭代更新, 相对残差:
| $ R=\sum\limits_{i=1}^{n_{d}} \frac{\left\|\sum\limits_{j=1}^{n_{d}} \boldsymbol{k}_{i j} \cdot \boldsymbol{d}_{j}-\boldsymbol{s}_{i}\right\|}{\left\|\boldsymbol{s}_{i}\right\|} $ | (23) |
低于要求的精度ε便得到方程组(13)的解。其中, ‖·‖表示对向量取模运算。
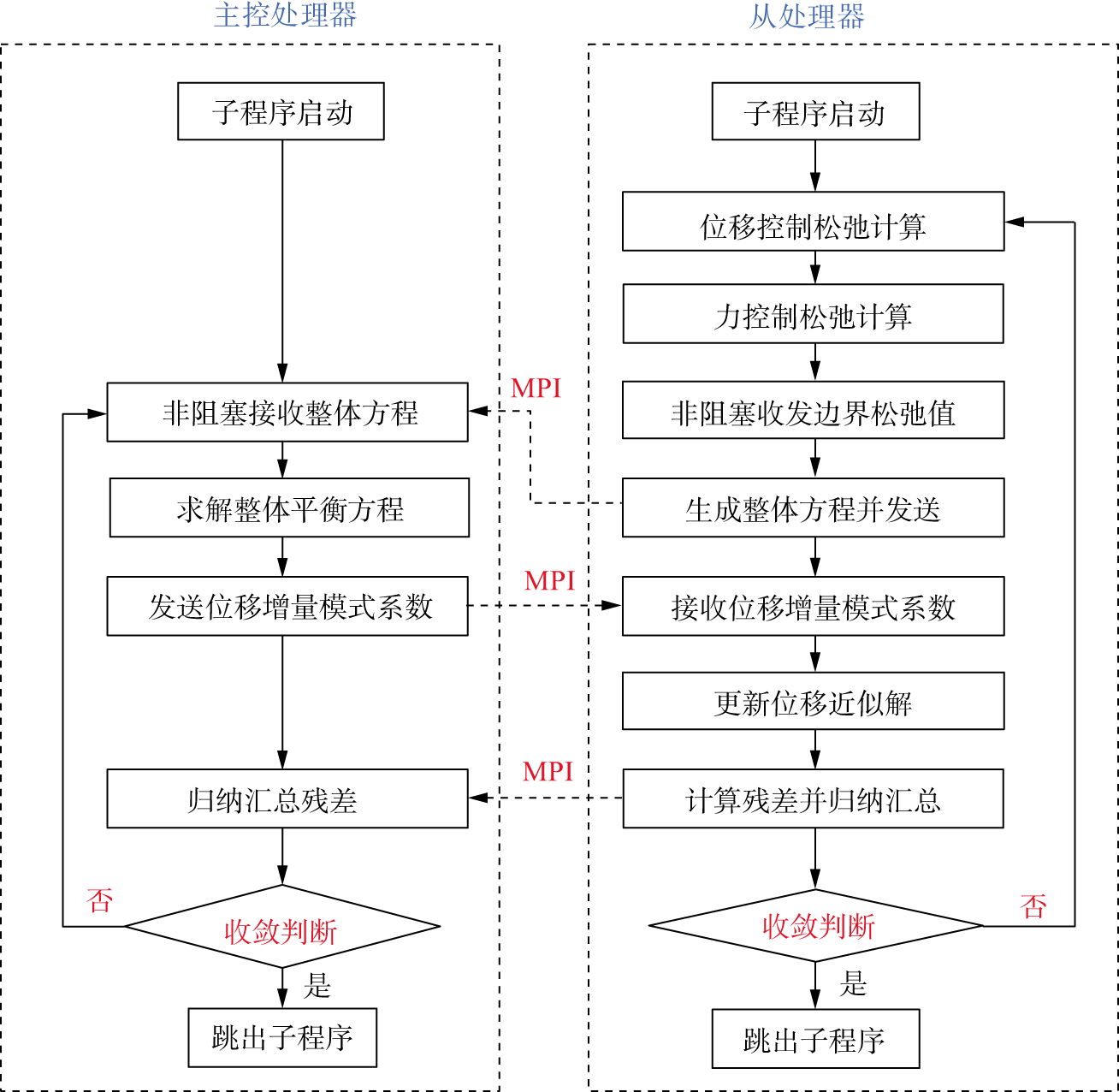
由公式(19)至公式(22)可知, 本算法不需要组合整体刚度阵。但考虑到仅使用很少的位移增量模式表示精细自由度, 相当于引入了附加限制, 因而迭代中需要通过分块内松弛计算自适应地调整位移增量模式。谱元法中节点只与周围数目非常少的节点有联系, 得到刚度阵通常是带状分布和稀疏的, 因此, 图 2中的每一个分块仅需和邻近分块交换界面信息, 产生的通信绝大部分都是局部的, 避免出现大规模的整体信息交换情况, 通信负担低。一个典型二级结构迭代方案的求解流程如图 4所示, 编程中可以使用MPI非阻塞通信实现通信与计算的重叠, 减少处理器等待时间, 图中虚线箭头表示通信数据流向。上述方法还可通过层层自由度凝聚, 建立多级平衡求解格式, 实现更大规模问题模拟。目前使用的位移增量模式包含常规位移增量模式和自适应位移增量模式两类, 其中常规位移增量模式用于捕捉分块的整体运动变形趋势; 自适应松弛位移增量模式用于捕捉分块内不均匀变形, 放在各分块所用的从处理器进行计算。
|
图 4 谱元法二级自由度凝聚迭代方案流程 |
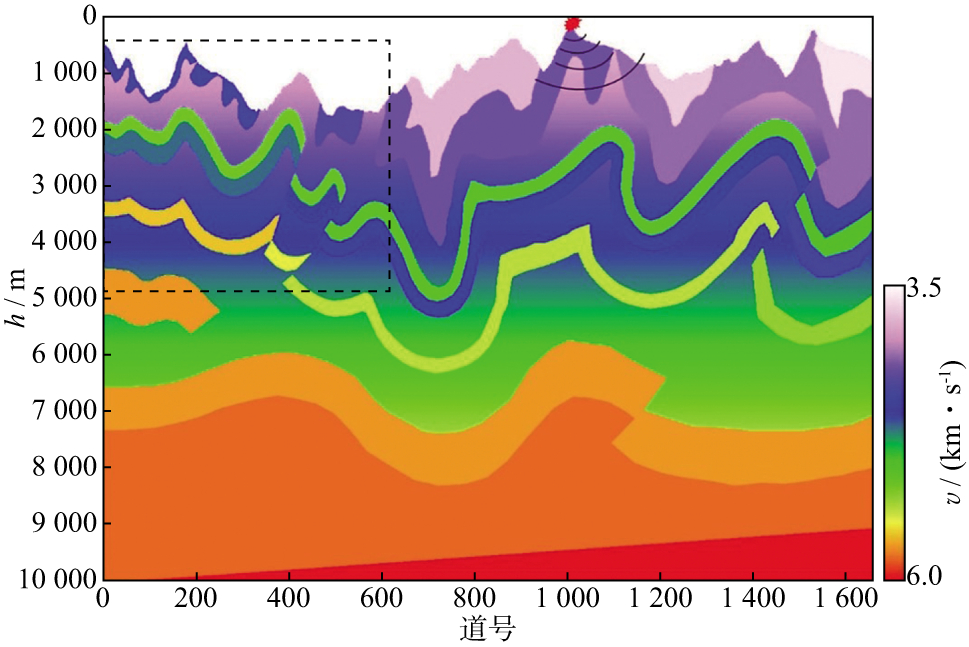
选择加拿大起伏地表逆掩断层速度模型(图 5)作为算例进行性能分析, 该模型横向24930m, 纵向10000m, 空间采样为15m×15m, 包含落差达1500m的起伏地表、高速体及低速体同时出露地表、众多高陡倾角断层以及逆掩推覆构造。在其地表高点进行切比雪夫谱元法单炮正演模拟来考察本文算法的收敛性、可扩展性及并行效率, 时间步长为1ms, 模拟长度为10s。
|
图 5 加拿大起伏地表逆掩断层速度模型 |
测试所用集群环境见表 1, 最多使用了2001个处理器, 求解有10×108个未知数的波场传播问题。
| 表 1 算法测试使用集群条件 |
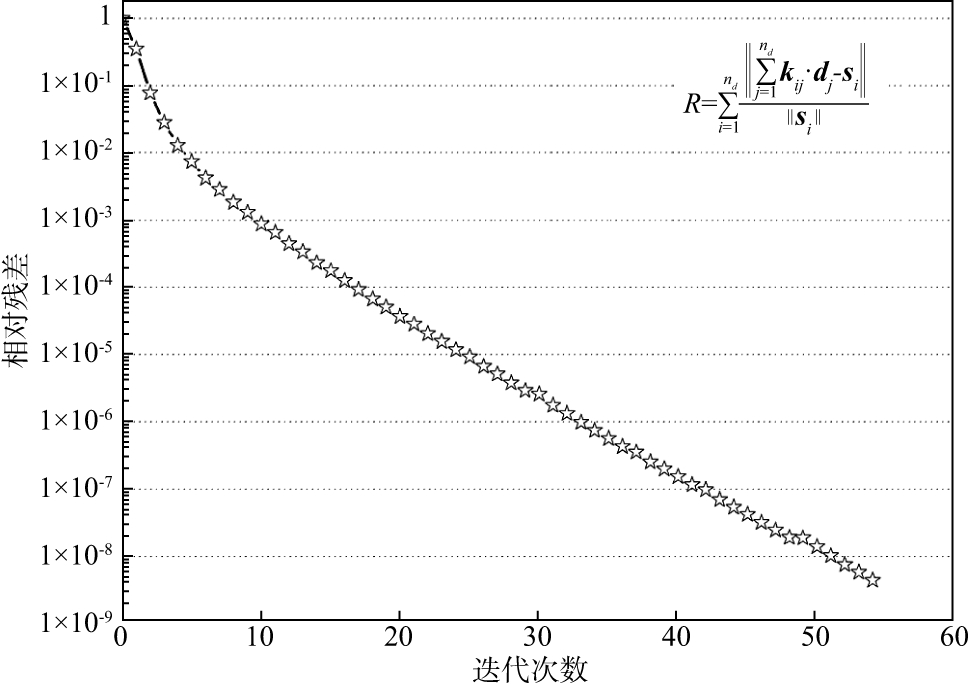
首先设计简单算例I分析算法的收敛性。采用的处理器数目是2400个核。将图 5模型剖分成具有10×108个节点规模的单元, 系统共有10×108个未知数, 分成2000块, 每块有50×104个自由度, 共使用了2001个处理器, 进行单炮的正演模拟, 得到该问题相对残差随迭代变化曲线(图 6), 可知每两个残差下降一个数量级, 收敛速度保持稳定。
|
图 6 图 5算例中相对残差变化曲线 |
在扩展性方面, 测试以下两类情况。
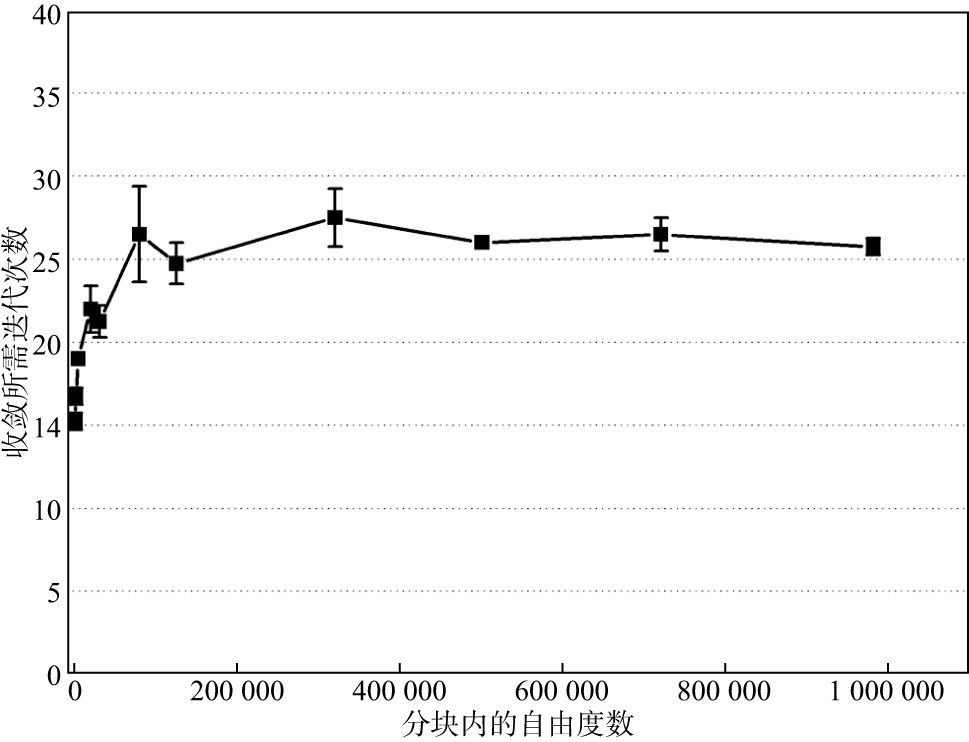
首先, 固定求解域分块数目, 增加分块内自由度数。将图 5所示模型分为8×8共64个分块, 不断增加分块内的未知数数量, 结果如图 7所示, 分块内的未知数从400个增长到了980000个, 可以看出, 无论是每个分块的未知数数量还是整个问题的规模都发生了巨大的变化, 但收敛所需迭代次数达到28次, 就不再增长。
|
图 7 收敛所需迭代次数与分块内未知数关系 |
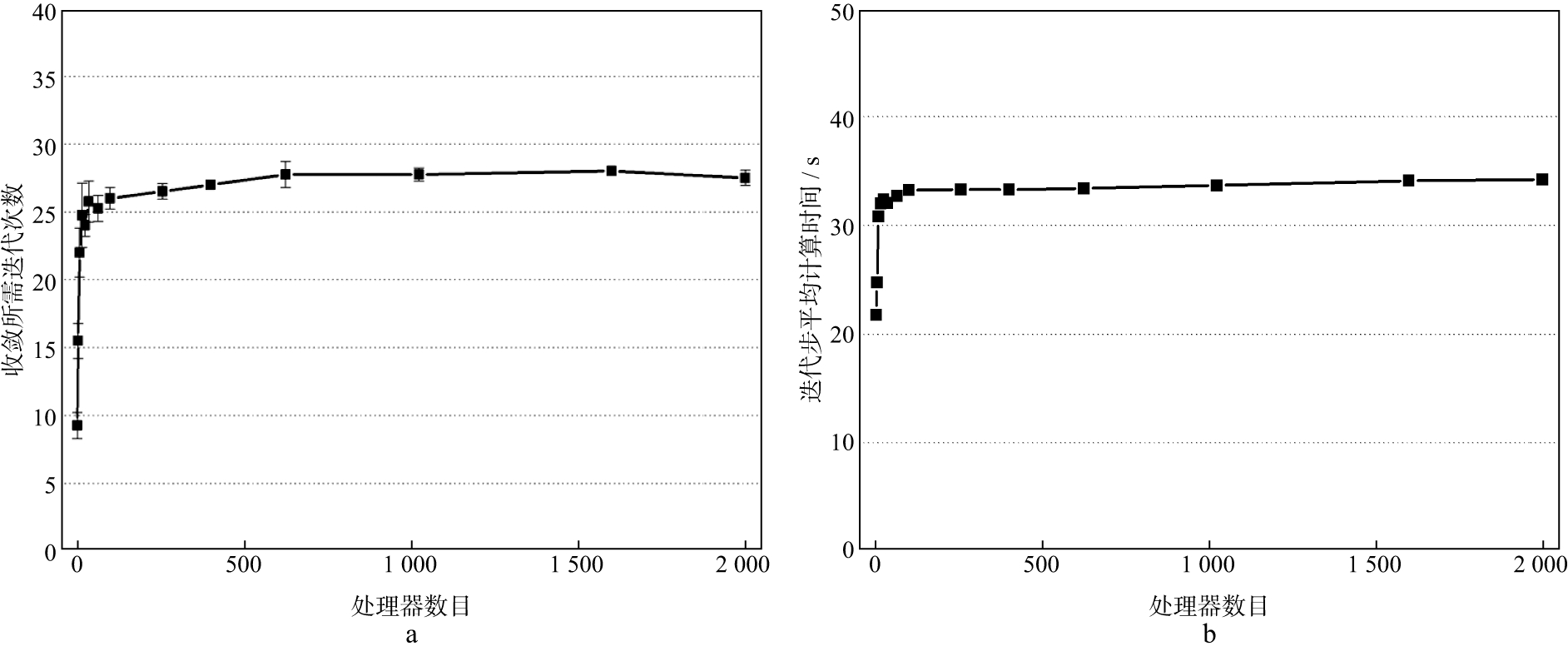
其次, 固定每个分块内的自由度数, 在每个分块内放置50×104个自由度, 像砌墙一样不断增加分块的数目, 由2个变化到2000个(10×108个未知数), 从图 8中可以看出, 当问题规模足够大时, 收敛所需迭代步数也不再变化, 同时, 每步迭代所需要的平均计算时间的增长速度也远远低于分块增长速度。
|
图 8 收敛所需迭代次数(a)、迭代步平均计算时间(b)与处理器数目关系 |
综合迭代次数和迭代时间说明, 本文提出的多级并行切比雪夫谱元逆时偏移方法有很好的扩展性, 借助集群系统能够有效提高成像问题大规模并行计算效率。
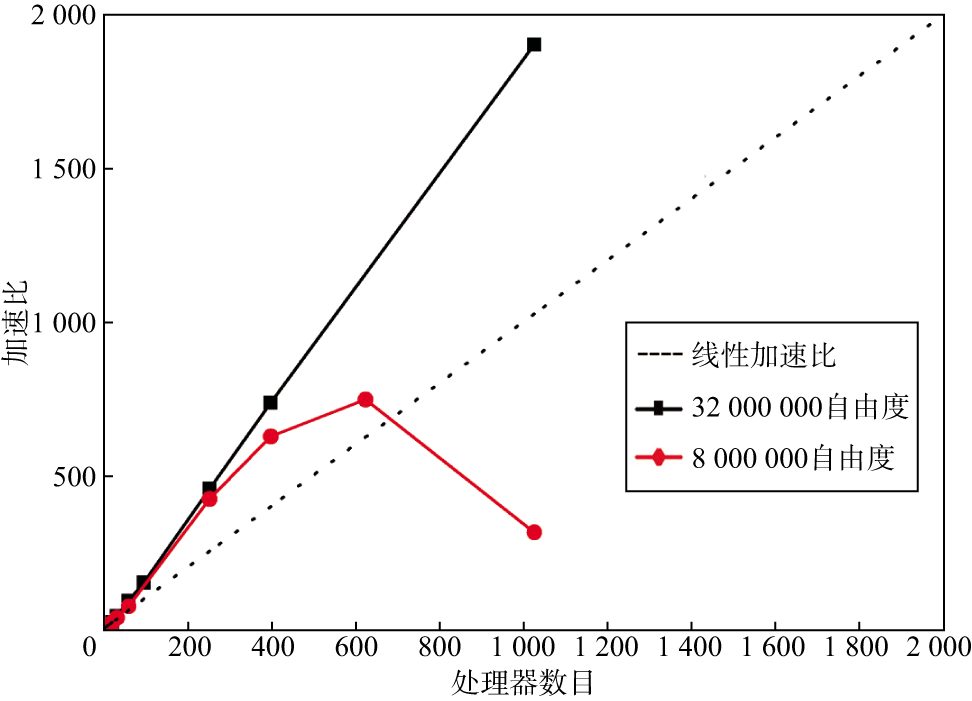
最后, 在并行效率方面, 使用800×104个未知数和3200×104未知数算例测试了谱元逆时偏移多级并行算法的并行加速比状况(图 9), 本文提出的算法具有很好的并行效率, 800×104的算例只有使用超过625个进程后, 加速比才出现下降的情况, 且对比两个算例可以看出, 规模越大, 加速比下降的位置出现越晚。
|
图 9 超大规模稀疏线性方程组并行算法加速比曲线 |
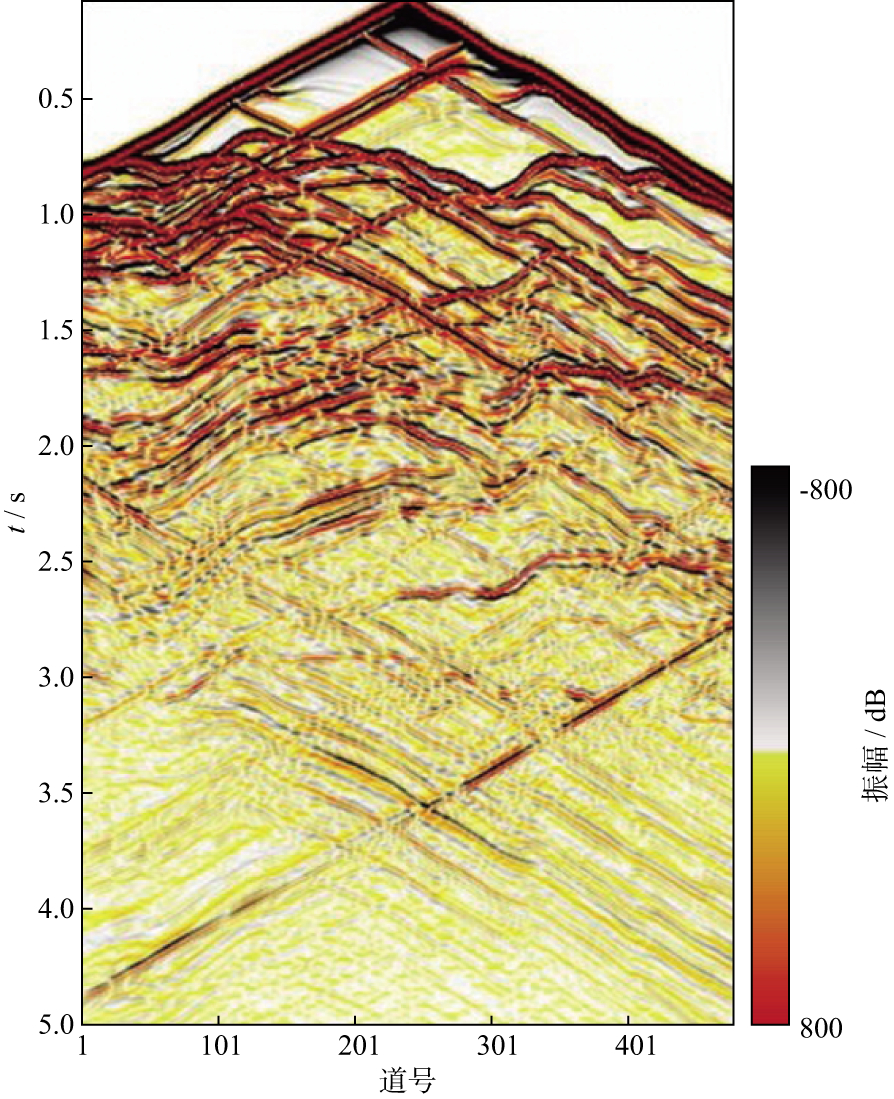
为了验证谱元逆时偏移多级并行算法在解决起伏地表复杂构造精确成像上的能力及效率, 选取图 5所示模型及数据包, 该数据包采用480道中间放炮对称观测系统进行正演模拟, 共采集278炮单炮数据, 道距为15m, 炮点距为90m, 最小炮检距为15m, 最大炮检距为3600m, 每道4ms采样, 道长为5s(图 10)。单元内采用4阶切比雪夫多项式插值, 模型按照4×4分块方案调用17个计算节点并行计算。
|
图 10 加拿大起伏地表逆掩断层正演单炮记录 |
有限差分法逆时偏移及谱元法逆时偏移的成像结果对比如图 11所示。有限差分法逆时偏移由于采用了双程波方程描述波场传播, 没有倾角限制, 可以实现回转波成像, 在近地表复杂构造、中深层复杂构造及逆掩推覆构造区都能成像, 特别是在深部逆掩推覆构造带, 构造边界刻画清晰干脆。然而, 由于有限差分法网格剖分通常采用矩形规则网格, 其在处理近地表速度突变区复杂构造成像时, 达不到理想的成像效果。

|
图 11 起伏地表模型偏移成像对比 a有限差分逆时偏移方法; b谱元逆时偏移多级并行算法 |
谱元逆时偏移方法由于采用谱元法求解波场传播问题, 求解域单元离散方式多样, 可以处理诸如起伏地表及速度突变区复杂构造成像, 其成像结果相对于有限差分发逆时偏移精度明显提高(图 11b)。两种方法的成像对比结果表明: 谱元逆时偏移方法具有较高的成像精度, 适应起伏地表及复杂构造, 可以精确刻画断裂系统, 具有明显成像优势。
从单炮成像及全数据体成像两方面分析有限差分逆时偏移方法(FD-RTM)和谱元逆时偏移多级并行算法的成像耗时, 单炮成像有限差分逆时偏移方法耗时7.28min, 谱元逆时偏移多级并行算法耗时6.62min; 有限差分逆时偏移方法全部278炮整体耗时33.88h, 而谱元逆时偏移多级并行算法全部728炮整体耗时30.86h。可以看出, 由于谱元法采用切比雪夫高阶多项式插值, 不论是单炮偏移, 还是全数据体偏移, 谱元法逆时偏移相对于有限差分法逆时偏移耗时均有所减少。
3.2 SEAM三维起伏地表复杂构造模型为了进一步验证谱元逆时偏移多级并行算法在解决三维起伏地表复杂构造精确成像上的能力及效率, 选取如图 12所示的SEAM三维起伏地表速度模型, 该速度模型x方向为12510m, y方向为14460m, z方向为10000m, 网格大小为12.5m×12.5m, 包含落差达1550m的起伏地表、出露地表的高速山体、三角洲低速沉积层及地下高陡断层推覆体构造。

|
图 12 SEAM三维起伏地表模型 |
正演单炮数据共25355炮, 采用正交对称观测系统采集, 全排列接收, 道距为12.5m, 线距为125m, 炮点距为25m, 炮线距为250m, 最小炮检距为12.5m, 横向最大炮检距为12500m, 纵向最大跑检距为14500m, 每道采样间隔为4ms, 道长为5s。选取图 12极高点附近部分炮集数据共1005炮, 进行过极高点剖面(图 13)局部三维成像, 单元内采用4阶切比雪夫多项式插值, 模型按照8×8分块方案调用65个计算节点并行计算。

|
图 13 SEAM三维起伏地表模型过最高点速度剖面(a)及正演单炮记录(b) |
有限差分法逆时偏移及谱元法逆时偏移的成像结果如图 14所示。同样地, 由于有限差分逆时偏移方法三维网格剖分通常采用正六面体等规则网格, 在处理三维近地表速度突变区复杂构造成像时, 采用该方法不能达到理想的成像效果。谱元逆时偏移方法求解域单元离散方式多样, 可以处理诸如三维起伏地表及速度突变区复杂构造成像, 其近地表浅层成像结果相对于有限差分法逆时偏移精度明显提高(绿框), 同时, 深层目标区(蓝框)背斜构造及其内幕成像也有明显的优势(图 14b)。两种方法的成像对比结果表明: 谱元逆时偏移方法适用于三维起伏地表及复杂构造成像且具有较高的成像精度。

|
图 14 SEAM起伏地表模型偏移成像结果对比 a有限差分法逆时偏移; b谱元逆时偏移多级并行算法 |
同样地, 从单炮成像及全数据体成像两方面分析有限差分逆时偏移方法和谱元逆时偏移多级并行算法的成像耗时, 单炮成像有限差分逆时偏移方法耗时12.5min, 谱元逆时偏移多级并行算法耗时13.8min; 有限差分逆时偏移方法整体耗时8.8d, 而谱元逆时偏移多级并行算法整体耗时9.7d。可以看出, 由于谱元法采用稀疏网格高阶多项式插值, 以及高扩展性多级并行计算方案, 同样地, 不论是单炮偏移, 还是全数据体偏移, 谱元法逆时偏移相对于有限差分法逆时耗时没有较大的增长, 并且通过进一步研究基于GPU集群系统的谱元逆时偏移, 该方法的运算效率有望进一步提高。
4 结论本文结合绝对稳定的隐式Newmark时间积分方法, 将切比雪夫谱元法应用于起伏地表复杂构造区地震波场模拟及成像, 推导了采用切比雪夫谱元方法模拟波场传播的逆时偏移算法。
为了提升该方法的并行效率, 基于自由度凝聚的思想, 推导出针对谱元波场模拟及逆时偏移成像处理的多级并行迭代求解算法, 该算法在控制收敛所需迭代次数的同时, 具有并行效率不随处理器数目增多而降低的优点。由于谱元法既有有限元方法的边界适应性, 又具有伪谱法的高精度快速收敛特性, 再结合多级并行计算方案, 谱元逆时偏移多级并行算法对起伏地表复杂构造的成像适应性及成像精度优于常规的有限差分逆时偏移方法, 同时其运算效率也与常规有限差分法逆时偏移相当。
虽然谱元逆时偏移方法具有起伏地表适应性强、精度高和收敛快等优点, 但也存在较低的时间精度与较高的空间谱精度不匹配问题, 这将是今后需要重点解决的问题。
| [1] |
冀国强, 石颖. 正则化形式的稳定粘声逆时偏移成像方法[J]. 石油物探, 2020, 59(3): 374-395. JI G Q, SHI Y. Stable and regularized visco-acoustic reverse time migration[J]. Geophysical Prospecting for Petroleum, 2020, 59(3): 374-395. DOI:10.3969/j.issn.1000-1441.2020.03.006 |
| [2] |
曲英铭, 魏哲枫, 刘畅, 等. 面向高陡构造的黏声棱柱波逆时偏移[J]. 石油地球物理勘探, 2020, 55(4): 793-802. QU Y M, WEI Z F, LIU C, et al. Viscoacoustic reverse time migration of prismatic wave for steeply dipped structures[J]. Oil Geophysical Prospecting, 2020, 55(4): 793-802. |
| [3] |
巩向博, 王升超, 韩立国. 小尺度散射体稀疏最小二乘逆时偏移方法研究[J]. 地球物理学报, 2019, 62(10): 4028-4037. GONG X B, WANG S C, HAN L G. Sparse least-squares reverse time migration of small scatters in seismic exploration[J]. Chinese Journal of Geophysics, 2019, 62(10): 4028-4037. DOI:10.6038/cjg2019M0420 |
| [4] |
李青阳, 吴国忱, 杨凌云, 等. 基于二阶系统的NCPML吸收边界三维声波逆时偏移方法[J]. 石油物探, 2020, 59(6): 901-911. LI Q Y, WU G C, YANG L Y, et al. Three-dimensional acoustic reverse time migration with a NCPML absorbing boundary condition in a second-order system[J]. Geophysical Prospecting for Petroleum, 2020, 59(6): 901-911. DOI:10.3969/j.issn.1000-1441.2020.06.008 |
| [5] |
段心标. 应用GPU的傅里叶有限差分逆时偏移[J]. 石油地球物理勘探, 2020, 55(5): 1039-1045. DUAN X B. Fourier finite-difference reverse time migration using GPU[J]. Oil Geophysical Prospecting, 2020, 55(5): 1039-1045. |
| [6] |
PETERA A T. A spectral element method for fluid Dynamics: laminar flow in a channel expansion[J]. Journal of Computational Physics, 1984, 54(3): 468-488. DOI:10.1016/0021-9991(84)90128-1 |
| [7] |
王秀明, SERIANI G, 林伟军. 利用谱元法计算弹性波场的若干理论问题[J]. 中国科学G辑: 物理学力学天文学, 2007, 37(1): 41-59. WANG X M, SERIANI G, LIN W J. Using spectral element method to calculate some theory problems about elastic wave field[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2007, 37(1): 41-59. DOI:10.3969/j.issn.1674-7275.2007.01.006 |
| [8] |
王童奎, 李瑞华, 李小凡. 横向各向同性介质中地震波场谱元法数值模拟[J]. 地球物理学进展, 2007, 22(3): 778-784. WANG T K, LI R H, LI X F. Numerical spectral-element modeling for seismic wave propagation in transversely isotropic medium[J]. Progress in Geophysics, 2007, 22(3): 778-784. DOI:10.3969/j.issn.1004-2903.2007.03.018 |
| [9] |
PRIOLO E, SERIANI G.A numerical investigation of Chebyshev spectral element method for acoustic wave propagation[C]//Proceeding of 13th IMACS World Congress on Computational and Applied Mathematics.Dublin: Criterion Press, 1991: 551-556
|
| [10] |
MADAY Y, PATERA A T. Spectral element methods for the incompressible Navier-Stokes equations[M]. York: State-of-the-Art Surveys on Computational Mechanics, 1989: 71-143.
|
| [11] |
李孝波, 薄景山, 齐文浩, 等. 地震动模拟中的谱元法[J]. 地球物理学进展, 2014, 29(5): 2029-2039. LI X B, BO J S, QI W H, et al. Spectral element method in seismic ground motion simulation[J]. Progress in Geophysics, 2014, 29(5): 2029-2039. |
| [12] |
林伟军, 苏畅, SERIANI G. 多网格谱元法及其在高性能计算中的应用[J]. 应用声学, 2018, 37(1): 42-52. LIN W J, SU C, SERIANI G. The poly-grid spectral element method and its implementation in high performance computing[J]. Journal of Applied Acoustics, 2018, 37(1): 42-52. |
| [13] |
KOMATITSCH D, VILOTTE J, VAI R, et al. The spectral element method for elastic wave equations-application to 2D and 3D seismic problems[J]. International Journal for Numerical Methods in Engineering, 1999, 45(9): 1136-1164. |
| [14] |
邵秀民, 蓝志凌. 各向异性弹性介质中波动方程的吸收边界条件[J]. 地球物理学报, 1995, 38(S1): 57-73. SHAO X M, LAN Z L. Absorbing boundary conditions for anisotropic elastic wave equations[J]. Chinese Journal of Geophysics, 1995, 38(S1): 57-73. |
| [15] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003: 468-522. WANG X C. Finite element method[M]. Beijing: Tsinghua University Press, 2003: 468-522. |
| [16] |
方秦. 隐式Newmark法分析波动问题精度的探讨[J]. 爆炸与冲击, 1992, 12(1): 45-53. FANG Q. Studies on the accuracy of finite element analysis of implicit Newmark method for wave propagation problems[J]. Explosion and Shock Waves, 1992, 12(1): 45-53. |



