2. 中国石油化工股份有限公司华东油气分公司勘探开发研究院, 江苏南京 210011
2. Research Institute of Exploration and Development, SINOPEC East China Oil & Gas Company, Nanjing 210011, China
多次波干扰普遍存在于勘探地震数据中, 多次波干扰可分为向下散射点位于表面和地下界面间的自由表面多次波和向下散射点位于地下界面之间的层间多次波[1-2]。在海上地震资料中常发育丰富的自由表面多次波, 而陆上地震资料相对于海上地震资料而言, 层间多次波更发育[3-4]。多次波对地震资料有多方面的影响, 例如, 多次波会降低地震资料的信噪比进而影响最终的成像精度; 当目的层的多次波能量较强时还会引起构造假象, 从而影响地震解释和勘探部署[5]。因此, 准确识别和有效压制多次波成为地震资料处理的关键环节。
目前, 自由表面多次波的压制已经取得了显著的成效[6-10], 然而层间多次波的形成机制以及波场特征更加复杂, 使得层间多次波的压制更具挑战性。预测反褶积作为最常用的多次波压制方法, 其原理是利用多次波的周期性将多次波和一次波分离, 该方法在消除由浅海海底产生的交响回声时有明显的效果, 但对于陆上地震资料, 由于子波的横向不一致和近地表的吸收衰减问题经常导致预测反褶积法压制多次波效果不佳[11]。无论是理论研究还是实际应用, Radon变换在多次波压制中都有良好的表现, 主要得益于其效率高、适应性强以及良好的信噪分离能力[5, 12]。Radon变换的假设条件是多次波与一次波存在校正量差, 而当层间多次波与一次波的旅行时和速度差异较小时, 利用Radon变换压制多次波则无法满足处理要求。BERKHOUT等[6]给出了基于反馈迭代自由表面多次波压制方法(SRME)的理论基础, JAKUBOWICZ[13]对该理论的物理意义做了进一步解释并进行了扩展, 提出层间多次波可用一次波构建。吴静等[14]将该方法扩展到多个界面的层间多次波压制, 只要通过少量的循环就能有效地完成所有阶次的层间多次波预测工作, 提高了计算效率。BERKHOUT等[15]和VERSCHUUR等[16]利用共聚焦点(CFP)道集, 将SRME拓展到层间多次波的预测, 但该方法高度依赖于宏观速度模型[17]。刘战等[18]在CFP方法的基础上证明了利用地表数据驱动消除层间多次波的可行性, 为层间多次波的压制开辟了新思路。WEGLEIN等[19]通过严格的理论推导将逆散射级数法(inverse scattering series, ISS)应用于多次波压制, 此后多位学者基于此方法进行了更深入的研究[20-22]。FU等[23]在逆散射理论的基础上首次推导出可用于陆上层间多次波压制的逆散射级数算法, 并将其成功应用于陆上地震资料的多次波压制。金德刚等[24]从降低算法空间复杂度的角度出发, 将逆散射级数法从1维拓展到1.5维, 在一定程度上提高了计算效率。自从WAPENAAR等[25]将Marchenko算法引入地球物理领域, 很多研究人员尝试利用Marchenko算法压制多次波并引起了广泛关注[26-27]。ZHANG等[28]从Marchenko算法出发, 给出一种可一步压制自由表面多次波和层间多次波的策略。然而Marchenko算法假设条件苛刻, 对地震数据的品质要求高, 目前大多只能应用于模型数据。
虽然层间多次波压制的研究取得了一定进展, 但目前还没有一种方法能够有效地压制实际数据中的层间多次波, 因此联合不同方法取长补短, 综合压制多次波的策略逐渐受到业界的重视和认可[29-31]。然而目前已有的综合方法仍存在一些不足: ①大多数的综合方法都是将波动方程预测与滤波法或预测反褶积方法相结合, 并且多数是在CMP道集(共中心点道集)进行波动方程预测, 这会极大增加波动方程的运算量, 而且CMP数据信噪比通常较低, 也很难满足波动方程方法对地震数据品质的要求, 另外也有研究发现在CMP道集压制多次波后再进行叠前偏移处理会放大剩余的多次波能量[32], 多次波的压制效果达不到最佳; ②综合方法通常要将预测的层间多次波从原始数据中减去, 如果直接运用自适应相减算法对两者求差, 很容易出现多次波衰减不干净或一次波受损的状况; ③有些综合方法的流程过于复杂, 计算效率低, 在过度追求多次波压制效果的同时也容易伤害到有效信号。
基于以上分析, 本研究提出了一种将逆散射级数法与抛物线Radon变换相结合压制层间多次波的新策略。目前逆散射级数法被认为是最先进的层间多次波预测方法, 该方法可较准确的预测层间多次波, 在CRP道集压制多次波能提高逆散射级数算法的计算效率, 还能在一定程度上弱化多次波的传播效应。在抛物线Radon域利用非线性滤波器, 先将未受多次波干扰的有效波分离出来, 再进行曲波域的匹配相减, 不但减小了多次波压制过程中对减法的依赖度, 还能有效地保护一次波。
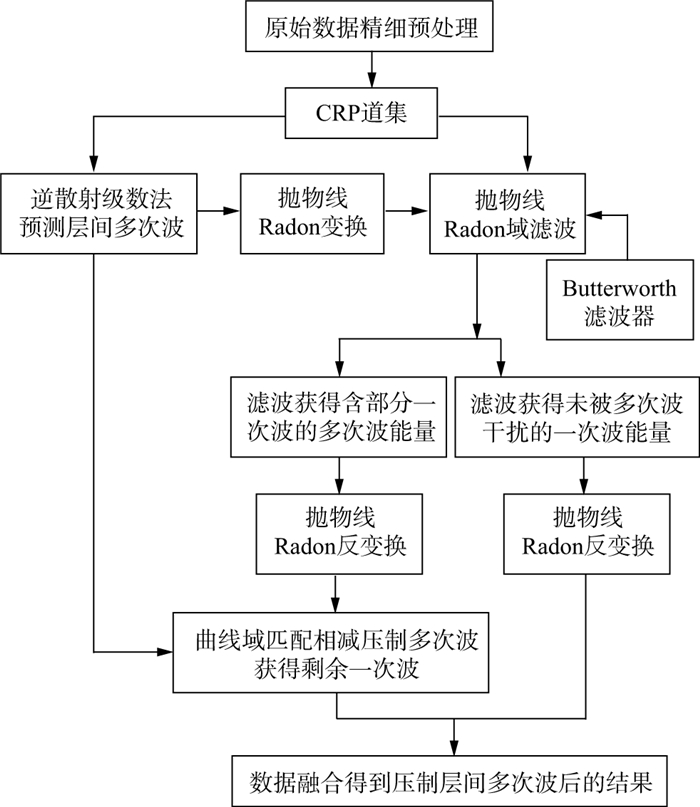
1 层间多次波压制策略及原理滤波法和波动方程预测法在层间多次波的压制中都有所应用, 但面对复杂的地质情况时, 单独使用一种方法很难较好地压制层间多次波。本文研究结合了逆散射级数法和抛物线Radon变换法的各自优势, 设计了图 1所示的层间多次波压制策略。如前文所述, 以逆散射级数为代表的波动方程预测层间多次波方法能够较准地预测层间多次波, 但对输入数据的振幅很敏感, 如果输入数据的品质较低, 处理后的结果可能出现极性相反甚至更强的内部多次反射。因此, 通过分析, 我们选择了叠前时间偏移的CRP道集(共反射点道集)作为层间多次波压制策略的输入数据。这是因为CRP道集相对于CMP道集信噪比更高、排列更整齐, 在CRP道集上层间多次波的周期性更明显, 利用波动方程能更好地预测多次波, 在计算效率上也会大大提高, 特别是在大规模的三维数据中这种策略是现实可行的。另外, 已有研究表明在CMP道集利用Radon变换压制多次波后, 剩余的多次波能量经由叠前偏移处理而被放大, 但在CRP道集上利用Radon变换压制多次波则能有效地弱化多次波的传播效应[27, 29], 而且在CRP道集上多次波的时距曲线更接近抛物线。因此, 我们选择将抛物线Radon变换与逆散射级数相结合在CRP道集压制层间多次波, 以达到更好的多次波压制效果。
|
图 1 层间多次波压制策略 |
考虑到逆散射级数法对数据质量有很高的依赖度, 本研究使用了杨金龙等[33]提出的一种改进的逆散射级数层间多次波压制方法。该方法在预测层间多次波前、后去除和补偿子波来提高层间多次波预测的准确性, 其推导出的层间多次波波场b3的预测算法如下:
| $ \begin{array}{l} b_{3}\left(k_{g}, k_{s}, q_{g}+q_{s}\right)=\frac{1}{(2 \pi)^{2}} \int_{-\infty}^{\infty} \mathrm{d} k_{1} \int_{-\infty}^{\infty} \mathrm{d} k_{2} \mathrm{e}^{-i q_{1}\left(\varepsilon_{g}-\varepsilon_{s}\right)} \cdot \\ \quad \mathrm{e}^{\mathrm{i}{\mathit{q}}_{2}\left(\varepsilon_{g}-\varepsilon_{s}\right)} \times \int_{-\infty}^{\infty} \mathrm{d} z_{1} b_{1}\left(k_{g}, k_{1}, z_{1}\right) \mathrm{e}^{\mathrm{i}\left(q_{g}+q_{1}\right) z_{1}} \cdot \\ \quad \int_{-\infty}^{z_{1}-\lambda} \mathrm{d} z_{2} b_{1}\left(k_{1}, k_{2}, z_{2}\right) \mathrm{e}^{-\mathrm{i}\left(q_{1}+q_{2}\right) z_{2}} \times \int_{z_{2}+\lambda}^{\infty} d z_{3} \cdot \\ \quad b_{1}\left(k_{2}, k_{s}, z_{3}\right) \mathrm{e}^{\mathrm{i}\left(q_{2}+q_{s}\right) z_{3}} \end{array} $ | (1) |
式中: b1为单频平面波场; εs, qs, k1和ks分别为震源的深度、垂向波数、水平波数积分变量和水平波数; εg, qg, k2, kg分别为检波器的深度、垂向波数、水平波数积分变量和水平波数; λ为条件参数; q1, q2为散射点垂向波数; z1, z2, z3为散射点的深度。一阶层间多次波产生的条件是3个一次波满足“低-高-低”约束关系; 二阶层间多次波产生的条件是两个一次波与一阶层间多次波满足“低-高-低”约束关系; 同理即可推出高阶层间多次波的产生条件。
基于波动方程压制层间多次波的实现过程通常分为两步: 第一步是多次波模型数据的预测; 第二步是通过减法运算将一次波从原始数据中分离出来。多数基于波动方程的层间多次波压制方法, 在预测出多次波模型后直接与原始数据进行自适应相减, 而在相减过程中很容易对一次波造成损害。本文新策略为了减小对减法运算的依赖程度, 提出使用非线性的掩蔽滤波器φ在多次波相减前先对数据的一次波进行保护处理。滤波器是自适应的, 因为其依赖于原始数据和多次波模型数据, Butterworth类型滤波函数如下[34]:
| $ \varphi=1-\frac{1}{\sqrt{1+\left[\frac{B}{\varepsilon A}\right]^{2 n}}} $ | (2) |
式中: B是多次波模型数据的振幅; A是原始数据的振幅; n是控制滤波平滑的参数; ε是加权因子。滤波后的原始数据被分成两部分: 含有部分一次波的多次波能量以及未被多次波干扰的一次波能量。让未被多次波干扰的一次波能量不参与相减运算, 从而保护一次波。在实际应用中, 滤波参数需要根据多次波压制和一次波保护的平衡关系进行适当选择。此外, 为了保证滤波效果, 在滤波前还需要对预测的多次波模型数据和原始数据进行平滑处理。
目前应用最广泛的多次波分离策略是基于L2范数的最小二乘分离方法, 如果多次波与一次波是分离的, 那么可通过该算法将多次波很好地去除, 而当一次波和多次波之间有重叠交叉时, 该方法无法有效去除多次波, 且容易对一次波造成损害。近年来, 结合了小波变换和脊波变换优势的曲波变换算法在多次波减法运算中受到广泛关注[35-37]。在曲波域地震数据可分解成类波前的短分量, 这使得地震数据可以被划分得更细致, 从而进行更细致地处理。因此, 新策略提出将地震数据和多次波在曲波域进行相减, 在曲波相减运算之前先利用最小二乘算法对原始数据和多次波数据进行匹配, 曲波系数表达式[38]如下:
| $ L(t)=h(t) * m(t)=\sum\limits_{\tau} h(\tau) m(t-\tau) $ | (3) |
| $ Q=\sum\limits_{t}[x(t)-L(t)]^{2} $ | (4) |
式中: L(t)为匹配得到的多次波数据; h(t)为匹配算子; m(t)为利用波动方程预测的多次波模型数据; x(t)为多次波压制前的原始数据; Q为总体误差。数据匹配后, 将地震数据和匹配得到的多次波数据进行曲波变换, 采用软阈值法将多次波从原始地震数据中分离出来, 曲波系数表达式[39]如下:
| $ C_{s p}=\left\{\begin{array}{cl} \operatorname{sgn}\left(C_{s p}\right)\left(\left|C_{s p}\right|-T_{m}\right) & \left|C_{s p}\right| \geqslant T_{m} \\ 0 & \left|C_{s p}\right|<T_{m} \end{array}\right. $ | (5) |
式中: Csp为原始地震数据经曲波变换后得到的曲波系数; Tm为经过匹配后的多次波数据曲波系数的模。将多次波数据从原始数据分离后, 再进行曲波反变换即得到了压制多次波后的地震数据。
新策略的实现过程中, 第1步对地震数据进行精细地预处理, 包括静校正、去噪、预测反褶积、高精度速度分析和叠前时间偏移, 最终得到数据品质较高的叠前CRP道集。在预处理阶段关键的步骤是去噪, 不但要保护原始数据的低频信息还要保证去噪过程中振幅不被破坏, 避免出现假振幅; 第2步利用杨金龙等[33]提出的改进逆散射级数方法对CRP道集进行层间多次波预测, 得到层间多次波模型数据; 第3步对预测的层间多次波模型数据和原始CRP道集都进行抛物线Radon变换, 根据预测的层间多次波模型数据和原始数据设计最优的Butterworth型滤波器, 然后根据解释质控调整滤波参数。利用设计的滤波器对原始CRP道集进行滤波, 得到含部分一次波的多次波能量和未被多次波干扰的一次波能量。第4步将逆散射级数法预测的多次波模型数据与含部分一次波的多次波能量进行曲波域匹配相减, 压制层间多次波后得到剩余一次波。第5步将剩余的一次波与第3步中分离出的未被多次波干扰的一次波能量进行匹配相加融合, 得到最终压制层间多次波后的地震数据, 在匹配融合过程中要注意数据之间能量的相对关系, 避免出现假象。
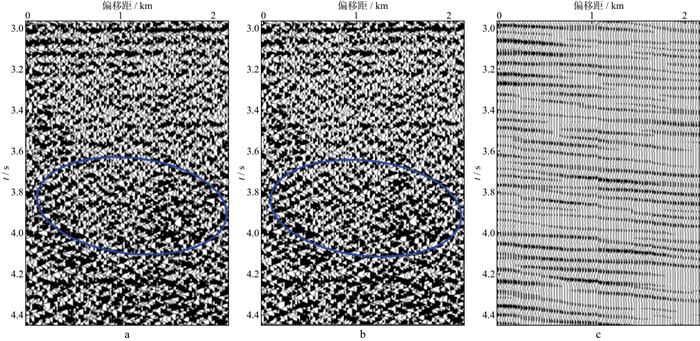
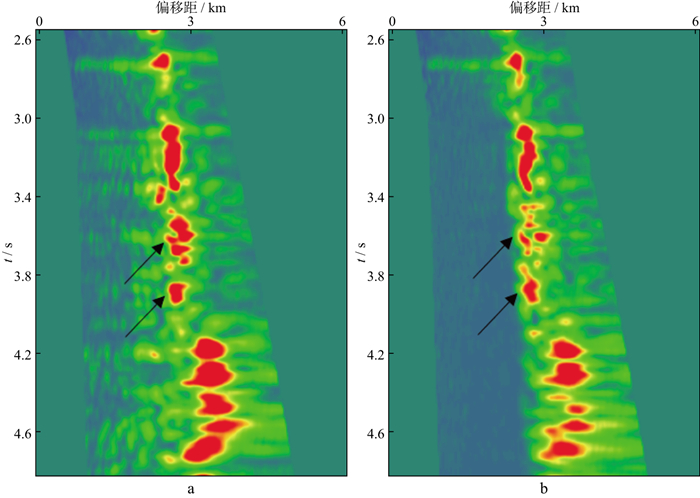
2 应用实例西部某探区上覆地层中发育几套速度异常体, 使得奥陶系内幕发育了能量较强的层间多次波。多次波的出现给地震成像、构造解释以及储层识别都带来很大干扰, 前期试验了多种压制方法, 但仍不能满足地震解释和勘探部署的需求。图 2是前期利用Radon变换在CMP道集压制多次波的结果, 对比图 2a和图 2b可以看出CMP道集的信噪比较低, 即使在层间多次波较发育的区域(蓝色圆圈处)也很难准确识别多次波, 因此图 2c所示被压制的层间多次波可信度不高。图 3a和图 3b分别是利用Radon变换在CMP道集压制多次波前后的速度谱, 由图可见, 该地区的层间多次波具有与一次波的旅行时和速度差异小、能量强等特点, 因此利用Radon变换只能压制速度差异很大的多次波能量团, 仍残存层间多次波的能量团(箭头所指处)。
|
图 2 Radon变换压制多次波的测试过程 a经过动校正后的CMP道集; b对图 2a数据利用Radon变换压制多次波后的结果; c被压制的多次波 |
|
图 3 利用Radon变换压制CMP道集多次波前(a)、后(b)的速度谱 |
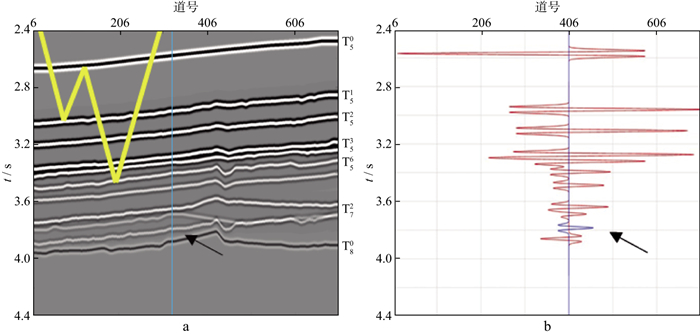
逆散射级数法不需要已知地下信息, 利用数据驱动就可预测出所有的多次波, 但在实际生产中要根据地质需求计算合理的多次波模型数据, 其关键是预测时窗的选取。为此, 我们先利用正演模拟分析了层间多次波的来源及其对目的层的干扰范围, 根据这些信息设计合理的预测时窗, 进而得到与目的层密切相关的层间多次波模型数据。本研究中利用解析方程法进行层间多次波模拟, 该方法理论基础可靠, 计算效率和精度均较高。将地质模型简化(图 4a), 根据速度和深度信息, 利用解析方程计算出每一个一次波和层间多次波准确的反射系数和走时, 解析并模拟出含一次波和多次波的地震数据(图 4b)。通过与原始地震剖面对比分析认为与T72和T80密切相关的多次波来源主要是T50, T51, T52和T56, 根据这些信息再对目的层附近层间多次的来源进行单独正演分析。如图 5a所示为正演模拟中的一种结果, 地震波在T50和T51中多震荡了一次, 因此在T72和T80中产生了层间多次波(图 5a和图 5b箭头所指处), 模拟发现不同来源的多次波可能会叠加成像, 使得层间多次波能量较强。
|
图 4 一次波数据(a)和正演模拟得到的含一次波和多次波的地震数据(b) |
|
图 5 正演模拟的结果(a)以及抽取的单道地震记录(b) |
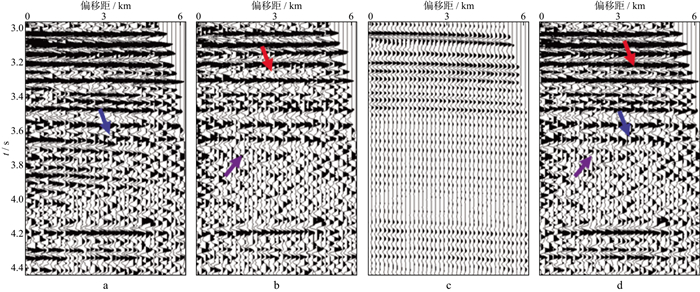
确定了层间多次波的来源后, 利用图 1所示的新策略对实际数据进行测试。图 6a所示是层间多次波压制前的CRP道集, 与图 2a CMP道集相比, 在CRP道集上层间多次波更容易识别。利用逆散射级数法在CRP道集上预测层间多次波模型数据, 并参照该结果设计自适应滤波器, 接着在Radon域对CRP道集进行滤波, 分离出未受多次波干扰的一次波(图 6b)和含有少部分一次波的多次波能量。随后在曲波域对多次波能量和逆散射级数法预测的多次波模型数据进行匹配相减, 得到如图 6c所示的剩余一次波。将剩余的一次波与滤波得到的一次波融合得到如图 6d所示的层间多次波压制后的结果。对比图 6b和图 6d, 可以看出最终结果要比最先分离出的一次波数据中增加了更多的有效信息(图中红色和紫色箭头所指位置)。对比图 6a和图 6d可知, 在CRP道集上层间多次波能量得到很好的压制, 而且目的层附近一次波的能量增强, 同相轴的连续性也有所改善(图中蓝色箭头所指位置)。
|
图 6 CRP道集层间多次波压制的测试过程 a多次波压制前的CRP道集; b利用滤波获得的未被多次波干扰的一次波数据; c曲波域匹配相减压制多次波后得到的剩余一次波数据; d新策略压制多次波后的CRP道集 |
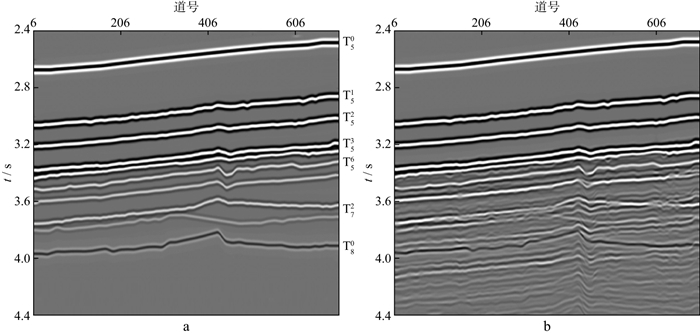
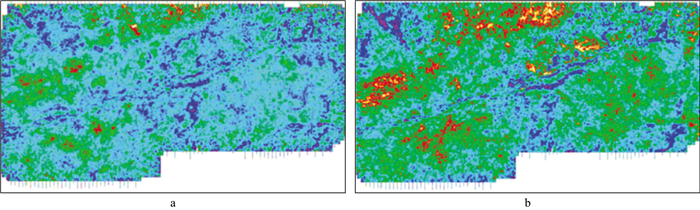
图 7为层间多次波压制前的时间偏移叠加剖面(图 7a)以及采用不同方法压制层间多次波后的偏移叠加剖面(图 7b至图 7d)。利用Radon变换在CMP道集压制多次波后的结果见图 7b, 可见主断裂右侧的层间多次波被部分压制(箭头①所指处), 但断裂左侧还有明显的多次波残余(箭头②所指处), 而且目的层的断裂特征(箭头③所指处)和储层特征(箭头④所指处)在压制多次波后也被破坏。分析可能原因是受Radon变换方法本身的限制, 只能对速度和时差差异较大的多次波进行压制, 还有一部分原因可能是在偏移后剩余的多次波能量被放大, 因此在剖面上仍有明显的多次波残余。利用新策略压制层间多次波的结果见图 7d, 与图 7b相比, 新策略能更好地压制层间多次波(箭头①、②所指处), 而且一次波的能量得到了很好的保护, 因此目的层的断裂特征(箭头③所指处)以及“串珠状”反射(箭头④所指处)更加清晰, 说明处理取得了良好的地质效果。图 7c与图 7d在处理方法上的区别在于新策略中的第4步, 图 7c使用的是常规的自适应相减压制多次波能量, 而图 7d使用的是曲波域匹配相减压制多次波能量。对比可见, 图 7c中主断裂右侧的层间多次波虽然被压制了但一次波的特征也受到一定的损害, 断裂左侧的层间多次波还有少量残余, 而且断裂特征和储层特征也没有图 7d的结果清晰, 说明曲波域匹配相减比常规的自适应相减具有一定的优势。图 8给出了采用新策略进行多次波压制前、后的T72均方根振幅属性, 可以看出在多次波压制后储层特征刻画的更加清晰, 进一步证明了新策略的有效性和实用性。

|
图 7 层间多次波压制前和采用不同方法压制层间多次波后的偏移叠加剖面 a未进行层间多次波压制; b利用Radon变换在CMP道集压制层间多次波; c利用自适应相减法压制层间多次波; d利用新策略压制层间多次波 |
|
图 8 多次波压制前(a)、后(b)T72界面提取的均方根振幅属性 |
层间多次波压制一直是地震资料处理中具有挑战性的工作, 本文提出了联合逆散射级数法和抛物线Radon变换法在CRP道集压制层间多次波的新策略。该策略避免了基于逆散射级数法在CMP道集预测工作带来的计算压力, 基于CRP道集压制多次波在一定程度上能避免偏移过程中多次波剩余能量的增强效应。在Radon域通过滤波先将有效波提前分离, 再进行匹配相减的方法能有效保护一次波。此外, 解析方程正演法在确定层间多次波的来源上也发挥了重要作用, 有效指导了多次波模型数据的预测。实际资料试算表明, 新策略较好地压制了层间多次波, 且保持了刻画储层特征的信息, 为地震解释提供了更合理的成像资料, 也为层间多次波的压制提供了新思路。
值得注意的是本研究仍存在一定的不足: 由于应用了逆散射级数法预测层间多次波, 对数据品质要求很高, 对于信噪比差的数据压制多次波的效果可能不够理想, 因此有必要进一步提高逆散射级数算法的抗噪性; 抛物线Radon变换对远偏移距或浅层数据的压制误差较大, 因此仍需要改进Radon算法; 基于曲波变换的匹配相减算法仍不能完全解决一次波和多次波交叉和重叠的情况, 因此未来的研究方向是利用多次波成像在成像过程中消除多次波的干扰。
| [1] |
陆基孟, 王永刚. 地震勘探原理[M]. 青岛: 中国石油大学出版社, 2009: 122-124. LU J M, WANG Y G. The principle of seismic exploration[M]. Qingdao: China University of Petroleum Press, 2009: 122-124. |
| [2] |
刘振, 张军华, 韩双, 等. 与界面有关的层间多次波预测及压制[J]. 石油地球物理勘探, 2014, 49(1): 61-67. LIU Z, ZHANG J H, HAN S, et al. Layer related interbed multiple elimination[J]. Oil Geophysical Prospecting, 2014, 49(1): 61-67. |
| [3] |
VERSCHUUR D J, BERKHOUT A J, WAPENAAR C P A. Adaptive surface-related multiple elimination[J]. Geophysics, 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [4] |
张宇飞, 苑昊. 陆上多次波识别与压制[J]. 岩性油气藏, 2015, 27(6): 104-110. ZHANG Y F, YUAN H. Recognition and attenuation of multiples in land seismic data[J]. Lithologic Reservoirs, 2015, 27(6): 104-110. DOI:10.3969/j.issn.1673-8926.2015.06.014 |
| [5] |
戴晓峰, 刘卫东, 甘利灯, 等. Radon变换压制层间多次波技术在高石梯-磨溪地区的应用[J]. 石油学报, 2018, 39(9): 1028-1039. DAI X F, LIU W D, GAN L D, et al. The application of Radon transform to suppress interbed multiples in Gaoshiti-Moxi region[J]. Acta Petrolei Sinica, 2018, 39(9): 1028-1039. |
| [6] |
BERKHOUT A J, VERSCHUUR D J. Estimation of multiple scattering by iterative inversion, Part Ⅰ: Theoretical considerations[J]. Geophysics, 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [7] |
VAN GROENESTIJN G J, VERSCHUUR D J. Estimating primaries by sparse inversion and application to near-offset data reconstruction[J]. Geophysics, 2009, 74(3): A23-A28. DOI:10.1190/1.3111115 |
| [8] |
LOPEZ G A, VERSCHUUR D J. Closed-loop surface-related multiple elimination and its application to simultaneous data reconstruction[J]. Geophysics, 2015, 80(6): V189-V199. DOI:10.1190/geo2015-0287.1 |
| [9] |
徐鹏, 刘亚辉, 王华忠. 编码与解码框架下的局部平面波域浅水多次波压制方法[J]. 石油物探, 2019, 58(3): 346-355. XU P, LIU Y H, WANG H Z. Shallow water multiple suppression method in local planar wave domain based on coding and decoding framework[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 346-355. DOI:10.3969/j.issn.1000-1441.2019.03.004 |
| [10] |
黎孝璋, 邓勇, 赫建伟, 等. 复杂海底自由表面多次波预测方法[J]. 石油地球物理勘探, 2020, 55(1): 64-70. LI X Z, DENG Y, HE J W, et al. Free-surface-related multiple prediction for complex seafloor[J]. Oil Geophysical Prospecting, 2020, 55(1): 64-70. |
| [11] |
甘利灯, 肖富森, 戴晓峰, 等. 层间多次波辨识与压制技术的突破及意义——以四川盆地GS1井区震旦系灯影组为例[J]. 石油勘探与开发, 2018, 45(6): 960-971. GAN L D, XIAO F S, DAI X F, et al. Breakthrough and significance of technology on internal multiple recognition and suppression: A case study of Sinian Dengying Formation in Central Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2018, 45(6): 960-971. |
| [12] |
熊登, 赵伟, 张剑锋. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报, 2009, 52(4): 1068-1077. XIONG D, ZHAO W, ZHANG J F. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple[J]. Chinese Journal of Geophysics, 2009, 52(4): 1068-1077. DOI:10.3969/j.issn.0001-5733.2009.04.024 |
| [13] |
JAKUBOWICZ H. Wave equation prediction and removal of interbed multiples[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1998, 1527-1530. |
| [14] |
吴静, 吴志强, 胡天跃, 等. 基于构建虚同相轴压制地震层间多次波[J]. 地球物理学报, 2013, 56(3): 985-994. WU J, WU Z Q, HU T Y, et al. Seismic internal multiple attenuation based on constructing virtual events[J]. Chinese Journal of Geophysics, 2013, 56(3): 985-994. |
| [15] |
BERKHOUT A J, VERSCHUUR D J. Removal of internal multiples with the common-focus-point(CFP) approach: Part 1—Explanation of the theory[J]. Geophysics, 2005, 70(3): V45-V60. DOI:10.1190/1.1925753 |
| [16] |
VERSCHUUR D J, BERKHOUT A J. From removing to using multiples in closed-loop imaging[J]. The Leading Edge, 2015, 34(7): 744-759. DOI:10.1190/tle34070744.1 |
| [17] |
刘嘉辉, 胡天跃, 彭更新. 自适应虚同相轴方法压制地震层间多次波[J]. 地球物理学报, 2018, 61(3): 1196-1210. LIU J H, HU T Y, PENG G X. Suppressing seismic inter-bed multiples with the adaptive virtual events method[J]. Chinese Journal of Geophysics, 2018, 61(3): 1196-1210. |
| [18] |
刘战, 刘洪, 孙军, 等. 地表数据驱动的与层相关的层间多次波消除方法及应用[J]. 地球物理学报, 2019, 62(6): 2227-2236. LIU Z, LIU H, SUN J, et al. Surface-based layer-related inter-layer multiple elimination method and its application[J]. Chinese Journal of Geophysics, 2019, 62(6): 2227-2236. |
| [19] |
WEGLEIN A B, GASPAROTTO F A, CARVALHO P M, et al. An inverse scattering series method for attenuation multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [20] |
WEGLEIN A B, ARAÚJO F V, CARVALHO P M, et al. Inverse scattering series and seismic exploration[J]. Inverse Problems, 2003, 19(6): R27-R83. DOI:10.1088/0266-5611/19/6/R01 |
| [21] |
ZHANG H Y, WEGLEIN A B. Direct nonlinear inversion of multiparameter 1D elastic media using the inverse scattering series[J]. Geophysics, 2009, 74(6): WCD15-WCD27. DOI:10.1190/1.3251271 |
| [22] |
LÖER K, CURTIS A, MELES G A. Relating source-receiver interferometry to an inverse-scattering series to derive a new method to estimate internal multiples[J]. Geophysics, 2016, 81(3): Q27-Q40. DOI:10.1190/geo2015-0330.1 |
| [23] |
FU Q, LUO Y, KELAMIS P G, et al. The inverse scattering series approach towards the elimination of land internal multiples[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg, 2010, 3456-3459. |
| [24] |
金德刚, 常旭, 刘伊克. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 2008, 51(4): 1209-1217. JIN D G, CHANG X, LIU Y K. Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method[J]. Chinese Journal of Geophysics, 2008, 51(4): 1209-1217. DOI:10.3321/j.issn:0001-5733.2008.04.032 |
| [25] |
WAPENAAR K, BROGGINI F, SLOB E, et al. Three-dimensional single-sided Marchenko inverse scattering, data-driven focusing, Green's function retrieval, and their mutual relations[J]. Physical Review Letters, 2013, 110(8): 084301. DOI:10.1103/PhysRevLett.110.084301 |
| [26] |
SLOB E, WAPENAAR K, BROGGINI F, et al. Seismic reflector imaging using internal multiples with Marchenko-type equations[J]. Geophysics, 2014, 79(2): S63-S76. DOI:10.1190/geo2013-0095.1 |
| [27] |
SINGH S, SNIEDER R, BEHURA J, et al. Marchenko imaging: Imaging with primaries, internal multiples, and free-surface multiples[J]. Geophysics, 2015, 80(5): S165-S174. DOI:10.1190/geo2014-0494.1 |
| [28] |
ZHANG L L, SLOB E. Free-surface and internal multiple elimination in one step without adaptive subtraction[J]. Geophysics, 2019, 84(1): A7-A11. DOI:10.1190/geo2018-0548.1 |
| [29] |
ZHANG J F, WANG W H. Multiple attenuation: An approach by incorporating multiple prediction with Radon transform[J]. Journal of Seismic Exploration, 2006, 15(1): 81-99. |
| [30] |
王艳香, 张军舵, 王圣, 等. 分级多域迭代组合压制多次波技术[J]. 天然气地球科学, 2014, 25(2): 243-251. WANG Y X, ZHANG J D, WANG S, et al. Multiple suppression technology using iteration combination in multi-domain step by step method[J]. Natural Gas Geoscience, 2014, 25(2): 243-251. |
| [31] |
曾华会, 王孝, 杨维, 等. 分级组合多次波压制技术——以玛湖地区为例[J]. 石油地球物理勘探, 2018, 53(S2): 13-19. ZENG H H, WANG X, YANG W, et al. Stepped-combination multiples suppression: An example in Mahu area[J]. Oil Geophysical Prospecting, 2018, 53(S2): 13-19. |
| [32] |
SAVA P, GUITTON A. Multiple attenuation in the image space[J]. Geophysics, 2005, 70(1): V10-V20. DOI:10.1190/1.1852789 |
| [33] |
杨金龙, 朱立华. 逆散射级数层间多次波压制方法及其应用[J]. 石油物探, 2018, 57(6): 853-861. YANG J L, ZHU L H. Inverse scattering series internal multiple attenuation method and its application[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 853-861. DOI:10.3969/j.issn.1000-1441.2018.06.007 |
| [34] |
HUO S D, WANG Y H. Improving adaptive subtraction in seismic multiple attenuation[J]. Geophysics, 2009, 74(4): V59-V67. DOI:10.1190/1.3122408 |
| [35] |
HERRMANN F J, WANG D L, VERSCHUUR D J. Adaptive curvelet-domain primary-multiple separation[J]. Geophysics, 2008, 73(3): A17-A21. DOI:10.1190/1.2904986 |
| [36] |
ZHAI Y Z, LIU J, SHENG B, et al. A hybrid crossgather curvelet domain multiple elimination method and its application[J]. Expanded Abstracts of 87th Annual Internat SEG Mtg, 2017, 4752-4757. |
| [37] |
AMARJEET K, RAJIV K, GARY H, et al. Adaptive subtraction using 3D curvelets: A linear optimisation framework[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 4504-4544. |
| [38] |
杨宇. 基于模型的水层多次波消除方法研究[D]. 青岛: 中国石油大学, 2016 YANG Y.The research of model-base water-layer demultiple[D].Qingdao: China University of Petroleum, 2016 |
| [39] |
王通, 王德利, 冯飞, 等. 三维稀疏反演多次波预测及曲波域匹配相减技术[J]. 吉林大学学报(地球科学版), 2017, 47(6): 1865-1874. WANG T, WANG D L, FENG F, et al. Multiple prediction with 3D sparse inversion and curvelet match[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(6): 1865-1874. |




