2. 福建省地震局, 福建福州 530001
2. Fujian Earthquake Agency, Fuzhou 530001, China
实际地球介质所表现出的非弹性、非均匀性、各向异性及多相态特征使得传统的均匀完全弹性介质理论受到严重的挑战。对于地震波在实际介质传播中的衰减特征的理论研究目前主要包括非弹性介质理论、非均匀散射理论和孔隙双相介质理论等。根据影响因素差异, 地震波传播衰减分为非固有衰减和固有衰减。其中, 非固有衰减与地震波传播路径有关, 即常规意义上的几何衰减; 固有衰减与介质的非弹性、含孔隙性及其渗透性、孔隙所含流体的黏性等相关[1], 即传统意义上的黏弹性。由于介质的黏弹性是导致地震波吸收衰减的主要原因, 因此, 黏弹性地震波传播的研究是地震波吸收衰减研究的重要方向之一。
在我国西部黄土塬区、沙漠覆盖区, 油气资源丰富, 近地表介质疏松多孔、弹性差, 从而使得地震波表现为强衰减、高频散、低信噪比、低分辨率的特征[2]; 若进一步考虑到浅表介质孔隙、裂隙发育, 孔隙流体多表现为黏滞性时就需要考虑强衰减模型[3]。因此, 本文在概要回顾黏弹性介质理论发展历程, 分析总结地震波衰减研究进展的基础上, 通过数值模拟分析对比强调了强衰减介质中地震波的衰减特征; 然后讨论了黏弹性理论未来的发展方向, 以期对地震波衰减研究提供一些有益的参考。
1 黏弹性介质模型黏弹性介质的研究始于STOKES[4]在弹性剪切模量上增加黏滞项建立因介质黏弹性而引起波场能量损失的Stokes方程。为了解决弹性理论模拟的脉冲地震记录与实际地震观测的正弦波记录之间明显存在的差异性问题, N.H.瑞克[5]在Stokes黏弹性理论中引入了地震子波的概念, 用Stokes方程取代弹性波动方程来刻画实际地震波的传播规律。
之后, 介质黏滞特征的描述更多是通过本构关系的确定而实现, 目前建立黏弹性本构方程的方法包括器件组合和累积积分两种。Kelvin-Voigt体和Maxwell体是两种最早能代表黏弹性理论发展的线性流变模型[6], 由于器件组合方式不同, 它们刻画介质性质的差异较大, 所以能为黏弹性衰减提供较广的研究范畴。但ZENER[7]研究表明, 这两种线性流变模型无法体现瞬间形变、剩余应变以及蠕变特征, 为此, ZENER等[8]和AKI等[9]先后构建了标准线性固体以克服这两种基本流变模型的缺陷。实际地球介质一般存在许多不同的松弛时间, 在地震频带范围内表现的常Q性是以往建立的黏弹性模型所不能刻画的, 因此多种广义线性固体(如广义Kelvin-Voigt模型(GKB)、广义Maxwell模型(GMB)和广义Zener体(GZB))应运而生。在线性黏弹性介质模型建立的基础上, 采用时间域微分型本构方程或Boltzmann介质理论的积分型本构方程研究介质的黏弹性是最常用的波场模拟研究思路; 而达朗贝尔(D'Alembert)理论则是从运动方程的角度出发, 在弹性介质的运动方程中引入与位移对时间一阶导数相关的阻尼项来研究介质黏弹性对地震波吸收衰减的影响, 该理论相对简单而且比较适用[10]。
一直以来, 黏弹性介质理论的发展都离不开介质非弹性影响因素, 一般情况下, 黏弹性介质中地震波能量损失的解释有两种: ①弹性滞后理论; ②内摩擦理论。这两种理论都可以定性地解释介质的非弹性衰减机理, 前者侧重于介质的剩余应变, 后者强调质点振动的阻尼损耗。在20世纪七八十年代, 一些学者先后对干燥岩石颗粒摩擦作用造成地震波的衰减做了一些计算, 验证了摩擦衰减效应的客观存在[11]。所以, 任何一种考虑非弹性衰减机制的黏弹性模型都有利于实际介质中地震波衰减和频散特征的刻画, 且具有研究意义。
1.1 线性黏弹性介质模型 1.1.1 基本线性黏弹性模型在线性小变形假设条件下, 非弹性应力、应变关系是黏弹性介质理论模型构建的基础。例如, Kelvin-Voigt体是地震勘探中最常用的一种线性黏弹性介质模型, 与建立Stokes方程时所用的模型相似, 它假设由于阻尼器的作用, 在恒定应力作用下Kelvin-Voigt体不会立即产生位移, 应力消失后将表现出应变滞后特征, 从而较好地刻画实际介质的非弹性特征。基于Kelvin-Voigt体, 国内外一些学者[12-16]利用不同数值算法模拟了黏弹性介质中地震波场的传播规律, 较好地印证了高频吸收衰减严重和速度频散现象。
Maxwell体是比Kelvin-Voigt体出现还早的一种线性黏弹性介质模型。它假设在给定应力作用后, 同时产生两类应变, 整体的应变率与应力和应力率线性相关; 施加瞬间应力后, Maxwell体上立即产生弹性形变, 这是Kelvin-Voigt体所不具备的, 而且常应变下应力呈指数衰减。但Maxwell体在发生弹性形变后, 其应变随时间线性增加, 即使在很小应力作用下Maxwell体也会无限变形, 显然不符合实际介质的蠕变特征。
早期有些地质学家利用Maxwell体研究了岩石的结构力学性质, 但由于它刻画介质的相态过于接近流相点, 以至于不能表现出岩石弹性极限的特征[17]。对于一些品质差的介质, 如海底沉积物, 需要利用Maxwell体的流变性刻画地震波的衰减机理, 不然将会弱化介质的衰减作用。在Maxwell体基础上, EMMERICH等[18]建立了广义Maxwell体, 并根据其流变特征推导出黏弹性模量的有理式; KRISTEK等[19]在广义Maxwell体的基础上使线性黏弹性模型的研究更具一般性。
1.1.2 标准线性黏弹性模型由于Maxwell体和Kelvin-Voigt体都存在固有缺陷, 不足以描述一般黏弹性介质, 于是人们发展出标准线性固体——“三元体”黏弹性介质模型。标准线性固体有两种等效形式, 一种是Maxwell体并联弹性体, 另一种是Kelvin-Voigt体串联弹性体, 二者的应力、应变关系完全一致[20]。标准线性固体蠕变和松弛的时变特征与实际基本相符, 可以有效克服Maxwell体和Kelvin-Voigt体的缺陷, 并保留二者的优点。
一些岩石物理实验表明, 在地震频带范围内, 介质的Q值几乎不随频率变化[21]。标准线性固体虽具一般性, 但也很难精准地刻画介质的常Q特征, 于是人们将标准线性固体组合发展出广义线性体。在构建方式上, 广义线性体是由许多Kelvin-Voigt体和(或)Maxwell体串联和(或)并联构成的一个总系统。作为系统性模型, 它能充分地考虑实际介质存在不同松弛时间的性质[22]。DAY等[23]利用Padé展开将黏弹性介质本构方程中的褶积形式转变为差分形式, 推动了广义线性固体理论的发展, 但这项研究对存储和计算的要求较高。之后, EMMERICH等[18]将系列Maxwell体并联建立了广义Maxwell模型(GMB), 并基于这种模型提出了能确定黏弹性模量有理近似函数的系数, 同时赋予其物理意义。此外, CARCIONE等[10]建立了广义Zener体(GZB), 并在此基础上发展了黏弹性介质的应力可由松弛函数与应变率褶积表示的理论。这项理论促进了多种各向同性和各向异性黏弹性介质波动方程的快速建立; 研究在此基础上的黏弹性地震波衰减发现, 具有频率依赖性的黏弹性模量是地震波耗散的主要原因。
广义标准线性体提出之后, 围绕GMB和GZB模型开展了大量的对比研究。EMMERICH等[18]、FÄH[24]和MOCZO等[25]对GMB理论公式进行了研究; 在随后几年里, MOCZO等[26]利用有限元、有限元与有限差分混合法模拟了GMB介质中的波场情况, 还定义了与位移分量相关的记忆变量; XU等[27]给出了复合记忆变量的概念, 但与之前提出的记忆变量区别甚微。GZB介质的黏滞衰减特征研究最先由LIU等[28]开展, ROBERTSSON等[29]基于GZB介质的流变机制, 利用有限差分交错网格法对速度-应力公式进行计算。众多学者在研究GZB和GMB这两种广义线性体时, 一般遵循研究一种流变机制而忽略另一种的思路, 所以常常造成难以确定两者关系的局面。直至MOCZO等[30]对比分析了GZB和GMB的流变机制后, 才发现它们未简化的松弛函数和流变机制均是一致的。CAO等[31]具体证明了广义标准线性体的一致性, 并重新定义记忆比变量, 统一两种广义线性体的波动方程。
1.1.3 品质因子与线性流变模型衰减机理黏弹性介质中地震波传播理论的研究初衷是反演地下介质的衰减特征。品质因子Q是描述介质衰减能力的重要参数, 可以反映地震波受地层吸收作用后不同频率成分能量的变化, 所以厘定地球介质的Q值分布将有利于后续的地震波能量补偿、消除大地滤波效应等工作的顺利进行。
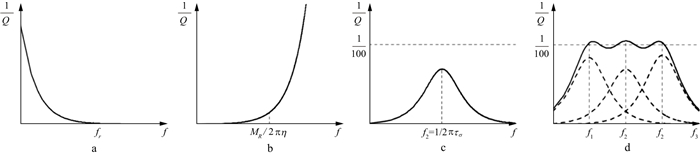
Maxwell体、Kelvin-Voigt体及标准线性固体等线性流变模型的本构关系不同, 对介质黏滞衰减的描述差异较大。在广义线性固体品质特征的研究中, 由于未松弛模量与地震波的传播速度直接相关, 而且非弹性系数取决于介质品质特征, KRISTEK等[19]定义了与介质性质无关的非弹性函数, 并利用未松弛模量重构黏弹性模量和松弛函数的公式。根据Maxwell体、Kelvin-Voigt体、标准线性体及广义线性体黏弹性模量的具体表达, 本文基于数值计算分析了各模型介质的品质特征和适用范围, 如图 1所示。
|
图 1 Maxwell体(a)、Kelvin-Voigt体(b)、标准线性(c)及广义线性体(d)逆品质因子随频率变化曲线 图中, fr、MR、η、τσ分别是松弛频率、松弛模量、黏滞系数和应力松弛时间。 |
图 1a和图 1b直观反映了Maxwell介质和Kelvin-Voigt介质相反的衰减特征, 符合这两种黏弹性模型所刻画介质的相态: 一种接近“流态”, 而另一种接近“固态”。图 1c和图 1d中的衰减曲线都是在Q=100、非弹性系数由品质因子公式直接求解的条件下计算而得, 而且本文采用的广义线性体由3个松弛频率分别为f1=0.1Hz, f2=1.0Hz, f3=10.0Hz的标准线性固体并联而成。从图 1c中可以清楚地看到, 介质的衰减作用在松弛频率处最强, 当频率趋于0或无穷大时, 介质表现出弹性性质。图 1d中的实线和虚线分别为广义线性体和3种标准线性体的衰减曲线, 对比曲线特征可看出, 在地震频率范围内广义线性体介质的衰减特征稳定, 而标准线性体则取决于介质的松弛频率。
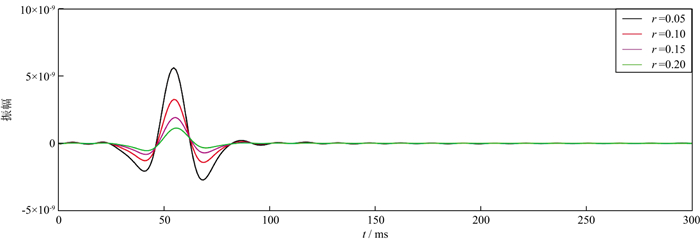
1.2 达朗贝尔(D'Alembert)模型相比于线性流变模型利用器件组合确定本构关系来描述介质的黏弹性, 达朗贝尔模型理论则认为介质质点在振动过程中受到的摩擦阻力与振动速度成正比, 于是直接在运动方程中加入黏滞特征项[10]。达朗贝尔介质“嵌入”黏滞力之后导致地震波发生非弹性吸收衰减, 如图 2所示, 黏滞力的存在如阻尼器一般损耗着介质质点振动的机械能。
|
图 2 达朗贝尔介质中不同黏滞系数(r)下单道地震记录 |
作为一种各向同性黏弹性介质模型, 达朗贝尔模型虽不如线性流变模型使用普遍, 但也是处理介质黏弹性问题的有效途径, 而且模型简单、有效。王美霞[32]和张金波等[33]分别计算出达朗贝尔波动方程的保辛算法解和间断有限元算法解, 并模拟黏弹介质中的波场特征; 对比分析不同耗散机制下地震波的衰减情况可知, 达朗贝尔模型基于运动方程考虑地球介质内流体与岩石颗粒之间的摩擦作用在刻画介质黏滞性方面是可行的。
黏弹性介质的研究在于波函数的求解, 达朗贝尔波函数是由与频率相关的复振幅函数和复相位函数组成, 确定这些函数后可以通过介质的品质因子刻画地震波的衰减特征。但是, 达朗贝尔模型所考虑的黏滞因素对纵、横波衰减的影响几乎相同, 这与直接在运动方程中增加黏滞项密切相关。因此, 鉴于通过运动方程研究介质黏滞衰减的有效性和便捷性, 弥补达朗贝尔模型缺陷, 改善黏弹性模型机制的意义重大。
2 复杂地震波非弹性吸收衰减介质理论 2.1 黏弹孔隙介质理论含流体孔隙介质的研究始于Gassmann提出的流体替换理论和所建立的Gassmann方程, 通过Gassmann方程可由矿物颗粒体积模量、干岩石体积模量及孔隙度等参数估计流体饱和岩石的体积模量。之后, 研究人员更多地认为造成流体孔隙介质中地震波衰减和频散特征的主要原因是流体流动机制, 于是根据流动特征尺度将流体流动分为宏观流动、微观流动和介观流动3种。在Gassmann方程的基础上发展出的Biot宏观流动理论则认为, 全局流体流动与岩石骨架间的相互作用是引起地震波损耗的主要机制, 但它却局限于超高频范围的地震波。MAVKO等[34]通过岩石物理实验提出微观喷射流理论, 但裂缝中流体的喷射作用仅是一定程度的耗散机制, 不能完全描述实际孔隙介质的衰减特征。因此, DVORKIN等[35]综合两种流动机制建立BISQ(Biot-Squirt)模型, 弥补以上两种模型的缺陷。
黏弹性介质理论和含流体孔隙介质理论在研究波场衰减时都各具缺陷, 若单独考虑介质黏弹性往往会忽略复杂孔隙结构和流体流动机制的影响, 而仅考虑含流体孔隙机制则不能准确地揭示固体骨架的黏滞衰减规律。CHENG等[36]指出, 对于含流体孔隙介质而言, 引起低频地震波频散和衰减的原因是岩石的黏弹性而非流体流动机制, 于是给出了与频率相关的描述岩石骨架黏滞性的黏弹性参数表达式, 并应用到BISQ波动方程中。与BISQ模型数值模拟结果相比, 黏弹性BISQ模型在描述孔隙介质(如扩张型各向异性(EDA)介质)中地震波的强衰减和高频散方面更有效, 尤其低频范围地震波衰减特征的刻画更真实。
在大多数流体孔隙介质的研究中, 一些地球物理学家致力于建立岩石物性参数与地震波传播速度及衰减之间的关系, 但NIE等[37]研究发现以上岩石物理模型和理论公式不能完整地预测大渗透范围内含泥质砂岩中地震波的衰减和频散性质, 尤其强衰减和高频散特征。于是, 他们应用微分型广义黏弹性本构关系描述孔隙介质固体骨架的应力、应变关系, 建立黏弹性BISQ模型, 并定义一个由渗透率和泥质含量控制的黏弹性参数修正因子。这种黏弹性BISQ模型能适用于更广渗透率范围(κ>0.05mD, 1mD≈0.987×10-3μm2)的含泥质砂岩衰减特征的研究。除了渗透率对流体孔隙介质中地震波衰减的影响明显, 饱和度也是用于研究固体骨架内所含软性杂质耗散性的关键因素。由于经典的Biot和BISQ理论都没有考虑饱和度的概念, 所以它们仅适用于饱和流体孔隙介质的情况, 对于一般情况如石油勘探中寻找剩余油是比较局限的。NIE等[38]利用线性Kelvin-Voigt体的本构方程描述BISQ模型固体骨架中应力与应变间的关系, 并通过引入饱和度概念建立能刻画一般流体孔隙介质中地震波传播响应的黏弹性介质模型。
对于一个完整的流体饱和岩石系统, 其体积模量在一定地震频率范围(10-2~106Hz)内一般有两次改变: ①岩石由松弛状态到未松弛状态; ②岩石由饱和状态到干燥状态。这两种状态的改变分别由岩石的黏弹性和孔隙流体流动所致, 均能引起地震波的衰减和频散特征[39]。凌云等[40]将线性Zener体的本构关系引入到BISQ模型中, 建立黏弹孔隙介质模型来描述以上两种岩石状态的变化。在这种黏弹性孔隙介质中, 岩石体积模量的两种改变分别由Zener特征频率和BISQ特征频率控制, 通过调整特征频率值可以研究不同类型储层介质中地震波的衰减和频散特征。
2.2 黏弹各向异性介质理论随着地震勘探工作的深入, 许多研究表明地下介质的物性参数在方向上存在差异, 尤其是充填流体的裂隙介质中的地震波, 不仅传播速度表现出各向异性, 而且非弹性衰减也具有各向异性, 并对裂缝的敏感性极强[41]。所以在精准预测地下波场衰减信息方面介质黏弹性和各向异性的考虑尤为重要, 油气勘探和开发更离不开黏弹各向异性介质理论的支撑。
描述介质黏弹各向异性的最一般模型是CHRISTENSEN[42]给出的等温黏弹各向异性本构关系, 之后CARCIONE[43]结合广义线性固体黏弹性机制构建出黏弹各向异性本构关系, 并建立与时间有关的松弛矩阵。CARCIONE建立的介质理论认为, 地震波的吸收衰减取决于介质的大量耗散机制, 每一种耗散机制均由黏弹性本构关系表示。在经过一些岩石物理实验之后, MAULTZSCH等[44]建立了品质因子与相角的关系式, 而且PRASAD等[45]发现了孔隙流体与方向应力都会引起介质衰减各向异性的现象; LIU等[46]利用VSP技术研究与方位角有关的介质衰减各向异性。为了进一步描述黏弹各向异性介质的衰减特征, ZHU等[47]在均匀常Q介质的假设条件下, 提出了与速度各向异性参数有函数关系且相似的衰减各向异性参数。早期国内对介质各向异性的研究主要针对与裂缝有关的问题, 那时侧重于研究地震波传播速度的各向异性, 而对介质的衰减和品质因子各向异性的研究较少。张中杰等[48]曾建立了考虑非弹性效应的EDA介质波动方程组, 基于平面波传播假设模拟了裂缝介质中地震波的频散和衰减特征。
裂缝方位和裂缝密度是刻画地层裂缝发育状况的关键因素[49], 并直接影响油气勘探效果。一般实际地震勘探中的测线非平行, 也非垂直于裂缝面, 所以需要对具任意方位角的各向异性介质展开研究; 基于同时具有任意方位角和水平对称轴的横向各向同性介质(AHTI)的黏弹性本构关系, 利用平面简谐波假设下的Christoffel方程正演分析介质的衰减特征也应运而生[50]。为解决裂缝检测中面临的确定裂缝相关参数与地震波场传播之间的定量关系这一难题, 杜启振等[51]在CARCIONE研究[43]的基础上建立了以位移场表示具任意方位角的黏弹各向异性介质的波动方程。该方程以裂缝的主轴作为其中的一个主要参数, 能定量地描述黏弹波场特征与裂缝走向之间的关系, 因此可以根据裂缝走向选择打井方式, 提高采收率。严红勇等[52]也在CARCIONE的研究基础上给出了观测坐标系下以任意方位角和倾角为参数的倾斜横向各向同性介质(TTI)的本构方程; 模拟发现波场中会出现横波分裂现象因此变得极为复杂, 地震记录中的同相轴也不再呈对称的双曲线型, 而且介质的黏滞性会严重地衰减地震波能量, 并造成波形畸变。
在地震勘探中, 储层中的流体对地震波的传播影响重大, 除了岩石中的裂隙等结构能造成储层介质的各向异性, 研究人员根据一些岩石物理实验发现裂缝空间内的流体也是造成介质衰减各向异性的主要原因[53]。而且实际地下岩石中常含有泥质及封闭流体等软物质, 它们对岩石骨架起到软化黏滞作用, 故需要用黏弹性本构方程来描述流体孔隙各向异性介质的应力与应变关系。聂建新等[54]综合考虑孔隙流体的宏观流动和微观喷射两种流动机制、岩石骨架黏弹各向异性及泥质含量, 并引入黏弹各向异性修正因子来探究含泥质的孔隙各向异性黏弹性介质中的波场衰减和频散特征。
薄储层如薄碳酸盐岩或致密砂岩层等是我国储层预测的难点, 若以黏弹各向异性介质作为实际地下介质模型, 可以有效描述薄层沉积、定向裂缝等结构引起的各向异性, 以及孔隙或裂缝流体充填等因素引起的非弹性。因此探究衰减及其各向异性所导致的地震动力学或运动学异常, 可以有效解决薄层反射问题; 郭智奇[55]基于黏弹各向异性基本理论推导了黏弹各向异性介质波动方程, 系统地研究了地震波在黏弹各向异性分界面及薄(互)层的反射、透射等问题。在前人对黏弹各向异性介质地震波AVO特征的研究背景下, 杨春颖等[56]分析对比了不同模型介质条件下PP波和PS波的反射特征, 研究发现, 黏弹各向异性因素对薄层振幅的影响强于速度各向异性, 单频振幅曲线的极值点振幅和极值点位置对黏弹各向异性薄层预测具有指导作用。综合考虑介质的黏弹性和各向异性, 杜启振等[57]、刘财等[58]和李桂华等[59]分别采用不同数值方法实现了黏弹各向异性波场的模拟, 印证了“高频强衰减”和“波面尖角”等诸多衰减各向异性地震波传播特征的存在, 为借助波场衰减的各向异性信息预测地层裂缝发育状况及流体性质提供了重要参考[60]。
3 波场强衰减理论探究 3.1 强衰减介质近地表介质由于长期受风化、剥蚀等自然外力作用, 相对于深层岩石常表现出疏松多孔、结构复杂、干燥、密度低、速度低等特点[61], 而且介质具有严重的非弹性特征。例如黄土塬近地表疏松黄土层厚度为50~300m、潜水面深80~150m。相对于深层介质中地震波因球面扩散及界面因素造成的衰减, 近地表介质的衰减作用突出体现在: ①介质岩性突变严重, 地表起伏及介质非均匀性强, 横向物理性质不连续, 散射作用明显; ②介质非弹性强, 对地震波吸收衰减严重, 使深层波场信息变得模糊失真[62]。近地表介质复杂的衰减机理是油气勘探所面临的主要问题之一, 强吸收衰减更与介质的黏滞性相关。不少学者[63-66]在近地表介质波场衰减规律、Q值估计、衰减补偿等方面做了很多工作, 但还需要综合考虑如介质孔隙特征、流体黏性以及固体骨架各向异性等影响因素, 从而更真实地揭示近地表介质的强衰减特征, 并实现高分辨勘探工作的目标。
稠油是目前油气地震勘探的主要目标之一。谢祥等[67]发现AVO技术尽管在气层和轻质油层识别上相对成熟, 但由于稠油层与水层密度相差不大, 故在稠油识别方面效果不佳; 研究发现储层孔隙度是影响稠油AVO特征的重要因素之一。一般情况下稠油流体黏度高达100~1000mPa·s, 其黏度值约为水的几百至几千倍或轻质油的几十倍, 故稠油与岩石颗粒之间存在明显的黏滞摩擦作用。由Biot基本思想可知, 流体与岩石骨架之间的相对作用是波场衰减的重要机制, 稠油的黏滞力过大必然会严重衰减地震波的能量。因此, 根据波场衰减信息分析稠油储层介质的黏弹性、孔隙度以及流体黏度等因素的影响, 研究波场强衰减性将利于稠油预测。
天然气水合物是天然气与水分子在一定温度、压力条件下形成的结晶固体物质[68]。它一般存储在海底300~500m厚度的浅层未固结砂泥岩互层结构的高孔隙度砂岩中, 因此介质的孔隙度、渗透率、泥质含量、流体的黏度以及饱和度等都是关系水合物储层地震波场衰减的重要物理因素。目前, 水合物层及其底部游离天然气层的衰减机制是一项研究热点, 勾丽敏等[69]在总结海洋水合物地震技术的研究进展中指出, 近十年国内外一些学者根据VSP和全波列测井资料发现真正起强衰减作用的是下伏含游离气层, 水合物储层的衰减能力较弱。但对于高达70%孔隙度的海底浅部沉积地层, 这一论断显然有值得进一步探究的必要。所以, 在黏弹性理论和孔隙双相介质理论的研究背景下, 研究海底水合物储层的衰减机制, 并通过波场衰减异常预测水合物的赋存情况是值得探索的。
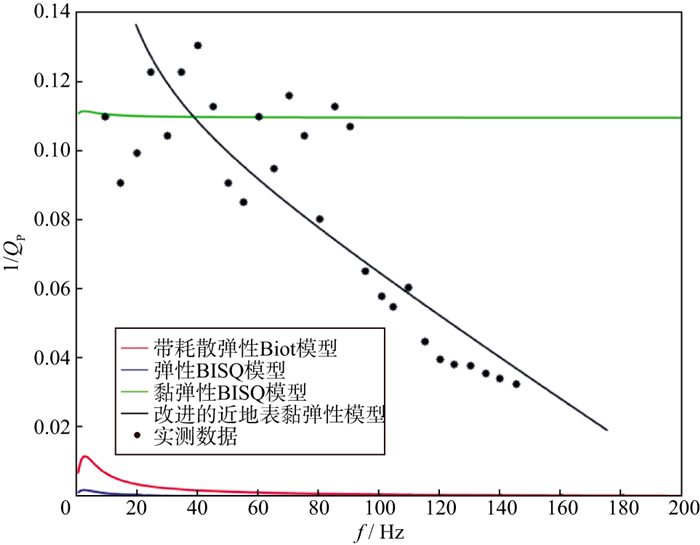
3.2 强衰减模型及频率-空间域波场特征分析强衰减模型是谢佩瑜等[70]应用Biot基本思想重新定义耗散系数, 并利用运动方程描述非常规油气储层近地表介质强吸收衰减特征的黏弹性介质模型。如图 3所示, 由于强衰减模型综合考虑了孔隙度、流体黏度及介质黏弹性等物理因素, 所以在预测波场衰减规律方面较一般的黏弹性介质和黏弹孔隙双相介质更简便、有效。强衰减模型波动方程具体如下:
|
图 3 不同模型纵波衰减值(1/QP)与实际数据对比[70] |
| $\rho \ddot{u}+\tilde{\eta} \dot{u}=\mu^{*} \nabla^{2} \boldsymbol{u}+\left(\lambda^{*}+\mu^{*}\right) \nabla(\nabla \cdot \boldsymbol{u})$ | (1) |
式中: ρ为介质密度; u为位移向量;
| $\lambda^{*}=\lambda^{\prime}+\mathrm{i} \lambda^{\prime \prime} \\ \lambda^{\prime}=\lambda_{0}\left(1+\frac{\tan \delta}{\pi} \ln \frac{\omega}{\omega_{0}}\right) \\ \lambda^{\prime \prime}=\lambda^{\prime} \tan \delta \\ \mu^{*}=\mu^{\prime}+\mathrm{i} \mu^{\prime \prime} \\ \mu^{\prime}=\mu_{0}\left(1+\frac{\tan \delta}{\pi \pi} \ln \frac{\omega}{\omega_{0}}\right) \\ \mu^{\prime \prime}=\mu^{\prime} \tan \delta$ | (2) |
其中, λ0和μ0是弹性拉梅系数, ω0是基准频率, tanδ是黏弹性参数。对于强衰减介质YANG等[71]定义了线性黏弹性参数表达式:
| $\tan \delta=\frac{\tan \delta_{2}-\tan \delta_{1}}{\omega_{2}-\omega_{1}}\left(\omega-\omega_{1}\right)+\tan \delta_{1}$ | (3) |
式中: tanδ2, tanδ1分别是最高频率ω2和最低频率ω1对应的黏弹性参数。
考虑波动方程中包含的黏弹性参数是与频率相关的复数型参数, 本文采用频率-空间域25点有限差分算法, 并根据表 1中实测近地表介质的物性参数, 进行二维均匀各向同性介质的波场模拟, 来分析不同频率下的波场衰减特征。模型大小为100×100网格, PML层厚为25个网格, 网格间距为2m, 时间采样间隔为1ms, 采样点数为1024, 频率间隔为0.976Hz, 地震子波为雷克子波, 主频为25Hz, 震源于模型中心激发。
| 表 1 近地表均匀各向同性介质模型物性参数 |
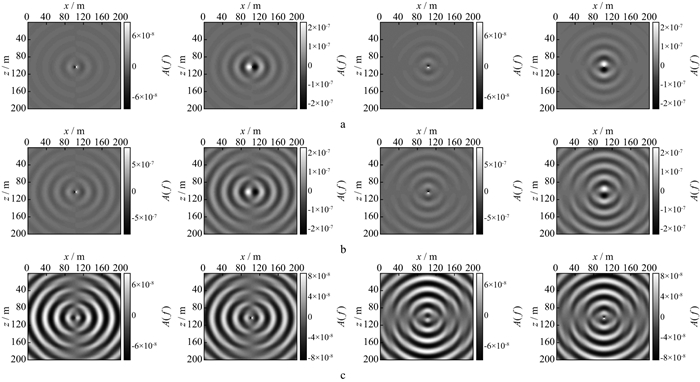
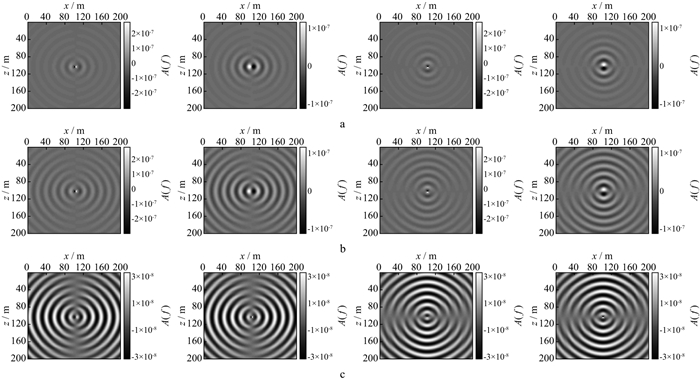
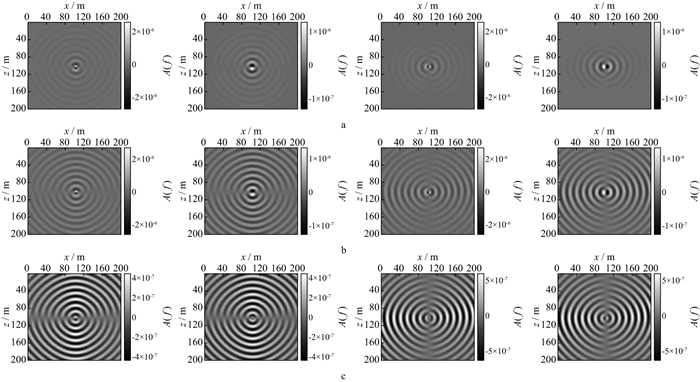
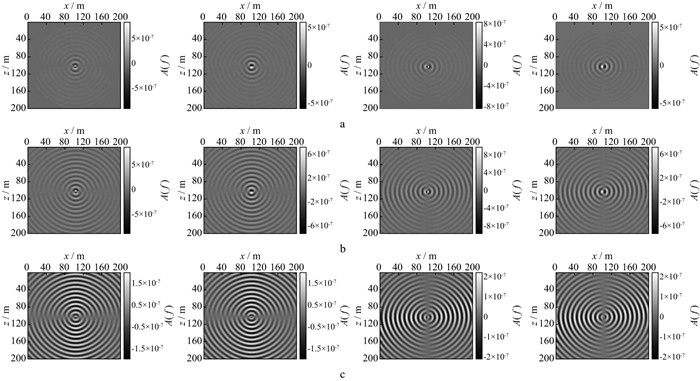
图 4至图 7分别给出了强衰减和完全弹性机制下34.18Hz和48.83Hz时的纵、横波单频切片及两种机制的差值。单频切片反映某一频率所有时刻的波场信息, 切片中同心圆的疏密程度与波长大小相关, 即高频切片中波峰与波谷的间隔小, 相同频率下横波切片同心圆分布较密。对比图 4至图 7中的信息可见, 强衰减单频切片较完全弹性单频切片而言, 同心圆轨迹变得模糊不清, 尤其传播时间长的波场信息几乎消失; 而且图 4c至图 7c中有关衰减部分的单频切片能量强, 相邻时间的波场信息完整。由此可知, 疏松多孔且弹性差的近地表介质对地震波各频率成分的能量吸收衰减严重, 若没有合理的补偿机制将难以判断深层波场信息。
|
图 4 不同条件下34.18Hz单频切片(纵波源)(从左至右依次为: 水平分量实部、虚部, 垂直分量实部、虚部) a强衰减单频切片; b完全弹性单频切片; c差值单频切片 |
|
图 5 不同条件下48.83Hz单频切片(纵波源)(从左至右依次为: 水平分量实部、虚部, 垂直分量实部、虚部) a强衰减单频切片; b完全弹性单频切片; c差值单频切片 |
|
图 6 不同条件下34.18Hz单频切片(横波源)(从左至右依次为: 水平分量实部、虚部, 垂直分量实部、虚部) a强衰减单频切片; b完全弹性单频切片; c差值单频切片 |
|
图 7 不同条件下48.83Hz单频切片(横波源)(从左至右依次为: 水平分量实部、虚部, 垂直分量实部、虚部) a强衰减单频切片; b完全弹性单频切片; c差值单频切片 |
介质黏弹性作为一种最重要的地震波吸收衰减机制, 国内外专家开展了大量关于黏弹性介质模型、正演模拟以及黏弹性衰减的理论探究, 综合调研与分析可以得出如下结论。
1) 实际地下介质比想象的复杂, 其对地震波的衰减机制更是多样, 黏弹性、孔隙度以及流体都有可能不同程度地造成地震波的频散和衰减, 所以建立适用于复杂介质的一般性黏弹孔隙介质模型是未来重要的研究方向。
2) 虽然已有学者建立并研究了黏弹孔隙介质模型, 但是基于线性流变模型的局限性和孔隙结构、流体流动机制的复杂性等的考虑首先需要开展一定的岩石物理实验。这种实验不仅要考虑地质环境、孔隙结构、孔隙中流体性质等对结果的影响, 更要探究岩石各向异性和骨架黏滞性的影响, 只有这样才能全面地掌握波的衰减与介质参数的关系, 建立逼近实际介质的模型并应用于地震反演。
3) 基于运动方程研究介质的黏弹性是值得考虑的, 它可以更多地避免广义线性体复杂器件组合和计算量需求大等问题, 所以, 这就需要剖析达朗贝尔模型问题的根本所在, 确定是否需要从介质性质本身出发对此进行改善。目前已有的强衰减模型是达朗贝尔模型的改进, 它较全面地考虑各种影响波场衰减的物理因素, 所以对此展开全面性的数值模拟, 并研究各种因素的强衰减机理以及建立强衰减补偿理论对油气勘探极具意义。
4) 鉴于介质的黏滞性对纵、横波的衰减机制存在差异, 介质的复杂性以及纵、横波对流体的响应差异, 需要从多分量地震、多波综合利用和更复杂的Q各向异性研究的角度考虑地震波传播的衰减特征, 从而提高对地震波衰减机制的理解和应用。
黏弹性介质理论发展至今已比较成熟, 但在论述中不难发现仍有一些问题值得思考, 例如: 多种黏弹性模型衰减机制不统一, 在波场信息利用方面存在多样性; 达朗贝尔模型从运动方程角度研究介质的黏滞性, 但是它却存在两种固有的缺陷, 即纵横波的黏滞衰减性质相同和黏滞系数物理意义不明确。本文模拟的强衰减模型初步综合考虑了多种介质因素对地震波衰减的影响。由模拟结果可知, 黏弹性和孔隙双相性都是造成地震波固有衰减的关键因素, 强衰减模型从介质本身的物理性质出发定义了地震波的耗散系数, 在近地表介质强衰减特征刻画方面更具有效性。而且, 从稠油层和海底游离气层强衰减物理特征的总结上来看, 若将强衰减模型应用到稠油层和海底游离气层波场衰减规律的研究中, 有可能实现更高分辨率的探测和流体识别。
| [1] |
牛滨华, 孙春岩. 地震波理论研究进展——介质模型与地震波传播[J]. 地球物理学进展, 2004, 19(2): 255-263. NIU B H, SUN C Y. Developing theory of propagation of seismic waves——medium model and propagation of seismic waves[J]. Progress in Geophysics, 2004, 19(2): 255-263. DOI:10.3969/j.issn.1004-2903.2004.02.008 |
| [2] |
宋吉杰, 禹金营, 王成, 等. 近地表介质Q估计及其在塔河北部油田的应用[J]. 石油物探, 2018, 57(3): 436-442. SONG J J, YU J Y, WANG C, et al. Q estimation for near-surface media and its application in the Northern Tahe Oilfield, China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 436-442. DOI:10.3969/j.issn.1000-1441.2018.03.013 |
| [3] |
李红梅. 基于孔隙粘弹性介质的AVO正演模拟及衰减分析[J]. 石油物探, 2013, 52(5): 464-474. LI H M. AVO forward modeling and attenuation analysis based on porous viscoelastic media[J]. Geophysical Prospecting for Petroleum, 2013, 52(5): 464-474. DOI:10.3969/j.issn.1000-1441.2013.05.004 |
| [4] |
STOKES G G. On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids[J]. Mathematical and Physical Papers, 2009, 1845(1): 75-129. |
| [5] |
N.H. 瑞克. 粘弹性介质中的地震波[M]. 许云, 译. 北京: 地质出版社, 1981: 1-220 RICKER N H.Transient waves in viscoelastic media[M].Xu Y, translator.Beijing: Geological Press, 1981: 1-220 |
| [6] |
汪勇, 段焱文, 王婷, 等. 近似解析离散化方法的粘弹声波方程数值模拟及波场特征分析[J]. 石油物探, 2017, 56(3): 362-372. WANG Y, DUAN Y W, WANG T, et al. Numerical simulation and the wave field characteristics analysis of viscoelastic acoustic wave equation based on the nearly-analytic discrete method[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 362-372. DOI:10.3969/j.issn.1000-1441.2017.03.006 |
| [7] |
ZENER C M. Elasticity and anelasticity of metals[M]. Chicago: University of Chicago Press, 1948: 1-170.
|
| [8] |
ZENER C M, SIEGEL S. Elasticity and anelasticity of metals[J]. The Journal of Physical Chemistry, 1949, 53(9): 1468-1468. DOI:10.1021/j150474a017 |
| [9] |
AKI K, RICHARDS P G. Quantitative seismology: Theory and methods[M]. New York: W H Freeman and Company, 1980: 1-932.
|
| [10] |
CARCIONE J M, KOSLOFF D, KOSLOFF R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 93(2): 393-401. DOI:10.1111/j.1365-246X.1988.tb02010.x |
| [11] |
牛滨华, 孙春岩. 黏弹性介质与地震波传播[M]. 北京: 地质出版社, 2007: 1-221. NIU B H, SUN C Y. Viscoelastic media and seismic wave propagation[M]. Beijing: Geological Press, 2007: 1-221. |
| [12] |
ČERVENÝ V, PŠENČÍK I. Time-averaged and time-dependent energy-related quantities of harmonic waves in inhomogeneous viscoelastic anisotropic media[J]. Geophysical Journal International, 2007, 170(3): 1253-1261. DOI:10.1111/j.1365-246X.2007.03476.x |
| [13] |
CARCIONE J M, POLETTO F, GEI D. 3-D wave simulation in anelastic media using the Kelvin-Voigt constitutive equation[J]. Journal of Computational Physics, 2004, 196(1): 282-297. DOI:10.1016/j.jcp.2003.10.024 |
| [14] |
刘财, 张智, 邵志刚, 等. 线性粘弹体中地震波场伪谱法模拟技术[J]. 地球物理学进展, 2005, 20(3): 640-644. LIU C, ZHANG Z, SHAO Z G, et al. Pseudospectral forward modeling of seismic wave in linear viscoelasic solid[J]. Progress in Geophysics, 2005, 20(3): 640-644. DOI:10.3969/j.issn.1004-2903.2005.03.010 |
| [15] |
单启铜, 乐友喜. PML边界条件下二维粘弹性介质波场模拟[J]. 石油物探, 2007, 46(2): 126-130. SHAN Q T, LE Y S. Wavefield simulation of 2-D viscoelastic medium in perfectly matched layer boundary[J]. Geophysical Prospecting for Petroleum, 2007, 46(2): 126-130. DOI:10.3969/j.issn.1000-1441.2007.02.005 |
| [16] |
严红勇, 刘洋. Kelvin-Voigt黏弹性介质地震波场数值模拟与衰减特征[J]. 物探与化探, 2012, 36(5): 806-812. YAN H Y, LIU Y. Numerical modeling and attenuation characteristics of seismic wavefield in Kelvin-Voigt viscoelastic media[J]. Geophysical and Geochemical Exploration, 2012, 36(5): 806-812. |
| [17] |
刘瑞珣. 流变学基础模型的地质应用及启示[J]. 地学前缘, 2007, 14(4): 61-65. LIU R X. Significance of a basic rheological model in geology and its application[J]. Earth Science Frontiers, 2007, 14(4): 61-65. DOI:10.3321/j.issn:1005-2321.2007.04.006 |
| [18] |
EMMERICH H, KORN M. Incorporation of attenuation into time-domain computations of seismic wave fields[J]. Geophysics, 1987, 52(9): 1252-1264. DOI:10.1190/1.1442386 |
| [19] |
KRISTEK J, MOCZO P. Seismic-wave propagation in viscoelastic media with material discontinuities: A 3D fourth-order staggered-grid finite-difference modeling[J]. Bulletin of the Seismological Society of America, 2003, 93(5): 2273-2280. DOI:10.1785/0120030023 |
| [20] |
孙成禹. 地震波理论与方法[M]. 东营: 中国石油大学出版社, 2007: 1-265. SUN C Y. Theory and method of seismic waves[M]. Dongying: China University of Petroleum Press, 2007: 1-265. |
| [21] |
孙成禹, 肖云飞, 印兴耀, 等. 黏弹介质波动方程有限差分解的稳定性研究[J]. 地震学报, 2010, 32(2): 147-156. SUN C Y, XIAO Y F, YIN X Y, et al. Study on the stability of finite difference solution of viscoelastic wave equations[J]. Acta Seismologica Sinica, 2010, 32(2): 147-156. |
| [22] |
常晓伟, 曹丹平, 梁锴, 等. 基于高阶广义标准线性体模型的三维黏弹性介质弹性波正演模拟[J]. 地球物理学进展, 2019, 34(3): 1010-1016. CHANG X W, CAO D P, LIANG K, et al. Forward modeling of elastic wave in 3D viscoelastic medium based on high order generalized standard linear body model[J]. Progress in Geophysics, 2019, 34(3): 1010-1016. |
| [23] |
DAY S M, MINSTER J B. Numerical simulation of attenuated wavefields using a Padé approximant method[J]. Geophysical Journal International, 1984, 78(1): 105-118. DOI:10.1111/j.1365-246X.1984.tb06474.x |
| [24] |
FÄH D.A hybrid technique for the estimation of strong ground motion in sedimentary basins[D].Switzerland: ETH Zurich, 1992
|
| [25] |
MOCZO P, BARD P Y. Wave diffraction, amplification and differential motion near strong lateral discontinuities[J]. Bulletin of the Seismological Society of America, 1993, 83(1): 85-106. |
| [26] |
MOCZO P, KRISTEK J, HALADA L. The finite-difference method for seismologists: An introduction[M]. Bratislava: Comenius University, 2004: 1-161.
|
| [27] |
XU T, MCMECHAN G A. Composite memory variables for viscoelastic synthetic seismograms[J]. Geophysical Journal International, 1995, 121(2): 634-639. DOI:10.1111/j.1365-246X.1995.tb05738.x |
| [28] |
LIU H P, ANDERSON D L, KANAMORI H. Velocity dispersion due to anelasticity; implications for seismology and mantle composition[J]. Geophysical Journal International, 1976, 47(1): 41-58. DOI:10.1111/j.1365-246X.1976.tb01261.x |
| [29] |
ROBERTSSON J O A, BLANCH J O, SYMES W W. Viscoelastic finite-difference modeling[J]. Geophysics, 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
| [30] |
MOCZO P, KRISTEK J. On the rheological models used for time-domain methods of seismic wave propagation[J]. Geophysical Research Letters, 2005, 32(1): L01306. |
| [31] |
CAO D P, YIN X Y. Equivalence relations of generalized rheological models for viscoelastic seismic-wave modeling[J]. Bulletin of the Seismological Society of America, 2014, 104(1): 260-268. DOI:10.1785/0120130158 |
| [32] |
王美霞. 双相及黏弹性介质中波传播方程的保辛算法及其波场模拟[D]. 北京: 清华大学, 2012 WANG M X.Symplectic stereomodelling method for wave equations in two-phase and viscoelastic media and its numerical simulations[D].Beijing: Tsinghua University, 2012 |
| [33] |
张金波, 杨顶辉, 贺茜君, 等. 求解双相和黏弹性介质波传播方程的间断有限元方法及其波场模拟[J]. 地球物理学报, 2018, 61(3): 926-937. ZHANG J B, YANG D H, HE Q J, et al. Discontinuous galerkin method for solving wave equations in two-phase and viscoelastic media[J]. Chinese Journal of Geophysics, 2018, 61(3): 926-937. |
| [34] |
MAVKO G, NUR A. Melt squirt in the asthenosphere[J]. Journal of Geophysical Research, 1975, 80(11): 1444-1448. DOI:10.1029/JB080i011p01444 |
| [35] |
DVORKIN J, NUR A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms[J]. Geophysics, 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [36] |
CHENG Y F, YANG D H, YANG H Z. Biot/Squirt model in viscoelastic porous media[J]. Chinese Physic Letters, 2002, 19(3): 445-448. DOI:10.1088/0256-307X/19/3/348 |
| [37] |
NIE J X, YANG D H, YANG H Z. A generalized viscoelastic Biot/Squirt model for clay-bearing sandstones in a wide range of permeabilities[J]. Applied Geophysics, 2008, 5(4): 249-260. DOI:10.1007/s11770-008-0038-y |
| [38] |
NIE J X, BA J, YANG D H, et al. BISQ model based on a Kelvin-Voigt viscoelastic frame in a partially saturated porous medium[J]. Applied Geophysics, 2012, 9(2): 213-222. DOI:10.1007/s11770-012-0332-6 |
| [39] |
SAROUT J. Impact of pore space topology on permeability, cut off frequencies and validity of wave propagation theories[J]. Geophysical Journal International, 2012, 189(1): 481-492. DOI:10.1111/j.1365-246X.2011.05329.x |
| [40] |
凌云, 杜向东, 曹思远. 基于Zener线性体的黏弹性介质衰减频散特征分析[J]. 地球物理学进展, 2017, 32(1): 205-209. LING Y, DU X D, CAO S Y. Attenuation and dispersion characteristics analysis in visco-poroelastic medium based on Zener linear solid[J]. Progress in Geophysics, 2017, 32(1): 205-209. |
| [41] |
滕吉文, 张中杰, 王爱武, 等. 弹性介质各向异性研究沿革、现状与问题[J]. 地球物理学进展, 1992, 7(4): 14-28. TENG J W, ZHANG Z J, WANG A W, et al. The study of anisotropy in elastic medium: Evolution, present situation and questions[J]. Progress in Geophysics, 1992, 7(4): 14-28. |
| [42] |
CHRISTENSEN R. Theory of viscoelasticity: An introduction[M]. 2nd ed. New York: Academic Press, 1982: 1-378.
|
| [43] |
CARCIONE J M. Constitutive model and wave equations for linear, viscoelastic, anisotropic media[J]. Geophysics, 1995, 60(2): 537-548. DOI:10.1190/1.1443791 |
| [44] |
MAULTZSCH S, CHAPMAN M, LIU E, et al. Modelling and analysis of attenuation anisotropy in multi-azimuth VSP data from the Clair field[J]. Geophysical Prospecting, 2007, 55(5): 627-642. DOI:10.1111/j.1365-2478.2007.00645.x |
| [45] |
PRASAD M, NUR A.Stanford rock physics laboratorys[EB/OL].[2020-01-10].https://srpl.stanford.edu/
|
| [46] |
LIU E, CHAPMAN M, VARELA L, et al. Velocity and attenuation anisotropy: Implication of seismic fracture characterizations[J]. The Leading Edge, 2007, 26(9): 1170-1174. DOI:10.1190/1.2780788 |
| [47] |
ZHU Y, TSVANKIN I. Plane-wave attenuation anisotropy in orthorhombic media[J]. Geophysics, 2006, 71(1): D9-D19. |
| [48] |
张中杰, 滕吉文, 贺振华. EDA介质中地震波速度、衰减与品质因子方位异性研究[J]. 中国科学(E辑), 1999, 29(6): 569-574. ZHANG Z J, TENG J W, HE Z H. Seismic wave velocity, attenuation and quality factor azimuthal heterosexuality in EDA media[J]. Science in China(Series E), 1999, 29(6): 569-574. |
| [49] |
王赟, 刘媛媛, 张美根. 裂缝各向异性地震等效介质理论[M]. 北京: 科学出版社, 2017: 1-144. WANG Y, LIU Y Y, ZHANG M G. Seismic equivalent medium theory for fractured anisotropy[M]. Beijing: Science Press, 2017: 1-144. |
| [50] |
杜启振, 杨慧珠. 线性黏弹性各向异性介质速度频散和衰减特征研究[J]. 物理学报, 2002, 51(9): 2101-2108. DU Q Z, YANG H Z. Velocity dispersion and attenuation inanisotropic linear viscoelastic media[J]. Acta Physica Sinica, 2002, 51(9): 2101-2108. DOI:10.3321/j.issn:1000-3290.2002.09.035 |
| [51] |
杜启振, 杨慧珠. 裂缝性地层黏弹性地震多波波动方程[J]. 物理学报, 2004, 53(8): 2801-2806. DU Q Z, YANG H Z. Viscoelastic wave equations of seismic multi-wave in fractured media[J]. Acta Physica Sinica, 2004, 53(8): 2801-2806. DOI:10.3321/j.issn:1000-3290.2004.08.070 |
| [52] |
严红勇, 刘洋. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 2012, 55(4): 1354-1365. YAN H Y, LIU Y. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
| [53] |
GUO Z Q, LIU X W, FU W, et al. Modeling and analysis of azimuthal AVO responses from a viscoelastic anisotropic reflector[J]. Applied Geophysics, 2015, 12(3): 441-452. DOI:10.1007/s11770-015-0498-9 |
| [54] |
聂建新, 杨顶辉, 巴晶. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究[J]. 地球物理学报, 2010, 53(2): 385-392. NIE J X, YANG D H, BA J. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay[J]. Chinese Journal of Geophysics, 2010, 53(2): 385-392. DOI:10.3969/j.issn.0001-5733.2010.02.016 |
| [55] |
郭智奇. 粘弹各向异性介质波场模拟与储层信息研究[D]. 长春: 吉林大学, 2008 GUO Z Q.Wave field modeling in viscoelastic anisotropic media and reservoir information study[D].Changchun: Jilin University, 2008 |
| [56] |
杨春颖, 杨春, 陈双全, 等. 各向异性衰减薄层地震响应特征研究[J]. 地球物理学报, 2017, 60(1): 316-326. YANG C Y, YANG C, CHEN S Q, et al. An analysis of seismic responses in thin anisotropic-viscoelastic reservoirs[J]. Chinese Journal of Geophysics, 2017, 60(1): 316-326. |
| [57] |
杜启振, 刘莲莲, 孙晶波. 各向异性粘弹性孔隙介质伪谱法波场正演模拟[J]. 油气地球物理, 2007, 5(1): 22-26. DU Q Z, LIU L L, SUN J B. Wavefield numerical modeling with the pseudo-spectral method in anisotropic viscoelastic porous media[J]. Petroleum Geophysics, 2007, 5(1): 22-26. |
| [58] |
刘财, 郭智奇, 杨宝俊, 等. 黏弹各向异性介质中波的反射与透射问题分析[J]. 地球物理学报, 2007, 50(4): 1216-1224. LIU C, GUO Z Q, YANG B J, et al. Analysis of reflection and transmission problems of waves in viscoelastic anisotropic media[J]. Chinese Journal of Geophysics, 2007, 50(4): 1216-1224. DOI:10.3321/j.issn:0001-5733.2007.04.031 |
| [59] |
李桂华, 冯建国, 朱光明. 黏弹性VTI介质频率空间域准P波正演模拟[J]. 地球物理学报, 2011, 54(1): 200-207. LI G H, FENG J G, ZHU G M. Quasi-P wave forward modeling in viscoelastic VTI media in frequency-space domian[J]. Chinese Journal of Geophysics, 2011, 54(1): 200-207. DOI:10.3969/j.issn.0001-5733.2011.01.021 |
| [60] |
YANG C Y, WANG Y, LI X Y. Amplitude anisotropy of shear-wave splitting and fluid detection in thin-layer reservoir[J]. Acta Geophysica, 2019, 67: 1563-1577. DOI:10.1007/s11600-019-00375-2 |
| [61] |
夏竹, 张少华, 王学军. 中国西部复杂地区近地表特征与表层结构探讨[J]. 石油地球物理勘探, 2003, 38(4): 414-424. XIA Z, ZHANG S H, WANG X J. Discussion on near-surface characters and structures in complex area of western China[J]. Oil Geophysical Prospecting, 2003, 38(4): 414-424. DOI:10.3321/j.issn:1000-7210.2003.04.015 |
| [62] |
王建民, 陈树民, 苏茂鑫, 等. 近地表高频补偿技术在三维地震勘探中的应用研究[J]. 地球物理学报, 2007, 50(6): 1837-1843. WANG J M, CHEN S M, SU M X, et al. A study of the near surface high-frequency compensation technology in 3-D seismic exploration[J]. Chinese Journal of Geophysics, 2007, 50(6): 1837-1843. DOI:10.3321/j.issn:0001-5733.2007.06.026 |
| [63] |
尹喜玲, 石战结, 田钢. 近地表低降速带地震波传播规律初探[J]. 地球物理学进展, 2009, 24(2): 398-407. YIN X L, SHI Z J, TIAN G. Study on transmittable laws of seismic waves in unconsolidated layers[J]. Progress in Geophysics, 2009, 24(2): 398-407. DOI:10.3969/j.issn.1004-2903.2009.02.005 |
| [64] |
宫同举. 近地表地震波衰减规律及品质因子提取方法研究[D]. 东营: 中国石油大学, 2010 GONG T J.Study on near surface seismic wave attenuation and methods of quality factor extraction[D].Dongying: China University of Petroleum, 2010 |
| [65] |
蒋立, 陈勇, 肖艳玲, 等. 地表过渡带近地表Q补偿与地表一致性反褶积处理效果对比研究[J]. 石油物探, 2018, 57(6): 870-877. JIANG L, CHEN Y, XIAO Y L, et al. A comparison of near-surface Q compensation and surface-consistent deconvolution in the near-surface transition zone[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 870-877. DOI:10.3969/j.issn.1000-1441.2018.06.009 |
| [66] |
沈鸿雁, 王鑫, 李欣欣. 近地表结构调查及参数反演综述[J]. 石油物探, 2019, 58(4): 471-485. SHEN H Y, WANG X, LI X X. Near surface structure survey and parameter inversion review[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 471-485. DOI:10.3969/j.issn.1000-1441.2019.04.001 |
| [67] |
谢祥, 吴奎, 张金辉, 等. 稠油油藏AVO影响因素分析[J]. 石油地球物理勘探, 2018, 53(3): 545-551. XIE X, WU K, ZHANG J H, et al. AVO influence analysis in heavy oil saturated reservoiors[J]. Oil Geophysical Prospecting, 2018, 53(3): 545-551. |
| [68] |
汪凯明. 我国非常规油气资源勘探开发前景[J]. 当代石油石化, 2009, 17(4): 24-27. WANG K M. Exploration and development prospects of unconventional hydrocarbon resources in China[J]. Petroleum & Petrochemical Today, 2009, 17(4): 24-27. DOI:10.3969/j.issn.1009-6809.2009.04.005 |
| [69] |
勾丽敏, 张金华, 王嘉玮. 海洋天然气水合物地震识别方法研究进展[J]. 地球物理学进展, 2017, 32(6): 2626-2635. GOU L M, ZHANG J H, WANG J W. Progres in seismic identification approach of marine gas hydrate[J]. Progress in Geophysics, 2017, 32(6): 2626-2635. |
| [70] |
谢佩瑜, 杨顶辉. 近地表强衰减介质中的地震波传播模型[J]. 地球物理学报, 2018, 61(3): 917-925. XIE P Y, YANG D H. Seismic wave propagation model in near-surface strong-attenuation media[J]. Chinese Journal of Geophysics, 2018, 61(3): 917-925. |
| [71] |
YANG D H, ZHANG Z J. Poroelastic wave equation including the Biot/squirt mechanism, and the solid/fluid couping anisotropy[J]. Wave Motion, 2002, 35(3): 223-245. DOI:10.1016/S0165-2125(01)00106-8 |




