随着油气勘探开发程度的提高, 地震勘探目标已由简单的构造油气藏转向岩性油气藏。在勘探地震频带范围内, 我国大多数岩性油气藏以薄层或薄互层的形式存在。因此, 薄互层的研究对于推动我国岩性油气藏勘探开发具有重要意义。
目前, 油气勘探领域对于薄互层的研究主要集中在薄层的厚度预测[1-4]、薄互层的分辨率[5-7]、薄层AVO响应特征[8-11]、敏感属性分析及提取[12-15]、内部结构预测反演[16-19]和长波长假设下的等效各向异性等方面[20-24]。对于薄互层内部结构反演, 由于涉及弹性参数众多, 现有的地震反射理论无法直接应用。因此, 前人在长波长假设条件下, 将薄互层近似等效为具有垂直对称轴的横向各向同性(vertical transversely isotropy, VTI)介质[20-21, 25-27]。POSTMA[20]给出了韵律型薄互层在长波长假设下的等效弹性参数计算公式, 开启了薄互层等效各向异性理论研究的序幕。随后的几十年, 不同学者从理论公式[20-24]、数值模拟[28-32]和物理模拟[33-37]等方面进行了深入的探索研究。
地震波在薄互层介质中的传播特征有别于厚层情况, 会产生与频率相关的调谐干涉, 这使得薄互层反演存在多解性。针对这一问题, 王赟等[38]提出利用对薄互层进行VTI近似, 并将薄互层中目标层的反演近似简化为VTI厚层介质背景下单薄层的反演问题。鉴于薄互层的等效各向异性理论对薄层油气勘探开发的基础支撑作用, 本文针对该理论的研究进展、适用条件、发展方向及遇到的瓶颈等现状进行了归纳总结, 分析了存在的问题, 对未来发展提出了几点展望。
1 理论基础 1.1 研究进展在POSTMA[20]研究的基础上, HELBIG[39]将薄互层的研究推广到多个不同层组成的薄互层, 但其未考虑薄互层内含各向异性层的情况。ANDERSON[40]弥补了HELBIG研究的不足, 将HASKELL矩阵[41]应用到含各向异性层的薄互层, 但该方法较为复杂且未考虑长波长假设的成立条件。BACKUS[21]综合前人的研究成果, 利用平均法将长波长假设下的薄互层等效各向异性理论拓展到含3种及以上不同弹性介质的非周期性薄互层, 使得该理论得到巨大发展。BACKUS平均公式建立了薄互层介质和等效VTI介质物性参数之间的关系。在BACKUS平均公式中存在以下近似假设: 若在一定的范围l′内, 函数a基本不变, 函数b在该范围内可随意变化, 则近似存在:
| $\langle a b\rangle=a\langle b\rangle$ | (1) |
式中: 符号“〈 〉”表示平均运算。若要(1)式严格成立, 则平均长度l′必须远远大于薄互层内的单层厚度, 同时要远远小于波长, 即长波长假设。
假设c11, c33, c13, c44, c66为薄互层内某一单层介质的弹性参数, 利用介质中的应力-应变关系[42], 求解得到平均运算后等效介质的弹性参数C11, C33, C13, C44, C66:
| $\left.\begin{array}{rl}C_{11} & =\left\langle c_{11}-c_{13}^{2} c_{33}^{-1}\right\rangle+\left\langle c_{33}^{-1}\right\rangle^{-1}\left\langle c_{13} c_{33}^{-1}\right\rangle^{2} \\ C_{33} & =\left\langle c_{33}^{-1}\right\rangle^{-1} \\ C_{13} & =\left\langle c_{33}^{-1}\right\rangle^{-1}\left\langle c_{13} c_{33}^{-1}\right\rangle \\ C_{44} & =\left\langle c_{44}^{-1}\right\rangle^{-1} \\ C_{66} & =\left\langle c_{66}\right\rangle\end{array}\right\}$ | (2) |
当薄互层为各向同性层时, 则有:
| $c_{11}=c_{33}=\lambda+2 \mu \\ c_{44}=c_{66}=\mu$ | (3) |
式中: λ、μ为拉梅常数。
将(3)式代入(2)式, 得到:
| $\left. \begin{array}{l} {C_{11}} = \left\langle {\frac{{4\mu (\lambda + \mu )}}{{\lambda + 2\mu }}} \right\rangle + {\left\langle {\frac{1}{{\lambda + 2\mu }}} \right\rangle ^{ - 1}}{\left\langle {\frac{\lambda}{{\lambda + 2\mu }}} \right\rangle ^2}\\ {C_{33}} = {\left\langle {\frac{1}{{\lambda + 2\mu }}} \right\rangle ^{ - 1}}\\ {C_{13}} = {\left\langle {\frac{1}{{\lambda + 2\mu }}} \right\rangle ^{ - 1}}\left\langle {\frac{\lambda}{{\lambda + 2\mu }}} \right\rangle \\ {C_{44}} = {\left\langle {\frac{1}{\mu }} \right\rangle ^{ - 1}}\\ {C_{66}} = \langle \mu \rangle \end{array} \right\}$ | (4) |
(4) 式的结果与POSTMA[20]研究的韵律型薄互层介质近似结果相同。该方法的应用范围很广, 是薄互层等效各向异性理论的基础。但是, BACKUS[21]只是给出了宽泛的适用条件, 即波长远大于单层厚度时近似成立。同时, 需满足入射波垂直或近似垂直于层面。
对于各向同性介质组成的随机型薄互层, LEVIN[25]利用各层纵波速度、横波速度和密度来表示等效弹性模量, 建立了薄互层弹性参数与等效VTI介质参数之间更为明显、直接的关系式:
| $\left. \begin{array}{l} {C_{11}} = \left\langle {4\rho v_{\rm{S}}^2\left( {1 - \frac{{v_{\rm{S}}^2}}{{v_{\rm{P}}^2}}} \right)} \right\rangle + {\left\langle {\frac{1}{{\rho v_{\rm{P}}^2}}} \right\rangle ^{ - 1}}{\left\langle {1 - \frac{{2v_{\rm{s}}^2}}{{v_{\rm{P}}^2}}} \right\rangle ^2}\\ {C_{33}} = {\left\langle {\frac{1}{{\rho v_{\rm{P}}^2}}} \right\rangle ^{ - 1}}\\ {C_{13}} = {\left\langle {\frac{1}{{\rho v_{\rm{P}}^2}}} \right\rangle ^{ - 1}}\left\langle {1 - \frac{{2v_{\rm{s}}^2}}{{v_{\rm{P}}^2}}} \right\rangle \\ {C_{44}} = {\left\langle {\frac{1}{{\rho v_{\rm{s}}^2}}} \right\rangle ^{ - 1}}\\ {C_{66}} = \langle \rho v_{\rm{s}}^2\rangle \end{array} \right\}$ | (5) |
式中: vP和vS分别为薄互层内某各向同性层中的纵波和横波速度。公式(5)是公式(4)的变形, 根据公式(5), 可以直接利用速度测井和密度测井计算等效VTI介质的弹性参数。
DALEY等[43]首次通过研究SH波的合成地震记录, 对比分析了两种等价模型(韵律型薄互层和与其相对应的等效VTI介质)的数值响应, 并发现两者模拟结果十分相似。HELBIG[22-23]利用韵律型薄互层介质的频散方程, 研究了薄互层等效各向异性理论成立的条件, 结果显示: 对于SH波, 当波长与互层单元厚度比≥3时, 薄互层等效各向异性理论成立; 并阐明了研究薄互层等效VTI介质在勘探地震中的意义。LYAKHOVITSKIY[44]指出韵律型薄互层所引起的地震各向异性存在以下3个问题: ①单薄层纵、横波速度比对薄互层等效介质理论成立的影响; ②SV型面波相速度交叉点与弹性参数的关系; ③由薄互层引起的各向异性与其它类型TI介质的区别。SCHOENBERG等[45]结合代数矩阵和群论方法将薄互层等效各向异性理论推广到任意各向异性薄互层情况。
张中杰等[24]利用运动学方程和界面的应力-位移连续性, 详细推导了薄互层引起的长波长等效各向异性介质的弹性参数计算公式。将公式(4)表示为如下形式:
| $\left. \begin{array}{l} {C_{11}} = \sum\limits_{i = 1}^n {{\eta _i}} \left( {{\lambda _i} + 2{\mu _i}} \right) + \\ \sum\limits_{i = 1}^n {\left[ {\left( {1 - \frac{{\sum\limits_{i = 1}^n {\frac{{{\eta _i}{\lambda _i}}}{{{\lambda _i} + 2{\mu _i}}}} }}{{{\lambda _i}\sum\limits_{i = 1}^n {\frac{{{\eta _i}}}{{{\lambda _i} + 2{\mu _i}}}} }}} \right)\frac{{{\eta _i}{\lambda _i}\left( {{\lambda _n} - {\lambda _i}} \right)}}{{{\lambda _i} + 2{\mu _i}}}} \right]} \\ {C_{33}} = \frac{1}{{\sum\limits_{i = 1}^n {\frac{{{\eta _i}}}{{{\lambda _i} + 2{\mu _i}}}} }}\\ {C_{13}} = \frac{{\sum\limits_{i = 1}^n {\frac{{{\eta _i}{\lambda _i}}}{{{\lambda _i} + 2{\mu _i}}}} }}{{\sum\limits_{i = 1}^n {\frac{{{\eta _i}}}{{{\lambda _i} + 2{\mu _i}}}} }}\\ {C_{44}} = \frac{1}{{\sum\limits_{i = 1}^n {\frac{{{\eta _i}}}{{{\mu _i}}}} }}\\ {C_{66}} = \sum\limits_{i = 1}^n {{\eta _i}} {\mu _i} \end{array} \right\}$ | (6) |
式中: ηi=di>/(∑di), di为薄互层第i层的厚度。(6)式与(4)式相比更明确地体现了薄层厚度与总厚度比值对等效VTI介质弹性参数的影响。
对于各向异性介质的弹性参数Cij, 其具体含义不够明确。因而, 引入了可以清晰描述VTI介质各向异性程度的Thomsen参数[46], 即
| $\left.\begin{array}{l}\varepsilon=\frac{C_{11}-C_{33}}{2 C_{33}} \\ \gamma=\frac{C_{66}-C_{44}}{2 C_{44}} \\ \delta=\frac{\left(C_{13}+C_{44}\right)^{2}-\left(C_{33}-C_{44}\right)^{2}}{2 C_{33}\left(C_{33}-C_{44}\right)}\end{array}\right\}$ | (7) |
等效的纵、横波速度分别为:
| $\left.\begin{array}{l}v_{\mathrm{P}}=\sqrt{\frac{p+q}{2 \rho}} \\ v_{\mathrm{SV}}=\sqrt{\frac{p-q}{2 \rho}} \\ v_{\mathrm{SH}}=\sqrt{\frac{C_{66} \sin ^{2} \theta+C_{44} \cos ^{2} \theta}{\rho}}\end{array}\right\}$ | (8) |
式中: θ为入射角, 且有:
| $p=\mathrm{C}_{11} \sin ^{2} \theta+C_{33} \cos ^{2} \theta+C_{44}$ |
| $\begin{aligned} q=\{&\left[\left(C_{11}-C_{44}\right) \sin ^{2} \theta-\left(C_{33}-C_{44}\right) \cos ^{2} \theta\right]^{2}+\\ &\left.4\left(C_{13}+C_{44}\right)^{2} \sin ^{2} \theta \cos ^{2} \theta\right\}^{\frac{1}{2}} \end{aligned}$ |
经过多年的研究, 薄互层等效各向异性理论逐渐得到完善, 但是尚未得到明确清晰且普遍认可的适用条件。地震波在层状介质中传播时, 根据地震波长与层厚的关系, 需要用不同的理论来研究, 即: 短波长理论(射线理论)、长波长理论(等效各向异性理论)或散射理论。地震波在短波长理论中的速度比长波长理论中要大, 即使用射线理论计算的波速比等效各向异性理论的波速要大[47-50]。而对于薄互层等效各向异性理论成立的基本条件就是波在介质中传播时的波长远远大于互层单元的层厚。但是, 这仅仅是一个定性且模糊的条件, 对于该理论的应用是不利的。因此, 需要一个清晰定量的适用条件, 使得薄互层等效各向异性理论可以更有效地应用于实际。
薄互层等效各向异性理论涉及的薄层是相对波长的“长”进行定义的, 但是仅满足波长远大于薄层厚度是不够的。BACKUS[21]认为波长在远大于单薄层厚度时, 还应同时满足大于BACKUS平均运算后的薄互层总厚度; DALEY等[43]认为震源主频对应的主波长大于2倍薄互层总厚度时, 薄互层等效各向异性理论成立; LEVIN[25]认为实验室建立薄互层物理模型并进行等效各向异性近似研究, 有助于得到薄互层等效各向异性理论的适用条件。随后, 前人从数值模拟[29-32]、物理实验[33-37]等不同角度对薄互层等效各向异性理论的适用性进行了深入研究。
2 韵律型薄互层韵律型薄互层是最常见的薄互层类型, 如砂岩被泥质条带分割而形成的砂泥岩薄互层[51]; 同时它也是最简单的薄互层类型, 其地震响应特征是研究其它类型薄互层的基础[52]。针对韵律型薄互层[20, 53-54], 不同学者利用数值模拟和物理模拟对薄互层等效各向异性理论成立的影响因素进行了研究。这些影响因素包括: 探测频率f(或波长λ)、薄互层中的单层厚度或互层单元厚度d(对于韵律型薄互层, 如无特殊说明, 层厚指的是互层单元的厚度)、互层单元中不同介质的厚度占比和层间阻抗比。
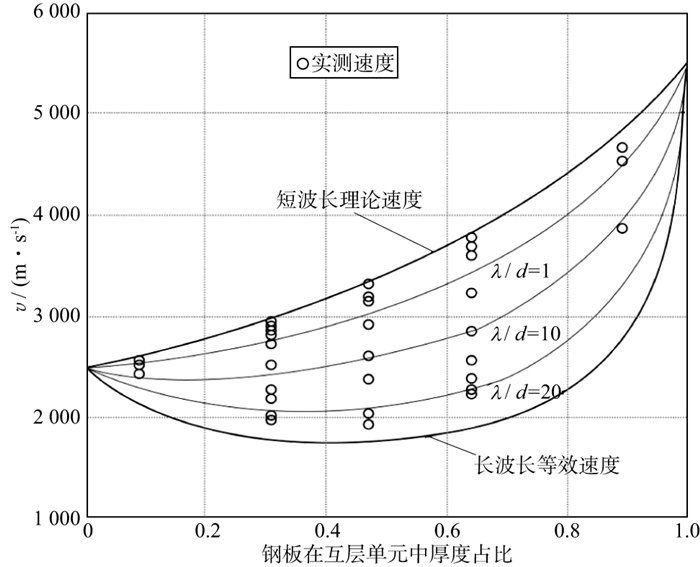
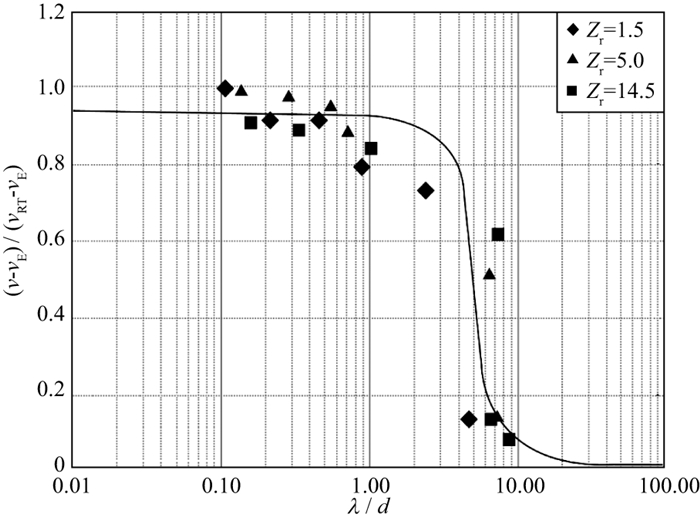
2.1 频率(波长)、单层或互层单元厚度的影响 2.1.1 不同材料的适用条件MELIA等[33]采用环氧树脂和玻璃制作薄互层模型, 并发现当波长λ比互层单元厚度d大1到2个量级(10~100倍)时, 薄互层等效各向异性理论近似成立。CARCIONE等[29]利用数值模拟方法研究发现, 在环氧树脂和玻璃组成的薄互层满足λ/d>8, 砂岩和石灰岩组成的薄互层满足λ/d>6时, 薄互层等效各向异性理论成立。MARION等[34]利用钢板和塑料板组成的薄互层进行实验研究, 对比物理模拟和数值模拟的结果发现, 薄互层等效各向异性理论成立的条件不同: 对于物理模拟, 需满足λ/d>15;而对于数值模拟, 需满足λ/d>10(图 1, 其中, v代表实际测量速度; vRT代表射线理论速度; vE代表等效介质速度)。李跃等[35]采用铝板、有机玻璃和蜡(板)3种材料制作了两种薄互层, 第一种为铝板和有机玻璃, 第二种为铝板和蜡(板), 用环氧树脂作为粘合剂。实验室测量结果证实了薄互层存在速度各向异性的现象, 即在波长远大于薄互层中各层的层厚di, 即λ/di>10(i=1, 2)时, 纵、横波均呈现明显的各向异性特征。杨晓松等[36]利用钢板和有机玻璃制作的薄互层进行实验研究, 结果表明: 当存在λi/di < 5(i=1, 2)(λi为超声波在介质i中传播时的波长, di为韵律层中介质i的厚度)时, 测量得到的波速与射线理论速度基本相同(表 1中样品1~3和样品6);当λi/di>5(i=1, 2), 但λsi/d < 10(λsi为波在样品i中的波长)时, 测量得到的波速趋向于等效介质波速, 但存在一定的差异(表 1中样品4和样品7~8)。魏建新等[37]采用灌注法构建了铝合金和环氧树脂组成的薄互层物理模型, 通过研究互层单元厚度d和探测频率对超声波特征的影响, 发现在λ/d>11时, 薄互层等效各向异性理论成立。
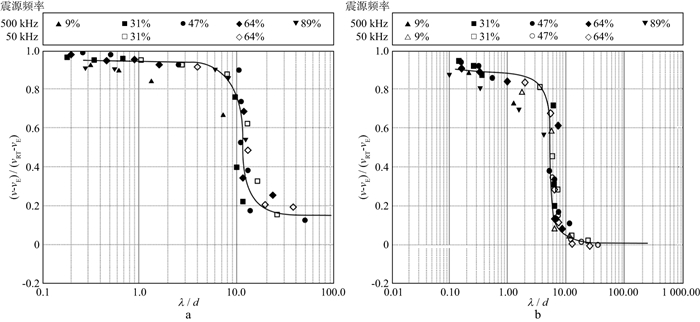
|
图 1 钢板和塑料板组成的韵律型薄互层中钢板厚度在互层单元中厚度占比对速度的影响 a物理实验结果; b数值模拟结果 |
| 表 1 λ/d和λi/di(i=1, 2)对实测速度、射线理论速度和等效介质速度的影响 |
综合以上结果可以发现, 不同材料对应的薄互层等效各向异性理论成立的波长与互层单元厚度比λ/d各不相同。此外, 杨晓松等[36]认为波在穿过不同介质时, 其对应的波长发生变化, 此时再统一使用探测震源的频率对应的波长进行研究会产生误差。因此, 需要考虑互层单元中不同介质对应的波长λi与该层厚度di的关系。他在研究互层单元中单层介质对应的波长与厚度比时发现, 当λi/di>5(i=1, 2, 表 1中样品4, 7, 8)时, 等效各向异性理论近似成立。但该结论尚未得到其它研究的证实, 需要进一步研究。目前, 在国际上普遍认可的仍是“波长与互层单元厚度比λ/d≥10”这一适用条件[32]。此外, 数值模拟和物理模拟结果也存在差别, 且使得薄互层等效各向异性理论成立的波长与互层单元厚度比λ/d, 在数值模拟时往往比物理模拟偏小, 存在系统性偏差。从现有的研究结果可以发现, 物理模拟结果小于数值模拟结果的1.5倍[33-34, 39]。这很有可能是由于物理实验在制作薄互层模型时, 工艺不够完善造成的。因此, 针对尚未进行物理实验的材料组成的韵律型薄互层的等效各向异性理论研究时, 可以将数值模拟结果的1.5倍作为其成立条件。
2.1.2 运动学特征对于运动学特征而言, 在互层单元厚度d不变时, 随着频率的减小, 波速由短波长极限值向长波长极限值变化, 但不会超过这两个极限值(图 2)[33]。但是, 短波长和长波长的转换带位置不随频率而变化(图 1)。
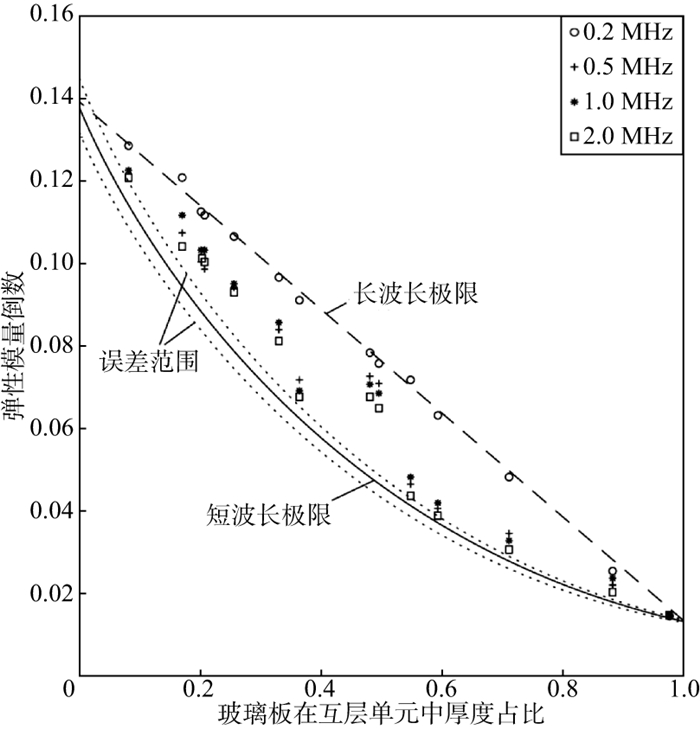
|
图 2 不同震源频率弹性模量倒数随玻璃板在互层单元中厚度占比的变化[33] |
在频率不变时, 随着互层单元厚度d的减小, 纵波速度首先保持基本不变, 近似等于互层单元的时间平均速度(射线速度), 随后会出现断崖式变小, 最后又逐渐变小并趋向于等效介质速度(长波长等效速度)(图 1)。
2.1.3 动力学特征对于动力学特征而言, 在探测频率不变时, 随着互层单元厚度d的减小, 波形到时会出现延迟现象, 振幅逐渐减小, 周期逐渐增大。同时, 会出现在低频波形上叠加高频信号的现象(图 3、图 4), 随后波形逐渐消失。随着互层单元厚度的进一步减小, 波形重新出现, 振幅逐渐增大, 周期逐渐减小[36-37]。波形消失的区域为短波长向长波长过渡的转换带, 此时波形衰减最为严重。因此, 简单的波形记录并非一定对应简单的介质结构[36]。
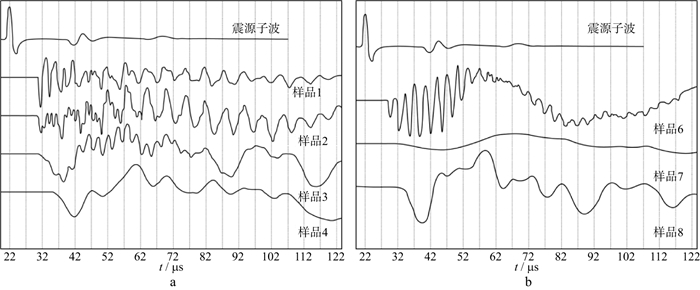
|
图 3 不同韵律层结构的透射纵波波形 a样品1, 2, 3, 4; b样品6, 7, 8 |
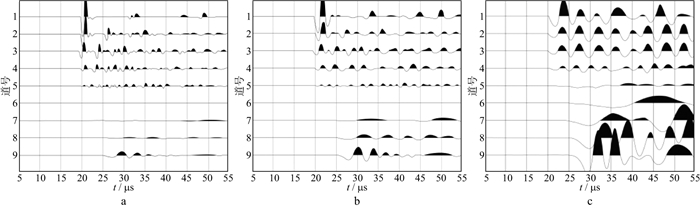
|
图 4 随互层单元厚度和频率变化的波形记录(地震道1~9自上而下互层单元厚度逐渐减小) a震源主频为1.0MHz; b震源主频为0.6MHz; c震源主频为0.2MHz |
在互层单元厚度d不变时, 随着探测频率的减小, 波形到时会出现延迟现象, 振幅在靠近短波长区域(第1~4道)逐渐减小, 在靠近长波长区域(第7~9道)逐渐增大, 周期逐渐增大(图 4)[37]。由于λ/d参数大小决定了薄互层介质满足长波长假设或者短波长假设的条件, 且速度一定时波长λ与探测频率成反比。因此, 互层单元厚度不变而探测频率减小时的地震动力学特征变化规律, 与探测频率不变而互层单元厚度减小时的规律一致。
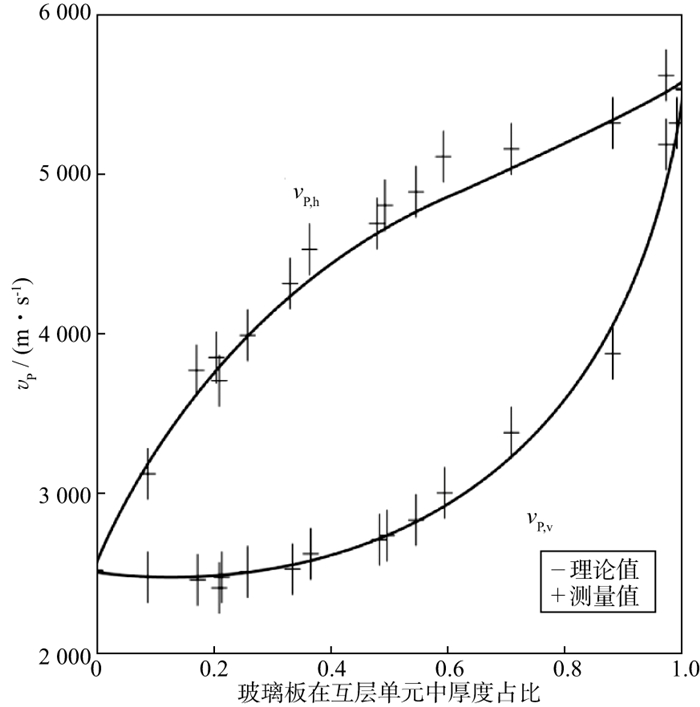
2.2 互层单元中介质厚度占比的影响薄互层的互层单元中两种介质的厚度占比发生变化时, 等效速度和各向异性参数均发生变化。对于等效速度, 其变化特征与波长互层单元厚度比λ/d有关(图 5)[34]。当λ/d较小时, 随着互层单元中目标介质(高速介质)厚度占比增大, 等效速度逐渐增大(图 5)。但是, 其垂向速度和水平速度增大的趋势不同, 且前者增大的幅度小于后者(图 6, 图中vP, h代表纵波水平速度; vP, v代表纵波垂直速度)[33]。当λ/d较大时, 随着目标介质所占比例增大, 可能出现等效速度先减小后增大的现象, 即等效速度小于组成薄互层的任意一种介质的速度(图 5中λ/d=20)[34]。因此, 厚的低速层可能是由两个高速层组成的薄互层。若选定薄互层中波速相对较低的介质进行研究, 其等效速度的变化趋势与上述结果相反。
|
图 5 钢板在互层单元中厚度占比变化时实测速度的变化规律 |
|
图 6 玻璃板在互层单元中的厚度占比对P波速度的影响 |
定义各向异性强度A[33]为:
| $A(\%)=\frac{200\left(v_{\mathrm{P}, \mathrm{h}}-v_{\mathrm{P}, \mathrm{v}}\right)}{v_{\mathrm{P}, \mathrm{h}}+v_{\mathrm{P}, \mathrm{v}}}$ | (9) |
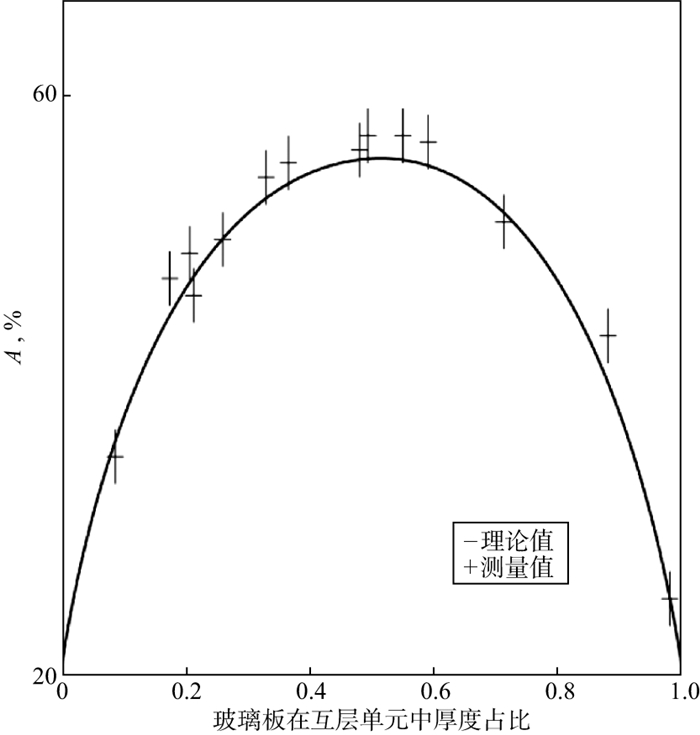
随着目标介质(玻璃)在互层单元中厚度占比增大, 等效各向异性强度先增大后减小, 在目标介质(玻璃)厚度占比为50%时, 纵波各向异性最强(图 7)。
薄互层的互层单元中不同介质厚度占比对短波长和长波长的转换带位置基本没有影响(图 1)[34]。
在探测频率、互层单元厚度不变的情况下, 组成薄互层的互层单元中不同介质厚度占比变化时, 穿过薄互层的透射波在振幅和周期上均会产生变化(图 3)。样品2和样品6、样品3和样品7互层单元厚度分别大致相同, 样品4和样品8的互层单元厚度相差较大, 且样品6, 7, 8中钢板在互层单元中厚度占比分别是样品2, 3, 4的2倍。对比样品2和样品6可以发现, 钢板厚度占比增大使得透射波的高频波动振幅更大, 周期也更长; 对比样品3和样品7可以发现, 钢板厚度占比更大的样品7中透射波仅存在低频成分, 高频成分已经消失(图 3)。
|
图 7 玻璃板在互层单元中的厚度占比对各向异性强度的影响 |
组成薄互层的介质层间阻抗比的大小对薄互层等效各向异性理论成立的影响较小, 弱阻抗比时转换带出现的λ/d值比强阻抗比时要稍小; 随着阻抗比的增大, 短波长速度和长波长等效速度的差别增大(图 8中Zr代表层间阻抗比)[34]。
|
图 8 归一化速度在不同层间阻抗比情况下随波长与互层单元厚度比的变化规律 |
综上所述, 对于韵律型薄互层, 长波长等效理论适用条件及波场特征的影响因素包括探测频率(波长)、层厚(单层或互层单元)、互层单元中厚度占比和层间阻抗比。对于薄互层等效各向异性理论的适用条件, 不同学者得到的结论不尽相同, 这可能是由两方面的原因造成的。一方面是由于短波长向长波长变化的过程是连续的, 转换带与长波长的临界点位置尚无明确的定义, 从而导致不同学者得到的适用条件有所偏差; 另一方面由于波在不同介质中的波长不同, 需考虑介质性质的影响, 即薄互层等效各向异性理论成立需满足λi/di>5(i=1, 2), 该结论尚未得到更多研究的证实。目前仍普遍认可波长与互层单元厚度比λ/d≥10为该理论的适用条件。而对于具体介质而言, 可以通过数值模拟的方法得到成立的临界λ/d, 并以该临界值的1.5倍作为薄互层等效各向异性理论的适用条件。
3 随机型薄互层虽然韵律型薄互层可以作为典型的薄互层模型进行薄互层等效各向异性适用性研究, 但随机型薄互层更符合实际介质的非均匀性特征。随机型薄互层建模的方法有两类: 基于数学方法的建模和基于测井数据的建模。KERNER[31]和郭乃川等[32]分别基于数学方法建立随机型薄互层模型, 并利用BACKUS平均法研究了薄互层等效各向异性理论的适用性; 而HSU等[28]、LINER等[30]、IMHOF[55]和曹丹平[56]则采用测井数据对该理论的适用性进行了研究。
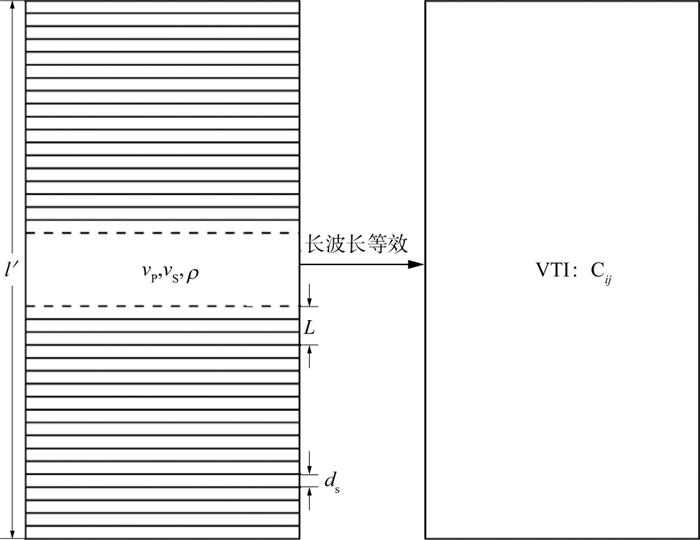
随机型薄互层等效各向异性理论的适用条件比韵律型薄互层的情况更为复杂[30-32]。KERNER[31]在对随机型薄互层的研究过程中提出了非均匀性尺度L(单层厚度dS的整数倍)的概念, 即描述薄互层介质时所采用的空间自相关长度。长波长等效时的平均长度可能是非均匀性尺度, 也可能是非均匀性尺度的倍数。随机型薄互层(图 9)需要确定单层厚度ds、非均匀性尺度L、平均长度l′和主波长λ之间的关系对薄互层等效各向异性理论的影响, 研究过程更为复杂, 得到的结果不确定性更强。
|
图 9 水平层状介质及其在长波长假设下的等效VTI介质[31] |
由于给出测井数据便可以进行随机型薄互层建模, 因此基于测井数据的建模方法不在本文赘述。基于数学方法的建模是在统计学基础上, 建立符合实际地层分布的地球物理建模方法。该方法建立的薄互层模型满足从测井数据或岩心样品中观测到的介质非均匀分布特征, 为实际地层的数值模拟研究提供了便利条件[32]。
为了描述沉积层的薄互层模型, KERNER[31]利用两种不同的基于随机过程的数学方法进行建模, 得到卷积模型和泊松模型。其中, 速度平缓波动的卷积模型是过渡式随机模型, 而两种岩石组成交替的泊松模型是周期式随机模型(图 10)。经过验证, 该建模方法可近似模拟不同类型的实际地层。
|
图 10 基于随机过程的数学方法建立的随机型薄互层模型[31] a卷积模型; b泊松模型 |
郭乃川等[32]基于自相关函数的扰动理论得到了随机型薄互层模型, 并在波数域计算时引入锥形函数压制离散计算造成的误差, 确保了随机型薄互层模型的可信度。此方法根据自相关函数的类型, 可分为高斯型和指数型两种随机薄互层模型。
3.2 等效各向异性参数用于表征各向异性强弱的参数有Thomsen参数[46]和BANIK定义的各向异性因子[57]。Thomsen参数的定义可参见(7)式, 其建立了与介质弹性参数的关系, 应用十分广泛。各向异性因子根据不同方向速度的线性关系, 直接表示出各向异性的强弱, 其定义相对于Thomsen参数更加简单清晰。为避免符号相同引起歧义, 将文献[57]中表示各向异性因子的量稍作修改(将εP、εSV、εSH分别替换为ξP、ξSV、ξSH), 表示为:
| $\left.\begin{array}{l}\xi_{\mathrm{P}}=\frac{v_{\mathrm{P}, \mathrm{h}}-v_{\mathrm{P}, \mathrm{v}}}{v_{\mathrm{P}, \mathrm{v}}} \\ \xi_{\mathrm{SV}}=\frac{v_{\mathrm{S}, 45}-v_{\mathrm{S}, \mathrm{v}}}{v_{\mathrm{S}, \mathrm{v}}} \\ \xi_{\mathrm{SH}}=\frac{v_{\mathrm{S}, \mathrm{h}}-v_{\mathrm{S}, \mathrm{v}}}{v_{\mathrm{S}, \mathrm{v}}}\end{array}\right\}$ | (10) |
式中: vS, h和vS, v分别表示横波水平和垂直速度; vS, 45表示横波在45°方向上的相速度。
对于韵律型薄互层模型, 在平均窗口滑动过程中(以互层单元厚度为滑动步长), 其局部等效各向异性参数曲线基本不变, 说明其等效介质为均匀横向各向同性介质。而对于随机型薄互层模型, 在平均窗口滑动过程中, 其局部各向异性参数曲线会有较大的波动, 其波动大小与随机薄互层中的参数波动和平均窗口大小(平均长度)有关。沿地层垂直方向自上而下利用BACKUS方法进行等效平均, 可获得不同深度各向异性参数的变化情况[30]。
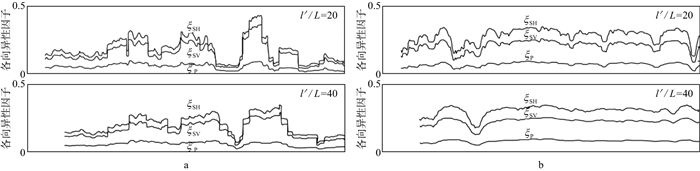
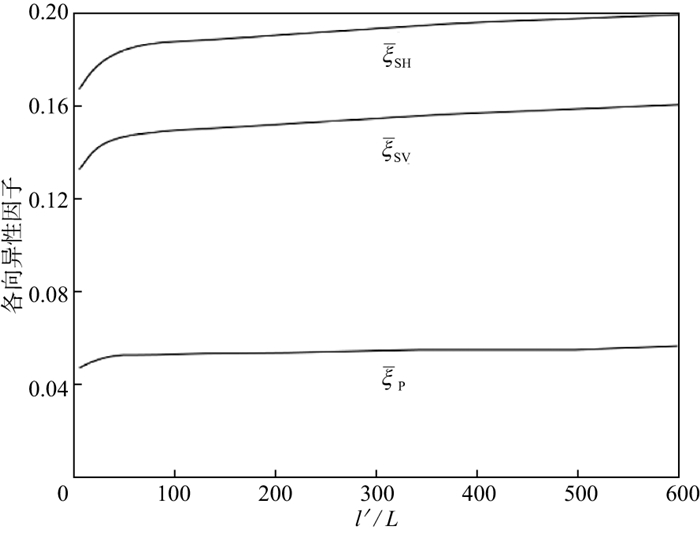
3.2.1 平均长度与非均匀性尺度的影响非均匀性尺度通常是单层厚度或测井采样长度的整数倍, 平均长度与非均匀性尺度的关系会影响局部各向异性因子和Thomsen参数的波动变化。平均长度与非均匀性尺度比值(l′/L)在增大的过程中, 随机薄互层的局部各向异性因子(图 11)和Thomsen参数变化(图 12)的波动逐渐减小, 消除了个别薄层对各向异性的影响(锯齿状起伏)[31]。当l′/L足够大时, Thomsen参数波动基本消失[32](图 12c); 各向异性因子会逐渐增大趋向于不变, 其标准差会逐渐减小, 在平均长度极大时趋于0, 即在平均长度远远大于(103倍以上)非均匀性尺度时, 等效介质近似为均匀介质(图 13)。
|
图 11 等效各向异性因子随深度的变化[31] a卷积模型; b泊松模型 |

|
图 12 不同平均长度的Thomsen参数曲线[32] a l′/L=20; b l′/L=40; c l′/L=333 |
|
图 13 局部各向异性因子平均值随平均长度的变化[31] |
当平均长度和横波速度扰动固定时, 随着纵波速度扰动的增大, 等效介质中纵波各向异性因子快速增大, 横波各向异性因子基本不变(图 14a); 当平均长度和纵波速度扰动固定时, 随着横波速度扰动的增大, 等效介质中纵、横波各向异性因子随之增大, 且两种横波的变化较纵波情况更快(图 14b); 随着纵、横波速度扰动之间的互相关系数增大, 纵波各向异性因子逐渐增大, 横波各向异性因子基本不受影响(图 14c)。
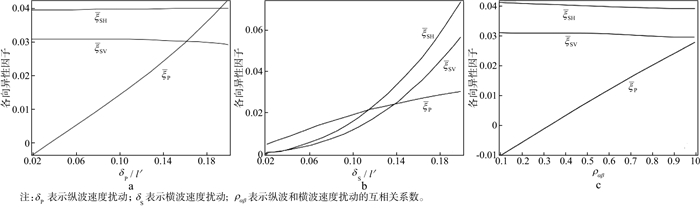
|
图 14 卷积模型中纵、横波速度扰动及其互相关系数对纵、横波各向异性因子的影响[31] a纵波速度扰动对纵、横波各向异性因子的影响; b横波速度扰动对纵、横波各向异性因子的影响; c纵、横波速度扰动的互相关系数对纵、横波各向异性因子的影响 |
图 15a、图 15b和图 15c分别给出了密度标准差σρ=0、纵横波速度比的标准差σP/S=0和密度标准差σρ=0且纵横波速度比的标准差σP/S=0时的局部等效各向异性曲线。当σρ=0且σP/S=0(图 15c)时, ε、γ曲线重合, δ曲线为水平直线。当仅存在σρ=0(图 15a)时, 纵横波速度比(泊松比)的波动使得ε、γ曲线远离0, γ曲线在ε曲线之上, 同时δ曲线不再是水平直线, 可见纵横波速度比对等效各向异性参数影响显著。当仅存在σP/S=0(图 15b)时, 密度的波动对δ曲线无影响, ε、γ曲线远离0, 但ε、γ曲线仍重合, 可见密度对等效各向异性参数影响较小[32]。

|
图 15 局部等效各向异性曲线[32] a σρ=0; b σP/S=0; c σρ=0, σP/S=0 |
LINER等[30]选取测井数据建立弹性水平薄互层模型, 利用基于BACKUS平均方法的薄互层等效各向异性理论, 计算得到的局部等效速度曲线与测井速度曲线趋势较为一致, 且更为平滑, 单点数据异常消失(图 16a, 图中测井速度(vP(右), vS(左))用黑线表示, 等效速度(vP0(右), vS0(左))用红线表示)。若组成薄互层的地层本身各向异性较强或各层层间阻抗比较大(JILH地层由石灰岩、白云岩和硬石膏薄互层组成), 计算得到的局部等效Thomsen参数曲线的绝对值较大(图 16b), 说明该层等效各向异性较强。
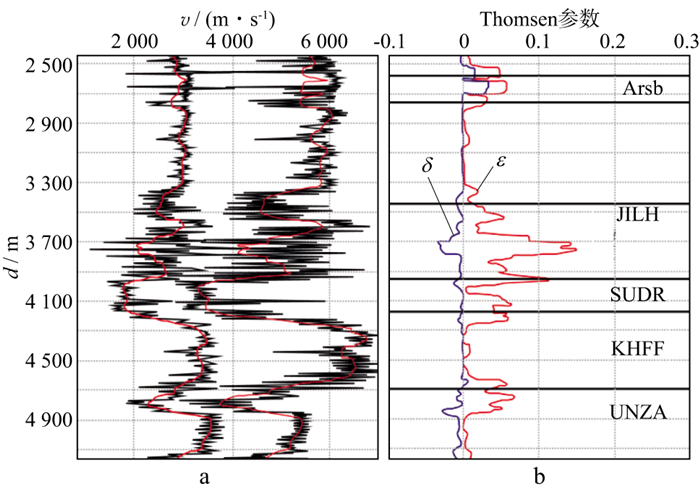
|
图 16 测井数据计算的等效速度(a)和各向异性参数(b)[30] |
在满足长波长假设时, 合成地震记录显示各向异性特征; 在波长满足强散射条件时, 合成地震记录显示散射特征; 在波长介于长波长假设和强散射条件之间时, 在合成地震记录中可同时观测到波场的各向异性特征和散射特征(图 17)[31]。
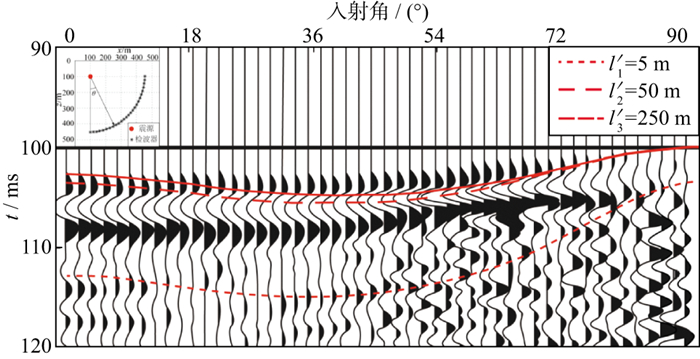
|
图 17 地震记录(Z分量)及不同平均长度对应的等效走时[32] |
为研究波长与平均长度的关系对波场的影响, LINER[30]根据测井中某段的最小主波长λmin, 选取不同平均长度进行研究。当λmin/l′≥3时, 随机型薄互层的长波长等效波场较精确。此时, 平均长度和波长都远远大于单层厚度。郭乃川等[32]通过波场数值模拟, 综合考虑了波长、平均长度和非均匀性尺度之间的关系对随机层状介质中的各向异性、频散和散射现象的影响。当λ/L>10(不满足强散射理论), 且λ < l′(不满足薄互层等效各向异性理论)时, 波长介于强散射理论极限值和薄互层等效各向异性理论极限值之间, 并不会出现强散射和显著的频散现象。当λ/L>10, 且λ < l′(不满足薄互层等效各向异性理论)时, 地震记录上同时存在各向异性和散射效应的影响(图 17)。地震波走时随入射角的增大而减小, 表现出介质的各向异性特征; 地震波垂向分量的尾波能量在大入射角时要显著高于小入射角时, 表现出介质的强散射特征; 入射角不同时, 地震波初至脉冲长度和振幅不同, 表现出介质的频散特征。
通过选取不同平均长度l′进行研究发现, 在平均长度较小(与非均匀性尺度相差不大)时, 等效走时明显大于波场数值模拟结果; 在平均长度很大(远远大于非均匀性尺度)时, 等效走时与波场数值模拟结果偏差明显减小, 在接近水平方向和垂直方向误差最小, 但在两者之间时误差仍较大(图 17)。所以, 主波长与非均匀性尺度之比λ/L < 10时, 即使平均长度远远大于非均匀性尺度(l′≫L), 仍无法准确计算地震波在随机型薄互层中的走时。
随机型薄互层长波长等效的适用条件及波场特征相对于韵律型薄互层更为复杂, 受到更多因素的影响, 仅仅根据主波长与非均匀性尺度的关系判断其成立条件是不严谨的。综合上述分析可以得到, 地震波在随机型薄互层中的传播特征依赖地震信号主波长λ、平均长度l′和非均匀性尺度L的关系: λ′≫l′′≫L时, 随机型薄互层才可等效为均匀横向各向同性介质; λ < l′时, 必然产生散射现象; λ < l′, λ/L>10时, 既不满足薄互层等效各向异性理论(λ < l′), 也不满足强散射理论(λ/L>10);λ < l′, λ/L < 10时, 同时存在强散射、频散和各向异性特征, 但此时的各向异性并非为均匀各向异性。
在随机型薄互层的研究中, 薄互层等效各向异性理论成立的极限值参考的仍然是韵律型薄互层的值(如波长与非均匀性尺度比满足λ/L≥10时, 近似成立), 需要找到适应其自身的参考值。基于统计学方法建立的随机型薄互层模型与测井实测的薄互层模型是有差异的。首先, 随机建模是建立在数学方法基础上, 将其应用到地球物理学的研究中需要满足实际的地质情况; 其次, 随机建模方法得到的类型有限, 不能考虑地层中所有类型的层状结构; 此外, 实际沉积岩中往往存在一定程度的内生各向异性(如页岩), 而不论是利用测井数据得到的薄互层模型还是随机建模的薄互层模型均假设组成层为各向同性介质。这种现象不仅存在于随机型薄互层中, 在韵律型薄互层中也存在, 从而导致建模计算的结果与地面实测数据不一致。
4 总结与展望等效各向异性理论是在BACKUS平均法的理论基础上进行变换和拓展, 从而建立起组成薄互层的单薄层与等效介质的弹性参数、波速等物理量之间的关系。前人研究已经证实, 对于韵律型薄互层而言, 短波长理论和长波长等效各向异性理论的适用范围与λ/d参数有关, 根据物理实验可以发现, 以上两种理论下等效速度之间存在一个过渡带, 且该过渡带的位置和宽度与λ/d值有关。同时, 不同材质的韵律型薄互层模型的物理模拟结果显示, 薄互层等效各向异性理论成立的λ/d有所不同。目前, 国际上普遍认可的是λ/d≥10。随机型薄互层的长波长等效相对于韵律型薄互层更为复杂, 地震波在随机型薄互层中的传播特征依赖地震信号主波长、平均长度、非均匀性尺度的关系, 而薄互层等效各向异性理论成立需满足平均长度远远大于非均匀性尺度, 且远远小于主波长的条件。
同时, 该理论仍存在一些不足, 需要进一步研究和验证。首先, 该理论应用的BACKUS平均法需满足假设: 波的传播方向与层面垂直(或近似垂直)。这大大局限了该方法的适用范围。因此, 需要对偏移距对长波长等效方法产生的误差进行更深入的研究。其次, 考虑到该理论的适用条件涉及到多个参数, 如薄互层总厚度、互层间阻抗比、震源频率等, 后续需要开展对上述各参数的研究, 以更全面地确定其适用条件。此外, 目前对该理论的适用条件研究主要基于纵波, 而横波是否有相同的结论, 需做进一步讨论分析。
长波长假设下, 薄互层可以等效成VTI介质, 在此过程中所涉及的参数个数大大减少, 使得薄互层反演成为可能。我国实际油气薄储层, 由于薄层调谐效应, 地震响应振幅微弱, 同相轴难以连续追踪, 因此, 在先验信息(测井、岩石物理实验等)约束下进行薄互层等效各向异性理论适用性的厘定, 进而确定适用模型及其参数来约束薄互储层的反演将成为实现油气薄储层参数反演的必由之路。
| [1] |
KOEFOED O, DE VOOGD N. The linear properties of thin layers, with an application to synthetic seismograms over coal seams[J]. Geophysics, 1980, 45(8): 1254-1268. DOI:10.1190/1.1441122 |
| [2] |
KALLWEIT R S, WOOD L C. The limits of resolution of zero-phase wavelets[J]. Geophysics, 1982, 47(7): 1035-1046. DOI:10.1190/1.1441367 |
| [3] |
陈守田, 孟宪禄. 薄互层储层预测方法[J]. 石油物探, 2004, 43(1): 33-36. CHEN S T, MENG X L. A method for prediction of reservoirs of thin interbeded layers[J]. Geophysical Prospecting for Petroleum, 2004, 43(1): 33-36. DOI:10.3969/j.issn.1000-1441.2004.01.008 |
| [4] |
宋维琪, 陈琛, 刘程, 等. 基于谱分析的谱峰数预测薄互层砂岩厚度[J]. 地球物理学进展, 2012, 27(6): 2470-2477. SONG W Q, CHEN C, LIU C, et al. Sandstone high prediction of alternating beds with spectral peak number on spectral analyses[J]. Progress in Geophysics, 2012, 27(6): 2470-2477. |
| [5] |
WIDESS M B. How thin is a thin bed[J]. Geophysics, 1973, 38(6): 1176-1254. DOI:10.1190/1.1440403 |
| [6] |
NEIDELL N S. Stratigraphic modeling and interpretation: Geophysical principles and techniques[J]. AAPG Special Memoir, 1977, 26: 389-416. |
| [7] |
徐伟慕, 郭平, 胡天跃. 薄互层调谐与分辨率分析[J]. 石油地球物理勘探, 2013, 48(5): 750-757. XU W M, GUO P, HU T Y. Thin interbed tuning and resolution analysis[J]. Oil Geophysical Prospecting, 2013, 48(5): 750-757. |
| [8] |
孙树海, 朱彦良. 薄互层条件下AVO技术的应用[J]. 地球物理学报, 1991, 34(1): 99-106. SUN S H, ZHU Y L. The application of AVO technique under the condition of thin interbed series[J]. Chinese Journal of Geophysics, 1991, 34(1): 99-106. DOI:10.3321/j.issn:0001-5733.1991.01.011 |
| [9] |
RVGER A, TSVANKIN I. Using AVO for fracture detection: analytic basis and practical solutions[J]. The Leading Edge, 1997, 16(10): 1942-1434. |
| [10] |
LIU Y, SCHMITT D R. Amplitude and AVO responses of a single thin bed[J]. Geophysics, 2003, 68(4): 1161-1168. DOI:10.1190/1.1598108 |
| [11] |
郭智奇, 刘财, 李向阳, 等. 非弹性层状介质地震波频变AVO响应模拟及分析[J]. 地球物理学报, 2016, 59(2): 664-672. GUO Z Q, LIU C, LI X Y, et al. Modeling and analysis of frequency-dependent AVO response in inelastic stratified media[J]. Chinese Journal of Geophysics, 2016, 59(2): 664-672. |
| [12] |
彭苏萍, 高云峰, 杨瑞召, 等. AVO探测煤层瓦斯富集的理论探讨和初步实践——以淮南煤田为例[J]. 地球物理学报, 2005, 48(6): 1475-1486. PENG S P, GAO Y F, YANG R Z, et al. Theory and application of AVO for detection of coalbed methane-A case from the Huainan coalfield[J]. Chinese Journal of Geophysics, 2005, 48(6): 1475-1486. DOI:10.3321/j.issn:0001-5733.2005.06.034 |
| [13] |
高静怀, 陈凤, 陈树民. 利用地震瞬时谱属性进行薄互层分析[J]. 煤田地质与勘探, 2005, 33(3): 67-71. GAO J H, CHEN F, CHEN S M. Using seismic instantaneous attributes to analyze thin interbeds[J]. Coal Geology & Exploration, 2005, 33(3): 67-71. DOI:10.3969/j.issn.1001-1986.2005.03.021 |
| [14] |
王濮, 金振奎, 李国发, 等. 薄层生物碎屑灰岩的地震属性检测[J]. 石油物探, 2007, 46(4): 390-393. WANG P, JIN Z K, LI G F, et al. Detection of thin-layer bioclastic limestone based on seismic attributes[J]. Geophysical Prospecting for Petroleum, 2007, 46(4): 390-393. DOI:10.3969/j.issn.1000-1441.2007.04.012 |
| [15] |
刘万金, 周辉, 袁三一, 等. 谱反演在地震属性解释中的应用[J]. 石油地球物理勘探, 2013, 48(3): 423-428. LIU W J, ZHOU H, YUAN S Y, et al. Application of spectral inversion in seismic attribute interpretation[J]. Oil Geophysical Prospecting, 2013, 48(3): 423-428. |
| [16] |
SAMS M S, ATKINS D, SAID N, et al.Stochastic inversion for high resolution reservoir characterization in the central Sumatra Basin[C]//Expanded Abstracts of SPE Asia Pacific Improved Oil Recovery Conference.Kuala Lumpur, Malaysia: Society of Petroleum Engineers, 1999: 257-260
|
| [17] |
SRIVASTVA R P, SEN M K. Stochastic inversion of prestack seismic data using fractal based initial models[J]. Geophysics, 2010, 75(3): R47-R59. DOI:10.1190/1.3379322 |
| [18] |
黄捍东, 赵迪, 任敦占, 等. 基于贝叶斯理论的薄层反演方法[J]. 石油地球物理勘探, 2011, 46(6): 919-924. HUANG H D, ZHAO D, REN D Z, et al. A thin bed inversion method based on bayes theory[J]. Oil Geophysical Prospecting, 2011, 46(6): 919-924. |
| [19] |
王保丽, 印兴耀, 丁龙翔, 等. 基于FFT-MA谱模拟的快速随机反演方法研究[J]. 地球物理学报, 2015, 58(2): 664-673. WANG B L, YIN X Y, DING L X, et al. Study of fast stochastic inversion based on FFT-MA spectrum simulation[J]. Chinese Journal of Geophysics, 2015, 58(2): 664-673. |
| [20] |
POSTMA G W. Wave propagation in a stratified medium[J]. Geophysics, 1955, 20(4): 780-806. DOI:10.1190/1.1438187 |
| [21] |
BACKUS G E. Long-wave elastic anisotropy produced by horizontal layering[J]. Journal of Geophysical Research, 1962, 67(11): 4427-4440. DOI:10.1029/JZ067i011p04427 |
| [22] |
HELBIG K. Anisotropy and dispersion in periodically layered media[J]. Geophysics, 1984, 49(4): 364-373. DOI:10.1190/1.1441672 |
| [23] |
HELBIG K. Transverse isotropy in exploration seismics[J]. Geophysical Journal of the Royal Astronomical Society, 1984, 76(1): 79-88. DOI:10.1111/j.1365-246X.1984.tb05024.x |
| [24] |
张中杰, 何樵登. N个薄层介质组合引起的视各向异性[J]. 吉林大学学报(地球科学版), 1990, 20(2): 223-234. ZHANG Z J, HE Q D. Apparent anisotropy produced by the coupling of N thin-layered media[J]. Journal of Jilin University(Earth Science Edition), 1990, 20(2): 223-234. |
| [25] |
LEVIN F K. Seismic velocities in transversely isotropic media[J]. Geophysics, 1979, 44(5): 918-936. DOI:10.1190/1.1440985 |
| [26] |
董良国, 李国治, 杨泉荣, 等. 横向各向同性介质中弹性波的物理模拟[J]. 石油物探, 1999, 38(1): 76-85. DONG L G, LI G Z, YANG Q R, et al. Physical modeling elastic waves in transversely isotropic medium[J]. Geophysical Prospecting for Petroleum, 1999, 38(1): 76-85. |
| [27] |
吴国忱, 罗彩明, 梁楷. TTI介质弹性波频率-空间域有限差分数值模拟[J]. 吉林大学学报(地球科学版), 2007, 37(5): 185-195. WU G C, LUO C M, LIANG K. Frequency-space domain finite difference numerical simulation of elastic wave in TTI media[J]. Journal of Jilin University(Earth Science Edition), 2007, 37(5): 185-195. |
| [28] |
HSU K, ESMERSOY C, SCHOENBERG M. Seismic velocities and anisotropy from high-resolution sonic logs[J]. Expanded Abstracts of 58th Annual Internat SEG Mtg, 1988, 114-116. |
| [29] |
CARCIONE J M, KOSLOFF D, BEHLE A. Long wave anisotropy in stratified media: A numerical test[J]. Geophysics, 1991, 56(2): 245-254. DOI:10.1190/1.1443037 |
| [30] |
LINER C L, FEI T W. Layer-induced seismic anisotropy from full-wave sonic logs: Theory, application, and validation[J]. Geophysics, 2006, 71(6): D183-D190. DOI:10.1190/1.2356997 |
| [31] |
KERNER C. Anisotropy in sedimentary rocks modeled as random media[J]. Geophysics, 1992, 57(4): 564-576. DOI:10.1190/1.1443270 |
| [32] |
郭乃川, 王尚旭, 董春晖, 等. 地震勘探中小尺度非均匀性的描述及长波长理论[J]. 地球物理学报, 2012, 55(7): 2385-2401. GUO N C, WANG S X, DONG C H, et al. Description of small scale inhomogeneities in seismic prospecting and long wavelength theory[J]. Chinese Journal of Geophysics, 2012, 55(7): 2385-2401. |
| [33] |
MELIA P J, CARLSON R L. An experimental test of P-wave anisotropy in stratified media[J]. Geophysics, 1984, 49(4): 374-378. DOI:10.1190/1.1441673 |
| [34] |
MARION D, MUKERJI T, MAVKO G. Scale effects on velocity dispersion: From ray to effective medium theories in stratified media[J]. Geophysics, 1994, 59(10): 1613-1619. DOI:10.1190/1.1443550 |
| [35] |
李跃, 徐果明, 施行觉, 等. 薄互层等效各向异性的实验研究[J]. 石油地球物理勘探, 1995, 30(4): 513-517. LI Y, XU G M, SHI X J, et al. Experiment in equivalent anisotropy of thin interbedded medium[J]. Oil Geophysical Prospecting, 1995, 30(4): 513-517. |
| [36] |
杨晓松, 马瑾, 刘力强. 周期性层状介质中超声波传播的实验研究[J]. 地震地质, 2004, 26(3): 484-491. YANG X S, MA J, LIU L Q. Experimental study on the propagation of acoustic waves through periodically layered media[J]. Seismology and Geology, 2004, 26(3): 484-491. DOI:10.3969/j.issn.0253-4967.2004.03.012 |
| [37] |
魏建新, 狄帮让. 周期层状介质对纵波速度影响的实验研究[J]. 石油地球物理勘探, 2010, 45(5): 661-666. WEI J X, DI B R. The experimental studies on influence of periodic layered media to P wave velocity[J]. Oil Geophysical Prospecting, 2010, 45(5): 661-666. |
| [38] |
王赟, 杨春, 芦俊. 薄互层弹性波反演面临的困境[J]. 地球物理学报, 2018, 61(3): 1118-1135. WANG Y, YANG C, LU J. Dilemma faced by elastic wave inversion in thinly layered media[J]. Chinese Journal of Geophysics, 2018, 61(3): 1118-1135. |
| [39] |
HELBIG K. Elastische wellen in anisotropen medien[J]. Gerlands Beiträge zur Geophysik, 1958, 67: 256-288. |
| [40] |
ANDERSON D L. Elastic wave propagation in layered anisotropic media[J]. Journal of Geophysical Research, 1961, 66(9): 2953-2964. DOI:10.1029/JZ066i009p02953 |
| [41] |
HASKELL N A. The dispersion of surface waves on multilayered media[J]. Bulletin of the Seismological Society of America, 1953, 43(1): 17-34. |
| [42] |
STONELY R. The seismological implications of aeolotropy in continental structure[J]. Monthly Notices of the Royal Astronomical Society, 1949, 5(8): 222-232. |
| [43] |
DALEY P F, HRON F. Computation of synthetic seismograms for a thin layered periodic structure[J]. Canadian Journal of Earth Sciences, 1982, 19(7): 1449-1453. DOI:10.1139/e82-125 |
| [44] |
LYAKHOVITSKIY F M. Transverse isotropy of thinly layered media[J]. Geophysical Journal of the Royal Astronomical Society, 1984, 76(1): 71-77. DOI:10.1111/j.1365-246X.1984.tb05023.x |
| [45] |
SCHOENBERG M, MUIR F. A calculus for finely layered anisotropic media[J]. Geophysics, 1989, 54(5): 581-589. DOI:10.1190/1.1442685 |
| [46] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [47] |
O'DOHERTY R F, ANSTEY N A. Reflections on amplitudes[J]. Geophysical Prospecting, 1971, 19(3): 430-458. DOI:10.1111/j.1365-2478.1971.tb00610.x |
| [48] |
SCHOENBERGER M, LEVIN F K. Apparent attenuation due to intrabed multiples[J]. Geophysics, 1974, 39(3): 278-291. DOI:10.1190/1.1440427 |
| [49] |
MARION D, COUDIN P. From ray to effective medium theories in stratified media: An experimental study[J]. Expanded Abstracts of 62nd Annual Internat SEG Mtg, 1992, 1341-1343. |
| [50] |
TANG X, BURNS D R. Seismic scattering and velocity dispersion due to heterogeneous lithology[J]. Expanded Abstracts of 62nd Annual Internat SEG Mtg, 1992, 824-827. |
| [51] |
王书伦. 薄互层合成地震记录制作方法研究[D]. 青岛: 中国海洋大学, 2012 WANG S L.The producing method research of synthetic seismogram of thin interbedding[D].Qingdao: Ocean University of China, 2012 |
| [52] |
李雪英, 文慧俭, 陈树民, 等. 等厚薄互层时频特征的正演模拟[J]. 地球物理学报, 2013, 56(3): 1033-1042. LI X Y, WEN H J, CHEN S M, et al. Forward modeling studies on the time-frequency characteristics of isopachous thin interbeding[J]. Chinese Journal of Geophysics, 2013, 56(3): 1033-1042. |
| [53] |
WHITE J E, ANGONA F A. Elastic wave velocities in laminated media[J]. Journal of the Acoustical Society of America, 1955, 27(2): 310-317. DOI:10.1121/1.1907520 |
| [54] |
RYTOV S M. Acoustical properties of a thinly laminated medium[J]. Soviet Physics Acoustics, 1956, 67(2): 68-80. |
| [55] |
IMHOF M G. Scale dependence of reflection and transmission coefficients[J]. Geophysics, 2003, 68(1): 322-336. DOI:10.1190/1.1543218 |
| [56] |
曹丹平. 基于Backus等效平均的测井资料尺度粗化方法研究[J]. 石油物探, 2015, 54(1): 105-111. CAO D P. The upscaling method of the well logging data based on backus equivalence average method[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 105-111. DOI:10.3969/j.issn.1000-1441.2015.01.015 |
| [57] |
BANIK N C. An effective anisotropy parameter in transversely isotropic media[J]. Geophysics, 1987, 52(12): 1654-1664. DOI:10.1190/1.1442282 |




