2. 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
2. Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
因地下岩石具有不同程度的弹性各向异性(以下简称各向异性)特征, 故地震波在地下岩石中传播时具有独特的传播机理, 主要包括以下6个方面的特点: ①地震波速度是传播方向的函数; ②地震波振幅与偏移距之间的关系是各向异性参数的函数; ③除几个特殊方向外, 各向异性介质中通常不存在理论意义上的纵波与横波, 只存在物理特性与之相似的准纵波与准横波; ④不同类型体波间相互耦合; ⑤横波在各向异性介质中传播时会发生分裂; ⑥面波的速度频散依赖于传播方向。
上述传播机理一方面增加了地震勘探的难度, 另一方面也为利用地震勘探资料确定岩石的各向异性参数提供了思路与依据。各向异性参数与岩石岩性、含裂隙性、裂隙发育参数以及裂隙内的充填物性质等因素密切相关, 因此, 研究地下岩石的各向异性问题对于提高裂缝型油气藏与岩性油气藏的勘探精度具有重要意义。目前, 解决地震勘探中地下岩石各向异性问题的思路主要包括以下两种: ①采集并利用反射纵波资料进行地下各向异性地层的准确成像并反演各向异性参数[1-4]; ②利用多分量地震勘探技术实现各向异性地层的纵、横波联合成像与反演[5-7]。前者不增加采集成本, 仅需在资料处理与解释阶段研发相应技术就可以实现各向异性地层的勘探, 但存在信息单一、地震解释的多解性严重等不足; 后者采用成本较高的多波地震技术获取纵、横波信息, 将地震波视作弹性波, 通过纵、横波联合解释降低地震解释的多解性。
利用多波地震技术解决各向异性地层勘探问题的优势包括以下5个方面: ①将地震波视作弹性波, 理论假设与实际情况接近, 具有理论基础的先天优势; ②横波对由裂隙引起的各向异性远较纵波敏感, 横波分裂为裂隙发育参数的确定和裂隙型油气藏探测提供了良好的思路; ③纵、横波速度比为岩性识别提供依据, 有利于提高岩性油气藏的勘探精度; ④综合应用纵、横波振幅信息可识别真假亮点, 有利于直接寻找油气藏; ⑤横波能在某些纵波勘探未能获得高质量地震资料的地区得到良好的成像结果。基于上述原因, 多波地震技术受到了业界的广泛重视, 并得到了快速发展。
多分量地震资料处理是各向异性多波地震技术的重要组成部分, 深度域地震资料成像是地震资料处理的关键步骤之一, 弹性波逆时偏移技术是当前业界重点发展的多分量地震资料深度域成像技术之一。
地震波逆时偏移思想起源于各向同性纵波成像领域, WHITMORE[8]、BAYSAL等[9]以及MCME-CHAN[10]几乎同时进行了二维声波方程逆时偏移算法的研究并发表了研究成果, 之后诸多学者从不同角度研究了声波方程的叠前逆时深度偏移技术[11-14], 并逐步形成了相对成熟的声波方程逆时偏移技术体系。与此同时, SUN等[15]将逆时偏移方法从声波推向了弹性波领域, 首先利用弹性波动方程进行了多分量地震数据的延拓, 然后在算法上实现了基于各向同性介质的弹性波逆时偏移, 最后利用三分量VSP模拟数据测试了算法的有效性。随后, 学者们又分别利用弹性波方程延拓算法[16-17]、纵、横波分离方法[18-19]、波场分解技术[20]、纵、横波成像方法[21]、偏移噪声压制技术[22]以及偏移效率提升方法[23-26]对弹性波逆时偏移技术进行了发展与完善。目前, 弹性波逆时偏移技术的研究已经从各向同性算法发展为各向异性算法[5, 27-43], 并在各向异性介质的弹性波方程数值求解方法[27-29, 33-35]、纵、横波解耦算法[30-32, 36-42]和纵、横波成像思路与方法[28-31]等方面取得了一系列研究成果。在偏移效率提升方面, 各向同性和声波领域的加速思路[23-26, 43]也适用于各向异性介质的弹性波逆时偏移研究。
本文主要分析各向异性介质中弹性波逆时偏移技术的研究现状与存在的问题, 由于横向各向同性(transverse isotropy, TI)介质模型是最具代表性的地层各向异性模型, 因此本文的综述对象仅限于TI介质。首先给出TI介质中弹性波方程逆时偏移的基本流程, 然后分析该流程中各个环节的研究现状和存在的主要问题, 最后提出下一步研究建议。依据对称轴倾角的不同, TI介质可以分为具有垂直对称轴的横向各向同性(vertical transverse isotropy, VTI)介质、具有水平对称轴的横向各向同性(horizontal transverse isotropy, HTI)介质和具有倾斜对称轴的横向各向同性(tilted transverse isotropy, TTI)介质3种, 其中VTI和HTI介质实质上是特殊的TTI介质, 因此, TTI与TI是等价的。除非显式说明, 本文中的TI介质一律是指TTI介质。
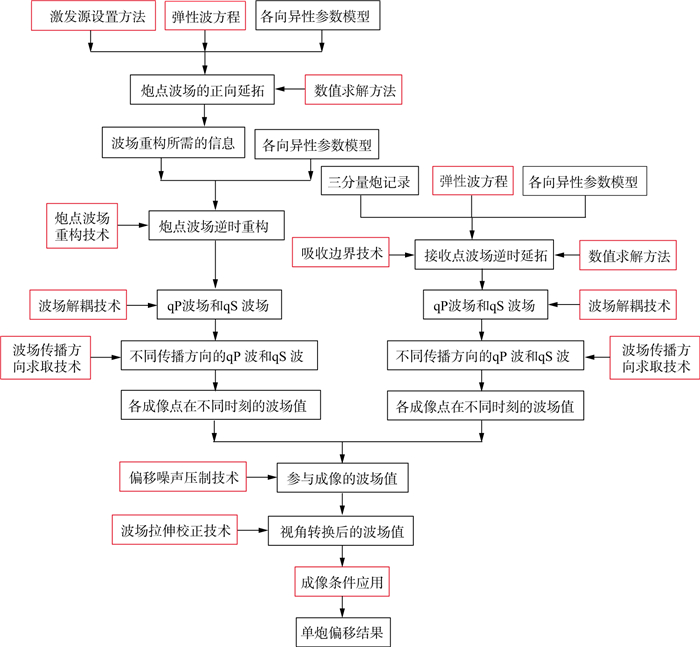
1 TI介质中弹性波方程逆时偏移的实现思路与基本流程与各向同性弹性波逆时偏移一样, TI介质的弹性波逆时偏移也由3部分组成: ①炮点波场的正向延拓; ②接收点波场的逆时延拓; ③纵、横波成像。为开拓并行机会, 在炮点波场正向延拓后还需要进行一次逆时重构, 实现炮点波场与接收点波场的同步延拓, 从而减少临时文件的读写量, 提升计算效率。同时, 为使偏移结果具有明确的物理意义, 在炮点波场重构和接收点波场逆时延拓过程中需要进行纵、横波的解耦, 将每一时间步长的炮点和接收点弹性波场解耦为准纵波(quasi-P, qP)和准横波(quasi-S, qS)场。此外, 为了压制层间反射等偏移噪声, 在延拓过程中需要按照传播方向对炮、检波场进行分解, 以得到沿不同方向传播的qP波和qS波, 后续只利用传播方向相反的波场进行纵、横波的互相关成像。TI介质弹性波逆时偏移计算流程如图 1所示。
|
图 1 TI介质弹性波逆时偏移计算流程 |
TI介质弹性波逆时偏移的核心技术包括矢量波场延拓算法和纵、横波成像方法两个方面。图 1中激发源设置方法、弹性波方程数值求解方法、吸收边界技术和炮点波场重构技术共同组成矢量波场延拓算法; 波场解耦技术、波场传播方向求取技术、偏移噪声压制技术、波场拉伸校正技术和成像条件应用共同组成纵、横波成像技术。本文从这两个方面对TI介质中弹性波逆时偏移研究现状进行综述, 深度域各向异性参数建模不在本文讨论之列。
2 TI介质中弹性波方程延拓技术的研究现状TI介质中矢量波场延拓算法的研究主要集中于方程的数值求解方法、吸收边界条件、随机边界炮点波场重构技术和计算效率提升等方面。激发源的设置方法是决定弹性波逆时偏移效果的关键因素之一。
2.1 激发源设置方法弹性波逆时偏移通常利用炮点波场和接收点波场的互相关实现地下地层的纵、横波成像, 炮点波场正向延拓时的震源设置方法对多分量逆时偏移的成像结果有显著影响。不合理的震源子波会弱化炮点波场与接收点波场之间的相关性, 降低成像准确性和分辨率[44]。相同条件下, 当震源子波与地震记录的子波一致时, 构造成像最准确, 当二者不一致时, 即使是水平反射界面的成像结果也会出现明显误差, 表现为: ①界面深度不准确; ②成像结果的频率与三分量地震记录的频率差别大导致偏移剖面的分辨率变差。因此, 设置合理的震源子波是获取准确的逆时偏移成像结果的前提。
杨仁虎等[45]通过模型实验表明: 各向同性声波方程逆时偏移中, 如果炮点波场延拓的震源主频与模型数据的主频不一致, 那么地震偏移结果会出现位置偏离和相位畸变, 采用正确的震源子波进行波场延拓, 这种误差则会消失, 这说明震源子波的主频对逆时偏移结果有着显著的影响。由于声波和弹性波逆时偏移的成像思路相同, 故上述结论同样适用于各向异性弹性波逆时偏移, 并可以进一步推论: 震源子波的类型、形态、能量以及频宽等参数均会严重影响各向异性弹性波逆时偏移的成像精度。但截至目前, 该领域的相关研究较少, 多数研究结论只停留在感性认识阶段, 尚未上升至理论高度, 无法用于生产实践。
实际资料处理中, 目前常用的震源设置思路主要包括以下两种: ①将理论子波作为炮点波场正向延拓的震源函数[2, 4-6, 9, 13-15], 理论子波主频和振幅由野外炮记录的频谱和能量分析结果确定; ②采用合适的反演方法由炮记录反演子波并将其作为炮点波场的震源函数[46-47]。第1种思路假定野外震源的子波与理论子波完全一致, 但实际情况往往不满足这一假设, 因此在对实际三分量地震数据进行各向异性偏移时往往很难得到满意的结果。第2种思路可以降低偏移子波与炮记录反演子波不一致对偏移结果产生的影响, 但受野外地震数据信噪比和地层对地震子波改造作用等因素的影响, 基于叠前单炮记录的子波反演存在许多技术难题。目前比较普遍的做法是利用地震反演领域中子波求取技术反演子波, 而后将其作为逆时偏移的震源函数进行炮点波场正向延拓[44], 这种方法一定程度上减小了由震源子波设置造成的误差, 但在采用这种方法进行子波求取时, 其输入数据往往是经过各种前期处理后的地震数据, 利用这样的地震数据求取的子波不一定能与炮记录的原始震源子波完全对应, 因此有必要就逆时偏移问题研发针对性的子波提取技术。
对于三分量地震数据, 震源子波函数的求取更为困难, 原因如下: 三分量地震数据包含一个垂直分量和两个水平分量, 采用基于单分量地震数据的子波求取技术可能会得到3个完全不同的子波, 而事实上该三分量地震数据对应同一个纵波源, 它们的震源子波应该是相同的, 但由于地层对纵、横波的改造作用不同, 三分量地震数据的纵、横波会具有截然不同的频谱, 因此设置弹性波逆时偏移中的震源子波时, 需要同时考虑炮记录的3个分量。目前相关研究工作与成果未见公开发表。
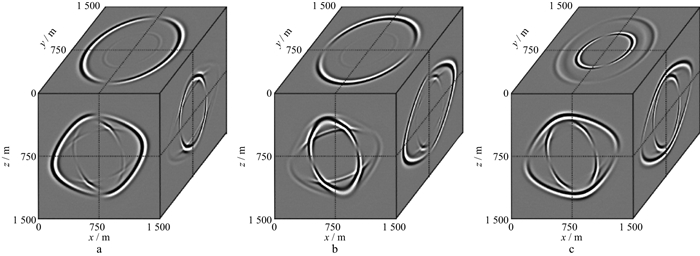
2.2 TI介质中弹性波方程的数值解法各向异性弹性波逆时偏移中, 炮点和接收点波场的延拓和重构都需要采用各向异性弹性波方程数值解法, 有限差分法是目前该领域最常用的方法, 有限差分中的常规网格技术、交错网格技术和旋转交错网格技术均可用于弹性波方程数值求解。但对于TI介质中一阶应力-速度弹性波方程的数值求解问题, 由于各向异性弹性波方程中的许多分量同时包含了多个坐标轴方向的偏导数项, 因此交错网格技术无法直接用于解决该问题, 只能将交错网格技术与空间插值技术相结合来实现TI介质弹性波方程的正向或逆时延拓。对于复杂模型而言, 空间插值处理不当会导致计算误差增大和不稳定性增加。为此SAENG-ER等[35]提出利用旋转交错网格求取一阶应力-速度方程的方法, 因为在旋转交错网格中, 所有应力分量和位移分量的位置相同, 求取空间导数无需插值, 所以在TI介质中利用旋转交错网格有限差分法求解弹性波方程, 得到的结果精度更高。此外, 由于旋转交错网格中的位移分量位于相同的网格点, 因此在波场分离时不需要进行位移分量的位置校正[35]。图 2为利用旋转交错网格有限差分技术得到的三维均匀TI介质正向延拓波前快照, 利用该技术能够实现TI介质中弹性波场的高精度延拓。图 2对应模型的各向异性参数如下: 沿对称轴方向的纵波速度为5000m/s, 沿对称轴方向的横波速度为3000m/s, 密度为2690kg/m3, Thomsen参数ε=0.2, γ=0.15, δ=-0.2, 对称轴倾角为20°, 测线方位角为30°。
|
图 2 利用旋转交错网格有限差分技术得到的三维均匀TI介质正向延拓波前快照 a vx分量; b vy分量; c vz分量 |
接收点波场逆时延拓时, 可利用吸收边界消除计算空间截断引起的误差。多用于地震正演的吸收边界技术可以解决接收点波场逆时延拓中的截断边界问题。在地震正演领域常用的边界条件主要包括单程波方程边界条件[48-49]、衰减边界条件[50]和完全匹配层(perfectly matched layer, PML)边界条件[51-53], 其中, PML边界条件对外行波的吸收性能优于前两类[54-55], 因此PML边界条件的应用范围最为广泛。
PML边界条件的研究始于电磁模拟领域[51], 其基本思路为: 首先在模拟区域外增加吸收层, 然后在该吸收层内将波场分裂为平行于坐标轴方向的3个分量, 再在各分量所满足的微分方程中增加阻尼项得到PML微分方程, 最后通过求解该微分方程来消除边界反射。BERENGER[51]证明了在不考虑离散误差的前提下, 该边界条件能够很好地吸收所有入射角和所有频率的外行波, 因此PML被迅速应用于地震波数值模拟[56-57]。之后, 学者们又采用复坐标变换法对PML层的微分方程进行了一般性推导[58-60], 简化了PML的实现步骤, 并将其应用于各向异性介质的地震模拟中[60]。研究发现PML边界条件存在两点不足: ①当入射波频率很低时, 衰减系数会出现奇异值, 使边界产生虚假反射; ②边界无法吸收高角度外行波。
为解决上述问题, JUZUOGLU等[61]通过引入避免衰减系数出现奇异值的频移因子和用于弯曲PML区内地震波传播方向的尺度因子, 对复坐标伸展变换形式进行了修正, 最终得到了复频移PML(complex frequency shifted PML, CFS-PML)边界条件, 该边界条件对瞬逝波吸收效果显著[62]。由于CFS-PML边界条件的应用需要引入过多的辅助变量以及进行大量的卷积运算, 因而导致计算量过大, 因此这种方法刚被提出时并未获得广泛认同, 目前多采用无需卷积运算的分裂PML边界条件来解决上述问题[54]。
分裂PML边界条件存在以下3点不足: ①三维条件下, 因波场分裂而导致引入的辅助变量个数过多, 增加了内存负担; ②边界处角点、棱边和面需采用不同公式进行处理, 增加了编程复杂性; ③波场分裂方式的物理意义不明确, 对分裂波场进行合并可能会引入误差。刘有山等[63]的工作降低了分裂PML边界条件的内存需求与编程复杂度, 但并未从根本上解决问题。此外, CFS技术的广泛应用会放大分裂PML边界条件的种种不足。
根据LUBBERS等[64]提出的卷积递归计算方法, RODEN等[65]提出的一种基于CFS的递归卷积PML边界条件, 该边界条件无需分裂波场, 也可提高大入射角外行波的吸收率并降低编程复杂度。随后MARTIN等[34]将其应用于各向异性介质, 提高了大入射角外行波的吸收效果。杜启振等[66]给出了二维TTI介质弹性波模拟的无分裂复频移PML, 并结合自由边界条件实现了自由地表条件下的各向异性弹性波数值模拟, 此后, 有学者采用递归思路先后提出了递归积分PML[67]和递归微分PML[68]。这3种PML边界条件对外行波的吸收效果接近, 但递归积分PML的实现过程过于复杂, 递归微分PML最容易编程实现。至此, 边界条件已基本满足低阶时间离散格式下的生产需求。
由于递归类PML所采用的递归方式难以应用于高阶时间离散格式的弹性波方程中, 为解决该问题, 又有学者提出了辅助微分PML(auxiliary differential equation PML, ADE-PML)[68-69]和近似PML(nearly PML, N-PML)边界条件[70], 这两种边界条件均可以较好地适应高阶差分格式的弹性波方程。
上述边界条件均通过在模型外增加PML来压制边界反射[71], 因此PML厚度影响着边界吸收效果。相关的研究工作还基本处在定性描述阶段[72], 尚未上升到定量层面, 这将是该领域的后续研究重点。
2.4 炮点波场逆时重构技术弹性波逆时偏移中, 通常在相反的时间方向上进行炮点和接收点波场的构建, 而互相关成像条件的应用前提要求二者必须具有相同的时间顺序, 这种不一致性增加了逆时偏移的实现难度。直观的方法是通过频繁的磁盘访问来获取相同时刻的炮、检波场值, 虽然这种方法不增加计算量, 但频繁的磁盘访问会降低并行程序的执行效率, 因此这种方法实用价值不高。
波场重构技术可以克服上述不足, 目前的波场重构方法包括以下4种。①基于检查点技术的炮点波场重构方法[25, 73], 该方法在炮点波场正传过程中每隔一定时间间隔设置检查点并储存该点波场, 重构时从检查点出发利用递推的方法重构任意时刻的波场。这种方法的波场重构精度取决于检查点数, 检查点数过少会降低重构精度, 增加检查点个数则会增大磁盘访问量。此外, 该方法还存在重算率过高的不足。陈桂廷等[74]对该方法进行了优化, 他们在满足采样定理的前提下首先对相邻检查点间的波场进行规则抽样, 然后将抽样波场作为插值节点, 最后利用多项式插值算法逆时重构炮点波场。该方法虽然降低了重算率, 但改进后的算法重算率仍大于2。②基于边界存储策略的炮点波场逆时重构方法[75]。其实现思路为: 在炮点波场正向延拓过程中记录镶边区域所有时刻的波场值和所有网格点最后两个时刻的波场值, 以此作为初始条件和边界条件来重构炮点波场。该方法的重算率为2, 可较大幅度地降低临时文件的存储量。边界临时文件存储量取决于镶边层数, 镶边层数过大造成存储量迅速增大, 镶边层数过小则会增大边界反射的影响。③基于有效边界存储策略的重构方法[23]。该方法改进了边界存储策略, 只需存储N层边界波场(N为差分阶数), 因此可在不改变重算率的前提下进一步减小存储压力。④基于随机边界技术的炮点波场重构方法[24]。随机边界技术通过在模型外面增加随机弹性参数层来散射边界区域的外行波, 以削弱边界反射波的相干性, 减少边界反射对成像的影响。该方法实现步骤如下: 首先在模拟外设置随机弹性参数层, 然后在所有计算区域进行炮点波场正向延拓, 最后以正向延拓的最后两个时刻的波场值为初始条件进行炮点波场的逆时重构。该方法的重算率为2, 无需进行磁盘读写。
综上可知, 现有的波场重构方法中, 基于随机边界技术的炮点波场重构方法具有最低的重算率和磁盘读写量, 并且计算效率最高。因此, 基于随机边界技术的炮点波场重构方法成为目前逆时偏移领域的主流方法。
随机边界技术的关键在于随机层内弹性参数的选择, 合理的随机弹性参数至少应该满足如下3个条件: ①具有很强的波场散射能力, 必须能破坏边界反射波场的相干性; ②随机弹性参数应能在一定的网格大小条件下确保数值求解算法的稳定与精度; ③随机弹性参数之间应满足岩石物理的一般规律与严格的物理理论。TI介质的各弹性参数并非独立, 它们之间应满足物理理论与岩石物理的一般规律, 独立产生的各个参数组合在一起很有可能会创造出一种根本不可能存在的介质, 在这样的介质中进行弹性波延拓可能会引起不可预知的错误。
上述3个条件是各向异性随机边界研究中亟待解决的问题。目前的研究主要以解决第1个问题为主, CLAPP[24]采用线性随机函数构建声波方程的随机边界, 这种方法要求随机层厚度较大, 否则会在边界外层形成强能量的相干反射。张丽美等[75]采用自相关函数类型、相关长度和速度扰动标准差3个参数描述随机介质, 并构建参数化的随机边界, 测试结果表明: 指数型自相关函数的随机介质对波场具有良好的散射效果, 提高扰动速度可以增强波场的散射效果, 考虑到算法稳定性, 当相关长度与波长接近且速度扰动标准差约为30%时, 随机边界的效果最佳。SHEN等[76]通过控制随机速度颗粒的大小和形态来构建随机边界, 研究结果显示, 在不增加随机边界厚度的情况下, 采用大尺度形态随机的速度颗粒可以有效地散射波场的低频分量, 削弱边界反射波的相干性。此外, 增大随机层厚度也可以在一定程度上解决该问题, 但需要更多内存和计算时间。
第3个问题的本质是多参数随机建模, 这些参数相互制约且必须满足相应的物理理论和岩石物理学规律。目前针对上述问题的研究很少, 也未见到理论严谨且具实用价值的成果。刘国峰等[77]在TI介质qP波方程逆时偏移中, 采用如下思路构建各向异性随机边界: 首先将随机层的Thomsen参数[78]设为常数, 该常数既可以是各向同性的, 也可以是各向异性的, 然后只对qP波速度进行随机建模, 并通过约束条件保持算法稳定。从表面上看, 似乎解决了上述两个问题, 但其实质是将多参数问题简化为单参数问题, 这种简化可能会导致随机边界绕射波场的相关性变强, 增加了偏移噪声。目前公开发表的文献中尚未检索到基于多参数的随机边界弹性参数建模相关研究成果。对于该问题, 目前存在两种可行的解决方案: ①首先将各弹性参数组合为一种新的数据类型, 确保组成该类型的各元素之间满足对应的约束关系, 即可将这种多参数问题简化为一种广义的单参数问题, 再将单参数领域的随机建模技术推广至广义单参数层面, 最终实现多参数随机建模。②由于随机介质领域的理论与方法相对完善, 引入各向异性随机介质领域的相关理论, 由此得到的各向异性随机参数自动满足数值稳定性条件与岩石物理规律。需要说明的是, 上述两种思路目前仅作初步设想, 实际操作中可能出现新的问题, 如背景参数与扰动参数之间的关系如何确定, 随机层厚度如何设置以及各参数扰动方向之间的关系等, 这些都将成为今后的研究重点。
3 TI介质弹性波方程逆时偏移纵、横波成像方法研究现状 3.1 成像条件TI介质弹性波方程逆时偏移的目标是实现纵、横波的准确成像, 这对成像条件提出了3个要求: ①偏移结果能够准确反映地层的构造形态; ②偏移结果要有明确的物理意义, 即成像结果必须是独立的纵波剖面和横波剖面, 而不是纵、横波耦合在一起的水平分量剖面和垂直分量剖面; ③偏移结果具有较高的信噪比。因此, 各向异性弹性波逆时偏移的理想成像条件可以表示为:
| $I_{\mathrm{P}}(x, y, z)= \ \frac{\sum\limits_{i=1}^{N}\left[\sum\limits_{t=0}^{t_{\max }} s_{\mathrm{P}, \phi_{i}}(x, y, z, t) r_{\mathrm{P}, \phi_{i}}(x, y, z, t)\right]}{\sum\limits_{t=0}^{t_{\max }} s_{\mathrm{P}}(x, y, z, t)^{2}}$ | (1a) |
| $I_{\mathrm{S}}(x, y, z)= \\ \frac{\sum\limits_{i=1}^{N}\left[\sum\limits_{t=0}^{t_{\max }} s_{\mathrm{P}, \phi_{i}}(x, y, z, t) r_{\mathrm{S}, \phi_{i}}(x, y, z, t)\right]}{\sum\limits_{t=0}^{t_{\max }} s_{\mathrm{P}}(x, y, z, t)^{2}}$ | (1b) |
式中: x, y, z分别为三维直角坐标系的3个坐标; t为时间; tmax为记录长度; IP、IS分别为纵、横波成像结果; sP和sP,ϕi均为炮点纵波场; rP,ϕi, rS,ϕi分别为接收点纵、横波场; i为波场传播方向, i=1, 2, 3, …, N; N为用于成像的波场传播方向数量。
(1) 式起初仅应用于各向同性逆时偏移[20-21], 应用于各向异性逆时偏移时, 需要得到不同时刻的空间域纵、横波解耦波场和各成像点在不同时刻的纵、横波传播方向两方面的信息。目前针对这两方面的研究尚不成熟, 有待进一步完善。
TI介质弹性波逆时偏移成像条件的研究过程就是将已有技术向(1)式所代表的各向异性逆时偏移技术不断逼近的过程。陈可洋[28]在二维VTI介质逆时偏移中, 利用激发时间成像条件得到了水平和垂直分量的偏移成像结果, 该结果反映了地层的构造形态, 但不满足后两个成像条件要求; 杜启振等[29]引入坡印廷矢量来压制二维VTI介质逆时偏移中的低频噪声, 以满足波场成像的第1个要求, 但得到的成像结果仍然不是纵波剖面和横波剖面; 周进举等[30]改进了二维VTI介质逆时偏移的成像条件, 在弹性波正向和逆时延拓时首先通过波场解耦得到qP波和qS波, 然后利用qP波和qS波的坡印廷矢量得到了纵、横波的传播方向并据此实现了波场分解, 最后利用分解后的波场得到纵、横波偏移成像结果, 上述方法兼顾了弹性波逆时偏移成像的3个要求, 但成像结果存在明显的波型泄露。王娟等[31]采用极化投影法实现了二维TI介质中的纵、横波解耦, 得到的结果最接近(1)式, 但由于缺乏TI介质中纵、横波传播方向的求取技术, 故未能实现基于波场分解的互相关成像, 此外, 该方法的效果还有待三维模型的检验。
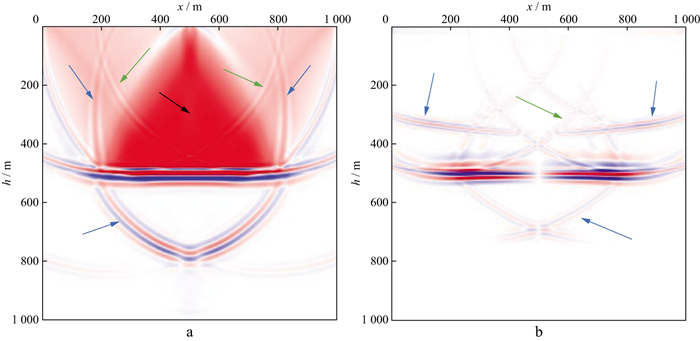
3.2 偏移噪声压制图 3为单界面TI介质模型单炮记录的弹性波逆时偏移结果, 偏移成像的条件为基于炮点波场归一和纵、横波解耦的互相关成像条件。图 3中主要存在3类偏移噪声: 第1类为由有限偏移孔径造成的绕射噪声(图 3中绿色箭头), 第2类为由层间反射产生的低频噪声(图 3中黑色箭头); 第3类为接收点波场逆时延拓时无法施加完整边界条件而造成的串扰伪像(图 3中蓝色箭头)。
|
图 3 单界面TI介质模型单炮记录的弹性波逆时偏移结果 a纵波; b横波 |
第1类噪声是由于接收点波场在测线两端突然截断而造成的, 通常只要采用适当算法对偏移输入炮记录的测线两端进行边缘道衰减, 即可消除此类噪声。
第2类噪声主要是由于炮、检波场中各种类型的波错误地参与互相关造成的[20, 79-87], 一般产生于浅层反射界面两侧波阻抗存在较大差异的区域, 在单炮偏移结果的纵波分量中表现为低频、低波数和强能量的特征。这类噪声的压制方法可归纳为以下3类。①在波场延拓过程中压制噪声[79-81]。典型的方法包括采用无反射波动方程进行炮、检波场延拓来减小层间反射[79]和在波场延拓前对弹性参数模型进行平滑来减弱层间反射波[80]。由于无反射波动方程是双程地震波方程的近似, 因此这种方法的本质是通过引入延拓方程误差来消除偏移误差。对于TI介质来说, 目前还不存在一个可用的单程弹性波方程, 利用平滑弹性参数模型来压制层间反射的思路本质上是通过引入新的模型误差来消除旧误差, 因此上述方法很难保证低频噪声的压制效果。②纵、横波成像时压制噪声[20, 82-86]。这类方法依据低频噪声的产生机理, 通过改变逆时偏移的成像条件来压制低频噪声。典型的做法是先依据传播方向对炮、检波场进行分解, 然后仅让传播方向相反的炮、检波场参与互相关成像, 实现低频噪声的压制。LIU等[84]将炮点和接收点波场分解为多个方向传播的单程分量, 在成像过程中对其重新组合, 以避开低频噪声的产生源头, 该方法具有良好的低频噪声压制效果; 黄杰等[85]采用类似思路实现了VTI介质中qP波方程的逆时偏移; SHU[86]根据LIU等[84]提出的方法对波场的传播方向进行了更为细致的划分, 并将其组成为多个扇形滤波器进行互相关成像, 取得了良好的低频噪声压制效果。我们根据SHU[86]的思路提出了(1)式, 这也是目前压制低频噪声最有效的方法。③成像后压制噪声。因为这类方法不对逆时偏移方法本身进行任何修改, 只将偏移结果看作信号, 然后采用适当算法对偏移结果进行滤波处理。许多地震去噪技术均可用于低频噪声压制, 目前常用的方法包括高通滤波法、扇形滤波法和拉普拉斯滤波法[87]等, 其中拉普拉斯滤波法最为常用, 该方法具有原理简单、操作方便且适应任意复杂构造的优点, 其本质是一种角度域去噪方法, 即按角度进行信号衰减。但是该方法会破坏偏移结果的振幅和相位信息, 通常需要对地震数据进行补偿校正。陈康等[88]提出了一种四阶拉普拉斯滤波算法, 解决了压制噪声不彻底及子波振幅和相位畸变的问题。实际应用中, 将后两类噪声压制方法相结合往往会取得更好的低频噪声压制效果[89]。
第3类噪声是由于接收点波场逆时延拓时, 只以3个速度分量作为边界条件而引起的, 如果能在此基础上增加应力或位移分量作为边界条件, 这类噪声就能得到部分压制, 但由于野外只能采集到接收点处的质点振动参数, 因此只能在后期处理时采用适当的方法计算接收点处的应力或位移分量, 以实现对这类偏移噪声的压制。针对第3类噪声压制, 目前尚未见到实质性的研究成果。
3.3 纵、横波解耦利用(1)式进行纵、横波成像首先需要得到不同时刻的sP, rP, rS值, 这说明在纵、横波成像前必须进行纵、横波解耦。在TI介质中, 由于qP波的偏振方向与传播方向不平行, qS波的偏振方向也与其传播方向不垂直, 因此基于散度和旋度算子的波场解耦方法不适用于TI介质。只要能够得到波场的传播方向以及沿该方向传播的纵、横波的偏振方向, 就可以利用纵、横波偏振方向相互垂直的性质对弹性波场进行分离。基于此, DELLINGER等[37]给出了一种利用波的偏振方向进行VTI介质纵、横波分离的方法, 其分离过程分为以下3个步骤: ①通过傅氏变换将弹性波场从空间域变换至波数域; ②求取平面简谐波中不同性质波的偏振方向, 并根据偏振方向构建波数域滤波算子, 利用该滤波算子分离平面简谐波中不同性质的波; ③利用反傅氏变换将波数域中分离出的波转换至空间域。
上述波场分离的关键在于构建波数域滤波算子, 滤波算子的构建需要已知波数值和沿该方向传播的平面波的偏振方向。实际计算时, 将波场从时间域变换至波数域, 可以在波数域中得到各平面波所对应的波数值, 该波数值中包含了波场的传播方向, 根据波场传播方向, 利用各向异性参数计算得到VTI介质中qP波, qSV波和SH波的偏振方向, 即可完成波数域中滤波算子的构建。后续的波场分离可以在波数域中进行, 也可以将滤波算子转换至空间域, 在空间域中完成波场分离[32]。对于已知各向异性参数的介质, 上述波场分离算法能够实现纵、横波解耦, 但解耦后的纵、横波中会产生新的噪声。唐怀谷[36]分析了这种噪声产生的原因, 并据此对波场分离算子进行了优化, 消除了由偏振方向中的异常值以及不合理的波场分离算子构建方式所引起的误差。
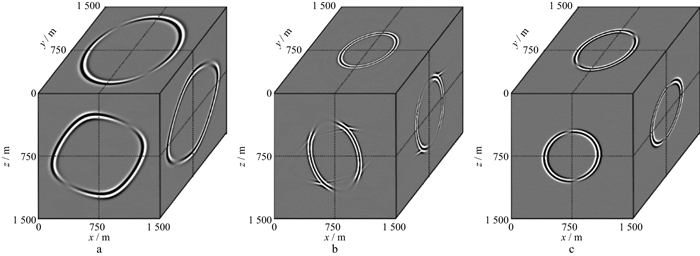
利用TI介质中的偏振向量可以构建TI介质中波场分离的滤波算子。由于难以直接通过Christoffel方程求取TI介质中的偏振向量解析式, 故可根据观测坐标系和本构VTI坐标系之间的关系, 先求取本构VTI介质坐标系中的偏振向量, 再将其投影至TI介质观测系统中, 得到观测系统中的偏振向量, 最后利用TI介质中的偏振向量得到滤波算子。采用上述方法将图 2的纵、横波分离, 结果如图 4所示, 当介质的各向异性参数已知时, 采用这种方法能够得到令人满意的纵、横波解耦结果。
|
图 4 三维均匀TI介质弹性波纵、横波分离结果 a qP波; b qSV波; c SH波 |
利用(1)式进行纵、横波成像还需要得到炮点和接收点波场中沿不同方向传播的纵波分量和横波分量, 这说明在纵、横波成像前必须先进行波场分解。由于纵、横波传播方向的准确求取是波场分解的前提, 所以如何准确求取各成像点在不同时刻的纵、横波传播方向成为纵、横波准确成像的关键。
声波方程逆时偏移通常根据坡印廷矢量来指示波的传播方向, 同样可以利用弹性波方程计算坡印廷矢量来指示波的传播方向, 但由这两个方程计算得到的坡印廷矢量的不同点在于: 声波方程中只包含纵波, 在声波方程波场延拓过程中求出的坡印廷矢量即为纵波的坡印廷矢量, 它代表了纵波的传播方向; 弹性波方程包含纵、横两种波型, 在弹性波方程波场延拓过程中求取的坡印廷矢量是混合波场的坡印廷矢量, 它既不是纵波的传播方向, 也不是横波的传播方向, 而是混合波场的传播方向, 利用这个方向进行波场分解必然引起误差。为解决这一问题, TANG等[90]推导了一个新的各向同性弹性波方程, 该方程将质点的振动速度矢量分解为胀缩振动速度矢量和剪切振动速度矢量, 这样就能在波场延拓过程中方便地求取不同波型的坡印廷矢量, 从而实现纵、横波的准确分解[91]。
对于各向异性介质中坡印廷矢量的求取问题, 采用常规一阶应力-速度方程得到的坡印廷矢量同样是纵、横波混合波场的坡印廷矢量, 它无法准确指示qP波或qS波的传播方向。我们认为, TANG等[90]用于求取各向同性介质中纵、横波坡印廷矢量的思路同样适用于各向异性问题。周进举等[30]采用类似思路求取了二维VTI介质中纵、横波坡印廷矢量。但在求取TI介质中纵、横波坡印廷矢量时, 由于振动速度分量的分解存在困难, 目前尚未见到有关求取纵、横波传播方向的最佳方法的文献。
4 存在的主要问题及今后的研究重点探讨各向异性弹性波逆时偏移是一个由众多关键技术组成的技术体系, 经过多年研究, 组成该体系的许多技术已趋于成熟, 但仍有许多技术需要继续深入研究。各向异性弹性波逆时偏移技术需要在以下几方面取得突破, 方可满足实际需求并广泛应用。
1) 三分量之间的频谱一致性处理技术。各向异性弹性波逆时偏移隐含了接收端的三分量记录具有相同频谱特征的假设。事实上, 实测三分量地震记录的频谱存在巨大差异, 特别是陆地三分量地震勘探中, 由于低速带对纵、横波的分频吸收机理不同, 造成实测资料的纵波频带宽、主频高, 横波频带窄、主频低。实测资料不满足处理算法的假设前提, 降低了弹性波逆时偏移技术解决实际问题的能力。因此有必要研究用于校正分量之间子波与频率一致性的新技术, 使校正后的各分量具有尽可能一致的子波与频谱, 此时的地震资料满足弹性波逆时偏移所隐含的假设, 实际地震资料处理时方可设置合理的震源子波。截至目前, 尚未见到这一领域研究成果的公开文献。
2) 各向异性随机边界构建技术。TI介质随机弹性参数的构建是一个多参数问题, 其特殊性表现在: 一方面随机层的波场散射效应必须能够破坏边界反射波的相干性; 另一方面构建的随机弹性参数必须满足数值求解弹性波方程的稳定性条件。此外, 各随机弹性参数之间还应该满足岩石物理的一般规律与严格的物理理论。独立产生的各个参数组合在一起无法保证波场延拓的稳定计算且难以符合岩石物理规律, 因此针对各向同性声波逆时偏移的随机边界构建技术不能直接用于解决各向异性问题。目前该领域的研究主要聚焦于提高单参数随机层的散射效应, 尚未对多参数随机层构建展开实质性研究。
3) 各向异性逆时偏移的噪声压制方法。弹性波逆时偏移会产生多种类型的偏移噪声, 其中, 由层间反射引起的低频噪声可以采用基于波场分解的互相关成像条件或拉普拉斯滤波技术进行压制, 由有限偏移孔径造成的绕射噪声可以采用边缘道衰减的方法消除。但对于图 3中蓝色箭头所示的偏移噪声, 目前未见对其产生机理的深入分析和压制方法的研究。
4) 数据驱动的TI介质中的纵、横波解耦技术。TI介质纵、横波解耦领域已有大量研究成果发表, 但现有成果都属于模型驱动类算法。这些算法在进行纵、横波分离时要求输入准确的各向异性模型, 当模型存在误差时, 解耦不彻底, 且解耦误差不收敛。对于逆时偏移这类成像处理技术而言, 这种误差不收敛的模型驱动类算法缺乏实用价值。因此研发一种数据驱动的TI介质中的纵、横波解耦技术, 可以使TI介质逆时偏移技术更易于工业应用。
5) 更准确的纵、横波传播方向求取技术。各向异性弹性波逆时偏移中需要准确求取qP波和qS波的传播方向以进行波场分解, 目前一般用坡印廷矢量来指示波的传播方向, 但现有算法求出的坡印廷矢量是纵、横波混合波场的坡印廷矢量, 它指示的方向也是混合波场的传播方向, 利用这个方向进行波场分解必然带来误差。各向同性和VTI介质弹性波逆时偏移中的此类问题已得到初步解决, 但对于更具一般性的TI介质, 由于理论上很难建立一个纵、横波解耦的一阶弹性波方程, 因此目前还无法准确求取同一成像点同一时刻多种波的传播方向。
6) 横波三叉区的处理与成像技术。横波三叉区对弹性波逆时偏移结果的影响在于: 在对炮、检波场中的横波成分进行互相关成像时, 三叉区的存在会造成偏移剖面产生虚假同相轴。现有算法均未考虑横波三叉区的处理问题, 如何消除横波三叉区的影响或利用横波三叉区得到更高精度的成像结果应成为该领域的研究重点之一。
5 结束语基于各向异性理论的地震波逆时偏移是一个庞大的技术体系, 受文章篇幅和作者水平限制, 本文无法就这一技术体系中每个细节的研究现状与存在的问题展开讨论, 只讨论了该体系中部分重点环节, 即便如此, 在这些重点讨论的环节中也可能因为作者水平问题遗漏其中的重要方法和文献。
本文未讨论各向异性建模问题, 而该问题又是逆时偏移必须解决的, 因此需另文讨论各向异性建模相关技术和难点问题。
| [1] |
DUVENCK E, MILIK P, BAKKER P M. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 2186-2190. |
| [2] |
王咸彬. TTI各向异性逆时偏移技术及应用[J]. 石油物探, 2017, 56(4): 534-542. WANG X B. Anisotropic reverse time migration technique in TTI media and its application[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 534-542. DOI:10.3969/j.issn.1000-1441.2017.04.009 |
| [3] |
康玮, 程玖兵. 横向各向同性介质拟声波方程及其在逆时偏移中的应用[J]. 地球物理学报, 2012, 55(3): 1033-1045. KANG W, CHENG J B. Pseudo-acoustic wave equations for reverse-time migration in TI media[J]. Chinese Journal of Geophysics, 2012, 55(3): 1033-1045. DOI:10.6038/j.issn.0001-5733.2012.03.034 |
| [4] |
郭成锋, 杜启振, 张明强, 等. 改进的TTI介质纯P波方程正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(1): 258-270. GUO C F, DU Q Z, ZHANG M Q, et al. Numerical simulation and reverse time migration using an improved pure P-wave equation in tilted transversely isotropic media[J]. Chinese Journal of Geophysics, 2017, 60(1): 258-270. |
| [5] |
FLETCHER R P, DU X, FOWLER P J. Reverse time migration in tilted transversely isotropic(TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [6] |
LI C, LIU G, LI Y. A practical implementation of 3D TTI reverse time migration with multi-GPUs[J]. Computers & Geosciences, 2017, 102(1): 68-78. |
| [7] |
ZHANG Y. Reverse time migration in 3D heterogeneous TTI media[J]. 27th SEG Technical Program Expanded Abstracts, 2008, 2196-2200. |
| [8] |
WHITMORE N D. Iterative depth migration by backward time propagation[J]. Expanded Abstracts of 53rd Annual Internat SEG Mtg, 1983, 382-385. |
| [9] |
BAYSAL E D, KOSLOFF J, SHERWOOD. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [10] |
MCMECHAN G A. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 1983, 31(3): 413-420. DOI:10.1111/j.1365-2478.1983.tb01060.x |
| [11] |
CHANG W F, MCMECHAN G A. 3D acoustic prestack reverse-time migration[J]. Geophysical Prospecting, 1990, 38(7): 737-755. DOI:10.1111/j.1365-2478.1990.tb01872.x |
| [12] |
杨佳佳, 何兵寿, 陈婷. 逆时深度偏移中的子波拉伸校正[J]. 石油地球物理勘探, 2016, 51(1): 135-140. YANG J J, HE B S, CHEN T. Wavelet stretch correction for reverse time migration[J]. Oil Geophysical Prospecting, 2016, 51(1): 135-140. |
| [13] |
郭鹏, 何兵寿, 郭敏. 基于坡印廷矢量的声波方程叠前逆时偏移成像条件[J]. 煤炭学报, 2011, 36(8): 1290-1295. GUO P, HE B S, GUO M. Acoustic equation pre-stack reverse-time migration imaging condition based on Poynting vector[J]. Journal of China Coal Society, 2011, 36(8): 1290-1295. |
| [14] |
刘守伟, 王华忠, 陈生昌, 等. 三维逆时偏移GPU/CPU机群实现方案研究[J]. 地球物理学报, 2013, 56(10): 3487-3496. LIU SW, WANG H Z, CHEN S C, et al. Implementation strategy of reverse time migration on GPU/CPU clusters[J]. Chinese Journal of Geophysics, 2013, 56(10): 3487-3496. DOI:10.6038/cjg20131023 |
| [15] |
SUN R, MCMECHAN G A. Pre-stack reverse-time migration for elastic waves with application to synthetic offset vertical seismic profiles[J]. Proceedings of the IEEE, 1986, 74(3): 457-465. DOI:10.1109/PROC.1986.13486 |
| [16] |
CHANG W F, MCMECHAN G A. Elastic reverse-time migration[J]. Geophysics, 1987, 52(10): 1365-1375. DOI:10.1190/1.1442249 |
| [17] |
DU Q Z, GONG X F, ZHANG M Q, et al. 3D PS-wave imaging with elastic reverse-time migration[J]. Geophysics, 2014, 79(5): S173-S184. DOI:10.1190/geo2013-0253.1 |
| [18] |
DU Q Z, ZHU Y, BA J. Polarity reversal correction for elastic reverse time migration[J]. Geophysics, 2012, 77(2): S31-S41. DOI:10.1190/geo2011-0348.1 |
| [19] |
SUN R, MCMECHAN G A, HSIAO H H, et al. Separating P-and S-waves in prestack 3D elastic seismograms using divergence and curl[J]. Geophysics, 2004, 69(1): 286-297. DOI:10.1190/1.1649396 |
| [20] |
CHEN T, HE B S. A normalized wavefield separation cross-correlation imaging condition for reverse time migration based on Poynting vector[J]. Applied Geophysics, 2014, 11(2): 158-166. DOI:10.1007/s11770-014-0441-5 |
| [21] |
王鹏飞, 何兵寿. 基于行波分离的三维弹性波矢量场点积互相关成像条件[J]. 石油地球物理勘探, 2017, 52(3): 477-483. WANG P F, HE B S. Vector field dot product coross-correlation imaging based on 3D elastic wave separation[J]. Oil Geophysical Prospecting, 2017, 52(3): 477-483. |
| [22] |
FLETCHER R P, FOWLER P J, KITCHENSIDE P, et al. Suppressing unwanted internal reflections in prestack reverse-time migration[J]. Geophysics, 2006, 71(6): E79-E82. DOI:10.1190/1.2356319 |
| [23] |
王保利, 高静怀, 陈文超, 等. 地震叠前逆时偏移的有效边界存储策略[J]. 地球物理学报, 2012, 55(7): 2412-2421. WANG B L, GAO J H, CHEN W C, et al. Efficient boundary storage strategies for seismic reverse time migration[J]. Chinese Journal of Geophysics, 2012, 55(7): 2412-2421. |
| [24] |
CLAPP R G. Reverse time migration with random boundaries[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 2809-2813. |
| [25] |
SYMESW W. Reverse time migration with optimal checkpointing[J]. Geophysics, 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [26] |
LIU H W, LI B, LIU H. The issues of prestack reverse time migration and solutions with Graphic Processing Unit implementation[J]. Geophysical Prospecting, 2012, 60(5): 906-918. DOI:10.1111/j.1365-2478.2011.01032.x |
| [27] |
张美根, 王妙月. 各向异性介质弹性波有限元叠前逆时偏移[J]. 地球物理学报, 2001, 44(5): 711-719. ZHANG M G, WANG M Y. Prestack finite element reverse-time migration for anisotropic elastic waves[J]. Chinese Journal of Geophysics, 2001, 44(5): 711-719. DOI:10.3321/j.issn:0001-5733.2001.05.015 |
| [28] |
陈可洋. 各向异性弹性波高阶有限差分法叠前逆时深度偏移[J]. 油气地球物理, 2011, 9(3): 23-28. CHEN K Y. Anisotropic elastic wave pre-stack reverse-time depth migration with high-order finite-difference scheme[J]. Petroleum Geophysics, 2011, 9(3): 23-28. |
| [29] |
杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移[J]. 地球物理学报, 2009, 52(3): 801-807. DU Q Z, QIN T. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic media[J]. Chinese Journal of Geophysics, 2009, 52(3): 801-807. |
| [30] |
周进举, 王德利, 李博文, 等. 基于解耦传播的波场分解方法在VTI介质弹性波逆时偏移中的应用[J]. 吉林大学学报(地球科学版), 2018, 48(3): 325-337. ZHOU J J, WANG D L, LI B W, et al. Application of wavefield decomposition based on decoupled propagation in elastic RTM for VTI media[J]. Journal of Jilin University(Earth Science Edition), 2018, 48(3): 325-337. |
| [31] |
王娟, 李振春. TTI介质矢量波成像及波型分解[J]. 地球物理学进展, 2014, 29(6): 2754-2760. WANG J, LI Z C. Vector wave imaging and wave separation in the TI media[J]. Processing in Geophysics, 2014, 29(6): 2754-2760. |
| [32] |
YAN J, SAVA P. Elastic wave-mode separation for VTI media[J]. Geophysics, 2009, 74(5): WB19-WB32. DOI:10.1190/1.3184014 |
| [33] |
IGEL H, MORA P, RIOLLET B. Anisotropic wave propagation through finite-difference grids[J]. Geophysics, 1995, 60(4): 1203-1216. DOI:10.1190/1.1443849 |
| [34] |
MARTIN R, KOMATITSCH D, GEDNEY S D. A variational formulation of a stabilized unsplit convolutional perfectly matched layer for the isotropic or anisotropic seismic wave equation[J]. Computer Modeling in Engineering and Sciences, 2008, 37(3): 274-304. |
| [35] |
SAENGER E H, BOHLEN T. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid[J]. Geophysics, 2004, 69(2): 583-591. DOI:10.1190/1.1707078 |
| [36] |
唐怀谷. TI介质中弹性波场的分离方法研究[D]. 青岛: 中国海洋大学, 2017 TANG H G, Decomposition of elastic wavefield in TI media[D].Qingdao: Ocean University of China, 2017 |
| [37] |
DELLINGER J, ETGEN J. Wave-field separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919. DOI:10.1190/1.1442906 |
| [38] |
CHENG J, FOMEL S. Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media[J]. Geophysics, 2014, 79(4): C97-C110. DOI:10.1190/geo2014-0032.1 |
| [39] |
CHENG J, ALKHALIFAH T, WU Z, et al. Simulating propagation of decoupled elastic waves using low-rank approximate mixed-domain integral operators for anisotropic media[J]. Geophysics, 2016, 81(2): T63-T77. DOI:10.1190/geo2015-0184.1 |
| [40] |
韩冬, 杜启振, 张明强, 等. 交错网格与旋转交错网格对VTI介质波场分离的影响分析[J]. 地震学报, 2016, 38(1): 111-121. HAN D, DU Q Z, ZHANG M Q, et al. Effects of staggered-grid and rotated-grid on the wavefield separation in VTI media[J]. Acta Seismologica Sinia, 2016, 38(1): 111-121. |
| [41] |
ZHANG Q, MCMECHAN G A. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media[J]. Geophysics, 2010, 75(3): D13-D26. DOI:10.1190/1.3431045 |
| [42] |
YAN J, SAVA P. Elastic wave mode separation for tilted transverse isotropy media[J]. Geophysical Prospecting, 2012, 60(1): 29-48. DOI:10.1111/j.1365-2478.2011.00964.x |
| [43] |
秦海旭, 吴国忱. TTI介质随机边界逆时偏移的实现[J]. 石油物探, 2014, 53(5): 570-578. QING H X, WU G C. The implementation of elastic reverse-time migration in TTI media based on random boundary[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 570-578. DOI:10.3969/j.issn.1000-1441.2014.05.010 |
| [44] |
刘学义. 海洋地震资料逆时偏移中的子波提取技术与应用研究[D]. 青岛: 中国海洋大学, 2017 LIU X Y.Research on Wavelet extraction technique and application in reverse time migration of marine seismic data[D].Qingdao: Ocean University of China, 2017 |
| [45] |
杨仁虎, 常旭, 刘伊克. 叠前逆时偏移影响因素分析[J]. 地球物理学报, 2010, 53(8): 1902-1913. YANG R H, CHANG X, LIU Y K. The influence factors analyses of imaging precision in pre-stack reverse-time migration[J]. Chinese Journal of Geophysics, 2010, 53(8): 1902-1913. DOI:10.3969/j.issn.0001-5733.2010.08.016 |
| [46] |
LAZEAR G D. Mixed-phase wavelet estimation using fourth-order cumulants[J]. Geophysics, 1993, 58(7): 1042-1051. DOI:10.1190/1.1443480 |
| [47] |
VELIS D R. Simulated annealing wavelet estimation via fourth-order cumulant matching[J]. Geophysics, 1996, 61(6): 1939-1948. DOI:10.1190/1.1444109 |
| [48] |
ENGQUIST B, MAJDA A. Absorbing boundary conditions for numerical simulation of waves[J]. Mathematics of Computation, 1977, 374(5): 1765-1766. |
| [49] |
CLAYTON R, ENGGUIST B. Absorbing boundary conditions for acoustic and elastic wave equations[J]. Bulletin of the Seismological Society of America, 1977, 67(6): 1529-1540. |
| [50] |
MUR G. Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic-field equations[J]. IEEE Transactions on Electromagnetic Compatibility, 1981, 23(4): 377-382. |
| [51] |
BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [52] |
CERJAN C, KOSLOFF D, KOSLOFF R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equation[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [53] |
SOCHACKI J, KUBICHEK R, GEORGE J, et al. Absorbing boundary conditions and surface waves[J]. Geophysics, 1987, 52(1): 60-71. DOI:10.1190/1.1442241 |
| [54] |
李景叶, 陈小宏. TI介质地震波场数值模拟边界条件处理[J]. 西安石油大学学报(自然科学版), 2006, 21(4): 20-23. LI J Y, CHEN X H. Treatment of the boundary conditions in the numerical simulation of the seismic wave field in transversely isotropic(TI) media[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2006, 21(4): 20-23. DOI:10.3969/j.issn.1673-064X.2006.04.005 |
| [55] |
付小波, 韩超, 原健龙, 等. 波动方程正演模拟边界条件的比较分析[J]. 成都理工大学学报(自然科学版), 2015, 42(4): 492-499. FU X B, HAN C, YUAN J L, et al. Comparison and analysis of boundary conditions for seismic wave equation forward modeling[J]. Journal of Chendu University of Technology(Science & Technology Edition), 2015, 42(4): 492-499. DOI:10.3969/j.issn.1671-9727.2015.04.13 |
| [56] |
HASTINGS F D, SCHNEIDER J B, BROSCHAT S L. Application of the perfectly matched layer(PML) absorbing boundary condition to elastic wave propagation[J]. The Journal of the Acoustical Society of America, 1996, 100(5): 3061-3069. DOI:10.1121/1.417118 |
| [57] |
严红勇, 刘洋. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 2012, 55(4): 1354-1365. YAN H Y, LIU Y. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
| [58] |
CHEW W C, WEEDON W H. A 3D perfectly matched medium form modified Maxwell's equations with stretched coordinates[J]. Microwave and Optical Technology Letters, 1994, 7(13): 599-604. DOI:10.1002/mop.4650071304 |
| [59] |
COLLINO F, MONK P B. Optimizing the perfectly matched layer[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 164(1/2): 157-171. |
| [60] |
陈浩, 王秀明, 赵海波. 旋转交错网格有限差分及其完全匹配层吸收边界条件[J]. 科学通报, 2006, 51(17): 1985-1994. CHEN H, WANG X M, ZHAO H B. A rotated staggered grid finite-difference with the absorbing boundary condition of a perfectly matched layer[J]. Chinese Science Bulletin, 2006, 51(17): 1985-1994. DOI:10.3321/j.issn:0023-074X.2006.17.002 |
| [61] |
JUZUOGLU M, MITTRA R. Frequency dependence of the constitutive parameters of causal perfectly match anisotropic absorbers[J]. IEEE Microwave and Guided Wave Letters, 1996, 6(12): 447-449. DOI:10.1109/75.544545 |
| [62] |
BERENGER J P. Application of the CFS-PML to the absorption of evanescent waves in wave guides[J]. IEEE Microwave and Wireless Components Letters, 2002, 12(6): 218-220. DOI:10.1109/LMWC.2002.1010000 |
| [63] |
刘有山, 刘少林, 张美根, 等. 一种改进的二阶弹性波动方程的最佳匹配层吸收边界条件[J]. 地球物理学进展, 2012, 27(5): 2113-2122. LIU Y S, LIU S L, ZHANG M G, et al. An improved perfectly matched layer absorbing boundary condition for second order elastic wave equation[J]. Progress in Geophysics, 2012, 27(5): 2113-2122. |
| [64] |
LUBBERS R J, HUNSBERGER F. FDTD for Nth-Order dispersive media[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(11): 1297-1301. DOI:10.1109/8.202707 |
| [65] |
RODEN J A, GEDNEY S D. Convolution PML(CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave and Optical Technology Letters, 2000, 27(5): 334-339. DOI:10.1002/1098-2760(20001205)27:5<334::AID-MOP14>3.0.CO;2-A |
| [66] |
杜启振, 孙瑞艳, 张强. 组合边界条件下二维三分量TTI介质波场数值模拟[J]. 石油地球物理勘探, 2011, 46(2): 187-195. DU Q Z, SUN R Y, ZHANG Q. Numerical simulation of three-component elastic wavefield in 2D TTI media in the condition of the combined boundary[J]. Oil Geophysical Prospecting, 2011, 46(2): 187-195. |
| [67] |
DROSSAERT F, GIANNOPOULOS A. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves[J]. Geophysics, 2007, 72(2): T9-T17. DOI:10.1190/1.2424888 |
| [68] |
秦臻, 任培罡, 姚姚, 等. 弹性波正演模拟中PML吸收边界条件的改进[J]. 地球科学, 2009, 34(4): 658-664. QIN Z, REN P G, YAO Y, et al. Improvement of PML absorbing boundary conditions in elastic wave forward modeling[J]. Earth Science, 2009, 34(4): 658-664. DOI:10.3321/j.issn:1000-2383.2009.04.012 |
| [69] |
RAMADAN O. Auxiliary differential equation formulation: An efficient implementation of the perfectly matched layer[J]. IEEE Microwave and Wireless Components Letters, 2003, 13(2): 69-71. DOI:10.1109/LMWC.2003.808706 |
| [70] |
CUMMER S A. A simple, nearly perfectly matched layer for general electromagnetic media[J]. IEEE Microwave and Wireless Components Letters, 2003, 13(3): 128-130. DOI:10.1109/LMWC.2003.810124 |
| [71] |
丁科. PML吸收边界条件影响因素分析[J]. 物探与化探, 2012, 36(4): 623-627. DING K. An analysis of factors affecting PML absorbing boundary condition[J]. Geophysical & Geochemical Exploration, 2012, 36(4): 623-627. |
| [72] |
廉西猛, 单联瑜, 隋志强. 地震正演数值模拟完全匹配层吸收边界条件研究综述[J]. 地球物理学进展, 2015, 30(4): 1725-1733. LIAN X M, SHAN L Y, SUI Z Q. An overview of research on perfectly matched layers absorbing boundary condition of seismic forward numerical simulation[J]. Progress in Geophysics, 2015, 30(4): 1725-1733. |
| [73] |
GRIEWANK A, WALTHER A. Algorithm 799 revolve: An implementation of checkpointing for the reverse or adjoint mode of computational differentiation[J]. ACM Transactions on Mathematical Software, 2000, 26(1): 19-45. DOI:10.1145/347837.347846 |
| [74] |
陈桂廷, 王真理. 基于插值原理的检查点技术波场重构与叠前逆时偏移[J]. 地球物理学报, 2018, 61(8): 3334-3345. CHEN G T, WANG Z L. A checkpoint-assisted interpolation algorithm of wave field reconstruction and prestack reverse time migration[J]. Chinese Journal of Geophysics, 2018, 61(8): 3334-3345. |
| [75] |
张丽美, 成谷. 参数组合优化的随机边界条件及其在地震RTM中的应用[J]. 物探与化探, 2017, 41(5): 890-898. ZHANG L M, CHENG G. Parameterized random boundary condition and its application on seismic RTM[J]. Geophysical and Geochemical Exploration, 2017, 41(5): 890-898. |
| [76] |
SHEN X K, CLAPP R G. Random boundary condition for memory-efficient waveform inversion gradient computation[J]. Geophysics, 2015, 80(6): R351-R359. DOI:10.1190/geo2014-0542.1 |
| [77] |
刘国峰, 李春, 吕庆田. 3D TTI介质逆时偏移计算关键问题研究[J]. 地球物理学进展, 2017, 32(6): 2498-2504. LIU G F, LI C, LV Q T. Key technologies about reverse time migration in TTI media[J]. Progress in Geophysics, 2017, 32(6): 2498-2504. |
| [78] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [79] |
FLETCHER R F, FOWLER P, KITCHENSIDE P. Suppressing artifacts in prestack reverse time migration[J]. Expanded Abstracts of 75th Annual Internat SEG Mtg, 2005, 2047-2051. |
| [80] |
LOEWENTHAL D, STOFFA P L, FARIA E L. Suppressing the unwanted reflections of the full wave equation[J]. The Leading Edge, 1987, 52(7): 1007-1012. |
| [81] |
BAYSAL E, KOSLOFF D D, SHERWOOD J W C. A two-way nonreflecting wave equation[J]. Geophysics, 1984, 49(2): 132-141. DOI:10.1190/1.1441644 |
| [82] |
YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 37(1): 102-107. DOI:10.1071/EG06102 |
| [83] |
李沁慈, 刘国峰, 孟小红, 等. 基于Poynting矢量的逆时偏移去噪[J]. 物探与化探, 2015, 39(6): 1223-1232. LI Q C, LIU G F, MENG X H, et al. The denoising of reverse time migration based on the Poynting vector[J]. Geophysical and Geochemical Exploration, 2015, 39(6): 1223-1232. |
| [84] |
LIU F Q, ZHANG G Q, MORTON S A, et al. Reverse-time migration using one-way wavefield imaging condition[J]. Expanded Abstracts of 77th Annual Internat SEG Mtg, 2007, 2170-2174. |
| [85] |
黄杰, 杨国权, 李振春. 基于Poynting矢量的全波场分离成像条件在VTI介质逆时偏移中的应用[J]. 地球物理学进展, 2018, 33(4): 1495-1500. HUANG J, YANG G Q, LI Z C. Application of full wavefield decomposition imaging condition based on Poynting vector in VTI media reverse time migration[J]. Progress in Geophysics, 2018, 33(4): 1495-1500. |
| [86] |
SHU S Y. Reverse-time migration bu fan filtering plus wavefield decomposition[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 2804-2807. |
| [87] |
ZHANG Y, SUN J. Practical issues of reverse time migration: true amplitude gathers, noise removal and harmonic-source encoding[J]. ASEG Expanded Abstracts 2009, 2009, 10. |
| [88] |
陈康, 吴国忱. 逆时偏移拉普拉斯算子滤波改进算法[J]. 石油地球物理勘探, 2012, 47(2): 249-255. CHEN K, WU G C. An improved filter algorithm based on Laplace operator in reverse-time migration[J]. Oil Geophysical Prospecting, 2012, 47(2): 249-255. |
| [89] |
张岩. TTI介质叠前逆时偏移成像研究[D]. 青岛: 中国石油大学(华东), 2013 ZHANG Y.Prestack reverse-time migration in TTI media[D].Qingdao: China University of Petroleum(East China), 2013 |
| [90] |
TANG H G, HE B S, MOU H B. P-and S-wave energy flux density vectors[J]. Geophysics, 2016, 81(6): T357-T368. DOI:10.1190/geo2016-0245.1 |
| [91] |
李凯瑞, 何兵寿, 胡楠. 基于一阶速度-胀缩-旋转方程的多分量联合逆时偏移[J]. 煤炭学报, 2018, 43(4): 1072-1082. LI K R, HE B S, HU N. Multicomponent joint reverse time migration based on first order veloci-ty-dilatation-rotation equations[J]. Journal of China Coal Society, 2018, 43(4): 1072-1082. |



