随着海上成熟油气区块勘探开发的不断深入, 薄互层岩性油气藏逐渐成为新增探明储量的重要研究领域, 但中深层地震资料频带宽度有限、分辨率低, 薄层刻画难度较大, 为了解决上述问题, 资料处理人员多采用地震数据高分辨率处理技术[1-2]。常用的高频恢复技术包括谱白化、反褶积、反Q滤波等[3-6], 这些技术都很好地改善了实际地震资料分辨率, 但存在各自的适用条件或缺陷。谱白化方法存在纵向时间、横向空间补偿不均衡问题; 反褶积方法对地层反射系数及子波均有一定假设条件, 且时变子波获取难度大; 反Q滤波在高频补偿问题上需要估算Q值[7]。
谱蓝化拓频首先对测井数据反射系数与地震信号进行频谱分析, 得到两者匹配的谱蓝化算子, 然后将其与原始地震反射系数褶积得到谱蓝化拓频数据, 其中, 谱蓝化算子的计算是核心步骤。BLACHE[8]认为谱蓝化拓频技术可以提高叠后地震资料分辨率, 并结合有色反演进行了叠后地震高分辨率处理及薄层识别。KAZEMEINI等[9]对比分析了叠后及叠前谱蓝化拓频技术在Ketzin区的二氧化碳预测效果, 论证了叠前谱蓝化压制边缘震荡效应的优势, 证明了其拓频效果更佳。近年, 国内学者杨瑞召等[10]、刘建伟等[11]、陈文雄等[12]、李贤兵等[13]利用谱蓝化技术拓宽地震数据中高频段信息, 实现地震数据的高分辨率处理, 较好地解决了薄煤层识别以及薄储层刻画中的一些问题, 但这些方法技术中的谱蓝化算子均基于地震整体频谱计算, 未考虑地震不同频带信息的特点, 导致了拓频后的地震数据出现分辨率不合理、低频震荡等问题。对此, 陈平等[14]提出基于谱反演的谱蓝化拓频技术, 通过压缩子波影响, 拓宽地震低频与高频, 提高地震资料分辨能力; 张璐等[15]提出地震分频谱蓝化思想, 借助S变换对地震数据分频, 然后分别求取谱蓝化算子, 较大程度地改善了薄层刻画的精度, 但S变换存在时频分辨率精度不够等问题。
为了优化谱蓝化地震拓频效果, 解决薄层刻画难等问题, 本文提出了一种基于同步压缩小波变换的分频谱蓝化拓频技术, 利用同步压缩小波变换时频分辨率优势完成地震数据的分频, 在分频数据体谱蓝化算子计算过程中, 利用不同频带频谱能量差异改进谱蓝化算子, 通过不同分频数据体振幅谱占比确定其对应的改进谱蓝化算子权重, 并将改进后的谱蓝化算子与地震数据进行褶积, 得到精度更高、更合理的拓频地震数据, 进而将其用于高分辨率薄层识别。
1 同步压缩小波变换 1.1 方法原理同步压缩小波变换(synchrosqueezing wavelet transform, SSWT)由DAUBECHIES等[16]在2011年提出, 其基本思想是在频率域压缩小波变换的时频结果, 使能量尽量集中到信号真正的频率附近, 使得计算结果的分辨率和能量聚集性更高。该技术的实现主要包括以下3步。
1) 求取信号的连续小波变换结果, 获取复小波系数谱Ws(a, b)。
对于信号s(t), 其连续小波变换公式计算如下:
| $ W_{\mathrm{s}}(a, b)=\frac{1}{\sqrt{a}} \int s(t) \psi^*\left(\frac{t-b}{a}\right) \mathrm{d} t $ | (1) |
式中: Ws(a, b)为待求信号的复小波系数谱; t为时间; a, b分别为尺度因子、时间平移因子; ψ*(t)为小波基函数的复共轭。结合Plancherel定理, 得到频率域复小波系数谱为:
| $ W_{\mathrm{s}}(a, b)=\frac{1}{2 \pi} \int \hat{s}(\varepsilon) a^{\frac{1}{2}} \hat{\psi}^*(a \varepsilon) \mathrm{e}^{\mathrm{i} \kappa} \mathrm{d} \varepsilon $ | (2) |
式中: ε为角频率; ŝ(ε), $\hat{\psi}$*(ε)分别是s(t), ψ*(t)的傅里叶变换结果。
2) 求取信号s(t)的瞬时频率Ws(a, b)。
DAUBECHIES等[16]的测试分析表明, 信号s(t)的小波系数在时间-尺度域容易发生扩散, 进而降低小波系数的可读性, 而信号的相位具有稳定性, 不随a值变化而改变。因此, 计算其相位偏导数就能求得瞬时频率Ws(a, b), 如下:
| $ \omega_{\mathrm{s}}(a, b)=\left\{\begin{array}{cc} \frac{-\mathrm{i} \partial_b W_{\mathrm{s}}(a, b)}{W_{\mathrm{s}}(a, b)} & \left|W_{\mathrm{s}}(a, b)\right|>0 \\ \infty & \left|W_{\mathrm{s}}(a, b)\right|=0 \end{array}\right. $ | (3) |
3) 在频率方向对小波系数压缩重组, 得到同步压缩小波变换量值Tx(a, b)。
将复小波系数从时间-尺度域Ws(a, b)转换到时间-频率域Ws[ωs(a, b), b], 在频率域将其压缩, 此时频率变量和尺度因子a被离散化。对复小波系数Ws[Ws(a, b), b]的任一中心频率ωl附近[ωl-Δω/2, ωl+Δω/2]的值进行压缩重组, 这样就将小波系数从频率方向发散的区域压缩到中心频率附近, 从而大幅度提高频率分辨率。由于实际信号处理过程中得到的均为时间域离散值, 所以要将尺度离散化, 同步压缩变量Ts(ωl, b)可表示为:
| $ \begin{gathered} T_{\mathrm{s}}\left(\omega_l, b\right)=\left(\Delta \omega_l\right)^{-1} \sum\limits_{a_k:\left|\omega\left(a_k, b\right)-\omega_l\right| \leqslant \Delta \omega / 2} W_{\mathrm{s}}\left(a_k, b\right) \cdot \\ a_k^{-\frac{3}{2}} \Delta a_k \end{gathered} $ | (4) |
式中; ωl是第l个离散频率值; ak为第k个离散尺度因子; Δak=ak-ak-1; Δωl=ωl-ωl-1。
采用上述技术, 可以使各时频脊线细化, 从而减弱频率混叠现象。分析可知, 同步压缩小波变换以小波变换为基础, 对相位求偏导数得到瞬时频率, 然后将小波系数进行压缩重组。在时间-尺度域到时间-频率域转变的过程中, 能量聚焦性得到提升, 从而提高了时频分析结果的分辨率。
1.2 模型测试为了验证同步压缩小波变换时频分析高分辨率特性, 建立如图 1a所示的地震信号, 模型长度为600ms, 采样间隔1ms, 纵向包含4个有效信号, 分别在100, 250, 400, 440ms, 信号振幅分别为0.4, 0.7, 0.6, 0.5, 其中400ms与440ms信号时间间隔较小。
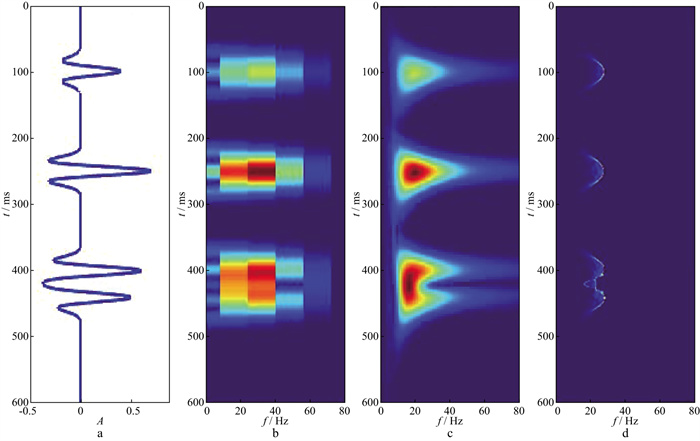
|
图 1 不同时频分析方法的效果 a地震信号; b短时傅里叶变换; c广义S变换; d同步压缩小波变换 |
对选取的地震信号分别进行短时傅里叶变换(STFT)、广义S变换(GST)及同步压缩小波变换(SSWT), 结果如图 1b、图 1c和图 1d所示, 可以看出短时傅里叶变换能量聚焦性差, 对400, 440ms的两个信号区分度不够。广义S变换后, 时频域分辨率明显提升, 纵向时间分辨率与信号匹配性高, 但当信号间隔较小时(400~440ms), 频率域能量聚焦存在一定误差。同步压缩小波变换效果最佳, 不仅时间分辨率高, 可以较好地区分400, 440ms的两个相邻信号, 且频率能量聚焦在25Hz附近, 时频域分辨率高。
为了进一步验证该本文所述方法的时频分析的稳定性, 设计如图 2所示的添加10%高斯噪声的模型, 图 2a为含噪声地震信号, 分别应用上述3种时频分析方法, 结果如图 2b, 图 2c和图 2d所示。分析可知, 相较于其它方法, 同步压缩小波变换抗噪性更强, 能量聚集性依然最好, 时频域分辨率最高。
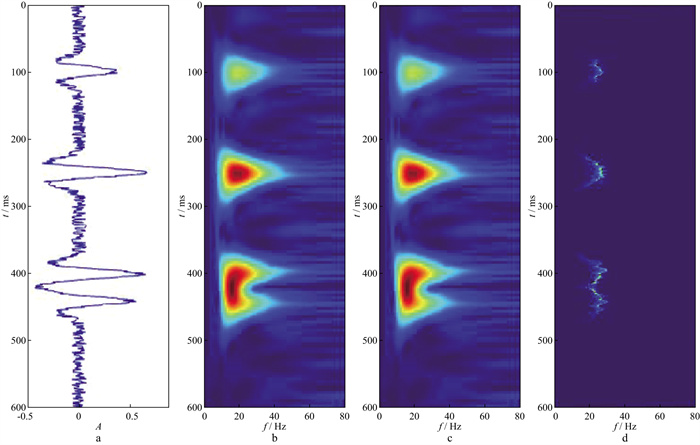
|
图 2 不同时频分析方法的效果对比(含10%噪声) a含噪地震信号; b短时傅里叶变换; c广义S变换; d同步压缩小波变换 |
传统谱蓝化拓频技术利用地震频率与振幅的正相关“蓝谱”特征, 先将地震和测井的反射系数振幅谱进行匹配以求取谱蓝化算子, 再利用井控的拓频思路来提高地震数据的分辨率。传统谱蓝化算子由地震数据整体平均频谱与测井数据对比计算得到, 因此缺乏对地震数据不同频带信息的充分匹配, 导致拓频后的地震数据出现低频信息损失、精度不够等问题。
本文在传统谱蓝化拓频基础上, 提出基于同步压缩小波变换的分频谱蓝化拓频技术, 其具体流程如下。
1) 对地震信号进行SSWT分频, 并计算不同频段的地震平均频谱Si(w)。
| $ \overline{S_i(w)}=\sum\limits_{j=1}^n S_{i j}(w) / n $ | (5) |
式中: Si(w)为第i个分频段的地震平均频谱; Sij(w)为第i个频段中第j道地震振幅谱; n为该分频段的地震道数。
2) 测井反射系数频谱计算。
目标井反射系数Rj表达式为:
| $ R_j=\left(\rho_{j+1} v_{j+1}-\rho_j v_j\right) /\left(\rho_{j+1} v_{j+1}+\rho_j v_j\right) $ | (6) |
式中: ρ为密度; v为速度; j为井上纵向第j个采样点; Rj为第j层反射系数。
利用傅里叶变换, 可以进一步得到:
| $ R(j w)=C(w) \mathrm{e}^{-j \varphi(w)} $ | (7) |
式中: R(jw)为测井反射系数频率域信号; C(w)为测井反射系数振幅谱; φ(w)为相位谱。
3) 不同分频段的谱蓝化算子计算。
计算不同分频段与测井反射系数频谱匹配的谱蓝化算子Bi(w), 使得两者差异最小化:
| $ \begin{gathered} \min \left\|T(w)\left[B_i(w) \cdot \overline{S(w)}-C(w)\right]\right\|^2+ \\ R\left[B_i(w)\right] \end{gathered} $ | (8) |
式中: T(w)为锥度函数; C(w)为测井反射系数振幅谱; S(w)为地震平均振幅谱; R[Bi(w)]为正则化函数。依据(8)式计算每一个分频段的谱蓝化算子。
4) 分频段谱蓝化权重因子计算。
首先对分频段振幅谱能量进行归一化处理, 具体如下:
| $ E_{\text {norm }}(i)=\frac{E(i)-E_{\text {min }}}{E_{\max }-E_{\text {min }}} $ | (9) |
式中: E(i)为第i个分频段振幅的谱能量; Emax, Emin分别为原始地震谱能量最大值和最小值; Enorm(i)为第i个分频段归一化后振幅谱能量。
根据不同分频段能量占比, 确定其谱蓝化权重因子λi。
| $ \lambda_i=E_{\text {norm }}(i) / \sum\limits_{i=1}^N E_{\text {norm }}(i) $ | (10) |
式中: N为分频段个数。
5) 对不同分频段的谱蓝化算子Bi(w)进行加权求和, 得到优化后的谱蓝化算子Bopt。
| $ B_{\mathrm{opt}}=\sum\limits_{i=1}^N \lambda_i B_i(w) $ | (11) |
6) 计算优化拓频数据。
先利用循环反褶积技术对地震数据进行重采样, 生成稀疏的反射系数体Rs, 然后将优化后的谱蓝化分频算子与Rs进行褶积, 得到拓频数据:
| $ S_{\mathrm{opt}}=R_{\mathrm{s}} * B_{\mathrm{opt}} $ | (12) |
因为求取了不同频段的谱蓝化算子, 故优化后的谱蓝化算子更能表征不同频段信号。利用分频谱蓝化算子拓频后的地震数据体精度高, 该技术不仅有效地拓宽了高频信息, 提高薄层刻画精度, 同时, 有效解决了传统谱蓝化技术低频段损失问题, 使得优化后的拓频数据对储层的刻画更加合理。
2.2 模型测试为了验证该技术高分辨率处理的优势, 设计如图 3所示的薄互层模型并添加10%高斯噪声, 黄色填充为砂岩, 灰色为泥岩, 3套砂岩均为10m薄层, 沿着CDP测线方向泥岩隔层厚度逐渐增大, 模型参数为实钻数据, 砂岩速度为3900m/s, 砂岩密度为2.50g/cm3, 泥岩速度为3800m/s, 泥岩密度为2.65g/cm3, 子波选用25Hz的零相位雷克子波。
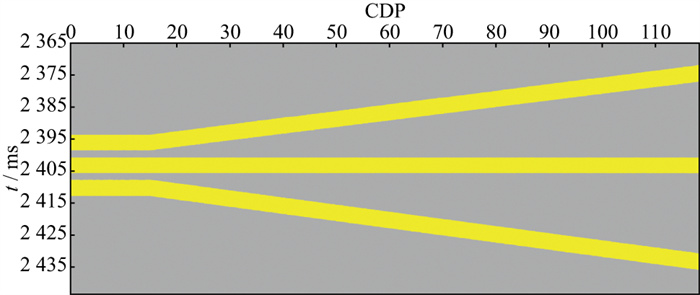
|
图 3 薄互层模型(含10%噪声) |
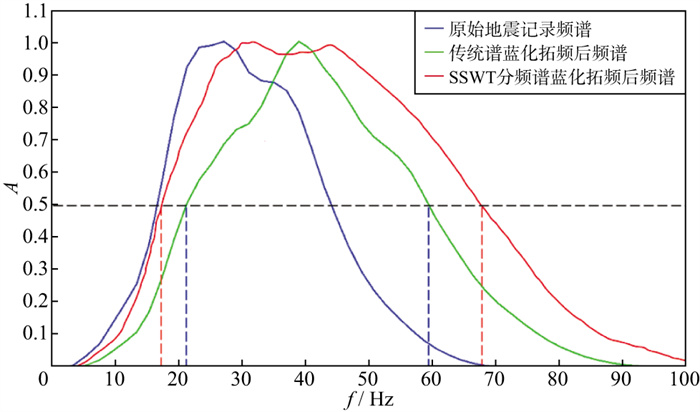
图 4为根据该模型正演得到的地震记录、传统谱蓝化拓频和SSWT分频谱蓝化拓频结果。分析可知, 泥岩隔层为14m处(图 4a红色箭头), 第一套砂岩底出现波峰, 而泥岩隔层厚度约为22m处(图 4a黑色箭头), 第二套砂岩底出现波峰, 且薄层的波形厚度明显超过实际厚度10m, 薄层分辨率整体不高。相较于原始地震记录, 图 4b中第一套砂底波峰出现在隔层厚度8m处(图 4b红色箭头), 传统谱蓝化拓频方法虽然无法有效区分第一套与第二套砂体, 但第二套砂岩底波峰较原始地震记录出现更早, 泥岩隔层厚度约15m(图 4b黑色箭头), 整体薄层分辨能力得到了较大程度的提升。对比图 4b和图 4c可知, SSWT分频谱蓝化的第一套砂岩底波峰相较于传统谱蓝化拓频结果有了进一步提升(图 4c红色箭头), 泥岩隔层厚度约为10m(图 4c黑色箭头)处第二套砂岩底出现波峰, 薄层识别精度更高。相较于传统谱蓝化拓频, SSWT分频谱蓝化技术的抗噪性更好, 在泥岩隔层偏薄的情况下, 薄层识别精度受噪声影响较小, 且厚度与实际模型匹配度更高(图 4c蓝色箭头)。图 5为原始地震记录频谱与两种谱蓝化拓频的频谱, 蓝色为原始地震记录频谱, 绿色为传统谱蓝化拓频得到的频谱, 红色为SSWT分频谱蓝化拓频得到的频谱。对比可知, 利用传统谱蓝化拓频方法得到的地震资料高频段信息得到了一定程度的拓宽, 但20Hz以下的低频信息存在损失, 有效频带(信噪比>1)范围为21~59Hz; 而利用SSWT分频谱蓝化拓频技术得到的结果中, 中、高频段信息更丰富, 且有效地保留了原始地震低频段信息, 有效频带范围为16~67Hz, 故该技术对地震资料拓频效果更好。
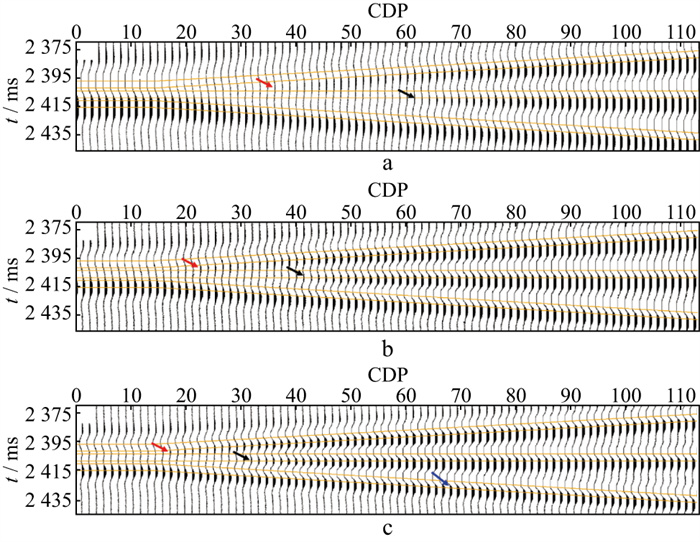
|
图 4 模型正演地震记录(a)、传统谱蓝化拓频结果(b)与SSWT分频谱蓝化(c)技术拓频结果 |
|
图 5 原始地震记录频谱与两种谱蓝化拓频技术得到的频谱 |
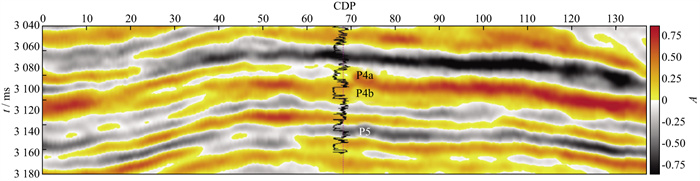
为了验证本文技术的有效性, 以XH凹陷中深层某气田N-1井为例进行分析。图 6为过该井的原始地震剖面, 该井在4050m附近钻遇两套优质薄气层P4a、P4b, 厚度分别为12m和13m, 两层之间泥岩隔层为6m。受限于XH凹陷中深层地震资料品质, 无法有效区分两套薄互层, 地震剖面上P4a砂顶表现为弱波峰, 与下覆P4b表现为典型复波叠置特征。
|
图 6 过N-1井的原始地震剖面 |
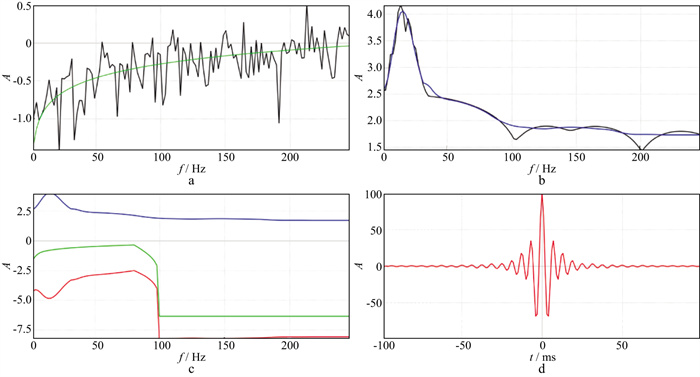
对此, 首先应用SSWT分频谱蓝化技术进行分频及优化谱蓝化算子求取。为了提高靶区拓频效果, 此次选用N-1井进行测井谱与不同频段地震谱匹配算子求取, 其中, 地震谱计算时采用N-1井邻道目的层段地震数据。图 7为中心频率为16.5Hz的分频段地震频谱与N-1井谱蓝化算子求取过程, 图 7a为N-1井目的层段反射系数谱, 图 7b为分频段地震数据在N-1井邻道目的层段的地震频谱, 蓝色为平滑后的振幅谱, 图 7c为分频段谱蓝化算子匹配结果, 其中蓝色为地震平均谱, 绿色为测井反射系数谱, 红色曲线代表该分频段的频率域谱蓝化算子, 图 7d为该算子的时间域形态。类似地, 对其它分频段分别求取分频段谱蓝化算子, 最后利用(11)式和(12)式分别计算优化后的谱蓝化算子及优化后的拓频地震数据。
|
图 7 中心频率为16.5Hz的分频段地震频谱与N-1井谱蓝化算子求取过程 a N-1井目的层段反射系数谱; b分频段地震数据在N-1井邻道目的层段地震频谱; c分频段谱蓝化算子匹配; d时间域分频段谱蓝化算子 |
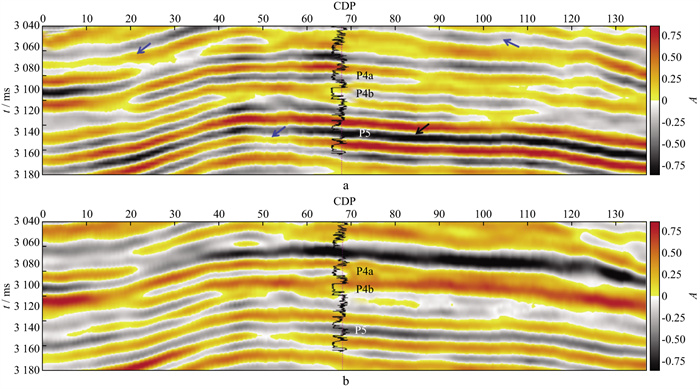
分别应用传统谱蓝化及SSWT分频谱蓝化两种技术对P4a段、P4b段地震资料进行拓频处理, 得到的剖面如图 8所示。不难发现, 两种技术均能提高P4两套薄互层地震分辨率, 且高频信息有所提高, 但在原始地震低频信息的保真上, 传统谱蓝化拓频在一定程度上破坏了低频段信息, 且横向分辨率存在损失(图 8a蓝色箭头), 而该技术的局限性也使得P5段振幅能量失真, 相较于原始地震剖面, 其振幅能量过强(图 8a黑色箭头)。
|
图 8 对P4a, P4b段地震资料应用两种分频谱蓝化拓频技术得到的剖面 a传统谱蓝化拓频; b SSWT分频谱蓝化拓频 |
图 9为分别应用两种谱蓝化拓频技术在3040~3180ms段得到的地震频谱, 黑色为原始地震频谱, 蓝色为传统谱蓝化拓频后的地震频谱, 红色为SSWT分频谱蓝化拓频后的地震频谱。对比可知, 对于中、高频信息, 两种技术相较于原始地震信号均有一定程度的拓宽, 其中, 采用SSWT分频谱蓝化拓频技术得到的结果中高频信息更丰富; 对于低频信息, 采用传统谱蓝化拓频技术造成15Hz以下的信息有较大损失, 而采用SSWT分频谱蓝化拓频技术可以有效地保留原始地震资料的低频段信息, 保幅性更好。
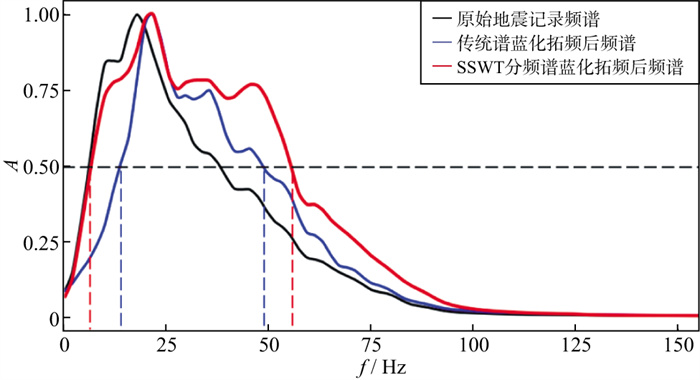
|
图 9 应用两种谱蓝化拓频技术得到的地震频谱(3040~3180ms) |
为了更直观地对比两种谱蓝化拓频处理得到的地震资料对薄储层的预测精度, 对拓频后的地震资料进行90°相移, 将地震界面信息判别转为更直观的岩性厚度识别。图 10a为90°相移后的原始地震资料岩性预测结果, 图 10b和图 10c分别为传统谱蓝化拓频后及SSWT分频谱蓝化拓频后90°相移地震资料岩性预测结果。分析可知, 受限于地震资料的分辨率, 原始地震资料对薄气层段P4a预测效果较差, 仅表现为虚弱反射(图 10a黑色箭头); 传统谱蓝化拓频技术可以明显改善对P4a段的岩性预测结果, 但由于拓频造成地震横向分辨率损失, 预测的砂体展布连续广泛, 故对P4b段下覆岩性假象有一定放大作用, 实钻泥岩段预测为砂岩(图 10b黑色箭头); 利用SSWT分频谱蓝化拓频技术得到的地震资料对P4a段岩性预测更合理, 在保留原始地震横向分辨率情况下, 该技术较好地提高了P4a段纵向分辨率, 且对P4b段下覆岩性假象有一定压制效果(图 10c蓝色箭头)。
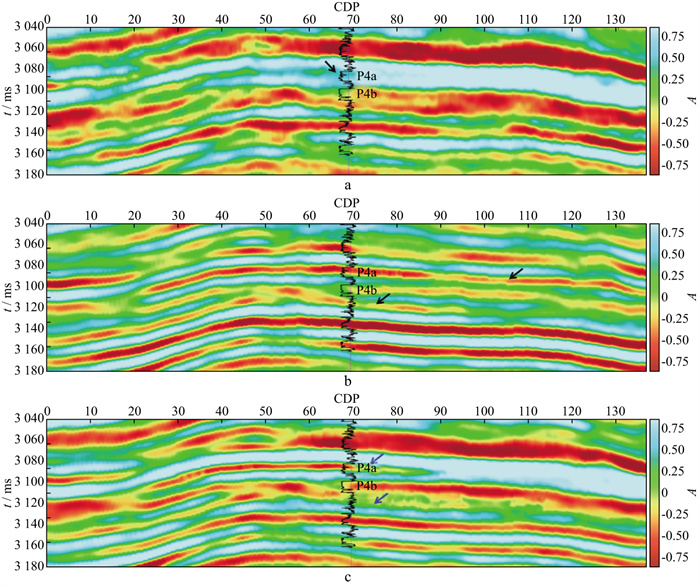
|
图 10 90°相移后的原始地震资料(a)、传统谱蓝化拓频后90°相移地震资料(b)和SSWT分频谱蓝化拓频后90°相移地震资料(c)岩性预测结果 |
图 11a、图 11b和图 11c分别显示原始地震资料以及分别采用传统谱蓝化及SSWT分频谱蓝化拓频得到的过N-1井P4a段砂体横向展布情况。相较于原始地震数据, 两种谱蓝化技术均可以较好地表征N-1井点P4a段砂体, 但其平面展布形态存在差异, 地质分析认为N-1井P4a段砂体为受潮汐改造、断坡遮挡形成的砂坝, 图 11c中SSWT分频谱蓝化拓频后砂体展布与上述认识一致, 在北侧断层尖灭处砂体不发育。图 11b中P4a段砂体表现为北东向连片展布, 在没有断坡遮挡的区域发育砂体, 这与实际地质认识不符。对比分析表明, SSWT分频谱蓝化拓频技术对薄互层砂体纵横向刻画精度更高。
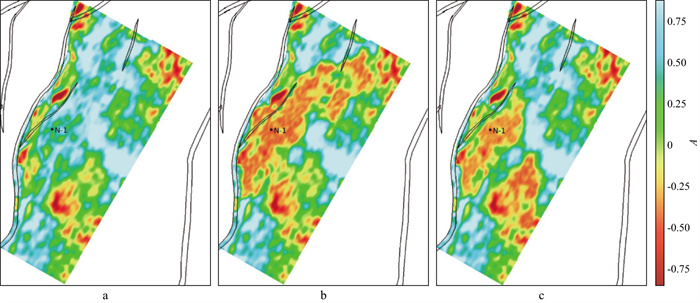
|
图 11 采用两种谱蓝化拓频技术得到的过N-1井P4a段砂体平面展布对比 a原始地震资料; b传统谱蓝化拓频; c SSWT分频谱蓝化拓频 |
谱蓝化地震高分辨处理技术的核心是谱蓝化算子。针对传统谱蓝化算子计算方法的单一性, 本文联合同步压缩小波变换时频分析对分频谱蓝化算子进行优化改进, 获取与实际更匹配的谱蓝化算子, 进而完成地震数据的高分辨处理, 提高地震薄储层识别能力。
SSWT分频谱蓝化拓频技术较好地克服了传统谱蓝化中高频带异常、低频损失等不足, 在高分辨处理的原则下, 较好地保留了低频段信息, 且信号保幅性更好。
中、深层地震资料普遍存在主频低、信噪比不高等问题, 进而影响了储层纵、横向的精细刻画, SSWT分频谱蓝化拓频技术在XH凹陷某气田应用表明, 其较好地提高了薄储层纵、横向分辨率, 砂体刻画结果与地质认识相符, 对薄互储层高分辨率处理具有较好的应用推广价值。
| [1] |
李庆忠. 走向精确勘探的道路—高分辨率地震勘探系统工程剖析[M]. 北京: 石油工业出版社, 1994: 3-8. LI Q Z. The way to obtain a better resolution in seismic prospecting-a systematical analysis of high resolution seismic exploration[M]. Beijing: Petroleum Industry Press, 1994: 3-8. |
| [2] |
王江, 涂国田, 王杰. 基于载波调制的高分辨率地震双向拓频技术及其应用[J]. 石油物探, 2021, 60(6): 954-963. WANG J, TU G T, WANG J. High-resolution seismic bidirectional frequency extension based on carrier modulation[J]. Geophysical Prospecting for Petroleum, 2021, 60(6): 954-963. |
| [3] |
范小冬, 曾濒, 刘益强. 地震资料时空变谱白化处理[J]. 石油地球物理勘探, 1995, 30(4): 550-555. FAN X D, ZENG B, LIU Y Q. Time-space variant spectrum whitening of seismic data[J]. Oil Geophysical Prospecting, 1995, 30(4): 550-555. |
| [4] |
YILMAZ Ö. Seismic data processing[M]. Tulsa: Society of Exploration Geophysics, 1987: 91-95.
|
| [5] |
郭廷超, 曹文俊, 陶长江, 等. 时变谱模拟反褶积方法研究[J]. 石油物探, 2015, 54(1): 36-42. GUO T C, CAO W J, TAO C J, et al. Research on time-varying spectral modeling deconvolution method[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 36-42. |
| [6] |
YAN H Y, LIU Y. Estimation of Q and inverse Q filtering for prestack reflected PP-and converted PS-waves[J]. Applied Geophysics, 2009, 6(1): 59-69. DOI:10.1007/s11770-009-0009-y |
| [7] |
姬战怀. Gabor小波变换在叠后地震数据处理中的应用研究[D]. 西安: 西北工业大学, 2018 JI Z H. Application and research of Gabor wavelet transform in post-stack seismic data processing[D]. Xi'an: Northwestern Polytechnical University, 2018 |
| [8] |
BLACHE F G, NEEP G J. Increasing seismic resolution using spectral blueing and colored inversion: Cannonball field, Trinidad[J]. Expanded Abstracts of 74th Annual Internat SEG Mtg, 2004, 1794-1797. |
| [9] |
KAZEMEINI S H, CAN Y, JUHLIN C, et al. Enhancing seismic data resolution using the prestack blueing technique: An example from the Ketzin CO2 injection site, Germany[J]. Geophysics, 2010, 75(6): 101-110. DOI:10.1190/1.3483900 |
| [10] |
杨瑞召, 赵争光, 马彦龙, 等. 利用谱蓝化和有色反演分辨薄煤层[J]. 天然气地球科学, 2013, 24(1): 156-161. YANG R Z, ZHAO Z G, MA Y L, et al. Thin coal bed resolution by using seismic spectral blueing and colored inversion[J]. Natural Gas Geoscience, 2013, 24(1): 156-161. |
| [11] |
刘建伟, 高秋菊, 师涛. 谱蓝化技术在大王庄油田储层预测中的应用[J]. 复杂油气藏, 2016, 9(1): 31-34. LIU J W, GAO Q J, SHI T. Application of spectral bluing frequency technology in reservoir prediction of Dawangzhuang area[J]. Complex Hydrocarbon Reservoir, 2016, 9(1): 31-34. |
| [12] |
陈文雄. 渤海西南部新近系超薄储层定量预测技术研究与应用[J]. 地球物理学进展, 2019, 34(2): 694-701. CHEN W X. Research and application of quantitative prediction technique for ultrathin reservoir in the neogene of southwestern Bohai sea[J]. Progress in Geophysics, 2019, 34(2): 694-701. |
| [13] |
李贤兵, 赵俊杰, 晋剑利, 等. 叠前谱蓝化提频技术在乍得Baob油田储层预测中的应用[J]. 石油地球物理勘探, 2020, 55(6): 1343-1348. LI X B, ZHAO J J, JIN J L, et al. Pre-stack spectrum blueing frequency increasing technique: A case study on reservoir prediction in Chad Baob Oilfield[J]. Oil Geophysical Prospecting, 2020, 55(6): 1343-1348. |
| [14] |
陈平, 谭辉煌, 秦童, 等. 基于谱反演的谱蓝化拓频方法研究及应用[J]. 东北石油大学学报, 2021, 45(6): 21-30. CHEN P, TAN H H, QIN T, et al. Research and application of spectrum bluing technology for frequency-broadening based on spectrum inversion[J]. Journal Of Northeast Petroleum University, 2021, 45(6): 21-30. |
| [15] |
张璐, 汪毓铎. 地震数据分频谱蓝化算子计算方法及应用[J]. 北京信息科技大学学报, 2020, 35(1): 63-68. ZHANG L, WANG Y D. Calculation and application of spectral blue operator of the frequency division seismic data[J]. Journal of Beijing Information Science & Technology University, 2020, 35(1): 63-68. |
| [16] |
DAUBECHIES I, LU J F, WU H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261. |



