2. 中国石油大学(北京)油气资源与探测国家重点实验室, 北京102249;
3. 中海油研究总院有限责任公司, 北京100028
2. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing), Beijing 102249, China;
3. CNOOC Research Institute Co., Ltd., Beijing 100028, China)
地震波在传播过程中会受到地下各种因素的影响, 使得地震数据并非通常假设的简单、平稳信号, 而是呈现时变特性的非平稳信号。常规傅里叶变换属于整体变换, 只能表征信号的整体频率分布, 不能精细地描述局部时间内信号的变化[1]。时频分析方法可以获取信号的局部时间-频率(时频)特征, 进而表述非平稳信号在不同时刻的频率变化, 因而该方法是地震勘探和储层表征的重要工具和手段[2-5]。
时频分析方法主要分为线性时频分析方法和二次型时频分析方法。线性时频分析方法在傅里叶变换的基础上加入不同的窗函数, 从而获得非平稳信号的时频信息, 其主要包括短时傅里叶变换(short-time fourier transform, STFT)、小波变换(continuous wavelet transform, CWT)和S变换(S-transform, ST)等方法[6]。二次型时频分析方法常用Wigner-Ville分布获取时频谱[7]。尽管该方法有较高的时间分辨率和频率分辨率, 但是将其应用于非平稳信号时, 时频分量之间存在的交叉项会严重影响时频分析结果。相比之下, 线性时频分析方法更适用于非平稳信号。
在地震勘探领域, STFT是最常用的线性时频分析方法, 但受限于固定长度的窗函数, STFT所获得的时频谱的时频分辨率对于所有频率分量是固定的, 因而限制了STFT的应用范围[8]。相比之下, CWT采用不同尺度的窗函数, 因而可以得到更高精度的结果。但在通常情况下, CWT得到的是时间-尺度谱, 不能直观地展现信号的频率变化[9]。ST结合了STFT和CWT的优点, 其窗函数随着频率的变化而变化, 在低频区域有较高的频率分辨率, 在高频区域有较高的时间分辨率, 满足实际生产的需求[10]。然而, ST的窗函数随着频率的变化是固定的, 无法针对不同信号灵活调整ST的时频分辨率, 因而限制了ST在地震勘探中的应用范围。
许多学者根据各自的实际勘探目标, 对S变换进行了不同的改进, 统称为广义S变换。MANSINHA等[11]通过加入单个系数, 从而调整ST的高斯窗长度的变化, 但是单系数只能粗略地调整ST的时频分辨率。因此, PINNEGAR等[12]引入两个参数来控制高斯窗的形状, 可以更为灵活地调整时频分辨率。陈学华等[13]通过加入指数项到高斯窗的标准差参数上, 进一步提高了时频分辨率。LI等[14]提出改进S变换(modified S transform, MST), 将原ST的标准差替换为随频率变化的线性函数, 从而提高了时频谱的时间分辨率。
综上所述, 这些广义S变换方法均是向ST的窗函数加入各自设计的参数, 从而获得满足其勘探需求的时频分辨率。然而, 这些方法均存在低频区域时间分辨率过低的问题和频率成分会向高频移动的现象, 因而得不到有效的低频信息。由于地震波的高频能量在通过油气藏时会被吸收, 会突显低频异常, 所以低频的地震振幅异常可用于指示油气藏区域[15]。因此, 为了提高ST在低频区域的时间分辨率并保持高频区域的时间分辨率, WANG[16]提出了W变换方法(W transform, WT)。WT方法的高斯窗函数不仅随频率变化, 而且受基于Hilbert变换的时变主频的影响, 因而WT方法在低频区域和高频区域均有较高的时间分辨率, 可以更好地应用于储层表征。但与MANSINHA等[11]提出的广义S变换相同, 由于WT方法只能用单参数控制, 因而只能粗略改变时频分辨率, 在实际应用中难以得到较为合适的时频分析结果, 导致其在分析应用方面受到限制。
在前人研究的基础上, 结合MST和WT方法的优点, 提出了改进型W变换(modified W-transform, MWT)的方法。MWT在WT方法的窗函数的标准差项中加入可调的斜率参数, 构建一个新的窗函数, 更为灵活调整WT的时频分辨率。通过替换W变换的窗函数, 从而得到时间域形式的MWT方法, 再将其由时间域转换到频率域。为了证明MWT方法的可行性, 设计了单子波与合成记录两组模拟实验并与ST与WT方法进行对比。最后, 将新方法应用于实际资料的处理, 证明了MWT方法的有效性和适用性。
1 理论方法 1.1 W变换(WT)给定一个时间信号x(t), 其中, t代表时间。对应的W变换为:
| $ {\rm{WT}}(\tau ,f) = \int_{ - \infty }^{ + \infty } x (t)g(\tau - t,f;\tau ){{\rm{e}}^{ - {\rm{i}}2{\rm{ \mathsf{ π} }}ft}}{\rm{d}}t $ | (1) |
式中: τ为窗函数中心对应的时间; f为频率; g(τ-t, f; τ)代表窗函数。表达式为:
| $ g(t, f;\tau ) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} p(\tau , f;k)}}{{\rm{e}}^{ - \frac{{{t^2}}}{{2p{{(\tau , f;k)}^2}}}}} $ | (2) |
式中: k为尺度因子; p(τ, f; k)代表窗函数g(τ-t, f; τ)的标准差函数。该标准差函数是尺度因子k, 时间τ和频率f的函数为:
| $ p(\tau, f ; k)=\frac{k}{f_0(\tau)+\left|f_0(\tau)-f\right|} $ | (i) |
式中: f0(τ)代表不同时间τ的波形主频。要获得该参数, 通常先用Hilbert变换得到信号的瞬时频率, 接着用高斯窗对其平滑就可以得到不同时刻的主频[16], f0(τ)的准确度对于WT的分辨率有极大的影响[17]。此外, 式中|·|代表求绝对值。
由(3)式可知, 因为引入了|f0(τ)-f|项, 使得W变换的时频谱能量主要集中在主频f0(τ)附近, 同时避免了ST的高频移动问题[18]。另外, 当f<f0(τ)时, (3)式分母可写作2f0(τ)-f, 使得标准差函数在0≤f<f0(τ)内小于主频处的函数值, 从而改变窗口大小。因此W变换的窗函数在低频区域(可以表示为0≤f<f0(τ))内依然有较高的时间分辨率。
1.2 改进型W变换(MWT)为了提高时频谱低频部分的分辨率和保持高频部分的时频分辨率, LI等[14]提出了MST方法, 公式为:
| $ {\mathop{\rm MST}\nolimits} (\tau , f) = \int_{ - \infty }^{ + \infty } x (t)G(t - \tau , f){{\rm{e}}^{ - {\rm{i}}2{\rm{ \mathsf{ π} }} ft}}{\rm{d}}t $ | (4) |
其中, 窗函数G(t-τ, f)为:
| $ G(t - \tau , f) = \frac{{|Af + B|}}{{\sqrt {2{\rm{ \mathit{\rm{ \mathsf{ π} }} }}} }}{{\rm{e}}^{ - \frac{{t2(Af + B)2}}{2}}} $ | (5) |
式中: A和B是实数参数, 分别代表G(t-τ, f)的标准差函数的斜率与截距, 用于调控MST方法的时频分辨率。
结合MST方法原理, 在原来的标准差函数p(τ, f; k)的基础上添加了一个新的斜率参数r, 从而构建了新的标准差函数, 减少了基于单参数的WT方法不能精细地调整时频分辨率的影响。新的标准差函数为:
| $ p(\tau, f ; m)=\frac{k}{f_0(\tau)+r\left|f_0(\tau)-f\right|} $ | (6) |
式中: m(k, r)是包含尺度因子k和斜率参数r的参数集, 二者作用类似于MST的参数A与B。通过斜率参数r, 可以更为精细地控制窗的标准差函数与频率之间的变化率。通过控制参数集m(k, r)两个参数, 就可以获得期望的时频分辨率。结合(2)式, 对应p(τ, f; m)的窗函数为:
| $ \begin{aligned} g_m(t, f ; \tau) & =\frac{f_0(\tau)+r\left|f_0(\tau)-f\right|}{\sqrt{2 {\rm{ \mathsf{ π} }}} k} \cdot \\ & \mathrm{e}^{-\frac{t^2\left(f_0(\tau)+r\left|f_0(\tau)-f\right|\right) 2}{2 k^2}} \end{aligned} $ | (7) |
将新构建的窗函数带入原来WT的(1)式中, 改进的WT(MWT)可以表示为:
| $ \begin{array}{*{20}{c}} {{\mathop{\rm MWT}\nolimits} (\tau , f) = \int_{ - \infty }^{ + \infty } x (t){g_m}(\tau - t, f;\tau ){{\rm{e}}^{ - {\rm{i}}2{\rm{ \mathsf{ π} }} ft}}{\rm{d}}t}\\ { = \frac{{{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|}}{{\sqrt {2{\rm{ \mathsf{ π} }} } k}}\int_{ - \infty }^{ + \infty } x (t) \cdot }\\ {{{\rm{e}}^{ - \frac{{(\tau - t)2\left( {{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|} \right)2}}{{2{k^2}}}}}{{\rm{e}}^{ - {\rm{i}}2{\rm{ \mathsf{ π} }} ft}}{\rm{d}}t} \end{array} $ | (8) |
如果r=1, (8)式等价于(1)式, 这代表通过改变参数集m(k, r)的斜率参数r, MWT方法也可以得到WT方法的时频分析结果。之后, 对应的逆MWT(inverse modified W transform, IMWT)表达式为:
| $ x(t) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{\mathop{\rm MWT}\nolimits} } } (\tau , f){{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }} ft}}{\rm{d}}\tau {\rm{d}}f $ | (9) |
如果要保证(9)式成立, 窗函数gm(t, f; τ)需要满足如下条件:
| $ \begin{array}{*{20}{l}} {\int_{ - \infty }^{ + \infty } {{g_m}} (t - \tau , f;\tau ){\rm{d}}\tau }\\ { = \int_{ - \infty }^{ + \infty } {\frac{{{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|}}{{\sqrt {2{\rm{ \mathsf{ π} }} } k}}} {{\rm{e}}^{ - \frac{{(t - \tau )2\left( {{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|} \right)2}}{{2k2}}}}{\rm{d}}\tau }\\ { \approx \frac{1}{{\sqrt {\rm{ \mathsf{ π} }} }}\int_{ - \infty }^{ + \infty } {{{\rm{e}}^{ - {\eta ^2}}}} {\rm{d}}\eta = 1} \end{array} $ | (10) |
如(10)式所示, 由于窗函数近似满足假设条件, 因此会对重构信号产生一定的影响。但对于类似实际资料的地震记录, WANG[16]通过模拟测试表明该假设的影响较小。
此外, 本文将时间域MWT转换到频率域MWT, 其形式为:
| $ {\mathop{\rm MWT}\nolimits} (\tau , f) = \int_{ - \infty }^{ + \infty } x (\alpha + f){G_m}(\alpha , f;\tau ){{\rm{e}}^{{\rm{i}}2{\rm{ \mathsf{ π} }} \alpha \tau }}{\rm{d}}\alpha $ | (11) |
式中: α代表频率域窗函数的频移量, 作用类似于时间域的τ; x(α+f)代表x(t)e-i2πft的傅里叶变换结果; Gm(α, f; τ)为窗函数gm(t, f; τ)的傅里叶变换结果。推导过程为:
| $ \begin{array}{*{20}{c}} {{G_m}(\alpha , f;\tau ) = \int_{ - \infty }^{ + \infty } {{g_m}} (t, f;\tau ){{\rm{e}}^{ - {\rm{i}}2{\rm{ \mathsf{ π} }} at}}{\rm{d}}t}\\ { = \int_{ - \infty }^{ + \infty } {\left[ {\frac{{{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|}}{{\sqrt {2{\rm{{\rm{ \mathsf{ π} }} }} } k}} \cdot } \right.} }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ {\left. {{{\rm{e}}^{ - \frac{{{t^2}{{\left( {{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|} \right)}^2}}}{{2{k^2}}}}}{{\rm{e}}^{ - {\rm{i}}2{\rm{ \mathsf{ π} }} \alpha t}}} \right]{\rm{d}}t}\\ { = \int_{ - \infty }^{ + \infty } {\frac{1}{{\sqrt {2\pi } }}} {{\rm{e}}^{ - \frac{{\xi 2}}{2}}}{{\rm{e}}^{ - \frac{{{\rm{i}}2{\rm{ \mathsf{ π} }} k \xi \alpha }}{{f0(\tau ) + r|f0(\tau ) - f|}}}}{\rm{d}}\xi }\\ \ \ \ \ { = \int_{ - \infty }^{ + \infty } {\frac{1}{{\sqrt {2\pi } }}} {{\rm{e}}^{ - \frac{{\xi 2}}{2}}}{{\rm{e}}^{ - i2\pi \mu \xi }}{\rm{d}}\xi }\\ { = \exp \left\{ {\frac{{ - 2{{\rm{ \mathsf{ π} }} ^2}{k^2}{\alpha ^2}}}{{{{\left[ {{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|} \right]}^2}}}} \right\}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{array} $ | (12) |
其中, ξ和μ的表达式为:
| $ \xi = \frac{{{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|}}{k}t $ | (13) |
| $ \mu = \frac{{k\alpha }}{{{f_0}(\tau ) + r\left| {{f_0}(\tau ) - f} \right|}} $ | (14) |
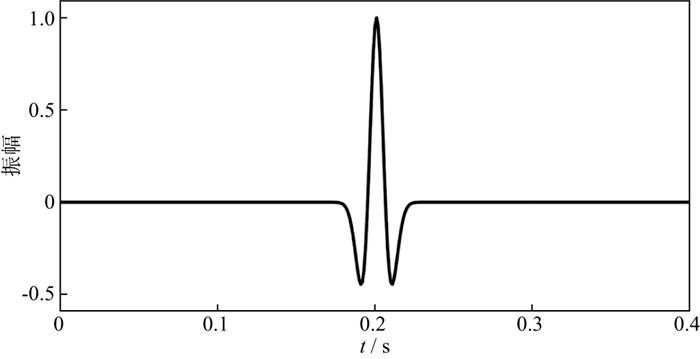
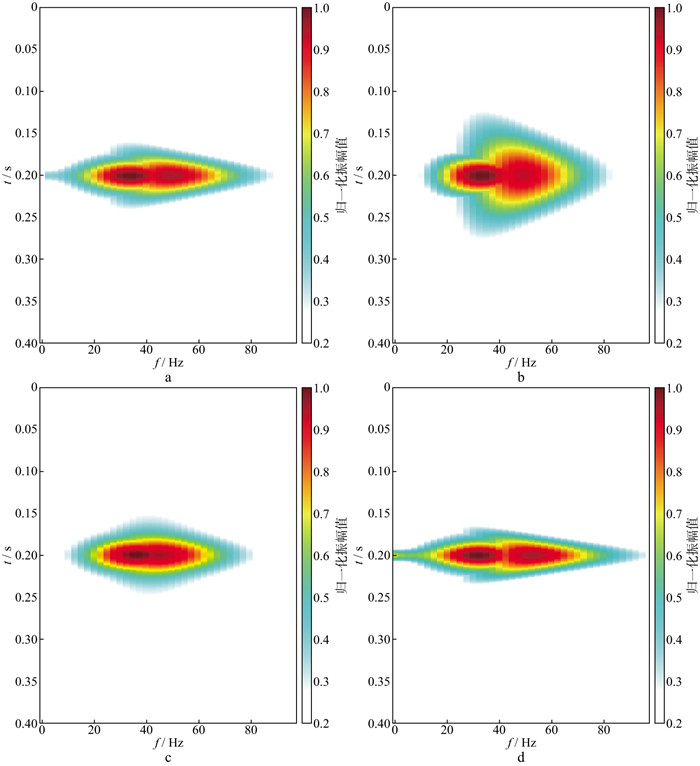
设计了一个简单的模型对WT和MWT方法进行测试。图 1是主频为40Hz的雷克子波, 子波中心位于0.2s处。图 2a和图 2b是选取不同的尺度因子k对应的W变换结果。设定MWT的参数集为m(1.0, 0.5), 其中, 第一项为尺度因子k, 第二项为斜率参数r, 如图 2c和图 2d所示。图 2a为k=1的时频谱, 图中能量集中在0.2s附近, 能量中心位于40Hz处。不同于常规S变换, WT在低于40Hz的区域内依然有较高的时间分辨率。根据Heisenberg测不准原理[20], 如果提高时间分辨率, 那么频率分辨率会对应下降。因此, 图 2a在低频区域内有较高的时间分辨率, 使得频率分辨率有所不足。当尺度因子k=2时, 对应的时频谱如图 2b所示。其中, 能量团在时间方向上主要集中在0.2s处, 频率方向上主要集中于40Hz处。总体的频率分辨率相比于图 2a有所提高, 但是也严重降低了时频谱的整体时间分辨率。同时, 图 2b中时频谱的能量过于发散, 远不如图 2a集中。可见, 尺度因子k是控制WT的时频分辨率的重要参数, k值越大, 时间分辨率越低, 频率分辨率越高, 能量越发散。相比于图 2a, MWT方法得到的时频谱的频率分辨率更高, 并且能量团的中心横向更为平滑。另外, 图 2c时频谱比图 2b时频谱的时间分辨率更高, 能量更为集中, 有效地证明了MWT方法的可行性。此外, 由于WT方法可看作r=1时的MWT, 通过比较图 2a、图 2c和图 2d, 可见斜率参数r越小, 总体频率分辨率更高, 时频谱更平滑; 当r增大时, 低频时间分辨率更高。因此, 提高斜率参数r或降低尺度因子k能改善低频时间分辨率; 反之, 则会提升整体的频率分辨率。
|
图 1 主频为40Hz的雷克子波 |
|
图 2 不同方法的时频结果 a WT对应k=1的时频谱; b WT对应k=2的时频谱; c MWT对应m(1.0, 0.5)的时频谱; d MWT对应m(1.0, 1.5)的时频谱 |
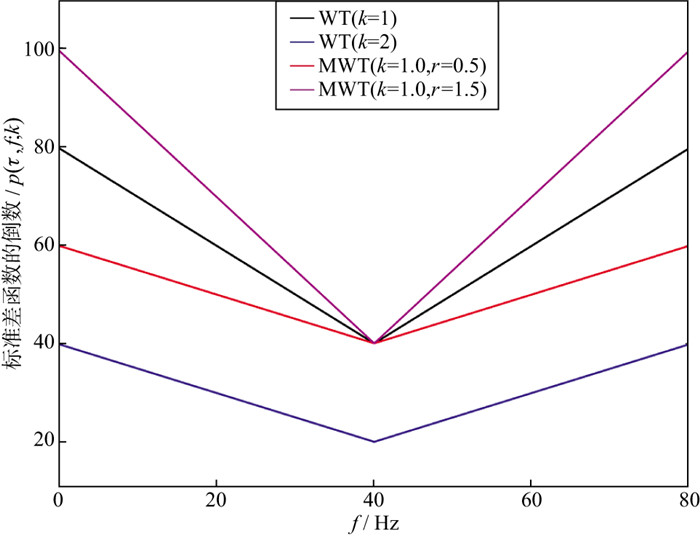
图 3中的黑色线、蓝色线、紫色线和红色线分别代表k=1和k=2时WT变换的标准差函数的倒数1/p(τ, f; k)以及参数集为m(1.0, 1.5)和m(1.0, 0.5)时MWT变换的标准差函数的倒数1/p(τ, f; m)。可见参数k呈倍数地改变标准差函数的大小, 不能精细地调整窗标准差与频率变化关系。而紫色线和红色线通过加入斜率参数r, 改变了标准差函数(k=1)的斜率, 从而修改了窗函数与频率之间的变化率。其中, 红色线通过加入斜率参数r, 使函数1/p(τ, f; m)的斜率等同于k=2时1/p(τ, f; k)的斜率, 使得图 2c的频率分辨率接近于图 2b。因此, 图 3表明MWT方法可以通过调整斜率参数r得到不同斜率的标准差函数, 通过改变尺度因子得到不同的最低点的标准差函数, 进而达到精细调整时频分辨率的目的。而经过测试, 通常尺度因子k取0~2, 双参数比值k/r最好在0.3~3.0。
|
图 3 标准差函数的倒数 |
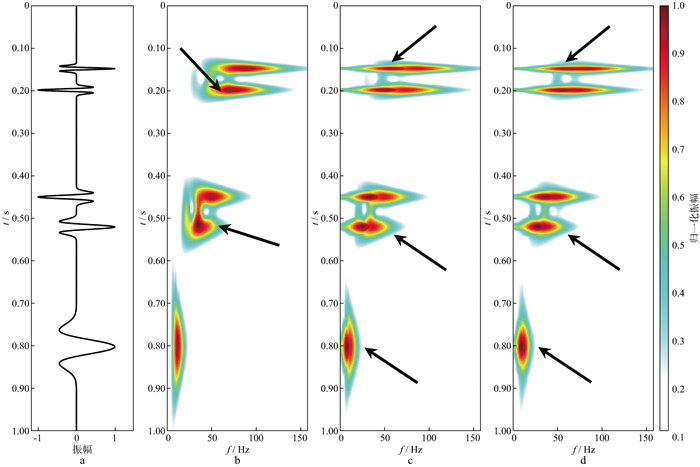
为了测试ST、WT和MWT方法的时间分辨能力, 设计了子波组合的合成记录, 如图 4a所示。记录中包括5个反射点, 分别位于0.15s, 0.20s, 0.45s, 0.52s和0.80s, 对应的振幅大小为1, -1, -1, 1和1。之后, 沿着时间方向从上到下, 分别对该记录的反射点褶积不同主频的雷克子波, 其主频大小由上到下分别为70Hz, 60Hz, 40Hz, 30Hz和10Hz。接着, 分别用ST、WT和MWT方法对该合成记录进行时频分析, 得到时频谱如图 4b至图 4d所示。WT和MWT方法的参数分别为k=0.8和m(0.6, 0.6)。
|
图 4 合成记录和不同方法对应的时频结果 a合成记录; b ST方法得到的时频谱; c WT方法(k=0.8)得到的时频谱; d MWT方法m(0.6, 0.6)得到的时频谱 |
由图 4b可见, 由于ST方法包含归一化项[16], 总体频率成分会向高频移动, 使得低频成分不足, 并且在低频区域时间分辨率过低, 因此在0.20s和0.52s的箭头处可以清晰看到相邻子波的低频区域互相干扰。而WT方法得到的时频谱避免了高频移动现象, 在图 4c的0.15s, 0.52s和0.80s的箭头处可见, 其低频区域内有较高的时间分辨率, 可以很好地分离0.20s和0.52s处的子波组合。但是WT方法只能通过参数k粗略调整整体的时频分辨率, 因此, 在提升频率分辨率的同时降低了时间分辨率, 0.52s的箭头处能量不够集中。而MWT方法得到的时频谱的时频分辨率更为合适, 如图 4d所示。不仅在低频区域有较高的时间分辨率, 并且很好地分离了0.20s和0.52s的子波组合。由于选择了合适的时间分辨率, 相比于ST方法和WT方法的时频分析结果, MWT方法得到的能量团在5个反射点处更为聚焦。该实验表明在低频区域内, WT方法和MWT方法比ST方法时间分辨率更高, 避免了高频移动现象。最后, 为了定量区分3种时频分布的优劣, 用时频聚焦算法[21]计算各方法的时频分布的聚焦度, 得到ST、WT、MWT方法的数值大小分别为6.76×10-5, 6.94×10-5, 7.51×10-5。数值越大对应能量更为聚焦, 可见MWT方法的能量最为集中。MWT方法相比于WT方法, 可以更灵活地调整时频分辨率, 在该记录中有更好的应用潜力。
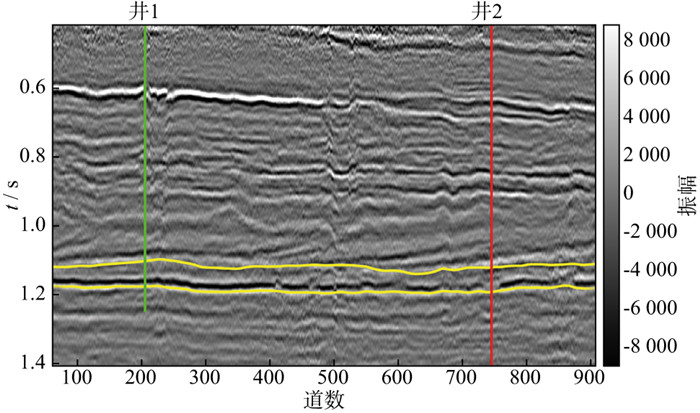
2.3 实际资料测试利用西北地区某实际工区的地震数据进行了方法测试。从叠后数据中选取一张连井剖面, CMP为851, 包含501个采样点, 对应的时间采样间隔为2ms, 如图 5所示。图中黄线指示两个层位, 二者之间即为储层区域。另外, 图中两条竖线分别代表井1和井2的位置, 井1用绿色表示, 为一口干井; 而井2则为一口含油井, 用红色表示, 该井在两个层位之间的储层区域为工业油层。通过提取井1和井2的井旁道数据, 分别用ST方法、WT方法和MWT方法对这些数据进行时频变换, 得到井旁道的时频谱分别对应图 6和图 7。印兴耀等[22]根据地震波穿过含油气储层时的衰减特征, 进而分析上述方法在储层描述方面的有效性。
|
图 5 实际工区叠后剖面 |
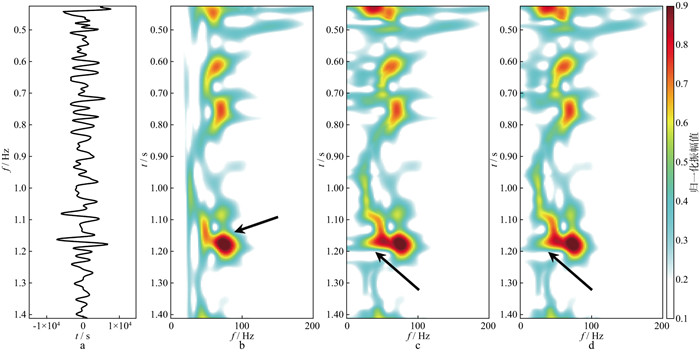
对于井1对应的井旁地震道(图 6a), 由于ST方法存在低频时间分辨率不足的问题, 从而使得图 6b时频谱在低频区域能量过于发散, 远低于高频区域能量。而WT方法(k=1)将时变主频加入到窗标准差函数, 很好地提升了低频区域的时间分辨率, 但是仅用单个参数k只能粗略调整整体时频分辨率, 使得图 6c中时间分辨率有所不足。而MWT方法通过构建参数集m(k, r), 从而更为精细地调整了原来WT方法的时频结果, 获得时间分辨率更高的时频谱, 此处MWT方法的参数为m(1.00, 0.65), 如图 6d所示。从1.15s的箭头处可见, 该方法可以很好地分离上、下层的能量。此外, 由于井1是干井, 因此在代表储层区域的箭头处, 低频到高频的能量变化应当较小。而ST方法在箭头处高频能量明显高于低频能量, 与实际干井结果不符。MWT方法得到的时频谱与WT方法较为接近, 二者均符合测井解释结果。
|
图 6 井1对应的井旁道和不同方法对应的时频结果 a井1对应的井旁地震道; b ST方法时频谱; c WT方法(k=1)时频谱; d MWT方法m(1.00, 0.65)时频谱 |
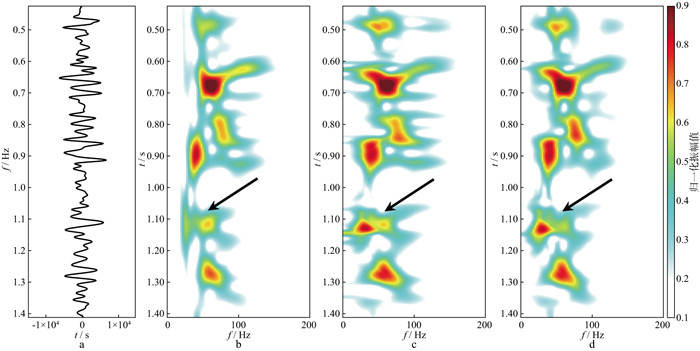
同样对于井2对应的井旁地震道(图 7a), ST方法得到的时频谱如图 7b所示。由于ST方法在低频区域的时间分辨率不足, 使得低频区域的能量在时间方向上极为发散。因为ST方法存在高频移动现象, 所以ST方法得到的时频谱总体能量分布更偏向高频区域, 导致20Hz以下区域能量极低。1.10s的箭头处代表井2的实际储层区域, 因此存在明显的高频衰减现象。而ST方法在此处的高频能量明显高于低频能量, 与井2对应的油井解释结果不符。WT方法(k=1)对应的时频谱如图 7c所示。不仅在低频区域提高了时间分辨率, 而且在高频区域保留了原有的时间分辨率。但是在实际储层高频区域依然有较强的能量分布。基于MWT方法m(1.00, 0.65)得到时频谱的时频分辨率更为恰当, 通过略微降低时间分辨率, 提高储层区域的频率分辨率。在1.15s箭头处可见, 图 7d储层区域能量主要集中在低频区域, 明显高于高频区域, 很好地对应了油井的测井解释结果。
|
图 7 井2对应的井旁道和不同方法对应的时频结果 a井2对应的井旁地震道; b ST方法时频谱; c WT方法(k=1)时频谱; d MWT方法m(1.00, 0.65)时频谱 |
本文在WT方法的基础上提出了改进的MWT时频分析方法。该方法加入新的斜率参数, 结合原有的尺度因子得到新的时变窗函数, 能够更加精细地调整时频分辨率, 其中尺度因子在参数集中影响更大。根据标准差函数随斜率参数与尺度因子的变化情况, 表明斜率参数和尺度因子分别经过调整函数斜率与最低点的大、小, 进而改变窗函数本身, 使得本文方法可以精细控制时频分辨率。将时间域的信号通过MWT变换转换到频率域, 实现简单高效地时频变换。单子波和合成记录的测试结果表明, MWT方法可以通过调整双参数来获得分辨率更为适中、能量更为集中的时频结果。实际工区叠后数据测试结果说明相较于传统的WT方法, 本文方法选取合适的参数集, 可以在油井储层区域对应较为明显的低频异常现象, 证明了该方法的储层表征能力。
值得注意的是, 本文仅对WT变换广义化改进, 并未加入常用时频谱二次处理手段, 如同步压缩、同步提取和反演谱分解等方法。这是我们后续需要开展的研究工作。
| [1] |
郭志伟. 时频分析在高精度地震资料处理中的应用研究[D]. 北京: 中国石油大学(北京), 2020 GUO Z W. Research on application of time-frequency analysis in high-precision seismic data processing[D]. Beijing: China University of Petroleum(Beijing), 2020 |
| [2] |
张付瑷, 陈学华, 罗鑫, 等. 改进的窗参数优化S变换及其在河道检测中的应用[J]. 石油地球物理勘探, 2021, 56(4): 809-814. ZHANG F A, CHEN X H, LUO X, et al. Improved window parameter optimized S-transform and its application in channel detection[J]. Oil Geophysical Prospecting, 2021, 56(4): 809-814. |
| [3] |
CASTAGNA J P, SUN S, SIEGFRIED R W, et al. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127. DOI:10.1190/1.1559038 |
| [4] |
周围, 杨巍, 朱鹏宇, 等. 基于叠前地震数据的流度属性计算方法[J]. 石油物探, 2022, 61(4): 683-693. ZHOU W, YANG W, ZHU P Y, et al. A mobility attribute calculation method based on pre-stack seismic data[J]. Geophysical Prospecting for Petroleum, 2022, 61(4): 683-693. DOI:10.3969/j.issn.1000-1441.2022.04.011 |
| [5] |
LIU W, CAO S Y, WANG Z M, et al. Spectral decomposition for hydrocarbon detection based on VMD and Teager-Kaiser energy[J]. IEEE Geoscience & Remote Sensing Letters, 2017, 14(4): 539-543. |
| [6] |
王克东. 致密砂岩储层地震流体识别方法研究[D]. 北京: 中国石油大学(北京), 2016 WANG K D. Seismic fluid identification method research of tight sandstone reservoir[D]. Beijing: China University of Petroleum(Beijing), 2016 |
| [7] |
赵迎月, 顾汉明, 李宗杰, 等. Wigner-Ville高阶时频谱及其在塔中奥陶系缝洞型储层预测中的应用[J]. 石油地球物理勘探, 2010, 45(5): 688-694. ZHAO Y Y, GU H M, LI Z J, et al. Wigner-Ville higher-order time&frequency spectrum and its application in prediction of Ordovician fractured-vuggy reservoir in Tazhong Area[J]. Oil Geophysical Prospecting, 2010, 45(5): 688-694. |
| [8] |
于豪, 李劲松, 张研, 等. 频谱分解技术在断层与储层识别中的应用[J]. 石油地球物理勘探, 2013, 48(6): 954-959. YU H, LI J S, ZHANG Y, et al. Spectral decomposition in fault and reservoir identifications[J]. Oil Geophysical Prospecting, 2013, 48(6): 954-959. |
| [9] |
AVIJIT C, DAVID O. Frequency-time decomposition of seismic data using wavelet-based methods[J]. Geophysics, 1995, 60(6): 1906-1916. DOI:10.1190/1.1443922 |
| [10] |
STOCKWELL R, MANSINHA L, LOWE R. Localization of the complex spectrum: The S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [11] |
MANSINHA L, STOCKWELL R, LOWE R. Pattern analysis with two-dimensional spectral localisation: Applications of two-dimensional S transforms[J]. Physica A: Statistical Mechanics and its Applications, 1997, 239(1/3): 286-295. |
| [12] |
PINNEGAR C R, MANSINHA L. The S-transform with windows of arbitrary and varying shape[J]. Geophysics, 2003, 68(1): 381-385. |
| [13] |
陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测[J]. 地球物理学报, 2009, 52(1): 215-221. CHEN X H, HE Z H, HUANG D J, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain[J]. Chinese Journal of Geophysics, 2009, 52(1): 215-221. |
| [14] |
LI D, CASTAGNA J, GOLOSHUBIN G. Investigation of generalized S-transform analysis windows for time-frequency analysis of seismic reflection data[J]. Geophysics, 2016, 81(3): V235-V247. |
| [15] |
DAN EBROM. The low-frequency gas shadow on seismic sections[J]. The Leading Edge, 2004, 23(8): 772-772. |
| [16] |
WANG Y. The W transform[J]. Geophysics, 2021, 86(1): V31-V39. |
| [17] |
CHEN X P, CHEN H, LI R, et al. Multisynchrosqueezing generalized S-Transform and its application in tight sandstone gas reservoir identification[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19(6): 1-5. |
| [18] |
WU L, CASTAGNA J. S-transform and Fourier transform frequency spectra of broadband seismic signals[J]. Geophysics, 2017, 82(5): O71-O81. |
| [19] |
WANG B F. An amplitude preserving S-transform for seismic data attenuation compensation[J]. IEEE Signal Process.Letters, 2016, 23(9): 1155-1159. |
| [20] |
HEISENBERG W. Vber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik[J]. Zeitschrift für Physik, 1927, 43(3/4): 172-198. |
| [21] |
JONES D L, PARKS T W. A high resolution data-adaptive time-frequency representation[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(12): 2127-2135. |
| [22] |
印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J]. 中国科学: 地球科学, 2015, 45(1): 8-21. YIN X Y, ZONG Z Y, WU G C. Research on seismic fluid identification driven by rock physics[J]. Science China(Earth Sciences), 2015, 45(1): 8-21. |




