2. 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都610059
2. Key Laboratory of Earth Exploration and Information Technology of Ministry of Education, Chengdu University of Technology, Chengdu 610059, China
随着地震勘探技术的发展, 多分量地震数据在油气勘探和工程勘查中得到了广泛应用[1-4]。三分量地震记录能携带更多的地下介质信息, 其中, 利用地震波极化特性研究地震波场已经成为多分量地震数据处理的重要内容之一[5-8]。
地震极化分析方法最早由FLINN[9]提出并给出了对应的数学算法, 其中, 时间域极化分析方法主要利用特定时间窗口内的三分量地震数据构造协方差矩阵, 解特征方程得到该协方差矩阵的特征值和特征向量[10-11]。利用特征值和特征向量构造一系列能够表征不同类型地震波极化特征的偏振特征函数, 同时, 利用不同偏振特征函数能够构造多种极化滤波器。由于不同震相的地震波质点振动状态不同, 可以利用极化滤波器保留具有某一极化特征的地震波, 达到滤波的目的[12-14]。MONTALBETTI等[15]使用突出线性偏振的特征函数提高地震记录中远震信噪比。SAMSON等[16-17]将偏振特征函数用于自适应地震数据极化滤波, 实现信噪分离。JURKEVICS[18]将偏振特征函数用于阵列地震数据处理, 以提高信噪比, 研究Pn、Sn和Lg波的极化特征。NGUYEN等[19]使用偏振特征函数设计极化滤波器实现了体波和面波分离。AKRAM[20]将线性偏振特征函数和时频阈值方法联合用于微地震数据去噪。PERELBERG等[21]使用不同类型的偏振函数实现了面波、转换波和折射波的分离。ZHANG等[22]使用偏振参数研究了面波的极化特征。上面所提到的偏振函数主要用于波形分离和特定波场衰减研究, 在面波分离和远震噪声衰减方面取得了较好的效果。但是, 大部分偏振特征函数在表征随机噪声时均出现偏差, 特征函数值振荡范围大, 一致性较差, 对有效信号和噪声识别不准确, 给极化滤波带来了干扰。
不同的偏振特征函数对地震信号的偏振特性表征不同, 准确的信号表征是进行高效极化滤波的前提。为提高微地震随机噪声极化滤波器的性能以及对有效信号和噪声的识别能力, 在总结多种偏振特征函数设计滤波器缺点的基础上, 提出了一种新的偏振特征函数极化滤波器。首先, 使用复协方差矩阵法分析地震信号的偏振特性, 同时分析传统偏振特征函数的特点, 对比不同偏振特征函数之间的差异。然后, 设计出一种新的偏振特征函数, 并与传统偏振特征函数进行对比分析, 分析其对噪声信号的表征能力。最后, 利用合成数据和实测数据进行测试与验证, 分别从信噪比、初至波到时和初至波振动方向等方面验证所提出的偏振特征函数设计的极化滤波器的应用效果。
1 方法原理 1.1 复协方差矩阵分析法VIDALE[23]使用复协方差矩阵进行偏振分析。首先, 将某一窗口内三分量地震信号uj(t)(j=x, y, z)进行希尔伯特变换, 然后, 再构造出解析信号, 即
| $ \begin{aligned} & \boldsymbol{X}(t)=u_x(t)+\mathrm{iH}\left[u_x(t)\right] \\ & \boldsymbol{Y}(t)=u_y(t)+\mathrm{iH}\left[u_y(t)\right] \\ & \boldsymbol{Z}(t)=u_z(t)+\mathrm{iH}\left[u_z(t)\right] \end{aligned} $ | (1) |
式中: H代表Hilbert变换。复协方差矩阵表示为:
| $ \boldsymbol{C}(t)=\left[\begin{array}{lll} \boldsymbol{X} \boldsymbol{X}^* & \boldsymbol{X} \boldsymbol{Y}^* & \boldsymbol{X} \boldsymbol{Z}^* \\ \boldsymbol{Y} \boldsymbol{X}^* & \boldsymbol{Y} \boldsymbol{Y}^* & \boldsymbol{Y} \boldsymbol{Z}^* \\ \boldsymbol{Z} \boldsymbol{X}^* & \boldsymbol{Z} \boldsymbol{Y}^* & \boldsymbol{Z} \boldsymbol{Z}^* \end{array}\right] $ | (2) |
式中: X*表示X的共轭。解特征方程
| $ \left[\begin{array}{r} V_k^x \\ V_k^y \\ V_k^z \end{array}\right]\left[\boldsymbol{C}-\lambda_k I\right]=0 $ | (3) |
可得到协方差矩阵C的3个特征值λk和特征向量Ik(Vkx, Vky, Vkz)(k=1, 2, 3)。将特征值降序排列并分别定义为λ1、λ2、λ3。与最大特征值λ1相关的特征向量(V1x, V1y, V1z)指向最大偏振量方向。
1.2 偏振特征函数与极化滤波首先, 通过特征值构造一系列能够表征不同类型地震波极化特征的偏振特征函数。良好的偏振特征函数可以准确地反映地震波的极化特性。表 1为总结归纳出的不同学者提出的特征函数。
| 表 1 偏振特征函数 |
在实际计算中, 当计算窗口位于有效信号段时, λ1≤λ2≈λ3, 其中P1、P3、P4、P5、P6、P7、P8、P9值均趋近于1。P2和P10主要由λ1决定。理论情况下, 当窗口位于随机噪声数据段时, 由于随机噪声数据没有方向性, 因此特征值λ1、λ2、λ3相差较小, 可近似认为λ1≈λ2≈λ3。于是, 在此假设前提下, 可近似认为P1、P3、P4、P6、P7、P8、P10值均趋于0, P2≈0.5, P5与参数ε、N的取值有关。但对于实测信号的处理, 此时特征值仍然以λ1>λ2>λ3为主, 不满足λ1≈λ2≈λ3条件, 各特征函数值也不再趋近于0, 缩小了有效信号和噪声间的差异, 增加了有效信号和噪声分离或噪声衰减的难度。为了设计可靠的极化滤波器, 将偏振特征函数定义为:
| $ P=F\left(p_{c 1}+p_{c 2}+p_{c 3}\right) $ | (4) |
式中: F(*)是归一化函数。pc1、pc2和pc3分别定义为:
| $ \left\{\begin{array}{l} p_{c 1}=\frac{\lambda_1}{\sqrt{\lambda_2+\lambda_3^2}} \\ p_{c 2}=\frac{\lambda_2}{\sqrt{\lambda_1+\lambda_3^2}} \\ p_{c 3}=\frac{\lambda_3}{\sqrt{\lambda_1+\lambda_2^2}} \end{array}\right. $ | (5) |
对于噪声数据段, 当λ1≈λ2≈λ3时,
| $ f(n)= \begin{cases}1 & P \geqslant P_0 \\ P & P<P_0\end{cases} $ | (6) |
式中: P0是临界极化率。ZHENG等[29]为偏振滤波器引入了矢量因子G, 定义为:
| $ \boldsymbol{G}=\left(\boldsymbol{u} \cdot \boldsymbol{I}_1\right) \boldsymbol{I}_1 $ | (7) |
式中: u是原始含噪地震记录; I1是最大特征值对应的特征向量。偏振滤波器的输出为:
| $ \boldsymbol{u}^{\prime}=f(n) \boldsymbol{G} $ | (8) |
式中: u′是滤波后的地震记录。
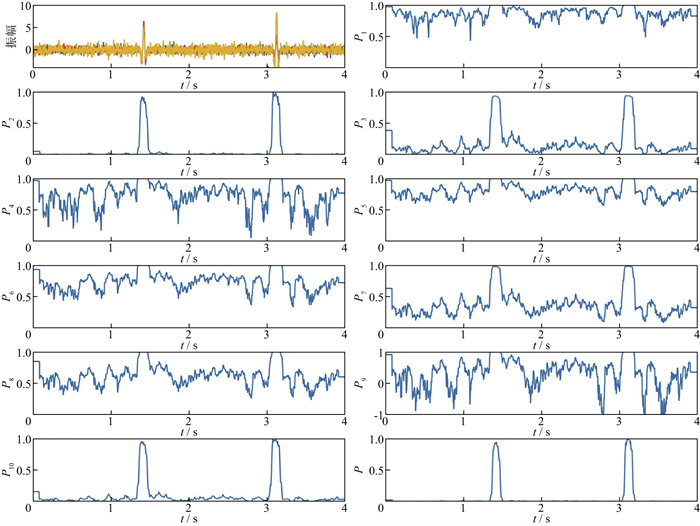
2 应用实例 2.1 合成信号滤波为比较上述偏振特征函数对滤波的影响, 使用一组合成三分量记录验证不同偏振函数对噪声信号的表征能力, 合成信号的三分量及不同偏振特征函数的计算结果如图 1所示。该信号Ricker子波主频为15Hz, 信号采样频率1000Hz, 记录时长4s, 并添加0.2dB随机噪声。P1中n=2;P4中q=1, p=2;P5中ε=1, N=1;P9中n=2;P10中n=1。由图 1可知, P2、P10和本文偏振特征函数P在噪声段接近0, 且有效信号段接近于1。虽然P3、P4、P5、P6、P7、P8和P9在有效信号段接近于1, 但在噪声段振荡幅度较大, 一致性差, 不利于噪声衰减。
|
图 1 合成噪声地震记录和不同偏振特征函数 |
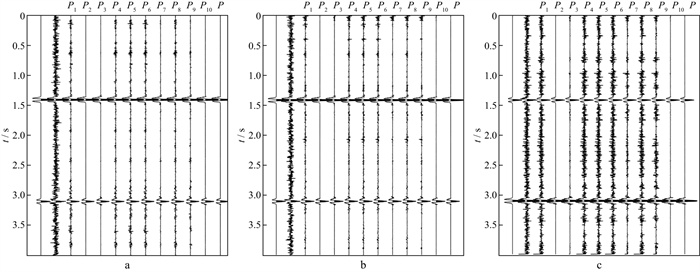
使用不同偏振特征函数构造极化滤波器对信号进行滤波处理后的结果如图 2所示。其中, (6)式中P0取0.5, 且对P2、P9和P10做归一化处理, 滤波过程中其它参数均一致。不难看出, P2、P3、P10和偏振特征函数P对应的极化滤波器对噪声的压制效果较好, 其它特征函数对噪声的压制效果不明显。
|
图 2 不同偏振特征函数所构造极化滤波器的滤波结果(第一道为不含噪信号, 第二道为含噪信号) a X分量; b Y分量; c Z分量 |
为检测极化滤波处理对地震数据初至相位的影响, 使用长、短时窗比(STA/LTA)法对初至时间进行拾取, 其中, STA取0.01s, LTA取0.30s, STA/LTA经归一化处理后阈值选为0.50。拾取初至误差如表 2所示。明显看出, 由于噪声的存在, 对初至时间的拾取均出现了偏差, 但本文偏振特征函数P的误差最小, 更接近原始记录的初至时刻。说明该偏振特征函数对初至波的相位影响较小。
| 表 2 初至误差 |
为量化评估不同的偏振函数对滤波性能的影响, 引入信噪比(SNR)、均方根误差(RMSE)和互相关归一化系数(NCC)。
| $ \mathrm{SNR}=10 \times \lg \frac{\sum \boldsymbol{u}^2}{\sum\left(\boldsymbol{u}-\boldsymbol{u}^{\prime}\right)^2} $ | (9) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\left(\boldsymbol{u}-\boldsymbol{u}^{\prime}\right)^2} $ | (10) |
| $ \mathrm{NCC}=\frac{\sum \boldsymbol{u} \boldsymbol{u}^{\prime}}{\sqrt{\sum \boldsymbol{u}^2 \sum \boldsymbol{u}^{\prime 2}}} $ | (11) |
式中: u表示原始信号; u′表示去噪后信号; N为信号长度。RMSE值可以测量原始信号和去噪信号之间的偏差, RMSE值越低, 表明该滤波器越好。NCC值可以用来评估原始信号和去噪信号之间的相似性。NCC值接近1表示该滤波器可以达到更好的去噪性能, 有效信号能量泄漏小。
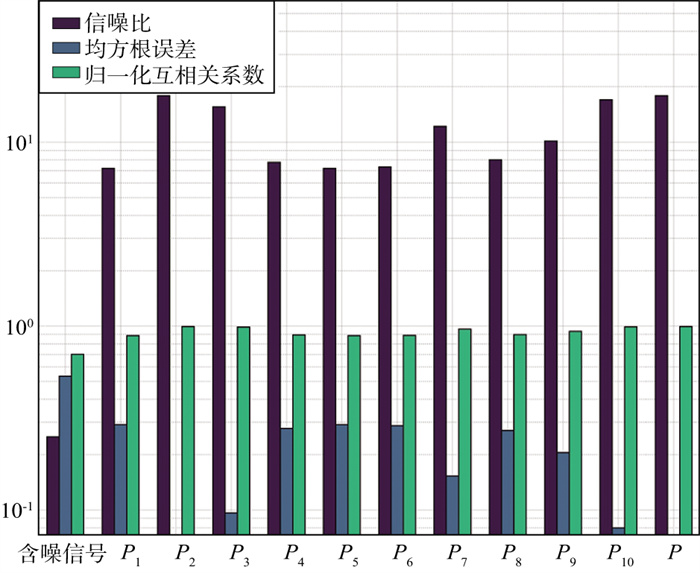
图 3为不同的偏振特征函数构造极化滤波器的输出性能对比, 不同的偏振特征函数均对噪声有衰减作用, 信噪比和归一化互相关系数均有所提升, 均方根误差下降。但采用偏振特征函数P构造的滤波器去噪效果明显优于其它偏振特征函数, 信噪比明显提高。当原始信号的信噪比为0.2dB时, 偏振特征函数P使信噪比提高了约16倍。类似地, 偏振特征函数P构造的滤波器使去噪信号和原始信号之间的RMSE值最低, NCC值最高。实验结果进一步表明, 偏振特征函数P构造滤波器在改善含噪地震记录的质量方面更加可靠。
|
图 3 不同的偏振特征函数构造极化滤波器的输出性能对比 |
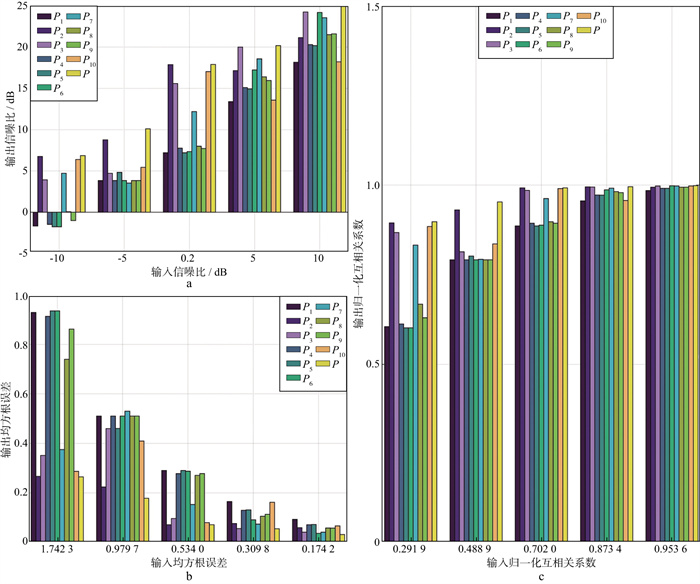
为进一步测试本文偏振特征函数P的有效性, 使用不同信噪比的合成信号作为输入, 对比不同偏振特征函数构造滤波器的输出。仍使用SNR、RMSE、NCC值量化不同偏振特征函数构造滤波器的输出性能, 输出结果如图 4所示。图 4a为输入信噪比-10.0dB、-5.0dB、0.2dB、5.0dB和10.0dB经不同偏振特征函数构造极化滤波器处理的信噪比输出结果; 图 4b为与之对应的输出均方根误差; 图 4c为与之对应的输出归一化互相关系数。
|
图 4 不同偏振特征函数构造极化滤波器处理不同信噪比信号的输出性能对比 a输出信噪比; b与a对应的输出均方根误差; c与a对应的输出归一化互相关系数 |
随着输入信号信噪比的提升, 不同偏振特征函数滤波器的输出信噪比也随之提升。不同偏振特征函数滤波器的输出均比原始输入信噪比高, 说明使用偏振特征函数P1至P10和本文偏振特征函数P所构造的极化滤波器均能压制噪声。但从图 4a可明显看出, 偏振特征函数P对提高信号的信噪比最为有效, 可以在传统偏振特征函数的基础上再提升约25%。此外, 在不同输入情况下, 经偏振特征函数P构造滤波器处理后均方根误差均保持最小, 归一化互相关系数最接近于1.0, 说明偏振特征函数P构造滤波器对有效信号的能量泄露最小, 可靠地保留了有效信号。
另外, 在实现可靠的噪声压制后, 有必要测试所提出方法对地震信号初至相位的影响。图 5对比了不同噪声水平和经不同偏振特征函数构造滤波器处理后的初至相位。初至拾取方法和前文一致, 拾取参数均与信号相适应。偏振特征函数P构造滤波器对初至的影响最小, 进一步表明所提出的方法对原始微地震记录的相位信息影响较小。

|
图 5 不同偏振特征函数构造极化滤波器处理信号后的初至误差 |
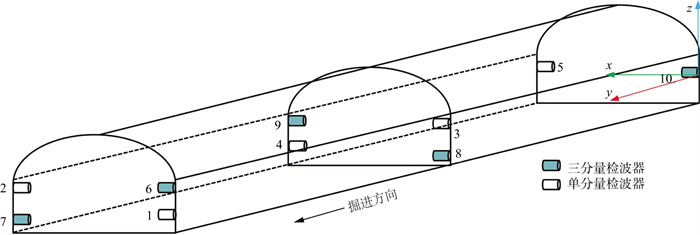
本研究使用的实测微地震信号来源于白鹤滩水电站左岸地下尾水1#施工支洞和尾水连接管监测部分, 采集设备为20通道微地震监测系统, 仪器采样频率为6000Hz。观测系统检波器布设如图 6所示。坐标如表 3所示。
|
图 6 微震监测检波器安装示意 |
| 表 3 检波器坐标 |
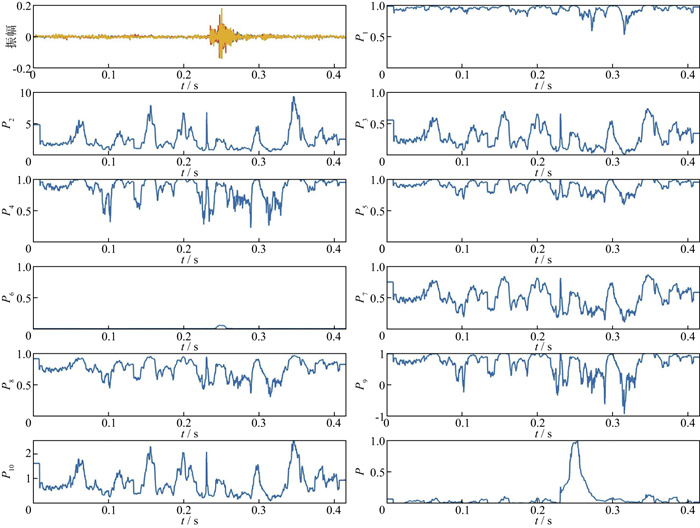
图 7为实际微地震信号的三分量记录和计算出的不同偏振特征函数。对于噪声信号段, 本文偏振特征函数P更接近于0, 且可以有效地识别有效信号与噪声信号。P1至P10均无法有效区分噪声和有效信号。
|
图 7 微地震信号记录和不同的偏振特征函数 |
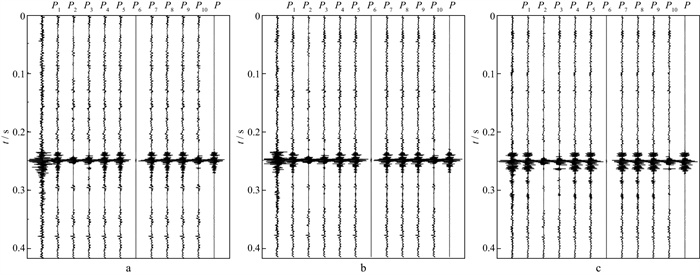
图 8为实测微地震信号经不同偏振特征函数所构造极化滤波器处理后的滤波结果。其中, (6)式中P0取0.154, P1、P4、P5、P9和P10中常量参数与合成信号中选择一致, 且对P2、P9和P10做归一化处理。经偏振特征函数P滤波器处理后噪声被明显压制, 其它偏振特征函数滤波器不能有效压制噪声, 且P6结果出现信号失真。
|
图 8 实测微地震信号的不同偏振特征函数所构造极化滤波器的滤波结果(第一道为含噪信号) a X分量; b Y分量; c Z分量 |
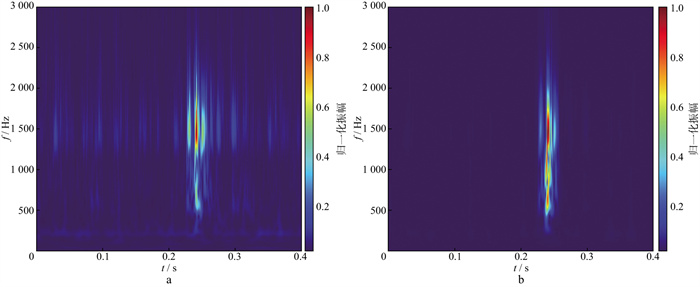
对于实测微地震信号, 经不同特征函数所构造滤波器处理后在时间域具有明显差异, 在同一组处理参数下, 不同的特征函数输出不同。将含噪信号和经偏振特征函数P构造滤波器处理后信号转换至时频域(图 9)。结果显示微地震信号噪声被明显衰减, 有效信号得到了较好地保留。此外, 在图 9a中可见信号存在一明显低频分量, 经过处理后该分量被明显压制。由于实测微地震信号的初至波到时未知, 且未知不含噪声信号, 主要从矢端曲线图对比处理前后的差异。极化滤波主要是根据质点的振动方向进行筛选, 原始含噪信号矢端曲线如图 10所示。
|
图 9 时频域信号 a含噪声信号; b偏振特征函数P构造极化滤波器滤波后的信号 |
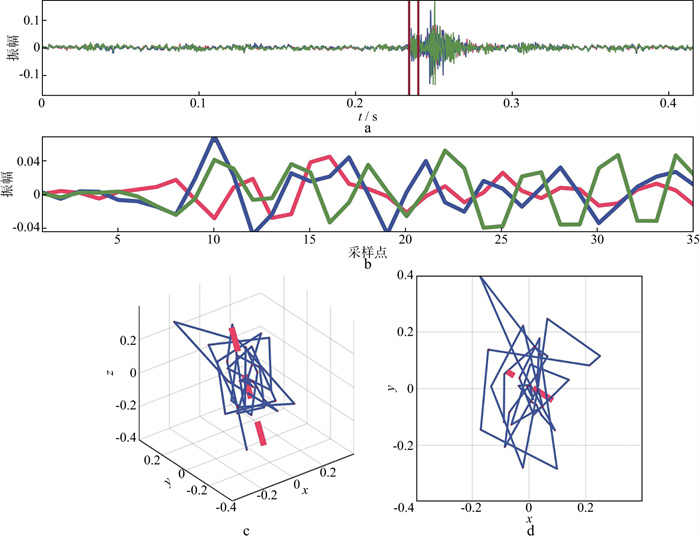
图 10c和图 10d中可见质点运动轨迹复杂, 没有明显的方向性, 不能有效识别初至波的极化方向。经偏振特征函数P构造滤波器处理后矢端曲线如图 11所示。由图 11c和图 11d可见, 质点振动轨迹清晰, 具有很好的方向指示性, 易于识别初至波极化方向。
|
图 10 原始含噪信号矢端曲线 a三分量含噪声信号(竖线标记为用于绘制矢端曲线区域); b a图中标记区域; c矢端曲线三维显示(红色虚线为拟合偏振方向); d矢端曲线xy面显示 |

|
图 11 极化滤波后信号矢端曲线 a三分量信号(竖线标记为用于绘制矢端曲线区域); b a图中标记区域; c矢端曲线三维显示(红色虚线为拟合偏振方向); d矢端曲线xy面显示 |
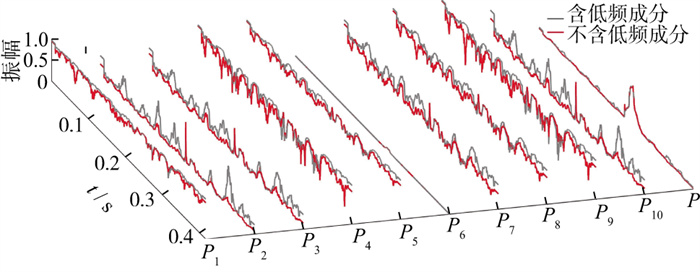
传统偏振特征函数在应用于上文实测微地震信号时效果不理想, 在图 9中可见持续低频背景信号, 因此有必要检查该低频成分对偏振特征函数求取的潜在影响。首先, 使用零相位FIR数字滤波器将该低频成分去除, 再分别计算含低频成分和不含低频成分时的偏振特征函数, 计算结果如图 12所示。由图 12可以看出, 由于低频分量存在, P1至P10在噪声数据段均引起了偏振特征函数的异常增大, 不能准确反映数据的偏振特性, 且不易识别有效信号。不含低频分量的偏振特征函数的值在噪声数据段总体低于含低频分量的偏振特征函数, 可见该低频分量确实影响了偏振特征函数的求取。当去除信号中的低频分量后, 构造偏振特征函数P在噪声数据段的值进一步减小, 对于整体有效信号和噪声信号区别更加明显, 利于后续处理。因此, 在使用偏振分析方法时可先对原始数据进行预处理, 减少低频噪声干扰, 提升偏振分析方法的准确性。
|
图 12 不同频率成分数据的偏振特征函数 |
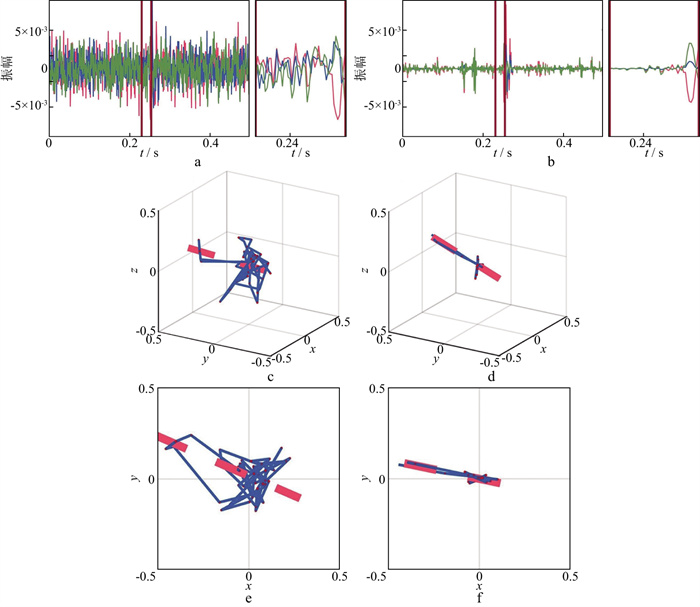
对于实测微地震信号, 其信噪比通常较低, 受到多种噪声干扰。选择一组信噪比较低的实测信号验证本文偏振特征函数P的有效性。实测三分量信号如图 13a所示。有效信号被噪声淹没, 使用本文偏振特征函数P构造的滤波器对其处理后的结果如图 13b所示。处理参数与前文实测微地震信号处理参数一致。经本文偏振特征函数P构造极化滤波器处理后, 保留了有效信号的偏振方向(图 13d), 压制了杂乱无规则振动(图 13c)。
|
图 13 低信噪比实测微地震信号滤波结果 a原始三分量记录(右图为左图中侧红线标注区域的放大显示); b经特征函数P构造极化滤波器处理后的结果(右图为左图中红线标注区域的放大显示); c原始记录矢端曲线三维显示(a图中标记区域); d滤波后矢端曲线三维显示(b图中标记区域); e矢端曲线c的xy面显示; f矢端曲线d的xy面显示 |
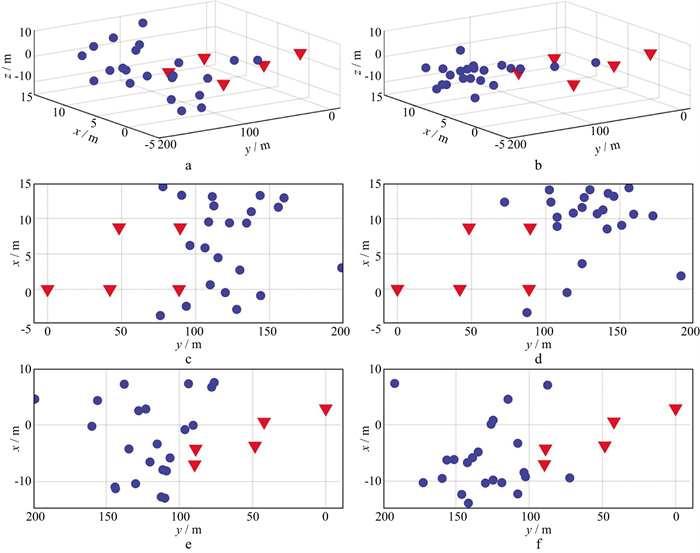
选择一段实际微地震监测记录, 检测筛选出22个微地震事件。得到有效信号准确偏振方向后进行震源定位。图 14为滤波前、后使用直达P波的偏振方向进行震源定位的结果。滤波处理前, 定位震源分布在工作面, 没有聚集性。结合现场施工情况, 可以判断微地震事件主要发生在开挖爆破之后, 位于挖断面和钻孔之间。滤波处理后定位震源主要分布在工作面的一侧, 定位结果与现场施工作业情况吻合, 符合实际情况。因此, 认为经偏振特征函数构造极化滤波器处理后可提高对直达P波偏振方向识别的准确性, 继而提高对微地震震源的定位精度。实测结果进一步证明了本文方法的可靠性与可行性。另外, 计算P波偏振方向构建协方差矩阵时, 数据窗长度对计算结果有影响。在实际计算中, 应根据不同应用对象数据的特征选取合理的数据窗长度, 以免产生较大误差。
|
图 14 滤波处理前、后微地震事件的定位结果 a原记录定位结果; b滤波数据定位结果; c a图的xy面; d b图的xy面; e a图的zy面; f b图的zy面 |
使用复协方差矩阵法分析信号的极化特征, 探究不同偏振特征函数对地震信号的表征能力, 设计了一种提升微地震极化滤波性能的偏振特征函数。经过对比、分析和研究, 得到如下结论。
1) 不同的偏振特征函数计算的信号偏振特性呈现出不同特征, 且对极化滤波器性能的影响也不同。新构建的偏振特征函数可以使噪声数据段趋近于0, 使有效信号和噪声表现出明显差异, 利于噪声衰减。
2) 使用新构建的偏振特征函数处理后, 信号的信噪比、均方根误差和归一化互相关系数均优于其它偏振特征函数。且对初至相位的影响更小, 使计算得到的初至波偏振方向更为准确, 更有利于后续微地震事件的定位。
| [1] |
HUANG W, WANG J, CHEN H, et al. Application of multi-wave and multi-component seismic data in the description on shallow-buried unconsolidated sand bodies: Example of block J of the Orinoco heavy oil belt in Venezuela[J]. Journal of Petroleum Science and Engineering, 2021, 205(10): 108786. |
| [2] |
李志军, 任华育, 杨德义, 等. 三分量微测井方法在转换波静校正中的应用[J]. 石油物探, 2021, 60(1): 114-122. LI Z J, REN H Y, YANG D Y, et al. Application of three-component micro-logging to converted wave static correction[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 114-122. DOI:10.3969/j.issn.1000-1441.2021.01.011 |
| [3] |
邱新明, 王赟, 韦永祥, 等. 多分量面波研究进展[J]. 石油物探, 2021, 60(1): 46-56. QIU X M, WANG Y, WEI Y X, et al. Advancements in multi-component surface waves: A review[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 46-56. DOI:10.3969/j.issn.1000-1441.2021.01.005 |
| [4] |
王赟, 孙丽霞, 李栋青, 等. 勘探地震中的六分量观测[J]. 石油物探, 2021, 60(1): 13-24. WANG Y, SUN L X, LI D Q, et al. Six-component observation for exploration seismology[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 13-24. |
| [5] |
MOHAMMADIGHEYMASI H, CROCKER P, FATHI M, et al. Sparsity-promoting approach to polarization analysis of seismic signals in the time-frequency domain[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60(1): 1-11. |
| [6] |
ZENHÄUSERN G, STÄHLER S C, CLINTON J F, et al. Low-frequency marsquakes and where to find them: Back azimuth determination using a polarization analysis approach[J]. Bulletin of the Seismological Society of America, 2022, 2204.12595. |
| [7] |
BVYVKAKPINAR P, AKTAR M, PETERSEN G M, et al. Orientations of broadband stations of the KOERI seismic network (Turkey) from two independent methods: P-and Rayleigh-wave polarization[J]. Seismological Research Letters, 2021, 92(3): 1512-1521. DOI:10.1785/0220200362 |
| [8] |
NASR M, GIROUX B, DUPUIS J C. A novel time-domain polarization filter based on a correlation matrix analysisA correlation matrix polarization filter[J]. Geophysics, 2021, 86(2): V91-V106. DOI:10.1190/geo2020-0002.1 |
| [9] |
FLINN E A. Signal analysis using rectilinearity and direction of particle motion[J]. Proceedings of the IEEE, 1965, 53(12): 1874-1876. DOI:10.1109/PROC.1965.4462 |
| [10] |
VIDALE J E. Complex polarization analysis of particle motion[J]. Bulletin of the Seismological Society of America, 1986, 76(5): 1393-1405. |
| [11] |
LI H, QU K, RONG W, et al. PolarGUI: A MATLAB-Based tool for polarization analysis of the Three-Component seismic data using different algorithms[J]. Bulletin of the Seismological Society of America, 2021, 92(6): 3821-3831. |
| [12] |
马见青. 多分量地震自适应极化滤波方法研究[D]. 西安: 长安大学, 2012 MA J Q. Researches on adaptive polarization filtering for multi-component seismic data[D]. Xi'an: Chang'an University, 2012 |
| [13] |
LANGSTON C A, LIANG C. Gradiometry for polarized seismic waves[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B8): B08305. |
| [14] |
MEZA-FAJARDO K C, PAPAGEORGIOU A S, SEMBLAT J F. Identification and extraction of surface waves from three-component seismograms based on the normalized inner product[J]. Bulletin of the Seismological Society of America, 2015, 105(1): 210-229. DOI:10.1785/0120140012 |
| [15] |
MONTALBETTI J F, KANASEWICH E R. Enhancement of teleseismic body phases with a polarization filter[J]. Geophysical Journal International, 1970, 21(2): 119-129. DOI:10.1111/j.1365-246X.1970.tb01771.x |
| [16] |
SAMSON J C, OLSON J V. Some comments on the descriptions of the polarization states of waves[J]. Geophysical Journal International, 1980, 61(1): 115-129. DOI:10.1111/j.1365-246X.1980.tb04308.x |
| [17] |
SAMSON J C, OLSON J V. Data-adaptive polarization filters for multichannel geophysical data[J]. Geophysics, 1981, 46(10): 1423-1431. DOI:10.1190/1.1441149 |
| [18] |
JURKEVICS A. Polarization analysis of three-component array data[J]. Bulletin of the Seismological Society of America, 1988, 78(5): 1725-1743. |
| [19] |
NGUYEN D T, BROWN R J, LAWTON D C. Polarization filter for multi-component seismic data[J]. CREWES Research Report, 1989, 1(7): 93-101. |
| [20] |
AKRAM J. An application of waveform denoising for microseismic data using polarization-linearity and time-frequency thresholding[J]. Geophysical Prospecting, 2018, 66(5): 872-893. DOI:10.1111/1365-2478.12597 |
| [21] |
PERELBERG A I, HORNBOSTEL S C. Application of seismic polarization analysis[J]. Geophysics, 1994, 59(1): 119-130. DOI:10.1190/1.1443522 |
| [22] |
ZHANG J, WALTER W R, LAY T, et al. Time-domain pure-state polarization analysis of surface waves traversing California[J]. Pure and Applied Geophysics, 2003, 160(8): 1447-1478. |
| [23] |
VIDALE J E. Complex polarization analysis of particle motion[J]. Bulletin of the Seismological Society of America, 1986, 76(5): 1393-1405. |
| [24] |
JENKINS G M, WATTS D G. Spectral analysis and its applications[M]. San Francisco: Holden Day, 1968: 1-525.
|
| [25] |
KANASEWICH E R. Time sequence analysis in geophysics[M]. 3rded. Edmonton: University of Alberta Press, 1981: 1-480.
|
| [26] |
ESMERSOY C. Polarization analysis, rotation and velocity estimation in three-component VSP[J]. Vertical Seismic Profiling, Part B.Advanced Concepts, 1984, 236-255. |
| [27] |
BAYER B, KIND R, HOFFMANN M, et al. Tracking unilateral earthquake rupture by P-wave polarization analysis[J]. Geophysical Journal International, 2012, 188(3): 1141-1153. |
| [28] |
JONES J P, EATON D W, CAFFAGNI E. Quantifying the similarity of seismic polarizations[J]. Geophysical Journal International, 2016, 204(2): 968-984. |
| [29] |
ZHENG Y, STEWART R R. Polarization filter: Design and testing[J]. CREWES Research Report, 1992, 4(8): 1-19. |


