浅海OBN地震勘探中, 舒尔特波和导波是两种常见的噪声。舒尔特波是地震波在水层和海底界面产生的面波, 具有低频、低速、频散和能量强等特点。导波是由平面波在自由表面和水底之间以超临界角的角度入射, 并在水面和海底之间多次传播产生的一种噪声, 具有频带宽、能量强, 高频端往往产生假频的特点。基于多道统计的滤波技术经常被用来压制这两种噪声, 但是此类方法对地震信号的采样密度有较高的要求, 压制效果取决于数据的采样密度以及信号的频率和视速度。为应对滤波过程中由采样率不足引起的假频问题, 通常在对地震数据进行滤波前采用插值的办法来对数据加大采样密度和规则化。一般情况下, OBN地震采集中的接收线距和道距较大, 采用插值的方法增大采样密度会带来计算资源需求的极大增加。在压制导波之前, 先用线性动校正改善导波的假频问题, 然后用FK滤波或者奇异值分解压制导波[1-2], 在实际应用中取得了不错的效果, 但是这种方法仍然对采样率有一定的要求。唐杰等[3]根据叠前高密度地震数据的特点, 建立面波去噪训练库, 利用去噪卷积神经网络衰减地震数据的面波噪声; 徐阳等[4]提出了广义S变换与二维离散小波变换相结合的面波压制方法。这些研究对压制舒尔特波都有积极意义。近年来, OBN在海洋地震勘探中应用越来越广泛, 有关OBN噪声的压制也得到越来越多的关注。张明强等[5]对OBN地震数据中与水层相关的某些噪声提出双检合并结合波动方程的方法进行压制。
在三分量数据处理中, 利用x、y和z分量地震数据的偏振特性, 设计偏振滤波器压制地滚波、随机噪声和分离纵横波有很多成果和实例。MOROZOV等[6]介绍了一种定向滤波方法, 根据瞬时偏振属性从多分量记录中分离不同类型的地震波; DIALLO等[7]将该方法扩展到连续小波变换, 通过在时频域中设计偏振滤波器来分离不同类型的地震波; 陈赟等[8]在引入多窗谱分析方法的基础上, 通过求解谱密度矩阵特征问题提取三分量数据的偏振参数, 设计滤波器压制随机噪声; 邱新明等[9]介绍了多分量面波的频散特征和偏振特性以及多分量地震数据处理中利用不同的偏振属性分离面波的方法和挑战; 金聪等[10]将偏振滤波应用到三维三分量井间地震的纵横波分离中, 分别利用水平方向和垂直方向的偏振方向分离SH和SV波; 马小军等[11]利用三分量地震数据的偏振特性, 采用滑动窗加权奇异值分解方法对背景噪声互相关波形进行分解、重构, 以达到去噪的目的。
浅海OBN地震采集中, 舒尔特波在水检和陆检的垂直分量数据中能量差异很大, 导波不但在两个分量中能量差异大, 而且是体波, 不能在原始数据上用椭圆率有效地进行分离。因此, 偏振滤波在压制浅海双检数据舒尔特波和导波中的应用几乎不被关注。实际数据处理中的一个发现是通过加权处理, 可以放大OBN数据中舒尔特波、导波和其它信号的偏振属性差异, 从而使得偏振滤波在压制OBN数据垂直分量中舒尔特波和导波的应用成为可能。本文研究了OBN采集中水检和陆检垂直分量地震信号的偏振特性, 提出使用加权偏振分析方法得到信号分离需要的偏振系数, 通过加权偏振滤波压制舒尔特波和导波, 在实际应用中取得了很好的效果。
1 方法原理DONG等[12]的经典著作《界面波》中详细描述了地震数据中舒尔特波在水固分界面的质点运动轨迹和偏振现象。其中介绍了在远离水固分界面的时候, 舒尔特波能量在水层中比在固体介质中衰减更快, 所以, 主要感应水层压力的水检中的舒尔特波振幅会远远小于感应水层和固体介质的陆检中的舒尔特波振幅。相反, 导波绝大部分能量在水层中传播, 只有一小部分能量被传播到水层下的固体介质中, 主要感应水层压力的水检中导波能量远大于陆检中导波能量。PRESS等[13]详细介绍了导波在海水中的产生和传播理论。舒尔特波和导波的能量差异从相同增益显示的水检和陆检记录中可以明显看出(图 1)。也正是因为这个原因, 常规的偏振分析一直不能很好地提取用于分离OBN双检数据中这两种噪声的偏振属性, 使得偏振滤波方法在压制OBN地震数据纵波分量中的这两种噪声一直没有得到广泛应用。

|
图 1 水检记录(a)和陆检记录(b) |
地震数据中的舒尔特波是椭圆偏振的, 与体波的偏振属性明显不同。给定一对水检和陆检垂直分量数据, 如果在舒尔特波到达的时窗周围绘制径向分量和垂向分量, 我们将观察到如图 2所示的椭圆, 其上升角α接近π/2。当数据集中在以体波为主的时窗内, 在零偏移距附近, 椭圆将塌陷成一条线(λ2≈0), 纵波的上升角接近π/2, 随着偏移距增大, 纵波的上升角减小。导波的上升角在零值附近, 质点振动呈线性偏振, 通常不能使用偏振滤波进行压制。但是, 在OBN双检数据中可以通过加权处理, 得到导波区别于其它信号的偏振属性。

|
图 2 具有几何属性的椭圆偏振示意 |
图 2中的θ是参与计算的水检和陆检之间的相位差, 通常是π/2。取n为整数, 根据偏振的定义, 如果θ=nπ时, 为线性偏振; 当θ=(n+π/2)时, 为椭圆偏振。椭圆率是短轴和长轴的比值, 其值的大小取决于参与计算的两个分量地震信号的振幅比值。使用加权偏振分析, 适当地对信号的振幅进行缩放, 可以放大噪声与有效波之间的偏振属性差异, 提取用于从OBN垂直分量数据中分离舒尔特波和导波的偏振参数, 并依据这些偏振参数设计滤波器, 压制这两种噪声。
1.1 双检数据的加权偏振分析偏振分析中, 对水检或者陆检某一分量进行加权处理, 可以很好地提取舒尔特波和导波区别于其它信号的偏振属性。以加权水检数据为例, 定义水检地震道H(t)和陆检地震道G(t)在某个时窗内的平均值:
| $ \bar{H}=\frac{1}{N} \sum\limits_{i=t_1}^{t_2}\left(H_i \cdot w\right) $ | (1) |
| $ \bar{G}=\frac{1}{N} \sum\limits_{i=t_1}^{t_2} G_i $ | (2) |
式中: 是H时窗内水检地震道的加权平均值; w是加权系数, 通过匹配噪声振幅获得, 即w=Gnoise/Hnoise, 其中, Gnoise为陆检数据中要压制的噪声的平均振幅, HnoiseG为水检数据中要压制的噪声的平均振幅; 是时窗内陆检地震道的平均值; t1-t2定义了计算时窗; N为样点数。
定义两个分量地震数据协方差:
| $ \begin{gathered} C_{H G}=\operatorname{COV}\left(H_{\mathrm{w}}, G\right)=\frac{1}{N} \sum\limits_{i=t_1}^{t_2}\left(H_i \cdot w-\right. \\ \bar{H}) \cdot\left(G_i-\bar{G}\right) \end{gathered} $ | (3) |
式中: Hw是加权后的水检数据。协方差数据组成协方差矩阵:
| $ \boldsymbol{C}=\left(\begin{array}{ll} C_{H H} & C_{H G} \\ C_{G H} & C_{G G} \end{array}\right) $ | (4) |
式中: CHH代表H分量的协方差; CGG代表G分量的协方差; CGH代表G分量和H分量的协方差。根据定义, 其特征值λ和特征向量u满足:
| $ C \boldsymbol{u}=\lambda \boldsymbol{u} $ | (5) |
对于二阶矩阵C, 满足等式(5)的特征值有两个, 分别记为λ1、λ2, 且λ1>λ2。
得到某时刻协方差矩阵特征值和特征向量, 可以用这些参数来描述质点振动的偏振特征, 这些参数包括椭圆率、偏振系数和偏振方向等。矩阵的最大特征值λ1和其对应的特征向量u1=(m1, n1)表示了质点振动的主要特征。这些表征质点振动的偏振特性可以用来分离不同类型的地震波。本文主要采用以下两个参数设计压制舒尔特波或者导波的偏振滤波器。
1) 椭圆率。在双分量数据中, 协方差矩阵的特征值λ1、λ2和对应的特征向量u1、u2定义了一个椭圆, 椭圆率
2) 偏振方向(上升角)
下面的讨论结合了OBN采集的地震数据中的两个垂直分量, 即水检数据和陆检数据的垂直分量, 使用由加权偏振分析得到的椭圆率和偏振方向, 设计偏振滤波器来压制浅海勘探中的舒尔特波和导波两种典型噪声。
1.2 利用加权偏振滤波压制舒尔特波OBN数据中, 纵波和舒尔特波都是大上升角信号, 但是它们的偏振形式不同, 反射纵波在空间的质点运动轨迹是直线, 其传播方向和质点位移方向保持一致, 而舒尔特波是椭圆偏振, 因此设计由椭圆率定义的滤波器F(ε), 利用该滤波器在舒尔特波的频率范围内(例如0~15Hz)进行偏振滤波, 从而压制舒尔特波。
| $ \tilde{f}(t)=f(t) F(\varepsilon) $ | (6) |
式中: f(t)为输入信号, 对应陆检数据或加权后的水检数据;
滤波后移除水检数据加权系数, 得到压制舒尔特波后的地震数据。
1.3 利用加权偏振滤波压制导波导波是在水层里传播的一种噪声。原始水检和陆检垂直分量数据偏振属性分析表明, 导波是线性偏振的, 它和地震反射波很难用椭圆率属性有效分离, 但是通过加权处理会使导波的椭圆率比反射纵波的椭圆率高, 这为用偏振滤波压制导波提供了独特的属性。另外, 导波的上升角集中在0值附近, 而反射波上升角则会远离0值, 因此, 偏振方向是可用于压制导波的另一个属性。所以设计滤波器F1(ε)F2(α), 并使用该滤波器进行偏振滤波, 从而压制导波。
| $ \tilde{f}(t)=f(t) F_1(\varepsilon) F_2(\alpha) $ | (7) |
式中: f(t)为输入信号, 对应陆检数据或加权后的水检数据;
滤波后移除水检数据加权系数, 得到压制导波后的地震数据。
2 正演模拟数据试算利用某浅海地区速度模型正演模拟含导波的水检和陆检记录。模拟数据中, 水检分量中导波的能量大约是陆检分量中导波能量的10倍, 因此使用0.1作为加权系数, 对数据进行加权偏振分析, 得到椭圆率谱(图 3)。

|
图 3 模拟记录及加权偏振分析 a水检记录; b陆检记录; c椭圆率谱 |
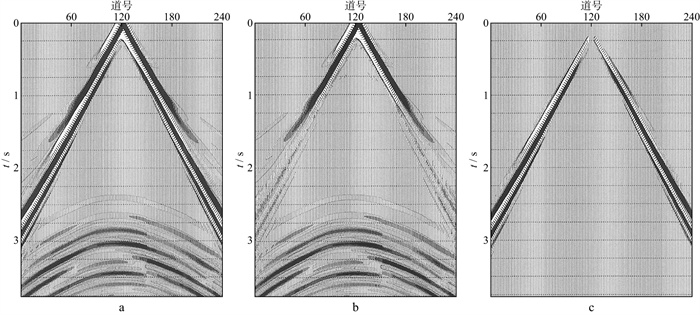
加权偏振分析得到椭圆率后, 设定合适的阈值, 用加权偏振滤波压制记录中的导波。在该实验中, 导波椭圆率范围在0.35~1.00, 因此, 滤除椭圆率0.35以上的信号, 即可得到压制导波之后的数据, 如图 4所示。图 4a为模拟水检记录; 图 4b为偏振滤波后水检记录; 图 4c为滤除的噪声。由图 4可以看出, 加权偏振滤波能够很好地压制双检数据的导波, 并且有效信号以及速度接近导波的初至得到了很好地保护。
|
图 4 模拟水检数据加权偏振滤波前、后记录及其差值 a偏振滤波前水检记录; b偏振滤波后水检记录; c滤除的噪声 |
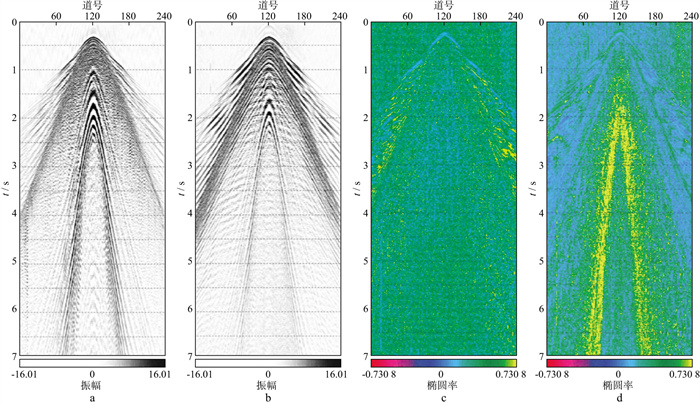
对实际OBN双检数据分别采用常规偏振分析和加权偏振分析求取椭圆率, 结果如图 5所示。图 5a为陆检数据; 图 5b为水检数据; 图 5c为常规偏振分析得到的椭圆率; 图 5d为加权偏振分析得到的椭圆率。前面提到, OBN双检数据中陆检分量中的舒尔特波能量远远大于水检分量中的舒尔特波能量, 如果采用常规偏振分析, 无法提取能够区分舒尔特波和其它信号的椭圆率参数, 如图 5c所示。根据两种检波器数据中舒尔特波振幅估算加权系数w, 以将该加权系数应用到数据中可以将两种检波器数据中的噪声振幅调整到同一数量级为依据, 使用加权偏振分析求取椭圆率, 如图 5d所示, 可以得到舒尔特波明显区别于其它信号的椭圆率。椭圆率谱中, 色标表示椭圆偏振的强弱, 图 5d中黄色部分高椭圆率为舒尔特波的椭圆率, 设计一个阈值, 在舒尔特波出现的频率范围内进行加权偏振滤波以压制舒尔特波。压制舒尔特波前、后的水检记录及其差值如图 6所示。图 6a为输入的地震记录; 图 6b为压制舒尔特波后的地震记录; 图 6c为压制掉的噪声。由图 6可以看出, 使用加权偏振滤波方法, 能够很好地压制舒尔特波, 并且有效信息得到有效保护。
|
图 5 双检数据常规偏振和加权偏振分析结果 a陆检记录; b水检记录; c常规偏振分析结果; d加权偏振分析结果 |

|
图 6 压制舒尔特波前、后水检记录及其差值 a输入的地震记录; b加权偏振滤波后的地震记录; c滤除的噪声 |
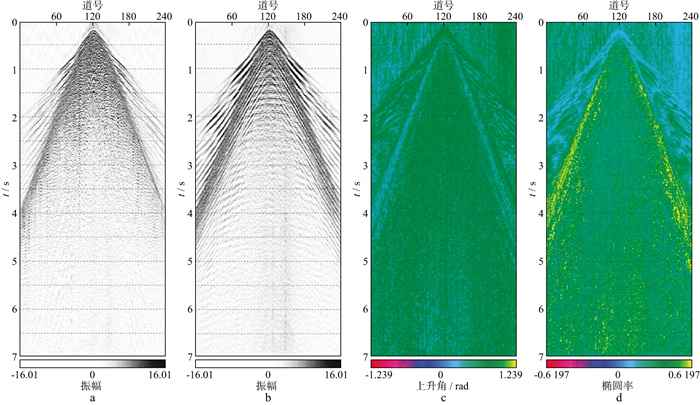
在压制舒尔特波后, 应用加权偏振滤波压制导波。在偏振分析之前, 根据双检数据中导波能量差异, 估算一个加权系数, 然后在估算的系数附近, 通过加权偏振分析找出最佳加权系数, 使用加权偏振分析求取偏振方向系数和椭圆率, 如图 7所示。图 7a为压制舒尔特波之后的陆检记录; 图 7b为压制舒尔特波之后的水检记录; 图 7c为上升角谱; 图 7d为椭圆率谱。由图 7可见, 和反射信号相比, 导波在上升角谱上表现为较小的值, 而在椭圆率谱上表现为较大的值。求取上升角和椭圆率后, 设定阈值, 在导波的速度范围内(例如1400~1650m/s)进行加权偏振滤波, 压制导波。
|
图 7 压制舒尔特波后的双检数据及其偏振方向和椭圆率分析结果 a陆检记录; b水检记录; c上升角谱; d椭圆率谱 |
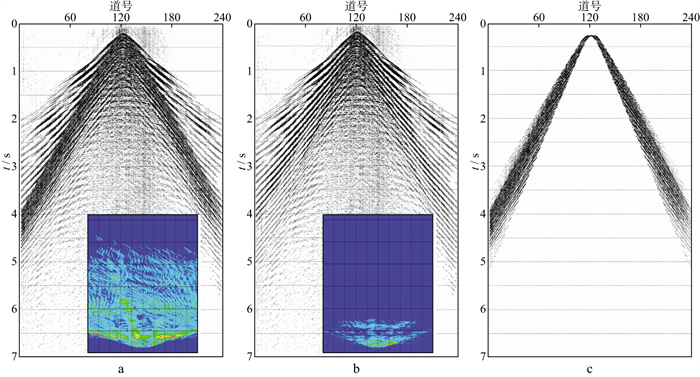
图 8对比了加权偏振滤波压制导波的效果。图 8a为压制导波前水检记录及其FK分析结果; 图 8b为加权偏振滤波后水检记录及其FK分析结果; 图 8c为滤除的噪声。压制前的水检记录上存在能量极强的导波, 从导波压制前的FK谱上可以明显看到导波的强能量及其20Hz以上频率的假频噪声, 偏振滤波后, 这些噪声得到了很好的压制。明显的优势是, 偏振滤波在压制导波的同时, 没有造成速度相近的其它线性信号的损失。
|
图 8 压制导波前、后水检记录及其FK分析结果和滤除的噪声 a压制导波前水检记录及FK分析结果; b加权偏振滤波后水检记录及FK分析结果; c滤除的噪声 |
图 9对比了使用加权偏振滤波压制舒尔特波和导波的效果。图 9a为输入的记录; 图 9b为噪声压制后的记录; 图 9c为滤除掉的噪声。使用本文方法后, 噪声得到压制, 并且低频有效信号和与导波速度接近的线性信号也得到了很好的保护。
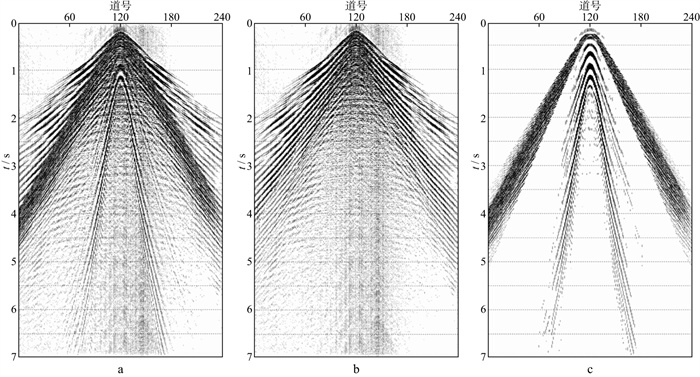
|
图 9 加权偏振滤波压制噪声前、后水检记录及滤除的噪声 a输入的记录; b加权偏振滤波压制噪声后的记录; c滤除的噪声 |
图 10对比了使用FK滤波压制舒尔特波和导波的效果对比。图 10a为输入的记录; 图 10b为噪声压制后的记录; 图 10c为滤除掉的噪声。实际处理中, 在十字排列中应用三维FK滤波压制舒尔特波, 用线性动校正后FK滤波压制导波。很明显, 在用FK滤波压制噪声后, 与导波速度接近的线性信号受到损伤, 在滤除掉的噪声记录中也可以观察到低频反射信号的损失, 并且压噪后的记录在近偏移距的初至信号有明显畸变。对比图 9和图 10可以看出, 使用加权偏振滤波压制这两种噪声以及在保护其它信号方面比常规FK滤波方法具有明显优势, 实现了“高保真”的噪声衰减。

|
图 10 使用FK滤波压制噪声前、后水检记录及滤除的噪声 a输入的记录; b FK滤波方法压制舒尔特波和导波后的记录; c滤除的噪声 |
1) 偏振滤波是根据波的偏振特性差异来分离波场的方法。在众多的偏振分析技术中, 协方差矩阵是可靠、有效的方法之一。由特征值和特征向量可以构造不同的偏振滤波器, 以适应不同噪声的压制。
2) OBN地震数据中, 水检和陆检垂直分量中的舒尔特波和导波能量差异大, 常规的偏振分析无法求取分离这两种噪声的偏振属性, 使用加权偏振分析和滤波很好地解决了这个问题。
3) 偏振滤波基于同一物理点的地震道计算, 并对每个接收点的多分量数据独立处理, 不受空间假频的影响, 因此也适用于空间欠采样地震资料的噪声衰减。
| [1] |
李江. 基于奇异值分解的角度域去噪方法[J]. 石油物探, 2019, 58(3): 427-432. LI J. Seismic denoising in the angle domain based on singular value decomposition[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 427-432. |
| [2] |
马继涛, 王建花, 刘国昌. 基于频率域奇异值分解的地震数据插值去噪方法研究[J]. 石油物探, 2016, 55(2): 205-213. MA J T, WANG J H, LIU G C. Seismic data noise attenuation and interpolation using singular value decomposition in frequency domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 205-213. |
| [3] |
唐杰, 韩盛元, 刘英昌, 等. 基于去噪卷积神经网络的面波噪声压制方法[J]. 石油物探, 2022, 61(2): 245-252. TANG J, HAN S Y, LIU Y C, et al. Seismic surface wave attenuation based on denoising convolutional neural networks[J]. Geophysical Prospecting for Petroleum, 2022, 61(2): 245-252. DOI:10.3969/j.issn.1000-1441.2022.02.006 |
| [4] |
徐阳, 罗明璋, 王智, 等. 广义S变换与二维离散小波变换联合压制面波[J]. 石油物探, 2018, 57(3): 395-403. XU Y, LUO M Z, WANG Z, et al. Surface wave suppression using generalized S-transform and 2D discrete wavelet transform[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 395-403. |
| [5] |
张明强, 焦叙明, 王炜, 等. OBN资料三维水层相关多次波压制方法研究[J]. 石油物探, 2020, 59(6): 872-879. ZHANG M Q, JIAO X M, WANG W, et al. 3D water-layer-related multiples attenuation for OBN data[J]. Geophysical Prospecting for Petroleum, 2020, 59(6): 872-879. |
| [6] |
MOROZOV I B, SMITHSON S B. Instantaneous polarization attributes and directional filtering[J]. Geophysics, 1996, 61(2): 872-881. |
| [7] |
DIALLO M S, KULESH M, HOLSCHNEIDER M. Instantaneous polarization attributes in the time-frequency domain and wavefield separation[J]. Geophysical Prospecting, 2005, 53(5): 723-731. |
| [8] |
陈赟, 高乐, 赵烽帆. 一种基于频率域偏振分析提高三分量地震资料信噪比的方法[J]. 地球物理学进展, 2007, 22(1): 255-261. CHEN Y, GAO L, ZHAO F F. A method to enhance the signal/noise ratio of three-component seismic data based on the polarization analysis in frequency domain[J]. Progress in Geophysics, 2007, 22(1): 255-261. |
| [9] |
邱新明, 王赟, 韦永祥, 等. 多分量面波研究进展[J]. 石油物探, 2021, 60(1): 46-56. QIU X M, WANG Y, WEI Y X, et al. Advancements in multi-component surface wave: A review[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 46-56. |
| [10] |
金聪, 吴遵红, 王薇, 等. 三维井间地震侧面波传播特征及其分离研究[J]. 地球物理学进展, 2021, 36(4): 1531-1540. JIN C, WU Z H, WANG W, et al. Study on the propagation characteristics and separation of 3D cross-well seismic lateral wave[J]. Progress in Geophysics, 2021, 36(4): 1531-1540. |
| [11] |
马小军, 吴庆举. 背景噪声互相关去噪的滑动窗加权SVD滤波方法[J]. 地球物理学进展, 2020, 35(6): 2083-2089. MA X J, WU Q J. Denoising noise cross-correlation via moving time-window weighted-SVD method[J]. Progress in Geophysics, 2020, 35(6): 2083-2089. |
| [12] |
DONG H F, JENS M H.Interface waves[M/OL].https://www.researchgate.net/publication/221916883
|
| [13] |
PRESS F, EWING M. Propagation of explosive sound source in a liquid layer overlaying a semi-infinite elastic solid[J]. Geophysics, 1950, 15(3): 426-446. |




