地震相是指一定分布范围内的地震反射单元, 该单元内的地震特征参数与相邻的单元不同, 它代表了产生其反射的沉积物的岩性组合、层理和沉积特征[1]。对地震相进行分类就是为了进行区域地层解释, 确定沉积体系、岩相特征和解释沉积发育史, 最后将地震相转换到沉积相, 以此作为研究石油地质分布规律的依据, 从而预测出有利生油区和储集相带。早期的地震相分析通常需要解释人员根据专业知识与地区经验, 以人的视觉为基础, 通过地震波运动学几何特征参数进行地震相识别[1], 或是根据客观的地震属性, 按一定的程序对地震相单元进行识别和作图[2]。近年来, 随着深度学习技术的发展, 以及所获取的地震资料的日益丰富, 人们将能够自动提取有用特征的监督学习方法应用于地球物理勘探中的岩性识别[3]、孔隙度预测[4]、波阻抗反演[5-6]等领域。
监督学习方法主要由模型、数据、标签三要素构成。在将深度学习方法应用于地震相预测等地震解释领域时, 国内外的学者大多注重于对模型的网络结构进行替换或改进。例如, 为了提高准确率, LEI等[7]使用基于循环神经网络进行地震波形分类的方法对地震相进行分类; QI等[8]融合了地震属性进行机器学习预测; 李祺鑫等[9]提出了一种基于深度嵌入网络的地震相聚类技术。为了能够评判地震相预测结果的不确定性, 贝叶斯深度学习网络被应用于地震相分类预测[10]。为了解决数据不均衡问题, 有学者在U-Net模型的基础了加入了金字塔池化模块[11]和注意力机制[12]。针对地震解释领域中训练数据难以获得这一问题, 也有学者进行了研究: 为了减少人工制作标签的繁杂工作, 可以只通过少量的带有标签的数据, 实现复杂的地震相分类的弱监督学习方法[13], 不需要标签数据的无监督学习方法[14-15]被引入了地震相预测; 在断层识别领域中, WU等[16]设计了一系列数学函数, 从而自动生成大量断层数据。
但关于地震训练数据标签的结构及地球物理意义几乎无人研究。在处理地震相分类这种多分类任务时, 现有的研究都是将地震相标签转换为独热编码, 这种静态标签包含的信息过于单一, 用于地震相数据训练时会产生以下3个问题: ①由于地层的沉积规律, 位于岩性过渡带的采样点应当兼具相邻地震相的特征, 并且与远离分界处的采样点具有明显的差异; 但用传统的独热标签表示则无法体现出差异, 相同地震相上的采样点会具有完全一样的标签; ②地震数据上地震相识别需要分类的种类较多, 且不同地震相之间可能会存在相似的地震波场特征, 如果一直训练由0, 1组成的独热标签, 强行将其它标签的概率都视为0, 会破坏模型的捕捉数据特征相似度的能力, 造成过拟合; ③地震相数据的标签都是由人工解释获得, 由于数据分辨率或是解释人员的主观因素, 容易误判, 从而使标签含有噪声; 如果直接使用独热标签, 这些噪声会影响模型的训练, 甚至使模型往错误的地方收敛。
本文引入了一种标签精炼方法, 首先对常规地震相深度学习预测结果进行分析, 根据地震数据上各个采样点所处的深度位置, 制作一个可以提取空间先验信息的“先验标签”; 随后引入了一种动态迭代生成地震相标签的标签精炼方法, 在不修改深度学习网络结构的前提下, 提高模型的泛化性, 使地震相预测结果更加准确。
1 方法原理 1.1 常规地震相深度学习预测结果分析在断层、溶洞、盐丘等单一的地震目标深度学习预测任务中, 需要区别的类别只有两类, 训练数据的标签通常为由0, 1组成的二分类标签(目标地质体处为1, 背景围岩处为0)。而对于地震相这种多目标识别任务, 需要区分的类别有C类(C>2)。由于各个地震相标签的数值之间不存在连续性, 所以在训练前将标签数据转化为独热编码, 以增强其稀疏性。对于地震剖面上第n个像素点, 其独热编码标签yn可以用一个由0, 1组成, 大小为1×C的向量来表示, 即yn=[y1, n, …, yc, n, …, yC, n], 若该点实际地震相为c, 则对应yc, n的值为1, 其余的值为0。以挪威北海F3工区数据体为例, 该工区共共划分出6类地震相, 各类地震相标签与对应的独热编码如表 1所示。
| 表 1 地震相标签与对应独热编码 |
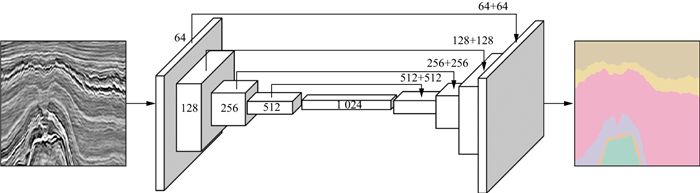
根据闫星宇等[11]的研究成果, 将独热编码应用到F3工区三维地震数据体的地震相深度学习分类任务中, 以分析其预测结果。其中, 网络模型采用现阶段最热门的U-Net深度学习模型[15](图 1), 损失函数采用交叉熵损失函数[17]。训练样本集的数据由人工标注好的三维地震数据体裁剪而来, 每个数据尺寸为256×256, 其中, 2413组数据作为训练集(用于模型的训练), 800组数据作为测试集(用于模型测试)。
|
图 1 U-Net地震相分类模型结构 |
建立好网络模型之后, 将之前准备的地震相训练样本数据分批次成对输入至U-Net模型中, 进行正向传播与反向传播, 计算网络的损失函数值, 更新网络的可调整参数, 并通过迭代训练令损失函数值越来越小。本次实验训练采用Adam优化算法, 学习率设置为10-4。首先将训练数据集中的2413组地震数据体及独热标签分成若干批次输入网络, 每批次输入神经网络的样本数为4。当一个完整的数据集全部通过神经网络完成一次正向与反向传播时, 这个过程称为一个epoch。本次实验中深度学习模型在经过20个epoch后基本达到收敛。
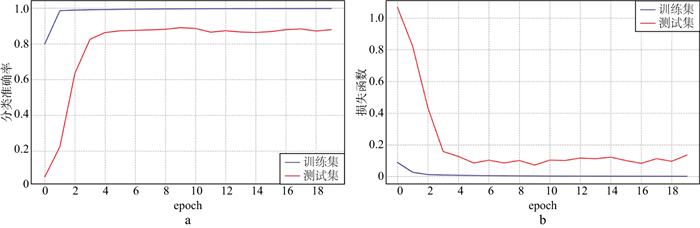
训练过程中准确率与损失函数随epoch变化的曲线如图 2所示, 其中, 蓝线表示训练集数据在训练中准确率与损失函数的变化; 红线表示测试集数据在训练中准确率与损失函数的变化。训练集的准确率最终达到了0.99800, 损失函数值收敛到0.00191附近; 测试集的准确率最终达到了0.879, 损失函数值收敛到0.0135。从图 2中可以看出, 模型在训练集上有着优越的表现, 最终准确率几乎达到了100%, 而测试集的效果却远远差于训练集, 这通常表示深度学习模型出现了过拟合的现象。
|
图 2 准确率(a)与损失函数(b)随epoch变化的曲线 |
出现上述这种过拟合现象的一个重要原因是独热标签包含的信息过于单一。一方面, 相同地震相上的采样点所处的深度位置不同, 结构也会有所差异, 但用传统的独热标签表示却是完全一样的标签; 另一方面, 不同地震相之间可能会存在相似的地震波场特征, 如果一直训练由0, 1组成的独热标签, 强行将其它标签的概率都打压到0, 会破坏模型捕捉数据相似度的能力, 造成过拟合。另外, 地震相等大部分地震数据的标签由人工解释获得, 由于数据分辨率等因素, 尤其是在交界处容易误判, 从而使标签产生噪声。如果直接使用独热标签, 这些噪声会影响模型的训练, 甚至往错误的地方收敛。
对于以上问题, 计算机视觉领域的学者通常使用“平滑标签”这一策略来提高泛化能力[18]。给定像素n的独热编码标签Yn=[y1, n, …, yc, n, …, yC, n], 若该点实际地震相种类为c, 则对应yc, n的值为1, 其余的值为0。“标签平滑”的思想是将真实类别的概率从1略微降低到1-ε, 并且同时将其它错误类别的概率从0增加到ε/(C-1), 其中ε是一个小常数。经过“标签平滑”后, 模型的判定标准不再是非对即错, 可以有效地降低模型过拟合的概率, 同时缓解标签中噪声的影响。但地震相分类时, 由于地质和构造的复杂性, 其中某些类别之间可能具有相似的特征。平滑后的标签对于其它各地震相给出的概率相同, 从而导致该方法无法提取到各个地震相之间的不同的相似关系。因此, 本文对地震相标签的分布特征进行改进。由独热编码构成的初始训练样本集d可以表示为:
| $ d=\left\{\boldsymbol{X}_n, \boldsymbol{Y}_n\right\} $ | (1) |
式中: Xn表示地震振幅图像; Yn表示对应的独热标签。
地震相的分布遵循沉积规律, 相邻越近的两个点, 其为同一种地震相的可能性较大; 另外, 地震相的边界处往往是不同沉积层的交界处, 也是一个岩石矿物物质逐渐转变的过渡带, 因此, 越靠近分界处的点, 其不确定性越高。针对以上特征, 本文利用一个高斯函数来定义不同地震相之间的空间信息关系。对于地震剖面上的每一地震道, 用wc, n评估像素点n与第c类地震相之间的相似度:
| $w_{c, n}=a \mathrm{e}^{-\frac{\left(l_c-b\right)^2}{2 \sigma^2}} $ | (2) |
其中, lc是像素点n与垂直距离最近的地震相种类为c的像素点之间相隔的距离, 这里用相隔的采样点个数表示距离, 若lc的地震相种类为c, 则距离lc=0;a, b, σ为常数, 用于调节高斯函数的形态, 本次研究分别取0.9, -3, 2。然后计算wc, n, 构成“先验标签”wn=[w1, n, …, wc, n, …, wC, n], 并替换训练集中的独热标签q, 此时, 新的训练样本集d0可以表示为:
| $ d_0=\left\{\boldsymbol{X}_n, \boldsymbol{W}_n\right\} $ | (3) |
为了进一步评价改进后标签所包含的信息量, 本文引入了信息论中的信息熵[19]。在信息论中, 信息熵用于度量信息中随机变量的确定性, 即发生概率越高的事件, 其所携带的信息熵越低。信息熵为0时, 为必然事件, 但也因此不携带任何信息量, 从信息论的角度来看, 该事件没有消除任何不确定性。用于地震相预测模型时, 地震剖面上第n个像素点处的信息熵En可表示为:
| $ E_n=-\sum\limits_{c=1}^C p_{c, n} \log p_{c, n} $ | (4) |
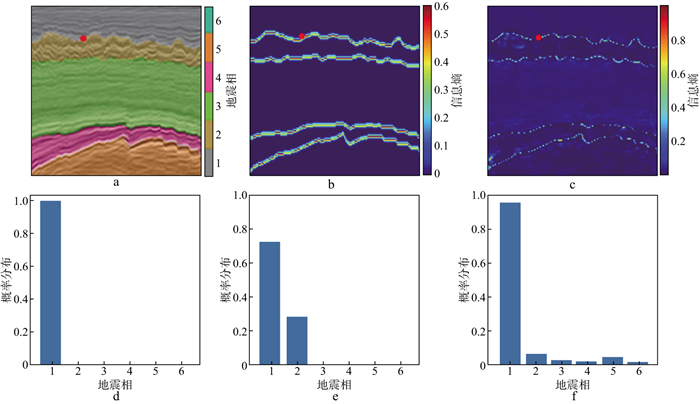
式中: pc, n表示像素点n为第c类地震相的概率。该点处的信息熵越高, 表示pc, n的分布越混乱, 不确定性越高; 信息熵越低, 表示预测结果的不确定性越低。当使用独热标签时, pc, n只有0和1两种可能, 其信息熵En为0, 即没有携带任何信息量。根据信息熵这一评价标准, 可以对本文提出的“先验标签”与地震相预测结果的携带信息量进行一个可视化的展现。图 3展示了不同地震数据携带信息量, 其中, 图 3a为地震相标签; 图 3b为“先验标签”信息熵; 图 3c为深度学习预测结果信息熵[10]; 图 3d、图 3e、图 3f分别为图 3a、图 3b和图 3c中红点处各类地震相的可能性概率分布。从图 3中可以进一步看出, 本文提出的“先验标签”的信息熵分布与深度学习模型的预测结果较为相似, 更加符合实际情况, 即在地震相的交界处具有较高的熵值。这一方面是由于交界处是矿物物质逐渐转变的过渡带, 本身具有较高的不确定性; 另一方面是由于人工标注标签时, 交界处往往难以划分, 容易出现误判等噪声。而“先验标签”则可以将这些信息融入标签之中, 使深度学习模型在训练时具有更为丰富的先验信息, 尤其是在预测交界处的地震相时, 给予更多的不确定性, 从而提高模型预测的泛化性, 减少过拟合的产生。
|
图 3 不同地震数据携带信息量可视化展现 a地震相标签; b “先验标签”信息熵; c深度学习预测结果信息熵; d独热标签概率分布; e “先验标签”概率分布; f深度学习预测结果概率分布 |
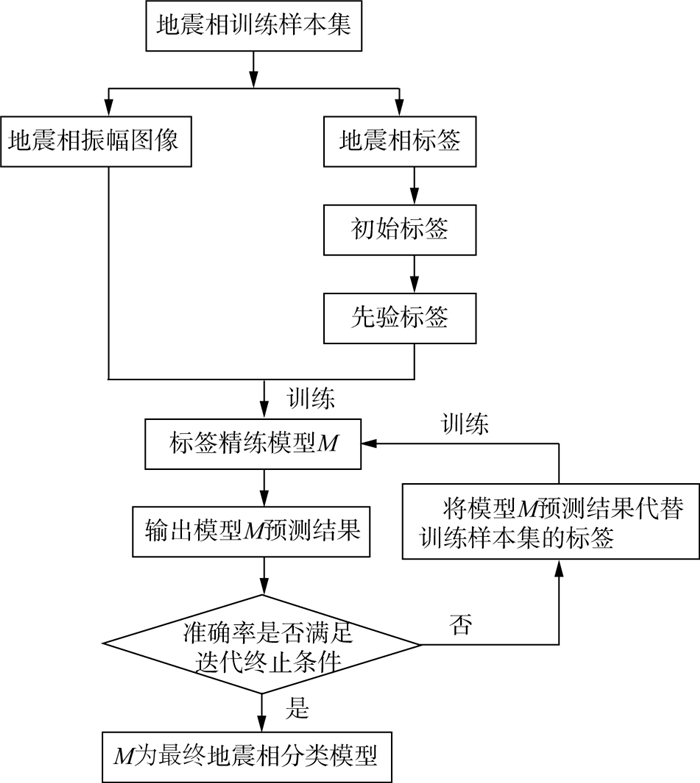
通过制作“先验标签”这一流程, 地震相标签数据获取了一定的空间信息, 但仍然属于静态标签, 无法通过动态迭代而进一步丰富信息, 为此, 本文引入“标签精炼”, 即将“先验标签”与对应的地震数据输入深度学习模型进行训练。训练完成后, 将该模型作为标签精炼器, 并将标签精炼器的输出结果作为“精炼标签”, 替换训练样本集中的地震相标签。将替换后的标签重新输入至相同结构的模型中进行训练, 完成后将该模型作为新的标签精炼模型, 其输出结果作为下次训练的“精炼标签”, 之后迭代进行该过程, 直至达到一定迭代次数或模型预测准确率达到阈值。迭代过程动态更新标签而不调整模型的超参数。标签精炼方法的流程如图 4所示。
|
图 4 标签精炼方法流程 |
建立“先验标签”后, 首先将修改后的数据集d0输入至深度学习模型M中进行训练, 待到损失函数收敛或达到一定迭代次数后训练完成, 并保存训练好网络权重的模型M1与对应的模型输出结果M1(Xn)。需要注意的是, 本方法对于深度学习模型的网络结构并没有具体限制, 一般的卷积神经网络模型均适用。训练好的模型M1视为第一个标签精炼模型, 并将该模型的输出结果M1(Xn)作为新的“精炼标签”, 替换训练样本集中的地震相标签。替换后的训练样本集d1可以表示为:
| $d_1=\left\{\boldsymbol{X}_n, M_1\left(\boldsymbol{X}_n\right)\right\} $ | (5) |
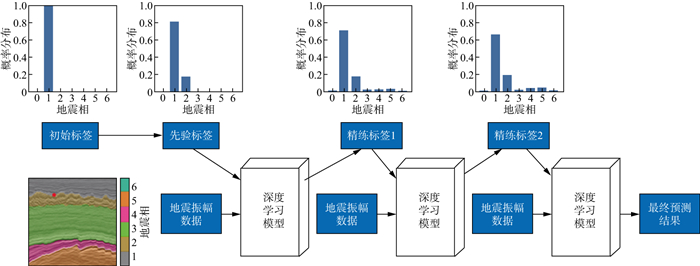
将替换标签后的训练样本集d1重新输入深度学习模型M进行训练。训练完成后同样保存具有新权重的模型M2, 作为新的标签精炼模型, 其输出结果M2(Xn)替换训练数据的标签作为下一轮的“精炼标签”, 从而得到新的训练样本集d2={Xn, M2(Xn)}。之后动态地迭代该过程, 直至达到迭代次数t或者深度学习模型输出结果Mt(Xn)的准确率大于某一判定条件为止。迭代结束后, 保存最后一次的标签精炼模型, 作为最理想的深度学习地震相分类模型, 具体流程如图 5所示, 上方直方图展示了每次迭代后的标签对各地震相的概率分布变化情况。该方法可以动态地更新地震相标签。在每次标签精炼后, 地震相标签的概率分布更加平滑, 同时具有更多的信息。
|
图 5 标签精炼流程 |
由于地震数据的非均衡性, 我们采用由交叉熵与Dice指数组合而成的复合损失函数[20]。第一个标签精炼模型M1的损失函数为:
| $\begin{aligned} L_{\mathrm{CE}} =-\sum\limits_n q_n \log \left[M_1\left(\boldsymbol{X}_n\right)\right] \end{aligned} $ | (6a) |
| $L_{\text {Dice }} =\frac{1}{N}\left[1-2 \frac{\sum\limits_n q_n M_1\left(\boldsymbol{X}_n\right)+\lambda}{\sum\limits_n q_n+\sum\limits_n M_1\left(\boldsymbol{X}_n\right)+\lambda}\right] $ | (6b) |
| $ L_{M_1} =L_{\mathrm{CE}}+e L_{\text {Dice }} $ | (6c) |
式中: N是地震数据包含的像素点总个数; qn为地震相的实际标签, 由0和1组成; λ为平滑算子, 为一个较小数, 本次研究取1; e为Dice损失函数的权重; Xn为输入数据, 第一个网络的输入数据的标签为“先验标签”。这里需要强调的是先验标签只用于交叉熵损失函数LCE。
对于之后的标签精炼模型Mt(t>1), 其损失函数采用KL散度(Kullback-Leibler divergence)。KL散度又被成为相对熵, 可以用于度量两个概率分布函数之间的差异[21], 差异越小, KL散度越小, 反之亦然。当两个概率分布一致时, 其KL散度为0。基于KL散度的性质, 可以将其应用于之后的标签精炼模型的损失函数, 即通过训练, 使模型的预测结果Mt(Xn)与其“精炼标签”Mt-1(Xn)之间的概率分布尽可能地相似, 其定义如下:
| $ \begin{aligned} L_{M_t}= & -\sum\limits_n M_{t-1}\left(\boldsymbol{X}_n\right) \log \left[\frac{M_t\left(\boldsymbol{X}_n\right)}{M_{t-1}\left(\boldsymbol{X}_n\right)}\right] \\ = & -\sum\limits_n M_{t-1}\left(\boldsymbol{X}_n\right) \log \left[M_t\left(\boldsymbol{X}_n\right)\right]+ \\ & \sum\limits_n M_{t-1}\left(\boldsymbol{X}_n\right) \log \left[M_{t-1}\left(\boldsymbol{X}_n\right)\right] \end{aligned} $ | (7) |
其中, 模型输出结果为Mt(Xn); 输入数据的标签为上一个标签精炼模型的输出结果Mt-1(Xn)。(7)式中的后半项为上一个精炼模型的交叉熵, 是一个定值, 因此在训练时可以省略。化简后的损失函数LMt为:
| $ L_{M_t}=-\sum\limits_n M_{t-1}\left(\boldsymbol{X}_n\right) \log M_t\left(\boldsymbol{X}_n\right) $ | (8) |
本次实验训练选用了两组数据。
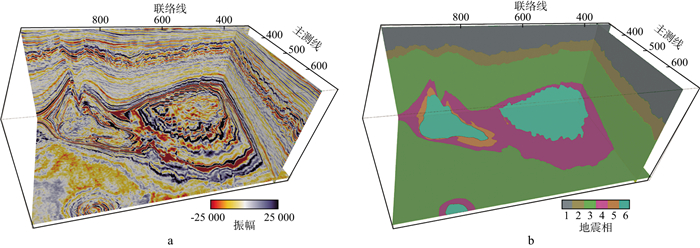
1) 第一组数据采用ALAUDAH等[22]手动标注地震相的位于北海F3工区公开数据集。手动标注地震相范围为主测线100~700, 共601条剖面, 701道。在F3区块的三维地震数据中, 根据岩性共划分了6组岩相单元: 上北海组、中北海组、下北海组、白垩组、莱茵兰组和蔡希斯坦统组[23](从最新到最老, 见图 6)。各组主要岩性为: ①上北海组, 中新世至新近系的粘土岩和砂岩; ②中北海组和下北海组, 从古新世到中新世的沙岩、沙石岩和粘土岩; ③白垩组, 上白垩世和古新世的碳酸盐岩; ④莱茵兰组, 上白垩世的粘土岩和砂岩; ⑤蔡希斯坦统组, 上侏罗纪和下白垩纪的粘土岩。
|
图 6 F3工区训练数据(a)和三维地震数据体地震相标签(b) |
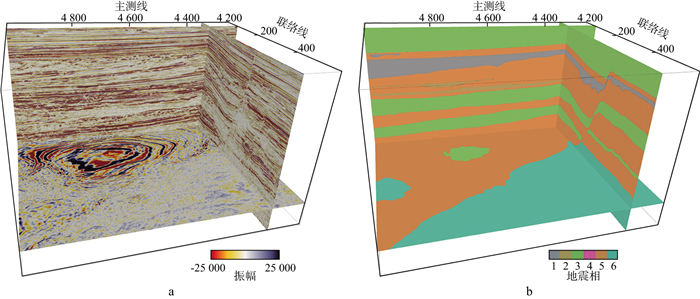
2) 第二组数据来自新西兰公共地震调查局开源的Parihaka工区三维地震数据。该数据同样经地质学家解释, 解释范围为主测线4200~5000, 共801条剖面, 550道(如图 7所示)。并划分了6种地震相: ①基准相(低信噪比、反射较弱, 可能在某些地方含有火山岩); ②坡地泥岩A相(主要为坡地至盆地底泥岩, 上下边界振幅较强; 内部反射较弱); ③大规模沉积相(杂乱反射与弱振幅平行反射混合组成); ④坡地泥岩B相(坡地至盆地底为泥岩和砂岩, 强振幅平行反射); ⑤坡谷(强振幅, 起伏相对较低); ⑥海底峡谷系统(侵蚀基底为U形, 局部起伏较高, 内部填充为低振幅的平行断层和杂乱反射)。
|
图 7 Parihaka工区训练数据(a)和三维地震数据体地震相标签(b) |
在任何领域的深度学习的应用中, 精心选择、划分训练集和测试集都是至关重要的。尤其在地震数据中更应谨慎, 因为地震数据中相邻线道号的数据是高度相似的。如果通过随机取样来划分训练集和测试集, 测试结果无法评估深度学习模型的效果, 而且这样的结果并不能代表被测试模型的实际性能。
因此, 我们应该尽可能地减少训练集和测试集数据之间的相似性, 同时也要确保训练集和测试集能充分代表数据集中所有地震相类别。经过数据分析, 在本次实验中, 将第一组数据体的300~700号剖面作为训练集, 100~299号剖面作为测试集, 用于评估模型的预测效果; 将第二组数据体的4200~4700号剖面作为训练集; 4701~5000号剖面作为测试集。
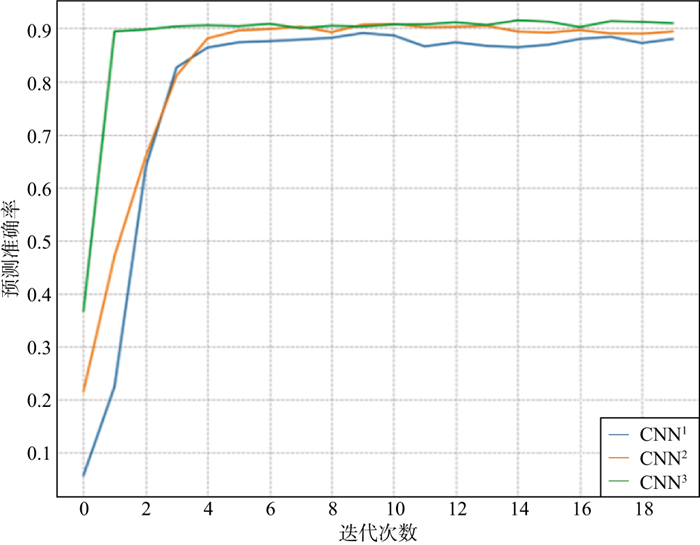
2.2 标签精炼过程在准备好训练数据与测试数据后, 按照本文引入的“标签精炼”流程, 将训练样本集数据输入深度学习模型进行迭代训练, 直到测试集的预测准确率大于0.9为止。两组工区的训练所用模型均为常规的U-Net模型(模型结构如图 1所示)。最终共进行了3次标签精炼, 其中, 在F3工区每次标签精炼过程中, 测试集中预测准确率随训练迭代次数变化的曲线如图 8所示, 蓝线表示第1次训练过程中准确率随迭代次数变化的曲线, 即未经过“标签精炼”的训练结果(CNN1); 橙线表示第2次训练过程中准确率随迭代次数变化的曲线(CNN2); 绿线表示第3次训练过程中准确率随迭代次数变化的曲线(CNN3)。从图 8中可以看出, 每进行一次标签精炼, 模型的预测准确率均有所提升。经过第1次标签精炼后, 模型的准确率最终稳定在0.879;第2次则稳定在0.893;第3次则达到了0.909, 达到了迭代终止条件。需要指出的是, 本研究的重点在于针对训练数据标签结构的研究, 因此并没有对深度学习模型超参数进行针对性的细致调参, 所有超参数均采用Keras深度学习库的默认值。
|
图 8 3次标签精炼的测试集预测准确率随训练迭代次数变化的曲线 |
对于输入的地震剖面, 深度学习模型会对剖面上的每个采样点计算出一个概率分布, 分别对应该点为各类地震相的概率, 从中选择概率最大的那一类作为该点的预测地震相。对每次标签精炼后的预测结果进行统计, 以评价该方法的效果。为了更加客观、全面地展示标签精炼方法在测试集数据上的表现, 本次研究采用了准确率(PA)、类准确率(CA)进行评价, 其结果如表 2所示。我们用γPA表示整个测试数据集中被正确分类的像素点与总像素点比值, 用于评估模型整体预测效果:
| $ \gamma_{\mathrm{PA}}=\frac{\sum\nolimits_{c=1}^C\left|P_c \cap Y_c\right|}{\sum\nolimits_{c=1}^C\left|Y_c\right|} $ | (9) |
| 表 2 不同标签精炼次数下地震相预测结果统计 |
式中: Yc表示在地震剖面上属于第c类地震相的像素点集合; Pc表示被网络模型预测为第c类地震相的像素点集合; 运算符|·|表示集合中的元素总数。
用CAc表示第c类地震相在整个数据集中的预测准确率, 用于评估模型对每一类地震相的预测效果:
| $\mathrm{CA}_c=\frac{\left|P_c \cap Y_c\right|}{\left|Y_c\right|} $ | (10) |
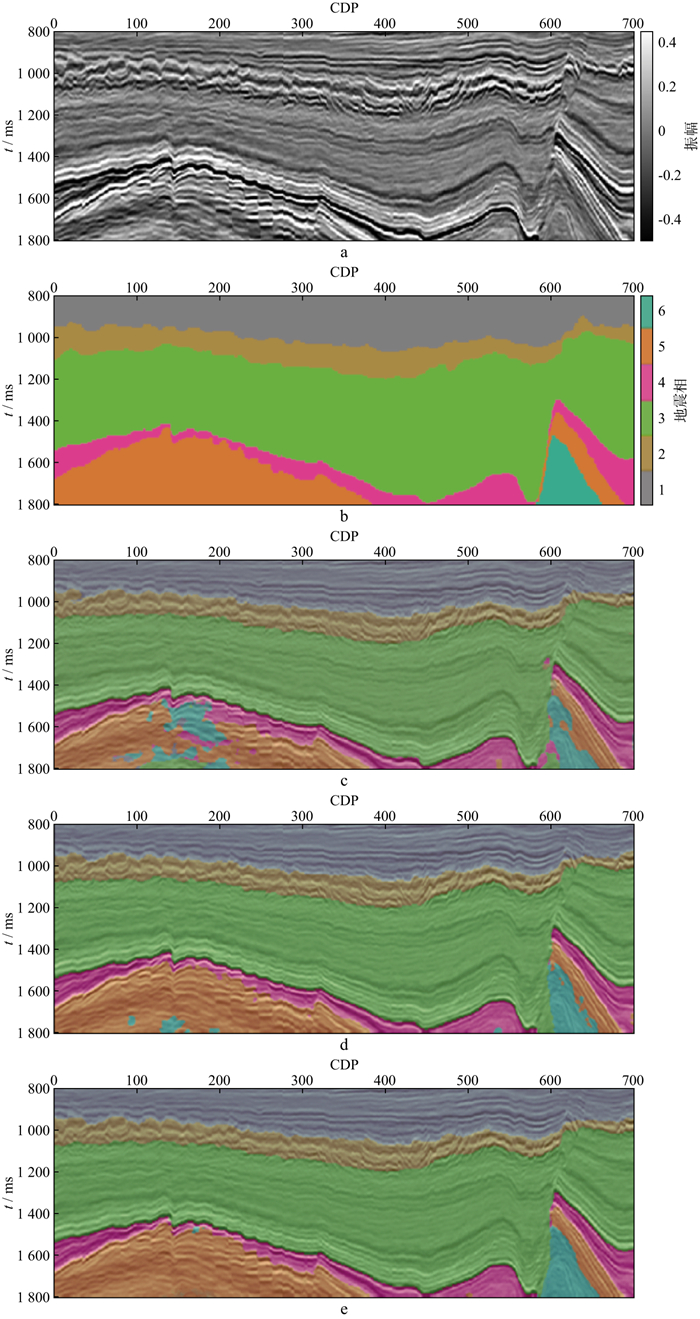
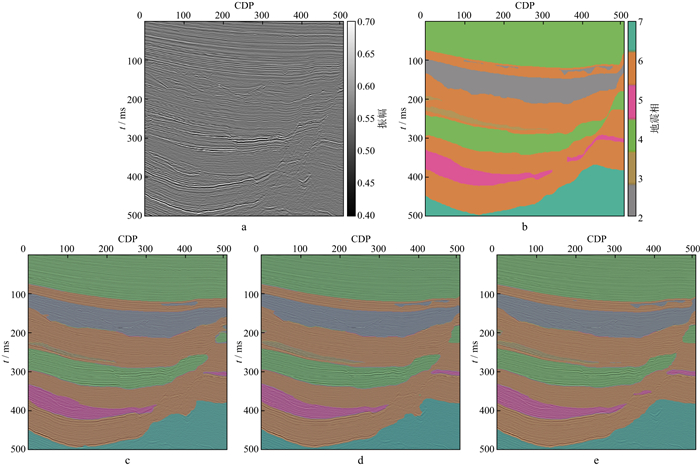
为了进一步验证本文方法的效果, 在两组测试工区的测试集的预测结果中, 分别选取一组剖面进行展示与对比, 结果如图 9和图 10所示, 其中, 图 9a和图 10a为地震剖面; 图 9b和图 10b为对应剖面的真实地震相; 图 9c和图 10c为模型第1次预测后, 深度学习模型对剖面的预测结果, 也可以看作是未经标签精炼的预测结果; 图 9d和图 10d为第2次标签精炼后, 深度学习模型对该剖面的预测结果; 图 9e和图 10e为第3次标签精炼后, 深度学习模型对剖面的预测结果。由图 9和图 10可知, 随着标签精炼流程的迭代次数增加, 同一个深度学习模型对于地震相的预测效果有着显著的提升。本研究在没有改变网络模型结构, 甚至是没有细致调整参数, 或是在没有增加训练数据的前提下, 仅通过对训练样本集的标签进行迭代改进, 就提高了深度学习模型的预测准确率。
|
图 9 F3工区标签精炼后深度学习模型对测试集中某剖面的预测结果 a地震剖面; b地震剖面的真实地震相; c第1次标签精炼后的预测结果; d第2次标签精炼后的预测结果; e第3次标签精炼后的预测结果 |
|
图 10 Parihaka工区标签精炼后深度学习模型对测试集中某剖面的预测结果 a地震剖面; b地震剖面的真实地震相; c第1次标签精炼后的预测结果; d第2次标签精炼后的预测结果; e为第3次标签精炼后的预测结果 |
1) 本文构建的“先验标签”可以较好地提取地震相的空间关系信息, 其信息熵的分布与深度学习模型的预测结果较为相似, 更加符合实际的概率分布情况;
2) 标签精炼方法可以在不改变深度学习网络模型结构的前提下, 提高预测结果的准确率。
当前的深度学习地震数据解释领域中, 人们对数据标签研究往往只局限于如何快速方便地给地震数据打上标签, 对于这些标签的数据结构以及其中蕴含的地球物理意义研究得并不多。希望本文研究能为领域内的学者提供思路。另外, 本文方法仍然存在许多不足, 例如对于空间信息的提取主要只用于不同地震相交界处的采样点, 如何进一步地使其它采样点同样拥有更丰富的地球物理信息仍需要研究。
| [1] |
朱剑兵, 赵培坤. 国外地震相划分技术研究新进展[J]. 勘探地球物理进展, 2009, 32(3): 167-171. ZHU J B, ZHAO P K. Advances in seismic facies classification technology abroad[J]. Progress in Exploration Geophysics, 2009, 32(3): 167-171. |
| [2] |
张林科, 覃丽君, 张国焘. 基于地震属性的地震相分析思路[J]. 工程地球物理学报, 2010, 7(6): 694-698. ZHANG L K, TAN L J, ZHANG G T. On seismic facies analysis based on seismic attributes[J]. Chinese Journal of Engineering Geophysics, 2010, 7(6): 694-698. |
| [3] |
牟丹, 张丽春, 徐长玲. 3种经典机器学习算法在火山岩测井岩性识别中的对比[J]. 吉林大学学报(地球科学版), 2021, 51(3): 951-956. MOU D, ZHANG L C, XU C L. Comparison of three classical machine learning algorithms for lithology identification of volcanic rocks using well logging data[J]. Journal of Jilin University(Earth Science Edition), 2021, 51(3): 951-956. |
| [4] |
侯贤沐, 王付勇, 宰芸, 等. 基于机器学习和测井数据的碳酸盐岩孔隙度与渗透率预测[J]. 吉林大学学报(地球科学版), 2022, 52(2): 644-653. HOU X M, WANG F Y, ZAI Y, et al. Prediction of carbonate porosity and permeability based on machine learning and logging data[J]. Journal of Jilin University(Earth Science Edition), 2022, 52(2): 644-653. |
| [5] |
宋磊, 印兴耀, 宗兆云, 等. 基于先验约束的深度学习地震波阻抗反演方法[J]. 石油地球物理勘探, 2021, 56(4): 716-727. SONG L, YIN X Y, ZONG Z Y, et al. Deep learning seismic impedance inversion based on prior constraints[J]. Oil Geophysical Prospecting, 2021, 56(4): 716-727. DOI:10.13810/j.cnki.issn.1000-7210.2021.04.005 |
| [6] |
伊小蝶, 吴帮玉, 孟德林, 等. 数据增广和主动学习在波阻抗反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 707-715. YI X D, WU B Y, MENG D L, et al. Application of data augmentation and active learning to seismic wave impedance inversion[J]. Oil Geophysical Prospecting, 2021, 56(4): 707-715. |
| [7] |
LEI L, YU L, XIONG Z, et al. Convolutional recurrent neural networks based waveform classification in seismic facies analysis[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 2599-2603. |
| [8] |
QI J, ZHANG B, LYU B, et al. Seismic attribute selection for machine learning based facies analysis Choosing the best seismic attributes[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 1853-1857. |
| [9] |
李祺鑫, 罗亚能, 马晓强, 等. 基于深度嵌入网络的地震相聚类技术[J]. 石油地球物理勘探, 2022, 57(2): 261-267. LI Q X, LUO Y N, MA X Q, et al. Seismic facies clustering technology based on deep embedding network[J]. Oil Geophysical Prospecting, 2022, 57(2): 261-267. |
| [10] |
MUKHOPADHYAY P, MALLICK S. Bayesian deep learning for seismic facies classification and its uncertainty estimation[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 2488-2492. |
| [11] |
闫星宇, 顾汉明, 罗红梅, 等. 基于改进深度学习方法的地震相智能识别[J]. 石油地球物理勘探, 2020, 55(6): 1169-1177. YAN X Y, GU H M, LUO H M, et al. Intelligent seismic facies classification based on an improved deep learning method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1169-1177. |
| [12] |
马江涛, 刘洋, 张浩然. 地震相智能识别研究进展[J]. 石油物探, 2022, 61(2): 262-275. MA J T, LIU Y, ZHANG H R. Research progress on intelligent identification of seismic facies[J]. Geophysical Prospecting for Petroleum, 2022, 61(2): 262-275. |
| [13] |
ALAUDAH Y, ALFARRAJ M, ALREGIB G. Structure label prediction using similarity-based retrieval and weakly supervised label mapping[J]. Geophysics, 2019, 84(1): V67-V79. |
| [14] |
LI J, WU X, YE Y, et al. Unsupervised contrastive learning for seismic facies characterization[J]. Geophysics, 2023, 88(1): WA81-WA89. |
| [15] |
QIAN F, YIN M, LIU X Y, et al. Unsupervised seismic facies analysis via deep convolutional autoencoders[J]. Geophysics, 2018, 83(3): A39-A43. |
| [16] |
WU X, SHI Y, FOMEL S, et al. Convolutional neural networks for fault interpretation in seismic images[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 1946-1950. |
| [17] |
PANCHAPAGESAN S, SUN M, KHARE A, et al. Multi-task learning and weighted cross-entropy for DNN-based keyword spotting[J]. Interspeech, 2016, 9: 760-764. |
| [18] |
SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision[J]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, 2818-2826. |
| [19] |
SHANNON C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3-55. |
| [20] |
SUDRE C H, LI W, VERCAUTEREN T, et al. Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations[C]//CARDOSO M J. Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Cham: Springer, 2017: 240-248
|
| [21] |
KULLBACK S, LEIBLER R A. On information and sufficiency[J]. The Annals of Mathematical Statistics, 1951, 22(1): 79-86. |
| [22] |
ALAUDAH Y, MICHAŁOWICZ P, ALFARRAJ M, et al. A machine-learning benchmark for facies classification[J]. Interpretation, 2019, 7(3): SE175-SE187. |
| [23] |
DUIN E J T, DOORNENBAL J C, RIJKERS R H B, et al. Subsurface structure of the Netherlands-results of recent onshore and offshore mapping[J]. Netherlands Journal of Geosciences, 2006, 85(4): 245-276. |



