2. 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
3. 中国石油天然气股份有限公司大港油田勘探开发研究院, 天津 300280;
4. 中国石油天然气股份有限公司大港油田分公司, 天津 300280
2. Key Laboratory of Geophysical Exploration of China National Petroleum Corporation, China University of Petroleum, Beijing 102249, China;
3. Research Institute of Exploration and Development, Dagang Oil Field, PetroChina, Tianjin 300280, China;
4. Dagang Oil Field Branch, PetroChina, Tianjin 300280, China
地震记录综合反映了地下构造和地层的岩性、流体等信息[1], 地震反演技术利用不同的反演方法从接收到的地震记录中提取这些信息并利用这些信息取得对地下沉积体空间结构的认识以及对于储层物性、含流体性质的预测。得益于近年来岩石物理理论和岩石物理建模方法的不断发展, 储层物性参数反演的方法研究取得了大量的研究成果[2-5]。但对于薄互层砂体来说, 首要目标是研究清楚储层的空间结构, 此类砂体的厚度薄且横向变化剧烈, 垂向叠置关系复杂, 储层的连通性难以正确认识, 针对这类储层, 落实砂体的叠置关系和横向展布极为重要。
对薄互层储集体空间结构的认识, 一方面依赖于地震数据的高分辨率处理, 另一方面则是通过各种反演方法对储层进行精细描述。储层精细描述对地震数据的分辨率提出了更高的要求。基于测井约束的反演方法是一种线性反演方法, 其依赖于初始模型的频带范围, 反演结果无法提供频带范围之外的频率成分, 提高分辨率的能力十分有限。反射系数服从稀疏分布的假设条件下, 稀疏脉冲反演方法可提供更高的分辨率, 在工业界取得了大规模的应用。但受限于反演问题解的非唯一性, 稀疏脉冲反演存在压制弱信号, 反演结果横向连续性差等问题[6-9]。为了解决这一问题, 发展了基于反射结构约束的多道地震反演方法[10-12], 在一定程度上改善了反演效果。但对于薄互层砂体来说, 分辨率依然满足不了砂体精细刻画的需求, 原因之一是单一地震数据所能提供的储层信息十分有限, 因此, 在基于地震数据开展的阻抗反演的基础上, 提出了多源信息融合理论[13-15], 尝试综合利用地质、测井、地震等信息, 实现单一地震数据驱动到多源信息驱动的高分辨地震反演, 为薄层结构的地震表征提供了新的思路和方法。
得益于大数据和人工智能的快速发展, 近年来, 基于机器学习技术开展的高分辨率地震阻抗反演技术推动了薄互层砂体结构的定量表征[16-18], 出现了基于字典学习(dictionary learning)[19]、卷积神经网络(convolutional neural networks, CNN)、生成对抗网络(generative adversarial networks, GAN)以及各种变体网络的地震阻抗反演技术。WANG等[20]通过KSVD(K-singular value decomposition)方法建立稀疏表征预测模型, 对基于模型反演得到的低频阻抗与测井的高频阻抗建立联系, 通过字典学习提取数据的本质特征, 用稀疏模型进行数据表征, 实现了有限数据下的高分辨率地震阻抗反演。DAS等[21]利用一维CNN实现了阻抗反演并将其应用于实际地震数据, 并对该方法的应用条件进行了分析。在实际数据处理中, 与标签数据具有相似的分布特征, 网络可以给出更好的预测结果。这也揭示了神经网络对于标签的需求以及在实际应用中的限制。阻抗反演中的高频信息通常来源于测井数据, 有限的测井数据限制了神经网络模型的实际应用。因此, 迁移学习技术[22]被引入, 用于克服有限标签数据的反演需求。除此之外, 在网络模型的搭建上, 出现了联合CNN与循环神经网络(recurrent neural networks, RNN)的复合网络模型[23], 或者在网络结构中引入残差模块[24-25]等来解决深层网络的退化问题。除此之外, 基于GAN模型[26]开展的高分辨率地震反演研究也在不断发展, 其通过生成器和判别器两个网络结构的联动调节, 使得生成网络生成高度逼近标签数据的高分辨率结果。
针对薄互层砂体的空间结构表征问题, 本文使用RNN的变种网络——长短期记忆(long short-term memory, LSTM)网络进行高分辨阻抗反演试验, 并在网络结构中引入双向系统, 使得网络尽可能地充分利用提供的标签数据, 在有限的标签数据下更好地表征薄互层砂体的空间展布。区别于CNN, LSTM网络模型更多地应用于序列数据的预测和生成[27], 利用其将多点数据与单点标签相映射的网络结构, 实现地震数据的地质结构特征表征。为了考察网络在薄层结构识别问题上的有效性, 构建了简单薄互层模型, 将基于模型的反演方法及CNN进行了对比, 并就标签数量及抗噪性进行了简单分析, 论证了BLSTM-Net(Bidirectional long short-term memory Network)模型对于薄层结构表征的有效性。在此基础上, 构建了更为复杂的陆相沉积薄互层地质模型, 针对不同频率的合成地震记录开展了阻抗反演试验, 讨论基于BLSTM-Net的反演方法与地震频带的关系, 对该方法的实际应用做进一步分析讨论。最后, 针对弱信号反演同稀疏脉冲反褶积进行了对比。对试验结果进行分析讨论, 取得了一些有意义的试验成果。
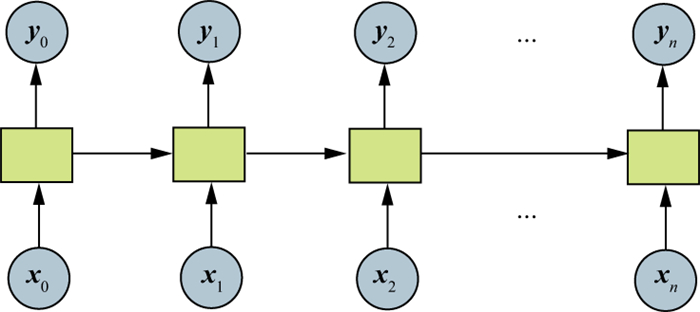
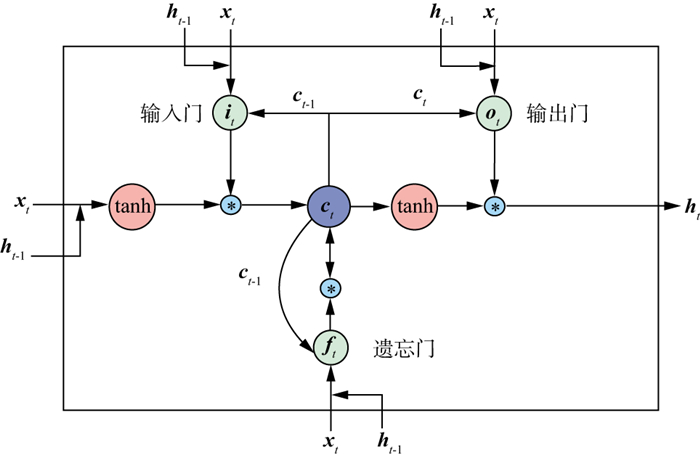
1 方法原理经典的RNN通过赋予网络“记忆”功能, 使得其区别于CNN可以考虑数据的内部联系, 因此, 在序列数据的预测和处理问题上取得了一定的应用成果[28]。图 1展示了RNN的数据处理过程, 这种按照时间序列循环展开的处理过程, 会导致激活函数的不断累乘, 从而出现梯度问题。因此, 为了训练过程的稳定和模型的收敛, 提出了RNN的变种网络——LSTM神经网络模型, 通过增加门控系统(输入门、输出门、遗忘门)来控制信息的输入和流通[29-30]。图 2展示了LSTM网络的内部结构, 每一个LSTM处理单元不仅接收当前时刻的输入(xt), 同时对前一时刻的状态(ht-1)做出判断, 通过激活函数, 完成输入数据与标签之间非线性映射关系的建立。细胞态联系着输入门、输出门和遗忘门, 使得网络得以进行信息的筛选, 摈弃冗余无用的信息, 保留对预测有用的“记忆”。因此, 网络的训练不会出现梯度爆炸或者梯度消失的问题, 进一步提高了循环神经网络的实际应用能力。
|
图 1 经典RNN的数据处理过程 |
|
图 2 LSTM网络的内部结构 |
在t时刻, RNN网络的具体计算过程如下:
| $ \begin{aligned} & \boldsymbol{h}_t=\sigma\left(\boldsymbol{W}_h \boldsymbol{x}_t+\boldsymbol{U}_h \boldsymbol{h}_{t-1}+\boldsymbol{b}_h\right) \\ & \boldsymbol{y}_t=\boldsymbol{W}_y \boldsymbol{h}_t+\boldsymbol{b}_y \end{aligned} $ | (1) |
式中: xt表示输入数据; ht表示隐藏层状态向量; yt表示输出向量; W, U, b是网络在训练中不断更新的参数矩阵和参数向量; σ表示激活函数, 将非线性映射引入到网络计算中。
在每一个LSTM单元中, 具体的计算过程如下:
| $ \begin{aligned} & \boldsymbol{f}_t=\sigma\left(\boldsymbol{W}_f \boldsymbol{x}_t+\boldsymbol{U}_f \boldsymbol{h}_{t-1}+\boldsymbol{b}_f\right) \\ & \boldsymbol{i}_t=\sigma\left(\boldsymbol{W}_i \boldsymbol{x}_t+\boldsymbol{U}_i \boldsymbol{h}_{t-1}+\boldsymbol{b}_i\right) \\ & \boldsymbol{o}_t=\sigma\left(\boldsymbol{W}_o \boldsymbol{x}_t+\boldsymbol{U}_o \boldsymbol{h}_{t-1}+\boldsymbol{b}_o\right) \\ & \boldsymbol{g}_t=\tanh \left(\boldsymbol{W}_g \boldsymbol{x}_t+\boldsymbol{U}_g \boldsymbol{h}_{t-1}+\boldsymbol{b}_g\right) \\ & \boldsymbol{c}_t=\boldsymbol{f}_t \odot \boldsymbol{c}_{t-1}+\boldsymbol{i}_t \odot \boldsymbol{g}_t \\ & \boldsymbol{h}_t=\boldsymbol{o}_t \odot \tanh \left(\boldsymbol{c}_t\right) \end{aligned} $ | (2) |
式中: ft, it, ot表示遗忘门、输入门和输出门在t时刻对应的向量; ct表示细胞态向量; ⊙表示Hadamard乘积, 即对应位置元素相乘。LSTM区别于RNN可以避免数据的长期依赖问题, 正是由于LSTM网络对细胞态的更新。W, U, b, σ等参数及输出向量yt的计算与RNN一致。
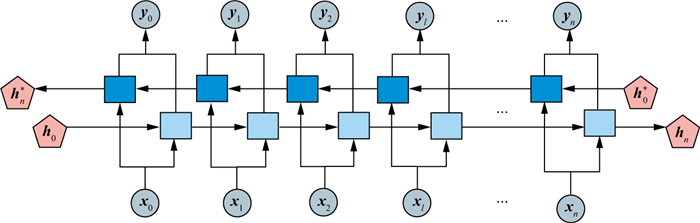
在上述LSTM网络的基础上, 本文引入双向系统建立了BLSTM-Net神经网络模型, 将两个LSTM网络进行叠加, 同时处理正向和反向输入的序列数据, 兼顾当前时刻、过去时刻以及未来时刻的信息, 充分利用有限的信息对输入做出判断, 建立起输入与标签数据的关系, 完成非线性映射关系的建立[31-33]。
在BLSTM-Net网络结构中的当前时间步中, 层的输出是来自两个相反方向隐藏层的输出的串联:
| $ \boldsymbol{h}_t=\left[\overrightarrow{\boldsymbol{h}}_t, \overleftarrow{\boldsymbol{h}}_t\right] $ | (3) |
式中:
| $ F=\frac{1}{N} \sum\limits_{i=1}^N\left(\boldsymbol{Y}_i-\boldsymbol{y}_i\right)^2 $ | (4) |
|
图 3 BLSTM-Net模型的数据处理过程 |
式中: N是样本个数; Y表示标签数据; y表示预测数据。在有限的迭代次数内, 通过误差反向传播算法[34]使F达到最小, 实现各神经元权重系数的调节, 从而不断地优化非线性映射函数, 以此来确定神经网络各节点的权重和偏置。使得预测值更加接近标签值, 得到最优的神经网络模型并将此时的神经元节点权重进行保存, 后续即可调用该网络模型即时完成地震数据的高分辨阻抗反演, 实现薄层结构的区分与刻画。
2 网络构建与模型测试 2.1 网络训练参数设置BLSTM-Net模型的输入为: 样本数量、时间步长、特征维度。通过其独特的网络结构, 可以将时间步长内的多个特征映射为标签数据中的一点。在不考虑干涉效应的影响下, 反射系数与子波的褶积将一点信息映射为地震数据内的多点信息, 反褶积即从地震记录中剔除子波的影响, 恢复反射系数, 这与BLSTM-Net模型的映射关系一致, 也是本文采取BLSTM-Net进行薄层结构表征的重要原因。相比于构建更为复杂的神经网络模型, 寻找网络的适用场景更为重要。
神经元的个数及神经网络的层数属于神经网络的架构参数, 指的是除了输入层和输出层之外添加隐藏层的个数及各个隐藏层所包含的节点数。在特定的应用场景中, 输入层和输出层的节点数量是确定的。对于较为复杂的非线性问题, 隐藏层的数目一般大于2, 层数越多, 理论上来说模型的拟合能力越强, 效果也会越好, 但是更多的层数可能会带来过拟合的问题, 从而增加网络的训练难度, 使模型难以收敛。隐藏层中神经元个数也遵循这一规律。同时, 相比于添加更多的神经元, 增加隐藏层的层数将获得更大程度的性能提升。对于神经网络中超参数的确定, 需要通过试验逐个进行确定, 从而得到适用于特定应用场景的最优模型。
除了神经网络层数、神经元的个数及样本数量等参数外, 本试验中重要的模型参数主要包括时间步长和学习率[35-37]。时间步长表征要提取地震记录中的多点建立与地层结构的关系, 与地震资料的分辨率密切相关。当地震资料干涉效应弱, 薄层结构基本可以区分时, 时间步长取半个波长至一个波长即可; 当地震资料分辨率低, 干涉严重时, 需要加大时间步长才可以将地质结构对应的地震信息完全包含。学习率类似优化算法中的步长这一参数, 其控制整个训练过程的稳定, 较高的学习率导致模型可能会跳过全局最优解, 从而达不到全局最小值。较小的学习率有助于网络收敛到全局最小值, 但需要花费更多的时间, 同时也可能使得神经网络在最小值附近来回震荡而达不到最小值。因此, 学习率的确定需要反复试验。
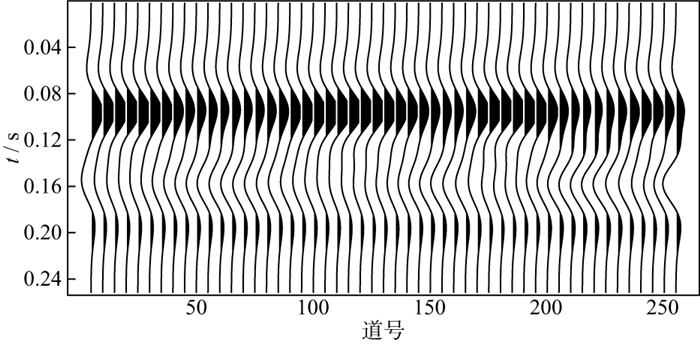
2.2 简单河道砂薄层模型为了测试前述方法识别薄层结构的有效性, 构建了如图 4所示的简单河道砂泥岩薄互层阻抗模型, 单层砂体的时间厚度约为8ms, 泥岩的速度为1800m/s, 砂岩储集层的速度为2400m/s, 上、下两层为水平层状介质, 中间层呈现河道沉积形态, 横向上弯曲变化, 将其与10Hz主频的雷克子波进行褶积, 得到如图 5所示的合成地震记录, 可以看出, 图 5中砂体结构和叠置关系难以区分, 尤其中间层砂体的构造形态几乎完全消失, 依靠地震数据识别薄层河道砂体存在困难。基于此合成地震记录, 采用不同的反演方法开展河道薄层砂体结构的识别试验。
|
图 4 河道砂泥岩薄互层阻抗模型 |
|
图 5 10Hz合成地震记录 |
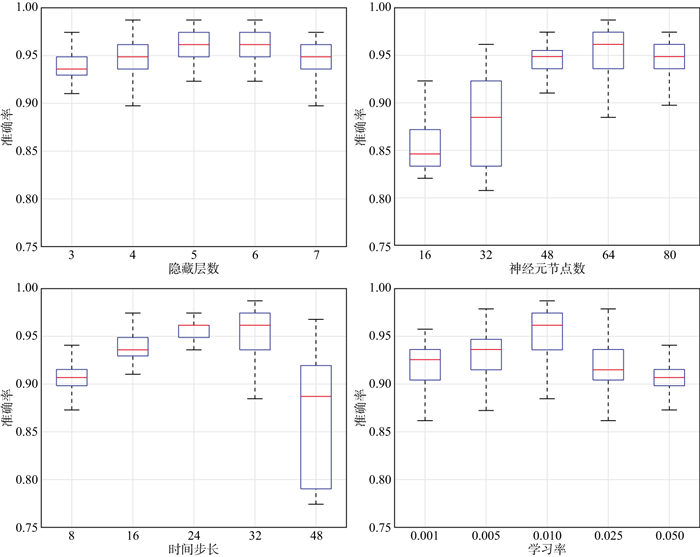
从阻抗模型中抽取3道(第25道、第125道、第175道)作为标签数据, 并按照75%∶25%的比例划分训练集和测试集, 通过考察不同超参数下网络在测试集上的表现来逐一选定最优的模型参数。图 6展示了超参数设置的试验过程, 并最终确定选用隐藏层数为5、神经元节点数为64、时间步长为32、学习率为0.010的超参数组合。基于此试验确定整个网络模型架构, 并将其保存用于后续的阻抗反演试验。
|
图 6 超参数试验过程 |
确定最优的神经网络参数后, 开展基于测井约束与基于BLSTM-Net模型的阻抗反演对比试验。从阻抗模型中抽取3道(第25道、第125道、第175道)作为“测井”数据, 依据地震数据拾取层位信息, 构建如图 7a所示的低频初始模型, 开展基于测井约束的阻抗反演试验。图 7b展示了相应的反演结果, 结果表明, 反演结果依赖于初始模型和层位信息, 提高分辨率的能力十分有限, 反演结果难以区分砂体结构。
|
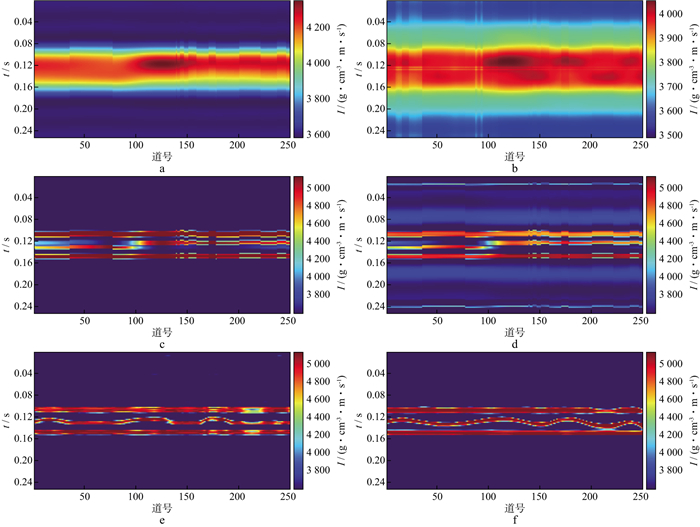
图 7 基于模型的反演与CNN、BLSTM-Net反演结果对比 a低频初始模型; b基于低频初始模型的反演结果; c全频带初始模型; d基于全频带初始模型的反演结果; e CNN模型反演结果; f BLSTM-Net模型反演结果 |
在此基础上, 构建如图 7c所示的全频带的初始模型, 充分利用“测井”所提供的高分辨率信息, 保证“井点”位置阻抗的正确性, 开展反演试验, 图 7d为基于全频带初始模型的反演结果, 图中所示的反演结果虽刻画了砂体的垂向叠置关系, 但无法刻画河道砂体的横向变化, 反演结果严重依赖于初始模型, 井间的反演结果更多地来自于初始模型的插值外推。
以上试验说明了基于测井约束反演方法表征薄层结构的局限性, 其根本原因是线性反演方法只能提供地震频带之内的频率成分, 反演结果受限于地震频带, 难以大幅提高分辨率。因此, 基于机器学习技术强大的非线性映射能力, 尝试利用数据驱动的神经网络技术恢复地震频带之外的高频成分并尽可能保证这种高频信息的可靠性。基于CNN[38-41]和BLSTM-Net两种神经网络模型开展反演试验, 采用同样的标签数据, 保持评价函数(MSE)、训练次数(500epochs)、学习率(0.01)等参数一致, 对两个网络进行训练, 通过误差反向传播算法调节神经网络各神经元的权重系数, 将训练得到的最佳网络模型进行保存。之后调用神经网络模型, 对各个地震道逐道进行反演。图 7e是基于CNN的反演结果, 很好地区分了砂体结构, 相较于基于测井约束的阻抗反演方法, 大幅提升了地震数据的分辨能力, 但其对于中间河道砂体的横向展布的刻画仅在标签的位置较为准确, 而图 7f所示的BLSTM-Net模型的反演结果, 不仅区分了砂体结构和叠置关系, 对中间层河道砂体的横向展布刻画准确, 表明在薄层砂体结构反演问题上, BLSTM-Net相较于CNN具有更强的泛化能力, 更加适用于薄层结构的反演。
与基于测井约束的反演方法相比, 基于数据驱动的反演方法获得了更高的分辨率和更好的应用效果, 准确区分了薄层砂体结构。与CNN方法相比, 基于BLSTM-Net模型的反演方法具有更强的泛化能力, 对河道薄砂体的横向展布刻画得更为准确。就薄层砂体结构反演这一问题, BLSTM-Net模型具有更好的适用性。
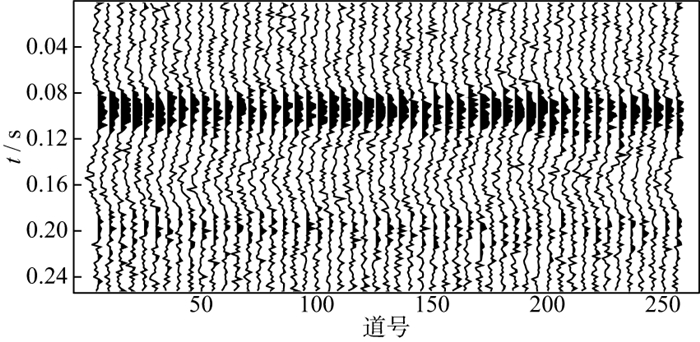
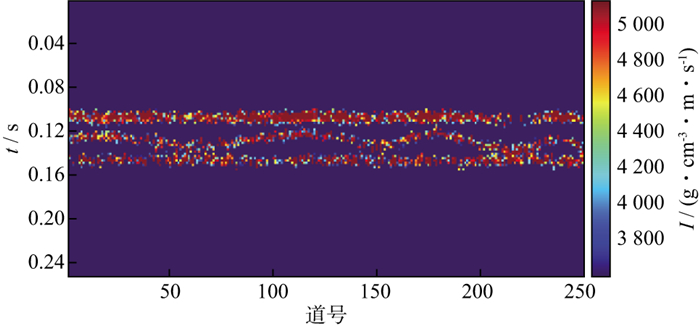
实际地震记录中总是包含很多噪声, 为了测试本文方法的抗噪能力, 在上述模型中添加噪声, 构建了如图 8所示的信噪比为5的模型数据, 同样抽取3道(第25道、第125道、第175道)含噪地震记录和阻抗标签作为训练样本进行模型训练。将建立的映射关系应用于整个合成地震记录, 图 9展示了含噪数据的阻抗反演结果。试验结果表明, 模型具有一定的抗噪能力, 依然可以区分薄层结构。这为该方法的实际应用提供了有力的理论支撑。
|
图 8 含噪合成地震数据(信噪比为5) |
|
图 9 含噪合成地震数据阻抗反演结果 |
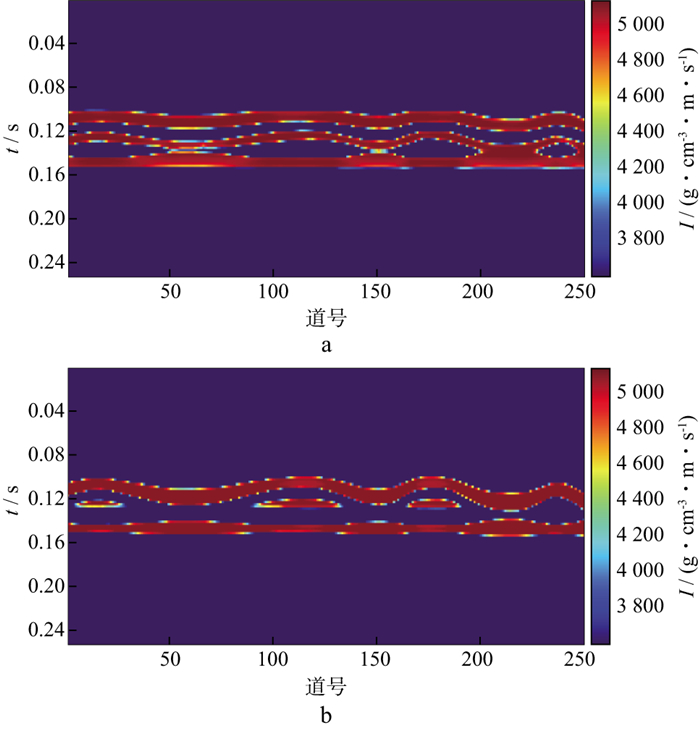
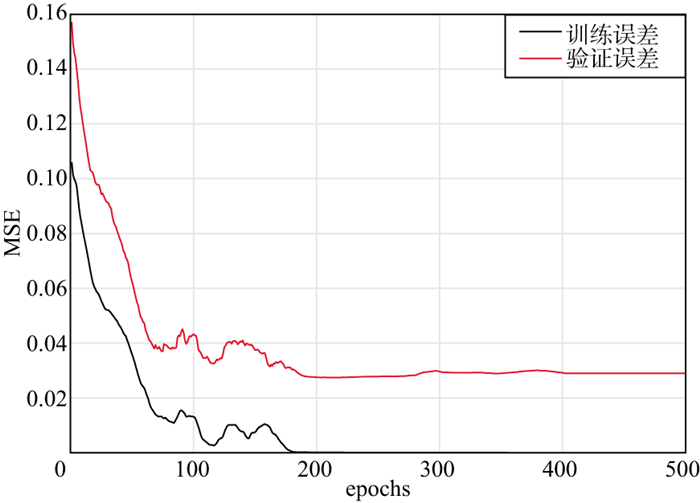
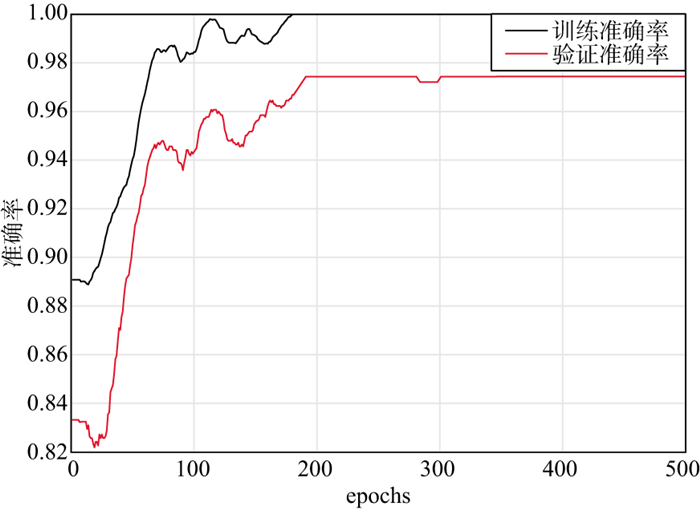
基于数据驱动的反演方法依赖于标签样本的数量, 多样且丰富的标签数据是神经网络提取数据特征、取得良好应用效果的前提。因此, 在验证了BLSTM-Net模型在表征薄互层空间结构问题上的有效性之后, 减少标签数量进行阻抗反演试验, 分别采用2道(第25道、第125道)和1道(第25道)阻抗数据进行反演试验, 反演结果如图 10所示, 结果表明, 数据驱动的反演方法在一定程度上依赖于标签样本的数量, 丰富的标签数据能够提高反演效果同时增强网络的适应性, 使其具有更强的泛化能力。与基于模型的反演方法相比, BLSTM-Net模型能提供更高分辨率的阻抗反演结果, 与此同时, 对于薄层结构的刻画及砂体叠置关系的区分受限于标签样本的数量。图 11和图 12分别展示了BLSTM-Net模型在3道标签样本数据下进行训练时对应的训练误差和准确率, 其中训练集和测试集的比例为75%∶25%, 可以看出, 模型在测试集上的准确率高达97%, 并且在测试集上没有表现出误差的上升及准确率的下降, 说明模型没有出现过拟合的问题, 超参数的选择是适用的。模型的训练过程稳定高效, 收敛速度快, 进一步说明了该模型在薄层结构反演问题上的适用性。
|
图 10 基于BLSTM-Net模型的阻抗反演 a 2道标签反演结果; b 1道标签反演结果 |
|
图 11 BLSTM-Net模型训练误差 |
|
图 12 BLSTM-Net模型训练准确率 |
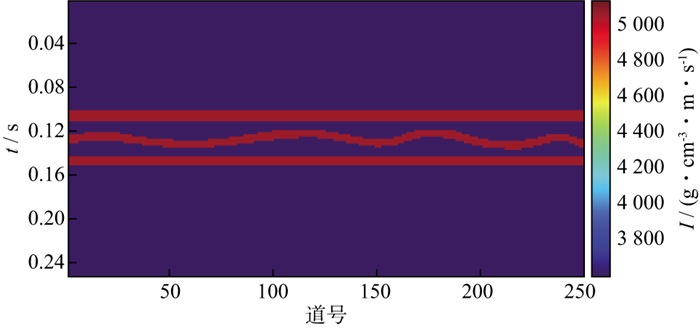
在前述河道砂泥岩薄互层简单模型反演的基础上, 为了进一步测试该方法在实际数据中的应用能力, 同时考虑到实际资料标签数据稀少, 难以建立正确的映射关系等因素, 基于东部某油田X构造带东营组实际地质特征构建了如图 13所示的陆相沉积薄互层阻抗模型。该构造带东三段时期发育大规模的扇三角洲, 且呈现“小平原, 大前缘”的特点, 主要发育广泛的砂泥岩薄互层。受沉积环境影响, 下部储层砂体连片发育, 横向连续性好; 上部砂体连续性较差, 横向变化快。垂向上砂泥岩互层结构发育, 非均质性强。该模型砂体空间关系复杂, 砂体厚度薄且变化幅度大, 最薄处为5ms, 最厚处为25ms。横向上厚度变化剧烈, 泥岩速度为2900m/s, 顶、底厚层砂体及部分透镜体砂岩的速度为3100m/s, 中间的薄层砂体速度为3000m/s, 速度差异小。基于此模型开展不同主频合成地震记录的阻抗反演试验, 用于说明本文方法对复杂薄互层结构识别的能力及地震频带对反演结果的影响。

|
图 13 陆相沉积薄互层阻抗模型 |
图 14a为30Hz主频的雷克子波合成地震记录, 可以看出, 砂体结构基本清晰可分, 与阻抗模型具有较好的对应关系, 地震数据的分辨率较高, 没有明显的干涉效应。等间隔选取5道(第25道、第65道、第105道、第145道和第185道)地震数据和阻抗标签作为训练样本, 进行BLSTM-Net模型的训练, 模型参数与简单河道砂泥岩薄互层模型一致, 将训练好的神经元权重进行保存, 并应用到整个地震数据上。反演结果如图 14b所示, 与模型数据具有很好的一致性, 各薄互层砂体可以清晰区分, 反演结果准确度高, 横向连续性好, 薄层分界干净利落, 对薄层结构的刻画准确, 尤其克服了砂体厚度横向变化的影响, 这说明该方法本身具有一定的泛化能力, 良好地展示了砂体的叠置关系和横向展布。
|
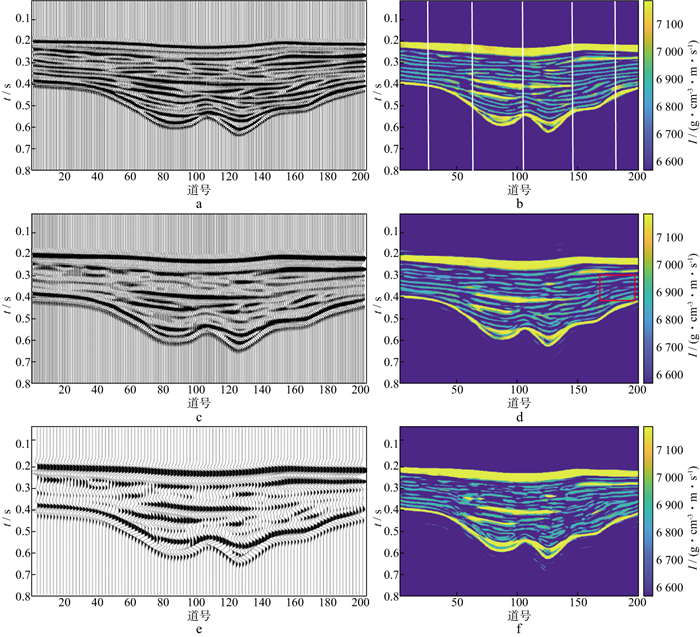
图 14 不同主频的合成地震记录及其阻抗反演结果 a 30Hz主频的合成地震记录; b 30Hz合成地震记录的阻抗反演结果; c 20Hz主频的合成地震记录; d 20Hz合成地震记录的阻抗反演结果; e 15Hz主频的合成地震记录; f 15Hz合成地震记录的阻抗反演结果 |
在30Hz地震数据反演的基础上, 降低地震子波主频至20Hz, 重新制作合成地震记录(图 14c)。此时, 合成地震记录的干涉效应严重, 砂体的叠置关系无法区分, 砂体的横向展布信息也被淹没, 已经无法基于此地震剖面建立合理的初始模型, 开展基于测井约束的地震反演。选用同样的地震道开展波阻抗反演试验, 反演结果依然清晰地刻画了砂体的垂向叠置关系和横向展布形态, 对于薄层结构的刻画准确可靠, 但与30Hz地震数据的反演结果相比, 表现出局部反演效果横向连续性差的问题(与图 14d中红框区域所展示的一样), 说明在相同标签数量的前提下, 地震数据的频宽影响反演的质量, 尤其影响其泛化性, 这种横向的不连续很好地证实了这一点。
20Hz主频的地震数据, 其反演结果的局部横向连续性虽然受到了地震频带的影响, 但其整体反演效果良好, 与地质模型具有较好的对应关系。进一步降低地震数据的主频至15Hz, 考察BLSTM-Net模型对于薄层结构刻画能力的上限。图 14e展示的地震记录上, 仅呈现出上、中、下3组强反射, 地震干涉效应严重, 砂体的边界、横向连通性、垂向叠置关系已经无法区分, 采用同样的标签开展反演试验, 反演结果如图 14f所示, 此时的反演质量明显下降, 主要表现在砂体的横向展布形态上, 模型的泛化能力受到了较大的影响, 砂体的横向连续性变差, 但其垂向结构依然可以较好的区分。
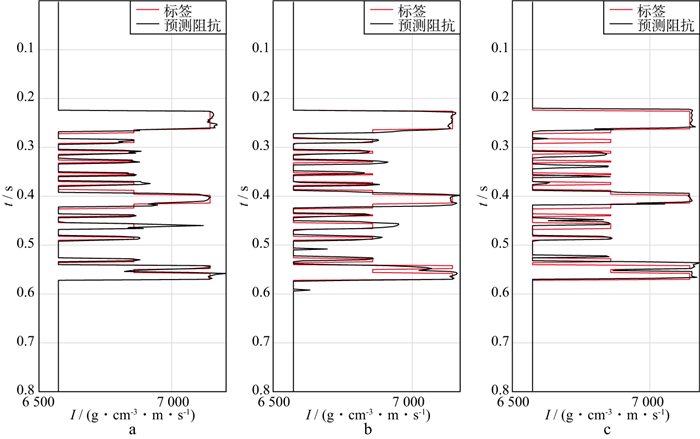
以上3组不同主频地震数据的波阻抗反演试验的对比分析说明BLSTM-Net模型在薄层结构表征问题上的有效性, 当地震频带降低至无法区分砂体结构, 基于模型的反演方法已经难以实现时, 基于数据驱动的反演方法依然可以清晰地刻画砂体结构和区分砂体边界, 准确可靠地提供了地震频带范围之外的高频信息, 大幅提升了地震数据的分辨能力。在相同标签样本数量的前提下, 反演结果受制于地震数据的频带, 反演结果的垂向叠置关系更易区分, 频带的限制主要表现在砂体的空间展布形态和横向连续性上, 低频的地震数据严重影响了模型的泛化能力。除了反演剖面的整体对比, 提取单道的反演结果(第96道)与标签数据进行了对比, 图 15展示的结果验证了地震数据频带对于模型泛化能力的限制及反演质量对于地震频带的依赖。
|
图 15 不同主频合成地震记录的阻抗反演结果(提取第96道) a 30Hz; b 20Hz; c 15Hz |
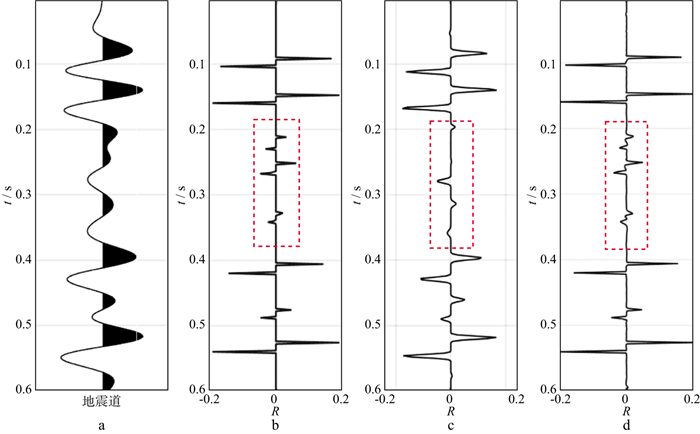
在地震勘探中, 当砂泥岩地层的速度相近或者有高速异常体存在时, 地震反射信号中就会出现强反射背景下的弱信号(图 16a)。随着勘探深度的加大, 加之地震数据中各种噪声的干扰, 这种弱信号更易被强背景掩盖。因此, 在选择反演方法时需要考量其对弱信号的保持能力。基于此, 我们构建了如图 16b所示的简单反射结构, 在0.2~0.4s设置了强反射背景下的一组弱信号, 采用不同反演方法进行弱信号的反演试验。
|
图 16 稀疏脉冲反演与本文方法反演结果 a地震道; b真实反射系数; c稀疏脉冲反演结果; d本文方法反演结果 |
稀疏脉冲反演技术通过假设反射系数服从稀疏分布大幅提高了地震资料的分辨率, 在工业界取得了良好的应用, 但同时存在着压制弱信号的问题, 图 16c展示的反演结果也证实了这一点, 0.2~0.4s的反射结构畸变, 反演方法本身压制了弱信号。
本文的BLSTM-Net神经网络模型可将数据中的多点与标签中的一点建立联系, 因此, 除了阻抗反演, 同样适用于反射系数的反演。整个反演流程与阻抗反演一致, 只需将标签数据由阻抗替换为反射系数。经过模型结构的调整和参数的优化, 得到最优的神经网络模型并进行保存, 其包括6个隐藏层, 每层神经元的组成为128+32+8+8+32+128, 时间步长为48, 学习率为0.002。将此最优模型直接应用在单一地震道上, 将反演得到的反射系数(图 16d)同稀疏脉冲反演的结果进行对比, 可以看出, 本文方法很好地保持了弱信号, 同时反射系数呈现脉冲状, 具有更高的分辨能力。
4 结论与认识本文采用BLSTM-Net网络结构针对机器学习地震反演对薄层结构的刻画能力进行模型试验, 试验结果表明:
1) 基于数据驱动的CNN和BLSTM-Net模型较常规地震反演具有更强的薄层结构预测和刻画精度, 具有较好的抗噪性和弱信号保护能力;
2) 基于BLSTM-Net模型的反演虽然对训练样本具有明显的依赖性, 但该方法不需要建立初始模型, 具有较好的稳定性和可靠性;
3) 对于薄层结构反演, BLSTM-Net网络结构较CNN网络结构更加适用, 具有更强的泛化能力, 可以更加准确地刻画砂体的横向展布;
4) 尽管基于BLSTM-Net神经网络模型开展的阻抗反演较常规方法具有更强的薄层结构预测能力, 但其反演精度仍然依赖于地震数据的有效频带, 在相同数量训练样本的情况下, 地震资料分辨率越低, 干涉越严重, 反演结果的精度越低。
最后需要指出的是, 基于BLSTM-Net模型开展的阻抗反演试验只是表明了机器学习反演在薄层预测和描述上的技术优势和内在潜力。与其它机器学习方法一样, 网络的泛化能力及其由此产生的对实际问题的适应能力依然是尚未解决的技术难题。希望本文能够起到抛砖引玉的作用, 与业内同行共同推动数据驱动智能反演技术在薄层结构预测中的实际应用。
| [1] |
李志勇. 储层物性参数地震叠前反演的确定性捜索方法[D]. 成都: 电子科技大学, 2017 LI Z Y. Deterministic searching methods of prestack seismic inversion for petrophysical parameters[D]. Chengdu: University of Electronic Science and Technology of China, 2017 |
| [2] |
白俊雨. 带先验约束的碎屑岩储层物性参数反演方法[J]. 地球物理学进展, 2020, 35(2): 530-535. BAI J Y. Inversion method for petrophysical parameters with prior constraints[J]. Process in Geophysics, 2020, 35(2): 530-535. |
| [3] |
潘新朋, 张广智, 印兴耀. 岩石物理驱动的储层裂缝参数与物性参数概率地震反演方法[J]. 地球物理学报, 2018, 61(2): 683-696. PAN X P, ZHANG G Z, YIN X Y. Probabilistic seismic inversion for reservoir fracture and petrophysical parameters driven by rock-physics models[J]. Chinese Journal of Geophysics, 2018, 61(2): 683-696. |
| [4] |
李坤, 印兴耀, 宗兆云. 岩石物理驱动的相约束叠前地震概率化反演方法[J]. 中国科学: 地球科学, 2020, 50(6): 832-854. LI K, YIN X Y, ZONG Z Y. Facies-constrained prestack seismic probabilistic inversion driven by rock physics[J]. Scientia Sinica(Terrae), 2020, 50(6): 822-840. |
| [5] |
张冰, 刘财, 郭智奇, 等. 基于统计岩石物理模型的各向异性页岩储层参数反演[J]. 地球物理学报, 2018, 61(6): 2601-2617. ZHANG B, LIU C, GUO Z Q, et al. Probabilistic reservoir parameters inversion for anisotropic shale using a statistical rock physical model[J]. Chinese Journal of Geophysics, 2018, 61(6): 2601-2617. |
| [6] |
KAZEMI N, SACCHI M D. Sparse multichannel blind deconvolution[J]. Geophysics, 2014, 79(5): V143-V152. DOI:10.1190/geo2013-0465.1 |
| [7] |
SUI Y H, MA J W. Blind sparse-spike deconvolution with thin layers and structure[J]. Geophysics, 2020, 85(6): V481-V496. DOI:10.1190/geo2019-0423.1 |
| [8] |
裴云龙. 稀疏约束反褶积及其波阻抗反演方法研究[D]. 北京: 中国地质大学, 2009 PEI Y L. The method research of sparse constraint deconvolution and wave impedance inversion[D]. Beijing: China University of Geoscience, 2009 |
| [9] |
刘金涛. 稀疏脉冲反褶积影响因素分析和适应性优选[D]. 北京: 中国石油大学, 2019 LIU J T. Influencing factors analysis and adaptive optimization of sparse pulse deconvolution[D]. Beijing: China University of Petroleum, 2019 |
| [10] |
魏吉贞. 块状地质结构约束下非线性反褶积方法研究[D]. 北京: 中国石油大学, 2016 WEI J Z. Non-linear deconvolution based on blocky geological structure constraint[D]. Beijing: China University of Petroleum, 2016 |
| [11] |
HAMID H, PIDLISECKY A. Structurally constrained impedance inversion[J]. Interpretation, 2016, 4(4): T577-T589. DOI:10.1190/INT-2016-0049.1 |
| [12] |
DU X, LI G F, ZHANG M, et al. Multichannel band-controlled deconvolution based on a data-driven structural regularization[J]. Geophysics, 2018, 83(5): R401-R411. DOI:10.1190/geo2017-0516.1 |
| [13] |
赵海波, 唐晓花, 李奎周, 等. 基于地震岩石物理分析与叠前地质统计学反演技术的齐家地区致密薄储层预测[J]. 石油物探, 2017, 56(6): 853-862. ZHAO H B, TANG X H, LI K Z, et al. Tight thin-bed reservoir prediction using rock physics analysis and prestack geostatistical inversion in the Qijia area[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 853-862. DOI:10.3969/j.issn.1000-1441.2017.06.011 |
| [14] |
GLINSKY M E, HAASE M C, CHAROING V, et al. Bayesian inversion whispers[J]. The Leading Edge, 2008, 27(5): 642-649. DOI:10.1190/1.2919583 |
| [15] |
钮学民, 张繁昌, 慎国强. 联合反演中多尺度地震资料自适应方法研究[J]. 石油物探, 2021, 60(2): 334-341. NIU X M, ZHANG F C, SHEN G Q. Adaptive method for the joint inversion of multiscale seismic data[J]. Geophysical Prospecting for Petroleum, 2021, 60(2): 334-341. |
| [16] |
闵超, 代博仁, 张馨慧, 等. 机器学习在油气行业中的应用进展综述[J]. 西南石油大学学报(自然科学版), 2020, 42(6): 1-15. MIN C, DAI B R, ZHANG X H, et al. A review of the application progress of machine learning in oil and gas industry[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2020, 42(6): 1-15. |
| [17] |
宋磊, 印兴耀, 宗兆云, 等. 基于先验约束的深度学习地震波阻抗反演方法[J]. 石油地球物理勘探, 2021, 56(4): 716-727. SONG L, YIN X Y, ZONG Z Y, et al. Deep learning seismic impedance inversion based on prior constraints[J]. Oil Geophysical Prospecting, 2021, 56(4): 716-727. DOI:10.13810/j.cnki.issn.1000-7210.2021.04.005 |
| [18] |
伊小蝶, 吴帮玉, 孟德林, 等. 数据增广和主动学习在波阻抗反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 707-715. YI X D, WU B Y, MENG D L, et al. Application of data augmentation and active learning to seismic wave impedance inversion[J]. Oil Geophysical Prospecting, 2021, 56(4): 707-715. |
| [19] |
SHE B, WANG Y J, LIU Z N, et al. Seismic impedance inversion using dictionary learning-based sparse representation and nonlocal similarity[J]. Interpretation, 2019, 7(3): SE51-SE67. DOI:10.1190/INT-2018-0196.1 |
| [20] |
WANG L Q, ZHOU H, LIU W L, et al. High-resolution seismic acoustic impedance inversion with the sparsity-based statistical model[J]. Geophysics, 2021, 86(4): R509-R527. DOI:10.1190/geo2020-0345.1 |
| [21] |
DAS V, POLLACK A, WOLLNER U, et al. Convolutional neural network for seismic impedance inversion[J]. Geophysics, 2019, 84(6): R869-R880. DOI:10.1190/geo2018-0838.1 |
| [22] |
SIAHKOOHI A, LOUBOUTIN M, HERRMANN F J. The importance of transfer learning in seismic modeling and imaging[J]. Geophysics, 2019, 84(6): A47-A52. DOI:10.1190/geo2019-0056.1 |
| [23] |
张昊, 朱培民, 顾元, 等. 基于深度学习的地震速度谱自动拾取方法[J]. 石油物探, 2019, 58(5): 724-733. ZHANG H, ZHU P M, GU Y, et al. Velocity auto-picking from seismic velocity spectra based on deep learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 724-733. |
| [24] |
WU X M, YAN S S, BI Z F, et al. Deep learning for multidimensional seismic impedance inversion[J]. Geophysics, 2021, 86(5): R735-R745. DOI:10.1190/geo2020-0564.1 |
| [25] |
王静, 张军华, 芦凤明, 等. 构建三维深度监督网络的断层检测方法[J]. 石油地球物理勘探, 2021, 56(5): 947-957. WANG J, ZHANG J H, LU F M, et al. Research on fault detection method based on 3D deeply supervised network[J]. Oil Geophysical Prospecting, 2021, 56(5): 947-957. |
| [26] |
ZHANG H J, WANG W, WANG X K, et al. An implementation of the seismic resolution enhancing network based on GAN[J]. Expanded Abstracts of 89th Annual Internat SEG Mtg, 2019, 2478-2482. |
| [27] |
陈云天. 基于机器学习的测井曲线补全与生成研究[D]. 北京: 北京大学, 2020 CHEN Y T. Research on well log completion and generation based on machine learning[D]. Beijing: Peking University, 2020 |
| [28] |
CHEN W, YANG L Q, ZHA B, et al. Deep learning reservoir porosity prediction based on multilayer long short-term memory network[J]. Geophysics, 2020, 85(4): WA213-WA225. |
| [29] |
YAO K S, PENG B L, ZHANG Y, et al. Spoken language understanding using long short-term memory neural networks[J]. IEEE Spoken Language Technology Workshop(SLT), 2014, 189-194. |
| [30] |
YOON D, YEEH Z, BYUN J. Seismic data reconstruction using deep bidirectional long short-term memory with skip connections[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(7): 1298-1302. |
| [31] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [32] |
GERS F A, SCHMIDHUBER J, CUMMINS F. Learning to forget: Continual prediction with LSTM[J]. Neural Computation, 2000, 12(10): 2451-2471. |
| [33] |
GRAVES A, SCHMIDHUBER J. Framewise phoneme classification with bidirectional LSTM networks[R]. 2005 IEEE International Joint Conference on Neural Networks. Montreal: IEEE, 2005
|
| [34] |
RAY S. A quick review of machine learning algorithms[C]//International Conference on Machine Learning, Big Data, Cloud and Parallel Computing(COMITCon). Faridabad, India: IEEE, 2019: 35-39
|
| [35] |
BERGSTRA J, BARDENET R, BENGIO Y, et al. Algorithms for hyper-parameter optimization[J]. Advances in Neural Information Processing Systems, 2011, 2546-2554. |
| [36] |
YANG L, SHAMI A. On hyperparameter optimization of machine learning algorithms: Theory and practice[J]. Neurocomputing, 2020, 415: 295-316. |
| [37] |
YANG J, WANG F. Auto-ensemble: An adaptive learning rate scheduling based deep learning model ensembling[J]. IEEE Access, 2020, 8: 217499-217509. |
| [38] |
杨翠倩, 周亚同, 何昊, 等. 基于全局上下文和注意力机制深度卷积神经网络的地震数据去噪[J]. 石油物探, 2021, 60(5): 751-762. YANG C Q, ZHOU Y T, HE H, et al. Global context and attention-based deep convolutional neural network for seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 751-762. |
| [39] |
周创, 居兴国, 李子昂, 等. 基于深度卷积生成对抗网络的地震初至拾取[J]. 石油物探, 2020, 59(5): 795-803. ZHOU C, JU X G, LI Z A, et al. A deep convolutional generative adversarial network for first-arrival pickup from seismic data[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 795-803. |
| [40] |
DI H B, LI Z, MANIAR H, et al. Seismic stratigraphy interpretation by deep convolutional neural networks: A semi-supervised workflow[J]. Geophysics, 2020, 85(4): WA77-WA86. |
| [41] |
WU X M, GENG Z C, SHI Y Z, et al. Building realistic structure models to train convolutional neural networks for seismic structural interpretation[J]. Geophysics, 2020, 85(4): WA27-WA39. |



