地震勘探野外采集的数据不可避免地含有噪声, 如果不能合理地压制这些噪声, 将会严重影响地震资料的品质, 因此噪声压制通常是地震数据处理中的第一个环节。本文着重讨论两种类型的噪声: 随机噪声和涌浪噪声。随机噪声作为地震数据中普遍存在的噪声类型, 具有随机性或相干性。涌浪噪声是海洋勘探中常见的噪声类型, 具有持续时间长、振幅相对更强的特点, 消除涌浪噪声是海洋地震数据处理的重要环节之一, 对提高海洋地震资料的品质具有重要意义[1]。
卷积神经网络(convolutional neural network, CNN)是一种经典的深度学习算法。由于其突出的图像处理性能被广泛应用于图像分类和图像去噪领域。与常规方法相比, 神经网络在图像处理方面不需要太多的先验经验, 只需要足够的训练样本即可具有良好的图像处理能力。由于其独特的优势, CNN在地震信号处理中有着广泛的应用, 如地震信号分类[2-3]、自动建模[4]和自动识别地震事件等[5]。此外, CNN也被应用于地震信号噪声压制[6-10], 在地震信号的随机噪声压制方面, CNN有着广泛的应用[11-15]。杨翠倩等[16]使用了含注意力机制的CNN方法对地震信号进行去噪。ZHANG等[17]使用基于深度卷积神经网络的无监督策略压制随机噪声。这些地震信号去噪方法大多是在时域进行的, 没有充分利用地震信号在频域的特性。YOU等[18]使用短时傅里叶变换(short-time Fourier transform, STFT)方法将时域信号转换为频域信号, 然后对处理后的信号进行噪声压制。由于STFT在时域的窗口宽度是固定的, 不能同时获得时域和频域的分辨率, 故该方法具有一定的局限性。与STFT相比, 连续小波变换(continuous wavelet transform, CWT)得到的结果具有更高的时域和频域分辨率。
为了充分利用时域和频域的信息, 本文倾向于采用CWT将时域的地震信号转换为频域信号, 这样既可以使时域和频域同时具有更好的分辨率, 又可以在噪声压制时利用更多的细节信息。将CWT计算得到的时频谱作为CNN的训练样本, 据此提出了基于CWT-CNN的地震噪声压制方法。通常情况下, 经过CWT计算之后的时频谱比较大, 难以直接作为CNN的训练样本。为了解决该问题, 本文提出采用双线性插值方法[19]调整图谱大小。为了量化所提出的CNN方法噪声压制效果, 本文引入了峰值信噪比(peak signal to noise ratio, PSNR)、结构相似性(structural similarity, SSIM)和均方根误差(root mean squared error, RMSE)等性能指标进行评估。为了进一步提升CNN方法对实际地震数据的处理能力, 本文将迁移学习方法用于预训练模型的训练, 解决了CNN方法的泛化性问题。
1 基本原理 1.1 基于CNN方法的噪声压制原理傅里叶变换实际上是将时域信号转换为不同频率三角函数的叠加, 在整体上将信号分解为不同的频率分量, 因而往往导致信号缺乏局域性信息。首先将傅里叶变换基函数乘以一个窗函数, 然后经过STFT得到STFT[20]基函数, 一维信号在此过程中转换为包含时间域和频率域信息的二维矩阵, 最终获得该信号的时频谱图。STFT不能够根据信号所需动态调整时域和频域分辨率, 因此我们利用连续小波变换(CWT)将傅里叶变换的三角函数基替换为小波基函数, 进而可以实现对不同频率信号分辨率的动态调整[21]。基于上述特性, 本文利用CWT将时域中的一维信号变换为二维矩阵, 因二维时频信号能将一维信号所携带的信息分散到一个矩阵上, 故更能体现信号特征, 便于图谱处理。
卷积神经网络包括卷积层、规范化层、激活层和池化层等元素。卷积层的功能是利用多个卷积核从输入数据中提取特征。激活层用于协助表达复杂的功能。在卷积层进行特征提取后, 输出的特征图被传递至池化层进行特征选择和信息过滤。本文将含噪声的图谱作为输入数据, 将无噪声的图谱作为输出结果, 采用梯度下降算法调整网络参数进行优化。经过多次训练, 卷积神经网络的参数将趋于稳定, 即完成训练。
实际情况中, 原始的时域地震信号Y(t)往往由两部分组成, 其表达式为:
| $ Y(t)=X(t)+S(t) $ | (1) |
式中: X(t)是有效信号; S(t)是噪声。地震数据进行噪声压制的目的是从含噪声信号Y(t)中估计有效信号X(t)。为了更多地显示Y(t)的特征, 我们根据CNN模型进行图谱处理, 然后利用CWT将Y(t)转换成Y(t, ω), 表达式为:
| $Y(t) \stackrel{\text { CWT }}{\longrightarrow} Y(t, \omega) $ | (2) |
对变换之后的时频谱再利用CNN方法进行网络训练和预测, 即:
| $ Y(t, \omega) * C(w, b)=X^{\prime}(t, \omega) $ | (3) |
式中: C(w, b)为卷积神经网络; w和b分别为网络的权重和偏置; X′(t, ω)为采用CNN方法预测得到的图谱。
在得到预测图谱之后, 利用逆连续小波变换(inverse continuous wavelet transform, ICWT)将二维图谱转换为一维地震信号, 如(4)式所示:
| $X^{\prime}(t, \omega) \stackrel{\text { ICWT }}{\longrightarrow} X^{\prime}(t) $ | (4) |
由(1)式至(4)式的描述可知, 本文方法的实现步骤如下: 首先, 利用连续小波变换将一维信号转换为二维时频谱Y(t, ω); 然后, 将变换后的结果作为CNN模型的输入, 并将无噪声地震信号时频谱X′(t, ω)作为CNN模型的输出, 使得经过训练的CNN模型具有针对地震信号时频谱去噪的能力; 最后, 利用ICWT将去噪后的时频谱转换回时域信号X′(t)。
经过CWT处理后的结果以复数形式表示为Y=a+ib。针对频率域噪声压制问题, 本文采用了两种策略: 基于时频谱中的振幅谱方法即能量谱策略(策略Ⅰ), 基于时频谱中的实部和虚部方法即复矩阵策略(策略Ⅱ)。策略Ⅰ是将Y写成Y=Ae-iθt的形式, 将连续小波变换后时频谱的振幅谱作为CNN模型训练输入图谱, 利用CNN模型输出的振幅谱和含噪声信号的相位谱重构时域信号; 策略Ⅱ是将复数Y写为Y=a+ib形式, 将连续小波变换后时频谱的实部和虚部作为CNN模型训练的双通道输入图谱。这两种策略流程如图 1所示。根据两种策略利用的信息差异, 对这两种策略的噪声压制效果进行对比研究。
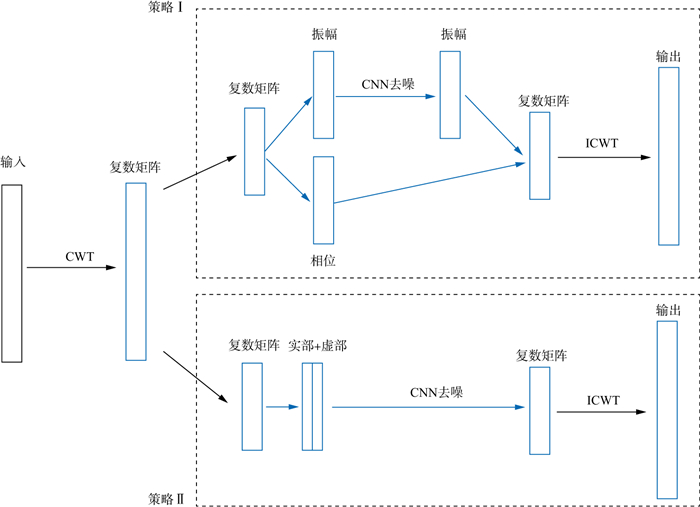
|
图 1 基于两种策略的CNN方法流程 |
首先, 将含有不同强度高斯噪声的信号和无噪声信号作为训练样本对, 通过连续训练, 使网络参数达到一个相对理想的状态。本文根据这两种训练策略分别训练了两个CNN模型, 然后对比分析这两种模型的应用效果。
迁移学习是一种在计算机视觉领域中被广泛应用的方法, 利用该方法可以在之前训练好的网络基础上建立更为精确的模型, 且耗时更短。通常, 在基于大量数据训练得来的预训练模型上, 使用不同于预训练数据集的少量新数据集对预训练的模型再次训练调整, 一方面节省了算力资源, 另一方面通过网络参数的微调, 使模型获得对新数据的处理能力。
1.2 定量评价指标为了定量地评价不同噪声压制方法的去噪效果, 本文使用了3个指标: 结构相似性(SSIM)、均方根误差(RMSE)和峰值信噪比(PSNR)来量化去噪效果, 其计算公式分别如下:
| $\operatorname{SSIM}=\frac{\left(2 \mu_x+\mu_y+c_1\right)\left(\sigma_{x y}+c_2\right)}{\left(\mu_x^2+\mu_y^2+c_1\right)\left(\sigma_x^2+\sigma_y^2+c_2\right)} $ | (5) |
式中: μx, μy分别代表x, y的平均值; σx, σy分别代表x, y的标准差; σxy代表x, y的协方差。c1, c2均为常数, 以避免分母为0带来的系统错误。
| $ \mathrm{RMSE}=\frac{1}{m n} \sum\limits_{i=0}^{m-1} \sum\limits_{j=0}^{n-1}\|\boldsymbol{I}(i, j)-\boldsymbol{K}(i, j)\|^2 $ | (6) |
式中: I, K分别为不同的图谱矩阵。
| $ \mathrm{PSNR}=10 \cdot \lg \left(\frac{M_{\mathrm{AXI}}^2}{M_{\mathrm{SE}}}\right) $ | (7) |
式中: MAXI表示图谱颜色的最大数值。
对于结构相似性和峰值信噪比这两个指标而言, 数值越大, 表明噪声压制的效果越好; 而均方根误差则相反, 该指标值越小, 表明噪声压制效果越好。
2 数值实验 2.1 地震数据随机噪声压制为了获得CNN的训练样本, 本文在无噪声地震信号中加入一定量的高斯白噪声得到含噪信号, 将含噪信号及其相应的原始信号组成训练样本集, 并使用少量与训练样本不同的数据组成验证数据集。在CNN训练过程中, 本文将均方根误差函数作为损失函数, 将峰值信噪比作为训练模型的评价指标。
本文采用卷积盲去噪网络(CBDNet)[22]开展噪声压制研究, 其网络结构如图 2所示。该网络结构主要是在UNet网络结构前面加入4个卷积层用于噪声估计。首先随机选取了400道地震信号, 然后在原始地震信号中加入-5dB高斯白噪声, 生成含噪地震信号, 并将原始地震信号作为CNN模型的输入样本。为验证方法的可行性, 利用基于策略Ⅰ的CNN方法进行初步实验。训练结束后, 对某个单道含噪地震信号进行噪声压制, 以验证方法的噪声压制效果。实验结果如图 3所示, 可以看出, 所采用的方法具有良好的去噪效果, 表明该方法在地震信号噪声压制上的有效性。
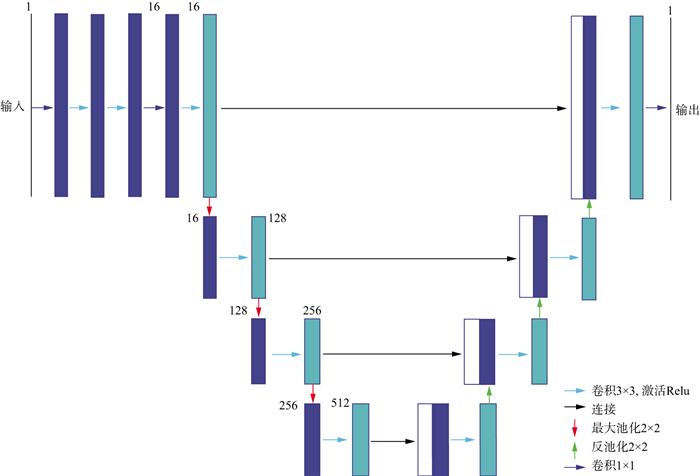
|
图 2 CBDNet网络结构(图中数字1, 16, 128, 256, 512代表卷积核数量) |
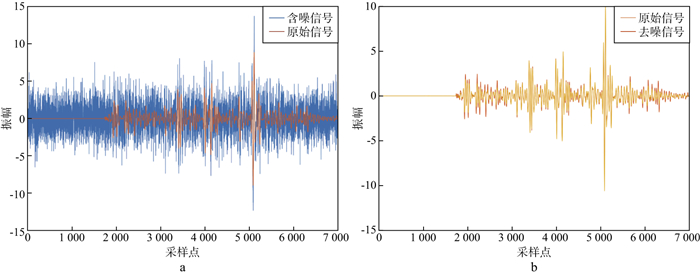
|
图 3 对单道地震信号采用基于策略Ⅰ的CNN方法得到的噪声压制结果 a含噪信号与原始信号; b原始信号与去噪后信号 |
对单道地震数据的随机噪声进行压制之后, 尝试对多道的炮集记录进行噪声压制研究。对600道地震数据利用基于策略Ⅰ的CNN方法计算其频谱, 再采用预训练的CNN模型对频谱进行噪声压制, 最后利用ICWT将频谱图转换回一维信号, 经过随机噪声压制之后的炮集记录如图 4所示, 可以看出, 基于策略Ⅰ的CNN方法对高斯白噪声的压制效果明显。
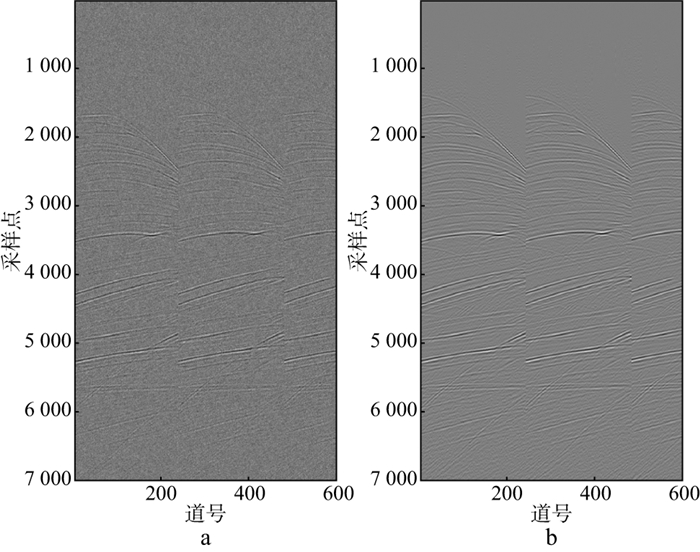
|
图 4 对600道地震信号采用基于策略Ⅰ的CNN方法进行噪声压制的结果 a加入-5dB高斯白噪声的炮集记录; b采用基于策略Ⅰ的CNN方法进行噪声压制后的炮集记录 |
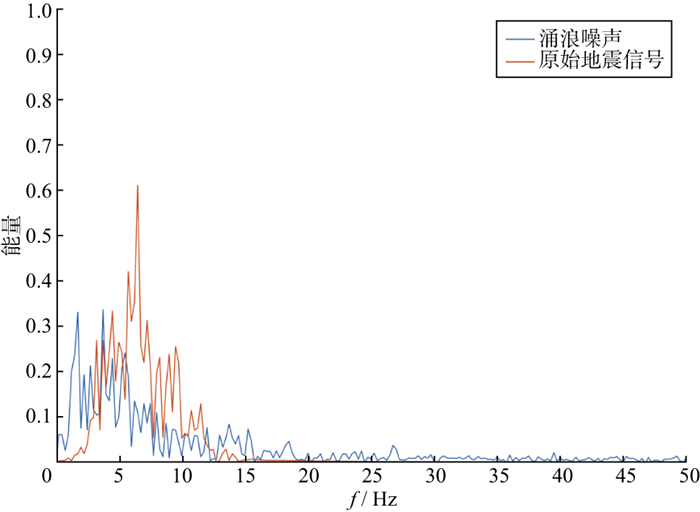
涌浪噪声是海洋地震勘探中常见的强随机噪声, 在原始地震记录上具有较强的低频背景。由于涌浪噪声的频谱与信号的频谱有较多的重叠, 故常规的带通滤波难以对这种含有噪声的地震信号进行处理。因此, 本文尝试采用基于策略Ⅰ的CNN方法对该噪声进行压制。如图 5所示, 原始地震信号频谱与涌浪噪声的频谱对比后发现, 在低频端, 原始信号和涌浪噪声具有很高的重合度, 地震信号的能量大多集中在0~15Hz, 涌浪噪声在这个范围内也有较高的能量分布, 因此很难在频率域将两者直接分开。利用基于策略Ⅰ的CNN方法分析含涌浪噪声的信号时, 可以发现, 干净的地震信号和噪声在时频域可分离(图 6)。这意味着它们在频率域中重叠的部分可能在时域中存在一些差异, 这为本文的研究奠定了基础。
|
图 5 原始地震信号与涌浪噪声的频谱 |
|
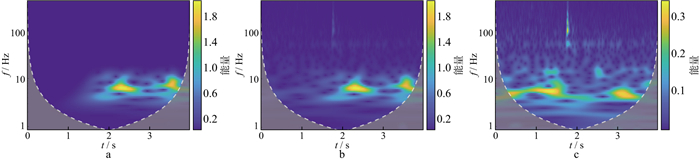
图 6 地震信号时频谱 a无噪声的原始地震信号; b含涌浪噪声的原始地震信号; c涌浪噪声 |
如图 6所示, 地震有效信号的主要能量分布在黄色区域。地震信号与涌浪噪声在频率域上的重叠部分为1~10Hz, 在此范围内, 地震信号主要分布于2.0~2.5s和3.5~4.0s, 涌浪噪声信号主要分布于0~1.5s和3.0~3.5s。时域重叠部分在1.5~2.0s和2.5~3.0s范围内。本文的目标是将信号从含涌浪噪声的地震信号时频谱(图 6b)处理为无噪声的地震信号时频谱(图 6a)。我们尝试采用基于不同策略的CNN方法来处理涌浪噪声, 同样以无噪声地震信号和含涌浪噪声的地震信号为训练样本, 训练用于处理含涌浪噪声地震信号的CNN模型。然后利用此模型对不同于训练样本的地震信号进行去噪处理, 结果如图 7和图 8所示。可以看出, 采用基于不同策略的CNN方法处理含涌浪噪声的地震信号时均具有较好的效果, 基于策略Ⅰ的CNN方法对涌浪噪声的压制效果比基于策略Ⅱ的CNN方法压制效果更加明显。
|
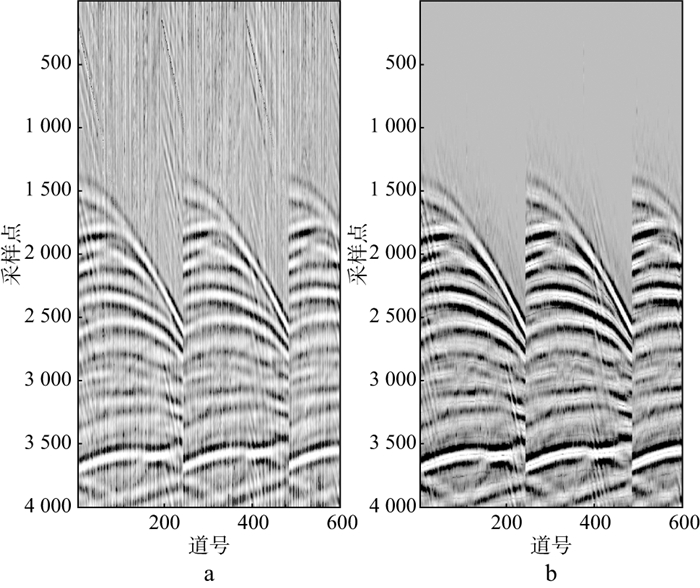
图 7 对含涌浪噪声的地震信号采用基于策略Ⅰ的CNN方法处理前(a)、后(b)的道集 |
|
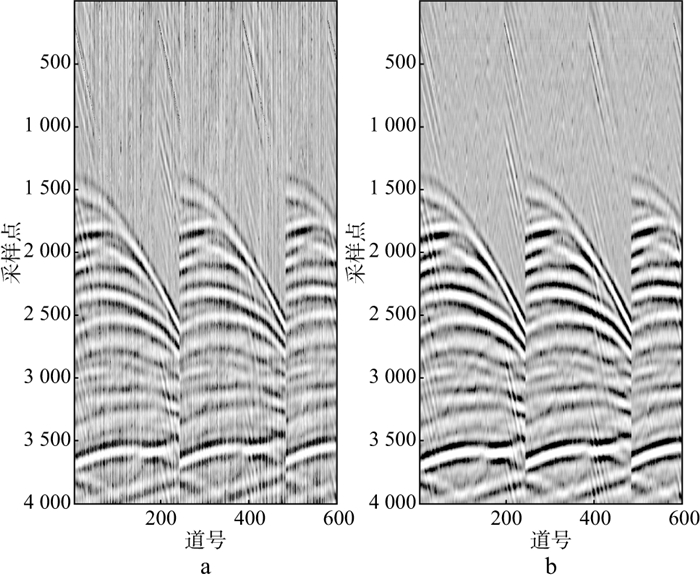
图 8 对含涌浪噪声的地震信号采用基于策略Ⅱ的CNN方法处理前(a)、后(b)的道集 |
为了对比本文提出的CNN方法与常规噪声压制方法的性能差异, 选取地震信号处理中比较常用的中值滤波(MF)、小波滤波器(WF)和低通滤波器(LF)及本文提出的基于策略Ⅰ(CNN(1))和策略Ⅱ(CNN(2))的CNN方法, 分别针对-10, -5, 5, 10dB噪声的数据进行处理, 并对结果进行量化统计。
如图 9所示, 当噪声为10dB时, 可以看出, 基于策略Ⅰ和策略Ⅱ的CNN方法在SSIM和PSNR指标上的表现都优于其它3种常规方法, 其中, 基于策略Ⅰ的CNN方法去噪效果最明显, 基于策略Ⅱ的CNN方法去噪效果略差于基于策略Ⅰ的CNN方法。就RMSE指标而言, 基于两种策略的CNN方法均明显优于常规方法, 基于策略Ⅰ的CNN方法优于基于策略Ⅱ的CNN方法。
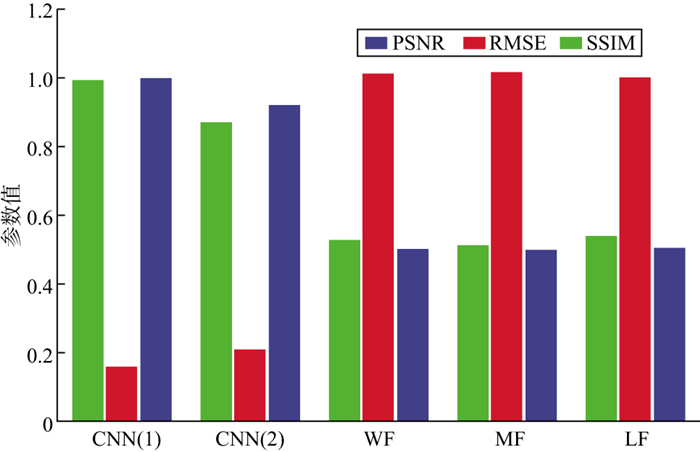
|
图 9 不同方法噪声压制效果的量化指标(10dB噪声) |
当噪声增加到5dB时, 不同方法噪声压制性能的量化评价指标如图 10所示。可以看出当增加噪声强度时, 各种方法的效果与之前的结论基本相似。常规方法与基于两种策略的CNN方法得到的SSIM、PSNR和RMSE指标值差距仍然很大; 和其它常规方法相比, 基于策略Ⅱ的CNN方法得到的SSIM和PSNR值较高, RMSE值较低, 该方法在去噪方面具有明显优势, 但整体表现略差于基于策略Ⅰ的CNN方法, 属于次好的噪声压制方法。
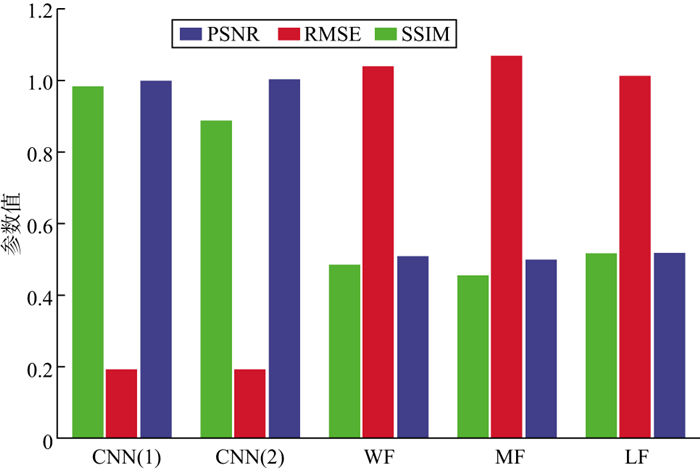
|
图 10 不同方法噪声压制效果的量化评价指标(5dB噪声) |
当噪声强度增加到-5dB时, 不同方法噪声压制效果的量化评价指标如图 11所示。不难发现, 采用常规方法得到的指标值不佳, 而分别采用基于两种策略的CNN方法得到的指标值仍然表现良好; 基于策略Ⅱ的CNN方法得到的3个指标略优于基于策略Ⅰ的CNN方法得到的3个指标, 采用基于策略Ⅱ的CNN方法得到的指标值均明显优于采用常规方法得到的指标值。
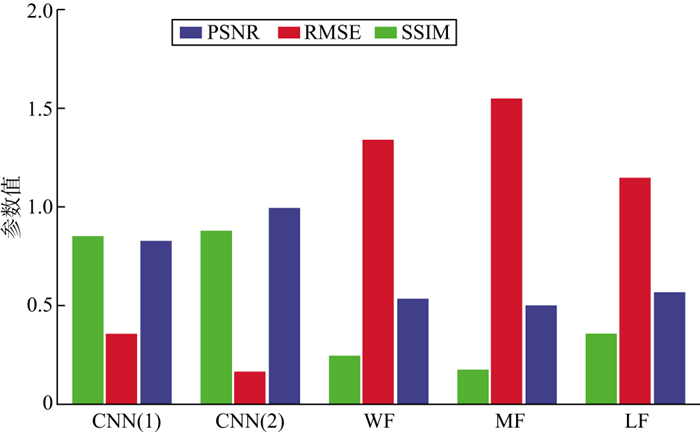
|
图 11 不同方法噪声压制效果的量化评价指标(-5dB噪声) |
当高斯噪声的强度增加到了-10dB时, 不同方法噪声压制效果的量化评价指标如图 12所示。就去噪效果而言, 基于两种策略的CNN方法均显著优于常规方法。基于策略Ⅱ的CNN方法在SSIM指标上的表现优于基于策略Ⅰ的CNN方法, 二者差距较小; 基于策略Ⅰ的CNN方法在PSNR和RMSE这两个指标上的表现优于基于策略Ⅱ的CNN方法。总体而言, 基于策略Ⅰ的CNN方法略优于基于策略Ⅱ的CNN方法, 二者差距不明显。
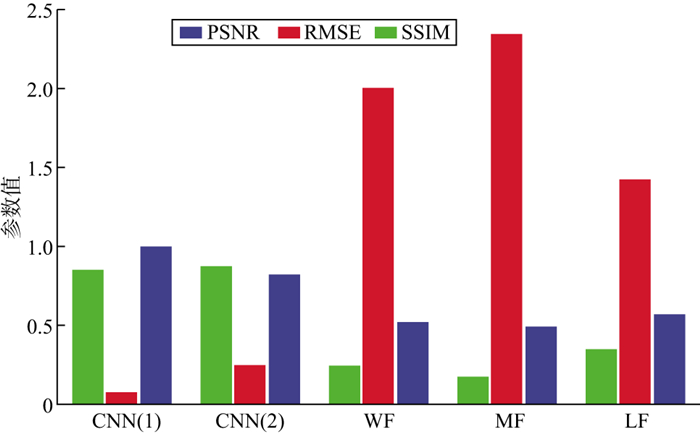
|
图 12 不同方法噪声压制效果的量化评价指标(-10dB噪声) |
在实际情况中, 通常难以测量随机噪声的强度, 因此本文将不同强度的随机噪声与地震信号混合, 形成一个新的训练集, 然后再使用基于策略Ⅰ和策略Ⅱ的CNN方法分别进行训练, 得到两种自适应去噪模型。
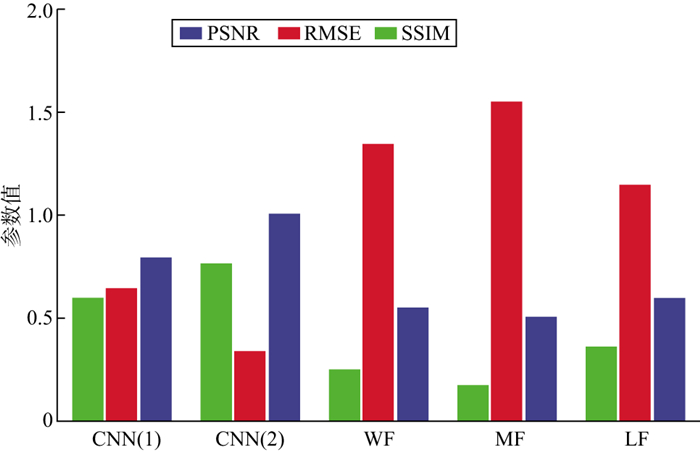
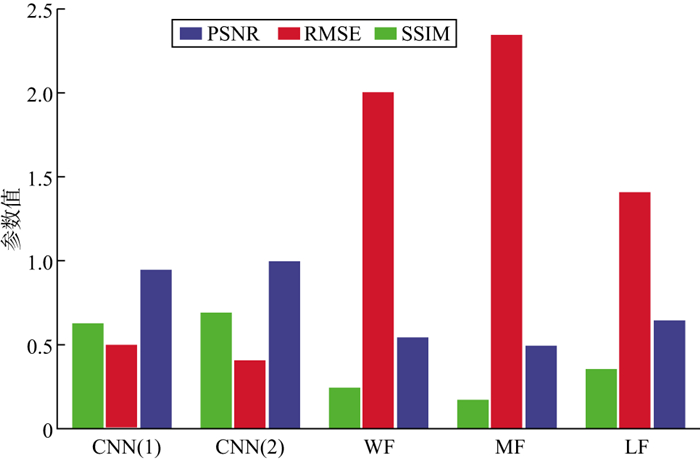
首先对加入-10dB噪声和-5dB噪声的地震信号应用基于策略Ⅰ和策略Ⅱ的CNN方法, 比较两种方法的随机噪声压制效果, 得到的结果与前面的结论基本一致, 基于策略Ⅰ和策略Ⅱ的CNN方法明显优于常规的去噪方法。当随机噪声为-5dB时, 得到的量化评价指标如图 13所示。基于策略Ⅰ和策略Ⅱ的CNN方法相较于常规去噪方法仍具有明显的优势。相较于采用基于策略Ⅰ的CNN方法, 采用基于策略Ⅱ的CNN方法得到的SSIM和PSNR值较高, RMSE值较低, 并且二者差距较大。这意味着基于策略Ⅱ的CNN方法整体表现明显优于基于策略Ⅰ的CNN方法。当随机噪声为-10dB时, 得到的量化评价指标如图 14所示, 基于策略Ⅰ的CNN方法和基于策略Ⅱ的CNN方法得到的结果差距进一步缩小, 整体表现较为相近, 但基于策略Ⅱ的CNN方法在3个量化评价指标上略有优势。
|
图 13 不同方法压制混合随机噪声效果的量化评价指标(-5dB噪声) |
|
图 14 不同方法压制混合随机噪声效果的量化评价指标(-10dB噪声) |
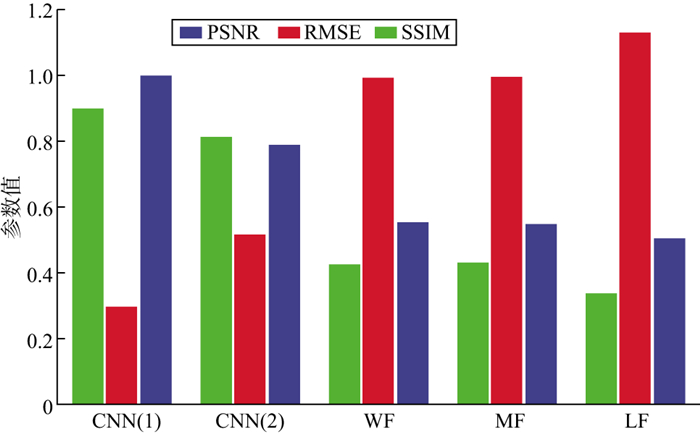
在涌浪噪声的压制研究中, 采用类似去除随机噪声的方法单独训练用于去除涌浪噪声的模型, 并进一步比较基于策略Ⅰ和策略Ⅱ的CNN方法和常规方法在压制涌浪噪声的效果, 不同方法得到的压制浪涌噪声的量化评价指标如图 15所示, 比较SSIM、PSNR和RMSE值, 不难发现两种策略下的CNN方法明显优于常规方法。在SSIM和PSNR指标方面, 基于策略Ⅰ的CNN方法和基于策略Ⅱ的CNN方法差距较小, 基于策略Ⅰ的CNN方法得到的PSNR值和SSIM值略高于基于策略Ⅱ的CNN方法, 基于策略Ⅰ的CNN方法得到的RMSE值明显低于基于策略Ⅱ的CNN方法得到的RMSE值。这表明基于策略Ⅰ的CNN方法优于基于策略Ⅱ的CNN方法。两种策略下的CNN方法对涌浪噪声都有较好的压制效果, 相较于常规方法更为有效。
|
图 15 不同方法压制涌浪噪声效果的量化评价指标 |
常规用于训练的数据噪声类型较为单一, 当实际资料中的噪声与用于CNN训练的噪声特征存在差异时, 预训练CNN模型的泛化能力面临巨大的挑战, 使用足够大量且特征足够多的数据进行网络训练可以解决该问题, 不足之处在于需要耗费巨大的计算量。为了解决大训练量问题和CNN模型的泛化性问题, 本文引入迁移学习概念, 即在训练好的预训练模型上, 使用少量的实际数据重新训练网络模型, 调整网络的权重, 然后再将训练好的网络模型用于处理实际地震数据。
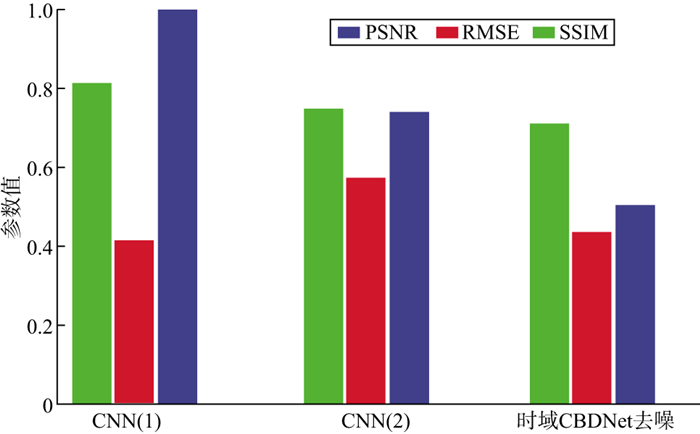
为了对比时域CBDNet方法与本文提出的基于两种策略的CWT-CNN方法在噪声压制上的差异, 本文将含噪和无噪地震剖面分割为大小320×160的网格, 然后制作训练集并优化训练时域CBDNet模型, 生成用于预训练的时域CBDNet模型; 再对原始地震剖面加入一定强度的随机噪声, 形成少量的训练样本, 分别对用于预训练的时域CBDNet模型和本文提出的基于不同策略的CNN方法得到的模型进行参数微调的迁移学习, 之后将其应用于叠加了-5dB随机噪声的实际地震数据, 进行噪声压制, 并定量评价噪声压制效果。不同方法压制随机噪声的量化评价指标如表 1和图 16所示, 采用不同方法压制-5dB噪声后的结果如图 17至图 19所示。基于策略Ⅰ的CNN方法在SSIM和PSNR指标上优于基于策略Ⅱ的CNN方法, 同时其RMSE值也小于基于策略Ⅱ的CNN方法得到的RMSE值。二者在SSIM和PSNR指标上的表现均优于时域CBDNet方法, 但基于策略Ⅱ的CNN方法在RMSE指标上的表现略逊于时域CBDNet方法。总体而言, 基于策略Ⅰ和策略Ⅱ的频域CNN方法充分利用了信号时频域的信息, 故去噪效果优于时域CBDNet方法。此外, 基于策略Ⅰ的CNN方法去噪效果优于基于策略Ⅱ的CNN方法的去噪效果, 且表现更为稳定。
| 表 1 不同方法压制随机噪声的量化评价指标 |
|
图 16 不同方法压制随机噪声效果的量化评价指标 |
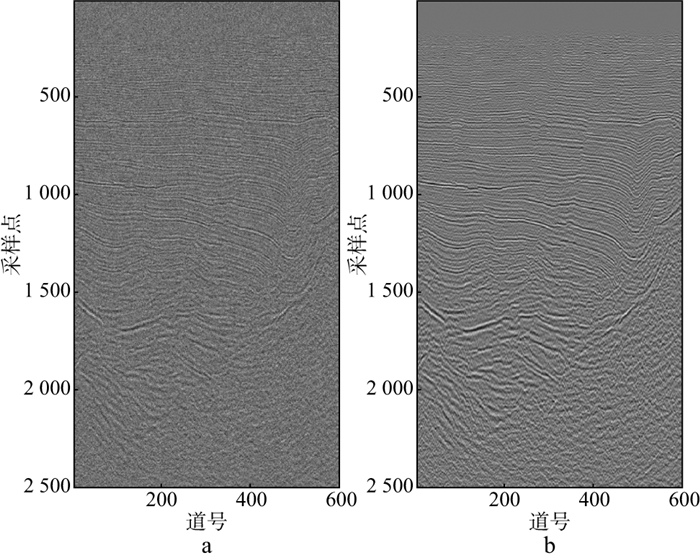
|
图 17 含-5dB噪声的地震信号(a)和基于策略Ⅰ的CNN方法得到的去噪结果(b) |
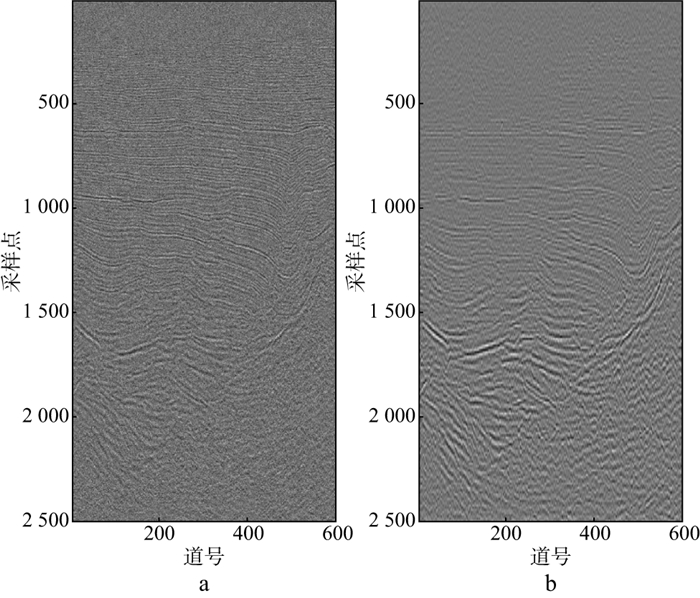
|
图 18 含-5dB噪声的地震信号(a)和基于策略Ⅱ的CNN方法得到的去噪结果(b) |
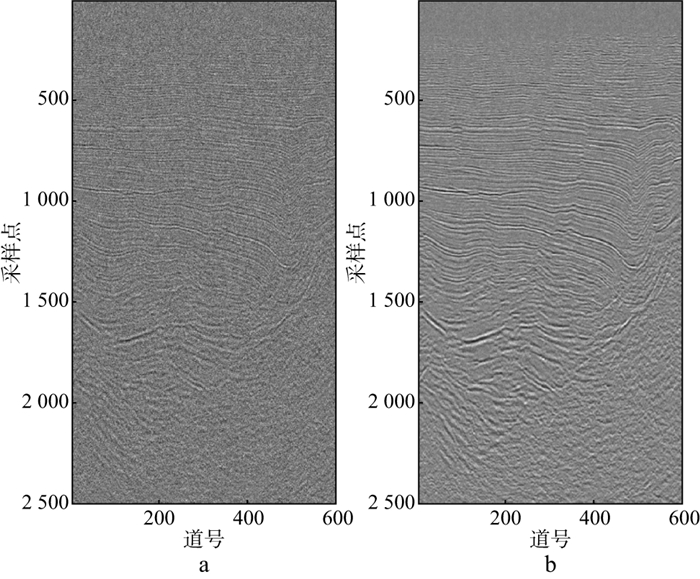
|
图 19 含-5dB噪声的地震信号(a)和时域CBDNet去噪方法得到的去噪结果(b) |
根据本文得到的噪声压制结果可知, 虽然在某些情况下基于策略Ⅱ的CNN方法噪声压制效果略好于基于策略Ⅰ的CNN方法噪声压制效果, 但是大部分情况下基于策略Ⅰ的CNN方法效果更优。原因可能和该算法执行原理有关。本文一开始便使用插值法将CWT计算得到的时频谱按照一定比例进行了缩小, 利用CNN模型进行噪声压制后又使用插值法将结果进行了放大(图 20)。基于策略Ⅰ的CNN方法在噪声水平较低的情况下, 因采用了较高分辨率相位频谱, 故保留有更多的相位细节信息, 因此相较于基于策略Ⅱ的CNN方法具有更好的细节表现能力。基于策略Ⅱ的CNN方法既需要对振幅谱进行处理, 又需要对相位谱进行处理, 因此基于策略Ⅱ的CNN方法在噪声强度较大时, 表现得更加稳健。在噪声水平更高的情况下, 由于基于策略Ⅱ的CNN方法将时频谱分布在实部和虚部两个通道上, 信号在各自通道上的特征相对于噪声的能量更小, 因此噪声压制效果变差。如果将利用基于策略Ⅱ的CNN方法处理后的原始图片尺寸加大, 其整体表现或许与利用基于策略Ⅰ的CNN方法得到的结果类似, 但是相应的处理计算量会增大很多。增大的计算量和提升的去噪效果之间的关系尚不确定, 该问题有待进一步研究讨论。
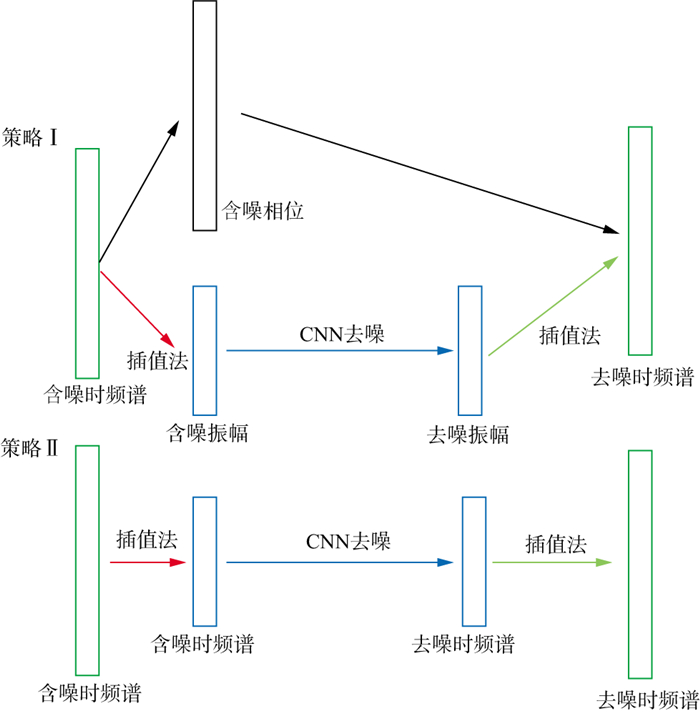
|
图 20 插值法在不同策略下应用的流程 |
针对地震数据的噪声压制, 相较于常规的时间域CNN去噪方法, 本文根据不同的时频谱处理方式, 提出了基于能量谱策略(策略Ⅰ)和基于复矩阵的策略(策略Ⅱ)的CNN方法。数值试验表明, 当随机噪声强度较低时, 基于策略Ⅰ的CNN方法总体的噪声压制效果要优于基于策略Ⅱ的CNN方法的噪声压制效果; 当随机噪声强度中等时, 基于策略Ⅰ的CNN方法和基于策略Ⅱ的CNN方法效果相当; 当随机噪声强度较高时, 基于策略Ⅰ的CNN方法的效果优于基于策略Ⅱ的CNN方法的效果; 与常规的噪声压制方法相比, 本文提出的基于两种策略的CNN方法在定量评价上均优于常规方法, 且能提供更高信噪比的地震数据。为了解决实际地震数据噪声压制的泛化性问题, 本文引入迁移学习技术, 利用少量实际训练样本微调预训练模型, 同时对比时间域和频率域CNN方法的性能差异。通过对实际地震数据的处理和定量评价可知, 在相同噪声强度情况下, 相较于时域CBDNet方法, 本文提出的基于两种策略的频率域CNN方法都具有稳健的噪声压制效果, 充分展示了本文方法的实际应用价值。
| [1] |
ELBOTH T, REIF B A, ANDREASSEN Ø. Flow and swell noise in marine seismic data[J]. Geophysics, 2009, 74(2): Q17-Q25. DOI:10.1190/1.3078403 |
| [2] |
DAI H C, MACBETH C. Automatic picking of seismic arrivals in local earthquake data using an artificial neural network[J]. Geophysical Journal International, 1995, 120(3): 758-774. DOI:10.1111/j.1365-246X.1995.tb01851.x |
| [3] |
SCARPETTA S, GIUDICEPIETRO F, EZIN E C, et al. Automatic classification of seismic signals at Mt.Vesuvius volcano, Italy, using neural networks[J]. Bulletin of the Seismological Society of America, 2005, 95(1): 185-196. DOI:10.1785/0120030075 |
| [4] |
张兵. 基于卷积神经网络和叠加速度谱的地震层速度自动建模方法[J]. 石油物探, 2021, 60(3): 366-375. ZHANG B. Automatic seismic interval velocity building based on convolutional neural network and velocity spectrum[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 366-375. DOI:10.3969/j.issn.1000-1441.2021.03.002 |
| [5] |
TITOS M, BUENO A, GARCíA L, et al. A deep neural networks approach to automatic recognition systems for volcano-seismic events[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(5): 1533-1544. DOI:10.1109/JSTARS.2018.2803198 |
| [6] |
WU H, ZHANG B, LIN T F, et al. White noise attenuation of seismic trace by integrating variational mode decomposition with convolutional neural network[J]. Geophysics, 2019, 84(5): V307-V317. DOI:10.1190/geo2018-0635.1 |
| [7] |
ZHANG Y S, LIN H B, LI Y, et al. A patch based denoising method using deep convolutional neural network for seismic image[J]. IEEE Access, 2019, 7: 156883-156894. DOI:10.1109/ACCESS.2019.2949774 |
| [8] |
WANG F, CHEN S C. Residual learning of deep convolutional neural network for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1314-1318. DOI:10.1109/LGRS.2019.2895702 |
| [9] |
张浩, 冯兴强, 付昌, 等. 基于卷积神经网络的倾角域弹性波逆时偏移噪声压制方法[J]. 石油物探, 2021, 60(3): 376-384. ZHANG H, FENG X Q, FU C, et al. Noise suppression during elastic reverse time migration in the dip-angle domain using a convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 376-384. DOI:10.3969/j.issn.1000-1441.2021.03.003 |
| [10] |
OTHMAN A, IQBAL N, HANAFY S M, et al. Automated event detection and denoising method for passive seismic data using residual deep convolutional neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. |
| [11] |
高有湖, 岳景杭, 孔军, 等. 一种基于卷积网络的地震探测数据随机噪声去除方法[J]. 科学技术与工程, 2021, 21(1): 103-108. GAO Y H, YUE J H, KONG J, et al. Random noise attenuation method for seismic exploration data based on convolutional network[J]. Science Technology and Engineering, 2021, 21(1): 103-108. |
| [12] |
YANG L Q, CHEN W, LIU W, et al. Random noise attenuation based on residual convolutional neural network in seismic datasets[J]. IEEE Access, 2020, 8: 30271-30286. DOI:10.1109/ACCESS.2020.2972464 |
| [13] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Y Q, LU W K, LIU J L, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [14] |
罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59. LUO R Z, LI Y Y. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59. |
| [15] |
程文婷, 方文倩, 付丽华. 基于自相似性和低秩先验的地震数据随机噪声压制[J]. 石油物探, 2020, 59(6): 880-889. CHENG W T, FANG W Q, FU L H. Seismic noise suppression via self-similarity and low-rank prior[J]. Geophysical Prospecting for Petroleum, 2020, 59(6): 880-889. DOI:10.3969/j.issn.1000-1441.2020.06.006 |
| [16] |
杨翠倩, 周亚同, 何昊, 等. 基于全局上下文和注意力机制深度卷积神经网络的地震数据去噪[J]. 石油物探, 2021, 60(5): 751-762. YANG C Q, ZHOU Y T, HE H, et al. Global context and attention-based deep convolutional neural network for seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 751-762. DOI:10.3969/j.issn.1000-1441.2021.05.006 |
| [17] |
ZHANG M, LIU Y, CHEN Y K. Unsupervised seismic random noise attenuation based on deep convolutional neural network[J]. IEEE Access, 2019, 7: 179810-179822. DOI:10.1109/ACCESS.2019.2959238 |
| [18] |
YOU J C, XUE Y J, CAO J X, et al. Attenuation of seismic swell noise using convolutional neural networks in frequency domain and transfer learning[J]. Interpretation, 2020, 8(4): T941-T952. |
| [19] |
OPPENHEIM A V, BUCK J R, SCHAFER R W. Discrete-time signal processing[M]. New Jersey: Prentice Hall, 2001: 504-509.
|
| [20] |
MITRA S K. Digital signal processing: A computer-based approach(2nd Ed)[M]. New York: McGraw-Hill, 2001: 117-137.
|
| [21] |
JONATHAN M L, SOFIA C O. Generalized morse wavelets as a superfamily of analytic wavelets[J]. IEEE Transactions on Signal Processing: A publication of the IEEE Signal Processing Society, 2012, 60(11): 6036-6041. |
| [22] |
GUO S, YAN Z, ZHANG K, et al. Toward convolutional blind denoising of real photographs[J]. Proceedings of the IEEE/CVF 2019 Conference on Computer Vision and Pattern Recognition, 2019, 1712-1722. |




