2. 中国石油东方地球物理公司西南物探研究院, 四川成都 610500
2. Southwest Geophysical Exploration Bureau of Geophysical Prospecting, China National Petroleum Corporation, Chengdu 610500, China
精确的地层岩性识别对地层对比、储层评价等具有十分重要的价值, 也是油藏描述、实时钻井监控及储层参数求解的基础。目前岩性识别方法主要包括岩屑录井、取心、测井资料的处理解释、地震属性分析和地震反演等方法。地震属性岩性预测方法取决于所选取的地震属性对岩性的敏感程度, 仅利用单一属性难以准确预测岩性。采用地震反演岩性预测方法统计岩性的某一弹性参数范围或进行弹性参数交会分析时, 若弹性参数之间分布范围存在大量重叠, 则无法有效划分岩性, 预测结果存在较大不确定性。
近年来, 人工智能技术应用于测井曲线岩性识别, 可从海量测井数据中自动提取特征值, 实现岩性的识别和分类。目前, 支持向量机[1]、BP神经网络[2、3]、决策树[4]、fisher[5]判别分析法以及贝叶斯决策法[6]等方法在测井岩性识别领域取得了明显的效果。ZOU等[7]、谷宇峰等[8]利用梯度提升决策树(gradient boosting decision tree, GBDT)模型对岩性进行分类, 该模型具有良好的分类性能。张野等[9]利用Inception-v3深度卷积神经网络模型, 采用迁移学习方法, 实现了岩石岩性的自动识别与分类。李曦等[10]将上述方法和粒子群算法优化支持向量机参数的方法相结合, 该方法的识别准确率达到97%。王恒等[11]将XGBoost和LightGBM的岩性识别方法的识别结果与KNN(K近邻分类器)、朴素贝叶斯和支持向量机等传统算法得到的识别结果进行对比, 发现前者的准确率远高于传统算法。赵武生等[12]根据层次聚类分析思想进行火成岩岩性识别, 准确率达到86.5%。WANG等[13]针对KNN模型鲁棒性不强的问题, 提出了一种基于加权余弦距离的KNN聚类方法, 将分类准确率从50.95%提高至61.39%。KAKOUEI等[14]使用反向传播神经网络(back propagation neural network, BPNN)模型对岩性进行识别, 对比径向基函数(radial basis function network, RBF)、概率神经网络(product-based neural network, PNN)、竞争学习(competitive learning, CL)和学习矢量量化器(learning vector quantization, LVQ)等方法的识别结果可知, BPNN模型的岩性识别率最高。王宗俊等[15]采用基于贝叶斯概率模型无监督学习的测井岩相分析方法, 该方法充分利用测井数据间的内在关系, 无需提供先验的岩性模型, 得到的岩性识别结果更为客观。段友详等[16]将集成学习应用于岩性识别, 岩性分类测试集的平均精度达到96.66%。
人工智能识别岩性方法同样存在缺点和局限性。对KNN而言, 随着样本维度的增高, 相似度高的样点之间的计算距离也随之变大, 容易导致分类出现误差。现有分类算法仅考虑通过模型提升分类准确率, 而忽略了少数类岩性数据与多数类岩性数据分布不平衡的影响, 导致岩性分类准确率低。苏赋等[17]采用改进合成少数类过采样方法(synthetic minority over-sampling technique, SMOTE)对不平衡数据集进行采样, 提高了支持向量机岩性识别准确率。王光宇等[18]采用针对不平衡样本集的随机森林预测方法, 在未考虑不同类别的少数类样本间也存在重叠的情况下, 将岩性识别的准确率提高至83%。
本文提出了一种针对不平衡样本集的集成学习岩性预测方法。其基本思想是以录井岩性数据为岩性样本标签, 以测井数据为岩性样本特征, 将K-means算法与合成少数类过采样相结合形成K-means合成过采样算法(KSMOSEL); 然后对岩性样本集进行平衡化处理; 再将采样后的数据集用于构建集成学习模型并训练, 将测试数据输入网络模型中进行测试, 建立测井曲线与岩性之间的非线性关系以实现岩性的识别与划分; 最后通过多组实验, 验证KSMOSEL算法的可行性, 并将该算法与其它算法进行对比, 证明KSMOSEL算法的岩性识别性能。
1 模型算法原理 1.1 不平衡数据集不平衡数据集是指数据集中的各个类别样本数量存在很大差距, 分布极不均衡, 有的类别岩性标签很少, 有的则很多。因此不平衡数据集分为少数类样本和多数类样本, 其中样本数量非常少的定义为稀缺类或少数类, 样本数量多的定义为多数类。我们定义少数类为负类样本(negative examples, NE), 多数类为正类样本(positive examples, PE)。数据集不平衡度D的计算公式如下:
| $ D=\frac{P_E}{N_E} $ | (1) |
式中: 数据集不平衡度D越大, 代表着数据集越不平衡; NE为负类样本; PE为正类样本。
当数据集不平衡度恒定时, 样本的规模对识别分类模型的性能影响很大。当样本规模较小时, 难以挖掘负样本中潜在的关系; 当样本规模逐渐增大时, 少数类中潜在的关系逐步被挖掘, 有利于提高模型的性能。
利用机器学习算法对测井数据进行岩性识别时发现, 由于地下岩石形成的环境和时间不同, 各类岩层厚度不同, 因此导致测井数据各类的样本数不同。由于测井数据的获取成本高昂, 不可能无限制地增加样本规模以消除测井数据不平衡对分类器的影响, 所以, 在识别之前, 有必要对测井数据的不平衡性进行处理, 即对岩性样本进行KS采样, 使测井数据达到平衡。
1.2 改进不平衡样本集过采样集成学习(K-means synthetic minority over sampling ensemble learning, KSMOSEL)原理采用KS采样处理不平衡测井数据, 是将K-means聚类与SMOTE过采样结合, 以平衡偏斜的测井数据集, 步骤包括聚类、过滤和过采样。为了保证训练模型的标签准确性, 只对测试集进行KS采样平衡, 将平衡后的数据重新输入模型中进行训练。具体过程如下。
1) 统计数据集中所有标签下样本的数量后求平均值K, 若样本少于K, 则判定为少数类, 如果样本多于K, 则判定为多数类。
K-means聚类思想: 用K-means算法将数据集X={X1, X2, …, Xi, …, Xn}聚类得到m个类别, 每个类别Cm有一个类别中心μi; 选取欧氏距离作为相似性和距离判断准则, 计算该类内各点到聚类中心的距离平方和:
| $ J(m)=\sum\limits_{x_i \in C_m}\left\|X_i-\mu_i\right\|^2 $ | (2) |
2) 对于少数类, 利用K-means聚类得到少数类样本聚类中心, 选择分类样本数目最多的一类样本的中心点作为负类的中心点, 记为XC, 去掉负类分类中聚类数目比较少的负类, 只保留数目较多的负类, 此过程为过滤。采用合成少数类过采样方法进行过采样处理, 在聚类中心与负类的样本点之间的连线上进行插值, 生成人工负类样本, 即少数类样本, 即得到s个新样本, 将s个新样本添加到该类中。
SMOTE过采样合成公式如下:
| $ s=x+\beta(x-y) $ | (3) |
式中: x代表种子样本在欧氏空间的坐标; y代表随机选取的m个近邻的坐标; β是一个随机值, β∈(0, 1)。
3) 对于上述少数类, 如果平衡样本数已经不小于K, 则停止进行聚类, 否则继续进行聚类, 最终得到多组均衡的新岩石样本。
在进行KS采样后, 样本集中的多类样本数量达到平衡状态, 在特征空间中能够很好地区分样本。利用该样本集训练分类器, 可有效降低少数类样本被误分的风险。
4) KS采样后, 将数据输入到集成学习模型中。KSMOSEL模型融合了各个单一机器学习模型的优势, 选择支持向量机(support vector machine, SVM, 适用于小样本数据和稀疏性好)、随机森林(适合高方差数据)、KNN算法(对异常值不敏感)以及GBDT模型(预测精度高、鲁棒性强)4个弱分类器进行融合, 采用“软投票”的方式计算分类概率, 最终形成一个岩性识别多层集成学习模型。该模型具有很强的抗干扰能力和特征组合能力, 可以减少数据分布振荡造成的模型效果不稳定。
依据模型判断某一类别属性的原理是将所有模型为同一类别的概率平均值作为该类别的最终概率, 计算出所有类别的概率, 概率值最大的类别为模型预测的结果。
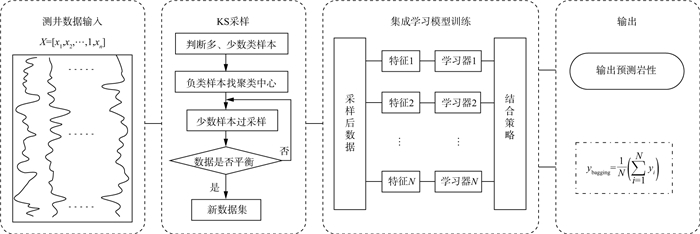
KSMOSEL模型包括测井数据输入、KS采样、集成学习模型与输出层。我们利用各层之间的连接关系, 挖掘出不同测井响应与对应岩性类别之间的非线性映射关系。KSMOSEL模型结构如图 1所示。
|
图 1 KSMOSEL模型结构 |
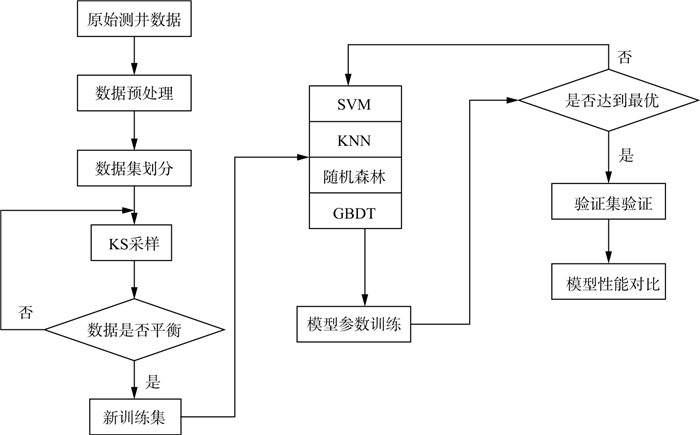
基于KSMOSEL模型的岩性识别方法主要由数据预处理、训练以及验证3部分构成, 具体流程如图 2所示, 关键步骤如下。
|
图 2 基于KSMOSEL模型的岩性识别流程 |
1) 数据预处理: 将数据集划分为训练集、测试集两部分, 并对数据进行归一化处理, 然后按照8∶2的比例对数据集进行分层抽采样法划分, 将80%的数据用于多层集成学习模型训练, 将20%的数据用于验证模型分类的效果。
2) 使用KS采样训练集得到新训练集, 搭建多层集成学习模型后, 开始训练集成学习算法分类模型, 再寻找最佳模型参数, 最后采用软投票方式得到分类结果。
3) 使用验证集数据来验证KSMOSEL分类算法模型的分类性能, 然后得到混淆矩阵, 再计算精准率、召回率和F1值, 最后进行实验结果分析。
2 数据准备与网络模型训练基于KSMOSEL分类算法的有监督分类模型可用于小数据集测井数据的岩性识别。首先利用带岩性标签的测井数据进行训练, 然后通过集成学习, 对未带标签的测井数据进行有效识别, 最终达到提高岩性识别精度的目的。
2.1 数据集的选取数据来自美国堪萨斯州西南部Hugoton盆地的Hugoton油气田10口井的测井数据, 采样间隔为半英尺(约0.15m), 标签数据由岩心、岩屑样品和测井数据综合确定。曲线特征包括自然伽马(GR)、深侧向电阻率(RLLD, 因属性值过大, 故取其关于10的对数)、中子密度孔隙度差异(DeltaPHI)、平均中子密度孔隙度(PHIND)、光电吸收截面指数(PE), 以及相对位置(RELPOS)和非海相/海相指标(NM_M)两种地质特征约束变量。将自然伽马、深侧向电阻率、中子密度孔隙度差异、平均中子密度孔隙度和光电吸收截面指数5种特征作为KSMOSEL模型的输入数据, 识别目标即输出数据为1-非海相砂岩(SS)、2-非海相粗粉砂岩(CSiS)、3-非海相粉砂岩(FSiS)、4-海相粉砂岩页岩(SiSh)、5-泥岩(MS)、6-泥灰岩(WS)、7-白云石(D)、8-泥粒灰岩-粒状石灰岩(PS)、9-叶状藻灰岩(BS)等9种岩性。岩性按分类号标记为1~9, 可作为标签, 部分测井数据及划分结果如表 1所示。
| 表 1 部分测井数据及划分结果 |
先取出一口完整井数据(包含全部9种岩性), 共计403组数据作为验证集, 验证集只用于验证KSMOSEL分类算法对数据的预测能力。余下2828组其它井数据按比例划分为训练集和测试集, 用于训练KS采样集成学习算法分类模型。通过KSMOSEL算法分类模型混淆矩阵得到的精准率、召回率以及F1值来分析模型的好坏。为了防止因采样导致的抽样误差, 本文采用分层抽样法。每层等比例进行抽样, 使得测试集包含数据集的基本信息, 而非仅包含易于分类的数据, 这解决了模型准确率高但泛化性低、鲁棒性不强的问题。训练集、测试集和验证集划分结果如表 2所示。可以看出, 相较于其它类别, 岩性1-非海相砂岩, 3-非海相粉砂岩, 4-海相粉砂岩页岩, 7-白云石, 9-叶状藻灰岩类别数量少, 在模型训练过程中获取到的特征少, 因此需要对样本进行KS采样, 使训练样本达到平衡。
| 表 2 训练集、测试集、验证集划分结果 |
由于测量误差以及评价指标的不同, 因而原始数据存在不同量纲和量级的异常值和干扰值。本文采用归一化方法对输入数据进行预处理, 使数据集样本值处于[0, 1], 以减少误差带来的不利影响, 并确保输入数据不溢出, 最大值和最小值处于合理的分布范围, 有助于梯度下降算法的收敛和提高模型的预测精度。具体计算公式为:
| $ \begin{aligned} & x_i^{\prime}=\frac{x_i-x_{i \min }}{x_{i \max}-x_{i \min}} \\ & i=1, 2, \cdots, n \end{aligned} $ | (4) |
式中: xi表示归一化前的第i个实测测井值, 即选取某类测井数据的某个实际测井值; x′i表示归一化后的第i个值; ximin表示第i个测井数据的最小值, ximax表示第i个测井数据的最大值。
2.4 评价指标评价指标包括精确率、召回率和F1值。在引入混淆矩阵的基础上计算得到上述3个指标, 用于综合评价分类的准确性。混淆矩阵为一个N×N矩阵(N=9), 其中, 矩阵的列数代表分类的预测值, 每一列的总数表示预测为该类别的数目总和; 行矩阵代表数据的真实类(标签值), 每一行的数据总数表示该类别的实际数目。混淆矩阵通过揭示样本数据的实际类别与预测类别之间的关系, 获得真正例(True Positive)、假正例(False Positive, )、真反例(True Negative)和假反例(False Negative)共4组数据, 具体表现形式如表 3所示(以二分类为例)。
| 表 3 分类结果混淆矩阵s |
表 3中TP是实际为多数类(正例)并预测为多数类的个数, FN是实际为多数类预测为少数类(负例)的个数, FP是实际为少数类预测为多数类的个数, TN是实际为少数类预测为少数类的个数。
在上述4组数据的基础上, 精确率(P)、召回率(R)和F1值(F1)3个评价指标的计算公式分别如下:
| $ P=\frac{T_P}{T_P+F_P} $ | (5) |
| $ R=\frac{T_P}{T_P+F_N} $ | (6) |
| $ F_1=\frac{2 \times P \times R}{P+R} $ | (7) |
式中: P用于衡量分类的总体精度, 精度越高, 分类效果越好; R用于衡量分类器对正例的识别效果, R值越高, 分类效果越好。
3 实验结果分析 3.1 KS采样效果分析为了验证KS采样之后各模型的有效性能, 采用K折交叉验证来验证算法性能。K折交叉验证是将数据集分成K份, 轮流将其中K-1份作为训练数据, 1份作为测试数据进行试验。每次试验都会得出相应的正确率, 其结果如表 4和表 5所示。本文中K=5, 称为5折交叉验证, 共验证10次。其中表 4为未进行KS采样时, 集成学习模型的训练集和测试集准确率结果, 表 5为进行KS采样平衡训练集后, 集成学习模型的训练集和测试集准确率结果。
| 表 4 未进行KS采样的集成学习模型准确度S |
| 表 5 KS采样后的集成学习模型准确度 |
从表 4可以看出, 未进行KS采样的集成学习模型10次5折交叉验证的训练集准确率基本稳定在98.00%, 测试集准确率基本稳定在75.00%, 而进行了KS采样的集成学习模型10次5折交叉验证的训练集准确率基本稳定在92.00%, 测试集准确率基本稳定在92.85%。训练过程中, 由于同一岩性的测井数据不断变化, 故结果存在差异。地质的非均质性、各向异性的影响, 使得训练数据在训练过程中不能达到100%。排除样本划分的偶然性所带来的模型评估不准确的情况, 表明KSMOSEL算法确实具有较高的稳定性。
为了验证KS采样是否对于岩性分类效果存在明显的提升, 本文对比了SVM、GBDT、随机森林、KNN以及XGBoost等模型在使用KS采样前、后分类的准确率, 其结果如表 6所示。
| 表 6 KS采样前、后模型分类准确率对比结果 |
由对各模型的混肴矩阵结果(表 7至表 11)以及表 6可以看出, KS采样可以实现对分类样品不平衡数据的扩充, 使得各分类数据平衡, 然后使各类分类效果得到显著提升。
| 表 7 KS-SVM模型分类混淆矩阵结果 |
| 表 8 KS-KNN模型分类混淆矩阵结果 |
| 表 9 KS-GBDT模型分类混淆矩阵结果 |
| 表 10 KS-随机森林模型分类混淆矩阵结果 |
| 表 11 KS-XGBoost模型分类混淆矩阵结果 |
为了测试模型以及评价模型的预测效果和性能, 本文引入混淆矩阵作为评价指标。通过测试集来验证基于KSMOSEL算法的分类性能, 表 12为未采样不同模型的岩性识别结果, 表 13为采样后不同模型的岩性识别结果, 包括精准率、召回率和F1值。
| 表 12 未采样不同模型的岩性识别结果 |
| 表 13 采样后不同模型的岩性识别结果 |
从表 12和表 13可以看出, 各模型的误识别主要出现在少数类样本识别差和岩性识别错误, 对泥岩识别效果不理想, 原因在于此样本数量少。KSMOSEL分类模型的分类结果与传统SVM、随机森林、XBoost等的分类结果比较可知, 非海相砂岩(SS)、非海相粗粉砂岩(CSiS)、非海相粉砂岩(FSiS)、海相粉砂岩页岩(SiSh)、泥岩(MS)、泥灰岩(WS)、白云石(D)、泥粒灰岩-粒状石灰岩(PS)、叶状藻灰岩(BS)最佳分类F1值分别为0.94, 0.94, 0.91, 0.97, 0.93, 0.95, 1.00, 0.96, 1.00, 白云岩和叶状藻灰岩的最佳分类F1值分别来自KS-KNN和KS-随机森林模型, 其余7类岩性最佳分类F1值来自KSMOSEL分类模型。整体而言, KSMOSEL模型的分类效果最佳。
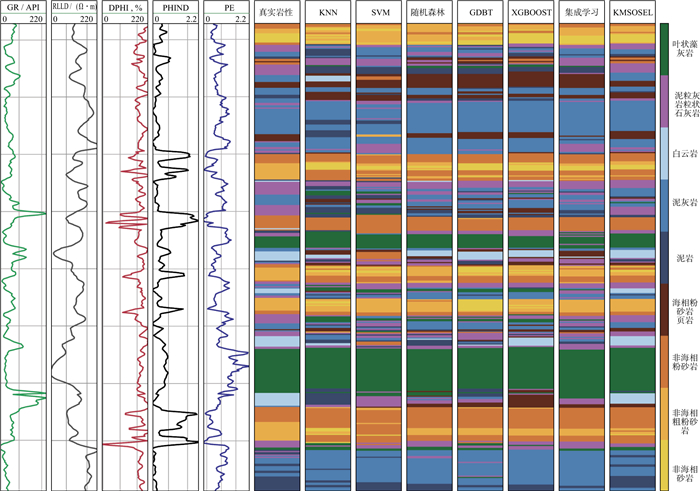
3.3 验证结果为了验证KSMOSEL分类模型的实际应用效果, 将该模型应用于工区中的CHURCHMAN BIBLE井的岩性识别, 同时将其与其它6种模型的识别结果进行对比分析。为了使识别的结果更加直观, 将9种岩性分别填充不同颜色。从图 3可以看出, 7种模型岩性识别结果与真实结果的对比情况。对比7种模型在井中的划分结果发现, XGBoost、决策树出现了乱序的问题, 并且识别精度低; GBDT划分误差较大; SVM、随机森林模型分类效果准确率较高, 但对于小样本的岩性分类准确率较低; KSMOSEL分类模型提取特征更全面, 分类模型预测的岩性分层效果更好, 与实际岩性吻合度高。
|
图 3 不同模型的岩性识别结果与真实结果 |
本文提出了基于KSMOSEL分类的测井岩性识别方法, 实现了使用测井数据对非海相砂岩、非海相粗粉砂岩、非海相粉砂岩、海相粉砂岩页岩、泥岩、泥灰岩、白云石、泥粒灰岩-粒状石灰岩、叶状藻灰岩等9类岩性的有效识别。通过实验得到以下结论。
1) 为解决数据不平衡问题, KS采样算法将K-means算法与SMOTE算法相结合, 对不平衡数据进行采样。进行KS采样后, 岩性分类效果明显提升, SVM模型提升了18.68%, 决策树模型提升了3.77%, GBDT模型提升了24.77%、KNN模型提升了12.03%, XGBoost模型提升了10.23%, KSMOSEL模型提升了16.69%、随机森林模型提升了19.37%。
2) 针对岩性识别率低的问题, 采用KSMOSEL分类算法得到的模型在岩性识别效果上最佳。与SVM、KNN、随机森林、GBDT、决策树和XGBoost模型的识别结果比较发现, KSMOSEL模型的分类精确度达到了94.28%。
| [1] |
韩启迪, 张小桐, 申维. 基于决策树特征提取的支持向量机在岩性分类中的应用[J]. 吉林大学学报(地球科学版), 2019, 49(2): 611-620. HAN Q D, ZHANG X T, SHEN W. Application of support vector machine based on decision tree feature extraction in lithology classification[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(2): 611-620. |
| [2] |
WANG Q S, ZHANG X J, TANG B, et al. Lithology identification technology using BP neural network based on XRF[J]. Acta Geophysica, 2021, 69(6): 2231-2240. DOI:10.1007/s11600-021-00665-8 |
| [3] |
张晗, 卢双舫, 李文浩, 等. ΔLogR技术与BP神经网络在复杂岩性致密层有机质评价中的应用[J]. 地球物理学进展, 2017, 32(3): 1308-1313. ZHANG H, LU S F, LI W H, et al. Application of ΔLogR technology and BP neural network in organic evaluation in the complex lithology tight stratum[J]. Progress in Geophysics, 2017, 32(3): 1308-1313. |
| [4] |
DUAN Y J, XIE J, LI B C, et al. Lithology identification and reservoir characteristics of the mixed siliciclastic-carbonate rocks of the lower third member of the Shahejie formation in the south of the Laizhouwan Sag, Bohai Bay Basin, China[J]. Carbonates and Evaporites, 2020, 35(2): 1-19. |
| [5] |
DONG S Q, WANG Z Z, ZENG L B. Lithology identification using kernel Fisher discriminant analysis with well logs[J]. Journal of Petroleum Science and Engineering, 2016, 143: 95-102. DOI:10.1016/j.petrol.2016.02.017 |
| [6] |
洪忠, 张猛刚, 朱筱敏. 基于岩石物理的致密碎屑岩气藏岩性及流体概率预测[J]. 石油物探, 2015, 54(6): 735-744. HONG Z, ZHANG M G, ZHU X M. Prediction on lithology and fluid probabilities of tight clastic gas reservoir based on rock physics[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 735-744. DOI:10.3969/j.issn.1000-1441.2015.06.012 |
| [7] |
ZOU Y H, CHEN Y T, DENG H. Gradient boosting decision tree for lithology identification with well logs: A case study of Zhaoxian gold deposit, Shandong peninsula, China[J]. Natural Resources Research, 2021, 30(5): 3197-3217. DOI:10.1007/s11053-021-09894-6 |
| [8] |
谷宇峰, 张道勇, 鲍志东, 等. GBDT识别致密砂岩储层岩性[J]. 地球物理学进展, 2021, 36(5): 1956-1965. GU Y F, ZHANG D Y, BAO Z D, et al. Lithology prediction of tight sandstone reservoirs using GBDT[J]. Progress in Geophysics, 2021, 36(5): 1956-1965. |
| [9] |
张野, 李明超, 韩帅. 基于岩石图像深度学习的岩性自动识别与分类方法[J]. 岩石学报, 2018, 34(2): 333-342. ZHANG Y, LI M C, HAN S. Automatic identification and classification in lithology based on deep learning in rock images[J]. Acta Petrologica Sinica, 2018, 34(2): 333-342. |
| [10] |
李曦, 范翔宇, 王兆峰, 等. 基于PSO-SVM的测井岩性识别方法研究: 以南图尔盖盆地K油田古生界(Pz)储层为例[J]. 地球物理学进展, 2022, 37(2): 617-626. LI X, FAN X Y, WANG Z F, et al. Logging lithology identification method research based on PSO-SVM: A case study of Paleozoic (Pz) reservoir in K oil field, South Turgay Basin, Kazakhstan[J]. Progress in Geophysics, 2022, 37(2): 617-626. |
| [11] |
王恒, 姜亚楠, 张欣, 等. 基于梯度提升算法的岩性识别方法[J]. 吉林大学学报(地球科学版), 2021, 51(3): 940-950. WANG H, JIANG Y N, ZHANG X, et al. Lithology identification method based on gradient boosting algorithm[J]. Journal of Jilin University (Earth Science Edition), 2021, 51(3): 940-950. |
| [12] |
赵武生, 谭伏霖, 王志章, 等. 准噶尔盆地腹部火成岩岩性识别[J]. 天然气工业, 2010, 30(2): 21-25. ZHAO W S, TAN F L, WANG Z Z, et al. Identification of the lithology of igneous rocks in central of the Junggar Basin[J]. Natural Gas Industry, 2010, 30(2): 21-25. |
| [13] |
WANG X D, YANG S C, ZHAO Y F, et al. Lithology identification using an optimized KNN clustering method based on entropy-weighed cosine distance in Mesozoic strata of Gaoqing field, Jiyang depression[J]. Journal of Petroleum Science and Engineering, 2018, 166: 157-174. |
| [14] |
KAKOUEI A, MASIHI M, SOLA B S, et al. Lithological facies identification in Iranian largest gas field: A comparative study of neural network methods[J]. Journal of the Geological Society of India, 2014, 84(3): 326-334. |
| [15] |
王宗俊, 董洪超, 范廷恩, 等. 基于无监督学习的测井岩相分析技术及其应用[J]. 石油物探, 2021, 60(3): 403-413. WANG Z J, DONG H C, FAN T E, et al. Logging lithofacies analysis based on unsupervised learning[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 403-413. |
| [16] |
段友祥, 赵云山, 马存飞, 等. 基于多层集成学习的岩性识别方法[J]. 数据采集与处理, 2020, 35(3): 572-581. DUAN Y X, ZHAO Y S, MA C F, et al. Lithology identification method based on multi-layer ensemble learning[J]. Journal of Data Acquisition and Processing, 2020, 35(3): 572-581. |
| [17] |
苏赋, 马磊, 罗仁泽, 等. 基于改进多分类孪生支持向量机的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2020, 35(1): 174-180. SU F, MA L, LUO R Z, et al. Research and application of logging lithology identification based on improve multi-class twin support vector machine[J]. Progress in Geophysics, 2020, 35(1): 174-180. |
| [18] |
王光宇, 宋建国, 徐飞, 等. 不平衡样本集随机森林岩性预测方法[J]. 石油地球物理勘探, 2021, 56(4): 679-687. WANG G Y, SONG J G, XU F, et al. Random Forests lithology prediction method for imbalanced data sets[J]. Oil Geophysical Prospecting, 2021, 56(4): 679-687. |



