地震反演是获取地下介质弹性参数的有效途径之一。以叠前AVO反演技术为例, 基于褶积模型理论及Zoeppritz方程近似式, 可以将带限地震振幅和频率等信息转换为纵、横波速度及密度等地层弹性信息, 进而指导岩性及流体预测[1-3]。由于地震信息的带限性、多解性及噪声干扰等, 如何构建合理、精细的初始反演模型, 获取更高精度、稳定的算法一直是反演研究的重点[4-5]。
常规低频建模在构造或地层格架约束下, 通过反距离加权、三角网格法或克里金等插值法[6], 将测井数据进行内插外推。但此类方法为数学插值, 不包含任何地质信息, 容易造成围绕井周边插值的“牛眼”模型化现象, 对井控程度低、地质体横向变化快等情况适用性较差。对此, 学者们提出通过多元统计、神经网络等方法, 利用地震速度、振幅等属性约束建模, 构建多属性与测井弹性参数关系。PRAMANIK等[7]采用Cokriging方法, 利用阻抗模拟孔隙度, 合理地利用弹性信息构建了油藏参数的空间模型。HANSEN等[8]利用地震属性(层速度、双程旅行时等)约束阻抗低频建模, 通过融入地质信息解决了振幅能量弱、反演效果不理想等问题。但是, 如何寻找最佳约束地震属性拟合的难度较大, 属性选择不当会产生过拟合现象或者插值存在“牛眼”问题。
叠前AVO三参数反演受地震资料品质影响, 求解方程存在病态性, 需通过先验信息进行合理约束。近年来, 基于贝叶斯理论框架的叠前三参数反演[9-11]成为主流, 其先验信息的正则约束可以较好地解决反演病态性问题, 贝叶斯似然函数符合高斯分布, 但先验信息并无统一分布假设, 对此前人作了很多研究。BULAND等[12]在现有方法基础上提出三参数自然对数服从三变量斜歪高斯分布; DOWNTON[13]通过研究贝叶斯两项和三项AVO反演, 发现单变量柯西分布先验约束反演优于高斯先验分布; RUSSELL等[14]在DOWNTON研究的基础上, 通过引入岩石物理关系约束, 采用协方差矩阵进行非对角线矩阵加权, 比传统的对角线加入白噪系数, 稳定性更好, 进一步提高了叠前AVO反演的鲁棒性; ALEMIE等[15]提出三参数反射系数服从三变量柯西分布, 通过引入相关矩阵来消除三参数反射系数之间的统计相关性, 具有较高的抗噪性, 降低了反演的不适定性。
为了解决勘探程度低的区块中深层目标勘探工区钻井少、井距大带来的低频模型构建不合理、储层与围岩反射系数差异小造成的反演预测精度低的问题, 基于前人研究成果[16-17], 提出联合岩石弹性趋势和岩相敏感地震信息开展低频建模, 同时采用基于贝叶斯理论框架的柯西约束叠前三参数反演方法, 以提高横、纵两个维度分辨率, 建立了一种基于目标最优双向建模的叠前三参数柯西约束反演技术。首先, 搜索或重构预测目标的敏感弹性参数和敏感地震属性, 在分析研究区已钻井岩石物理垂向变化趋势的基础上, 加入对预测岩相敏感的地震横向信息, 构建更符合地质规律的目标最优双向约束初始低频模型, 以提高初始模型横向指示砂体边界的能力; 然后, 在叠前AVO三参数反演目标函数的基础上, 结合双向约束初始模型, 采用三参数柯西分布先验约束反演技术, 利用柯西分布长尾巴特征凸显弱反射系数, 提高储层预测的纵向分辨能力。最后, 利用目标最优双向建模的柯西约束反演技术提高井距大、岩相变化快背景下的低勘探区块储层预测精度。
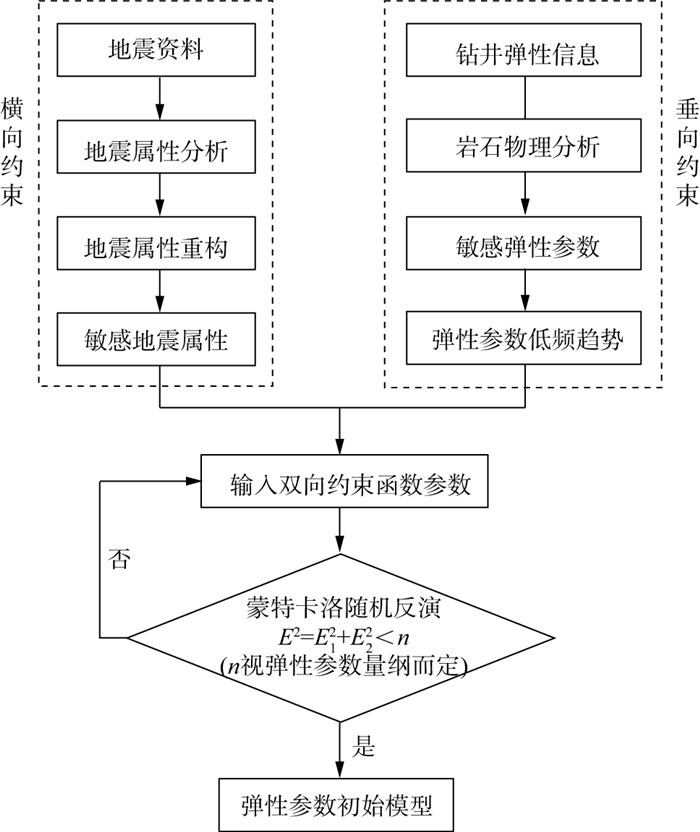
1 方法原理 1.1 目标最优双向约束建模常规地震资料通常为缺少低频成分的带限数据, 而初始低频模型的精度对于反演极为重要, 因此, 本次研究根据地震反演预测的目标(不同的岩性或流体), 将岩石物理垂向趋势与横向地震属性相结合, 实现目标最优双向建模, 技术流程如图 1所示。
|
图 1 目标最优双向约束建模流程 |
1) 通过岩石物理分析, 优选能识别预测目标的敏感弹性参数, 并结合反演算法需求, 建立靶区不同岩性的弹性参数RP趋势线[18], 其数学表达式为:
| $ R_{\mathrm{P}}=a \times \exp (b \times Z) $ | (1) |
式中: Z为埋深; a和b为不同岩性值。趋势线反映了不同岩性0~3 Hz低频信息。
2) 优选或重构符合地质沉积规律的敏感地震属性并将其作为空间约束条件。在属性优选部分, 对测井岩性弹性参数进行与地震频带相匹配的带通滤波, 获得带通弹性参数信息, 统计各种地震属性与带通弹性参数的相关性, 按照相关系数高低进行排序, 优选相关系数较高的属性。在属性重构部分, 以属性的相关系数作为该属性权重, 根据(2)式进行属性重构。
| $ A=w_0 \times A_0+w_1 \times A_1+\cdots+w_n \times A_n $ | (2) |
式中: A为空间约束属性; w表示权重; An为不同地震属性。
3) 分层统计(2)式中最大、最小值, 并映射到(1)式趋势线内, 实现双向约束建模。
| $ \begin{array}{c} R_{\mathrm{PMod}}\left(R_{\mathrm{Pmin}}, R_{\mathrm{Pmax}}, A_{\min }, A_{\max }, R_{\text {Plow }}\right)= \\ \alpha\left[R_{\mathrm{Pmin}}+\left(R_{\mathrm{Pmax} }-R_{\mathrm{Pmin}}\right)\left(A-A_{\min }\right) /\right. \\ \left.\quad\left(A_{\max }-A_{\min }\right)\right]+\beta \times R_{\text {Plow }} \end{array} $ | (3) |
式中: RPmin, RPmax为(1)式中弹性参数最小、最大值; Amin和Amax为(2)式中地震属性最小、最大值。(3)式中: [RPmin+(RPmax-RPmin)(A-Amin)/(Amax-Amin)]是将空间属性A的量纲调整为与测井岩性弹性参数RPlow一致, RPlow为测井低频弹性参数; α和β为权重系数。利用(3)式, 将空间属性A与测井低频弹性参数统一量纲后建立该弹性参数的目标最优双向模型。在实际叠前反演中所应用的纵、横波阻抗与密度低频模型均可应用该式进行目标最优双向建模。
4) 优化目标函数为:
| $ E_1^2=\sum\limits_{i=1}^M \sum\limits_{j=1}^N\left(R_{\text {PMod } i j}-R_{\text {Plow2} _{i j}}\right)^2 $ | (4) |
| $ E_2^2=\sum\limits_{i=1}^{M_1} \sum\limits_{j=1}^{N_1}\left(R_{\text {PMod } i j}-R_{\operatorname{Plow2}_ {i j}}\right)^2 $ | (5) |
| $ E^2=E_1^2+E_2^2 $ | (6) |
(4) 式为参与井双向约束模型与测井低频模型的均方根误差。(5)式为后验井双向约束模型与测井低频模型的均方根误差。其中, M, N为参与井纵、横向约束最大采样点数; M1, N1为后验井纵、横向约束最大采样点数; RPModij为(i, j)位置的RP岩性弹性参数值。给定a, b和Amin, Amax, α及β初始值和扰动区间, 利用蒙特卡洛随机反演算法寻找最优参数, 使得(6)式的误差达到最小, 从而实现高精度双向约束建模。
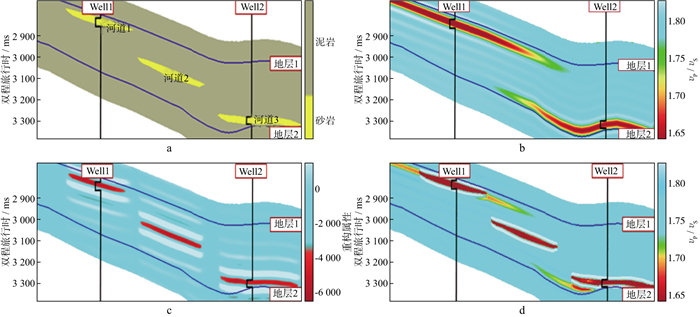
设计一个分流河道砂体模型(泥岩背景下发育三期分流河道), 如图 2a所示, 图中棕绿色为泥岩, 黄色为砂岩, 砂、泥岩弹性参数见表 1。图 2a中河道1和河道3分别被Well1井与Well2井钻遇, 河道2未被钻遇。图 2b为受层位约束的常规测井插值初始低频模型。Well1井与Well2井在砂岩段模型以低vP/vS特征为主, 泥岩段以高vP/vS特征为主。由于河道2砂体未被井钻遇, 该砂体信息受已钻井泥岩插值背景影响, 在初始低频模型上没有反应。此外, 由于常规建模多应用反距离加权方法, 该方法并不考虑岩性体边界的信息, 因此, 图 2b模型砂岩发育段横向展布特征与所设计河道砂(河道1和河道3)边界特征也不吻合。图 2c为统计岩性-属性相关性后优选重构出的岩性敏感属性, 属性低值(图 2c红色)与地质模型河道对应关系良好, 能够表达出设计模型中三期河道的信息。通过目标最优双向约束建模, 将敏感属性与弹性参数低频趋势进行综合表达, 得到图 2d的初始低频模型。相较于图 2b, 图 2d低频模型中通过敏感属性加入了河道2信息, 同时三期分流河道边界信息更为突出, 该低频模型与地质模型更为吻合。
|
图 2 分流河道砂体模型及不同方法建模得到的模型 a 分流河道砂体模型; b 常规测井插值建模; c 优选地震属性建模; d 双向最优约束建模 |
| 表 1 正演模型参数 |
基于贝叶斯理论框架的叠前三参数反演是将似然函数与先验地质信息结合, 通过求解最大后验概率来建立反演的目标函数, 进而反演弹性参数。中深层储层与围岩阻抗差异小, 反射系数能量弱, 研究表明, 三参数柯西约束比高斯约束能更好地凸显弱反射系数[19]。本次研究采用三变量柯西先验分布对反演参数进行正则化约束, 利用柯西分布长尾巴特征保护弱反射信息, 提高储层反演的预测精度。
由贝叶斯公式得到待反演弹性参数R的后验概率密度函数:
| $ P(\boldsymbol{R} \mid \boldsymbol{D})=P(\boldsymbol{D} \mid \boldsymbol{R}) P(\boldsymbol{R}) $ | (7) |
式中: P(D|R)表示似然函数; P(R)为研究区地质条件背景下的先验分布; D表示随入射角变化的叠前地震数据; R为待反演弹性参数, 在此为纵、横波及密度等相对变化量。
通常假设地震噪声服从高斯正态分布且相互独立, 似然函数可表示为:
| $ \begin{array}{l} P(\boldsymbol{D} \mid \boldsymbol{R})=\frac{1}{\delta_m^{m n}(2 \pi)^{\frac{mn}{2}}} \times \\ \;\;\;\;\;\;\;\;\exp \left[\frac{-(\boldsymbol{D}-\boldsymbol{G} \boldsymbol{R})^{\mathrm{T}}(\boldsymbol{D}-\boldsymbol{G} \boldsymbol{R})}{2 \delta_m^2}\right] \end{array} $ | (8) |
式中: G为子波矩阵; δm为噪声标准方差。
假设不同采样点参数相互独立, 采用三变量柯西分布描述三参数相对变化率的先验分布, 进一步消除三参数之间相关性, 公式为:
| $ P(\boldsymbol{R})=\frac{1}{\pi^{2 n}\left|\boldsymbol{C}_x\right|^{n / 2}} \exp \left[-2 \sum\limits_{i=1}^N \ln \left(1+\boldsymbol{R}^{\mathrm{T}} \mathit{\pmb{\Phi}}^i \boldsymbol{R}\right)\right] $ | (9) |
式中: Cx为协方差矩阵; Φi= DiTCxDi, Di为3×3n的矩阵, 其定义为:
| $ \left[\boldsymbol{D}_{p l}^i\right]=\left\{\begin{array}{cc} 1 & \text { if } p=1 \text { and } l=1 \\ 1 & \text { if } p=2 \text { and } l=i+n \\ 1 & \text { if } p=3 \text { and } l=i+2 n \\ 0 & \text { else } \end{array}\right\} $ | (10) |
将(9)式和(10)式代入(8)式, 求解最大后验概率, 得到反演目标函数:
| $ \left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+2 \boldsymbol{Q}\right) \boldsymbol{R}=\boldsymbol{G}^{\mathrm{T}} \boldsymbol{D} $ | (11) |
式中:
Zoeppritz近似式有效描述了入射纵波与反射纵波之间的关系, 且物理意义明确, 本次研究采用以阻抗形式的Fatti近似式计算纵、横波及密度反射率, 即:
| $ \begin{aligned} R(\theta)= & \frac{1}{2} r_{\mathrm{P}}(1+\tan 2 \theta)-4 \gamma^2 r_{\mathrm{S}} \sin 2 \theta- \\ & r_\rho\left(\frac{1}{2} \tan 2 \theta-2 \gamma^2 \sin 2 \theta\right) \end{aligned} $ | (12) |
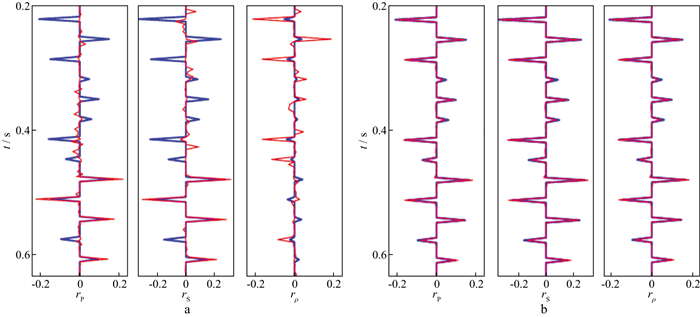
式中: rP, rS及rρ分别表示纵波阻抗、横波阻抗及密度反射率; γ表示横波与纵波速度比值。图 3显示了基于高斯约束和柯西约束的纵波阻抗、横波阻抗及密度反射率理论试算结果。其中, 图 3a为基于高斯约束, 图 3b为基于柯西约束, 蓝色为实际模型参数, 红色为两种约束下正演结果。对比可知, 三参数柯西约束反演具有更好的抗噪性, 与实际反射率吻合度更高。
|
图 3 基于高斯约束(a)、柯西约束(b)的理论试算的纵波阻抗、横波阻抗及密度反射率 |
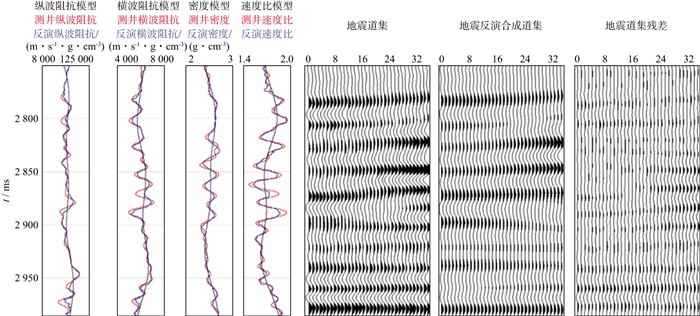
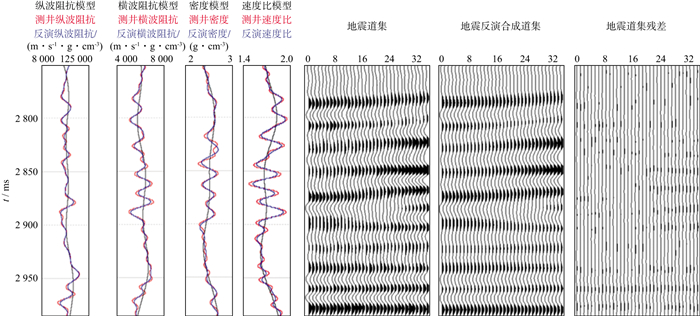
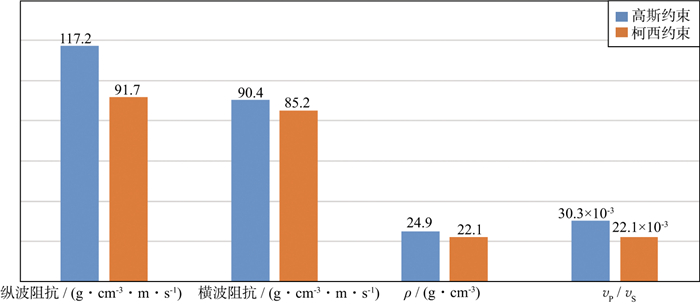
最后, 基于实际测井模型应用共轭梯度算法, 求解纵、横波阻抗、密度及纵横波速度比数据体。图 4、图 5分别为基于高斯约束和柯西约束的纵、横波阻抗、密度及纵横波速度比试算结果, 图 6为两种方法反演结果与测井曲线均方根误差统计。图 4和图 5中左侧部分红色为测井弹性参数曲线, 黑色为反演所用的初始模型曲线, 蓝色为两种约束下反演结果曲线;右侧地震道集部分第一列地震道集为利用测井曲线(左侧红色曲线)正演合成后加入20%噪声的地震道集, 第二列是基于反演结果曲线(左侧蓝色曲线)合成的地震道集, 第三列为二者残差指示反演方法的抗噪性。对比图 4和图 5可知, 对加入20%噪声的地震道集数据开展两种方法的反演, 基于柯西约束的反演纵波阻抗、横波阻抗、密度及纵横波速度比曲线均方根误差(统计目的层段2 750~2 980 ms)均小于基于高斯反演结果(图 6), 同时柯西约束结果地震道集残差更小, 表明三参数柯西约束反演具有更好的抗噪性, 与实际地震资料吻合度更高。
|
图 4 基于高斯约束方法反演的纵、横波阻抗, 密度以及纵横波速度比 |
|
图 5 基于柯西约束方法反演的纵、横波阻抗, 密度以及纵横波速度比 |
|
图 6 基于高斯约束与柯西约束反演结果与测井曲线均方根误差统计 |
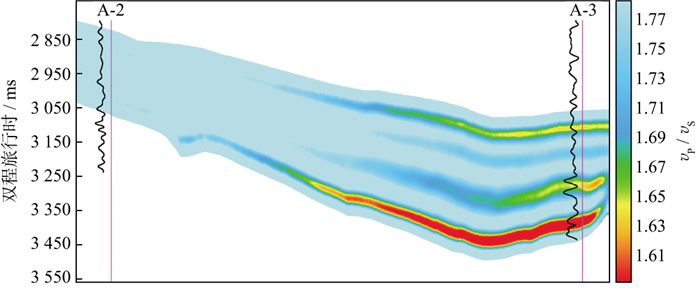
研究区位于XH凹陷斜坡带, 目的层段为受潮汐控制或潮-河联控的潮坪、三角洲沉积环境[20], 砂体横向变化快(图 7)。在海上少井条件下, 若仅利用井资料建立初始低频模型, 由于该模型仅参考地层格架进行数学横向插值, 未结合地震资料考虑砂体横向变化, 因而无法有效表征地质模式。如图 8所示, A-2井在目的层段钻遇砂体少、A-3井在目的层段钻遇砂体较多, 由于两口已钻井钻遇砂体情况差别较大, 导致井插值的初始模型不符合目的层多发育分流河道与潮道沉积的认识(图中测井曲线为滤波到地震频带的自然伽马(GR)曲线)。

|
图 7 研究区联井相分析 |
|
图 8 常规层位约束井插值初始模型(测井曲线为GR曲线) |
为解决这一问题, 我们采用了纵向岩石物理约束和横向敏感地震信息约束的目标最优双向约束建模方法。为增强建模的针对性、提高迭代计算效率, 首先通过岩石物理分析寻找岩性敏感的弹性参数, 确定相应弹性参数的数值分布范围; 再通过地震正演及井震联合分析, 搜索或重构能够反映不同岩性的敏感地震属性, 作为双向约束建模的主要属性。
图 9为目的层岩石物理分析结果, 其中图 9a为纵波阻抗与vP/vS的交会分析, 从图中可以看出, 煤层(黑色点)为低阻抗, 阻抗值小于7 000 m/s·g/cm3, 但泥岩(绿色点)和砂岩(红色点)重叠在一起, 其中泥岩的阻抗分布范围为7 000~13 000 m/s·g/cm3, 砂岩的阻抗分布范围为8 500~12 500 m/s·g/cm3。而vP/vS对岩性有较好的识别能力, 其中砂岩的vP/vS最低, 煤层最高, 泥岩居中, 结合图 9b的vP/vS频数分析, 砂岩vP/vS分布在1.500~1.655, 泥岩约为1.610~1.855, 煤层的vP/vS>1.9。因此, 可通过反演vP/vS进行岩性识别。

|
图 9 目的层岩石物理分析 a vP/vS与纵波阻抗交会分析; b 不同岩性vP/vS的阈值范围 |
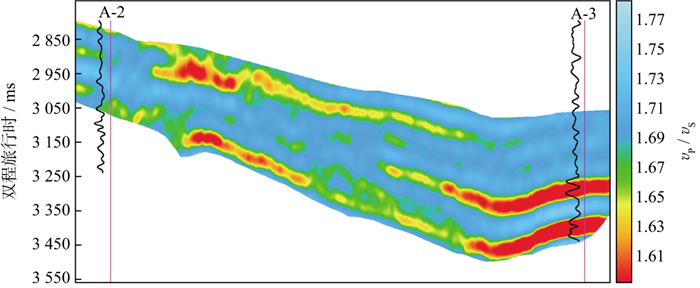
在建立初始低频模型方面, 基于最优双向建立初始模型思路首先分析研究区敏感地震属性。统计研究区含砂率与叠后地震振幅类(RMS、能量半衰时、弧长)、相位类(平均瞬时相位)、频率类(平均瞬时频率、弧长)和叠前道集(梯度RMS)等属性相关系数发现, 筛选与岩性相关性较高的敏感属性。表 2为研究区敏感地震属性统计结果, 对比表中相关系数发现, 只有梯度属性(梯度RMS)与含砂率相关性较高(0.89), 其余属性相关性均低于0.50, 因此优选该属性参与最优双向约束建模。为进一步论证梯度属性可靠性, 开展已钻井弹性参数及井旁地震信息的联合分析(图 10)。从图中可以看出, vP/vS能够较好地识别砂岩, 而梯度(AVO-G)的-90°相移为储层的敏感地震信息。因此, 分别以这两种信息为纵、横向约束的主要信息, 通过迭代建立双向约束低频模型, 如图 11所示, 双向约束建模在保留已钻井岩石物理趋势的同时, 因敏感地震属性的融入, 横向细节更丰富。
| 表 2 地震属性统计分析 |

|
图 10 敏感参数与敏感属性井震联合分析 |
|
图 11 目标最优双向约束初始模型 |
图 12为靶区主力层初始模型两种建模方法的平面属性展布结果, 其中图 12a应用常规建模方法, 图 12b应用双向约束建模方法, 相比于前者, 双向约束建模消除了常规方法简单数学内插外推的“牛眼”现象, 同时所建初始模型与该层沉积模式吻合度更高。

|
图 12 常规初始模型(a)与双向约束初始模型(b)平面属性 |
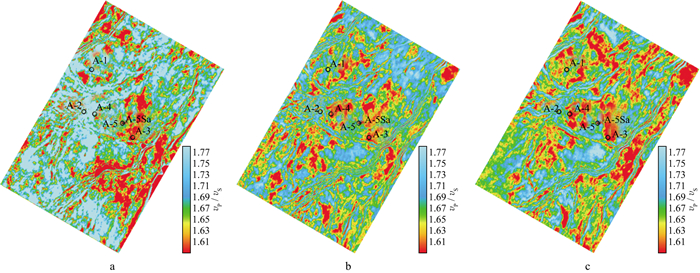
在最优双向约束模型基础上, 开展目的层段储层精细反演。根据上述岩石物理分析结果, 储层反演弹性参数为vP/vS, 其中砂体为低vP/vS特征。图 13(剖面)与图 14(平面)为基于不同初始模型和反演方法的反演结果, 其中, 图 13a和图 14a为基于常规井插值的高斯约束反演结果, 图 13b和图 14b为基于双向约束模型的高斯约束反演结果, 图 13c和图 14c为基于双向约束模型的柯西约束反演结果。对比可知, 基于常规井插值模型, 反演受A-2井富泥的影响, 存在较为典型的模型化特征, 反演结果(图 13a, 图 14a)指示A-4井处砂体不发育, 基于双向约束模型的反演(图 13b, 图 13c, 图 14b, 图 14c)较好地避免了模型化问题, 提高了横向分辨能力, 反演指示A-4井处砂体较发育, 这与A-4井的实钻结果更吻合。图 13b和图 13c分别为基于双向约束模型的高斯约束反演与柯西约束反演的结果, 对比可以看出, 柯西约束进一步提高了反演的分辨能力, A-5钻遇的薄气层柯西约束反演结果上有所指示(图 13c)。同时, 图 14c相较于图 14b砂体平面展布特征与研究区潮坪、三角洲沉积环境更为吻合, 印证了双向约束模型的柯西约束反演结果的合理性。

|
图 13 基于不同初始模型的反演结果的剖面显示(A-4、A-5/5Sa钻前预测) a 基于井插值建模的高斯约束反演; b 基于双向约束建模的高斯约束反演; c 基于双向约束建模的柯西约束反演 |
|
图 14 基于不同初始模型的目的层反演结果的平面显示(A-4、A-5/5Sa钻前预测) a 基于井插值建模的高斯约束反演; b 基于双向约束建模的高斯约束反演; c 基于双向约束建模的柯西约束反演 |
1) 常规低频建模方法多在构造或地层格架约束下将测井数据进行内插外推, 但当低勘探区钻井少且井距大时, 极易出现不符合地质模式的“牛眼”现象, 对储层识别造成较大干扰。目标最优双向约束建模方法, 综合考虑纵向岩石弹性趋势和横向岩相敏感地震信息, 相比于常规井插值建模方法, 能够提供更加符合地质规律的初始低频模型, 进而提高储层预测的横向分辨能力。
2) 针对低勘探区中深层储层与围岩阻抗差异小导致的反演预测精度低的问题, 采用基于贝叶斯理论框架的柯西约束叠前三参数反演方法, 通过三变量柯西先验分布对反演参数进行正则化约束, 相较于传统的高斯先验约束分布, 该方法利用柯西约束长尾巴特征对弱反射的保护提高了储层预测的纵向分辨能力。
3) 基于目标最优双向建模的柯西约束反演方法在XH凹陷斜坡带的应用表明, 该技术能有效提高储层纵、横向预测精度, 反演结果得到钻探证实。
| [1] |
印兴耀, 刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探, 2016, 55(3): 309-325. YIN X Y, LIU X X. Research status and progress of the seismic rock-physics modeling methods[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 309-325. |
| [2] |
TARANTOLA A. Inversion problem theory and methods for model parameter estimation[M]. Philadelphia: Society of Industrial and Applied Mathematics, 2005: 1-342
|
| [3] |
印兴耀, 曹丹平, 王宝丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34. YIN X Y, CAO D P, WANG B L, et al. Progress in fluid identification methods based on prestack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34. |
| [4] |
晓宇, 凌云, 孙德胜, 等. 叠前地震反演应用研究[J]. 石油物探, 2010, 49(4): 384-389. XI X Y, LING Y, SUN D S, et al. Application research of pre-stack seismic inversion[J]. Geophysical Prospecting for Petroleum, 2010, 49(4): 384-389. |
| [5] |
田军, 吴国忱, 宗兆云. 鲁棒性AVO三参数反演方法及不确定性分析[J]. 石油地球物理勘探, 2013, 48(3): 443-449. TIAN J, WU G C, ZONG Z Y. Robust three-term AVO inversion and uncertainty analysis[J]. Oil Geophysical Prospecting, 2013, 48(3): 443-449. |
| [6] |
林承焰, 陈仕臻, 张宪国, 等. 多趋势融合的概率体约束方法及其在储层建模中的应用[J]. 石油学报, 2015, 36(6): 730-739. LIN C Y, CHEN S Z, ZHANG X G, et al. Probability constraint method based on multiple trend integration and its application in reservoir modeling[J]. Acta Petrolei Sinica, 2015, 36(6): 730-739. |
| [7] |
PRAMANIK A G, SINGH V, et al. Estimation of effective porosity using geostatistics and multiattribute transforms: A case study[J]. Geophysics, 2004, 69(2): 352-372. |
| [8] |
HANSEN T M, MOSEGAARD K, PEDERSEN-TATALOVIC R, et al. Attribute guided well log interpolation — applied to low frequency impedance estimation[J]. Geophysics, 2008, 73(6): R83-R95. |
| [9] |
印兴耀, 周琪超, 宗兆云, 等. 基于t分布为先验约束的叠前AVO反演[J]. 石油物探, 2014, 53(1): 84-92. YIN X Y, ZHOU Q C, ZONG Z Y, et al. AVO inversion with t-distribution as priori constraint[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 84-92. |
| [10] |
张丰麒, 金之钧, 盛秀杰, 等. 贝叶斯三参数低频软约束同步反演[J]. 石油地球物理勘探, 2016, 51(5): 965-975. ZHANG F Q, JIN Z J, SHENG X J, et al. Bayesian prestack three-term inversion with soft low-frequency constraint[J]. Oil Geophysical Prospecting, 2016, 51(5): 965-975. |
| [11] |
印兴耀, 王慧欣, 曹丹平, 等. 利用三参数AVO近似方程的深层叠前地震反演[J]. 石油地球物理勘探, 2018, 53(1): 129-135. YIN X Y, WANG H X, CAO D P, et al. Three term AVO approximation of Kf-fm-pand prestack seismic inversion for deep reservoir[J]. Oil Geophysical Prospecting, 2018, 53(1): 129-135. |
| [12] |
BULAND A, OMRE H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(1): 185-198. |
| [13] |
DOWNTON J E. Seismic parameter estimation from AVO inversion[M]. Calgary: University of Calgary, 2005: 1-371
|
| [14] |
RUSSELL B H, GRAY D, HAMPSON D P. Linearized AVO and poroelastic[J]. Geophysics, 2011, 76(3): C19-C29. |
| [15] |
ALEMIE W, MAURICIO D. High-resolution three-term AVO inversion by means of a Trivariate probability distribution[J]. Geophysics, 2011, 76(1): R43-R55. |
| [16] |
张世鑫, 印兴耀, 张繁昌. 基于三变量柯西分布先验约束的叠前三参数反演方法[J]. 石油地球物理勘探, 2011, 46(5): 737-743. ZHANG S X, YIN X Y, ZHANG F C. Prestack three term inversion method based on Trivariate Cauchy distribution prior constraint[J]. Oil Geophysical Prospecting, 2011, 46(5): 737-743. |
| [17] |
张丰麒, 魏福吉, 王彦春, 等. 基于精确Zoeppritz方程三变量柯西分布先验约束的广义线性AVO反演[J]. 地球物理学报, 2013, 56(6): 2098-2115. ZHANG F Q, WEI F J, WANG Y C, et al. Generalized linear AVO inversion with the priori constraint of trivariate Cauchy distribution based on Zoeppritz equation[J]. Chinese Journal of Geophysics, 2013, 56(6): 2098-2115. |
| [18] |
李阿伟, 孙东生, 王红才. 致密砂岩波速各向异性及弹性参数随围压变化规律的实验研究[J]. 地球物理学进展, 2014, 29(2): 754-760. LI A W, SUN D S, WANG H C. Seismic anisotropy and elastic parameter of tight sandstone with confining pressure[J]. Progress in Geophysics, 2014, 29(2): 754-760. |
| [19] |
袁焕, 王宇超, 石兰亭, 等. 一种基于修正Cauchy分布的高分辨率AVO三参数反演方法[J]. 岩性油气藏, 2011, 23(6): 93-96. YUAN H, WANG Y C, SHI L T, et al. A high resolution three-parameter AVO inversion method based on modified Cauchy distribution[J]. Lithologic Reservoirs, 2011, 23(6): 93-96. |
| [20] |
王泽宇, 徐清海, 侯国伟, 等. 东海陆架盆地西湖凹陷W井区平湖组潮汐沉积模式[J]. 海相油气地质, 2021, 26(2): 159-169. WANG Z Y, XU Q H, HOU G W, et al. Tidal depositional model of Pinghu Formation in well W area of Xihu Sag, East China Sea Shelf Basin[J]. Marine Origin Petroleum Geology, 2021, 26(2): 159-169. |



