2. 中国石化弹性波理论与探测技术重点实验室, 北京 100083;
3. 中国石油化工股份有限公司石油勘探开发研究院, 北京 102206
2. Sinopec Key Laboratory of Seismic Elastic Wave Technology, Beijing 100083, China;
3. Sinopec Exploration and Production Research Institute, Beijing 102206, China
我国致密砂岩气地质资源量为17.4×1012~25.1×1012 m3, 可采储量为8.8×1012~12.1×1012 m3[1], 目前已形成四川盆地须家河组和鄂尔多斯盆地上古生界等2个致密砂岩气大气区。自2009年以来, 四川盆地须家河组天然气勘探潜力逐渐引起关注[2-5], 该致密砂岩储层成层性明显且具有储层厚度薄的特点, 优质储层的单层厚度在4~9 m。使得基于精确Zoeppritz方程和相应近似正演模拟不再适用于致密砂岩薄储层。这是因为Zoeppritz方程只适用于单一反射界面, 对于层状模型, 尤其是含有薄互层的储层, 地震记录中的多次波、转换波和透射损失等更为复杂, Zoeppritz方程难以适用。
为解决上述问题, 需要能模拟薄储层波场响应的正演模拟算法。反射率法使用了波动方程的解析解, 可模拟层内的复杂波场响应, 包括反射波、透射波、转换波和多次波。MALLICK等[6]和KENNETT[7-8]指出, 虽然反射率法基于一维模型假设, 但由于采用了波动方程的解析解, 因此该类方法比有限差分法等正演方法有更高的模拟精度且计算速度更快。FUCHS[9]首次提出将反射率法用于合成地震记录, 该方法可模拟层内的复杂地震波场响应, 包括反射波、透射波、转换波和多次波。在此基础上, KENNETT等[7-8, 10-11]首次提出了用于计算层状地层的总反射和透射系数的递归算法, 该方法的特点是对所有频率和慢度无条件稳定。为提高计算速率, PHINNEY等[12]在KENNETT研究成果的基础上提出了快速反射率法, 即将原有的反射率法进行重组, 实现矢量化, 使计算速度提高了约20倍。YANG等[13]基于反射率法推导了针对单薄层的二阶近似公式, 并利用递归算法将其推广到薄互层。
在地震叠前反演方面, 国内外学者已经尝试将反射率法用于薄储层AVA反演。SEN等[14]比较了KENNETT的反射率法与快速反射率法, 并建立基于Gauss-Newton的反演方法用于叠前波形反演。王建花[15]在层参数等效的情况下, 推导了P波入射到单薄层时的波场能量再分配的简化公式, 并进行了初步的P波反演试验。在这些研究中, 反演均是在截距时间和射线参数域(即τ-p域)进行的。然而, 当可用偏移距数据较少时, τ-p域变换会受到混叠现象的影响。为了避免混叠现象, MALLICK等[16]建议可生成角道集与实际道集数据相匹配。LIU等[17]针对P波AVA反演, 提出基于快速反射率法的Bayesian反演方法。YANG等[18]基于快速反射率法对PP波进行反演, 并在反演中考虑到稀疏约束。LIU等[19]提出基于快速反射率法的遗传算法, 用于AVA叠前联合反演。尽管已有多位学者发表相关文章, 但受到公式本身复杂性的制约, 基于反射率法的叠前反演并没有被广泛应用, 仍需要进一步的研究。
本文将基于快速反射率法的AVA反演应用于致密砂岩储层。在快速反射率法理论的基础上, 利用Gauss-Newton法建立目标函数。为了估计弹性参数(纵波和横波速度以及密度), 目标函数是通过角度域中模拟数据和观测数据之间的最小差异实现。最后, 分别使用薄互层模型和实际数据进行基于反射率法的反演, 并与基于精确Zoeppritz方程的反演方法进行比较, 结果表明, 基于快速反射率法的反演结果与真实值更加接近。
1 技术方法 1.1 反射系数的计算KENNETT[7-8]推导出了反射率法的迭代公式, 可以计算目标区域的总反射系数及总透射系数, 包括多次波和转换波等。为提高运算速度, PHINNEY等[12]对KENNETT[7-8]反射率法进行了改进, 将最内层的循环改为计算频率, 并拓展到整个频率域, 实现矢量化, 不仅加快了计算速度, 还能实现对弹性参数偏导数的解析计算, 提高了后续反演工作的精度和效率。据PHINNEY等[12]的研究成果, 频率域PP波的总反射系数公式可以写为:
| $ R(p, \omega)=\frac{\boldsymbol{v}_{04}}{\boldsymbol{v}_{01}} $ | (1) |
式中: p为慢度; ω为角频率; v01、v04分别为数组v0的第1个和第4个元素; v0为PHINNEY基于Haskell-Dunkin minor matrix方法在慢度-频率域(p, ω)定义的含有6个元素的数组, 则有:
| $ \begin{array}{l} \boldsymbol{v}_0= \\ {\left[\begin{array}{llllll} \Delta & -R_{\mathrm{PS}} \Delta & -R_{\mathrm{SS}} \Delta & R_{\mathrm{PP}} \Delta & R_{\mathrm{SP}} \Delta & \operatorname{det} R \Delta \end{array}\right]^{\mathrm{T}}} \\ \end{array} $ | (2) |
式中: Δ为比例系数; Rij(i=P或S, j=P或S)为对应波类型的总反射系数; detR为反射系数行列式。
v0可以通过递归法计算得到:
| $ \boldsymbol{v}_0=\boldsymbol{Q}_0 \boldsymbol{Q}_1 \cdots \boldsymbol{Q}_n \cdots \boldsymbol{Q}_{N-1} \boldsymbol{v}_N $ | (3) |
其中, vN为初始项。
| $ \boldsymbol{v}_{N}=\left[\begin{array}{llllll} 1 & 0 & 0 & 0 & 0 & 0 \end{array}\right]^{\mathrm{T}} $ | (4) |
Qn为地层n的传播矩阵。
| $ \boldsymbol{Q}_n=\boldsymbol{E}_n \boldsymbol{F}_n $ | (5) |
式中: En为层穿越矩阵, 描述了平面波在第n层地层中传播时相位的移动; Fn为界面矩阵。En和Fn可以具体写为:
| $ \boldsymbol{E}_n=\operatorname{diag}\left[\mathrm{e}^{-\mathrm{i} \omega d_n\left(q_n^{\mathrm{P}}+q_n^{\mathrm{S}}\right)}\right.\;\;\;1 \;\;\;\mathrm{e}^{-\mathrm{i} \omega d_n\left(q_n^{\mathrm{P}}-q_n^{\mathrm{S}}\right)} \quad \mathrm{e}^{\mathrm{i} \omega d_n\left(q_n^{\mathrm{P}}-q_n^{\mathrm{S}}\right)}\;\;\;1\;\;\;\left.\mathrm{e}^{\mathrm{i} \omega d_n\left(q_n^{\mathrm{P}}+q_n^{\mathrm{S}}\right)}\right] $ | (6) |
| $ \boldsymbol{F}_n=\boldsymbol{T}_n^{\boldsymbol{- 1}} \boldsymbol{T}_{n+1} $ | (7) |
式中: qP, qS分别为纵波、横波的垂直慢度; Tn源自Dunkin矩阵, 是第n层大小为6×6的矩阵, 与频率无关, 依赖于第n层的水平慢度p和弹性参数, 具体形式可以参看PHINNEY等[12]的文献。
1.2 反演原理本文的反演基于Gauss-Newton法, 其核心思想是利用快速反射率法计算层状地层PP波反射系数, 最大程度地模拟目标地震记录, 以此来估算目标区域的弹性参数(纵波速度α, 横波速度β和密度ρ)。为得到合适的模型参数, 使得模型响应和观测数据的差异最小, 反演的目标函数定义为:
| $ Q(M)=\left\|\mathit{\pmb{\Phi}}-\mathit{\pmb{\Phi}}^{\mathrm{obs}}\right\|^2 $ | (8) |
式中: M=(α, β, ρ)为模型弹性参数向量; Φobs为实际地震记录; Φ为模拟地震记录。
需要注意的是, 这里使用的Φobs和Φ均为时间域角道集, 而本文所述的快速反射率法在慢度-频率域计算反射系数, 因此需要进行域的转换。由慢度-频率域转换到时间-角度域的过程可以分成以下两个步骤:
1) 慢度转换为角度。在反射系数R(p, ω)的计算中有3个循环, 即最外层循环是慢度p, 中间循环为层循环(n)和最内层循环为频率循环。一般来说, 慢度在每一个最外层循环上是固定的, 入射角在每一层上都会发生变化, 即θn=arcsin(αnp)。但将入射角设置在最外层循环, 每层的慢度都会发生变化, 因此, 通过公式(9), R(p, ω)被重采样为R(θ, ω), 最后得到角度道集。
| $ p_n=\frac{\sin \theta}{\alpha_n} $ | (9) |
式中: 下角标n表示第n层。
2) 频率域转到时间域。类比FRYER[20], KENNETT[7-8]的处理方法, 对反射系数做一次逆Fourier变换, 最终得到截距时间-角度域(τ-θ)的反射系数为:
| $ R(\tau, \theta)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} R(\theta, \omega) \mathrm{e}^{\mathrm{i} \omega t} \mathrm{~d} \omega $ | (10) |
得到时间-角度域的反射系数后, 地震记录Φ可以通过反射系数R与子波W的褶积得到。
| $ \mathit{\pmb{\Phi}}=\boldsymbol{W} * \boldsymbol{R} $ | (11) |
给定符合假设条件的初始模型M0(能反映出地层的大致形态), 利用Gauss-Newton法[21-24], 模型的更新参数公式可以写为:
| $ \Delta \boldsymbol{M}=\left[\boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}\right]^{-1} \boldsymbol{J}^{\mathrm{T}}\left(\mathit{\pmb{\Phi}}-\mathit{\pmb{\Phi}}^{\text {obs }}\right) $ | (12) |
式中: J为雅可比矩阵。
| $ \boldsymbol{J}=\frac{\partial(\boldsymbol{W} * \boldsymbol{R})}{\partial \boldsymbol{M}}=\boldsymbol{W} * \frac{\partial \boldsymbol{R}}{\partial \boldsymbol{M}} $ | (13) |
通过迭代ΔM更新初始弹性参数向量M0直到目标函数Q足够小, 得到反演结果。公式(12)的难点在于其不稳定性, 这里应用Levenberg-Marquardt方法修改公式(12), 得到:
| $ \Delta \boldsymbol{M}=[\boldsymbol{H}+\lambda \boldsymbol{I}]^{-1} \boldsymbol{J}^{\mathrm{T}}\left(\mathit{\pmb{\Phi}}-\mathit{\pmb{\Phi}}^{\mathrm{obs}}\right) $ | (14) |
式中: H = JTJ, 为海森矩阵; λ为比例系数; I为单位矩阵。
根据公式(10)和公式(13), 雅可比矩阵J具体可以写为:
| $ \boldsymbol{J}=\boldsymbol{W} * \frac{1}{2 \pi} \int_{-\infty}^{\infty} \frac{\partial \boldsymbol{R}(\omega, \theta)}{\partial \boldsymbol{M}_n} \mathrm{e}^{\mathrm{i} \omega t} \mathrm{~d} \omega $ | (15) |
其中,
| $ \frac{\partial \boldsymbol{R}(\omega, \theta)}{\partial \boldsymbol{M}_n}=\frac{\boldsymbol{v}_{01} \frac{\partial \boldsymbol{v}_{04}}{\partial \boldsymbol{M}_n}-\boldsymbol{v}_{04} \frac{\partial \boldsymbol{v}_{01}}{\partial \boldsymbol{M}_n}}{\left(\boldsymbol{v}_{01}\right)^2} $ | (16) |
其中, v0对Mn的偏导数为:
| $ \frac{\partial \boldsymbol{v}_0}{\partial \boldsymbol{M}_n}=\boldsymbol{Q}_0 \boldsymbol{Q}_1 \cdots \frac{\partial\left(\boldsymbol{Q}_{n-1} \boldsymbol{Q}_n\right)}{\partial \boldsymbol{M}_n} \cdots \boldsymbol{Q}_{N-1} \boldsymbol{v}_N $ | (17) |
其中,
| $ \frac{\partial\left(\boldsymbol{Q}_{n-1} \boldsymbol{Q}_n\right)}{\partial \boldsymbol{M}_n}=\frac{\partial \boldsymbol{Q}_{n-1}}{\partial \boldsymbol{M}_n} \boldsymbol{Q}_n+\boldsymbol{Q}_{n-1} \frac{\partial \boldsymbol{Q}_n}{\partial \boldsymbol{M}_n} $ | (18) |
| $ \frac{\partial \boldsymbol{Q}_n}{\partial \boldsymbol{M}_n}=\frac{\partial \boldsymbol{E}_n}{\partial \boldsymbol{M}_n} \boldsymbol{F}_n+\boldsymbol{E}_n \frac{\partial \boldsymbol{F}_n}{\partial \boldsymbol{M}_n} $ | (19) |
式中: Mn代表第n层的α, β, ρ。
对于Fn的偏导数具体可以写为:
| $ \frac{\partial \boldsymbol{F}_n}{\partial \boldsymbol{M}_n}=\frac{\partial \boldsymbol{T}_n^{-1}}{\partial \boldsymbol{M}_n} \boldsymbol{T}_{n+1}+\boldsymbol{T}_n^{-1} \frac{\partial \boldsymbol{T}_{n+1}}{\partial \boldsymbol{M}_n} $ | (20) |
其中,
| $ \frac{\partial \boldsymbol{T}_{n+1}}{\partial \boldsymbol{M}_n}=\left\{\begin{array}{l} \frac{\partial \boldsymbol{T}_{n+1}}{\partial \alpha} \\ \frac{\partial \boldsymbol{T}_{n+1}}{\partial \beta} \\ \frac{\partial \boldsymbol{T}_{n+1}}{\partial \rho} \end{array}\right. $ | (21) |
En对M的偏导数可以求出解析解, 具体可以写成以下形式:
| $ \frac{\partial \boldsymbol{E}_n}{\partial \boldsymbol{M}_n}=\left\{ {\begin{array}{*{20}{l}} {\frac{\partial \boldsymbol{E}_n}{\partial \alpha}=\frac{\mathrm{i} \omega d_n}{\alpha} \operatorname{diag} \left[ {A \mathrm{e}^{-\mathrm{i} \omega d_n\left(q^{\mathrm{P}}+q^{\mathrm{S}}\right)}\;\;\;\;0\;\;\;B \mathrm{e}^{-\mathrm{i} \omega d_n\left(q^{\mathrm{P}}-q^{\mathrm{S}}\right)}\;\;\;-B \mathrm{e}^{\mathrm{i} \omega d_n\left(q^{\mathrm{P}}-q^{\mathrm{S}}\right)}\;\;\;0\;\;\; -A \mathrm{e}^{\mathrm{i} \omega d_n\left(q^{\mathrm{P}}+q^{ \mathrm{S}}\right)} } \right] }\\ { \frac{\partial \boldsymbol{E}_n}{\partial \beta}=\frac{\mathrm{i} \omega d_n}{q^{\mathrm{S}} \beta^3} \operatorname{diag}\left[ { \mathrm{e}^{-\mathrm{i} \omega d_n\left(q^{\mathrm{P}}+{ }q^{\mathrm{S}}\right)}\;\;\;\;0\;\;\;-\mathrm{e}^{-\mathrm{i} \omega d_n\left(q^{\mathrm{P}}-q^{\mathrm{S}}\right)}\;\;\;\mathrm{e}^{\mathrm{i} \omega d_n(q^{\mathrm{P}}-q^{\mathrm{S}})}\;\;\;0\;\;\;-\mathrm{e}^{\mathrm{i} \omega d_n\left(q^{\mathrm{P}}+q^{\mathrm{S}}\right)} } \right] \frac{\partial \boldsymbol{E}_n}{\partial \rho}=0 } \end{array}} \right. $ | (22) |
式中: A=qP-p2/qS, B=qP+p2/qS。
为了加快计算速度, 按照与PHINNEY[12]相似的方法, 将E对M的偏导数拓展到整个频率域。假定频率是等间隔分布, 将维数定义为频率域的点个数NF, 此时将E拓展到整个频域, 变成一个维数是6*NF的复数数组
| $ \boldsymbol{g}_n^{\prime}=\left[\begin{array}{lllll} \frac{\omega_m}{\omega_{m-6} s_n^{+}} & 0 & \frac{\omega_m}{\omega_{m-6} s_n^{+}} & \frac{\omega_m s_n^{-}}{\omega_{m-6}} & 0 \end{array}\right]\\ m=7, 13, \cdots, 6 *\left(N_F-1\right)+1 $ | (23) |
其中,
通过初始值(初始频率所对应的
| $ \begin{array}{l} {\left[\begin{array}{c} \hat{E}_m \\ \hat{E}_{m+1} \\ \vdots \\ \hat{E}_{m+5} \end{array}\right]=\left[\begin{array}{c} g_n^{\prime}(1) \\ g_n^{\prime}(2) \\ \vdots \\ g_n^{\prime}(6) \end{array}\right]\left[\begin{array}{c} \hat{E}_{m-6} \\ \hat{E}_{m-5} \\ \vdots \\ \hat{E}_{m-1} \end{array}\right]} \\ m=7, 13, \cdots, 6 *\left(N_F-1\right)+1 \end{array} $ | (24) |
在E拓展后, 对应的v0也需要做同样的拓展, 拓展方法可参考PHINNEY[12]。
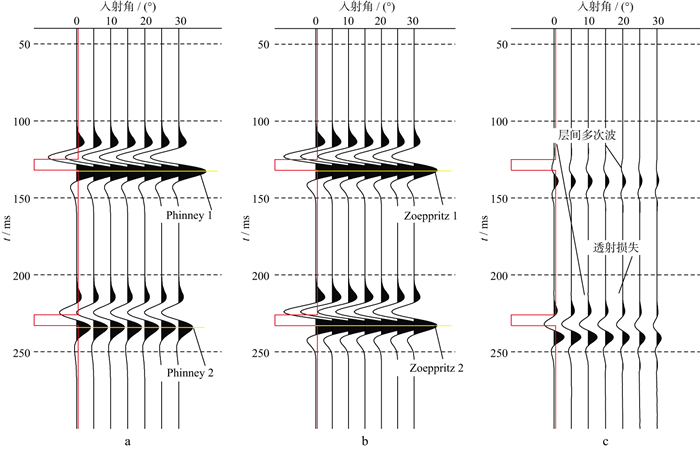
2 模型测试 2.1 反射系数对比鉴于实际地层中薄层不能单独存在的原因, 为验证快速反射率法在AVA建模和反演中的有效性, 采用多层模型测试其中薄层的AVA曲线特点, 模型参数如表 1所示。PP波合成角道集由快速反射率法和精确Zoeppritz方程分别进行模拟, 子波采用40 Hz的Ricker子波。与基于精确Zoeppritz方程的AVA道集相比(图 1), 基于快速反射率法的AVA道集包含更完整的信息, 例如图 1c中所示的多次波。这是因为使用精确Zoeppritz方程的合成地震记录没考虑多次波, 可能会导致解释和反演中出现错误。反射率法考虑了波在地层中传播时的传播效应, 可以计算传播过程中所有的反射系数, 由于现有的地震资料处理技术难以在不影响初级反射振幅的情况下去除波在地层中的传播效应, 如透射损失、层间多次波和几何扩散等, 因此, 采用快速反射率法可以更逼真地模拟地震记录。
| 表 1 等厚模型参数 |
|
图 1 PP波AVA道集对比(红色曲线代表P波速度) a 基于快速反射率法的AVA道集; b 基于精确Zoeppritz方程的AVA道集; c 两种方法模拟的AVA道集之间的差异 |
为了进一步显示快速反射率法和精确Zoeppritz方程方法之间的差异, 沿图 1中黄线位置提取瞬时振幅随入射角的变化数值, 如图 2所示。受到传播效应的影响, 使用快速反射率法计算两个界面的振幅随深度的增加而逐渐减小, 比使用Zoeppritz方程模拟的振幅小, 主要是由于该方法考虑了波在传播时的透射损失。而基于Zoeppritz方程计算的AVA曲线不会随深度的变化而变化。如果在地震数据处理程序中未正确校正传输损耗和层间多次波, 则不建议基于Zoeppritz进行正演模拟, 利用快速反射率法模拟的道集将与现场数据更匹配。
2.2 薄互层模型反演将薄互层模型的单个薄层的厚度设置为8 m, 具体参数如表 2所示。利用快速反射率法计算反射系数时, 频率的计算范围为0~125 Hz, 合成地震记录所用子波为40 Hz Ricker子波, 采样率为1ms。考虑到实际数据的角道集数据入射角范围通常较窄, 该薄互层模型角道集的角度范围是5°~30°, 如图 3a所示。图 3b为对地震记录添加15%随机噪声后的地震记录。此外, 该模型为深度域模型, 后续反演得到的模型更新量是时间域模型, 需将深度域模型转换到时间域(PP波时间域), 各个界面对应于表 2中的双程旅行时。
| 表 2 薄互层模型参数 |

|
图 3 薄互层模型PP波角道集记录(入射角为5°~30°, 红色曲线为纵波速度) a 不加噪声的地震记录; b 添加15%噪声的地震记录 |
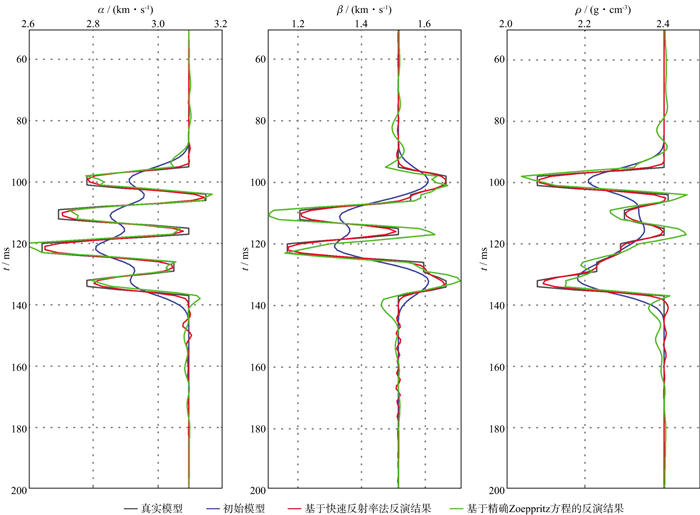
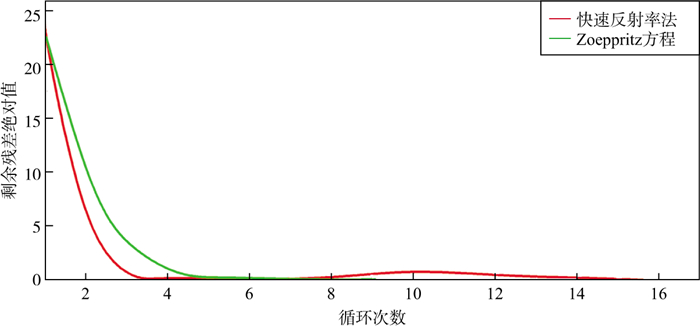
以平滑后的真实模型为初始模型, 反演的目标数据为图 3所示地震记录。分别采用基于快速反射率法和精确Zoeppritz的反演方法进行反演, 反演结果如图 4所示。由反演结果可以看出, 基于快速反射率法的反演结果基本与真实值重合。而基于Zoeppritz方程的反演结果会有一些波动, 与地震记录中的多次波有关。图 5为反演迭代次数收敛曲线, 红色为基于快速反射率法的收敛曲线; 绿色为基于Zoeppritz方程的收敛曲线。若是将收敛精度定义在剩余误差绝对值小于1时反演收敛, 那么基于快速反射率法的反演在迭代3次后收敛, 基于Zoeppritz方程的反演在迭代4次后收敛。
|
图 4 基于快速反射率法和精确Zoeppritz方程的反演结果 |
|
图 5 不添加噪声的薄互层模型AVA反演迭代次数收敛曲线 |
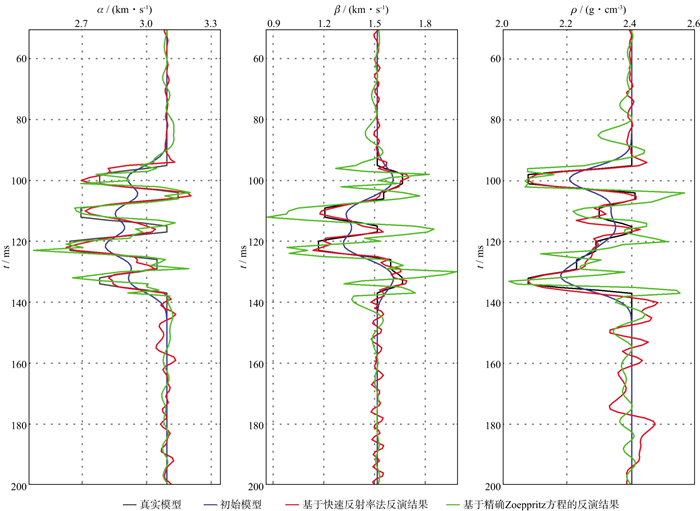
与之前的反演类似, 均以平滑模型为初始模型, 图 6为两种反演方法的反演结果。受地震记录中随机噪声的影响, 两种反演方法的反演结果中均含有随机噪声。但是在目标层位置处, 特别是单独的PP波反演, 反演结果仍然能较好地反演地层的真实参数。同时, 基于快速反射系数法的反演结果更逼近于真实值, 说明该方法具有更强的抗噪性。
|
图 6 基于快速反射率法和精确Zoeppritz方程的反演结果(对模型地震记录添加15%随机噪声后) |
需要强调的是, 这里的模拟地震记录包含层间多次波, 并考虑了透射损失, 因此将该方法应用到实际数据的时候, 实际数据含透射损失和多次波。此外, 本反演方法没有反演地层厚度参数, 未讨论厚度对反演结果的影响, 这要求使用的初始模型能大体反应地层厚度的变化。
3 应用实例实际数据选自四川某工区, 其目的层段为须家河组的须三段。由于龙门山造山带北段和西部山系的持续隆升, 造成须三段沉积时期盆地边缘大量沉积物快速堆积, 物源以近南北向为主, 在盆地中央深处发育湖相沉积, 目的层岩性组合为致密砂岩、泥岩互层, 埋深4 000~5 000 m。
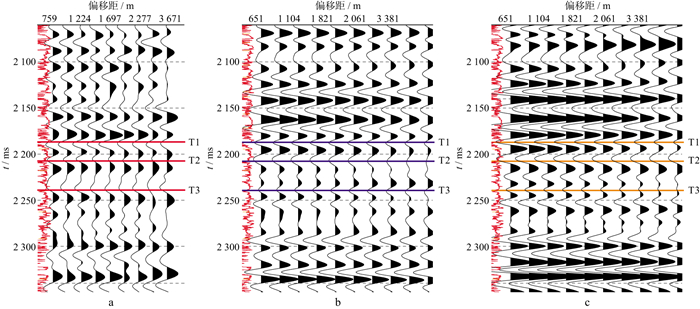
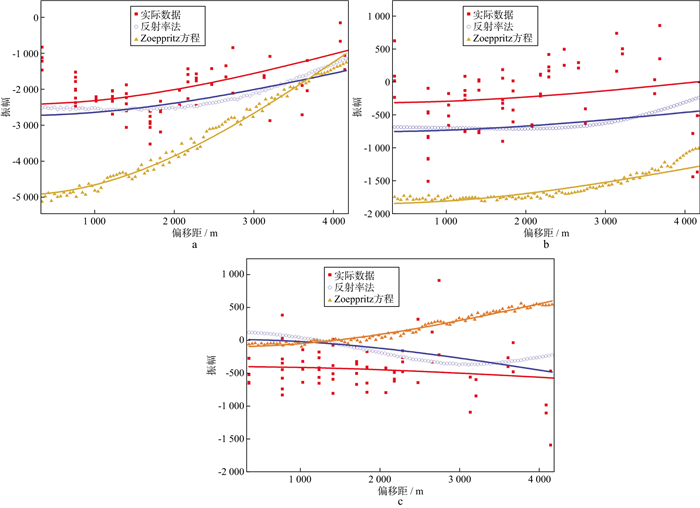
在应用本文反演方法之前, 首先, 要确保数据已经被合理地处理过。由于反射率法在计算反射系数时会考虑透射损失以及多次波, 因此地震数据处理时, 可以不用考虑透射损失以及多次波的处理。其次, 利用井数据做正演模拟, 然后对地震数据进行标定, 这个过程是将井数据(深度域)与地震数据(时间域)进行对应, 对于该数据, 标定是基于商业软件完成, 所以标定的过程是在Zoeppritz方程的基础上完成的。标定完成后, 模拟的地震记录与实际数据之间的相似度约0.78。基于Zoeppritz和基于反射率法的合成地震记录与实际数据的对比如图 7所示, 为了更细致地观察二者的区别, 在图 7中选3个时间点(T1, T2, T3)提取AVO曲线, AVO曲线对比如图 8所示。由图 8可以看出, 无论是数据振幅的幅值, 还是AVO曲线的走向趋势, 均是基于反射率法的地震记录与实际地震记录更加接近。最后是初始模型的选择, 将实际测井数据限频后的曲线作为初始模型, 频率的选取范围为0~60 Hz。需要注意的是, 反射率法的基本假设条件是数据为局部一维数据或是水平层状。结合叠前时间偏移, 该方法可以适用于地质条件简单的地区。在地质条件复杂的地区, 需要进行叠前时间偏移或逆时偏移。本文数据因经过叠前偏移处理, 所以是水平地层的剖面。
|
图 7 井旁地震道及不同方法合成地震记录(红色曲线为纵波速度测井曲线) a 实际地震数据; b 基于快速反射率法的合成地震记录; c 基于Zoeppritz方程的合成地震记录 |
|
图 8 图 7中T1, T2, T3位置处的AVO曲线对比(散点代表振幅数据点; 曲线代表回归曲线) a T1时间; b T2时间; c T3时间 |
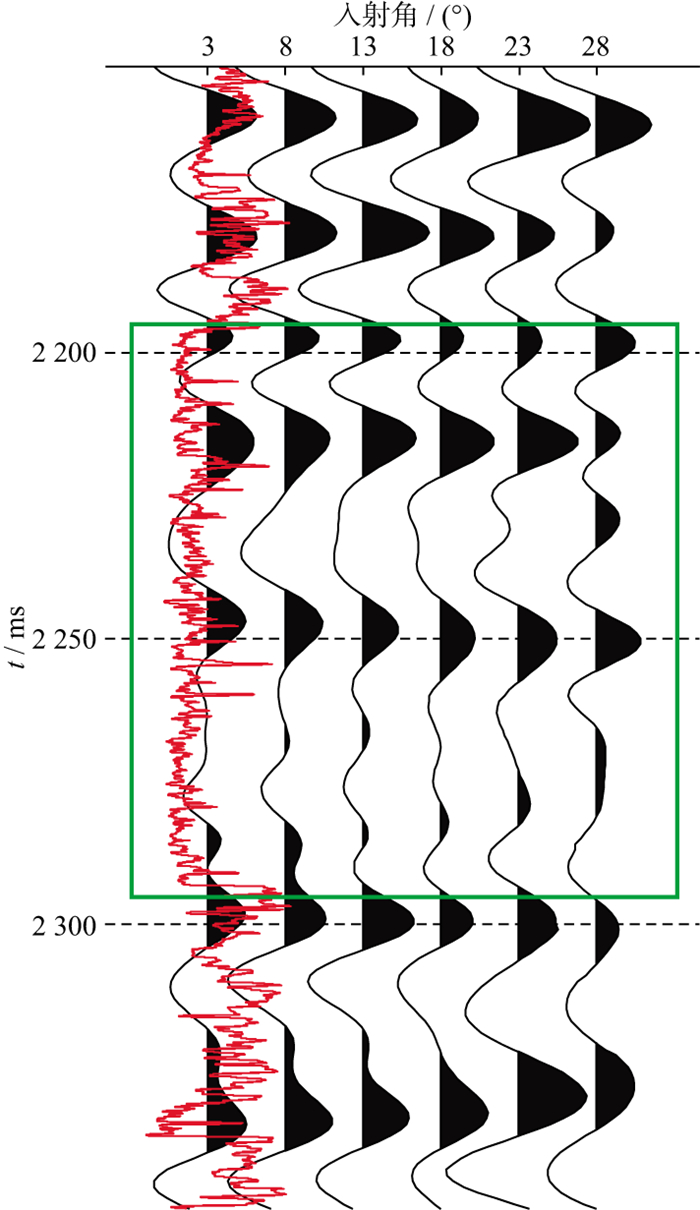
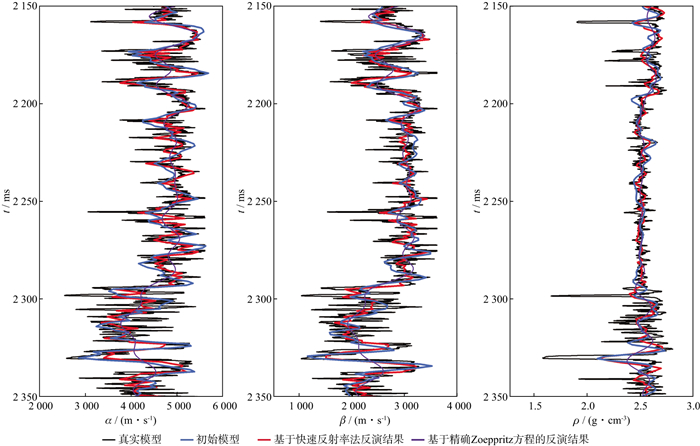
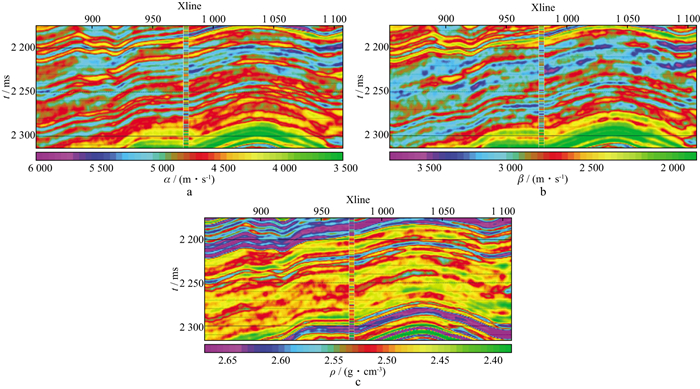
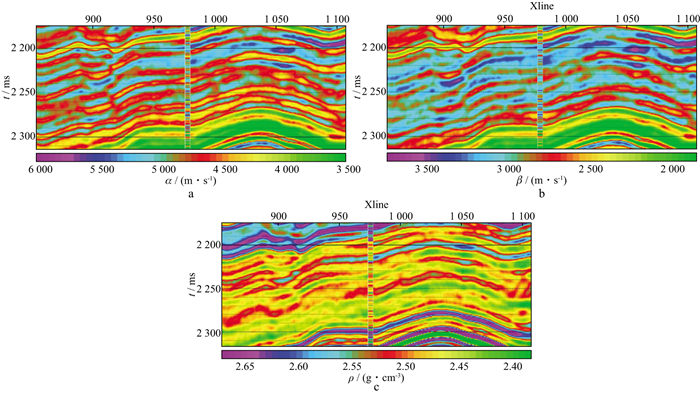
为了验证基于反射率法反演的优越性, 分别基于精确Zoeppritz方程和反射率法对实际资料进行AVA反演。反演的目标区是2 150~2 350 ms, 井旁角道集数据如图 9所示。共有6个角道集, 范围为3°~28°。该区域主要的地层特征为砂泥岩互层, 图中绿色方框所圈出区域为目标层段。图 10为井旁道地震数据反演结果, 由反演结果可以看出, 基于反射率法的反演结果与测井曲线更加贴合, 能显示出更多的细节。值得注意的是, 相对于纵波速度反演结果, 横波速度和密度的反演结果相对较差, 这是因为反射系数公式本身对纵波速度更加敏感[25]。图 11和图 12分别为过井的基于快速反射率法和基于精确Zoeppritz方程的反演剖面。反演中所使用的子波需要对每个入射角分别提取。尽管受到地震分辨率的限制, 反演结果与测井相比频率较低, 但从反演结果可以看出, 基于反射率法的反演结果要更接近于测井曲线, 能更准确地反映地层变化的趋势, 对识别有效的致密砂岩储层非常有帮助。
|
图 9 目标区域井旁角道集(红色曲线为伽马测井曲线; 绿色的方框为目标层) |
|
图 10 井旁道反演结果对比 |
|
图 11 基于反射率法的反演结果 a 纵波速度反演结果; b 横波速度反演结果; c 密度反演结果 |
|
图 12 基于Zoeppritz方程的反演结果 a 纵波速度反演结果; b 横波速度反演结果; c 密度反演结果 |
讨论了基于快速反射率法的叠前反演理论, 展示了其在致密砂岩储层中的应用效果。该反演是在时间-角度域而不是τ-p域中实现, 从而避免了积分变换中的混叠。
实际地震数据与基于快速反射率法和精确Zoeppritz方程合成地震记录的比较, 证明在地震数据的幅值及AVO曲线趋势方面, 基于快速反射率法的模拟结果与实际地震记录更加接近。
模型数据的反演结果表明, 基于快速反射率法的反演方法收敛速度更快且具有一定的抗噪能力。此外, 基于快速反射率法的反演结果更加准确。实际数据的反演结果显示, 基于快速反射率法的反演结果在精度和连续性方面优于基于精确Zoeppritz方程的反演结果。
虽然展示了PP波反演的应用结果, 但该反演方法也可应用于PP和PS波的联合反演, 这需对正演模拟算子进行修改, 并考虑如何匹配PP波和PS波。需要强调的是, 反演前的处理过程应包括与地表相关的多次波衰减、几何扩展补偿等, 但应排除透射损失补偿和层间多次波。
| [1] |
贾承造, 郑民, 张永峰. 中国非常规油气资源与勘探开发前景[J]. 石油勘探与开发, 2012, 39(2): 129-136. JIA C Z, ZHENG M, ZHANG Y F. Unconventional hydrocarbon resources in China and the prospect of exploration and development[J]. Petroleum Exploration and Development, 2012, 39(2): 129-136. |
| [2] |
郭彤楼, 张汉荣. 四川盆地焦石坝页岩气田形成与富集高产模式[J]. 石油勘探与开发, 2014, 41(1): 28-36. GUO T L, ZHANG H R. Formation and enrichment mode of Jiaoshiba shale gas field, Sichuan Basin[J]. Petroleum Exploration and Development, 2014, 41(1): 28-36. |
| [3] |
王志刚. 涪陵页岩气勘探开发重大突破与启示[J]. 石油与天然气地质, 2015, 36(1): 1-6. WANG Z G. Breakthrough of Fuling shale gas exploration and development and its inspiration[J]. Oil and Gas Geology, 2015, 36(1): 1-6. |
| [4] |
赵文智, 卞从胜, 徐春春, 等. 四川盆地须家河组须一、三和五段天然气源内成藏潜力与有利区评价[J]. 石油勘探与开发, 2011, 38(4): 385-393. ZHAO W Z, BIAN C S, XU C C, et al. Assessment on gas accumulation potential and favorable plays within the Xu-1, 3 and 5 Members of Xujiahe Formation in Sichuan Basin[J]. Petroleum Exploration and Development, 2011, 38(4): 385-393. |
| [5] |
赵正望, 谢继容, 李楠, 等. 四川盆地须家河组一、三、五段天然气勘探潜力分析[J]. 地质勘探, 2013, 33(6): 23-28. ZHAO Z W, XIE J R, LI N, et al. Gas exploration potential of the 1st, 3ed and 5th members of Xujiahe Fm reservoirs in the Sichuan Basin[J]. Geology Exploration, 2013, 33(6): 23-28. |
| [6] |
MALLICK S, ADHIKAR S. Amplitude-variation-with-offset and prestack-waveform inversion: A direct comparison using a real data example from the Rock Springs Uplift, Wyoming, USA[J]. Geophysics, 2015, 80(2): B45-B59. |
| [7] |
KENNETT B L N. Seismic wave propagation in stratified media[M]. Cambridge: Cambridge University Press, 1983: 1-350.
|
| [8] |
KENNETT B L N. Seismic wave propagation in stratified media[M]. Canberra: ANU E Press, 2009: 1-298.
|
| [9] |
FUCHS K. The reflection of spherical waves from transition zones with arbitrary depth-dependent elastic moduli and density[J]. Journal of Physics of Earth, 1968, 16(S1): 27-41. |
| [10] |
KENNETT B L N. Reflections, rays and reverberations[J]. Bulletin of the Seismological Society of America, 1974, 64(6): 1685-1696. |
| [11] |
KENNETT B L N, KERRY N J. Seismic waves in a stratified half space[J]. Geophysical Journal of the Royal Astronomical Society, 1979, 57(3): 557-583. |
| [12] |
PHINNEY R A, ODOM R I, FRYER G J. Rapid generation of synthetic seismograms in layered media by vectorization of the algorithm[J]. Bulletin of the Seismological Society of America, 1987, 77(6): 2218-2226. |
| [13] |
YANG Z, LU J. Second-order approximation of the seismic reflection coefficient in thin interbeds[J]. Energies, 2020, 13(6): 1465. |
| [14] |
SEN M K, ROY I G. Computation of differential seismograms and iteration adaptive regularization in prestack waveform inversion[J]. Geophysics, 2003, 68(6): 2026-2039. |
| [15] |
王建花. 叠前弹性参数反演新方法[D]. 青岛: 中国海洋大学2006 WANG J H. A new method on prestack elastic parameters inversion[D]. Qingdao: Ocean University of China, 2006 |
| [16] |
MALLICK S, FRAZER L N. Practical aspects of reflectivity modeling[J]. Geophysics, 1987, 52(10): 1355-1364. |
| [17] |
LIU H X, LI J Y, CHEN X H, et al. Amplitude variation with offset inversion using the reflectivity method[J]. Geophysics, 2016, 81(4): R185-R195. |
| [18] |
YANG Z, LU J. Thin interbed AVA inversion based on a fast algorithm for reflectivity[J]. Acta Geophysica, 2020, 68(1): 1007-1020. |
| [19] |
LIU W, WANG Y C, LI J Y, et al. Prestack AVA joint inversion of PP and PS waves using the vectorized reflectivity method[J]. Applied.Geophysids, 2018, 15(3/4): 448-465. |
| [20] |
FRYER G J. A Slowness approach to the reflectivity method of seismogram synthesis[J]. Geophysical Journal International, 1980, 63(3): 747-758. |
| [21] |
TARANTOLA A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(10): 1893-1903. |
| [22] |
SHEEN D H, TUNCAY K, BAAG C E, et al. Time domain Gauss-Newton seismic waveform inversion in elastic media[J]. Geophysical Journal International, 2006, 167(3): 1373-1384. |
| [23] |
LU J, YANG Z, WANG Y, et al. Joint PP and PS AVA seismic inversion using exact Zoeppritz equations[J]. Geophysics, 2015, 80(5): R23-R250. |
| [24] |
LU J, WANG Y, CHEN J, et al. Joint anisotropic AVO inversion of PP and PS seismic data[J]. Geophysics, 2018, 83(2): N31-N50. |
| [25] |
LUO C, BA J, CARCIONE J M, et al. Joint PP and PS pre-stack seismic inversion for stratified models based on the propagator matrix forward engine[J]. Surveys in Geophysics, 2020, 41(5): 987-1028. |




