作为渤海油田的主力探区, 渤南探区历经近50年的勘探, 发现了一批大中型油气田, 贡献了渤海油田近1/4的产量[1]。但随着渤南探区勘探程度越来越高, 大中型油田发现难度越来越大。为寻求勘探突破, 渤南探区的勘探方向由成熟的构造油气藏转向更为复杂的岩性油气藏, 并选择莱北地区作为岩性油气藏勘探的主攻方向[2]。莱北地区新近系地层埋深较浅(800~1 500 m), 主要表现为高孔低胶结特征, 该区断裂和气云发育, 现有地震资料频带范围有限、保幅性差, 导致难以有效判断储层发育模式, 严重制约了探区岩性勘探进程, 亟需提高地震资料的成像品质。
在岩性勘探领域, 国内外学者已进行了大量研究。邸志欣等[3]针对复杂岩性油气藏提出了高精度、高密度地震采集技术, 该技术在胜利油田多个工区的应用显著提高了原始地震资料的品质。马光克等[4]针对分辨率低的地震资料, 采用多次波联合建模、四维插值规则化及精细的地震速度分析技术, 提高了地震分辨率, 并使得砂体接触关系更加清晰。王艳冬等[5]针对浅水区宽频处理问题, 研发了针对τ-p域鬼波和浅水多次波的压制技术。冯波等[6]针对岩性勘探中层析反演计算精度不足的问题, 提出了一种特征波反射层析反演方法, 有效提升了建模精度和计算效率。徐嘉亮等[7]针对层析反演计算效率低的问题, 建立剩余时差与剩余速度之间的关系, 在保证建模精度的同时有效提高了计算效率。徐德奎等[8]针对大型气云发育区成像质量问题, 模拟了多种地震采集方法及不同因素的影响, 为海上气云区采集观测系统设计提供了重要的参考依据。夏同星等[9]针对渤海湾盆地气云区发育问题, 研究了Q值层析反演气云区能量吸收衰减补偿技术, 解决了气云区地震能量吸收衰减严重的问题。TENG等[10]利用基于Q吸收补偿的叠前深度偏移成像来消除气云屏蔽的影响。李振春等[11]针对常规反Q偏移方法存在的稳定性问题, 提出在反演框架下求解黏声介质成像问题的方法, 有效改善了成像结果分辨率及精度。匡斌等[12]针对实际地震资料子波不确定性问题以及深度偏移速度场不够精确的问题, 利用三维自适应最小二乘逆时偏移技术, 改善了复杂断块的成像质量。目前, 针对渤海油田岩性油气藏勘探面临的难题研究相对较少, 实际地震资料处理面临诸多挑战。
本文针对渤海气云发育区高孔低胶结地层地震资料品质差的问题, 以研究区地质情况和现有拖缆地震资料为基础, 首先结合正演模拟分析了处理难点, 然后针对浅水环境下多次波压制、气云发育区速度建模、浅层Q值估算以及保幅偏移成像等影响地震资料成像的主控因素进行了一系列关键技术的探索和研究, 最终形成了渤海浅水环境下气云发育区高孔低胶结地层地震资料成像策略, 该策略有效改善了地震资料成像品质, 并在渤海莱北地区A油田取得良好的应用效果。
1 地震资料处理难点莱北地区位于渤海南部海域, 紧邻黄河口富生烃凹陷, 油源充足, 主要目的层新近系为曲流河和浅水三角洲沉积, 河流相砂体发育, 储盖组合较好。储层以大型复合河道砂体为主, 孔隙度高(平均孔隙度约为35%), 胶结程度低, 地层疏松[1-2]。这种高孔低胶结地层对地震波具有极强的衰减效应, 从而导致地震资料频带窄、保幅性差。莱北地区砂体受上覆气云等复杂地质体的屏蔽和散射效应影响, 导致地震速度横向变化快, 地震资料信噪比低, 构造及砂体成像质量差(图 1中红色框所示), 给地震资料处理带来极大挑战, 主要表现在以下3个方面。
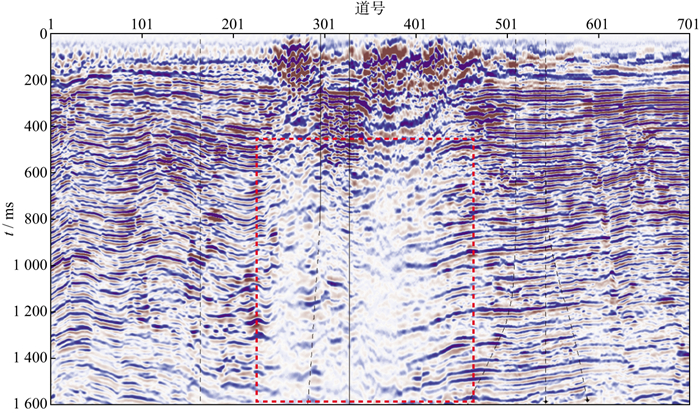
|
图 1 莱北地区过气云发育区地震剖面 |
1) 海上地震勘探采集的资料中存在大量的多次波, 它们与有效反射波相互混叠, 导致有效反射波波形发生变化, 地震资料信噪比和保幅性降低。其中, 与海面和海底相关的鬼波和浅水多次波的旅行时与有效反射波的旅行时差异较小, 故难以有效压制鬼波和浅水多次波。
2) 受浅层气云的影响, 地震资料信噪比明显降低, 甚至出现异常强反射或空白反射, 通常进行反射波初至拾取时, 在气云区内和远离气云区的远偏移距处初至拾取不准确, 与实际地震资料初至误差大, 导致求取的速度模型不准确, 进而影响最终速度模型的精度。
3) 高孔低胶结地层对地震波具有强烈的吸收衰减作用, 尤其是高频反射波能量衰减严重, 导致地震资料有效信息缺失, 成像结果保幅性差, 岩性圈闭识别困难。
2 方法技术针对上述难点, 本文系统研究了浅水环境下气云发育区高孔低胶结地层的地震资料处理技术, 形成了浅水环境下气云发育区高孔低胶结地层地震资料成像策略, 有效提高了渤海气云发育区高孔低胶结地层地震资料的成像质量。
2.1 浅水环境下多次波压制方法海洋地震勘探采集资料中鬼波和浅水多次波发育, 导致地震资料波组关系混乱, 地震资料有效频带变窄, 相位发生变化, 严重影响后续储层发育模式的判别[13]。从图 2可知, 鬼波的存在导致地震子波相位发生明显改变, 低频能量缺失(图 2b中绿色箭头所示); 浅水多次波的存在使得地震子波出现“拖尾”现象, 频谱出现“陷波”现象(图 2b中红色箭头所示)。因此, 开展鬼波和浅水多次波压制工作, 恢复和拓展地震资料频带尤为必要。
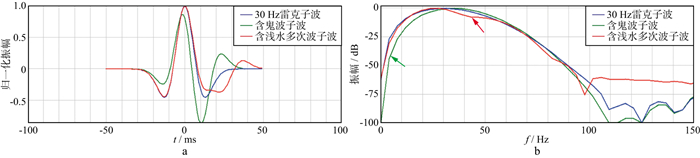
|
图 2 时间域子波(a)及对应频谱(b) |
反鬼波算子的求取通常与采集记录的电缆深度相关, 但受海浪、潮汐等影响, 采集记录的电缆深度与实际电缆沉放深度误差较大, 导致鬼波压制结果中出现明显的噪声(图 3a红色箭头所示)。因此, 本文根据残差能量最小准则, 求取准确的电缆沉放深度和海水反射系数, 进而得到精确的反鬼波算子。图 3b为采用精确反鬼波算子得到的鬼波压制结果, 压制后的地震资料信噪比明显提升。
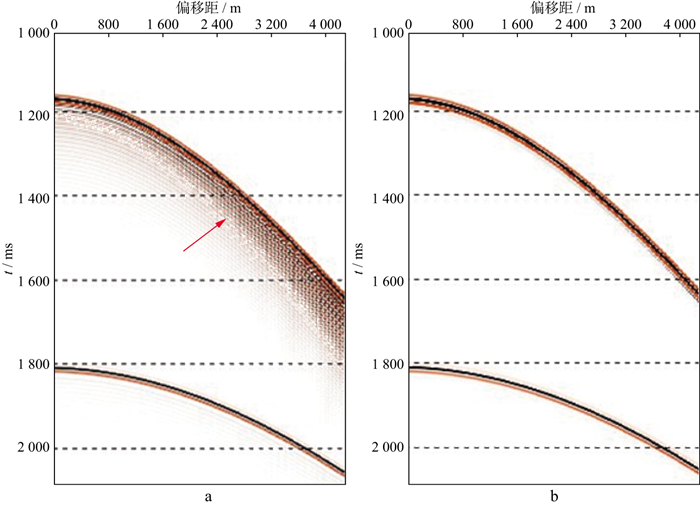
|
图 3 水平层状模型数据的鬼波压制结果 a 常规鬼波压制结果; b 采用精确反鬼波算子的鬼波压制结果 |
由于渤海平均水深仅为18 m, 最大水深不超过40 m, 属于极浅水环境, 海底反射与直达波混叠, 因而常规自由表面多次波衰减方法(surface-related multiple elimination, SRME)难以有效压制浅水多次波[14]。基于水层(自由表面下的海水层)模型的格林函数浅水多次波预测方法克服了常规方法在浅水多次波预测中的不足, 无需识别海底反射, 利用采集过程中记录的水深和速度信息建立水体模型, 能够更准确地预测出浅水多次波[15]。
在建立准确水层模型的基础上, 构建含有角度信息的双程格林函数, 对构建的格林函数与原始地震记录进行计算, 获得各地震道在目标地震道产生的浅水多次波预测结果, 再对预测结果进行叠加即可获得浅水多次波预测结果:
| $ M\left(x_r, x_s ; \omega\right)=\sum\limits_{x_r} G_0\left(x_r, x_k ; \omega\right) D\left(x_k, x_s ; \omega\right) $ | (i) |
式中: M为预测的浅水多次波; G0为格林函数; D为地震记录; xr为接收点位置; xs为震源点位置; xk为目标地震道位置; ω为角频率。
并非上述所有的地震道计算结果对目标道浅水多次波的预测结果都有贡献, 冗余的数据将会导致预测结果信噪比降低, 而且计算和叠加全部地震道所需的运算量大, 对内存要求高。因此, 本文采用菲涅尔带约束方法筛选出对目标地震道处浅水多次波有贡献的地震道, 而后进行地震数据的优势加权叠加, 从而得到预测精度更高、计算效率更高的浅水多次波预测结果:
| $ M\left(x_r, x_s ; \omega\right)=\sum\limits_{x_i}^{x_j} G_0\left(x_r, x_k ; \omega\right) D\left(x_k, x_s ; \omega\right) $ | (2) |
式中: xi和xj分别为菲涅尔带范围内的起、止地震道位置。
从图 4所示的浅水多次波预测结果可以看出, 采用常规方法得到的浅水多次波预测结果信噪比低, 存在明显的线性噪声(图 4b中红色箭头所示), 而采用菲涅尔带约束方法得到的浅水多次波预测结果信噪比明显提升。在此基础上, 对原始地震记录与预测的浅水多次波结果进行自适应相减, 最终得到波组关系有效改善的压制结果。
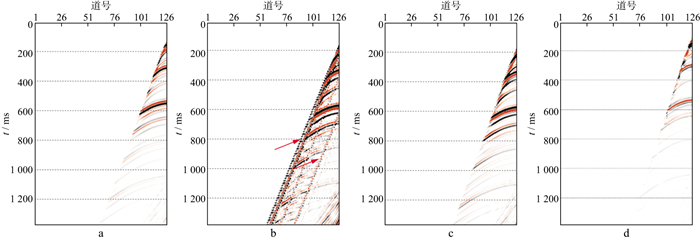
|
图 4 浅水多次波压制效果 a 含浅水多次波记录; b 采用常规方法得到的浅水多次波预测结果; c 采用菲涅尔带约束方法得到的浅水多次波预测结果; d 浅水多次波压制结果 |
由于莱北地区目的层为新近系, 主要反射信息多为近偏移距数据, 射线密度不足, 且受气云影响, 利用反射波层析方法反演得到的浅层速度存在较大的不确定性, 进而影响最终速度模型的精度[16]。回转波在地震记录上总是以初至波的形式出现, 易于拾取, 并且射线密度能够满足反演需求, 因此利用回转波层析能够较为准确地反演浅层速度模型。分析莱北地区实际地质条件可知, 浅层主要为薄互层, 回转波发育。因此, 本文提出了采用回转波与反射波联合层析的速度建模方法, 首先利用回转波层析反演建立浅层速度模型, 并将该模型作为反射波层析初始模型进一步更新中、深层速度, 然后多次反演迭代, 最终获得高精度速度模型。
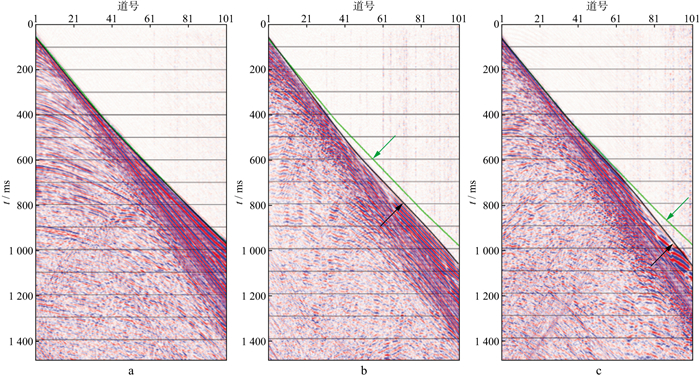
作为一种初至波层析建模的方法, 回转波层析反演利用回转波走时和路径, 反演介质速度结构。该方法不仅适用于纵向连续沉积的介质模型, 还适应于横向变化和速度倒转的介质模型, 即对复杂模型有较好的适应性[17]。从图 5可以看出, 非气云区地震资料信噪比高, 初至拾取准确, 而在气云区内和气云区附近的远偏移距地震资料信噪比低, 初至拾取困难。由于自动拾取方法受地震资料信噪比影响较大, 导致图 5b和图 5c中初至拾取不准确(图 5中绿色箭头所示为初至自动拾取结果), 与实际地震资料初至误差大, 这会导致后期求取的速度模型不准确。因此, 在气云发育区附近进行了精细初至拾取, 人工调整后, 得到了更加准确的拾取结果, 从图 5中人工调整后的拾取结果(黑色箭头所示)可以看出, 无论是信噪比高的非气云区还是信噪比低的气云区, 初至拾取结果均较为准确, 与实际地震资料的旅行时相符合, 这也为获得精度更高的浅层回转波层析反演结果奠定了基础。
|
图 5 单炮记录拾取结果 a 非气云区单炮记录; b 气云区单炮记录; c 气云区附近单炮记录 |
回转波与反射波联合层析速度建模方法的具体流程如下: 首先, 对叠前时间偏移速度场进行时深转换得到初始的深度域速度模型; 然后利用回转波层析得到较为准确的浅层速度场; 再结合工区内典型的构造层位信息建立地质模型; 而后将回转波层析得到的浅层速度场与地质层位进行融合, 得到浅层速度较为准确的层速度模型; 在此基础上, 对中、深层进行沿层速度拾取和分析, 利用反射波层析反演迭代修改速度-深度模型, 最终获得精度更高的速度模型。上述方法具有地质格架约束含义, 能够表达复杂的地质模型, 所建立的地质模型受地质构造约束, 具有地质意义, 故方法具有较强的稳定性。
上述速度建模方法在浅层采用回转波层析方法, 保证了浅层速度模型的准确性; 在中、深层采用沿地质层位的反射波层析反演方法, 控制了速度模型的低频趋势。该方法既保留了回转波反演得到的高精度浅层模型, 又在中、深层体现了地质格架约束的特征, 最终得到的速度模型整体精度高。
2.3 基于复谱分解的井震联合Q值估算技术谱比法是常用的Q值估计方法, 但该方法要求地震反射子波为非调谐平稳信号, 而实际地震资料中的反射子波为调谐非平稳信号, 故利用该方法难以获得准确的储层顶、底反射。因此将时频分析技术引入到Q值估计中, 以获得更加准确的地震反射子波振幅谱。短时傅里叶变换、S变换和小波变换等常规时频分析方法的稳定性和聚焦性仍存在一定不足, 在薄互层处的时频谱误差仍较大。复谱分解方法的理论基础是基于非平稳地震褶积模型反演得到的时频谱, 可以用于去除子波的影响, 还可以在一定程度上降低薄层调谐的影响[18]。
复谱分解方法是一种高分辨率地震信号时频分析方法, 该方法将谱分解描述为一个线性反演问题, 然后采用稀疏约束正则化策略求解该线性反演问题, 最终得到一个具有高时频分辨率的时频谱[19]。该高分辨率稀疏反演复谱分解方法的数学模型公式为:
| $ \boldsymbol{A} \boldsymbol{x}+\boldsymbol{n}=\left(\begin{array}{llll} \boldsymbol{W}_1 & \boldsymbol{W}_2 & \cdots & \boldsymbol{W}_N \end{array}\right)\left(\begin{array}{c} \boldsymbol{r}_1 \\ \boldsymbol{r}_2 \\ \vdots \\ \boldsymbol{r}_N \end{array}\right)+\boldsymbol{n}=\boldsymbol{s} $ | (3) |
式中: s表示地震记录; Wi表示以频率fi为主频的与频率相关的复子波褶积矩阵; ri表示与Wi相对应的与频率相关的复反射系数; N表示参与计算的频率个数, 且i=1, 2, …, N; A表示复子波卷积矩阵库; x表示与频率相关的复反射系数矩阵; n表示随机噪声。
(3) 式是一个欠定问题, 为了降低解的不确定性并获得稀疏的时频谱, 需要对x执行稀疏约束, 进而转化为基追踪去噪问题进行求解, 即:
| $ \min\limits_{x \in \mathbb{C} n}\|\mathit{\boldsymbol{x}}\|_1+\frac{1}{2 \mu}\|A x-s\|_2^2 $ | (4) |
式中: 权重参数μ>0, 用于在最小化过程中控制(4)式中前、后两项的相对权重; ||·||22表示L2范数;
我们采用高效、稳健的交替方向算法(alternating direction method, ADM)求解无约束基追踪去噪问题以实现复谱分解。首先引入辅助变量υ∈
| $ \min\limits_{x \in \mathbb{C}^n, v \in \mathbb{C}^m}\left\{\|x\|_1+\frac{1}{2 \mu}\|v\|_2^2: \boldsymbol{A} \boldsymbol{x}+\boldsymbol{v}=\boldsymbol{s}\right\} $ | (5) |
由图 6中合成信号的时频分析结果可以看出, 复谱分解得到的时频谱比连续小波变换(continuous wavelet transform, CWT)方法得到的时频谱分辨率更高, 这也为后续Q值估计打下了坚实基础。

|
图 6 合成信号的时频分析结果 a 合成信号; b 连续小波变换结果; c 复谱分解结果 |
然后利用复谱分解方法求取初始时频谱CSD(t0, f), 并根据地震波在均匀介质中传播的衰减规律, 可获得衰减振幅谱计算公式:
| $ C_{\mathrm{SD}}(t, f)=A(t) C_{\mathrm{SD}}\left(t_0, f\right) e^{\frac{-\pi f\left(t-t_0\right)}{Q}} $ | (6) |
式中: t为时间; t0为初始时间; f为频率; Q为品质因子; CSD(t0, f)为地震信号的初始振幅谱; A(t)为与时间相关的因子。对(6)式两边取自然对数, 可得:
| $ \begin{gathered} \ln \left[C_{\mathrm{SD}}(t, f)\right]=\frac{-1}{Q} \cdot\left[\pi f\left(t-t_0\right)\right]+ \\ \ln \left[C_{\mathrm{SD}}\left(t_0, f\right)\right]+\ln [A(t)] \end{gathered} $ | (7) |
为了方便计算、减少计算时间, 我们采用降维的方法, (7)式可进一步化简为以频率f为自变量的一次函数:
| $ y(\chi)=-\frac{\pi}{Q} \cdot \chi+C $ | (8) |
式中: y(χ)表示频谱比值; χ=(t-t0)·f; C表示常量。
最后, 我们对数据进行拟合, 采用最小平方法估算Q值:
| $ J=\left\|y+\frac{1}{Q} x\right\|_2^2 \rightarrow \min $ | (9) |
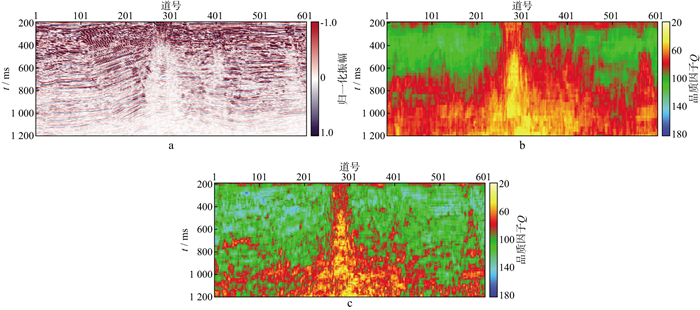
式中: J为目标函数。再利用典型井的最佳匹配Q曲线, 对根据地震资料求取的Q值数据体(简称Q体)进行数值校正, 使Q体的数值精度在合理的范围内, 从而得到井震匹配的最佳Q体并用于后续的黏声逆时偏移成像处理。图 7a所示为过气云发育区地震剖面, 图 7b和图 7c分别为利用连续小波变换方法和复谱分解方法求取的Q剖面, 可以看出, 利用复谱分解方法求取的Q剖面分辨率更高, 与地震剖面中气云发育区吻合更好。
|
图 7 地震剖面与实际Q剖面 a 过气云发育区地震剖面; b 利用连续小波变换方法求取的Q剖面; c 利用复谱分解方法求取的Q剖面 |
通常, 我们对地震数据进行反Q滤波处理以补偿吸收衰减, 但这种处理方法基于一维波反向传播, 故只需要一维Q模型。实际上, 地震波的吸收衰减不仅与传播时间相关, 还与速度场的分布、子波的频率、地下构造、射线路径等多个因素有关系, 仅利用反Q滤波方法进行一维补偿显然不能准确处理实际地质情况[20]。因为地震波场的衰减和相位频散是在地震波传播过程中发生的, 所以在基于波动方程的叠前深度偏移过程中, 补偿这些影响更加准确。因此, 本次研究采用了黏声介质逆时偏移成像技术。
假设地下介质为黏声介质, 并且地震波在地下介质中传播时衰减并频散, 为了反映成像过程中吸收衰减的影响, 需要改进黏声介质的平面波解, 即声介质的平面波解乘以一个指数衰减项A, 它是衰减系数和传播距离的函数。地震波由震源激发、传播到反射层并被反射到检波点处, 地震波在黏声介质中传播时, 在下行和上行过程中受黏性累积的影响, 检波点处接收到的波场为:
| $ \widetilde{R}(x, t)=A_{\mathrm{D}} A_{\mathrm{U}} R(x, t) $ | (10) |
式中:
在黏声介质中, 正向传播的震源波场在反射点处为ADS(x, t), 反向传播的检波点波场R(x, t)经补偿后在反射点处为AU-1ADAUR(x, t), 若要达到振幅补偿的目的, 或者实现完全的振幅补偿, 可以在反向延拓过程中补偿检波点处的波场, 令震源波场为AD-1S(x, t), 此时有:
| $ \tilde{I}(x)=\int_0^T A_{\mathrm{D}}^{-1} S(x, t) A_{\mathrm{D}} R(x, t) \mathrm{d} t $ | (11) |
式中:
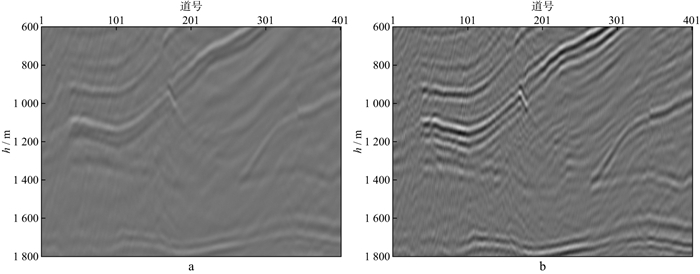
对某吸收衰减模型分别进行常规逆时偏移和黏声介质逆时偏移, 结果如图 8所示, 虽然常规方法和黏声介质逆时偏移方法均能对构造形态进行成像, 但是随着深度逐渐增加, 吸收衰减作用越来越明显, 常规逆时偏移成像剖面中能量逐渐减弱, 而黏声介质逆时偏移成像剖面中整体能量均衡, 而且剖面中同相轴的分辨率也得到了明显的提高。
|
图 8 逆时偏移成像剖面 a 常规逆时偏移; b 黏声介质逆时偏移 |
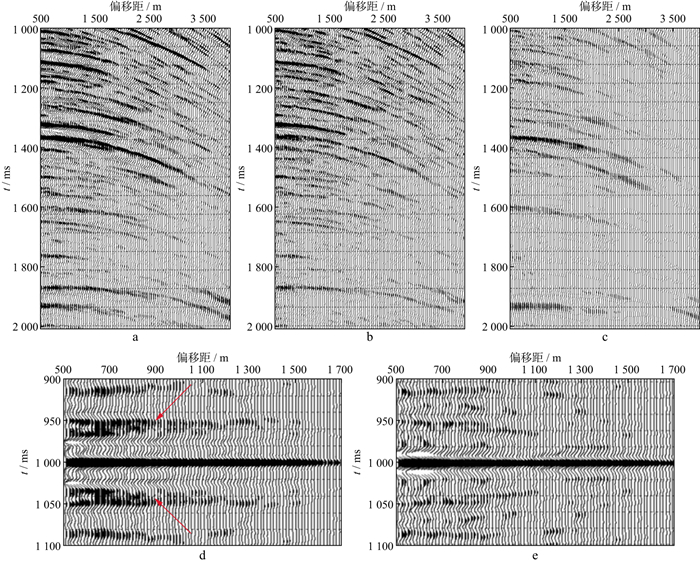
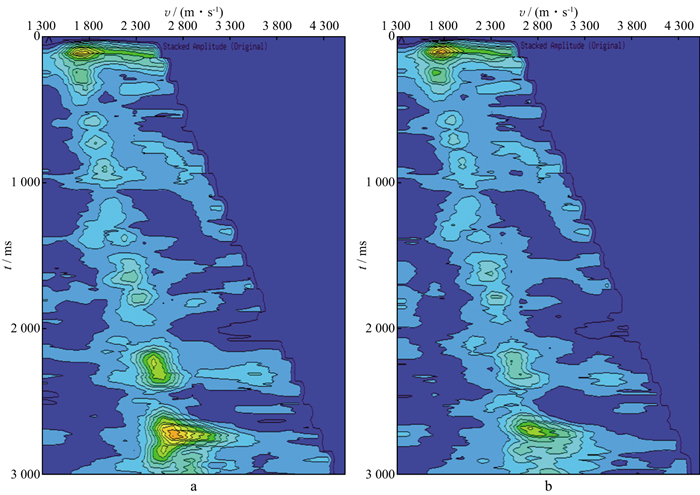
渤海莱北地区A油田主要目的层段为典型的气云发育区高孔低胶结地层, 平均水深约为18 m, 拖缆地震采集得到的地震资料中鬼波和浅水多次波发育。针对该问题, 首先进行了鬼波和浅水多次波压制。如图 9所示, 鬼波和浅水多次波压制后的地震资料波组特征明显改善, 波组关系更明确, 自相关剖面中有效反射能量更加集中, 周期性多次波得到了很好的压制(图 9d中红色箭头所示)。图 10a中鬼波和浅水多次波压制前的速度谱能量团横向聚焦性差, 图 10b中鬼波和浅水多次波压制后的速度谱能量团更加聚焦。
|
图 9 鬼波和浅水多次波压制前、后的地震资料 a 压制前单炮记录; b 压制后单炮记录; c 压制的多次波; d 压制前自相关剖面; e 压制后自相关剖面 |
|
图 10 鬼波和浅水多次波压制前(a)、后(b)速度谱 |
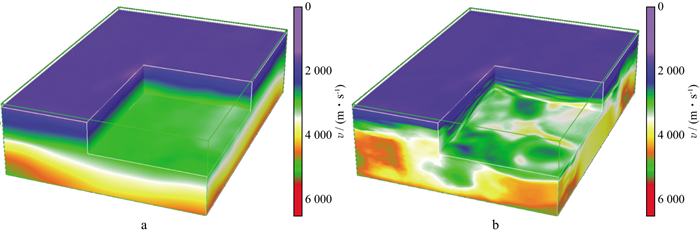
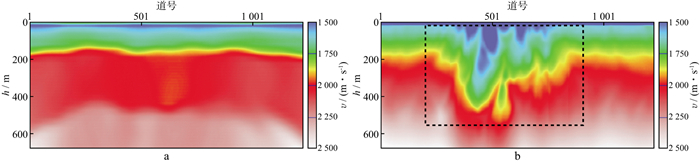
由于莱北地区浅层气云发育, 地震资料信噪比低, 故采用常规方法拾取初至困难, 进而导致速度场精度不足。因此, 结合莱北地区的地质地震特点, 对该区开展了回转波与反射波联合层析速度建模, 从图 11速度体的“椅状”切片可以看出, 相比初始输入速度, 经过沿层层析速度反演后的速度模型的精度更高, 细节刻画更为清晰。尤其是在浅层气云发育区, 常规反射波层析速度建模结果精度较低(图 12a), 与实际气云发育区的复杂地质情况匹配度较差。基于回转波与反射波联合层析速度建模方法得到的速度建模结果精度大幅提升(图 12b), 较为准确地反映了气云发育情况(图 12b中黑色方框所示)。
|
图 11 速度模型 a 初始速度模型; b 回转波与反射波联合层析速度建模结果 |
|
图 12 浅层层析速度建模结果 a 常规反射波层析; b 回转波与反射波联合层析 |
为了进一步对比回转波与反射波联合层析速度建模方法和常规反射波层析速度建模方法的精度, 在研究区随机选择了部分井对速度模型进行验证, 结果如图 13所示。图 13a为研究区V油组顶面等T0图, 包括在工区抽取的7口井分布情况。抽取过A井点处地震速度曲线与真实测井速度, 利用回转波与反射波联合层析速度建模方法得到的速度(图 13b红线)比利用常规反射波层析方法得到的速度(图 13b蓝线)精度更高, 与测井真实速度(图 13b黑线)一致性更高。对比研究区内7口井井震速度吻合率(图 13c)可知, 利用回转波与反射波联合层析速度建模方法(图 13c所示红线)可以极大地提高速度建模精度, 相较于常规层析方法(图 13c所示蓝线), 建模精度提升了约13%。

|
图 13 不同方法速度建模结果与真实速度 a V油组顶面等T0图; b 过A井不同方法得到的速度与真实速度对比; c 不同方法得到的速度模型与真实速度吻合率 |
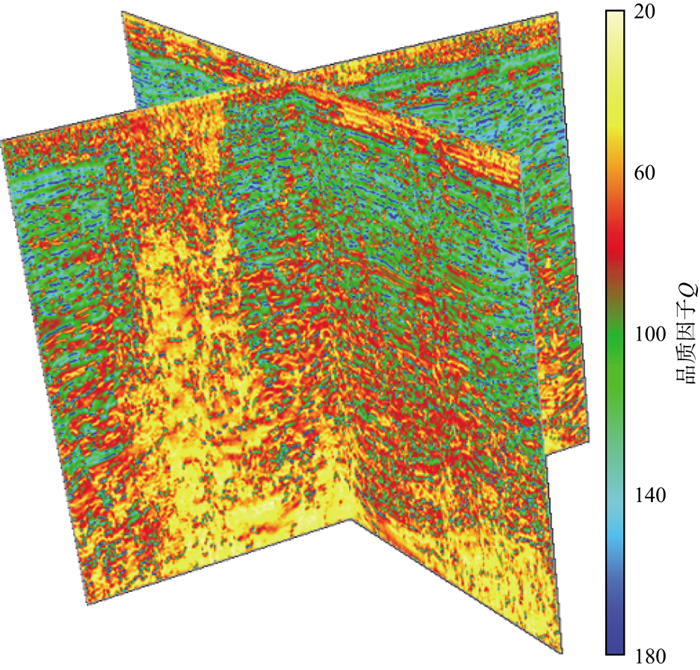
受气云和高孔低胶结地层的吸收衰减作用影响, 研究区地震资料有效频率缺失, 保幅性差, 为提高成像质量, 首先进行了Q值估算, 再基于得到的Q体(图 14)进行黏声介质逆时偏移成像。图 15为过气云发育区常规逆时偏移剖面与采用本文策略得到的黏声介质逆时偏移剖面(深时转换到了时间域)。常规逆时偏移未考虑地层衰减影响, 气云区(图 15a中蓝框所示)振幅明显减弱, 采用本文策略得到的黏声介质逆时偏移剖面中气云造成的振幅衰减得到了有效恢复。
|
图 14 三维Q体 |

|
图 15 采用不同方法得到的逆时偏移剖面 a 常规逆时偏移; b 本文策略 |
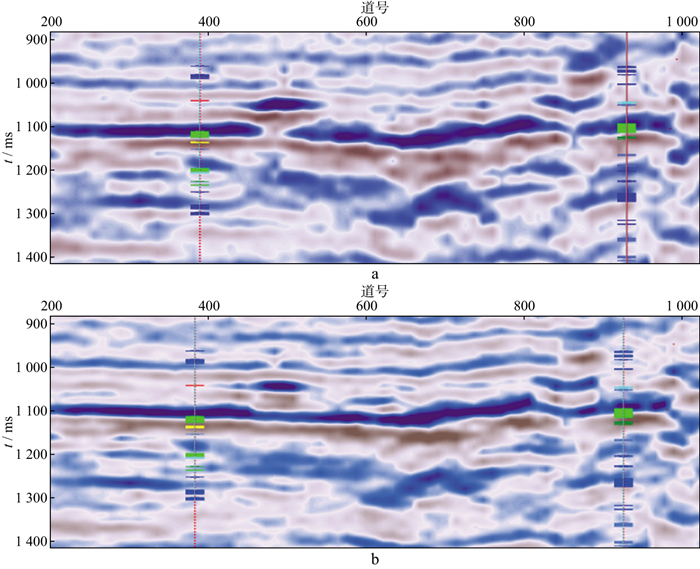
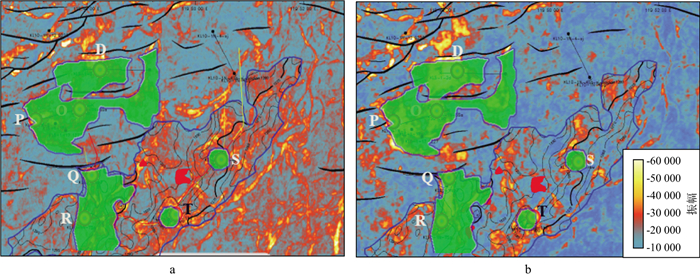
根据莱北地区某油田研究区的地震地质情况, 首先对采集的原始地震资料开展了鬼波和浅水多次波压制等宽频处理工作, 然后采用回转波与反射波联合层析方法进行速度建模, 最后基于估算的Q场信息进行了黏声介质逆时偏移成像。对比图 16中常规偏移方法和根据本文策略得到的偏移剖面(深时转换到了时间域)可知, 相较于常规偏移方法, 根据本文策略得到的地震资料成像品质明显提升, 地震资料中波组关系更加清晰(图 16b)。分别提取不同方法策略得到的目的层段偏移结果属性, 对比分析发现, 根据本文策略得到的偏移结果中, 砂体地震响应与已钻井更加吻合, 横向展布更加符合地质规律(图 17)。对比分析常规方法和根据本文策略得到的偏移结果在目的层段的频谱可知, 根据本文策略得到的地震资料有效频带由8~59 Hz拓展至4~96 Hz, 增加了1.5个倍频程(图 18)。
|
图 16 常规偏移剖面(a)与利用本文策略得到的偏移剖面(b) |
|
图 17 常规偏移结果振幅属性(a)与根据本文策略得到的偏移结果振幅属性(b) |

|
图 18 常规方法偏移与利用本文策略得到的偏移成像结果的频谱 |
针对渤海气云发育区高孔低胶结地层地震资料成像质量差的问题, 本文从多次波压制、速度建模精度提升、Q场估算和保幅偏移等方面分别进行了研究。结合模型测试和实际地震资料应用效果进行分析, 获得以下3个方面的认识。
1) 由于渤海为极浅水环境, 鬼波和浅水多次波发育, 导致地震波组关系变化, 频带变窄, 因此需要开展鬼波和浅水多次波压制, 以恢复和拓宽地震频带, 提高地震资料分辨率。
2) 气云区地震资料信噪比低, 利用常规层析方法拾取初至困难, 故采用浅层回转波层析和中、深层反射波层析联合的方式, 可以有效提升速度建模精度。
3) 气云和高孔低胶结地层对于地震波具有明显的吸收衰减作用, 开展黏声介质逆时偏移是提升地震资料保幅性的关键环节之一。
本文从渤海浅水环境下气云发育区高孔低胶结地层的地震地质特点出发, 分析了影响地震资料成像的主要因素, 针对性地应用并改进了一系列处理关键技术, 研究了相应的处理策略, 有效提高了研究区地震资料的成像质量, 为莱北地区某亿吨级油田规模性岩性圈闭的发现奠定了地震资料基础, 对于类似地区地震资料处理也具有一定的推广应用价值。
| [1] |
薛永安, 杨海风, 黄江波, 等. 渤海海域浅层油气运移成藏理论技术创新与勘探突破[J]. 中国海上油气, 2020, 32(2): 14-23. XUE Y A, YANG H F, HUANG J B, et al. Technological and theoretical innovations in the shallow hydrocarbon migration and accumulation of the Bohai Sea and the exploration breakthroughs[J]. China Offshore Oil and Gas, 2020, 32(2): 14-23. |
| [2] |
薛永安, 牛成民, 王德英, 等. 渤海海域浅层油气运移新认识与勘探新进展[J]. 石油学报, 2019, 40(增刊2): 29-37. XUE Y A, NIU C M, WANG D Y, et al. New understanding of shallow hydrocarbon migration and new exploration progress in the Bohai Sea[J]. Acta Petrolei Sinica, 2019, 40(S2): 29-37. |
| [3] |
邸志欣, 丁伟, 吕公河, 等. 五号桩地区滩浅海高精度三维地震采集技术[J]. 石油物探, 2012, 51(4): 388-397. DI Z X, DING W, LV G H, et al. 3D high-precision seismic acquisition techniques in Wuhaozhuang beach and shallow sea area[J]. Geophysical Prospecting for Petroleum, 2012, 51(4): 388-397. DOI:10.3969/j.issn.1000-1441.2012.04.012 |
| [4] |
马光克, 李雷, 刘巍, 等. 高密度地震勘探技术在莺歌海盆地M气田岩性勘探中的应用[J]. 石油物探, 2019, 58(4): 591-599. MA G K, LI L, LIU W, et al. Application of high-density seismic acquisition technology for lithological exploration of M gas field in the Yinggehai Basin[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 591-599. DOI:10.3969/j.issn.1000-1441.2019.04.014 |
| [5] |
王艳冬, 王小六, 桑淑云, 等. 渤海海域水平拖缆数据宽频处理关键技术[J]. 石油地球物理勘探, 2020, 55(1): 10-16. WANG Y D, WANG X L, SANG S Y, et al. Key techniques for broadband processing of plane streamer data in Bohai Sea[J]. Oil Geophysical Prospecting, 2020, 55(1): 10-16. |
| [6] |
冯波, 吴成梁, 王华忠. 反射波层析反演速度建模方法[J]. 石油物探, 2019, 58(3): 371-380. FENG B, WU C L, WANG H Z. Velocity model building using reflection tomography[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 371-380. DOI:10.3969/j.issn.1000-1441.2019.03.006 |
| [7] |
徐嘉亮, 张冰, 王维红, 等. 基于一步法层析速度建模方法建立[J]. 地球物理学报, 2021, 64(4): 1412-1418. XU J L, ZHANG B, WANG W H, et al. Establishment of an one-step method for modeling tomographic velocity[J]. Chinese Journal of Geophysics, 2021, 64(4): 1412-1418. |
| [8] |
徐德奎, 张志军, 夏同星, 等. 海上大型气云发育区地震数据采集参数论证分析[J]. 石油物探, 2020, 59(2): 186-197. XU D K, ZHANG Z J, XIA T X, et al. Demonstration analysis of seismic acquisition in a large-scale gas cloud area in the sea[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 186-197. DOI:10.3969/j.issn.1000-1441.2020.02.004 |
| [9] |
夏同星, 刘垒, 明君, 等. 渤海湾X油田气云区地震资料关键处理技术研究[J]. 石油物探, 2018, 57(2): 283-291. XIA T X, LIU L, MING J, et al. Key processing technologies of seismic data for a gas cloud area in the X oilfield, Bohai Bay Basin[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 283-291. DOI:10.3969/j.issn.1000-1441.2018.02.014 |
| [10] |
TENG K H, ZHOU J, WU X, et al. Compensating attenuation due to gas cloud through QPSDM: Case study from offshore Brunei[J]. Proceedings of EAGE Workshop on Seismic Attenuation, 2013, cp-363-00023. |
| [11] |
李振春, 郭振波, 田坤. 黏声介质最小平方逆时偏移[J]. 地球物理学报, 2014, 57(1): 214-228. LI Z C, GUO Z B, TIAN K. Least-squares reverse time migration in visco-acoustic medium[J]. Chinese Journal of Geophysics, 2014, 57(1): 214-228. |
| [12] |
匡斌, 唐祥功, 张猛, 等. 三维自适应最小二乘逆时偏移技术[J]. 石油地球物理勘探, 2018, 53(1): 73-76. KUANG B, TANG X G, ZHANG M, et al. 3D adaptive least-squares reverse-time migration[J]. Oil Geophysical Prospecting, 2018, 53(1): 73-79. |
| [13] |
顾元, 文鹏飞, 张宝金, 等. 水平缆地震数据的鬼波压制方法及其应用[J]. 地球物理学进展, 2017, 32(4): 1764-1772. GU Y, WEN P F, ZHANG B J, et al. Receiver de-ghosting method in τ-p domain and its application to flat streamers pre-migration data[J]. Progress in Geophysics, 2017, 32(4): 1764-1772. |
| [14] |
杨佳佳, 潘军, 栾锡武, 等. 浅水多次波衰减技术在多道地震数据处理中的应用[J]. 海洋地质与第四纪地质, 2020, 40(1): 167-174. YANG J J, PAN J, LUAN X W, et al. Application of attenuation technology to shallow water multiples in multi-channel seismic data processing[J]. Marine Geology & Quaternary Geology, 2020, 40(1): 167-174. |
| [15] |
徐强, 王征, 史增园, 等. 浅水多次波衰减[J]. 石油地球物理勘探, 2015, 50(2): 238-242. XU Q, WANG Z, SHI Z Y, et al. Shallow water multiple attenuation[J]. Oil Geophysical Prospecting, 2015, 50(2): 238-242. |
| [16] |
周东红, 夏同星, 曹盛, 等. 气云区地震成像关键处理技术: 以渤海湾某油田为例[J]. 地球物理学进展, 2018, 33(6): 2613-2618. ZHOU D H, XIA T X, CAO S, et al. Key imaging technologies of gas cloud area: A case study in Bohai Bay[J]. Progress in Geophysics, 2018, 33(6): 2613-2618. |
| [17] |
徐嘉亮, 周东红, 贺电波, 等. 高精度深度域层析速度反演方法[J]. 石油地球物理勘探, 2018, 53(4): 737-744. XU J L, ZHOU D H, HE D B, et al. High-precision velocity tomography inversion in the depth domain[J]. Oil Geophysical Prospecting, 2018, 53(4): 737-744. |
| [18] |
GAO F, WEI J X, DI B R. Ultrasonic attenuation estimation based on time-frequency analysis[J]. Applied Geophysics, 2019, 16(4): 414-426. |
| [19] |
韩利, 刘春成, 张益明, 等. 地震复谱分解技术及其在烃类检测中的应用[J]. 地球物理学报, 2016, 59(3): 1095-1101. HAN L, LIU C C, ZHANG Y M, et al. Seismic complex spectral decomposition and its application on hydrocarbon detection[J]. Chinese Journal of Geophysics, 2016, 59(3): 1095-1101. |
| [20] |
李振春, 王清振. 地震波衰减机理及能量补偿研究综述[J]. 地球物理学进展, 2007, 22(4): 1147-1152. LI Z C, WANG Q Z. A review of research on mechanism of seismic attenuation and energy compensation[J]. Progress in Geophysics, 2007, 22(4): 1147-1152. |



