2. 中国石油新疆油田分公司勘探开发研究院, 新疆克拉玛依 834000
2. Petroleum Exploration and Development Institute, PetroChina Xinjiang Oilfield Company, Karamay 834000, China
品质因子Q是地球物理勘探中的重要地层参数, 其不仅可用于基于吸收补偿的高分辨率地震资料处理[1], 还可用于指示地下介质的流体特征、孔隙度、渗透率等信息[2]。自FUTTERMAN[3]提出地层吸收衰减理论和相关计算方法以来, 许多学者在时间域和频率域发展了一系列的Q因子估计方法。时间域Q因子估计方法根据地震子波形态变化与衰减的关系进行Q值估计, 如振幅衰减法、上升时间法等[4]。由于几何扩散、透射损失等非地层吸收因素会引起子波振幅的改变, 降低了时间域Q因子估算精度, 因此, 目前很少采用时间域方法进行Q值估算。相对而言, 频率域Q因子估计方法能够很方便地分离出几何扩散等与频率无关的影响因素, 逐渐成为Q值估算的主流方法[5]。谱比法[6]和质心频移法[7]是目前频率域Q因子估算最为常用的方法。谱比法基于地震信号衰减函数的斜率对Q进行估算, 该方法的物理意义明确, 计算方法直观, 但其估算结果易受噪声干扰和层间干涉等因素的影响。质心频移法基于地震信号质心频移的变化对Q进行估算。质心频移的估算具有一定的统计效应, 其抗噪性要优于谱比法。但是, 质心频移法假设地震子波的频谱为高斯函数, 当地震子波的频谱偏离高斯函数时, 估算结果也随之产生误差[8]。为提高这两种方法的稳定性和适应性, 许多学者从不同角度对以上方法进行了修改和完善。ZHANG等[9]将质心频率修改为峰值频率, 提出了基于峰值频率的Q估算方法。WANG等[10]提出了基于对数谱面积差值法的Q值估计方法, 提高了Q估计的稳定性和抗噪性。李拥军等[11]将非零相位雷克子波的复数域快速匹配追踪分解法与对数谱比法相结合, 进行了微测井数据近地表Q值估计。刘国昌等[12]以地震波射线传播为基础, 根据同相轴局部斜率和射线参数的映射关系, 将多射线频谱同时代入谱比法进行联合反演, 有效避免了速度误差对Q值估计的影响。李波等[13]将Lucy-Richardson算法与广义S变换相结合, 提高了Q因子估算精度。LI等[14]提出了一种双参数回归方法, 从非线性地震衰减中估计与频率相关的Q因子。另外, LEI等[15]借助于小波变换和时频分析技术, 提高了谱比法和质心频移法进行Q值估计的精度。赵秋芳等[16]对近地表品质因子估算方法进行了总结和梳理, 指出井地联合及多源信息融合是未来近地表Q反演的主要研究方向。云美厚等[17-18]就品质因子地震反演问题进行了系统分析, 并指出了基于品质因子进行储层预测的风险。
常用Q值估计方法利用两个不同位置的地震信号或者相同位置两个不同时间的地震信号进行Q值估算, 当利用多个地震信号同时对地下吸收参数进行估算时, 这种方法不能充分利用所有地震信号的频率变化及其相互关系进行Q参数反演。随着速度层析反演技术的发展[19], Q值估算逐渐与各种层析反演技术结合, 通过衰减信号与Q值的关系建立矩阵方程进行Q值估计。WONG等[20]首先将VSP数据与层析反演相结合进行Q值估算。BREGMAN等[21]利用初至波信息, 结合基于射线理论的层析反演与谱比法来进行Q值估计, 并分析了大量实例, 指出Q值层析反演中数据预处理的重要性。JAMES[22]利用不同深度地震子波的对数谱构建层析反演方程来估计层间衰减, 并将数据的高信噪比部分和模型约束作为先验信息加入到反演方程, 提高了反演的抗噪能力和稳定性。HU等[23]基于质心频移法, 加入一个源振幅谱函数使Q层析成像很好地适应实际地震数据, 提高了衰减层析反演的精度。基于全波形反演的吸收参数建模是近年来的热点研究内容[24], 这类方法具有明显的理论优势, 但在实际应用中也遇到了诸多困难。
就工业界应用现状而言, 谱比法与质心频移法依然是目前应用最为广泛的Q值估算方法。但是, 这两种方法只是利用了地震频谱的某个单一属性(衰减斜率或者质心频移), 未能充分考虑地震频谱及其空间变化的完整信息, 估算结果很容易受干扰因素的影响, 另外, 质心频移法还需要高斯谱等基本假设。为此, 本文提出了一种频谱一致性Q因子估算方法, 其基本思想是: 基于粘弹性介质地震波传播理论, 将不同位置或不同时间的多个地震信号反向传播到同一位置, 以反向传播之后地震频谱的一致性作为目标函数, 采用全局优化算法对Q模型进行非线性反演。该方法既不需要已知震源子波函数, 也不需要对震源子波的性质进行任何假设, 其估算结果不依赖于地震频谱的某个单一属性, 而是基于地震频谱的整体变化, 因而增强了Q估算的稳定性、抗噪性和适应性。本文对模型数据采用频谱一致性Q因子反演方法进行实验分析和效果对比, 并利用实际数据进行了Q因子反演和吸收补偿的试验处理。
1 方法原理根据粘弹性介质波动理论, 地震波的传播过程在频率域表示[3]为:
| $ R(f)=G \cdot H(f) \cdot S(f) $ | (1) |
式中: f为频率; S(f)为震源信号振幅谱; R(f)是接收点信号的振幅谱; G表示不依赖频率的衰减, 包括几何扩散、反射、透射损失等; H(f)为地层吸收衰减函数。H(f)表示为[25]:
| $ H(f)=\exp \left(-\pi f \sum\limits_{j=1}^N \frac{\Delta t_j}{Q_j}\right) $ | (2) |
式中: N为地层数目; Qj是第j个地层的品质因子; Δtj是地震波在第j个地层的旅行时间。将公式(2)代入公式(1)中, 忽略不依赖于频率的衰减因子G的影响, 有:
| $ R(f)=S(f) \cdot \exp \left(-\pi f \sum\limits_{j=1}^N \frac{\Delta t_j}{Q_j}\right) $ | (3) |
(3) 式完整地表达了地层吸收对地震信号频谱的改造效应。
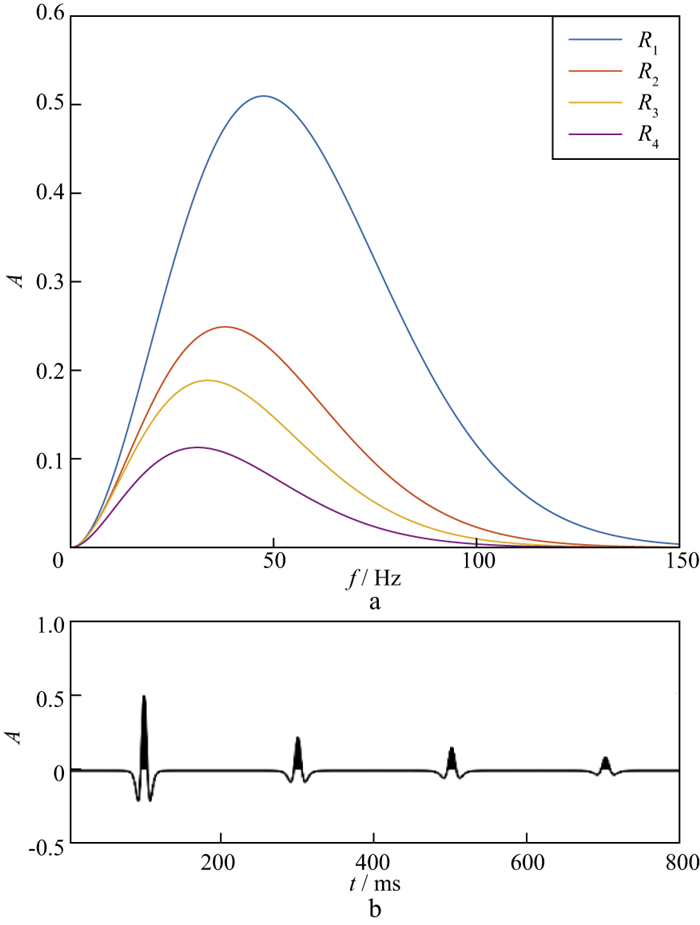
为了更加直观地展示地层吸收对地震频谱的影响, 进而引出本文方法的基本原理, 在一维层状介质假设条件下, 建立了一个4层吸收介质模型, 模型参数见表 1。假设震源子波为50 Hz的雷克子波, 利用(3)式计算地层吸收后每个界面反射信号的振幅谱, 图 1a给出了这4个反射信号的振幅谱。再利用傅里叶反变换得到图 1b所示的合成地震记录。可以看出, 从浅至深, 来自4个不同界面(R1, R2, R3, R4)地震信号的主频逐渐降低, 有效频宽逐渐变窄, 振幅谱的形态发生了较大变化, 相应时间反射记录振幅逐渐减弱, 主波瓣宽度不断增大。
| 表 1 合成地震记录的模型参数(反射时间、反射系数和Q值) |
|
图 1 不同反射界面地震信号的振幅谱(a)及其合成地震记录(b) |
可以设想, 若将不同深度的地震信号反向传播到同一位置, 在反向传播的过程中, 依据地层Q模型对地震信号进行吸收补偿, 此时, 所采用的Q模型与实际模型越接近, 则这些信号反向传播之后所重构的振幅谱一致性越好, 否则, 不同信号重构振幅谱的差异性越大。此即本文方法的基本思想, 称之为频谱一致性Q因子反演方法。通常, 可以采用不同的数学准则对重构频谱的一致性进行评价和分析, 本文采用方差函数作为评价准则, 其目标函数为:
| $ \begin{aligned} & F(\mathit{\boldsymbol{Q}})= \\ & \sum\limits_{f=f_{\min }}^{f_{\max }} \sqrt{\frac{1}{N-1} \sum\limits_{i=1}^N\left[\frac{1}{n} \sum\limits_{j=1}^N S_j(f, \mathit{\boldsymbol{Q}})-S_i(f, \mathit{\boldsymbol{Q}})\right]^2} \end{aligned} $ | (4) |
式中: N为不同深度或时间地震信号数目; Q=(Q1, Q2, …, QN)T为待反演的吸收模型; Si(f, Q)表示第i个地震信号的重构振幅谱; Sj(f, Q)表示第j个地震信号的重构振幅谱; fmin和fmax分别为地震信号的最低和最高有效频率。
(4) 式给出了频谱一致性Q因子反演的一般性目标函数, 适用于地面地震和VSP地震等各类野外观测数据的Q模型反演。如将不同位置接收的地震信号反向传播到同一位置, 需要在已知速度模型的情况下进行射线追踪以确定地震信号衰减的轨迹和大小。为简化问题, 在后面的模型试验和实际资料试算中均采用了一维层状介质模型假设进行反向逆推计算。
基于(4)式所示的目标函数对Q模型进行估算是典型的非线性反演问题, 该目标函数呈现明显的非线性特征, 模拟退火法、遗传算法、蚁群算法和粒子群算法等是目前非线性反演问题的常用算法, 相对而言, 粒子群算法的基本思想更加简洁, 其结果也较稳定[26]。
粒子群算法(particle swarm optimization, PSO)是KENNEDY等[27]受大自然中鸟类觅食的启示而提出的一种全局寻优智能算法。该算法的核心在于, 鸟群在觅食时每只鸟作为一个单独的信息源, 它将自己所获得的信息反馈到鸟群中去, 通过每只鸟不停移动并反馈自身认知、更新群体认知, 从而加快了整个群体获得最佳食物的进程。PSO对鸟类觅食过程进行了高度概括和总结, 数学模型简单、适用范围大、收敛较快, 被广泛应用于解决全局优化问题[28]。
在对目标函数((4)式)进行全局寻优时, 首先对“Q模型”这种粒子进行初始化, 假设该粒子群有M个粒子在N维空间寻找全局最优位置, 第i个粒子的初始位置为Qi=(Qi1, Qi2, …, QiN), 其中, i=1, 2, …, M, 每个粒子的位置为一个潜在解, 其成为真解的可能性通过适应度函数来计算。就本文而言, 适应度函数就是(4)式所示的目标函数。在每一次寻找过程中, 每个粒子当前的最优位置记为pi=(pi1, pi2, …, piN), 其中, i=1, 2, …, M, 则所有粒子在这次寻找中的最优解即可作为当前最优解, 记为pt, 通过对粒子的位置(即Q模型)进行更新达到反复迭代目的, 直至达到最大迭代次数或者搜索精度, 在t+1时刻粒子速度与Q模型的更新公式如下:
| $ \begin{aligned} v_i^j(t+1)= & \omega v_i^j(t)+c_1 r_1\left[p_i^j(t)-Q_i^j(t)\right]+ \\ & c_2 r_2\left[p_t^j(t)-Q_i^j(t)\right] \end{aligned} $ | (5) |
| $ Q_i^j(t+1)=Q_i^j(t)+\alpha v_i^j(t) $ | (6) |
式中: i=1, 2, …, M; j=1, 2, …, N; ω为惯性因子, 用于控制算法的收敛; pi, pt分别为局部和全局最优位置; c1, c2为学习因子; r1, r2为0~1内的随机数; α为控制速度权重的约束因子。
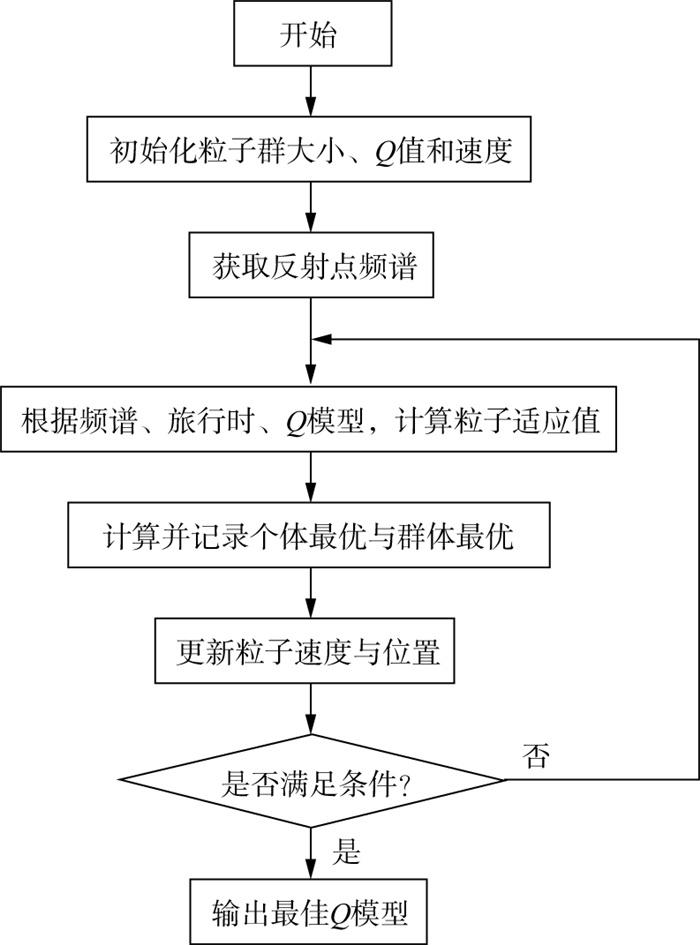
本文频谱一致性Q反演的基本流程表述如下。
1) 对地震记录进行频谱分析, 获得不同反射时间tk及其对应的振幅谱Sk(f)。
2) 给定ω, c1, c2, r1和r2等粒子群算法的控制参数。
3) 粒子群初始化。给定Q的最大值和最小值, 随机生成M个Q模型。
4) 计算每个粒子的适应度值。亦即将反射时间tk、振幅谱Sk(f)和Q模型代入(4)式, 计算频谱一致性函数。
5) 计算每个粒子在当前时刻的最优值, 也就是说, 每个初始Q模型迭代之后的当前最优值。然后, 由每个粒子的最优值再筛选出整个粒子群在当前时刻的最优值。
6) 利用(5)式和(6)式更新粒子的速度与位置, 即计算下一个时刻的Q模型及其更新速度。
7) 更新每个粒子的局部最优值与整个粒子群的全局最优值。
8) 重复步骤5)和步骤6), 直至满足搜索精度或到达最大迭代次数。
图 2给出了利用PSO反演Q值的流程。
|
图 2 利用PSO反演Q值的流程 |
基于一维层状介质模型对频谱一致性Q因子反演方法的结果与谱比法和质心频移法Q因子估算结果进行对比分析。
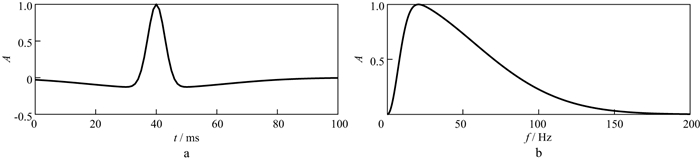
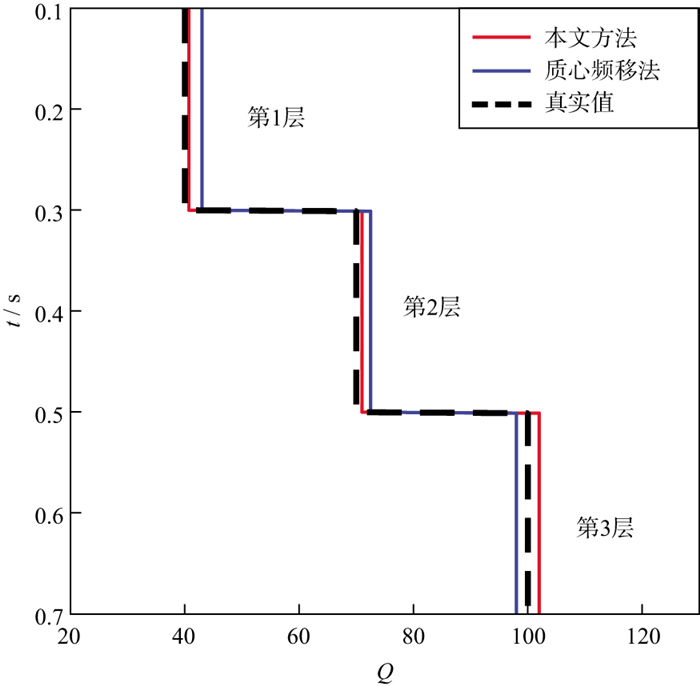
2.1 非高斯谱源子波试验质心频移法假设地震子波的频谱为高斯函数, 频谱一致性Q因子反演方法(本文方法)基于重构频谱的一致性对Q因子进行反演估算, 无需对震源子波及其频谱进行任何假设。为此采用表 1所示的模型基于非高斯谱对两种估算方法的影响进行测试。俞氏子波的振幅谱是非高斯的[29], 因此, 选择图 3所示的主频为50 Hz的俞氏子波作为震源函数。图 4显示了采用本文方法和质心频移法的Q值估算结果, 其中, 黑虚线代表真实值, 蓝实线代表质心频移法估算结果, 红实线代表本文方法的估算结果。采用质心频移法在第1, 2, 3层的误差分别为8.50%, 4.10%, 3.70%;采用本文方法在第1, 2, 3层的误差分别为1.20%, 1.70%, 0.92%, 由此可知, 当震源子波不满足高斯谱假设时, 采用质心频移法进行Q估计的准确性会下降, 而采用本文方法则准确性会高很多。
|
图 3 俞氏子波(a)及其归一化振幅谱(b) |
|
图 4 采用本文方法与质心频移法的Q值估算结果 |
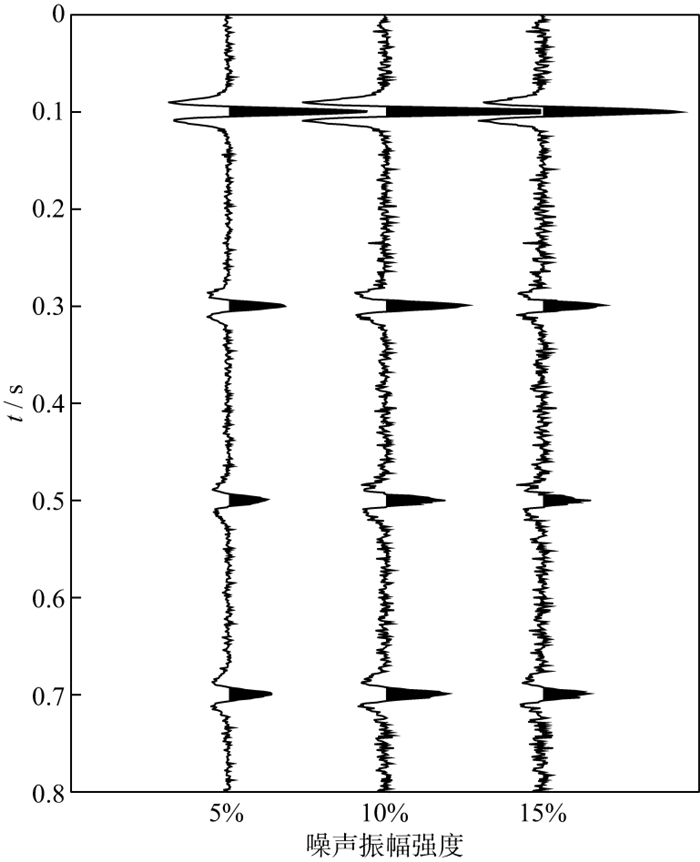
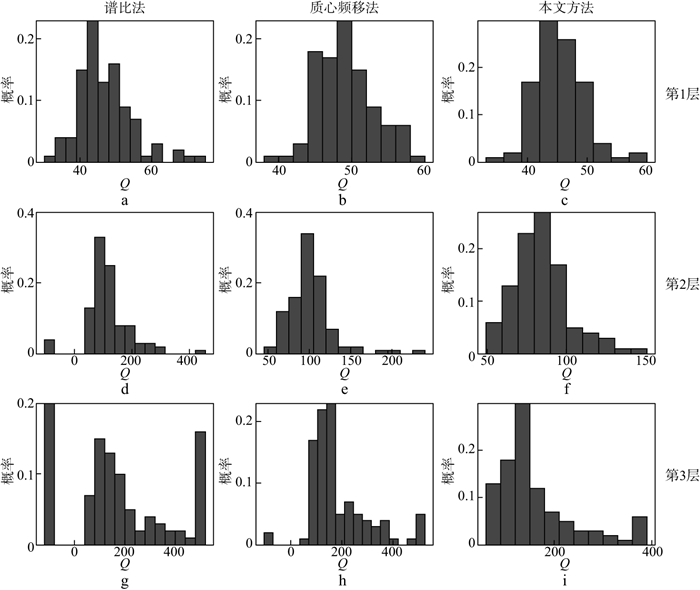
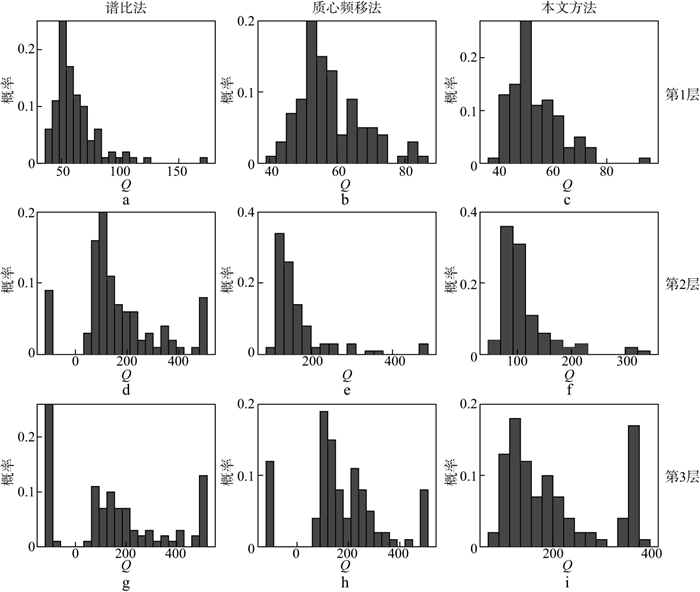
对图 1b所示的雷克子波合成地震记录分别加入振幅强度为5%, 10%, 15%的高斯噪声, 获得如图 5所示的含噪地震记录。在这3种强度的噪声下分别计算100次, 图 6和图 7分别给出了10%和15%噪声环境下采用谱比法、质心频移法和本文方法得到的Q值估计结果的概率分布, 表 2给出了3种噪声环境下估算结果的均值和方差。
|
图 5 加入不同振幅强度随机噪声后的合成地震记录 |
|
图 6 加入10%随机噪声时不同方法得到的Q因子概率分布结果 a~c, d~f, g~i分别为3种方法对第1层、第2层、第3层估算的Q值(这3层的Q理论值分别为40, 70, 100) |
|
图 7 加入15%随机噪声时不同方法得到的Q因子概率分布结果 a~c, d~f, g~i分别为3种方法对第1层、第2层、第3层估算的Q值(这3层的Q理论值分别为40, 70, 100) |
| 表 2 不同噪声环境下3种方法Q值估计结果的均值与方差 |
分析图 6、图 7和表 2可以发现: 在5%噪声环境下, 采用这3种方法均能得到可接受的反演结果; 在10%噪声环境下, 采用谱比法、质心频移法和本文方法在第3层的方差分别为257.12, 142.35, 63.37;在15%噪声环境下, 采用谱比法、质心频移法和本文方法在第3层的方差分别为361.15, 183.20, 97.96。可见, 随着噪声强度的增大, 谱比法和质心频移法的反演误差迅速增大, 本文方法的优势逐渐凸显出来。
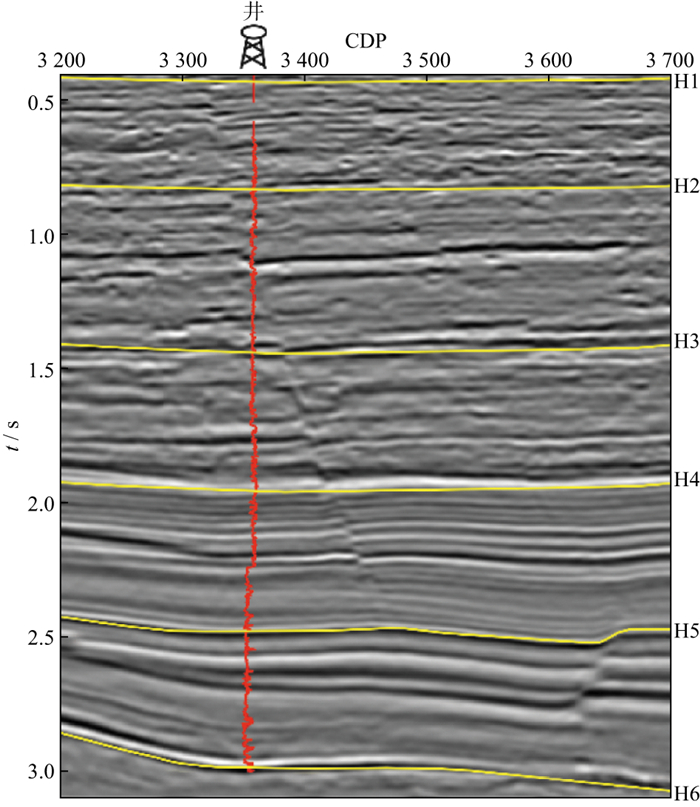
3 实际数据测试图 8是叠前时间偏移后的地震剖面, 该数据在叠前经过了地表一致性反褶积处理, 但没有进行预测反褶积等提高分辨率的处理, 因此, 地震数据一定程度上保持了实际地层的吸收特征。
|
图 8 叠前时间偏移地震剖面 |
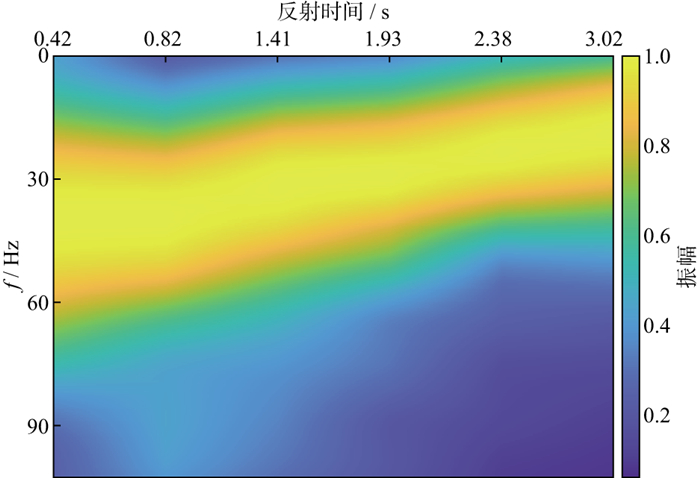
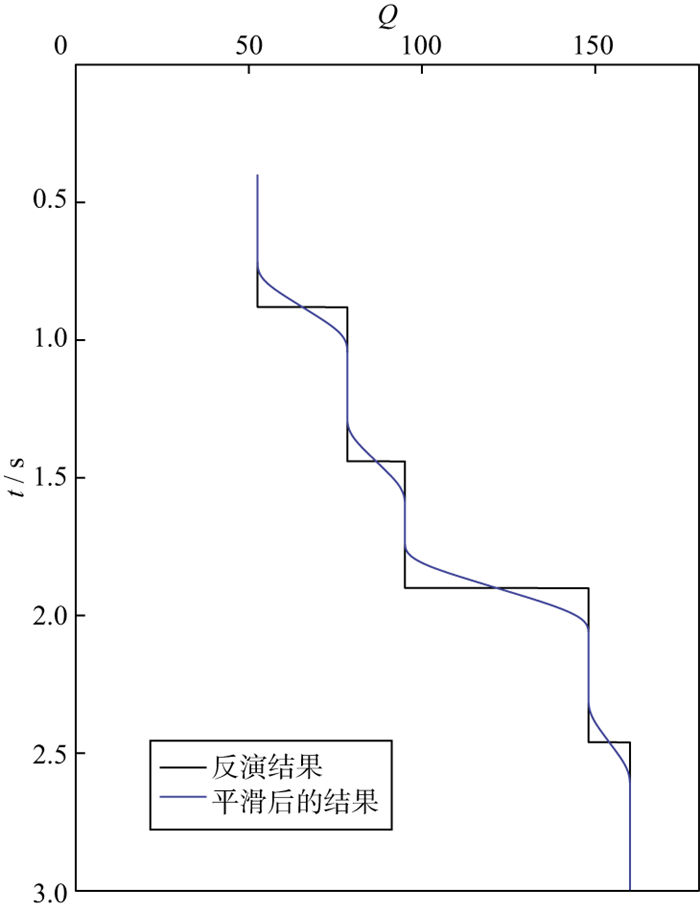
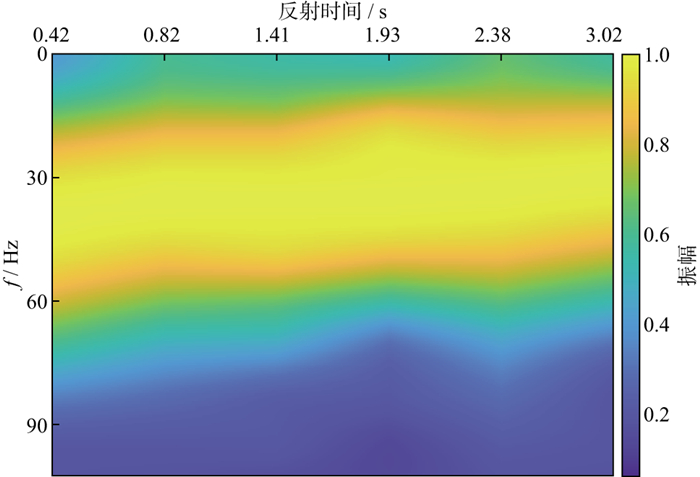
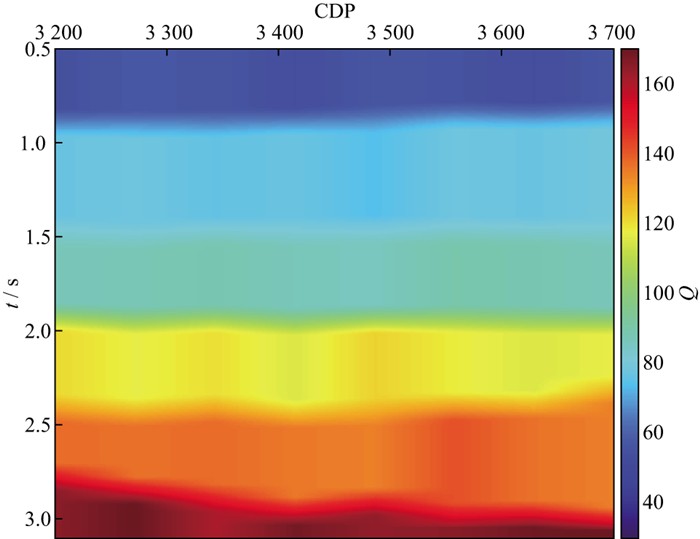
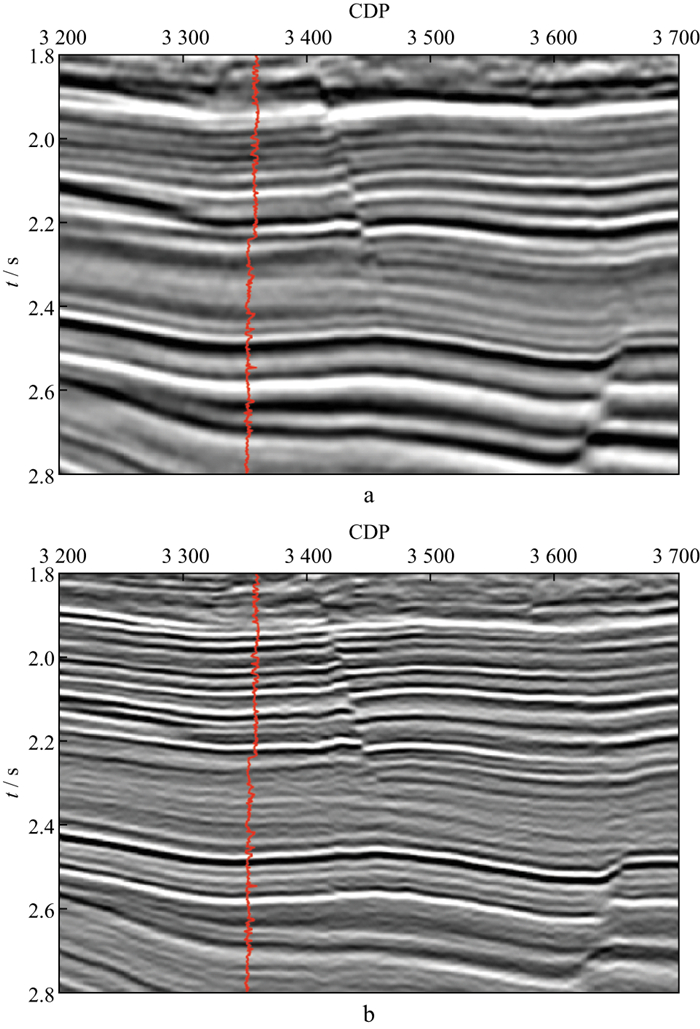
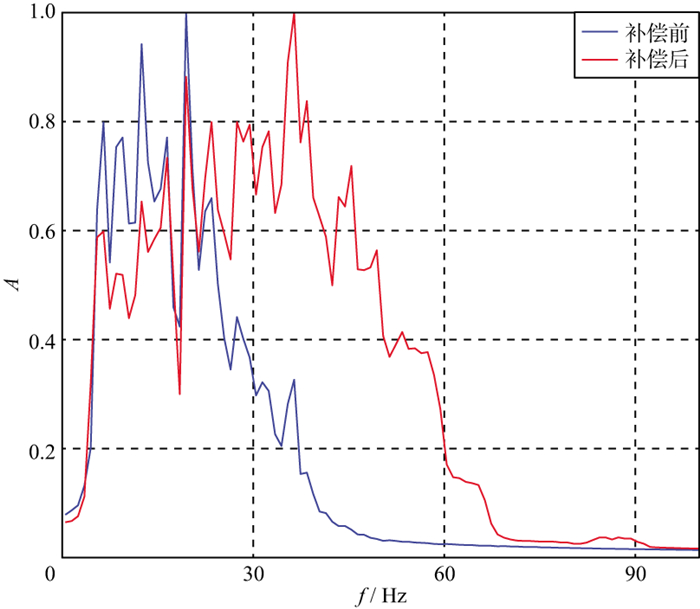
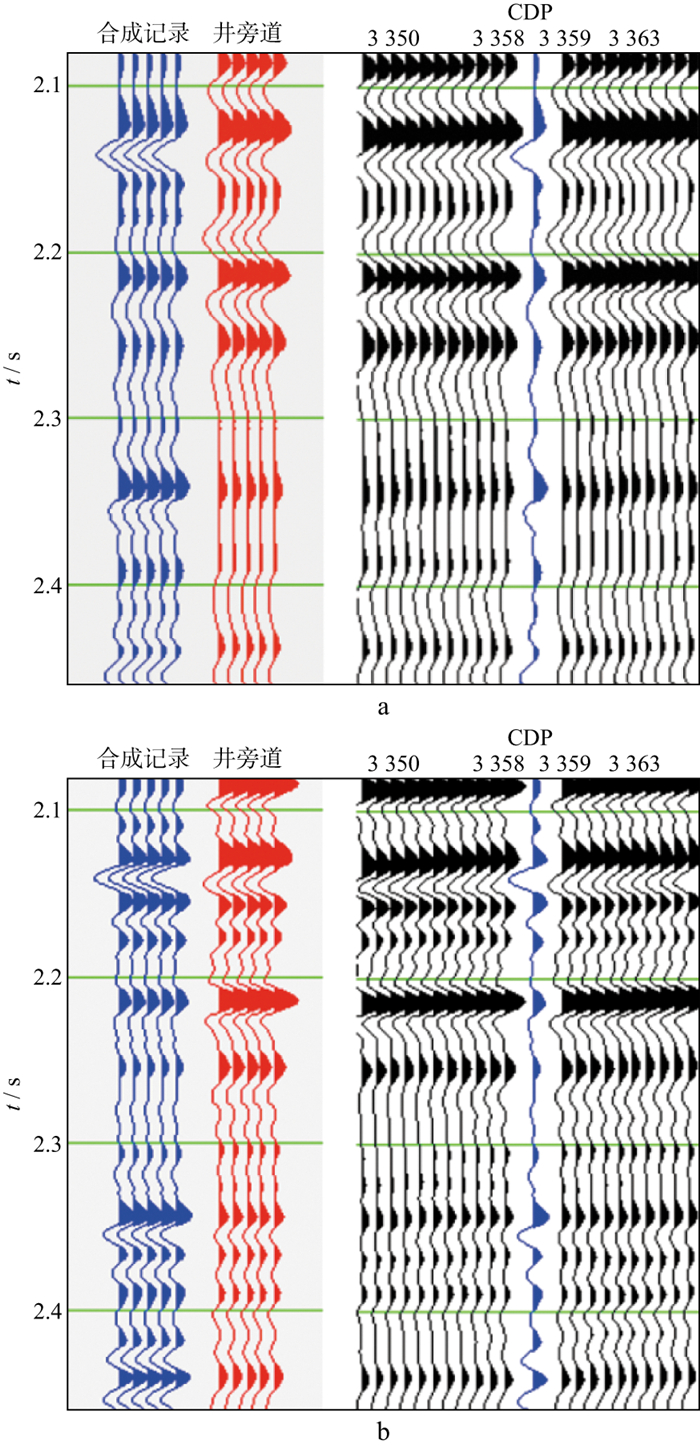
不同于表 1所示的模型数据, 实际地震数据中不同时间的地震反射相互干涉, 很难得到不同时间的孤立子波及其频谱, 需要采用Gabor变换等时频分析方法尽量降低子波干涉对频谱分析的影响。另外, 吸收估算所依据的是不同时间地震频谱的差异, 只有在时间间隔较大时, 其频谱差异才能保证Q反演的稳定性。为此, 本文试验选择了图 8中黄线所示的6个反射层(H1~H6), 其时间间隔大致在500 ms。以CDP3358的地震道为例, 说明Q反演的具体过程。首先对地震道进行时频分析, 然后再以反射层为中心, 在200 ms的时窗内, 沿时间方向进行三角加权平均, 得到反射时间分别为0.42, 0.82, 1.41, 1.93, 2.38, 3.02 s这6个反射层的振幅谱(图 9), 可见, 主频随反射时间增大而减小的趋势十分明显。然后, 进行频谱一致性Q因子反演, 反演结果如图 10所示。进一步利用反演的Q因子对该地震道进行吸收补偿, 图 11显示了补偿之后6个反射时间的振幅谱, 可以看出, 不同深度地震反射在吸收补偿之后, 其振幅谱在整体趋势上趋于一致, 表明反演的Q模型较好地刻画了实际地层的吸收特征。图 12是采用本文方法反演得到的Q模型。图 13是基于图 12的Q模型进行吸收补偿前、后的地震剖面, 可以看出, 补偿之后地震剖面的分辨率得到了明显改善, 更好地揭示了大套地层之间的层序结构及其接触关系。图 14是吸收补偿前、后的振幅谱对比结果, 振幅谱是图 13所有地震道的平均值, 可以看出, 地震信号的主频和频宽得到了明显提升。为了更好地展示吸收补偿对地震反射特征的恢复能力, 图 15展示了吸收补偿前、后地震数据与合成地震记录的标定结果, 其中, 补偿前、后合成地震记录的子波分别从其地震剖面统计估算, 可以看出, 补偿之后的地震记录与合成地震记录在反射特征上具有较好的一致性, 表明采用频谱一致性反演方法估算的Q模型较好地描述了实际地层的吸收特征。
|
图 9 CDP3358位置处的6个不同反射时间的振幅谱 |
|
图 10 CDP3358位置处反演的Q值曲线 |
|
图 11 CDP3358位置处的6个不同反射时间的振幅谱(补偿之后) |
|
图 12 采用本文方法反演得到的Q模型 |
|
图 13 吸收补偿前(a)、后(b)的地震剖面 |
|
图 14 吸收补偿前、后的振幅谱 |
|
图 15 实际数据吸收补偿前(a)、后(b)与合成地震记录对比结果 |
谱比法和质心频移法基于地震频谱的某个单一属性对Q参数进行反演和估算, 反演结果易受噪声干扰和地震干涉等因素的影响。不同于以上两种方法, 频谱一致性反演方法基于吸收补偿之后地震频谱在整体形态上的一致性对Q因子进行评价和反演, 反演结果的稳定性和抗噪性更好。另外, 本文采用的粒子群算法能较好地适应Q因子的全局寻优过程。
需要指出的是, 尽管本文方法的模型试验和实际资料分析都采用了叠后地震数据, 但是, 无论是理论方法还是实现过程, 频谱一致性反演方法很容易扩展到叠前地震数据、VSP数据甚至微测井地震数据。
| [1] |
MA X, LI G F, LI H, et al. Multichannel absorption compensation with a data-driven structural regularization[J]. Geophysics, 2020, 85(1): V71-V80. DOI:10.1190/geo2019-0132.1 |
| [2] |
王小杰, 印兴耀, 吴国忱. 基于S变换的吸收衰减技术在含气储层预测中的应用研究[J]. 石油物探, 2021, 51(1): 37-42. WANG X J, YIN X Y, WU G C. The application of an S transform based absorption and attenuation technique for prediction of gasbearing reservoir[J]. Geophysical Prospecting for Petroleum, 2021, 51(1): 37-42. DOI:10.3969/j.issn.1671-0657.2021.01.011 |
| [3] |
FUTTERMAN W L. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(18): 5279-5291. |
| [4] |
TONN R. The determination of the seismic quality factor Q from VSP data: A comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39(1): 1-27. DOI:10.1111/j.1365-2478.1991.tb00298.x |
| [5] |
LI G F, SACCHI MAURICIO D, ZHENG H. In situ evidence for frequency dependence of near-surface Q[J]. Geophysical Journal International, 2016, 204(2): 1308-1315. DOI:10.1093/gji/ggv523 |
| [6] |
BATH M. Spectral analysis in geophysics[M]. New York: Elsevier, 1974: 46-48.
|
| [7] |
QUAN Y, HARRIS J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. DOI:10.1190/1.1444197 |
| [8] |
LI G F, ZHENG H, ZHANG X M, et al. Frequency-dependent near-surface Q factor measurements via a cross-hole survey[J]. Journal of Applied Geophysics, 2015, 121: 1-12. DOI:10.1016/j.jappgeo.2015.07.006 |
| [9] |
ZHANG C J, ULRYCH T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(10): 1542-1547. |
| [10] |
WANG S D, YANG D F, LI J N, et al. Q factor estimation based on the method of logarithmic spectral area difference[J]. Geophysics, 2015, 80(6): V157-V171. DOI:10.1190/geo2014-0257.1 |
| [11] |
李拥军, 宋炜, 唐传章, 等. 复数域匹配追踪近地表Q值估计及深度学习建模[J]. 石油物探, 2021, 60(1): 123-135. LI Y J, SONG W, TANG C Z, et al. Complex domain-matching pursuit for near-surface Q-estimate and deep learning modeling[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 123-135. DOI:10.3969/j.issn.1000-1441.2021.01.012 |
| [12] |
刘国昌, 李超. 基于多射线联合反演的速度无关叠前地震数据Q值估计[J]. 地球物理学报, 2020, 63(4): 1569-1584. LIU G C, LI C. Velocity-independent prestack seismic Q estimation based on multi-ray joint inversion[J]. Chinese Journal of Geophysics, 2020, 63(4): 1569-1584. |
| [13] |
李波, 文晓涛, 张懿疆, 等. 基于Lucy-Richardson算法和广义S变换的Q值提取[J]. 石油物探, 2019, 58(5): 689-699. LI B, WEN X T, ZHANG Y J, et al. Combined generalized S transform and Lucy-Richardson algorithm for Q-value extraction[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 689-699. DOI:10.3969/j.issn.1000-1441.2019.05.007 |
| [14] |
LI G F, HUANG W, ZHENG H, et al. Estimate error of frequency-dependent Q introduced by linear regression and its nonlinear implementation[J]. Journal of Geophysics and Engineering, 2016, 13(1): 11-17. DOI:10.1088/1742-2132/13/1/11 |
| [15] |
LEI X, MORGAN E. A comparison of methods for estimating Q[J]. Expanded Abstracts of 86th Annual Internat SEG Mtg, 2016, 3021-3025. |
| [16] |
赵秋芳, 云美厚, 朱丽波, 等. 近地表Q值测试方法研究进展与展望[J]. 石油地球物理勘探, 2019, 54(6): 1397-1418. ZHAO Q F, YUN M H, ZHU L B, et al. Progress and outlook of near-surface quality factor Q measurement and inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1397-1418. |
| [17] |
云美厚, 党鹏飞, 李伟娜, 等. 地层品质因子Q值地震反演问题剖析[J]. 石油地球物理勘探, 2017, 52(1): 189-198. YUN M H, DANG P F, LI W N, et al. On issues of formation quality factor inversion[J]. Oil Geophysical Prospecting, 2017, 52(1): 189-198. |
| [18] |
云美厚, 李伟娜, 党鹏飞, 等. 基于品质因子Q反演预测含气储层的潜在风险[J]. 地球物理学进展, 2018, 33(1): 304-310. YUN M H, LI W N, DANG P F., et al. Risk of gas reservoir prediction based on inverting quality factor Q[J]. Progress in Geophysics, 2018, 33(1): 304-310. |
| [19] |
秦宁, 李振春, 杨晓东, 等. 自动拾取的成像空间域走时层析速度反演[J]. 石油地球物理勘探, 2012, 47(3): 392-398. QIN N, LI Z C, YANG X D, et al. Image domain travel-time tomography velocity inversion based on automatic picking[J]. Oil Geophysical Prospecting, 2012, 47(3): 392-398. |
| [20] |
WONG J, HURLEY P, WEST G F. Crosshole seismology and seismic imaging in crystalline rocks[J]. Geophysical Research Letters, 1983, 10(8): 686-689. DOI:10.1029/GL010i008p00686 |
| [21] |
BREGMAN N D, BAILER R C. Crosshole seismic tomography[J]. Geophysics, 1989, 54(2): 200-215. DOI:10.1190/1.1442644 |
| [22] |
JAMES R. Integrated estimation of interval attenuation profiles[J]. Geophysics, 2006, 71(4): A19-A23. DOI:10.1190/1.2209722 |
| [23] |
HU W, LIU J, BEAR L, et al. A robust and accurate seismic attenuation tomography algorithm[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011, 2727-2731. |
| [24] |
CHEN H M, ZHOU H. Estimating velocity and Q by fractional Laplacian constant-Q wave equation-based full-waveform inversion[J]. Expanded Abstracts of 87th Annual Internat SEG Mtg, 2017, 1648-1653. |
| [25] |
WARD R W, TOKSOEZ M N. Causes of regional variation of magnitudes[J]. Bulletin of the Seismological Society of America, 1971, 61(3): 649-670. DOI:10.1785/BSSA0610030649 |
| [26] |
SHI Y, EBERHART R. A modified particle swarm optimizer[J]. IEEE International Conference on Evolutionary Computation Proceedings, 1998, 69-73. |
| [27] |
KENNEDY J, EBERHART R. Particle swarm optimization[J]. Proceeding of IEEE International Conference on Neural Networks, 1995, 1942-1948. |
| [28] |
陈愿愿, 邓小江, 王小兰, 等. 粒子群优化支持向量机算法在页岩储层总有机碳含量预测中的应用——以渝西地区Z井区为例[J]. 石油物探, 2021, 60(4): 652-663. CHEN Y Y, DENG X J, W X L, et al. Application of a PSO-SVM algorithm for predicting the TOC content of a shale gas reservoir: A case study in well Z in the Yuxi area[J]. Geophysical Prospecting for Petroleum, 2021, 60(4): 652-663. |
| [29] |
赵宝银, 陈思远, 陶钰, 等. 应用宽带Ricker子波的期望目标频谱整形[J]. 石油地球物理勘探, 2020, 55(3): 541-547. ZHAO B Y, CHEN S Y, TAO Y, et al. Spectrum shaping of desired targets based on broadband Ricker wavelets[J]. Oil Geophysical Prospecting, 2020, 55(3): 541-547. |



