2. 中海油田服务股份有限公司物探事业部, 天津 300451;
3. 海洋油气勘探国家工程研究中心, 北京 100028
2. China Oilfield Services Limited Geophysical Division, Tianjin 300451, China;
3. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China
拖缆地震数据采集是海上油气地震勘探的主要采集方式, 由勘探船拖拽枪阵与电缆沿设计测线行驶, 并控制枪阵激发地震波进行放炮, 拖缆上的检波器阵列接收并记录由海底反射回来的地震波信号, 经过地震数据处理即可反演海底地下的地质构造, 从而达到油气勘探的目的[1-2]。拖缆定位在海上地震数据处理中起到至关重要的作用, 其检波器阵列的位置精度直接影响地震数据的成像精度与可靠性[3]。为了确定检波器阵列在放炮时刻的位置信息, 通常会在勘探船及其拖拽的载体上安装各种定位设备, 主要包括: 安装于勘探船上, 用于获取船的三维坐标的差分全球定位系统(Differential GPS, 简称DGPS); 安装于勘探船上, 用于获取船头朝向的电罗经; 安装于勘探船、枪阵以及拖缆尾标上, 用于获取船参考站与枪阵、拖缆尾标移动站之间的基线向量的相对GPS(Relative GPS, 简称RGPS); 安装于拖缆上, 用于获取拖缆在该处的切线方位角的罗经鸟; 安装于枪阵、拖缆以及拖缆尾标上, 用于获取各声学节点之间的相对距离, 构成声学网络的声学鸟[4]。
海上三维地震勘探通常采用多缆作业, 每条拖缆一般长达数公里。水下的环境复杂多变, 难以确定拖缆的真实形状, 且定位观测值种类多、观测量大、观测质量不稳定, 这些因素都给拖缆定位数据的处理以及实现高精度拖缆定位带来了困难。长期以来, 我国在海上地震勘探拖缆导航方面主要依赖于进口。国内也有学者对拖缆定位数据处理方法进行了研究与探讨, 如易昌华等[5]对水下拖缆的形状确定进行了研究, 介绍了弧段模型、曲线积分模型以及多项式模型, 并进行了对比分析; 周波等[6]介绍了二维地震勘探中的拖缆定位数据处理算法及系统设计, 其单缆定位结果与国外软件相比偏差约10 m;姚宜斌等[7]对三维地震勘探中拖缆定位数据处理的关键算法进行了研究, 提出使用约束网平差与拟稳平差来对声学网络进行解算, 取得了较好的结果; 易昌华[8]比较全面地介绍了拖缆定位数据处理的预处理算法以及网络平差算法, 并对其进行了系统实现; 陈育才等[9]对水下拖缆的形态进行了分析, 对拖缆移动实现了可视化模拟; 孔振兴等[10]使用曲线多项式拟合算法进行缆形解算, 并对比分析了选择不同多项式阶数时的解算结果; 张昊楠等[11]在定位网络解算算法中加入卡尔曼滤波, 提升了多历元解算结果的稳定性。但国内目前仍缺少较为成熟的自主研发的三维拖缆导航数据处理系统。
本文针对目前海上三维地震勘探拖缆定位数据处理中存在的难点问题, 对数据预处理算法以及拖缆定位网络平差算法进行了研究, 设计并实现了一套数据处理系统, 并利用实际案例验证了系统的可行性与有效性。
1 难点分析水下拖缆受勘探船转向、洋流以及海浪的影响, 其缆形动态变化。为了获取各放炮时刻检波器阵列的位置信息, 需要使用定位传感器的观测值进行拖缆定位网络解算, 解算过程包括定位节点坐标推算与网络平差。定位节点坐标推算是对位于勘探船、枪阵以及拖缆尾标上的定位节点进行坐标推算, 为网络平差提供起算基准; 网络平差则通过建立拖缆数学模型, 使用拖缆定位网络观测值进行网络平差, 对拖缆的缆形与位置信息进行解算。
勘探船在一条测线上的放炮次数一般达到上千次, 采样率为1次/炮的定位传感器(如罗经鸟、声学鸟以及深度传感器, 炮间间隔约12 s)会在作业中产生上千个观测值, 而采样率为1次/s的定位传感器(如DGPS、RGPS以及电罗经)则会产生上万个观测值。海上地震勘探中大部分拖缆定位传感器位于水下, 测量环境复杂多变, 其观测值中普遍带有粗差与强噪声, 且各传感器的数据采集历元不同。由于这些客观因素的存在, 定位网络中的原始观测值不能直接用于平差计算, 需要先进行预处理, 主要包括粗差探测与剔除、滤波降噪以及数据同步。
2 算法设计 2.1 粗差探测与剔除由于水下观测环境较复杂, 拖缆定位观测值中普遍带有粗差, 有必要对观测数据进行粗差探测, 并剔除带有粗差的观测值。针对定位数据观测量大、观测时间长、观测值变化受海况影响等特点, 采用基于中值滤波的梯度算法对观测数据进行粗差探测。令原始观测数据序列为{xn}, 共包含n个观测历元, 其对应的观测时刻为{tn}, {yn}为原始数据序列{xn}经中值滤波处理之后的中位数序列, 即:
| $ y_i=\operatorname{median}\left\{x_j, |i-j| \leqslant \frac{l-1}{2}\right\} $ | (1) |
式中: l为中值滤波的采样窗口大小, 可根据不同观测值类型手动选择, 一般为奇数; 下标i, j为该数据在其对应数据序列中所在的位置。采样窗口大小l在数据序列的边界会进行自适应缩小, 保证中值滤波可以在边界处正常计算。滤波后得到的中位数序列{yn}与原始观测数据序列{xn}具有相同的长度。梯度算子▽定义为:
| $ \left\{\begin{array}{l} {\mathit{\nabla}} x_{i, j}=\frac{x_j-x_i}{t_j-t_i} \\ {\mathit{\nabla}} y_{i, j}=\frac{y_j-y_i}{t_j-t_i} \end{array}\right. $ | (2) |
基于中值滤波的梯度算法对观测值序列进行双向探测, 包括正向探测与反向探测。正向探测即从数据序列前端开始向尾端探测, 反向探测即从数据尾端开始向前端探测。正向探测流程如下:
1) 令i=1, j=i+1;
2) 计算▽xi, j与▽yi, j;
3) 计算梯度差值d=|▽xi, j-▽yi, j|;
4) 若d小于设定的阈值, 则令i=j, j=i+1, 否则认为观测值xj中可能带有粗差, 并令j=j+1, 转到步骤2)。
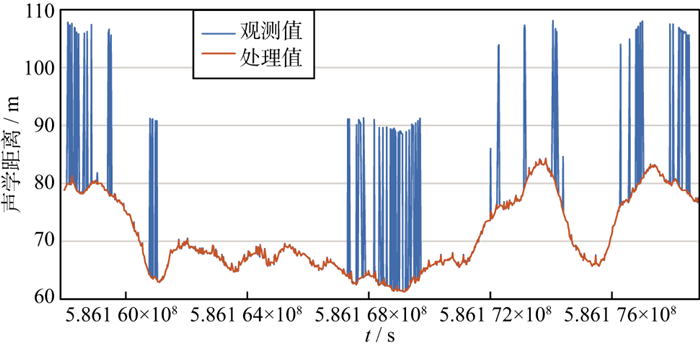
反向探测过程以此类推, 在双向探测中都被认为带有粗差的观测值则会被剔除。该算法的核心思想是将中值滤波后的数据作为参考, 并以双向梯度计算来达到探测粗差的目的。中位数并不会由于异常值过大或过小而变化, 使用中值滤波数据序列计算得到的梯度作为参考梯度可以反映出观测数据的真实变化水平。图 1给出了声学数据粗差探测结果。由图 1可见, 相比于对所有历元的观测值梯度设置一个经验的、固定的阈值的方法, 这种粗差剔除算法能在每个历元的数据点单独计算出一个梯度阈值, 能够更好地适应不同类型、不同采样率的观测值, 更好地应对作业过程中的不同海况。
|
图 1 声学数据粗差探测结果 |
经过粗差探测与剔除之后的观测值序列中还带有随机噪声以及一些未被成功剔除的小粗差, 需要使用滤波来对观测值序列进行降噪与平滑处理。低通维纳滤波是一种频率域滤波, 其频率响应函数w(f)可写为:
| $ w(f)=\left\{\begin{array}{cc} \frac{P(f)-N(f)}{P(f)} & f \leqslant f_{\mathrm{c}} \\ 0 & f>f_{\mathrm{c}} \end{array}\right. $ | (3) |
式中: f为数据频率; fc为截止频率, 可根据不同观测值的频谱信息进行手动选择; P(f)为总的信号功率; N(f)为噪声功率。对于位于截止频率以下的低频分量, 低通维纳滤波通过噪声功率来对其进行降噪处理。随机噪声可看作在所有频率上都具有相同的功率, 可将N(f)作为一个常量并对其进行估计。而位于截止频率以上的高频分量则会被全部去除。
观测数据通过快速傅里叶变换(FFT)算法从时域转换至频域进行处理, 再通过快速傅里叶逆变换(IFFT)算法由频域转换回时域。在这一过程中, 观测数据受到“边缘效应”的影响, 序列两端的数据通常会出现失真的情况。为了解决这一问题, 可以在序列两端进行增补数据, 且增补数据应与原始数据在时域图像中构成中心对称。增补后的数据序列长度应正好达到2的整数次幂, 这样可大幅度提高FFT与IFFT算法的计算效率。由于用于增补的数据与原始数据序列高度相关, 增补后的数据序列可看作与原始数据序列具有相同的噪声水平。综合上述因素, 这种增补方式可将“边缘效应”的影响降至最低, 提升计算效率, 且不会影响原始数据的噪声水平。
2.3 历元同步经过粗差探测与滤波降噪处理之后的观测数据还处于原始观测历元, 而地震数据处理需要的是放炮时刻的检波器位置, 所以, 在进行拖缆定位网络平差解算之前, 还需通过内插与外推的方法将原始观测数据同步至放炮时刻。在放炮时刻相邻两侧都存在正常观测值的情况下, 可以直接使用一阶线性内插来计算该放炮时刻的观测值。部分放炮时刻位于定位传感器开始记录数据之前或结束观测之后, 这时应使用时间上最相近的两个观测值进行外推计算。
2.4 定位节点坐标推算为了给拖缆定位网络提供必要的起算基准, 需先对枪阵与拖缆尾标上的定位节点进行坐标推算。拖船DGPS可获得三维坐标, 电罗经可获得拖船的船头朝向方位角。通过拖船上各节点之间在拖船坐标系之下的设计偏移, 即可推算出拖船上任意节点与定位传感器的坐标。设拖船上某点相对于DGPS节点的设计偏移为(xo, yo), xo以船右舷方向为正方向, yo以船头朝向为正方向。该点坐标(x, y)计算公式如下:
| $ \left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{cc} \cos\alpha_{\mathrm{v}} & -\sin\alpha_{\mathrm{v}} \\ \sin\alpha_{\mathrm{v}} & \cos\alpha_{\mathrm{v}} \end{array}\right]\left[\begin{array}{l} y_0 \\ x_0 \end{array}\right]+\left[\begin{array}{l} x_{\mathrm{DGPS}} \\ y_{\mathrm{DGPS}} \end{array}\right] $ | (4) |
式中: αv为船头朝向方位角, 由电罗经获得; (xDGPS, yDGPS)为DGPS节点获得的绝对坐标。
拖船上的RGPS参考站与枪阵以及拖缆浮标上的RGPS流动站形成基线向量观测值, 利用该观测值可以推算出各RGPS浮标的坐标。各RGPS流动站的坐标(xmob, ymob)可由(5)式获得:
| $ \left\{\begin{array}{l} x_{\mathrm{mob}}=S_{\mathrm{b}} \times \cos\alpha_{\mathrm{b}}+x_{\mathrm{ref}} \\ y_{\mathrm{mob}}=S_{\mathrm{b}} \times \sin\alpha_{\mathrm{b}}+y_{\mathrm{ref}} \end{array}\right. $ | (5) |
其中, Sb为基线长度, αb为基线方位角, 均由RGPS观测获得, (xref, yref)为拖船RGPS参考站坐标。
由于船上DGPS、电罗经以及RGPS观测值采样率较高, 观测质量稳定, 因此采用这种方式推算得到的RGPS节点坐标精度较高, 可作为拖缆定位网络的起算基准。
2.5 拖缆定位网络平差拖缆在水下可以看作一条光滑的曲线, 要获得高精度的拖缆位置与缆形, 必须对拖缆建立准确的数学模型并采取合适的算法对模型参数进行解算。目前有如下3种网络平差算法可供选择。
2.5.1 弧段模型算法弧段模型将拖缆缆形曲线离散为若干段相连的圆弧来表示, 以罗经鸟作为圆弧的端点, 以罗经鸟读数作为圆弧在该端点处的切线方位角。用这种方式可以获得拖缆的近似缆形, 此时, 从拖缆的一端开始可以逐个推算拖缆上所有定位传感器与检波器的近似坐标。之所以称之为近似缆形与近似坐标, 是因为其还需要通过边角网平差来进行二次调整。
边角网平差时选取拖缆上的声学节点坐标为待估参数, 除了声学节点之间的声学距离观测值之外, 还需要加入“派生观测值”, 包括由近似缆形推算得到的同缆相邻声学节点之间的“派生距离观测值”与“派生方位观测值”。派生观测值有两个作用: ①派生观测值可以将前、中、后声学网络联系起来, 进行整体平差; ②派生观测值是由近似缆形派生得到的观测值, 而近似缆形是由罗经鸟观测值所确定的, 加入派生观测值使得罗经鸟观测值能够以另一种形式参与边角网平差。
边角网平差可以得到相对精确的声学节点坐标, 而这些声学节点在平差后必然会偏离其原来的近似位置。此时, 需要对缆形进行二次调整, 使其上的声学节点能够吻合边角网平差的结果, 同时也能使拖缆整体获得更高精度的位置。缆形二次调整时, 以声学节点为端点进行分段调整, 每一段拖缆需要经过平移、旋转与缩放来吻合声学节点的位置。经过调整后的拖缆与检波器坐标即可作为最终的输出结果。
2.5.2 多项式拟合算法多项式拟合模型将拖缆上任意里程处的三维坐标用多项式来表示, 以拖缆上各点的里程为自变量, 其参数方程表示如下:
| $ \left\{\begin{array}{l} x=f_x(s)=a_0+a_1 s+a_2 s^2+\cdots+a_n s^n=\boldsymbol{S}^{\mathrm{T}} \boldsymbol{A} \\ y=f_y(s)=b_0+b_1 s+b_2 s^2+\cdots+b_n s^n=\boldsymbol{S}^{\mathrm{T}} \boldsymbol{B} \\ z=f_z(s)=c_0+c_1 s+c_2 s^2+\cdots+c_n s^n=\boldsymbol{S}^{\mathrm{T}} \boldsymbol{C} \end{array}\right. $ | (6) |
式中: x, y, z为拖缆上各点坐标的三维分量; s为该点在拖缆上沿缆线方向的里程; a0, a1, a2, …, an, b0, b1, b2, …, bn, c0, c1, c2, …, cn为待估计的多项式系数, A=[a0 a1 a2 … an]T, B=[b0 b1 b2 … bn]T, C=[c0 c1 c2 … cn]T; S=[1 s s2 … sn]T; n为多项式阶数。罗经方位观测值与声学距离观测值可通过(6)式建立起其与待估参数A, B, C之间的函数关系, 推导相应的误差方程, 并通过最小二乘准则对参数进行估计。在确定了待估参数A, B, C后, 再由(6)式计算拖缆上任意里程处的检波器坐标。
2.5.3 曲线积分算法曲线积分模型利用定位网络中的罗经观测值来拟合整条拖缆的方位角变化, 并沿拖缆进行坐标积分来确定拖缆上检波器的位置。拖缆的方位角函数α(s)可以写为:
| $ \alpha(s)=a_0+a_1 s+a_2 s^2+\cdots+a_n s^n $ | (7) |
若拖缆上已知某点里程为s0, 坐标为(x0, y0), 则拖缆上任意里程s处的坐标(x, y)可由积分得到:
| $ \left\{\begin{array}{l} x=x_0+\int_{s 0}^s \cos\alpha(s) \mathrm{d} s \\ y=y_0+\int_{s 0}^s \sin\alpha(s) \mathrm{d} s \end{array}\right. $ | (8) |
其中, 罗经方位观测值可通过(7)式建立其与待估参数的函数关系, 声学距离观测值可通过(8)式建立其与待估参数的函数关系, 并通过最小二乘估计获得参数a0, a1, …, an的最优估值。在确定(7)式中的待估参数后, 可由(8)式计算得到检波器坐标。
3种网络平差方法中, 多项式拟合算法与曲线积分算法估计的参数个数较少, 计算效率较高; 而弧段模型算法需要利用边角网平差来对所有的声学节点坐标进行估计, 在缆数较多的情况下计算效率比较低。在缆形解算方面, 利用多项式拟合算法与曲线积分算法解算得到的缆形光滑, 符合水下拖缆的物理特性, 但其在拖缆出现较大的弯曲时解算精度不佳; 弧段模型算法需要对拖缆进行分段调整, 解算得到的缆形存在分段过渡不平滑的现象, 但它可以较好地适应拖缆出现较大弯曲的情况。
3 系统实现数据处理系统基于Qt平台, 使用C++语言设计与实现, 并将本文数据处理算法集成于其中。该系统采用面向对象的设计思路, 将整套拖缆作业设备划分为载体类与观测值类并进行定义。载体类包括拖船、枪阵、拖缆以及尾标, 其中存储了各载体的配置信息以及所属关系; 观测值类包括DGPS观测值、电罗经观测值、RGPS观测值、深度观测值、罗经鸟观测值以及声学观测值, 均采用配置信息加数据体的结构, 配置信息中存储了观测值的ID号、系统改正、质量因子以及所在传感器信息, 数据体则采用变长队列的形式存储观测数据, 包括各个观测值的读数、观测历元等信息。
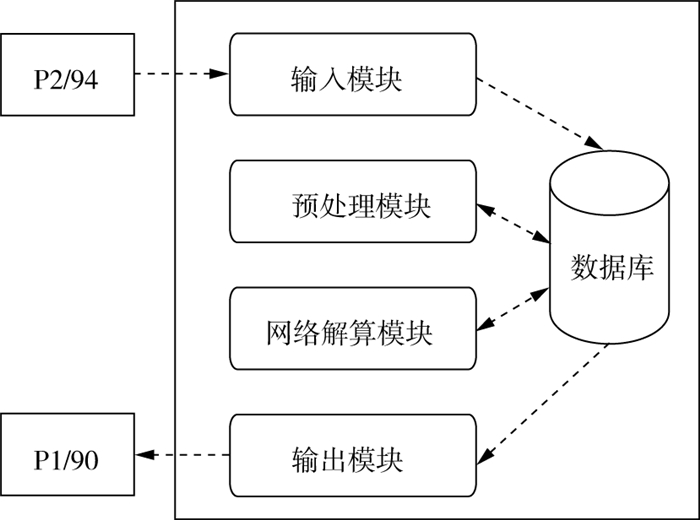
如图 2所示, 海上拖缆导航定位数据处理系统主要包括4个功能模块: 输入模块、预处理模块、网络解算模块以及输出模块。
|
图 2 拖缆导航定位数据处理系统架构 |
1) 输入模块。输入模块主要负责导入勘探作业时记录的导航数据P2/94(海上定位原始数据交换格式)文件, 并对其进行解析后写入数据库。
2) 预处理模块。预处理模块支持对观测值进行分组处理, 支持观测数据可视化, 在可视化界面中可以对原始观测数据进行手动剔除操作, 支持调用预处理算法时手动配置参数, 也支持观测值批量处理, 并生成批处理报告。
3) 网络解算模块。网络解算模块使用经预处理后的数据逐个历元进行网络平差解算。可在配置界面选择解算时使用的拖缆数学模型并手动配置模型参数, 解算时可根据每炮输出结果对定位网络及定位节点误差椭圆进行可视化, 解算后可对网络平差质量进行评估并形成平差报告, 检波器定位结果直接存入数据库。
4) 输出模块。输出模块将数据库中的解算结果输出至P1/90(海上定位成果数据交换格式)文件, 可选择输出的放炮历元范围, 输出船位、震源、尾标以及检波点的位置信息。
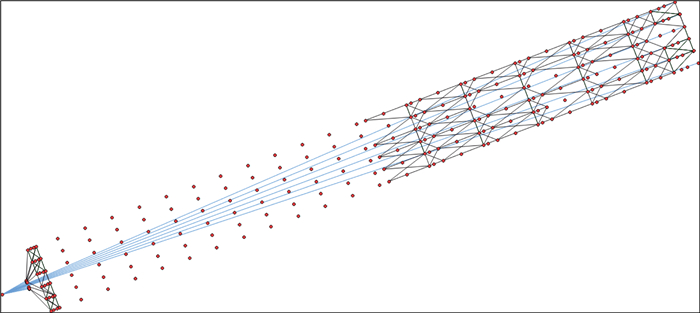
4 实际应用为了验证本文拖缆定位数据处理算法及系统的有效性, 选取两套三维勘探作业数据进行测试, 该次作业为6缆配置, 每套文件包含1 200个放炮历元。在数据处理系统中导入P2/94文件, 其作业配置如图 3所示, 声学网络为前-中后网络配置, 每条拖缆挂载26个罗经鸟, 15个声学鸟, 长度约为7 100 m, 且尾标挂载RGPS。
|
图 3 数据处理系统网络配置可视化界面 |
使用数据处理系统的预处理模块进行处理, 预处理模块中使用的算法参数配置如表 1所示。
| 表 1 预处理算法参数配置 |
完成数据预处理后, 在网络解算模块中选用多项式拟合算法进行网络平差解算。将两套P2/94数据的解算结果分别导出为P1/90文件, 由于海上勘探无法获取拖缆的准确定位坐标, 只能将其与国外主流商业软件解算输出的P1/90文件结果进行对比。作业时每条拖缆挂载检波器564个, 将6条拖缆共3 384个检波器1 200个放炮历元的解算结果与国外软件的解算结果进行对比, 统计各历元的检波器平均坐标偏差, 并将其坐标偏差投影到沿测线方向(DA)与垂直测线方向(DC), 对比结果如表 2所示。
| 表 2 检波器平均坐标偏差统计 |
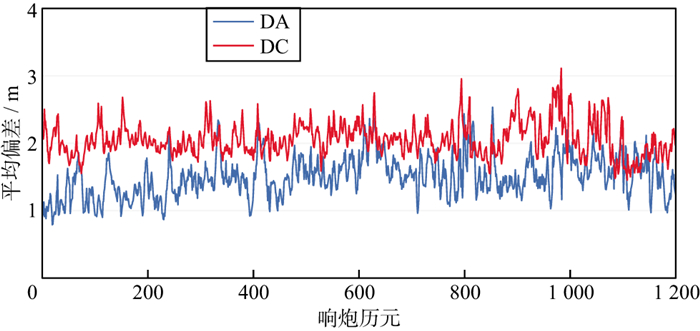
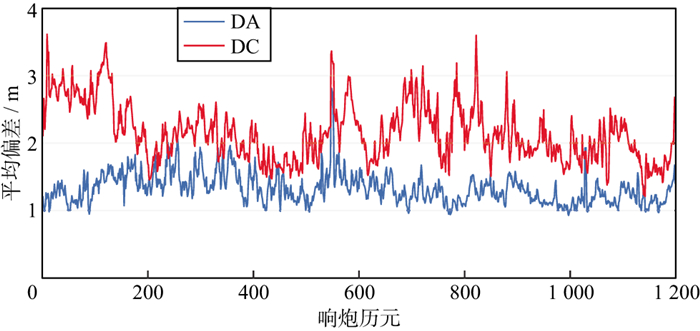
由表 2可以看出, 与国外软件的处理结果相比, 各历元的检波器平均DA偏差小于2.0 m, 标准差小于0.5 m, 最大值小于3.0 m;平均DC偏差小于2.5 m, 标准差小于0.5 m, 最大值小于4.0 m;平均点位偏差小于3.0 m, 标准差小于0.5 m, 最大值小于5.0 m。两套数据各个历元的平均检波器DA、DC偏差变化如图 4和图 5所示。
|
图 4 数据1各历元平均定位偏差变化 |
|
图 5 数据2各历元平均定位偏差变化 |
由图 4与图 5可以看出, 与国外软件的处理结果相比, 各个历元的检波器平均DA偏差均小于3 m, 平均DC偏差均小于4 m, 精度变化比较稳定, 说明设计与实现的数据处理系统解算结果与国外软件相近。
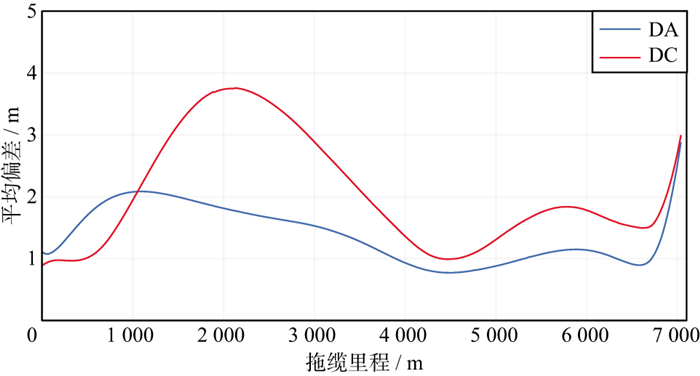
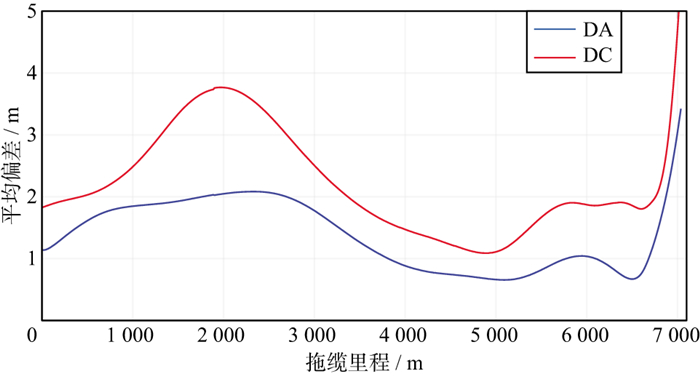
图 6与图 7展示了两套数据的检波器平均定位偏差在拖缆上不同里程处的变化情况。可以看出, 拖缆上各处的检波器定位精度变化比较平缓。两套数据的DA、DC偏差均在拖缆的前中部与尾部出现了峰值, 这是因为作业采用前-中后声学网络配置, 拖缆的前中部未挂载声学鸟, 定位观测值较少, 导致其定位精度会低于拖缆上有声学网络覆盖的部分; 而拖缆尾部的检波器定位偏差较大可能是由于拖缆在此处存在一定的弯曲, 且其最尾端未挂载声学鸟。
|
图 6 数据1拖缆各里程处平均定位偏差变化 |
|
图 7 数据2拖缆各里程处平均定位偏差变化 |
本文针对海上三维地震勘探拖缆导航定位数据处理难点问题, 对其数据预处理与定位网络平差关键算法进行了研究, 提出的基于中值滤波的梯度算法能有效地对拖缆定位观测值进行粗差探测, 给出的一整套数据处理流程成功地应用于三维拖缆导航定位, 并基于算法对数据处理系统功能进行了设计与实现。实际应用案例表明, 本文数据处理系统解算结果与国外主流商业软件相比, 检波器定位偏差小于3.0 m, 标准差小于0.5 m, 可以认为精度与国外主流商业软件相当, 能够满足海上三维拖缆勘探地震数据成像的精度需要。目前, 该系统已完成试应用, 将在实际生产中投入使用。
| [1] |
杜向东. 中国海上地震勘探技术新进展[J]. 石油物探, 2018, 57(3): 321-331. DU X D. Progress of seismic exploration technology in offshore China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 321-331. DOI:10.3969/j.issn.1000-1441.2018.03.001 |
| [2] |
王学军, 全海燕, 刘军, 等. 海洋油气地震勘探技术新进展[M]. 北京: 石油工业出版社, 2017: 1-7. WANG X J, QUAN H Y, LIU J, et al. New progress of offshore oil and gas seismic exploration technology[M]. Beijing: Petroleum Industry Press, 2017: 1-7. |
| [3] |
王守君, 杨凯, 唐进. 海洋地震勘探新技术与应用[M]. 北京: 石油工业出版社, 2016: 8-25. WANG S J, YANG K, TANG J. New technology and application of marine seismic exploration[M]. Beijing: Petroleum Industry Press, 2016: 8-25. |
| [4] |
张振波, 王征, 董水利, 等. 海上多源多缆地震采集综合导航定位数据处理技术[J]. 石油物探, 2013, 52(6): 630-635. ZHANG Z B, WANG Z, DONG S L, et al. Integrated navigation and positioning data processing in offshore multi-sources and multi-streamers seismic survey[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 630-635. |
| [5] |
易昌华, 曹国发, 方守川, 等. 深海拖缆勘探电缆形状确定方法研究[J]. 武汉大学学报(信息科学版), 2010, 35(6): 702-704. YI C H, CAO G F, FANG S C, et al. Fitting of offshore towed streamer shapes[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 702-704. |
| [6] |
周波, 宋伟伟, 易文婷. 二维深海勘探导航定位数据处理系统的设计[J]. 武汉大学学报(信息科学版), 2010, 35(6): 705-707. ZHOU B, SONG W W, YI W T. Navigation data processing for deep-sea exploration[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 705-707. |
| [7] |
姚宜斌, 易文婷, 宋伟伟. 深海拖缆导航勘探数据处理算法研究[J]. 武汉大学学报(信息科学版), 2010, 35(6): 698-701. YAO Y B, YI W T, SONG W W. Processing methods for navigation data of offshore towed streamer exploration[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 698-701. |
| [8] |
易昌华. 拖缆式石油勘探导航定位数据处理关键技术研究及系统实现[D]. 武汉: 武汉大学, 2013 YI C H. Study on key techniques of navigation & positioning data processing and system development in marine seismic streamer operation[D]. Wuhan: Wuhan University, 2013 |
| [9] |
陈育才, 叶美芬, 郑贵洲. 海洋地震勘探电缆形态算法分析与模拟[J]. 海洋技术学报, 2018, 37(3): 106-111. CHEN Y C, YE M F, ZHENG G Z. Analysis and simulation of cable shape algorithms in marine seismic exploration[J]. Journal of Ocean Technology, 2018, 37(3): 106-111. |
| [10] |
孔振兴, 赖祖龙. 地震导航定位算法研究[J]. 测绘通报, 2018(增刊1): 22-26. KONG Z X, LAI Z L. Key positioning algorithm of marine 3D towed streamer[J]. Bulletin of Surveying and Mapping, 2018(S1): 22-26. |
| [11] |
张昊楠, 阮福明, 胡广浩, 等. 海上三维拖缆综合导航系统关键定位算法[J]. 测绘科学技术学报, 2019, 36(5): 441-446. ZHANG H N, RUAN F M, HU G H, et al. Key positioning algorithm of marine 3D towed streamer integrated navigation system[J]. Journal of Geomatics Science and Technology, 2019, 36(5): 441-446. |




