2. 中石化石油物探技术研究院有限公司, 江苏 南京 211103
2. Sinopec Geophysical Research Institute Co., Ltd., Nanjing 211103, China
油气地震勘探最终目的是精确地描述油气藏并对其进行准确的含油气性分析, 做出最佳的钻井决策, 得到最高的油气勘探效益。油气地震勘探核心问题是由叠前地震数据及与待估计参数相关的先验信息, 进行宽波数带的弹性参数估计(或称广义的高精度地震波成像), 与岩石物理知识结合, 进行精确的油气藏描述和准确的含油气性评价。宽波数带的弹性参数估计问题是基于叠前地震数据和待估计参数相关的先验信息, 基于地震波理论和波动方程(及其各种简化形式), 基于Bayes参数估计理论, 提出并求解一个信息不足情形下的(强)非线性反问题(系统参数反演问题)。高精度地震波成像的信息源是“两宽两高(宽方位、宽频带、高密度、高信噪比)”的地震数据。而仅靠大炮数据采集的“两宽两高”叠前地震数据还远不能满足高精度、定量、针对岩性储层描述的高精度地震波成像的需求, 还需要补充待估计的与地下介质岩性变化相关的先验信息。可以说, 油气地震勘探的整个发展历史, 就是在地震波成像理论的指导下, 由地震数据采集技术(也包括其它先验信息收集技术)不断向前发展的牵引下而向前发展的。而地震数据采集技术的进步奠基于装备技术的发展。这些构成了当前油气地震勘探领域的核心技术概念。
地震波成像理论和技术将叠前地震数据及与待估计参数相关的先验信息映射成地下介质弹性参数、物性参数, 进而实现高精度的油气藏描述及高效油气开发。
常规的地震波成像以地下界面的带限反射系数为成像目标, 高精度的速度建模为保真和高分辨的带限反射系数成像提供更精确的背景速度场。由于震源激发端和检波端各种因素的不可控, 地震波成像方法技术并不能完全消除地震波传播过程中的各种影响因素, 即便做到保真和高分辨的带限反射系数的成像也非常不容易。但是, 深水、深层情况下碎屑岩储层、火山岩储层、碳酸盐岩储层和非常规储层都已成为油气勘探的常规目标。针对这些复杂岩性油藏地震勘探的需求, 地震波成像技术由定性的、带限反射系数为成像目标转为定量的、宽带波阻抗为成像目标成为必然选择。
当前, 石油工业界开展岩性油藏勘探的地震波成像主要依赖3项关键技术, 即层析速度反演技术、保真和高分辨方位角度带限反射系数成像方法技术、AVA分析/反演方法技术。3项技术是串联的, 最后一项技术反映了角度反射系数反演界面两边弹性参数的变化(ΔvP为纵波速度扰动; ΔvS为横波速度扰动; Δρ为密度扰动)。存在的主要问题是AVA分析/反演的基本理论基础是Zoeppritz方程, 而Zoeppritz方程是在平面波入射到广大的平反射界面上的假设情况下推导出的。在碳酸盐岩油藏、火山岩油藏等情形下是不合适的假设。另一方面, 保真带限反射系数估计本身就很困难, 反演结果存在很大的不确定性。常规1D波阻抗反演是当前波阻抗建模的主要方法技术, 但是1D波阻抗反演仅适用于水平层状介质情形[1]。历史上, 该项技术主要用于缓横向变化的碎屑岩沉积地层下的油气勘探中, 显然已经完全不适用于目前横向变化剧烈的复杂油气藏的勘探。
Bayes参数估计理论下的全波形反演(FWI)技术已经成为业界公认的高精度地震波成像的标志性技术[2]。从理论本质上看, FWI技术的目标是估计宽波数带的速度变化(或者波阻抗变化), 它是定量的地震波成像方法。众所周知, 当前FWI被定义为主要利用透射波估计高精度的背景速度模型, 为逆时偏移(RTM)或最小二乘逆时偏移(LS_RTM)提供更好的初始速度模型。即便如此, 也需要退化成利用透射波走时信息, 并且在海上低频长偏移距数据情形下, 才有可能产生实用的效果。根本的困难在于实际观测数据不能满足FWI反演的理论假设以及复杂介质变化(小尺度、强变化)情形下FWI反演的高度非线性性。因此, 实际数据情形下利用FWI反演技术进行宽带波阻抗为目标的成像显然是不可能的。
实际数据的地震波反演成像从来不是一个纯数学问题, 即便“两宽两高”的叠前地震数据依然不能满足岩性储层定量反演成像的需求, 必须发展出地质信息约束下的地震波成像新理论与新方法。定性的地震波偏移成像技术的研究已经趋于完善。但是, 任何更为高端的技术都是在现有技术基础上发展出来的。充分保留现有方法技术的优点, 充分借鉴Bayes参数估计理论下的FWI的理论优势, 充分利用大数据和机器学习(ML)中的理念和算法[3], 发展信息融合的深度域真三维宽带波阻抗成像, 认为是合理的针对岩性储层的定量地震波成像技术路线。
宽波数带波阻抗可以被分为低波数带(0~3Hz)、中波数带(4~8Hz)、高波数带(9~50Hz)和超高波数带(51~80Hz)4个部分[4](注: 其中的数字划分是相对的)。背景阻抗的信息来源一定是背景速度场和背景密度场; 高波数带阻抗的信息源一定是宽带反射系数(或宽带的速度扰动)。中波数波阻抗的信息来源更多地依赖于与地下介质波阻抗变化有关的(地质)先验信息; 超高波数波阻抗的信息源应该是测井数据和岩石物理知识。
分析可知, 由不同炮检对地震道中透射波和/或反射波地震子波传播的旅行时估计背景速度/各向异性参数(等于各向异性背景速度v(x, θ)), 背景速度估计结果是定量的。因为估计背景速度所用的正问题本质上由
另外, 分析可知, 实际数据情形下的FWI也不能得到由低波数, 到中波数, 再到高波数的波阻抗(或速度)反演结果。众所周知的关系式FWI=Tomography+LS_RTM仅仅在反演骗局(Inverse Crime)意义下是成立的[5]。对于实际数据, 这个公式会引起误导。在实际数据情形下, 基于反射地震子波振幅的LS_RTM方法并不能得到与地下反射系数同等量级的反演结果, 因此高波数速度扰动的估计过程是不可能收敛的(连反演结果量级都不能与低波数反演结果保持一致, 如何能产生收敛的反演结果?)。
依据上述分析, 我们(WPI研究组)提出了特征波反演成像(characteristic wave inversion imaging, CWI)与基于信息融合的宽带波阻抗建模(wide band impedance modeling, WBIM)的技术路线[6], 是一种针对岩性储层的定量地震波成像方法技术系列。关键技术包括: 背景速度模型建立方法、背景密度模型建立方法、保真的宽带反射系数估计方法和基于信息融合的宽带波阻抗建模方法。必须说明的是, 提高各环节建模精度的先验信息获取方法(包括先验信息的正则化约束方法)也是十分重要的关键方法技术。原因是即便有“两宽两高”的叠前地震数据还是不能很好地满足定量地震波成像的需求, 必须引入尽可能多的先验信息, 才有可能进一步提升各波数带的波阻抗建模精度。这与当前大数据、人工智能和机器学习等技术越来越多地渗透到勘探地震全流程中的趋势是完全一致的。因此, 基于信息的、定量的地震波成像代表了地震波成像技术的发展趋势。
理论数据和实际数据的应用实践证明了我们提出的特征波反演成像(CWI)与基于信息融合的宽带波阻抗建模(WBIM)流程及方法技术的有效性。
1 定量地震波成像理论基础前已述及, 油气地震勘探的核心是宽波数带的弹性参数估计, 它提供了高精度油藏描述的基础信息, 结合井数据、岩石物理和油气地质知识, 由高精度油藏描述和含流体性评价提供最佳的井位决策, 获得最佳的勘探效益。很显然, 油气勘探中宽波数带的弹性参数估计(或称高精度地震波成像)占据核心地位。我们将其定位成提出并求解一个信息不足情形下的(强)非线性反问题(系统参数反演问题)。
宽波数带的弹性参数估计(或称高精度地震波成像)的信息源包括叠前地震数据(尽可能是“两宽两高”的)及与待估计参数有关的先验信息。
Bayes估计理论奠定了宽波数带的弹性参数估计(或称高精度地震波成像)的理论基础。叠前地震数据被记为dobs(xS, xR, t); 待估计的宽波数带的弹性参数被记为m(x)。叠前地震数据一般被认为是五维数据体, 反演成像结果是深度域真三维的。叠前地震数据被认为是随机过程, 实际野外数据采集被认为是该随机过程的一次实现。认为波动方程(或某种变种)建立起了m(x)与dobs(xS, xR, t)之间一定的预测关系。很显然, 这样的预测关系是不确定的, 波动方程(或某种变种)并不能完全地预测dobs(xS, xR, t)中包含的各种复杂的波现象。实测数据的不确定性, 波动方程预测结果的不确定性, 使得我们有理由认为估计的结果也是不确定的。这就构成了Bayes估计理论的思想基础。
经典的Bayes公式为:
| $ P\left(\boldsymbol{m} \mid \boldsymbol{d}^{\mathrm{obs}}\right)=\frac{P\left(\boldsymbol{d}^{\mathrm{obs}} \mid \boldsymbol{m}\right) P(\boldsymbol{m})}{P\left(\boldsymbol{d}^{\mathrm{obs}}\right)} $ | (1) |
式中: P(m)代表先验的表达待估计参数的不确定性的概率密度函数; P(dobs|m)代表先验的波动方程(或某种变种)预测实测数据时不确定性的概率密度函数(也称似然函数), 这里面既有波动方程的不合适引起的预测结果的不确定性, 也有实际数据观测中各种复杂因素导致的观测结果的不确定性, 震源激发和检波器性能引起的不确定性也都包容在这个概率密度函数中。可以看出, (1)式中包含了实际地震数据观测、波动方程对高精度地震波成像的不满足; 也包含了引入与待估计参数有关的先验信息的必要性。仅仅靠波动方程对实际数据的预测误差很小(或似然函数P(dobs|m)取最大), 并不能(远远不能)保证反演结果的可靠性。P(dobs)是描述采集数据过程表现出的不确定性的概率密度函数。一般地, 我们很难获取这方面的先验信息, 索性假设P(dobs)满足均匀分布, 不再引入先验信息。因此, (1)被改写为:
| $ P\left(\boldsymbol{m} \mid \boldsymbol{d}^{\text {obs }}\right) \propto P\left(\boldsymbol{d}^{\text {obs }} \mid \boldsymbol{m}\right) P(\boldsymbol{m}) $ | (2) |
很显然, P(m|dobs)是后验条件概率密度函数。所谓后验概率是指实际数据观测已经获取的情况下, 待估计参数m(x)发生的概率。参数估计的合理逻辑选择自然是后验条件概率密度函数P(m|dobs)取最大时对应的
实际上, P(m)和P(dobs|m)都是很难实际计算得到的。因此, 先验地假定它们均满足Gauss概率分布。很多实际随机过程被假定满足Gauss概率分布, 这是有大数定理和中心极限定理支持的。因此, 有:
| $ P(\boldsymbol{m})=\frac{1}{\sqrt{(2 \pi)^M \operatorname{det}\left(\boldsymbol{C}_{\boldsymbol{m}}\right)}} \exp \left(-\frac{1}{2} \boldsymbol{m}^{\mathrm{T}} \boldsymbol{C}_m^{-1} \boldsymbol{m}\right) $ | (3a) |
| $ \begin{gathered} P\left(\boldsymbol{d}^{\mathrm{obs}} \mid \boldsymbol{m}\right)=\frac{1}{\sqrt{(2 \pi)^N \operatorname{det}\left(\boldsymbol{C}_{\boldsymbol{d}}\right)}} \exp \left\{-\frac{1}{2}\left[\boldsymbol{d}^{\mathrm{obs}}-\right.\right. \\ \left.\boldsymbol{K}(\boldsymbol{m})]^{\mathrm{T}} \boldsymbol{C}_{\boldsymbol{d}}^{-1}\left[\boldsymbol{d}^{\mathrm{obs}}-K(\boldsymbol{m})\right]\right\} \end{gathered} $ | (3b) |
式中: Cm代表待估计参数的协方差矩阵, M是它的维度; Cd代表观测数据的协方差矩阵, N是它的维度。K(m)=d抽象地表示波动方程(或其变种)对实测数据的预测关系, 数学上更多用第一类Fredholm积分方程来表示, 而非用微分形式的波动方程。地震勘探中Born近似后的散射场计算式就是典型的第一类Fredholm积分方程, 它建立起了地下介质参数的扰动量与波场扰动量之间的数学关系式。
将(3)代入(2)式得到:
| $ \begin{gathered} P\left(\boldsymbol{m} \mid \boldsymbol{d}^{\mathrm{obs}}\right) \propto L \cdot \exp \left\{-\frac{1}{2}\left\{\left[\boldsymbol{d}^{\mathrm{obs}}-\boldsymbol{K}(\boldsymbol{m})\right]^{\mathrm{T}} \cdot\right.\right. \\ \left.\left.\boldsymbol{C}_{\boldsymbol{d}}^{-1}\left[\boldsymbol{d}^{\mathrm{obs}}-\boldsymbol{K}(\boldsymbol{m})\right]+\boldsymbol{m}^{\mathrm{T}} \boldsymbol{C}_m^{-1} \boldsymbol{m}\right\}\right\} \\ =L \cdot \exp \left[-\frac{1}{2} \boldsymbol{S}(\boldsymbol{m})\right] \end{gathered} $ | (4) |
式中:
很显然, 根据指数函数的单调性, 后验概率密度最大化等价于S(m)取极小。S(m)被称为代价函数或误差泛函。Bayes参数估计问题转化为了误差泛函求极小问题。
| $ \begin{gathered} \hat{\boldsymbol{m}}=\underset{\boldsymbol{m} \in M}{\operatorname{argmin}} \boldsymbol{S}(\boldsymbol{m})=\underset{\boldsymbol{m} \in M}{\arg \min }\left\{\left[\boldsymbol{d}^{\mathrm{obs}}-\boldsymbol{K}(\boldsymbol{m})\right]^{\mathrm{T}} \cdot\right. \\ \left.\boldsymbol{C}_{\boldsymbol{d}}^{-1}\left[\boldsymbol{d}^{\mathrm{obs}}-\boldsymbol{K}(\boldsymbol{m})\right]+\boldsymbol{m}^{\mathrm{T}} \boldsymbol{C}_{\boldsymbol{m}}^{-1} \boldsymbol{m}\right\} \end{gathered} $ | (5) |
这就是最经典的FWI反演理论。其目标显然是全频带的、定量的参数估计。理论上看, Bayes估计理论下的FWI似乎是最完美的地震波成像方法。
(5) 式求解根本的困难在于实际观测数据不能满足FWI反演的理论假设; 在于复杂介质变化(小尺度、强变化)情形下它表现出高度非线性性。
经典的勘探地震中, 我们并没有硬解(5)式定义的反问题, 而是把正问题(波动方程对数据的预测关系)退化成线性关系, 即
| $ \begin{gathered} \boldsymbol{d}=\boldsymbol{K}(\boldsymbol{m})=\boldsymbol{K}\left(\boldsymbol{m}_0\right)+\frac{\partial \boldsymbol{K}}{\partial \boldsymbol{m}} \Delta \boldsymbol{m}+\frac{1}{2} \frac{\partial^2 \boldsymbol{K}}{\partial \boldsymbol{m}^2} \Delta \boldsymbol{m}^2+\cdots \\ \approx \boldsymbol{d}_0+\frac{\partial \boldsymbol{K}}{\partial \boldsymbol{m}} \Delta \boldsymbol{m} \end{gathered} $ | (6a) |
| $ \Delta \boldsymbol{d}=\boldsymbol{d}-\boldsymbol{d}_0=\frac{\partial \boldsymbol{K}}{\partial \boldsymbol{m}} \Delta \boldsymbol{m}=\boldsymbol{F} \Delta \boldsymbol{m} $ | (6b) |
式中: d0=K(m0), F=∂K/∂m。将(6)式代入(5)式, 得到:
| $ \begin{gathered} \Delta \hat{\boldsymbol{m}}=\underset{\Delta \boldsymbol{m} \in M^{\prime}}{\arg \min }\left[( \Delta \boldsymbol { d } ^ { \mathrm { obs } } - \boldsymbol { F } \Delta \boldsymbol { m } ) ^ { \mathrm { T } } \boldsymbol { C } _ { \Delta \boldsymbol { d } } ^ { - 1 } \left(\Delta \boldsymbol{d}^{\mathrm{obs}}-\right.\right. \\ \left.\boldsymbol{F} \Delta \boldsymbol{m})+\Delta \boldsymbol{m}^{\mathrm{T}} \boldsymbol{C}_{\Delta \boldsymbol{m}}^{-1} \Delta \boldsymbol{m}\right] \end{gathered} $ | (7) |
(7) 式是地震波层析成像和LS_PSDM共同遵循的参数估计反问题提法。因此有FWI=Tomography+LS_PSDM的说法。层析成像解决背景速度估计问题; LS_PSDM解决带限反射系数(或速度扰动量)估计问题。通过(6)式表示的线性化过程, (5)式定义的非线性反问题被转化为线性的。线性化的反问题理论上具备凸性, 存在唯一解。因此(7)式的求解理论上应该更稳定、迭代解的收敛性更好、反演结果更精确[7-8]。实际上, 常规的地震波成像过程中的三项关键技术: 层析成像、偏移成像和AVA反演成像都是线性反演理论在勘探地震中的应用实践。可以看出, 常规的地震波反演成像目的也是期望得到宽波数带的弹性参数估计。但核心问题出在Zoeppritz方程的理论假设(平面波入射到广大的地下介质平反射界面上)不适应当前常见的横向变化剧烈的介质情形; 偏移成像给出的反射系数不保真, 与地下介质反射界面的“真”反射系数差异可能很大, AVA反演缺乏可靠的数据基础。常规的1D波阻抗反演本质上是地下介质水平层状假设下的FWI反演, (5)式定义的FWI遇到的问题, 1D FWI同样不能回避。更重要的是, 目前油气勘探遇到的复杂介质和复杂油藏情形已经不符合其水平层状介质假设。
因此, 针对岩性油藏的定量地震波成像需要新的更合理的技术路线。我们是通过修改(5)式定义的FWI形成由特征波反演成像+基于信息融合的宽带波阻抗建模构成的定量地震波成像路线。
由前述Bayes估计理论可知, 波动方程(或各种变种)对实测数据(中的波现象)的预测关系, 本质是待估计参数与波现象之间的关系是否接近线性决定了形成的反问题是否凸的, 反问题是否有很好的凸性决定了反问题的求解是否能得到稳定可靠的解。先验信息的引入可以促进解的稳定性和精度进一步提升, 但过分依赖初始模型或先验信息提高解的精度逻辑上是不合理的。因为先验信息的获取往往比“两宽两高”的地震数据采集更困难, 代价更大。比如我们不可能钻很多井来获取关于地下介质弹性参数、物性参数的先验信息。
为此, 我们提出了特征波反演成像的概念, (5)式被改写成:
| $ \begin{gathered} \hat{\boldsymbol{m}}=\underset{\boldsymbol{m} \in M}{\operatorname{argmin}}\left[\left(\boldsymbol{d}_C^{\mathrm{obs}}-\boldsymbol{d}_C^{\mathrm{cal}}\right)^{\mathrm{T}} \boldsymbol{C}_{d^{\prime}}^{-1}\left(\boldsymbol{d}_C^{\mathrm{obs}}-\boldsymbol{d}_C^{\mathrm{cal}}\right)+\right. \\ \left.\boldsymbol{m}^{\mathrm{T}} \boldsymbol{C}_{\boldsymbol{m}}^{-1} \boldsymbol{m}\right] \end{gathered} $ | (8) |
式中: dCobs=T(dobs), T(·)代表一个特征波现象提取算子, 把实测炮集中的特征波现象dCobs提取出来。譬如初至波; 特征反射层对应的反射波都可以认为是特征波。而且dCobs也可以是特征波的走时。dCcal=KC(m)代表特征波传播算子KC模拟出的特征波现象。
我们认为, 特征波成像主要包括初至波层析成像和特征反射层导引下的特征反射波层析成像。常规的射线理论折射波层析、基于各种反射波时距关系的NMO速度分析、共成像点道集射线层析成像也可归于特征波成像的范围。
很显然, 特征波成像是基于不同波现象同相轴上地震子波的走时估计背景速度, 这是一个定量反演过程。所得的背景速度与地下介质速度量级是一致的。它们可被认为是定量的成像方法。
(7) 式规定的另一个线性化反演问题是最小二乘叠前深度偏移(LS_PSDM)或LS_RTM。常规的地震波偏移成像是LS_PSDM或LS_RTM的简化实现。(7)式的数学求解可以表示为:
| $ \begin{aligned} & -\boldsymbol{F}^{\mathrm{T}} \boldsymbol{C}_{\Delta \boldsymbol{d}}^{-1}\left(\Delta \boldsymbol{d}^{\mathrm{obs}}-\boldsymbol{F} \Delta \boldsymbol{m}\right)+\boldsymbol{C}_{\Delta \boldsymbol{m}}^{-1} \Delta \boldsymbol{m}=0 \\ & \left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{C}_{\Delta \boldsymbol{d}}^{-1} \boldsymbol{F}+\boldsymbol{C}_{\Delta \boldsymbol{m}}^{-1}\right) \Delta \boldsymbol{m}=\boldsymbol{F}^{\mathrm{T}} \boldsymbol{C}_{\Delta \boldsymbol{d}}^{-1} \Delta \boldsymbol{d}^{\mathrm{obs}} \end{aligned} $ | (9) |
常规的地震波偏移成像的数学表述式为:
| $ \Delta \boldsymbol{m} \approx \boldsymbol{F}^{\mathrm{T}} \boldsymbol{C}_{\Delta \boldsymbol{d}}^{-1} \Delta \boldsymbol{d}^{\mathrm{obs}} $ | (10) |
实际上, 石油工业界常用的偏移成像思想和方法技术并非由上述Bayes估计理论退化产生的, 而是由物理直觉与波传播算子相结合导出。认为地表观测的波场是由地表主动源产生的下行波激活地下介质波阻抗异常体, 产生上行绕射波场, 所有地下介质中的波阻抗异常体产生的上行波场的叠加形成地表观测波场。尤其考虑到多次覆盖的地表数据激发接收方式, 地震波成像就是把所有地表接收的、由所有炮激发的上行绕射波场推到或收敛到产生它们的波阻抗异常体上。Kirchhoff积分偏移成像就是直接地按上述物理逻辑实现的; 单平方根波动方程偏移是按正向外推炮端激发波场与反向外推接收端波场并在波阻抗异常体处的相关(相关最大对应偏移速度模型是正确的)进行成像的; 双平方根波动方程偏移是按炮点和检波点同时沉降的方式, 把炮点和检波点外推到波阻抗异常体处按成像条件(上行波出发时刻为零)提取成像值进行成像的。但是, 这些具体的实现方法本质上与Bayes估计理论退化出的(10)式是统一的。只不过前者物理意义和几何意义更清晰; 后者的数学算法更严谨。
很显然, 石油工业界常用的偏移成像只不过是对地下波阻抗异常体的位置进行定位, 定位精度依赖于背景速度。定位结果的表现是由地震子波的振幅体现出来的, 正是“放置或搬家”到成像点处反射子波的振幅体现出地下介质反射系数的相对变化(并期望这种相对变化能比较真实地反映地下介质反射系数真实情况)。直到目前的油气地震地质解释主要还是利用了地震波成像提供的波阻抗异常体的空间定位信息和保真的反射强度信息。事实上, 相关成像条件得到定位结果是由下行波场与外推到成像点处的下行波场中子波的相关系数体现出来的, 与地震子波的振幅关系更远。如果不强调偏移成像的保真处理, 成像结果得到的带限反射系数与地下介质反射系数之间可能相差极大。
实际观测波场中, 各震源激发产生的地震波能量(振幅)有复杂的影响因素, 炮和炮之间差异很大; 检波器测震结果的物理意义不同, 有位移检波器、速度检波器、加速度检波器和压力检波器, 各检波器与介质的耦合相差很大, 检波器本身对不同频率响应的一致性很难保证, 导致检波器检测的地震波振幅是相对的。而且各检波器对同一炮激发的震动的响应差异很大, 即便相邻检波器测量的同一反射层的反射子波振幅也很不相同。这些复杂的因素并不能被正问题K(m)=d所描述。地震波反演成像中的正算子很简单, 常密度声波方程最常用, 而且又被引入了Born近似, 复杂介质对波场的改造作用不能在成像过程中得到消除。因此, 实际数据情况下, 即便使用LS_RTM方法也得不到收敛的定量成像结果。理论框架下的FWI和LS_RTM在自身的理论假设下可以得到可靠的定量成像结果, 遗憾的是, 这只是个反演骗局(Inverse Crime)。
当前, FWI_Imaging[9-11]或全波数带FWI[12]试图由透射波FWI估计低波数带背景速度, 然后进到反射波FWI估计中波数带的背景速度, 再进展到估计高波数带的速度扰动量(这已经是LS_RTM解决的问题, 这是LS_RTM被称为高波数参数反射波FWI的原因)。事实上, 由于FWI反演迭代过程中, 由利用波现象同相轴上地震子波的走时信息到利用地震子波的振幅信息, 迭代反演中的梯度项由定量变为“定性”, 不受控制的FWI根本不可能由定量的背景速度的更新自动地转到定量的高波数扰动量的更新。因此, 尽管在Inverse Crime意义下, FWI的梯度项由背景速度的更新自动地转到高波数扰动量的更新似乎是理所当然的(事实上, 也不是那么的理所当然); 但对于实际数据, 这是不可能自动发生的。
影响地震波振幅的因素非常复杂, 基于地震子波振幅的参数估计或定量成像到目前为止并没有完善的解决方案。上述分析清楚地说明, 针对岩性储层的定量地震波成像的真正困难在于高波数参数的定量化估计。更明确地, 保真与宽带反射系数成像是定量地震波成像的难点。
假定已经获得了定量的背景速度、背景密度、保真与宽带反射系数, 基于上述3种成像结果的地震地质解释依然不是深度域真三维空间的油气地质信息的真实反映。深度域真三维空间的宽带波阻抗才是更能反映地下介质岩性变化情况的成像结果。深度域真三维空间的宽带波阻抗自然不能作为FWI的成像目标, 这只会徒然增加反问题的非线性性, 求解过程更不收敛, 多解性更严重。这正是我们提出信息融合宽带波阻抗建模的本质原因, 信息融合宽带波阻抗建模避开了FWI反演宽带波阻抗的强非线性性, 可以将更多的与阻抗有关的先验信息融入到宽带波阻抗建模过程中, 从而充分借用当前机器学习领域发展的新思想和新算法。
定量地震波反演成像是工业界有急迫需求且理论上也存在待解决问题的研究方向。我们(WPI研究组)提出的CWI(Characteristic Wave Inversion)+WBIM(Wide Band Impedance Modeling)策略就是一种定量的地震成像技术路线。
2 定量地震波成像技术路线前已述及, 当前油气地震勘探主要还是利用了地震波成像提供的地下介质波阻抗异常体的定位信息, 以及偏移成像算法附带产生的相对保真的反射强度信息, 进行地震地质解释, 在井数据和油气地质知识的辅助下进行井位决策和钻井方案决策。
很显然, 地震波成像由定性的、主要反映地下介质几何形态附带表现地下介质反射强度变化的带限反射系数成像发展到定量的、反映地下介质岩性变化的宽带波阻抗成像, 显然满足了油气工业的重大需求。图 1展示了由叠前地震数据与待估计参数相关的先验信息映射成油藏描述需要的定量地震成像结果的3条技术路线。
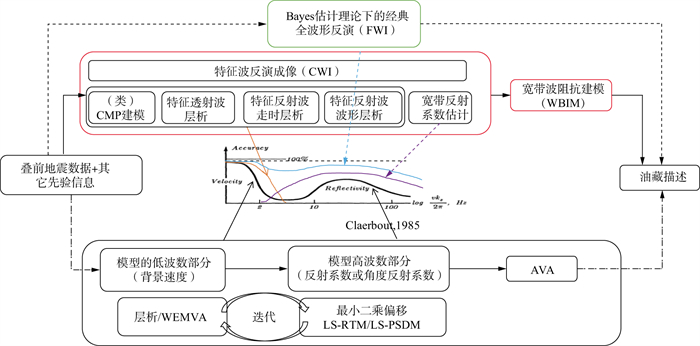
|
图 1 由叠前地震数据与待估计参数相关的先验信息映射成油藏描述需要的定量地震成像结果的3条技术路线 |
由前述理论分析知道, Bayes估计理论下的FWI是定量地震波成像最为完善的方法技术。但是, 在实际数据情况下, FWI直接反演宽带波阻抗是不可能的。这是一个高度非线性的反演问题。
常规的做法包括3项核心技术, 即背景速度层析成像; 带限的角度反射系数成像和AVA反演(也包括1D波动方程波阻抗反演), 存在的问题(分析后认为)主要是AVA反演的Zoeppritz方程理论假设不适应当前复杂的勘探目标和角度反射系数成像结果存在严重的不确定性。另外, 1D波动方程波阻抗反演的理论假设与当前勘探实际差异过大, 横向变化剧烈的介质情况下, 根本不存在满足1D波动方程的1D数据。
可以看出, 图 1中所示的走向定量油藏描述的常规技术路线越来越不适应当前复杂介质与复杂油藏的勘探实际。
HAFFINGER等[13]提出基于FWI反演的AVA弹性参数反演流程(wave-equation based AVO inversion, WEB-AVO)试图解决定量储层描述问题。但是, 基于FWI背景速度及叠前深度偏移成像道集和1.5D弹性参数反演这三项关键技术的WEB-AVO存在很多逻辑上令人质疑的地方, 譬如叠前深度偏移给出的零偏移距地震剖面是否满足1.5D弹性波方程的要求?1.5D弹性波反演依然是个强非线性问题, 如何能得到稳定的反演解?另外, 1.5D弹性参数反演假设地下介质水平层状也不适应当前横向变化复杂的勘探目标。
根据上一节的理论分析, 我们(WPI研究组)提出了另外一条定量地震波成像技术路线(图 2)。
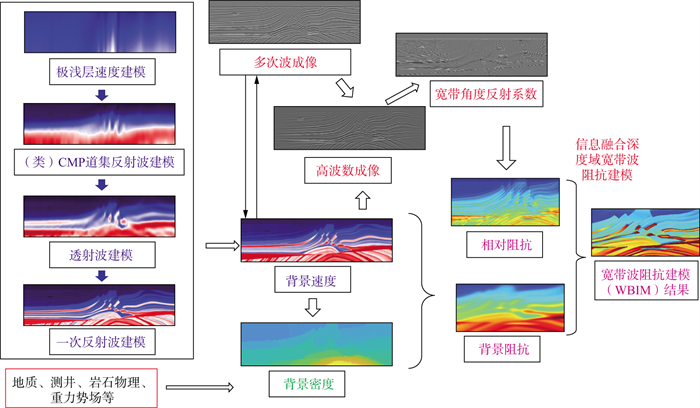
|
图 2 基于特征波成像+宽带波阻抗建模的定量地震波成像技术路线 |
该技术路线中包括背景速度建模、背景密度建模、宽带反射系数(或高波数参数扰动量)估计及信息融合宽带波阻抗建模四大部分。
背景速度和背景密度构成的背景阻抗对于岩性油藏的描述与评价具有重要意义。背景速度模型的构建包含如下5项关键技术。
1) 可靠的初至波识别与初至走时拾取方法技术。我们提出, 弱初至掩埋在强噪声的情形下, 基于高维、多属性、Markov最佳状态转移理论框架, 充分利用机器学习领域发展出的新算法, 实施初至波识别与走时拾取。不能认为初至波FWI可以避开可靠的初至波识别与初至走时拾取的困难。事实上, 复杂初至情形下初至波FWI也不能提供好的背景速度反演结果。除了初始模型差异过大之外, 这正是初至波走时测量精度不能保证所引起的。单独处理初至波识别与初至波走时拾取可以通过各种预处理和先验信息的引入解决实际数据(尤其是陆上地震数据)不满足初至波FWI理论假设引起的问题。到目前为止, 弱初至掩埋在强噪声情形下的初至波识别与初至走时拾取依然是没有得到很好解决的问题。
2) 高效率且适应非水平地表的初至波走时波动理论层析成像方法技术。
3) (类)CMP道集动校正扫描速度分析方法技术。类CMP道集是指PSTM或PSDM后成像道集反动校正后得到的所谓的CMP道集, 反动校正用偏移速度。类CMP道集受横向变速的影响小, 动校正速度分析结果更符合地质实际。
4) 特征反射结构导引下的特征反射波层析成像方法技术。利用反射波建立中深层背景速度不需要所有层位的反射波信息, 基本原则是先用一些特征反射结构(特征反射层)对应的反射波同相轴(走时), 进行大套地层的层速度估计。然后, 逐渐放入一些相对弱一些的反射层对应的反射波同相轴(走时), 提高层速度估计结果的分辨率。
5) 反射波FWI层析成像方法技术。在步骤4提供的初始速度模型的基础上, 进行少许几次反射波FWI层析成像迭代。其中的关键是要引入对梯度有地质含义的正则化, 并尽可能压制掉偏移响应梯度项的影响。
油气地震勘探中, 背景密度模型的构建是比较困难的。原则上, 选择包含密度的波动方程(譬如变密度声波方程), 利用FWI进行多参数反演是可以反演密度的。但这是另一个反演骗局。实际数据情形下, 密度变化会影响速度, 速度影响波的到达时, 因而似乎可以由波的到达时反演密度。但是, 密度和波的到达时的数学关系是什么?目前缺乏这样的数学物理关系式。它们的关系可能是非线性的异常复杂的关系。密度变化影响同相轴上地震子波的振幅是确定的, 密度变化导致波阻抗和反射子波振幅变化是确定的。但是, 影响振幅的因素太多, 这些因素构成了由叠前地震数据基于Bayes估计理论下的FWI反演密度, 因为非线性性很强, 极难在实用中见到效果的根本原因。据此, 我们提出两条构建背景密度模型的技术路线。首先, 由测井数据提供的密度信息和地震波成像提供的反射结构信息, 提出多信息约束下的密度场插值反问题, 这是多约束条件下的非线性性优化问题, 解此优化问题, 得到背景密度场。其次, 如果探区内有重力势场观测数据, 再提一个重力势场约束下多信息约束的密度反演问题, 把前一步插值方法获得的背景密度场作为初始值, 求解该反问题得到所要的背景密度场。由背景速度场和背景密度场就可以得到背景波阻抗。为了方便, 也可以借用已有的速度和密度之间的岩石物理关系式, 计算出密度场, 从而得到背景密度场。
宽带反射系数(或高波数参数扰动量)估计在宽带波阻抗建模中提供高波数带(譬如9~50Hz)的(相对)波阻抗变化信息。理论上, 我们需要的是零角度反射系数。实际情况下, 一般由角度反射系数的加权叠加作为零角度反射系数的近似。理论上, 我们需要的是只有主瓣没有旁瓣的零角度反射系数, 主瓣宽度也要尽可能地小。实际上, 这也是地震波成像的期望目标。有限频带的震源激发和有限孔径的地表接收下的叠前地震数据不支持我们得到这样的期望成像目标。实际数据情况下, 适用于宽带波阻抗建模的反射系数获取方法应该是: ①做好地表一致性处理; ②做好保真的偏移成像(至少要消除球面扩散和吸收衰减)得到最佳的Imig(保真的偏移成像结果); ③用H*ITrue=Imig定义一个其它信息约束(主要是三维空间中的构造约束)下的图像反褶积问题(其中H是Hessian矩阵), 求解该反问题得到更宽带的Itrue(频带拓宽后的保真的偏移成像结果); ④井震结合标定Itrue的幅值大小。至此, 可以认为得到了定量的宽带反射系数估计结果。
目前, 油气地震勘探地震地质解释的主要信息来源就是带限反射系数成像结果。但是, 很显然反射系数R=(I2-I1)/(I2+I1)仅仅反映界面处的岩性变化。深度域全三维空间中大量的岩性变化信息并不包含在带限反射系数成像结果中, 而地质解释人员关心的是深度域全三维空间中介质岩性的变化。这也是为什么一定要追求深度域全三维空间中岩性变化信息完整刻画的地震波成像结果的根源。众所周知, 宽波数带的纵波速度vP(x, y, z)、横波速度vS(x, y, z)、密度ρ(x, y, z), 波阻抗I(x, y, z), 泊松比σ(x, y, z)都可以从不同的角度描述深度域全三维空间中的岩性变化, 它们之间并不是相互独立的, 而是紧密关联的。目前, 我们的成像目标是宽波数带的波阻抗I(x, y, z)。事实上, 宽波数带的纵波速度vP(x, y, z)也是很合适的选择。我们不是将它定为Bayes估计理论下FWI方法技术的成像目标, 而是在已知背景阻抗和宽带反射系数(或高波数参数扰动量)估计结果的基础上, 提一个在其他先验信息约束下的信息融合反问题, 进一步融入更多的有地质意义的先验信息(譬如地震相), 将背景阻抗和宽带反射系数融合成宽带波阻抗。这样做避开了Bayes估计理论下FWI方法技术估计宽带波阻抗的强非线性性, 得到的结果更稳定、更符合地质逻辑, 而且没有降低背景阻抗和宽带反射系数所包含信息的分辨率。
3 宽带波阻抗建模影响因素分析定义并求解一个约束优化问题实现信息融合宽带波阻抗建模, 目的是把背景阻抗和宽带反射系数在其他信息的约束下, 有机地融合在一起, 得到低波数带(0~3Hz)、中波数带(4~8Hz)和高波数带(9~50Hz)成分都合理存在的宽带波阻抗模型。通过数值实验在Marmousi模型上分析背景阻抗的精度和宽带反射系数的精度对宽带波阻抗建模结果的影响。目的是依据分析结果得到提高宽带波阻抗建模精度的合理做法。
3.1 背景阻抗的生成将图 3所示的不同平滑半径的高斯平滑算子施加在Marmousi模型上, 得到不同平滑程度的背景速度。用描述速度密度之间关系的Gardner关系式产生密度场, 从而生成平滑程度的背景阻抗。图 4展示了平滑半径分别为40m, 120m, 240m, 360m的背景阻抗。
|
图 3 半径为R的Gauss平滑算子示意 |
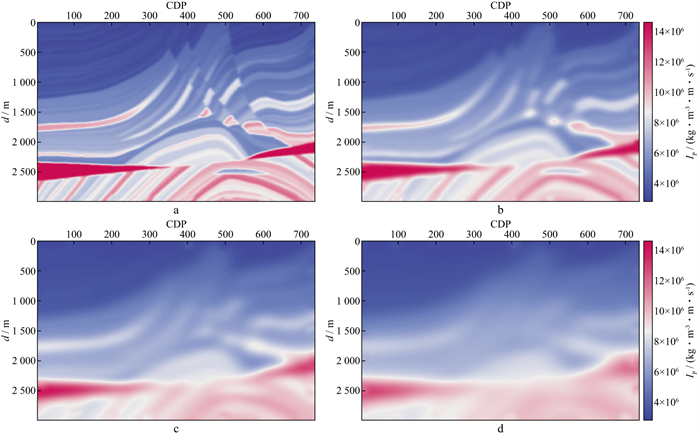
|
图 4 不同平滑半径的背景阻抗 a 平滑尺度R=40m的阻抗结果; b 平滑尺度R=120m的阻抗结果; c 平滑尺度R=240m的阻抗结果; d 平滑尺度R=360m的阻抗结果 |
为了更清楚地看出平滑算子的影响, 从图 4中各子图抽出第200道(模型中间一道)进行阻抗曲线展示, 其中图 5a为真值, 图 5b至图 5e分别是40m, 120m, 240m和360m平滑后的结果。

|
图 5 平滑后的背景阻抗抽线对比 a 第200道的真值; b 40m平滑后的结果; c 120m平滑后的结果; d 240m平滑后的结果; e 360m平滑后的结果 |
由于频率广为大家熟知, 通过关系式f/(df*nf)=k/(dk*nk)把深度域模型Fourier变换对应的波数折算成频率。其中, df, nf分别代表频率域采样间隔以及采样点数; dk, nk代表波数域采样间隔以及采样点数。图 6所示为图 5中各曲线对应的振幅谱。
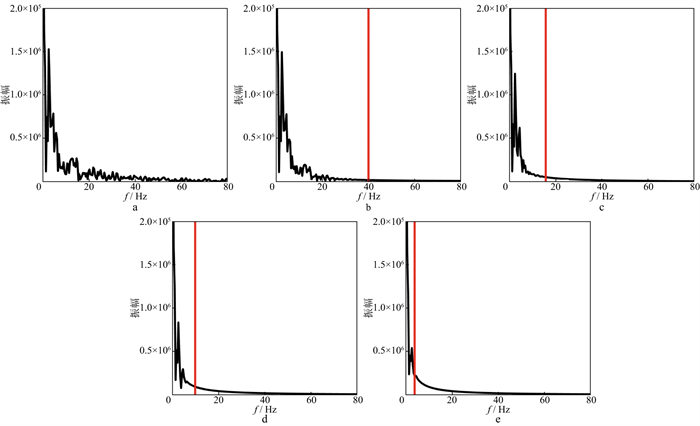
|
图 6 图 5中各曲线对应的振幅谱 a 真实模型对应的振幅谱(波数谱); b 平滑尺度R=40m的阻抗结果对应的振幅谱(波数谱); c 平滑尺度R=120m的阻抗结果对应的振幅谱(波数谱); d 平滑尺度R=240m的阻抗结果对应的振幅谱(波数谱); e 平滑尺度R=360m的阻抗结果对应的振幅谱(波数谱) |
从图 6可以看出, 随着平滑尺度的增大, 高波数的成分逐渐降低。平滑半径R=40m时, 波阻抗中40Hz以上的频率完全衰减; 平滑半径R=120m时, 16Hz以上的频率完全衰减; 平滑半径R=240m时10Hz以上的频率完全衰减; 平滑半径R=360m时4Hz以上的频率基本完全衰减。
3.2 宽带波阻抗建模需要什么样的反射系数成像结果?即便最高精度的叠前深度偏移成像, 由于受实测地震数据中激发接收的地震子波频带有限和仅在地表观测的观测方式的孔径有限, 得到的带限反射系数必然是雷克(Ricker)子波型反射系数。雷克(Ricker)子波型反射系数的典型特征是主瓣比较宽、旁瓣比较深。主要原因是缺低中频和频带窄。我们认为, 各种地震子波的分辨率取决于完整的振幅谱, 而相位谱的影响是次要的。低中频优势成分的存在是让子波旁瓣变浅, 从而提高弱层分辨能力的重要信息源。由于雷克(Ricker)子波型反射系数主瓣比较宽、旁瓣比较深, 因而它不是宽带波阻抗建模所期望的反射系数。
3.3 宽带波阻抗建模需要什么样的带限反射系数?为了回答这个问题, 我们测试了4种类型的反射系数。这4种类型的反射系数见图 7。首先是脉冲型反射系数, 这是我们最想要得到的反射系数, 它是全频带的。其次是(我们WPI称谓的)高斯型反射系数, 高斯型反射系数相对于脉冲型反射系数主要是衰减了高频信息, 但低中频信息丰富。然后, 是(我们WPI称谓的)期望子波型反射系数, 具有窄主瓣、低旁瓣的特征。最后, 是雷克(Ricker)子波型反射系数。这是宽带波阻抗建模中最不想要的。雷克(Ricker)子波型反射系数的低频和高频都大幅度衰减, 并且旁瓣的能量比较强, 会引入较多的假的波阻抗高频信息。需要说明的是期望子波是我们根据地质分辨率要求, 用子波的主旁瓣宽度比和高度比为参数定义的高分辨子波。
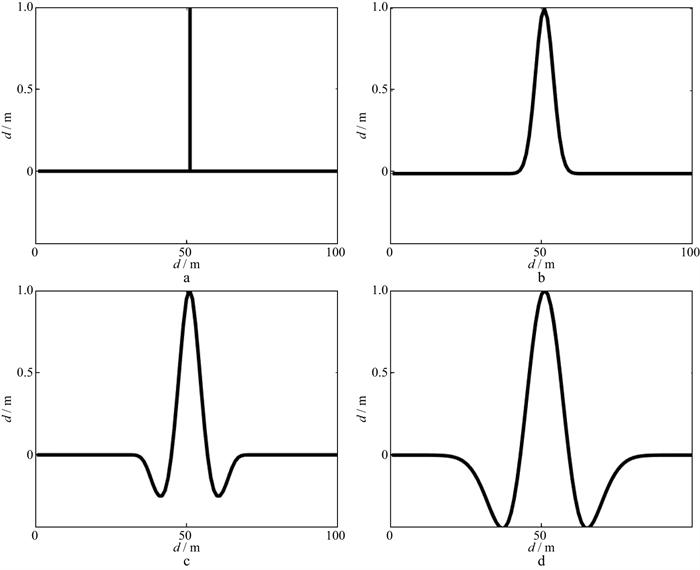
|
图 7 四种类型的反射系数示意 a 脉冲型反射系数; b 高斯型反射系数; c 期望子波型反射系数; d 雷克子波型反射系数 |
图 8展示了上述4种反射系数表示的Marmousi模型。相当于我们假定用叠前深度偏移成像方法得到了图 8展示的偏移成像剖面。由图可见, 脉冲型反射系数和高斯型反射系数表示的Marmousi模型成像剖面是理想的和期望的。
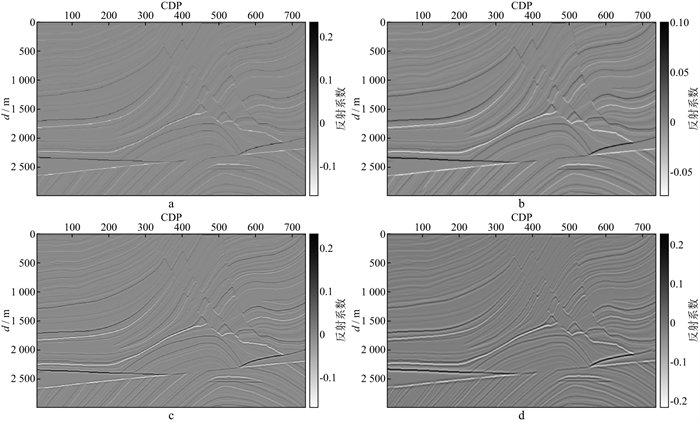
|
图 8 4种反射系数表示的Marmousi模型 a 采用脉冲型反射系数表示的结果; b 采用高斯型反射系数表示的结果; c 采用期望子波型反射系数表示的结果; d 采用雷克子波型反射系数表示的结果 |
首先对4种反射系数剖面中CDP200道进行抽线, 并进行频谱分析, 结果如图 9所示。可以明显看出, 脉冲型反射系数的频带展布较广, 全频带均有能量; 高斯型反射系数在高频端的能量明显衰减, 但低中频成分有很好的保留; 期望子波型反射系数在低频和高频端均有一定程度的衰减, 但有效频带比较宽; 雷克子波型反射系数的频带最窄, 既缺低频也缺高频。
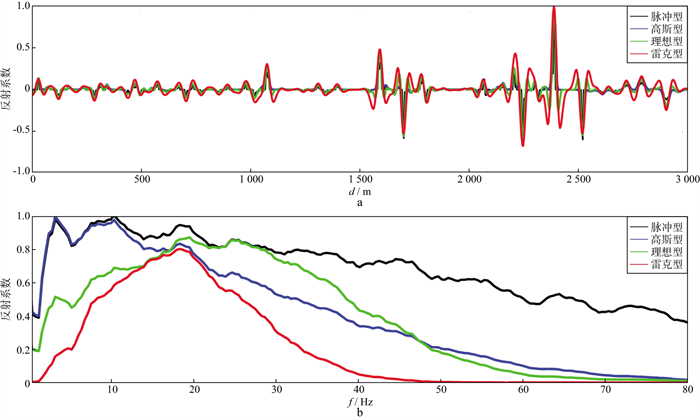
|
图 9 宽带反射系数抽线及频谱分析 a 宽带反射系数结果; b 宽带反射系数频谱(波数谱) |
使用这4种反射系数剖面分别与平滑半径为R=240m的背景阻抗进行融合, 得到的结果如图 10所示。此处, 我们把信息融合宽带波阻抗问题提成一个约束非线性优化问题, 具体提法如下:
| $ \begin{gathered} \min \|\boldsymbol{R}\|_1 \quad \text { s.t. }\left\|\boldsymbol{W} * \boldsymbol{R}-\boldsymbol{r}_{\text {mig }}\right\|{ }^2 \leqslant \varepsilon_1 \\ \left\|\boldsymbol{R}-\nabla_z \boldsymbol{X}\right\|^2 \leqslant \delta_1 \end{gathered} $ | (11a) |
| $ \begin{gathered} \min \|\boldsymbol{X}\|_{\text {TV }} \text { s.t. } \quad\left\|\boldsymbol{L} * \boldsymbol{X}-\boldsymbol{X}_b\right\|^2 \leqslant \varepsilon_2 \\ \left\|\boldsymbol{R}-\nabla_z \boldsymbol{X}\right\|^2 \leqslant \delta_2 \end{gathered} $ | (11b) |
|
图 10 不同宽带反射系数与平滑半径为240m的背景阻抗融合得到的阻抗结果 a 采用脉冲型反射系数融合的波阻抗结果; b 采用高斯型反射系数融合的波阻抗结果; c 采用期望子波型反射系数融合的波阻抗结果; d 采用雷克子波型反射系数融合的波阻抗结果 |
式中: R是宽带反射系数; rmig是偏移成像及各种后处理得到的保真的宽带反射系数; W类似地震子波的滤波器; X=lnI/2是宽带波阻抗I的半对数表示; Xb是背景阻抗的半对数表示; L是低通滤波器; ‖·‖1和‖·‖2分别代表L1和L2范数; ‖·‖TV代表总变差(TV)范数; ▽z代表沿深度(z)方向的导数。迭代串联求解(11)式得到后续展示的信息融合宽带阻抗结果。约束非线性优化问题的具体求解是一个相当复杂的议题。(11)式的具体解法不是此文讨论的重点, 为简单计, 略去关于具体解法的冗长讨论。
图 10展示了不同宽带反射系数与平滑半径240m作用下的背景阻抗融合得到的阻抗结果; 图 11展示了从CDP200处抽取的各种融合阻抗与对应的背景阻抗和真阻抗的对比。从图中可以看出, 脉冲型反射系数与背景阻抗的融合结果趋于真解, 与真波阻抗的相关度达到99.83%;高斯型反射系数由于高频部分受损, 融合阻抗的分辨率降低, 但与真波阻抗的相关度达到99.47%;期望子波尽管是宽带子波, 但由于中低频成分的缺失, 旁瓣加深, 融合结果中的低中频成分难以补全, 且已经引入了假的高波数成分, 与真波阻抗的相关度只能达到96.36%。雷克子波型反射系数融合效果最差, 融合后波阻抗与真阻抗的相关度只有90.20%, 从图 11中明显可以看出它们之间的差异。
|
图 11 不同宽带反射系数融合结果抽线(CDP200)对比 a 采用脉冲型反射系数融合的波阻抗结果抽线对比; b 采用高斯型反射系数融合的波阻抗结果抽线对比; c 采用期望子波型反射系数融合的波阻抗结果抽线对比; d 采用雷克子波型反射系数融合的波阻抗结果抽线对比 |
从融合过程可以清楚地看出, 油气地震勘探中宽带成像子波对于介质岩性刻画的重要性, 宽带成像子波的获取最重要的是既要有宽带的激发接收子波, 还要有宽方位长偏移距的观测。尤其低中频成分的缺失, 成像结果对地下介质岩性描述的误差会很大。高密度和高信噪比的观测对于岩性成像的贡献是从其它角度体现的。
然后, 再分析背景阻抗建模结果和宽带反射系数成像结果对宽带波阻抗建模结果的不同波数带成分的贡献。图 12展示了用不同类型宽带反射系数剖面与背景阻抗(R=240m)融合后背景阻抗、融合阻抗和真阻抗的振幅谱对比。
|
图 12 不同类型宽带反射系数剖面与背景阻抗融合后, 背景阻抗、融合阻抗和真阻抗的振幅谱对比 a 对应脉冲型反射系数; b 对应高斯型反射系数; c 对应理想子波型反射系数; d 对应雷克子波型反射系数 |
从图 12可以清楚地看出, 融合阻抗的背景成分都是由背景阻抗贡献出来的, 其它部分是由反射系数成像结果贡献出来的。这是很自然的逻辑结果。但是, 中波数带(譬如4~8Hz)也可以由反射系数成像补充出来, 只要反射系数成像结果中包含有波阻抗中波数段的信息。事实上, 脉冲型反射系数中包含了除零波数成分外所有波数成分的波阻抗变化信息。因此, 道积分方法重建波阻抗时, 对于脉冲型反射系数, 理论上只要提供任意一层的正确波阻抗就可以得到真波阻抗的恢复。当然, 这又是一个反演骗局。实际上道积分方法受到的影响很多, 根本不可能得到实际可用的波阻抗建模结果[14]。高斯型反射系数成像结果除了超高频部分不能正确贡献外, 其他部分的波阻抗贡献结果都是可靠的。应该注意这个结论与高斯函数的方差是密切联系的。较大方差下的高斯函数也会滤除过多的低中频和超高频成分, 从而降低波阻抗建模的精度。理想子波型反射系数成像结果对宽带阻抗的贡献, 误差较大的是中波数段。雷克子波型反射系数对宽带阻抗的贡献, 误差较大的既包括中波数段, 也包括高波数带, 高波数带中明显地引入了假的成分(图 11)。
上述融合过程再次告诉我们, 地震波成像的真正目标既包括精确的背景速度(背景阻抗), 也包括最好是高斯型反射系数呈现出的成像结果(追求脉冲型反射系数成像结果过于理想)。即便得到高斯型反射系数呈现出的成像结果, 成像分辨率也会有本质性的提升。但是, 高斯型反射系数成像结果也很难得到, 叠前地震数据提供的信息不足以得到这样的成像结果。无论如何, 我们知道了地震波叠前偏移成像的目标不是带限的反射系数, 尤其不是具有宽主瓣、深(宽)旁瓣特征的雷克(Ricker)子波型的反射系数, 期望的偏移成像结果应该是方差较小的高斯型反射系数。常规的偏移成像无论如何都不可能得到高斯型反射系数成像结果, 但是约束反演成像方法有可能得到实用的高斯型反射系数成像结果, 只不过要引入其它的先验信息。
3.4 背景阻抗对宽带波阻抗建模的影响为了分析不同平滑半径获得的背景阻抗(实质上是不同精度的背景阻抗)对融合阻抗的精度影响, 将图 4中4种背景阻抗与高斯型的宽带反射系数(图 8)进行融合, 得到图 13所示的融合结果。图 14为CDP200处的抽线对比。
|
图 13 不同平滑尺度的背景阻抗与高斯型反射系数融合得到的融合阻抗 a 采用平滑尺度R=40m的背景阻抗融合结果; b 采用平滑尺度R=120m的背景阻抗融合结果; c 采用平滑尺度R=240m的背景阻抗融合结果; d 采用平滑尺度R=360m的背景阻抗融合结果 |
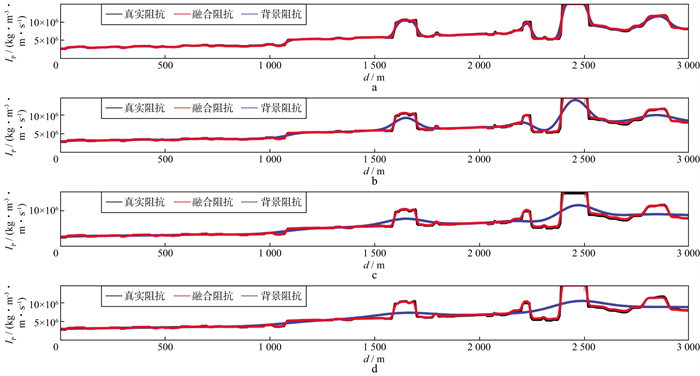
|
图 14 CDP200处的抽线对比 a 采用平滑尺度R=40m的背景阻抗融合结果抽线对比; b 采用平滑尺度R=120m的背景阻抗融合结果抽线对比; c 采用平滑尺度R=240m的背景阻抗融合结果抽线对比; d 采用平滑尺度R=360m的背景阻抗融合结果抽线对比 |
从图 13和图 14可以看出, 4种不同平滑半径得到的背景阻抗剖面与高斯型反射系数剖面的融合结果, 精度都相当高。说明当地震成像剖面表现为高斯型反射系数时, 其中包含了波阻抗中的丰富的低中波数信息, 即使用很平滑的背景阻抗, 也能把宽波数带的波阻抗重构出来。各个波数带中没有显著的成分缺失, 重构精度很高。
为了看到不同背景阻抗剖面与不同类型反射系数剖面融合结果之间的差异, 又做了上述4种不同平滑半径得到的背景阻抗剖面与期望子波型反射系数剖面(图 8)的融合, 结果如图 15所示。图 16为CDP200处的抽线对比, 图 17还对比了CDP200处各种融合阻抗、背景阻抗与真阻抗的振幅谱。
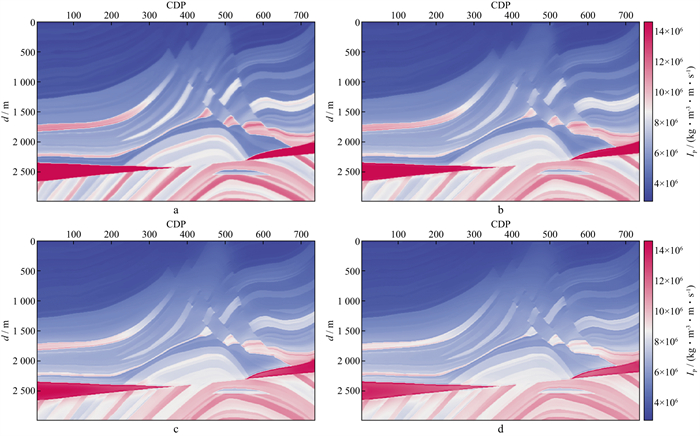
|
图 15 不同平滑尺度的背景阻抗与期望子波型反射系数进行融合得到的阻抗 a 采用平滑尺度R=40m的背景阻抗融合结果; b 采用平滑尺度R=120m的背景阻抗融合结果; c 采用平滑尺度R=240m的背景阻抗融合结果; d 采用平滑尺度R=360m的背景阻抗融合结果 |
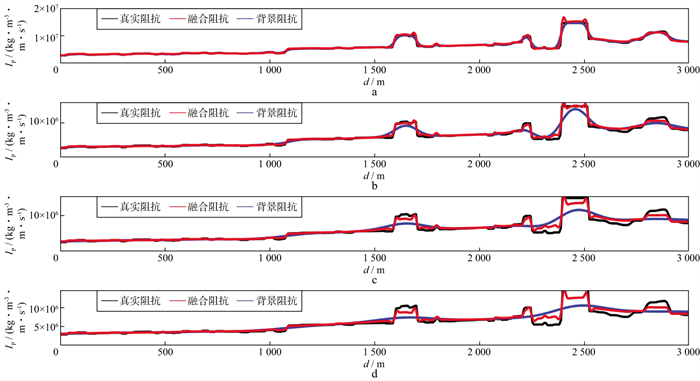
|
图 16 CDP200处的抽线对比 a 采用平滑尺度R=40m的背景阻抗融合结果抽线对比; b 采用平滑尺度R=120m的背景阻抗融合结果抽线对比; c 采用平滑尺度R=240m的背景阻抗融合结果抽线对比; d 采用平滑尺度R=360m的背景阻抗融合结果抽线对比 |
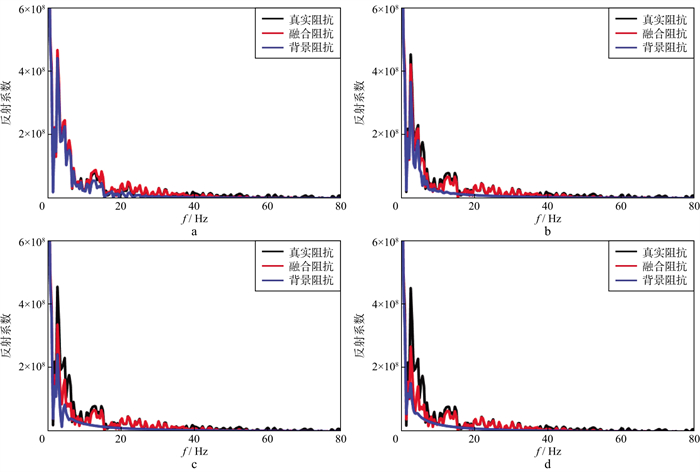
|
图 17 CDP200处各种融合阻抗、背景阻抗与真阻抗的振幅谱 a 平滑尺度R=40m时的对比情况; b 平滑尺度R=120m时的对比情况; c 平滑尺度R=240m时的对比情况; d 平滑尺度R=360m时的对比情况 |
图 15给出的最主要的结论是: 平滑半径增大导致了背景波阻抗中中波数成分损失, 理想子波型反射系数剖面也缺乏中波数成分, 从而导致中波数阻抗不能被重构(图 16和图 17)。中波数段成分的损失, 使得重构的波阻抗与真波阻抗出现明显差异, 重构的波阻抗不能真实反映地下介质岩性的变化。很显然, 拓宽成像子波的频带, 提高背景阻抗的建模精度都是补充中波数阻抗成分的措施。
前述分析时, 背景阻抗成分是正确的。但是对于实际情况, 背景阻抗也会存在一定的误差。因此我们又分析了背景阻抗错误情况下的信息融合宽带波阻抗重构结果。背景阻抗误差引入方式为: 真实阻抗进行R=240m的高斯平滑后, 整体减小15%;整体增加15%;加入15%量级的随机扰动。用高斯型反射系数成像结果与它们分别进行信息融合重构, 重构结果如图 18和图 19所示。
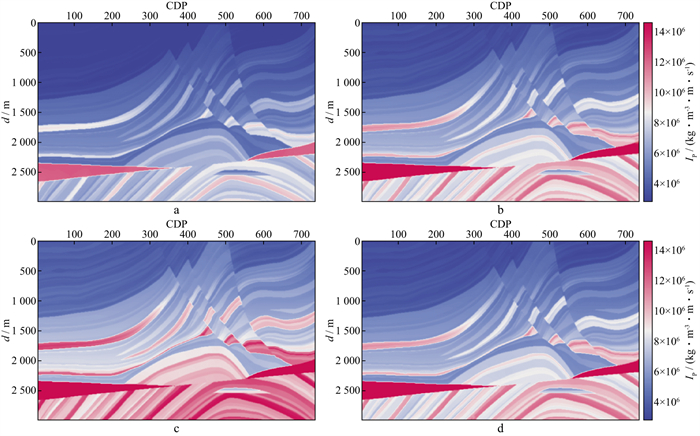
|
图 18 错误背景阻抗与高斯型反射系数进行融合得到的阻抗 a 采用真实波阻抗平滑240m后整体减小15%的背景波阻抗融合的结果; b 采用真实波阻抗平滑240m后的背景波阻抗融合的结果; c 采用真实波阻抗平滑240m后整体增大15%的背景波阻抗融合的结果; d 采用真实波阻抗平滑240m后整体加入15%量级的随机扰动的背景波阻抗融合的结果 |
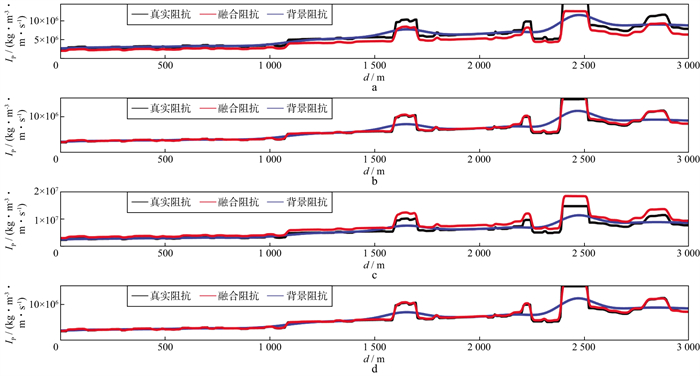
|
图 19 错误背景阻抗与高斯型反射系数进行融合得到的阻抗在CDP200处的抽线对比 a 采用真实波阻抗平滑240m后整体减小15%的背景波阻抗融合的结果抽线对比; b 采用真实波阻抗平滑240m后的背景波阻抗融合的结果抽线对比; c 采用真实波阻抗平滑240m后整体增大15%的背景波阻抗融合的结果抽线对比; d 采用真实波阻抗平滑240m后整体加入15%量级的随机扰动的背景波阻抗融合的结果抽线对比 |
当背景阻抗为真实阻抗经过半径为240m的高斯平滑时, 重构阻抗与真阻抗匹配度达到99.27%;但是若此时背景速度由上述背景速度整体减小15%时, 匹配度仅达到89.28%;若此时背景速度由上述背景速度整体增加15%时, 匹配度仅达到77.55%;若此时背景速度由上述背景速度加入15%量级的随机扰动, 对重构结果影响不大, 匹配度可达99.26%。值得庆幸的是, 在实际情况下建立背景速度模型时, 出现系统误差的概率不大。
4 宽带波阻抗建模及定量地震波成像的基本认识油气地震勘探的目的就是通过地震波成像提供的对地下介质弹性参数的准确刻画, 结合钻井、测井、岩石物理和油气地质学知识, 准确识别与评价油气藏, 进行高效益的油气开发。
深度域真三维空间中地下介质弹性参数的准确刻画是地震波成像的本质目标, 也是油气地震勘探中的核心问题。无论是深度域真三维空间中的宽波数带纵波速度vP(x, y, z)或是宽带波阻抗I(x, y, z)都能反映地下介质岩性的变化, 而带限反射系数仅揭示介质岩性在某些地方(波阻抗跃变的地方)发生突变, 反映的是介质波阻抗的相对变化量(不是绝对变化量)。很显然, 对于准确识别与评价油气藏而言, 宽波数带纵波速度vP(x, y, z)或是宽带波阻抗I(x, y, z)建模结果比带限反射系数更适合基础数据。很长时间以来, 地震波成像及后续的地震地质解释之所以总是基于带限反射系数成像结果, 首要原因是带限反射系数的估计(或成像)是一个更稳健的问题, 更容易得到可靠的解。以带限反射系数为目标的偏移成像甚至不能称为是一个真正的反问题。偏移成像是油气地震勘探领域独创的方法技术。遗憾的是, 理论上说, 它仅是一种地下绕(反)射点的空间定位方法技术, 振幅相对保真的成像结果只是偏移成像方法技术的附带结果而已。
油气地震勘探发展到现在, 地震波成像进入定量的、以估计介质弹性参数绝对变化为目标的阶段已不可避免。Bayes估计理论下的FWI技术本质上就是要达到此目标。实际数据不满足它的理论假设, 估计(全)宽波数带的介质弹性参数的绝对变化是一个强非线性问题, 至少这两个主要原因限制了它的实用化。我们提出的特征波成像(CWI)+宽带波阻抗建模(WBIM)也是为了估计(全)宽波数带的介质弹性参数的绝对变化。当前的目标是信息融合宽带波阻抗建模(或重构)。用石油工业的术语讲, 这是一种针对岩性储层描述的、定量的地震波成像路线与方法技术系列。FWI的提法侧重于强调算法; 针对岩性储层描述的、定量的地震波成像更强调油气勘探的目标和需求。
依据信息融合宽带波阻抗建模(或重构)的思路, 定量地震波成像被分成背景阻抗建模、宽带反射系数估计和信息融合宽带波阻抗建模3个核心环节。
第2节的分析指出, 背景阻抗建模主要利用炮集中透射波(直达波、折射波和Diving Wave)和反(绕)射波的走时信息, 求解线性反演问题(即所谓的层析成像), 得到定量的背景速度估计。基于走时信息估计得到的背景速度与介质层速度的背景部分在量级上是一致的, 不是特别复杂的情形下, 低波数的速度估计结果精度也是很高的。为了给背景速度补充进更多的中波数成分, 仅仅靠算法的改进(譬如用FWI算法)和提高叠前数据的品质(譬如“两宽两高”数据)是不够的, 引入其他先验信息非常必要。目前认为, 最重要的先验信息就是地下介质的结构信息。首先是大套的反射层位信息、断层信息和不规则地质体信息, 如果可能, 再继续引入地震相这样更细节的地质信息, 会大幅度补充背景速度中的中波数段速度成分, 从而提升整个背景速度建模的精度。上述分析可知, 低中波数波阻抗成分的缺失对于定量地描述岩性变化会引起很大的误差。在当前“两宽两高”地震数据采集逐渐成为常态, 高精度的速度建模算法越来越多的情况下, 通过机器学习算法提取更多的用于补充速度建模中波数成分的先验信息, 进而获得可靠的、包含丰富的低、中波数信息的背景阻抗模型, 可以保证最终定量的岩性成像结果的可靠性。
众所周知, 利用地震波同相轴上子波的振幅(波形)变化, 估计介质参数的扰动是地震波成像中更关键的步骤。宽带反射系数估计利用的就是炮集中反(绕)射波同相轴上地震子波的振幅信息。但是, 影响同相轴上地震子波振幅的因素太多。理论上, 应该剥离其它因素对振幅的改变, 仅留下介质阻抗扰动引起的振幅扰动, 才能用适当的算法由波场振幅扰动反演地下介质阻抗扰动。
实际上, 地震数据(波场)是经过人工震源的激发, 大地介质系统的滤波和检波器系统的检测和记录才被获取到的。这是一个非常复杂的过程。通过对震源和检波器系统的简化, 把地震波成像(或参数反演)更广义地抽象如图 20所示。
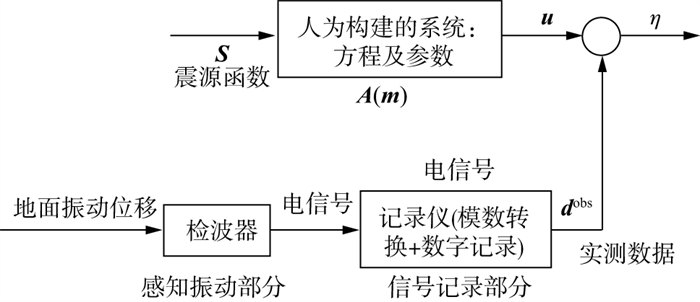
|
图 20 反演成像系统示意 |
观测的地震波场可以抽象表示为:
| $ d\left(\boldsymbol{x}_{\mathrm{R}}, \boldsymbol{t}, \boldsymbol{x}_{\mathrm{S}}\right)=\boldsymbol{C}\left[u\left(\boldsymbol{x}, \boldsymbol{t}, \boldsymbol{x}_{\mathrm{S}}\right)\right]+\eta $ | (12) |
| $ \boldsymbol{A}(\boldsymbol{m}) \boldsymbol{u}=f $ | (13) |
式中: f是震源函数, u为波动方程的解。A为人为构建的波动方程, C为地震数据的采样算子, 将连续的地震波场转换为指定观测点的离散的空间时间函数, η为采集过程引入的噪声函数。
忽略对震源激发的振幅的影响分析, 通过对检波器系统的抽象过程可以看出:
1) 对地面振动位移的感知, 检波器将地面震动位移线性地转化为电信号。在该过程中, 要求电信号强度与振动强度存在常比例关系, 并且需要检波器响应动态范围较大, 最强振动与最弱振动都能够被有效地感知到并按上述要求产生电信号。此时需要注意的是, 地震子波(波前面)平稳下来之后才能把地面的近似振动幅度当成源的强度, 平稳之前的振动位移应该舍弃。因此, 能否保真感知并产生电信号, 动态范围是否能适应勘探需求, 弱振动能否保真地记录下来, 都使检波器的感知面临巨大的挑战。
2) 能否把检波器输出的被认为保真感知的电信号转换并记录为有效数字, 最关键的是模拟转换设备。在当前高性能计算机系统下, 模拟转换数字信号的存储并不存在问题。然而模拟转换的动态范围是个问题, 过粗的采样忽略了弱信号。也说明感知到的大动态范围的振动(电信号)不一定能被保真地转化成数字信号记录下来。因此, 在检波器的设计过程中, 需要考虑深层弱信号的动态范围、感知部分能做到保真感知的动态范围和记录部分能做到保真记录的动态范围。
另外, 检波器的方向选择性(不同分量对振动位移方向的感知不同)能否应对野外观测的实际变化和检波器是否能与地表介质耦合以及引起的振幅畸变会有多大, 对保真成像带来了巨大的挑战。
定量的地震波成像不仔细考察震源激发与检波器接收的振幅保真性是不可能做好的。
3) 基于线性成像系统分析保真成像的影响因素。首先, 分析观测系统中的单个炮检对情况下成像系统的照明及分辨率。在高频近似下, 单个炮检对对应的射线与地下某一点作用的几何关系如图 21所示。
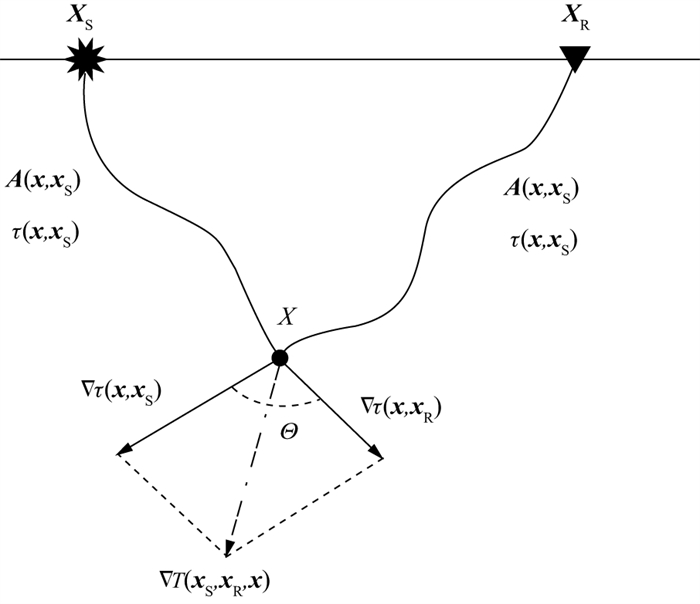
|
图 21 高频近似下, 单个炮检对对应的射线与地下单点作用的几何关系 |
图 21中, ▽τ(x, xS)与▽τ(x, xR)分别代表在地下x点处, 源端波场、检端波场对应的慢度矢量, 其方向分别垂直于入射、散射波前面。散射张角Θ为源、检端慢度矢量的夹角, 散射张角的大小取决于震源点、检波点相对于散射点的位置, 以及波场在背景速度模型中的传播情况。▽T(xS, xR, x)为源、检端慢度矢量的矢量和, 称为双程慢度矢量, 也称为照明矢量, 各向同性情况下, 有:
| $ \begin{gathered} \boldsymbol{I}_{\mathrm{SR}}=\nabla T\left(\boldsymbol{x}_{\mathrm{S}}, \boldsymbol{x}_{\mathrm{R}}, \boldsymbol{x}\right)=\nabla \tau\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{S}}\right)+ \\ \nabla \tau\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{R}}\right)=\frac{2 \cos \left(\frac{\mathit{\Theta}}{2}\right)}{v_0(\boldsymbol{x})} \boldsymbol{n}_{\mathrm{SR}} \end{gathered} $ | (14) |
式中: ISR代表照明矢量, nSR为照明矢量方向上的单位矢量, v0(x)为散射点处的背景速度。照明矢量模的长短决定着分辨率的高低。可以看出, 散射张角的大小对照明矢量的模长有重要影响, 对于相同的背景速度, 当Θ=0时, 照明矢量的模最长, 分辨率最高, 此时对应正入射(自激自收)情形; 当散射张角增大, 照明矢量的模变短, 分辨率降低; 当Θ=180°时, 照明矢量长度为零, 此时对应透射情形, 对散射点没有成像分辨率。散射张角对分辨率的影响可以解释角度域成像道集(或偏移距域成像道集)中, 大角度(或大偏移距)产生子波拉伸。另外, 背景速度的大小也影响着照明矢量模的长度, 背景速度越大, 照明矢量模长越短, 分辨率越低。一般情况下, 地下介质从浅到深, 速度逐渐增大, 解释了通常深层成像结果分辨率比浅层低的原因。
观测系统中, 通过一对炮检对在地下某一点对应的照明矢量ISR, 可以计算出该炮检对在地下该点对应的波数矢量kSR, 即
| $ \boldsymbol{k}_{\mathrm{SR}}=\omega \boldsymbol{I}_{\mathrm{SR}} $ | (15) |
式中: ω代表角频率。图 22为单个炮检对波数矢量的投影。通过上式, 可将地震波场波前面上(时间域)的子波的频谱投影至波数域, 波数矢量的方向与照明矢量相同, 其幅值取决于波场子波的频谱以及照明矢量的模长。波数矢量是分辨率分析中的关键量, 将波数域中的kSR进行Fourier反变换, 可在空间域成像点处, 得到一个带限局部平面波前面。波前面延续方向与双程走时场T(xS, xR, x)的等时面(偏移画弧曲面)在成像点位置相切, 与波数矢量kSR的方向正交。
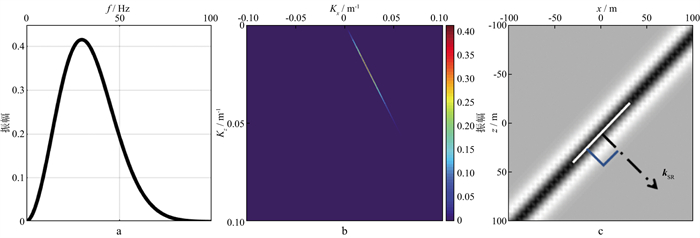
|
图 22 单个炮检对波数矢量的投影 a 成像点处, 地震波场波前面上时间域地震子波的频谱(此处为主频30Hz Ricker子波的频谱); b 假定成像点处速度为2000m/s, 炮检对对应的散射张角为0, 利用照明矢量以及投影关系, 将a中的频谱投影至波数域, 获得的波数矢量, 注意波数矢量展布的方向与选定的照明矢量方向相同; c 通过Fourier反变换, 将b中波数矢量变换到空间域, 得到带限的局部平面波波前面, 波前面的“厚度”决定了成像分辨率, 其与照明矢量模的长度以及子波频带有关, 波前面的延续方向与波数矢量方向正交 |
由上述分析可知, 子波频带、成像点处速度以及散射张角是影响分辨率的3个重要因素。
实际情形下, 由于观测系统的孔径有限, 并且炮检点分布不均匀, 加上地下复杂的速度结构对波传播路径的影响, 理想照明情形无法实现。实际上, 观测系统中在地下每个成像点处满足某一反射角及方位角的炮检对, 对成像点的角度照明是不完备且不均匀的。图 23展示了在仅有一定角度照明范围的情形下, 波数矢量的展布及其对应的空间域点扩散函数(point spread function, PSF)。从图中可以看出, 将所有波数矢量进行矢量求和, 可以得到一个平均波数矢量kmean, 其方向决定了空间PSF的高分辨率轴以及低分辨率轴。高分辨率轴沿着kmean的方向, 在该方向上, PSF具有最高的分辨率, PSF在该方向上的“厚度”决定了成像系统的“纵向”分辨率, “纵向”分辨率受到子波频带以及照明矢量模长的影响; 低分辨率轴的方向垂直于kmean的方向, 在该方向上PSF的分辨率最低, PSF在该方向上的延续宽度决定了成像系统的“横向”分辨率, “横向”分辨率受到波数矢量在角度上覆盖范围的影响, 角度覆盖范围越大, “横向”分辨率越高。由图 23可以看出, 所谓的“纵向”与“横向”, 实质上是沿kmean以及垂直kmean的方向。
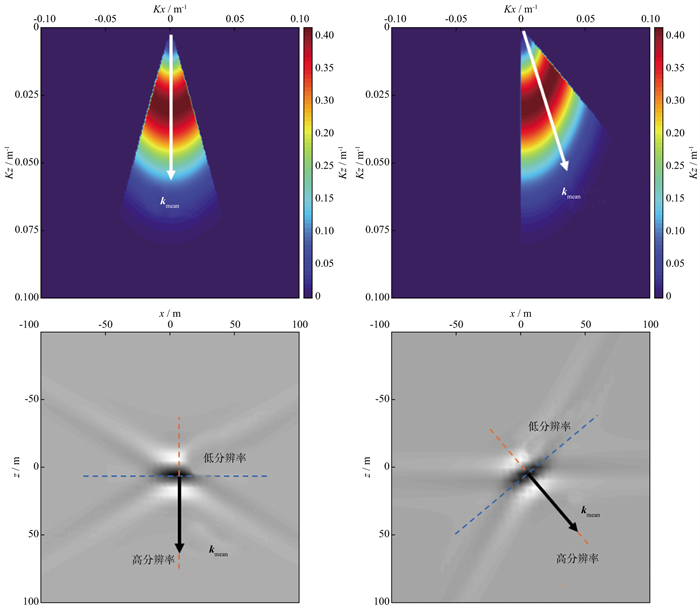
|
图 23 在不完备的角度照明情形下, 波数矢量在波数域的展布及其对应的空间PSF |
从上述分析可知, 影响成像系统在某一成像点分辨率的本质原因, 是观测系统中的炮检对在该成像点对应的波数矢量在波数域的展布范围。展布范围包含两方面, 一是单个波数矢量的长度, 其次是所有波数矢量在不同角度方向上的分布范围。成像点处的速度越小、散射张角越小、成像点处波前面上子波的频带越宽时, 波数矢量的长度越长, 对应的PSF有越高的“纵向”分辨率。其中, 波前面上的子波频带取决于震源子波频带以及波传播过程中的吸收衰减、频散等效应。观测系统中的炮检对, 在成像点处对应的波数矢量在波数域分布的角度范围越宽, 对应的PSF有越高的“横向”分辨率。波数矢量的展布方向取决于炮检对相对于地下成像点的位置, 同时也受到背景速度对入射、散射波场传播方向的影响。综上所述, 从观测系统设计的角度而言, 想要使成像系统有较高的分辨率以及较均衡的照明, 震源子波需要有宽频带, 炮检对的分布需要有较宽的孔径, 并且排列要尽可能规则。另外, 为了使得成像结果有较高的信噪比, 需要高密度的炮检点的分布。对于高分辨率的成像系统, 需要“两宽一高”(宽频带、宽方位、高密度)的观测系统。
综上所述, 由于震源函数未知(实际采集过程中震源函数变化较为复杂)、声波波动方程过于简单(地震波在复杂介质中的传播需要复杂的波动方程描述), 检波器系统的振幅保真问题, 导致观测数据中的数据误差η远偏离高斯分布, 使得保真成像变得异常困难。
我们认为, 宽带反射系数估计不是一个数学算法可以解决的, 需要一个合理的技术流程, 结合合理的关键技术, 基本上能得到与地下介质波阻抗扰动量一致的、定量的成像结果。为此提出如下的宽带反射系数定量化估计的技术流程。
1) 地表一致性振幅校正。消除激发端和接收端导致的地震子波的振幅变化, 余下的振幅变化仅由传播过程和阻抗扰动引起;
2) 球面扩散校正。偏移成像过程能处理球面扩散校正时, 不必单独处理;
3) 吸收衰减校正。偏移成像过程能处理吸收衰减校正时, 不必单独处理;
4) 透射损失校正、薄层干涉校正和散射损失校正。这些因素引起的振幅变化往往被忽略;
5) 保真的叠前深度偏移成像。当前, 我们的建议是做好常规的叠前深度偏移(PSDM), 产生(方位)角度道集, 进行照明优选的保真叠加。不建议用LS_PSDM和LS_RTM, 因为这二种方法施加的理论假设过多, 实际数据很难满足;
6) 成像域点扩散函数(PSF)反褶积。目的是校正照明不均匀, 进一步提升反射系数成像结果保真度和分辨率;
7) 进行测井反射系数与地震成像反射系数的量级标定。我们建议在上述保真成像尽可能做好的情况下, 仅仅对大套标志性反射层的反射系数进行一致性标定。
总之, 带限反射系数的相对保真性由保真成像处理各环节保障。带限反射系数的频带展宽, 甚至扩展成高斯型反射系数, 需要提一个合适的约束非线性反问题并进行有效的求解; 宽带反射系数成像结果的定量化要靠测井反射系数标定。可以认为, 井反射系数是一种质控信息。
在上述认识基础上, 我们将特征波成像(CWI)+宽带波阻抗建模(WBIM)流程及技术系列应用于理论和实际数据的处理, 验证了方法技术系列的有效性。
5 定量地震波成像数值实验我们对西北某探区抽象出的三维模型数据和三维实际数据, 用特征波成像(CWI)+宽带波阻抗建模(WBIM)技术流程进行数据处理。
5.1 三维模型数据宽带波阻抗建模首先, 利用三维模型来模拟西北某探区实际地质情况。其中, 背景速度由模型真速度经过半径为375m的高斯平滑产生, 用Garder速度密度关系生成背景密度, 从而得到背景阻抗。宽带反射系数rmig由Kirchhoff叠前深度偏移结果生成。利用(11)式定义的信息融合宽带波阻抗重构方法生成宽带波阻抗建模结果。
图 24显示了三维模型数据宽带波阻抗建模的结果。可以看出, 重构阻抗和真实阻抗有良好的一致性, 图 25的抽线对比了宽带波阻抗建模的结果。由图 25可以看出, 重构的宽带阻抗在低波数段和高波数段都是比较可靠的, 5~10Hz左右的中波数段重构阻抗的振幅谱值与真实阻抗的振幅谱值差异比较大。可以认定, 这是因为Kirchhoff叠前深度偏移成像结果中没有提供中波段的信息。其中, 由于带限反射系数成像结果频带有限, 反射系数旁瓣太深, 导致波阻抗建模中出现假的波阻抗跃变。在之前的影响因素分析中已经介绍过。中波数段部分缺失也可以归结为半径为375m的平滑半径过大, 导致背景阻抗中也没有包含这部分中波数成分的信息。
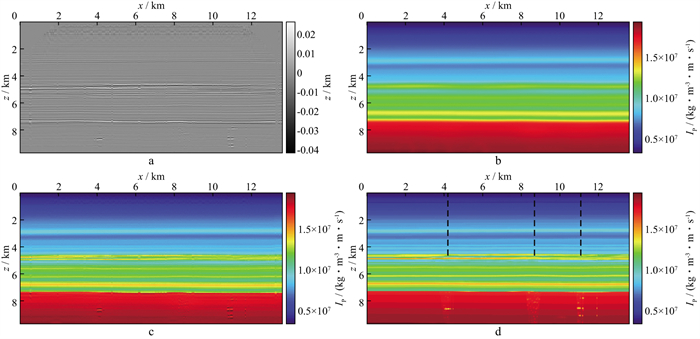
|
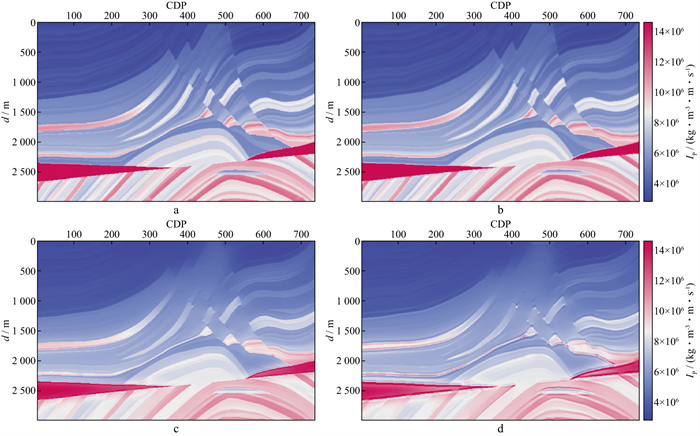
图 24 三维模型数据宽带波阻抗建模结果的剖面显示 a 反射系数振幅标定后的Kirchhoff叠前深度偏移结果剖面; b 基于真速度平滑(半径375m)后的背景速度产生的背景阻抗; c 信息融合宽带阻抗建模结果; d 真阻抗模型 |
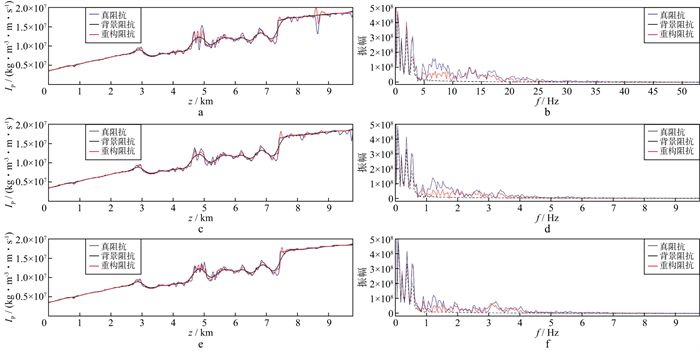
|
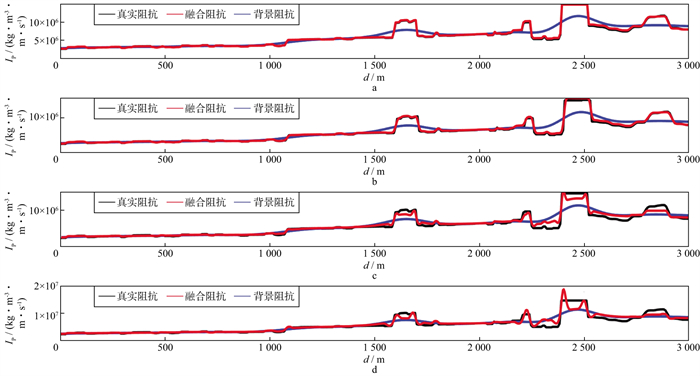
图 25 对应图 24d虚线所示位置处的宽带波阻抗建模结果的抽线对比 a 图 24d左边虚线位置处背景阻抗、重构阻抗和真阻抗的对比; b 背景阻抗、重构阻抗和真阻抗的振幅谱对比; c 图 24d中间虚线位置处背景阻抗、重构阻抗和真阻抗的对比; d 背景阻抗、重构阻抗和真阻抗的振幅谱对比; e 图 24d右边虚线位置处背景阻抗、重构阻抗和真阻抗的对比; f 背景阻抗、重构阻抗和真阻抗的振幅谱对比 |
由图 26可以看出, 振幅标定后的Kirchhoff叠前深度偏移成像结果的深度切片并没有很好地展示出地下岩性变化的真实情况。与真实阻抗相比, 即便在几何形态上, 也与真实的阻抗扰动差异较大。尤其在7.35km的深度切片上, 这一点看得很清楚。理论上, 这是不应该出现的现象。如果叠前深度偏移做得符合理论预期, 叠前深度偏移结果至少在几何形态上能很准确地反映地下介质波阻抗扰动情况。问题当然出在Kirchhoff叠前深度偏移成像受偏移速度和成像算法的影响上。应该提及的是, 由于三维模型正演模拟数据量巨大, 此处用的Kirchhoff叠前深度偏移成像结果是由模拟数据一方提供的。即便如此, 宽带波阻抗重构结果与真实阻抗的一致性很高, 显然更适于岩性油藏的地质解释。
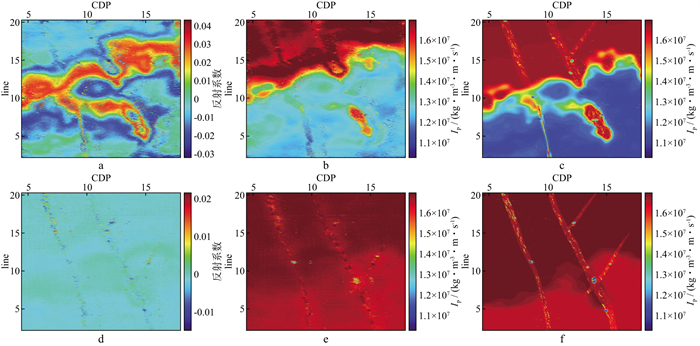
|
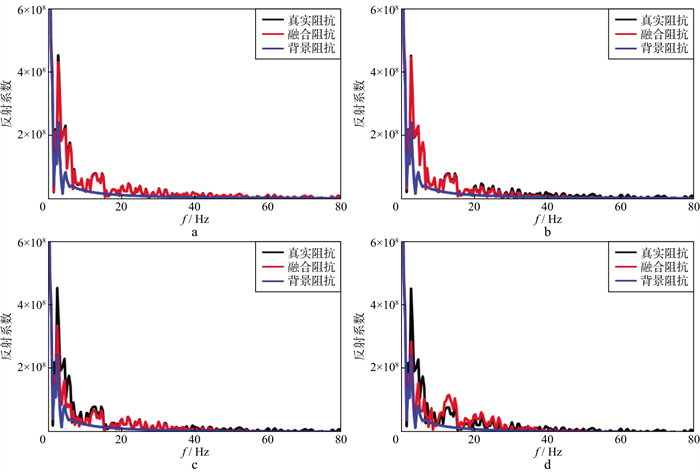
图 26 三维模型数据宽带波阻抗建模结果不同深度的切片显示 a 7.35km深处标定后的偏移成像结果显示; b 7.35km深处重构宽带波阻抗切片显示; c 7.35km深处真波阻抗切片显示; d 8.675km深处标定后的偏移成像结果显示; e 8.675km深处重构宽带波阻抗切片显示; f 8.675km深处真波阻抗切片显示 |
这就从理论模型数据上证明了我们提出的信息融合宽带波阻抗建模路线及方法技术的有效性。
5.2 实际数据宽带波阻抗建模选择西北某探区的实际数据进行宽带波阻抗建模处理。关键技术环节包括: ①背景波阻抗模型的建立; ②波动方程叠前深度偏移; ③方位角度成像道集的输出; ④成像道集后处理, 包括道集拉平、最佳照明选择、最优加权叠加; ⑤成像域反褶积; ⑥基于信息融合的宽带波阻抗建模。
背景阻抗建模中的背景速度来自于叠前深度偏移所用的速度场, 背景密度用Gardner关系由背景速度转换得到。宽带反射系数由前段中的步骤②~⑤产生。步骤⑥由求解(11)式完成。
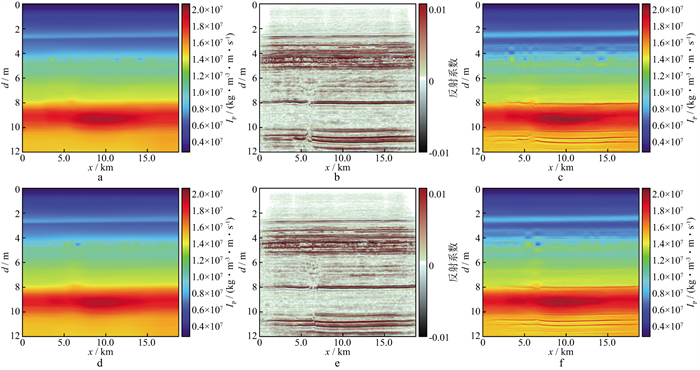
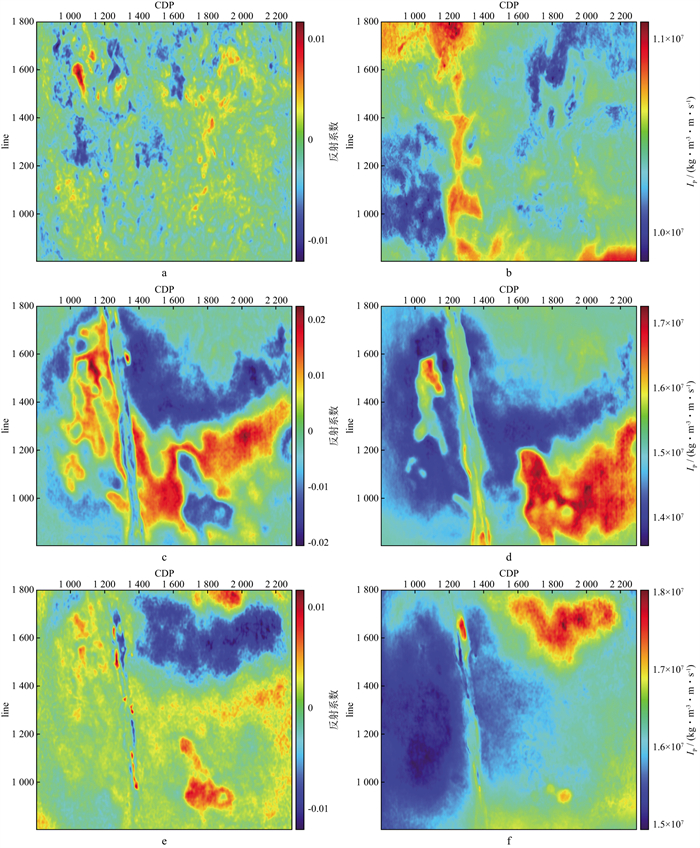
图 27按剖面展示了实际数据信息融合宽带波阻抗重构结果。图 28以深度切片的方式展示了实际数据信息融合宽带波阻抗重构结果。由于不知道真实阻抗, 信息融合宽带波阻抗重构结果好坏的判断比较困难, 只能从成像分辨率和地质逻辑合理性来评判。从信息融合的角度, 算法不会伤害原有信息的分辨率。理论上, 反射系数是绝对阻抗的微分, 反射系数剖面的视觉分辨率应该会高于宽带阻抗。但是, 从图 28展示的深度切片看, 反射系数成像结果的地质合理性不如重构阻抗, 在5.5km处显得十分杂乱。宽带阻抗成像结果的地质合理性还要与该探区的地质解释人员结合再做进一步判断。
|
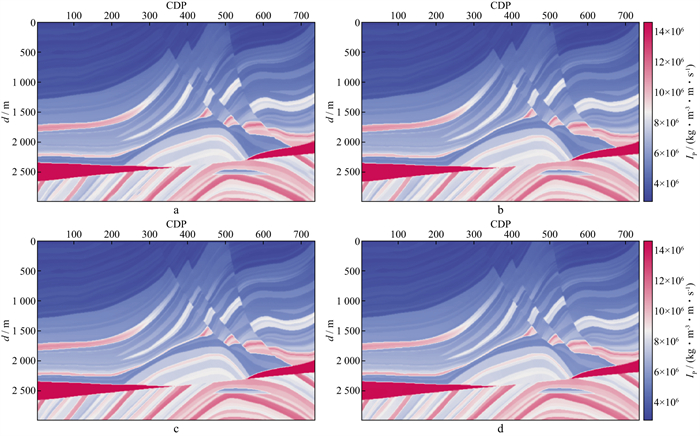
图 27 实际数据信息融合宽带波阻抗重构结果 a 背景阻抗剖面; b 标定后的宽带反射系数剖面; c 重构的宽带波阻抗剖面; d 背景阻抗剖面; e 标定后的宽带反射系数剖面; f 重构的宽带波阻抗剖面 |
|
图 28 实际数据信息融合宽带波阻抗重构结果的深度切片显示 a 振幅标定后的叠前深度偏移结果深度切片(5.5km); b 重构波阻抗深度切片(5.5km); c 振幅标定后的叠前深度偏移结果深度切片(7.9km); d 重构波阻抗深度切片(7.9km); e 振幅标定后的叠前深度偏移结果深度切片(8.1km); f 重构波阻抗深度切片(8.1km) |
从实际数据处理结果看, 我们提出的信息融合宽带波阻抗建模路线及方法技术是可行的。但宽带阻抗成像结果在油藏描述中的有效性, 还要进一步检验。
无论如何, 实际数据情况下, 针对岩性储层的定量地震波成像, 要求地震数据采集环节、地震数据预处理各环节、背景速度建模、背景密度建模、宽带反射系数定量估计, 都要全面提升质量和精度, 才有可能得到能显著提升油藏描述精度和勘探效益的结果。因此, 沿着针对岩性储层的定量地震波成像方向提升勘探技术, 比用FWI技术引领勘探技术的发展更合理。
6 结论与讨论随着油气勘探的新领域(深水、深层、复杂储层、非常规储层等)逐步扩展, 油气勘探的目标越来越复杂。但是, 精确描述油气藏、确定最佳井位和最佳钻井方案、获得最高油气勘探效益的需求并没有变化; 精确描述油气藏需要更精确的地震波成像结果的需求也没有改变。总体上讲, 提供宽波数带的、能反映介质岩性变化的、定量的地震波成像结果是油气勘探的核心问题。
地震波成像的本质就是利用叠前地震数据和与待估计参数相关的先验信息, 利用人为提出的地下介质参数变化和实测数据中波场变化之间的数学物理关系, 利用Bayes参数估计理论下提出的(非)线性化反演方法, 得到介质参数变化的估计结果。FWI方法、层析成像方法、LS_PSDM/LS_RTM和一般的偏移成像就是典型的地震波成像方法。基于时距关系的动校正和静校正本质上也应归于地震波成像的范畴。宽波数带的参数估计结果是地震波成像的根本目标。带限反射系数成像在石油工业界广为应用, 主要是因为对应的偏移成像算法稳定而且物理意义清楚, 并非带限反射系数成像结果更能满足精确油藏描述的需求, 仅是深度域真三维空间中波阻抗相对变化的体现。实际上, 在一个三维油气勘探空间中, 仅有很少部位有显著的波阻抗相对变化。当然, 油气勘探主要是对波阻抗发生变化的部位感兴趣。
宽带的、定量的地震波成像结果(譬如纵波速度vP(x, y, z)或波阻抗I(x, y, z))是在深度域真三维空间中对地下介质岩性变化进行准确刻画的物理量, 具有明确的油气地质意义, 适于进行高精度的、定量的油藏描述。FWI反演方法的真正目的也就是获得宽带的、定量的参数估计结果, 但这是个强非线性反问题, 极难得到稳定收敛的、有地质意义的、能实用的解。
李庆忠[14]在《走向精确勘探的道路》一书中详细分析了波阻抗建模的各种实际影响因素, 很受启发。但他的工作还没有提升到信息融合的高度, 没有奠基在FWI反演成像理论基础上, 留下了很多未解的疑问。
我们提出的特征波成像(CWI)+信息融合宽带波阻抗建模(WBIM)方法技术系列, 本质上是把FWI宽带波阻抗反演, 分解成背景速度建模、背景密度建模、线性化的宽带反射系数估计这3个凸性更好的反问题进行求解。考虑到实际数据的复杂性, 这3个关键技术中的任何一个技术都还需要做进一步的变通, 目的是在实际数据的限制下还能得到“最佳”的成像结果。关键是我们并没有把宽带波阻抗估计提成一个非线性的反演问题来求解, 而是转化成一个信息融合问题。将已有的、认为最好的背景速度建模、背景密度建模、线性化的宽带反射系数估计结果, 通过提出和求解一个约束非线性优化问题, 重构出宽带波阻抗模型。这样做完全避开了反演求解宽带波阻抗时的不稳定和不收敛问题, 同时在此过程中还可以进一步引入其他先验信息, 在信息融合这一步继续提升宽带阻抗建模的精度。
本文提出的由背景速度、背景密度和宽带反射系数, 结合其他先验信息, 融合后得到宽带波阻抗, 是不同于目前常规波阻抗反演的一种新的宽带波阻抗建模方法技术。建模结果稳定, 地质含义更清楚。宽带波阻抗模型各波数带的信息来源清楚, 低频(低波数)来自背景波阻抗, 高频(高波数)来自高分辨反射系数成像。中频成分的补充依赖于背景速度建模和构造成像精度的提高(背景速度的波数带向中波数段展宽), 也依赖于高分辨反射系数成像精度的提升(宽带反射系数的波数带向中波数段展宽)。
期望的宽带反射系数是高斯型反射系数, 其次是理想子波型宽带反射系数。Ricker子波型反射系数成像结果因为有较宽的主瓣和较为宽深的旁瓣, 导致在宽带波阻抗建模中引入很大的误差。Ricker子波型反射系数成像结果之所以有这样的特点主要是当前很多实际观测数据缺低中频(譬如2~8Hz)有效成分, 且观测方位不够宽和偏移距不够长导致的。数据的低信噪比对成像精度的影响首先体现在影响速度建模的精度上, 然后体现在影响偏移成像的精度上。高精度宽带波阻抗建模需要有低中频(中波数)段优势成分的宽带反射系数(譬如方差较小的高斯型反射系数)。宽带反射系数中的低频(包括中频)成分的来源与宽频子波、宽方位长偏移观测又是密切关联的。背景速度的估计精度事实上也严重依赖宽频子波和宽方位长偏移观测。“两宽两高”地震数据观测对定量地震波成像具有核心作用。另外, 即便做了保真的地震波成像, 宽带反射系数(量级)依然需要测井反射系数的标定, 宽带反射系数的量级对波阻抗反演结果影响很大。说明定量的地震波反演成像需要井与震的结合, 这是无法回避的。
尽管“两宽两高”地震数据采集已经成为业界的共识, 也已经得到广泛应用, 但是, 满足油藏描述期望的、定量的宽带成像结果依然很难达成。我们一直认为, 宽带地震波成像(或宽带参数估计)是(一直是)一个信息不足情况下的最佳估计问题。高精度的地震波成像(宽带参数估计)必须要引入更多的地质、测井和岩石物理信息。针对岩性储层描述的、定量的地震波成像过程与油藏描述过程逐渐融为一体。在大数据、人工智能和机器学习算法的赋能下, 测井数据中与岩性变化相关的信息要充分地挖掘出来; 地震成像剖面上与地下构造、沉积相关的信息要尽可能地挖掘出来; 岩石物理知识, 也包括定性的地质知识也要能被计算机表达, 所有这些信息都会有助于提升宽带参数估计的精度, 在深度域全三维空间中尽可能准确地描述地下介质岩性的状态。因此, 今后的地震波成像技术发展, 我们认为应该在定量的岩性成像概念引领下向前发展, 而不是在FWI的理念下向前发展。追求定量的岩性成像, 针对的是石油工业的需求; 追求FWI成像, 更多的是算法方面的深究。
尽管文中数值实验显示我们提出的特征波成像(CWI)+信息融合宽带波阻抗建模(BWIM)这种定量的岩性成像方法技术路线是合理且有效的, 但要实现在油气勘探中广泛应用的目标, 还有很多工作要做。我们认为当前要深化的工作主要不是体现在发展更复杂的反演成像算法上, 而是充分利用机器学习算法提取更多的能提升宽带参数估计精度的先验信息, 并把这些先验信息合理地融入当前已有的反演成像算法中。对实际应用而言, 定量地震波成像对于成像处理各环节是否做到了保真的要求很高, 因此质量控制是十分重要的。一项好的方法技术要落地应用, 不仅仅是靠理念正确和方法技术的有效, 各环节的质控往往起到决定成败的作用。
致谢: 感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中石化物探技术研究院、胜利油田分公司和西北油田分公司对波现象与反演成像研究组(WPI)研究工作的资助与支持。| [1] |
SHERIFF R E, GELDART L P. Exploration seismology[M]. London: Cambridge University Press, 1995.
|
| [2] |
TARANTOLA A. Inverse problem theory and methods for model parameter estimation[M]. Pairs: Society for Industrial and Applied Mathematics, 2005.
|
| [3] |
THEODORIDIS S. Machine learning: A Bayesian and optimization perspective[M]. Pittsburgh: Academic Press, 2015.
|
| [4] |
王华忠, 盛燊. 走向精确地震勘探的道路[J]. 石油物探, 2021, 60(5): 693-708. WANG H Z, SHENG S. Pathway toward accurate seismic exploration[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 693-708. |
| [5] |
KAIPIO J, SOMERSALO E. Statistical and computational inverse problems[M]. New York: Springer Science & Business Media, 2006.
|
| [6] |
王华忠, 冯波, 王雄文, 等. 特征波反演成像理论框架[J]. 石油物探, 2017, 56(1): 38-49. WANG H Z, FENG B, WANG X W, et al. The theoretical framework of characteristic wave inversion imaging[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 38-49. |
| [7] |
ASTER R C, BORCHERS B, THURBER C. Parameter estimation and inverse problems[M]. New York: Academic Press, 2005: 1-320.
|
| [8] |
STOLT R H, WEGLEIN A B. Seismic imaging and inversion: Application of linear inverse theory[M]. London Cambridge University Press, 2012
|
| [9] |
ZHANG Z G, WU Z D, WEI Z Y, et al. FWI imaging: Full-wavefield imaging through full-waveform inversion[J]. Expanded Abstracts of 90th Annual Internat SEG Mtg, 2020, 656-660. |
| [10] |
WEI Z Y, MEI J W, WU Z D, et al. FWI imaging: Revealing the unprecedented resolution of seismic data[J]. Expanded Abstracts of First International Meeting for Applied Geoscience & Energy, 2021, 682-686. |
| [11] |
HE Y, XING H, HUANG Y, et al. Inversion-based Imaging: FWI beyond Velocity[J]. Expanded Abstracts of 82nd EAGE Annual Conference & Exhibition, 2021, 1-5. |
| [12] |
KALINICHEVA T, WARNER M, MANCINI F. Full-bandwidth FWI[J]. Expanded Abstracts of 90th Annual Internat SEG Mtg, 2020, 651-655. |
| [13] |
HAFFINGER P, GISOLF D, PANOS D P, et al. Wave-equation based seismic AVO inversion: A pragmatic approach to use the full elastic wave-field for exploration and production[J]. Expanded Abstracts of Second International Meeting for Applied Geoscience & Energy, 2022, 3087-3091. |
| [14] |
李庆忠. 走向精确勘探的道路[M]. 北京: 石油工业出版社, 1993. LI Q Z. The way to obtain a better resolution in seismic prospection[M]. Beijing: Petroleum Industry Press, 1993. |



