宽方位五维地震数据是指通过地震宽(全)方位观测系统采集, 并经过炮检距向量片(OVT)等技术处理获得的包含五维(即空间三维+炮检距+方位角)信息的叠前地震道集, 宽方位五维地震数据逐渐成为复杂油气勘探及高精度地震解释的重要基础数据^[1-3]。针对储层的有效压力预测在油气勘探开发中降低钻井成本、保障钻井安全、保护油气层等方面发挥着关键作用^[4-6]。国内外学者针对压力的岩石物理研究已经开展了大量基础与实践研究, 主要包括纵横波速度、岩石模量或速度比与有效压力之间的经验关系式^[7-11], 有效压力与软孔隙纵横比变化的关系式^[12]或气饱和超压页岩岩石物理模型^[13]等, 但在实际裂缝型储层有效压力预测方面仍面临挑战, 瓶颈在于现有有效压力预测方法多以岩石物理模型为主, 或通过有效压力与上覆地层压力与孔隙压力的关系间接计算, 缺少针对综合五维地震资料进行裂缝型储层有效压力稳定预测的研究。

裂缝型储层五维地震有效压力预测的关键是寻找对有效压力敏感的参数及建立相应表征反射系数方程。学者们基于岩石物理实验建立了岩石模量与有效压力之间的线性关系^[11]或对数关系^[14], 在一定程度上可以通过岩石的模量反映其受到的有效压力情况。借助统计岩石物理模型将岩石物理学关系和地质统计学相结合, 可以建立起岩石弹性参数和地震响应之间的联系^[15], 进而指导有效压力的预测。但统计岩石物理模型是通过数据拟合和随机误差获得的^[16], 具有较强的随机性。SMITH^[17]建立了有效压力与孔隙度间的指数关系式, 为有效压力参数的预测提供了良好的途径。目前广泛使用间接方法预测有效压力, 如利用纵横波速度进行孔隙压力预测, 利用地层埋藏深度求取上覆地层压力, 然后再进行有效压力的求解^[18], 该方法容易受其它干扰因素(岩性和断裂等)影响, 因此该方法需要在预测结果的基础上考虑校正因子^[19]。此外, 从地震岩石物理理论出发, 构建压力敏感参数的刚度矩阵, 基于Born近似和稳相法求解, 可推导与待反演参数有关的反射系数近似方程, 再通过概率化方法可进行反演预测^[20], 目前针对有效压力的研究已从各向同性储层^[21]发展到各向异性储层^[22]。本文的特点是在于联合有效压力关系式^[17]、Nur临界孔隙度模型^[23]以及各向异性Gassman方程^[24]构建新的刚度矩阵方程, 优化参数组成, 构建OA介质有效压力敏感参数表征的方位反射系数方程。

裂缝型储层的特殊性以及地下埋藏条件的复杂性给裂缝型储层五维地震反演带来了挑战, 多裂缝参数同时反演更是导致储层参数精度下降。针对裂缝型储层, 常用的直接反演方法是弹性阻抗反演方法^[25-39]和基于贝叶斯框架的AVAZ反演方法^[40-42], 除单纯利用地震纵波信号反演外, 学者们也进行了多波联合反演^[42]及非线性反演方法研究^[43-44]。时间域地震反演的抗噪性能相比频率域有所增强, 但是时间域地震反演的分辨率不及频率域地震反演。因此在裂缝型储层压力预测中结合时频域地震反演的优势^[45], 充分利用五维地震资料中多波(纵、横)多特征(振幅、频率及相位)信息, 采取不同的反演策略, 可提高有效压力预测的可靠性。

根据各向异性Gassman方程及Schoenberg线性滑动模型, 联合有效压力关系式^[17]和Nur临界孔隙度模型^[23]构建OA介质新的岩石物理刚度矩阵方程, 推导出利用有效压力参数及流体模量和裂缝参数直接表征的新的裂缝型储层五维地震反射系数方程, 并分析方程的适用条件, 从理论上阐明了采用该方程开展裂缝型储层有效压力参数预测及流体识别的可行性。在此基础上, 创新了有效压力参数预测方法, 采用五维地震时频域分步反演的方法, 基于分步反演及时频域联合反演策略, 在贝叶斯理论框架下构建五维地震时频域分步反演目标泛函, 基于五维地震频率和振幅信息及岩石、测井和地质资料, 实现了裂缝型储层有效压力参数及流体参数和裂缝法向及切向裂缝弱度参数的直接预测。

1 方法原理 1.1 OA介质五维地震有效压力参数刚度矩阵构建及分析

各向异性Gassmann方程提供了描述裂缝型储层等效参数的理论基础, GUREVICH^[46]结合线性滑动理论将各向异性Gassmann方程推导为:

$ \boldsymbol{C}_{i j}^{\mathrm{sat}}=\boldsymbol{C}_{i j}^{\mathrm{dry}}+\beta_{i} \beta_{j} K_{p}^{\mathrm{ani}} \quad i, j=1,2, \cdots, 6 $

(1)

式中: C_ij^sat是饱和流体裂缝岩石的等效刚度弹性矩阵, C_ij^dry是干裂缝岩石的等效刚度弹性矩阵。以完全各向同性背景下发育水平裂缝和垂直裂缝为例, 等效OA介质C^dry可表示为^[47]:

$ \boldsymbol{C}^{\mathrm{dry}}=\left[\begin{array}{cccccc} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ C_{12} & C_{22} & C_{23} & 0 & 0 & 0 \\ C_{13} & C_{23} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{array}\right] $

(2)

其中,

$ C_{11} \approx M_{b}^{\mathrm{dry}}\left[1-\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \delta_{\mathrm{N} 1}-\delta_{\mathrm{N} 2}\right] $

$ C_{12} \approx \lambda_{b}^{\mathrm{dry}}\left(1-\chi_{b}^{\mathrm{dry}} \delta_{\mathrm{N} 1}-\delta_{\mathrm{N} 2}\right) $

$ C_{13} \approx \lambda_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{N} 1}-\delta_{\mathrm{N} 2}\right) $

$ C_{22} \approx M_{b}^{\mathrm{dry}}\left[1-\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \delta_{\mathrm{N} 1}-\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \delta_{\mathrm{N} 2}\right] $

$ C_{23} \approx \lambda_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{N} 1}-\chi_{b}^{\mathrm{dry}} \delta_{\mathrm{N} 2}\right) $

$ C_{33} \approx M_{b}^{\mathrm{dry}}\left[1-\delta_{\mathrm{N} 1}-\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \delta_{\mathrm{N} 2}\right] $

$ C_{44}=\mu_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{T} 1}\right) $

$ C_{55}=\mu_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{T} 1}-\delta_{\mathrm{T} 2}\right) $

$ C_{66} \approx \mu_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{T} 2}\right) $

式中: M_b^dry=λ_b^dry+2μ_b^dry是背景弹性介质纵波模量; λ_b^dry和μ_b^dry为拉梅常数。另外, χ_b^dry=1－2μ_b^dry/M_b^dry, δ_N1, δ_N2分别表示水平裂缝法向与切向弱度参数; δ_T1, δ_T2分别表示垂直裂缝的法向与切向弱度参数。公式(1)中, β_i或β_j表示各向异性类Biot系数, 统一记为β_p, K_p^ani表示各向异性类Gassmann孔隙空间模量, 展开式分别为:

$ \beta_{p}=\left(1-\frac{\sum\limits_{n=1}^{3} C_{l n}^{\mathrm{dry}}}{3 K_{m}}\right) \vartheta_{p} $

(3a)

$ \vartheta_{p}= \begin{cases}1 & l=1,2,3 \\ 0 & l=4,5,6\end{cases} $

(3b)

$ K_{p}^{\mathrm{ani}}=\frac{K_{g}}{\left(1-\frac{K_{\mathrm{dry}}^{\mathrm{ani}}}{K_{m}}\right)-\varphi\left(1-\frac{K_{m}}{K_{f}}\right)} $

(3c)

$ K_{\mathrm{dry}}^{\mathrm{ani}}=\frac{\sum\limits_{i=1}^{3} \sum\limits_{j=1}^{3} C_{i j}^{\mathrm{dry}}}{9} $

(3d)

式中: K_dry^ani表示干岩石有效体积模量; K_m和K_f分别为固体矿物颗粒体积模量和流体等效体积模量; φ是含等径孔隙裂缝岩石的总孔隙度; β₀=1－K_b^dry/K_m为常用的Biot系数^[48]; K_b^dry表示背景介质有效体积模量。

结合Nur临界孔隙度模型^[23], 利用临界孔隙度参数φ_c可以将干岩石等效体积模量表示为基质矿物模量与孔隙度的形式, 即

$ K_{b}^{\mathrm{dry}}=K_{m}\left(1-\frac{\varphi}{\varphi_{c}}\right) $

(4)

SMITH^[17]提出了一种简易的指数形式的用孔隙度表示的有效压力参数函数, 即

$ \varphi \approx \varphi_{0} \mathrm{e}^{-\alpha P _\mathrm{eff}} $

(5)

式中: φ₀为初始孔隙度; α是有效压力系数, 与岩石压实程度有关。令α=0.096MPa^－1[49], P_eff为有效压力, 其矢量形式为有效应力, 指的是地层岩石骨架和岩石基质所受的应力^[50]。由公式(5)可知, 储层有效压力与储层孔隙度存在指数关系, 该经验公式适用于致密储层及裂缝发育的页岩储层。为便于后续反演研究, 构造有效压力敏感参数P_e=e^{－αP_eff[21]}, 有效压力敏感参数P_e仅与有效压力系数α和有效压力P_eff相关; 有效压力敏感参数P_e可反映储层有效压力的大小。进而公式(5)可表示为孔隙度与有效压力的线性关系φ≈φ₀P_e; 有效压力敏感参数也可表示为P_e≈φ/φ₀, 由储层孔隙度求得。另外, P_eff=P_z－P_p, 其中, P_z为上覆地层压力或垂直压力。其矢量形式为垂直应力, 是由上覆地层的岩石骨架, 岩石基质及裂缝、孔隙中流体所受的重力对地层作用产生的; P_p为孔隙压力, 是由裂缝、孔隙中的流体对地层作用产生的^[49]。

考虑到流体体积模量通常远远小于基质固体颗粒的体积模量, 即K_f≤K_m^[48], 结合公式(4)和公式(5)可以得出:

$ \frac{\beta_{0}^{2}}{\varphi}=\frac{\left(1-\frac{K_{b}^{\text {dry }}}{K_{m}}\right)^{2}}{\varphi}=\frac{\varphi}{\varphi_{c}^{2}} \approx \frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} $

(6)

$ \begin{gathered} \frac{\beta_{0}\left(1-\beta_{0}\right)}{\varphi} K_{f}=\frac{\left(1-\frac{K_{b}^{\mathrm{dry}}}{K_{m}}\right)\left(\frac{K_{b}^{\mathrm{dry}}}{K_{m}}\right)}{\varphi} K_{f} \\ =\frac{\left(\frac{\varphi}{\varphi_{c}}\right)\left(\frac{K_{b}^{\mathrm{dry}}}{K_{m}}\right)}{\varphi} K_{f}=\frac{1}{\varphi_{c}} \frac{K_{b}^{\mathrm{dry}}}{K_{m}} K_{f} \approx 0 \end{gathered} $

(7)

将公式(3)代入公式(1), 结合公式(6)和公式(7), 可获得裂缝介质纵波模量、有效压力参数、两组裂缝的干裂缝弱度参数及流体体积模量表征的饱和流体OA介质的刚度矩阵, 即:

$ \boldsymbol{C}_{\mathrm{OA}}^{\mathrm{sat}}=\left[\begin{array}{cccccc} C_{11}^{\mathrm{sat}} & C_{12}^{\mathrm{sat}} & C_{13}^{\mathrm{sat}} & 0 & 0 & 0 \\ C_{12}^{\mathrm{sat}} & C_{22}^{\mathrm{sat}} & C_{23}^{\mathrm{sat}} & 0 & 0 & 0 \\ C_{13}^{\mathrm{sat}} & C_{23}^{\mathrm{sat}} & C_{33}^{\mathrm{sat}} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44}^{\mathrm{sat}} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55}^{\mathrm{sat}} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66}^{\mathrm{sat}} \end{array}\right] $

(8)

$ C_{11}^{\mathrm{sat}} \approx M_{b}^{\mathrm{dry}}\left[1-\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \delta_{\mathrm{N} 1}-\delta_{\mathrm{N} 2}\right]+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} K_{f} $

(9a)

$ C_{12}^{\mathrm{sat}} \approx \lambda_{b}^{\mathrm{dry}}\left(1-\chi_{b}^{\mathrm{dry}} \delta_{\mathrm{N} 1}-\delta_{\mathrm{N} 2}\right)+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} K_{f} $

(9b)

$ C_{13}^{\mathrm{sat}} \approx \lambda_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{N} 1}-\delta_{\mathrm{N} 2}\right)+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} K_{f} $

(9c)

$ C_{22}^{\mathrm{sat}} \approx M_{b}^{\mathrm{dry}}\left[1-\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \delta_{\mathrm{N} 1}\right]+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} K_{f} $

(9d)

$ C_{23}^{\mathrm{sat}} \approx \lambda_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{N} 1}^{2}-\delta_{\mathrm{N} 2}^{\mathrm{dry}} \delta_{\mathrm{N} 2}\right)+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} K_{f} $

(9e)

$ C_{33}^{\mathrm{sat}} \approx M_{b}^{\mathrm{dry}}\left[1-\delta_{\mathrm{N} 1}-\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \delta_{\mathrm{N} 2}\right]+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} K_{f} $

(9f)

$ C_{44}^{\mathrm{sat}}=\mu_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{T} 1}\right) $

(9g)

$ C_{55}^{\mathrm{sat}}=\mu_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{T} 1}-\delta_{\mathrm{T} 2}\right) $

(9h)

$ C_{66}^{\mathrm{sat}}=\mu_{b}^{\mathrm{dry}}\left(1-\delta_{\mathrm{T} 2}\right) $

(9i)

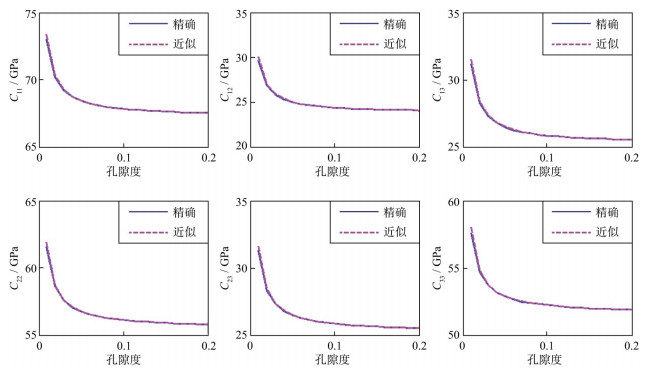
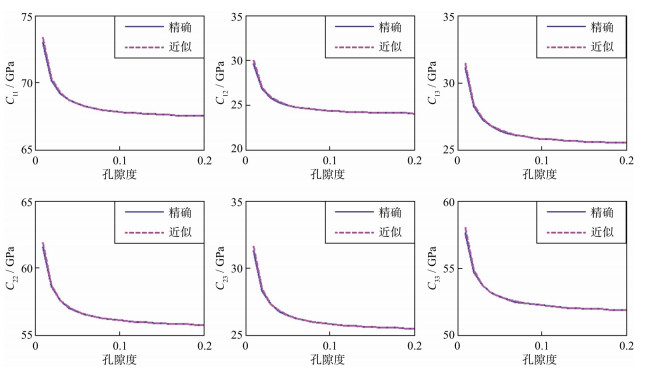
设置模型验证上述模型近似刚度参数的准确性。模型储层孔隙中饱含气和水, 含水饱和度Sw分别为30%和70%, 矿物成分由石英和黏土组成, 比例为1∶1, 使用Wood公式计算岩石的混合流体模量, 使用VRH方程计算矿物平均模量^[48], 裂缝弱度参数分别为δ_N1=0.02和δ_N1=0.04及δ_N2=0.06和δ_N2=0.12, 进而对弱各向异性近似刚度方程(9)与精确刚度表征方程(2)进行对比, 如图 1~图 8是不同含气饱和度及裂缝弱度情况下, 裂缝岩石弱各向异性近似(粉色)与精确(蓝色)刚度参数随孔隙度变化的对比, 孔隙度变化范围为0~0.2, 比较图 1至图 8可知,在含水饱和度不变的情况下, 法向裂缝弱度越小, 则近似刚度参数越准确, 故推导的近似公式更适用于弱各向异性介质; 图 1至图 8对比可知, 在裂缝弱度不变的情况下, 含水饱和度越低, 则近似刚度参数越准确, 故推导的近似公式更适用于低体积模量裂缝型储层。

1.2 裂缝型储层五维地震有效压力参数地震反射方程推导

反射系数与散射函数之间的关系可简单地表示为^[51-52]:

$ R_{\mathrm{PP}}(\theta)=\frac{1}{4 \rho_{b} \cos ^{2} \theta} S_{\mathrm{PP}}\left(\boldsymbol{r}_{0}\right) $

(10)

其中,

$ S_{\mathrm{PP}}\left(\boldsymbol{r}_{0}\right)=\Delta \rho \xi^{P P}+\Delta C_{m n} \eta_{m n}^{\mathrm{PP}} $

(11)

$ \xi^{P P}=\left.\left[g_{i}^{\prime \mathrm{PP}} g_{k}^{\mathrm{PP}}\right]\right|_{\boldsymbol{r}=\boldsymbol{r}^{\prime} 0} $

(12a)

$ \eta_{m n}^{\mathrm{PP}}=\left.\left[p_{j}^{\prime \mathrm{PP}} g_{i}^{\prime \mathrm{PP}} p_{l}^{\mathrm{PP}} g_{k}^{\mathrm{PP}}\right]\right|_{\boldsymbol{r}=\boldsymbol{r}^{\prime} 0} $

(12b)

式中下标符号m和n与i, j, k及l的关系可表示为:

$ m=i \delta_{i j}+(9-i-j)\left(1-\delta_{i j}\right) $

(13a)

$ n=k \delta_{k l}+(9-k-l)\left(1-\delta_{k l}\right) $

(13b)

$ (i, j, k, l=1,2,3) $

式中: δ_ij和δ_kl均为Kronecker函数。

根据公式(9)推导OA等效介质的饱和流体扰动刚度参数(假设|ΔM_b^dry/M_b^dry|≤1, |Δλ_b^dry/λ_b^dry|≤1)及(δ_N1, δ_T1≤1、δ_N2, δ_T2≤1), 忽略含ΔM_b^dryδ_N1, Δλ_b^dryδ_N1, ΔM_b^dryδ_N2和Δλ_b^dryδ_N2的项, 则OA介质扰动刚度矩阵表示为:

$ \begin{aligned} &\Delta \boldsymbol{C}_{\mathrm{OA}}^{\mathrm{sat}}= \\ &{\left[\begin{array}{cccccc} \Delta C_{11}^{\mathrm{sat}} & \Delta C_{12}^{\mathrm{sat}} & \Delta C_{13}^{\mathrm{sat}} & 0 & 0 & 0 \\ \Delta C_{12}^{\mathrm{sat}} & \Delta C_{22}^{\mathrm{sat}} & \Delta C_{23}^{\mathrm{sat}} & 0 & 0 & 0 \\ \Delta C_{13}^{\mathrm{sat}} & \Delta C_{23}^{\mathrm{sat}} & \Delta C_{33}^{\mathrm{sat}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \Delta C_{44}^{\mathrm{sat}} & 0 & 0 \\ 0 & 0 & 0 & 0 & \Delta C_{55}^{\mathrm{sat}} & 0 \\ 0 & 0 & 0 & 0 & 0 & \Delta C_{66}^{\mathrm{sat}} \end{array}\right]} \end{aligned} $

(14)

式中:

$ \begin{gathered} \Delta C_{11}^{\mathrm{sat}} \approx \Delta M_{b}^{\mathrm{dry}}-M_{b}^{\mathrm{dry}}\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \Delta \delta_{\mathrm{N} 1}-M_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{N} 2}+ \\ \frac{\varphi_{0}}{\varphi_{c}^{2}} \Delta P_{e} K_{f}+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} \Delta K_{f} \end{gathered} $

$ \begin{gathered} \Delta C_{12}^{\mathrm{sat}} \approx \Delta \lambda_{b}^{\mathrm{dry}}-\Delta \lambda_{b}^{\mathrm{dry}} \chi_{b}^{\mathrm{dry}} \delta_{\mathrm{N} 1}-\Delta \lambda_{b}^{\mathrm{dry}} \delta_{\mathrm{N} 2}+ \\ \frac{\varphi_{0}}{\varphi_{c}^{2}} \Delta P_{e} K_{f}+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} \Delta K_{f} \end{gathered} $

$ \begin{gathered} \Delta C_{13}^{\mathrm{sat}} \approx \Delta \lambda_{b}^{\text {dry }}-\Delta \lambda_{b}^{\text {dry }} \delta_{\mathrm{N} 1}-\Delta \lambda_{b}^{\text {dry }} \delta_{\mathrm{N} 1}+ \\ \frac{\varphi_{0}}{\varphi_{c}^{2}} \Delta P_{e} K_{f}+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} \Delta K_{f} \end{gathered} $

$ \begin{gathered} \Delta C_{22}^{\mathrm{sat}} \approx \Delta M_{b}^{\mathrm{dry}}-M_{b}^{\mathrm{dry}}\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \Delta \delta_{\mathrm{N} 1}-M_{b}^{\mathrm{dry}}\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \cdot \\ \Delta \delta_{\mathrm{N} 2}+\frac{\varphi_{0}}{\varphi_{c}^{2}} K_{f} \Delta P_{e}+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} \Delta K_{f} \end{gathered} $

$ \begin{gathered} \Delta C_{23}^{\mathrm{sat}} \approx \Delta \lambda_{b}^{\mathrm{dry}}-\lambda_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{N} 1}-\lambda_{b}^{\mathrm{dry}} \chi_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{N} 2}+ \\ \frac{\varphi_{0}}{\varphi_{c}^{2}} \Delta P_{e} K_{f}+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} \Delta K_{f} \end{gathered} $

$ \begin{gathered} \Delta C_{33}^{\mathrm{sat}} \approx \Delta M_{b}^{\mathrm{dry}}-M_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{N} 1}-M_{b}^{\mathrm{dry}}\left(\chi_{b}^{\mathrm{dry}}\right)^{2} \Delta \delta_{\mathrm{N} 2}+ \\ \frac{\varphi_{0}}{\varphi_{c}^{2}} K_{f} \Delta P_{e}+\frac{\varphi_{0}}{\varphi_{c}^{2}} P_{e} \Delta K_{f} \end{gathered} $

$ \begin{gathered} \Delta C_{44}^{\mathrm{sat}}=\Delta \mu_{b}^{\mathrm{dry}}-\mu_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{T} 1} ; \Delta C_{55}^{\mathrm{sat}}=\Delta \mu_{b}^{\mathrm{dry}}- \\ \mu_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{T} 1}-\mu_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{T} 2} \end{gathered} $

$ \Delta C_{66}^{\mathrm{sat}}=\Delta \mu_{b}^{\mathrm{dry}}-\mu_{b}^{\mathrm{dry}} \Delta \delta_{\mathrm{T} 2} $

式中: 符号Δ表示裂缝型储层参数的扰动量。

将方程(14)扰度刚度矩阵代入公式(10), 可以建立有效压力敏感参数、流体体积模量、介质剪切模量、密度、水平裂缝与垂直裂缝法向弱度、切向弱度等参数直接表征的反射系数方程, 即:

$ \begin{gathered} R_{\mathrm{PP}}(\theta, \varphi)=a_{K_{f}^{\mathrm{PP}}}(\theta) \frac{\Delta K_{f}}{K_{f 0}}+a_{\mu^{\mathrm{PP}}}(\theta) \frac{\Delta \mu}{\mu_{0}}+a_{{Pe}}^{\mathrm{PP}}(\theta) \cdot \\ \frac{\Delta P_{e}}{P_{e 0}}+a_{\rho}{ }^{\mathrm{PP}}(\theta) \frac{\Delta \rho}{\rho_{0}}+a_{\delta_{\mathrm{N} 1}^{\mathrm{PP}}}(\theta) \Delta \delta_{\mathrm{N} 1}+a_{\delta_{\mathrm{T} 1}}^{\mathrm{PP}}(\theta) \Delta \delta_{\mathrm{T} 1}+ \\ a_{\delta_{\mathrm{N} 2}^{\mathrm{PP}}}(\theta, \varphi) \Delta \delta_{\mathrm{N} 2}+a{\delta_{\mathrm{T} 2}}^{\mathrm{PP}}(\theta, \varphi) \Delta \delta_{\mathrm{T} 2} \end{gathered} $

(15)

式中:

$ \begin{gathered} a_{K_{f}}^{\mathrm{PP}}(\theta)=\left(1-\frac{\gamma_{d}^{2}}{\gamma_{s}^{2}}\right) \frac{\sec ^{2} \theta}{4}, a_{\mu}^{\mathrm{PP}}(\theta)=\frac{\gamma_{d}^{2}}{\gamma_{s}^{2}} \frac{\sec ^{2} \theta}{4}- \\ \frac{2}{\gamma_{s}^{2}} \sin ^{2} \theta, a_{P_{e}}^{\mathrm{PP}}(\theta)=\left(1-\frac{\gamma_{d}^{2}}{\gamma_{s}^{2}}\right) \frac{\sec ^{2} \theta}{4} \end{gathered} $

$ \begin{gathered} a_{\rho}^{\mathrm{PP}}(\theta)=\frac{1}{2}-\frac{\sec ^{2} \theta}{4}, a_{\delta_{\mathrm{N} 1}}^{\mathrm{PP}}(\theta)=-\frac{\gamma_{d}^{2}}{\gamma_{s}^{2}} \frac{\sec ^{2} \theta}{4}(1- \\ \left.\frac{2}{\gamma_{d}^{2}} \sin ^{2} \theta\right)^{2}, a_{\delta_{\mathrm{T} 1}}^{\mathrm{PP}}(\theta)=\frac{1}{\gamma_{s}^{2}} \sin ^{2} \theta \end{gathered} $

$ \begin{gathered} a_{\delta_{\mathrm{N} 2}}^{\mathrm{PP}}(\theta, \varphi)=-\frac{\gamma_{d}^{2}}{\gamma_{s}^{2}} \frac{\sec ^{2} \theta}{4}\left[1-\frac{2}{\gamma_{d}^{2}}\left(\sin ^{2} \theta \sin ^{2} \varphi+\right.\right. \\ \left.\left.\cos ^{2} \theta\right)\right]^{2} \end{gathered} $

$ a_{\delta_{\mathrm{T} 2}}^{\mathrm{PP}}(\theta, \varphi)=\frac{2}{\gamma_{s}^{2}} \sin ^{2} \theta \cos ^{2} \varphi\left(1-\tan ^{2} \theta \sin ^{2} \varphi\right) $

式中: θ表示地震波的入射角; φ表示地震观测方位与裂缝法向的方位角差值; 裂缝方位角可以通过椭圆拟合方法预测^[53]得到。分母K_f0表示流体体积模量的均值; P_e0表示岩石的有效压力参数均值; μ₀表示剪切模量的均值。γ_s²=M_s/μ, γ_d²=M_d/μ, 其中, M_s表示含流体各向同性介质纵波模量, M_d表示干燥各向同性介质纵波模量, 可以利用测井数据和Gassmann公式^[24]计算。令水平裂缝参数为0, 即完全各向同性介质背景中发育一组垂直裂缝时, 公式(15)退化为HTI介质方程, 经验证该方程与PAN^[54]以及LI^[25]中的公式一致, 进而验证了该方程的准确性。裂缝参数可通过岩石物理模型^[52]估算得到。

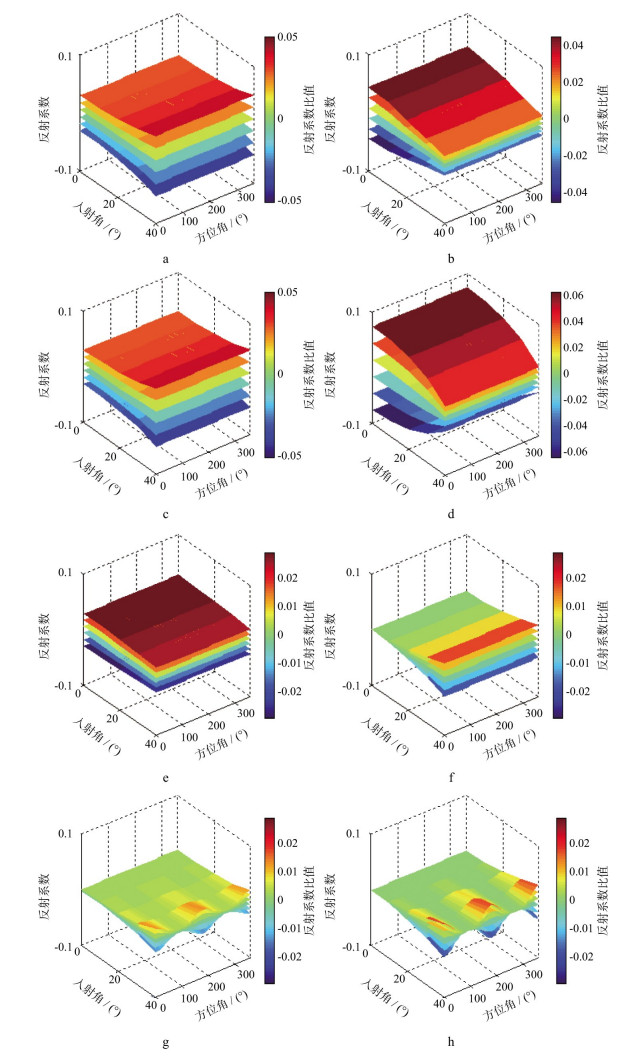
为研究有效压力敏感参数、流体体积模量、介质剪切模量、密度、水平裂缝与垂直裂缝法向弱度、切向弱度参数变化对公式(15)的贡献度差异, 逐一分析每个参数对反射系数产生的影响。图 9分别展示了在参数统一变化范围(-0.30∶0.15∶0.30)内引起的地震反射系数变化特征, 整体分析可以看出, 各向同性参数的贡献度要远大于各向异性部分, 重点分析有效压力敏感参数项, 即图 9c所示内容, 随着入射角及参数扰动范围的变化, 有效压力敏感参数对OA介质反射系数的贡献较明显, 相较裂缝参数更容易实现稳定反演, 其它各向同性介质参数如流体体积模量和介质剪切模量对反射系数影响同样较明显, 图 9d中密度参数对反射系数引起的变化较小, 但仍比裂缝参数的明显。由图 9e至图 9h分析可知, 裂缝参数对反射系数整体贡献度较低, 裂缝参数之间贡献度差异不明显, 随着地震波入射角的增大, 裂缝参数对反射系数的贡献度逐渐增加, 因此, 相较小角度地震数据, 裂缝参数对大角度方位地震数据更敏感, 利用大入射角的宽方位五维地震资料更容易实现上述参数的稳定反演。

1.3 裂缝型储层五维地震有效压力参数反演方法

对于有效压力敏感参数地震反射方程(15), 将其中的非裂缝待反演参数的相对差值用自然函数的差值Δln(·)近似代替, 即ΔK_f/K_f0≈Δ(lnK_f), Δμ/μ₀≈Δ(lnμ), ΔPe/Pe₀≈Δ(lnPe)和Δρ/ρ₀≈Δ(lnρ), 进而消除了反射系数方程中的分式项。针对弱各向异性裂缝型储层, 各向异性特征及非均质特征较弱, 储层地球物理参数变化连续, 因此可将待反演参数的差值形式表示为: Δ(lnK_f)≈d(lnK_f), Δ(lnμ)≈d(lnμ), Δ(lnPe)≈d(lnPe)和Δ(lnρ)≈d(lnρ), 其中裂缝弱度参数同样表示为Δδ_N1≈dδ_N1, Δδ_T1≈dδ_T1, Δδ_N2≈dδ_N2和Δδ_T2≈dδ_T2, 上述参数表征为利用五维地震资料反演奠定了基础。

将方程(15)与时间域和频率域地震子波分别褶积, 得到时间域和频率域的正演方程, 可表示为:

$ \begin{gathered} s(t)=W(t) \boldsymbol{a}_{K_{f}}^{\mathrm{PP}}(\theta) D \ln K_{f}+W(t) \boldsymbol{a}_{\mu}^{\mathrm{PP}}(\theta) D \ln \mu+ \\ W(t) \boldsymbol{a}_{P_{e}}^{\mathrm{PP}}(\theta) D \ln P_{e}+W(t) \boldsymbol{a}_{\rho}^{\mathrm{PP}}(\theta) D \ln \rho+ \\ W(t) \boldsymbol{a}_{\delta_{\mathrm{N} 1}}^{\mathrm{PP}}(\theta, \varphi) D \delta_{\mathrm{N} 1}+W(t) \boldsymbol{a}_{\delta_{\mathrm{T} 1}}^{\mathrm{PP}}(\theta, \varphi) D \delta_{\mathrm{T} 1}+ \\ W(t) \boldsymbol{a}_{\delta_{\mathrm{N} 2}}^{\mathrm{PP}}(\theta, \varphi) D \delta_{\mathrm{N} 2}+W(t) \boldsymbol{a}_{\delta_{\mathrm{T} 2}}^{\mathrm{PP}}(\theta, \varphi) D \delta_{\mathrm{T} 2} \end{gathered} $

(16)

$ \begin{gathered} S^{\prime}(\omega)=W^{\prime}(\omega) \boldsymbol{E} \boldsymbol{a}_{K_{f}}^{\mathrm{PP}}(\theta) D \ln K_{f}+W^{\prime}(\omega) \boldsymbol{E} \boldsymbol{a}_{\mu}^{\mathrm{PP}}(\theta) \cdot \\ D \ln \mu+W^{\prime}(\omega) \boldsymbol{E a}_{P_{e}}^{\mathrm{PP}}(\theta) D \ln P e+W^{\prime}(\omega) \boldsymbol{E} \boldsymbol{a}_{\rho}^{\mathrm{PP}}(\theta) \cdot \\ D \ln \rho+W^{\prime}(\omega) \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N} 1}}^{\mathrm{PP}}(\theta, \varphi) D \delta_{\mathrm{N} 1}+W^{\prime}(\omega) \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{T} 1}}^{\mathrm{PP}}(\theta, \varphi) \cdot \\ D \delta_{\mathrm{T} 1}+W^{\prime}(\omega) \boldsymbol{E}_{\delta_{\mathrm{N} 2}}^{\mathrm{PP}}(\theta, \varphi) D \delta_{\mathrm{N} 2}+W^{\prime}(\omega) \cdot \\ \boldsymbol{E a}_{\delta_{\mathrm{T} 2}}^{\mathrm{PP}}(\theta, \varphi) D \delta_{\mathrm{T} 2} \end{gathered} $

(17)

式中: s(t)和S′(ω)分别是时间域和频率域地震记录; W(t)和W′(ω)分别为时间域和频率域子波; E=e^-iωτ_k代表傅里叶算子, 令l=1∶T, ω_l表示第l个有效频率成分, D是差分算子。

将公式(16)和公式(17)写成矩阵的形式:

$ \left[\begin{array}{c} \boldsymbol{S}(t) \\ \boldsymbol{S}^{\prime}(\omega) \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{G}_{\text {iso }}(t) & \boldsymbol{G}_{\mathrm{ani}}(t) \\ \boldsymbol{G}^{\prime}{ }_{\text {iso }}(\omega) & \boldsymbol{G}^{\prime}{ }_{\text {ani }}(\omega) \end{array}\right] *\left[\begin{array}{l} \boldsymbol{m}_{\text {iso }} \\ \boldsymbol{m}_{\mathrm{ani}} \end{array}\right] $

(18)

在贝叶斯框架下, 基于五维地震时频域分步反演算法, 对于入射角数量为M, 方位角数量为N, 反射界面的数量为K的五维地震道集, 时间域和频率域各向同性正演算子G_iso(t), G′_iso(ω)和各向异性正演算子G_ani(t), G′_ani(ω)为:

$ \begin{aligned} &{\left[\boldsymbol{G}_{\mathrm{iso}}(t)\right]_{M N K \times 4 K}=} \\ &\boldsymbol{W}(t) \boldsymbol{D}\left[\boldsymbol{A}_{K_{f}}(\theta) \quad \boldsymbol{A}_{\mu}(\theta) \quad \boldsymbol{A}_{P e}(\theta) \quad \boldsymbol{A}_{\rho}(\theta)\right] \end{aligned} $

(19)

其中,

$ \begin{array}{c} \begin{array}{l} \left[\boldsymbol{A}_{K_{f}}(\theta)\right]_{M N K \times K} \end{array}=\left[\begin{array}{llll} \boldsymbol{a}_{K_{f}}\left(\theta_{1}\right) & \cdots & \boldsymbol{a}_{K_{f}}\left(\theta_{M}\right) & \boldsymbol{a}_{K_{f}}\left(\theta_{1}\right)\cdots & \boldsymbol{a}_{K_{f}}\left(\theta_{M}\right) & \cdots & \boldsymbol{a}_{K_{f}}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}}\\ \left[\boldsymbol{A}_{\mu}(\theta)\right]_{M N K \times K}=\left[\begin{array}{llllllll} \boldsymbol{a}_{\mu}\left(\theta_{1}\right) & \cdots & \boldsymbol{a}_{\mu}\left(\theta_{M}\right) & \boldsymbol{a}_{\mu}\left(\theta_{1}\right) & \cdots & \boldsymbol{a}_{\mu}\left(\theta_{M}\right) & \cdots & \boldsymbol{a}_{\mu}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}}\\ \left[\boldsymbol{A}_{P e}(\theta)\right]_{M N K \times K}\left[\begin{array}{llllllll}\boldsymbol{a}_{P e}\left(\theta_{1}\right) & \cdots & \boldsymbol{a}_{P e}\left(\theta_{M}\right)&\boldsymbol{a}_{P e}\left(\theta_{1}\right) & \cdots & \boldsymbol{a}_{P e}\left(\theta_{M}\right) & \cdots & \boldsymbol{a}_{P e}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}}\\ \left[\boldsymbol{A}_{\rho}(\theta)\right]_{M N K \times K}=\left[\begin{array}{lll} \boldsymbol{a}_{\rho}\left(\theta_{1}\right) & \cdots & \boldsymbol{a}_{\rho}\left(\theta_{M}\right)&\boldsymbol{a}_{\rho}\left(\theta_{1}\right) & \cdots &\boldsymbol{a}_{\rho}\left(\theta_{M}\right) & \cdots & \boldsymbol{a}_{\rho}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}} \end{array} $

$ \begin{array}{c} \left[\boldsymbol{a}_{K_{f}}\left(\theta_{i}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{K_{f}}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{K_{f}}^{K}\left(\theta_{i}\right)\right]\\ \left[\boldsymbol{a}_{\mu}\left(\theta_{i}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{\mu}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{\mu}^{K}\left(\theta_{i}\right)\right]\\ \left[\boldsymbol{a}_{P e}\left(\theta_{i}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{P_{e}}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{P e}^{K}\left(\theta_{i}\right)\right]\\ \left[\boldsymbol{a}_{\rho}\left(\theta_{i}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{\rho}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{\rho}^{K}\left(\theta_{i}\right)\right] \end{array} $

$ \left[\boldsymbol{G}_{\mathrm{ani}}(t)\right]_{M N K \times 4 K}=\boldsymbol{W}(t)\left[\boldsymbol{A}_{\delta_{\mathrm{N} 1}}(\theta, \varphi) \quad \boldsymbol{A}_{\delta_{\mathrm{T} 1}}(\theta, \varphi) \quad \boldsymbol{A}_{\delta_{\mathrm{N} 2}}(\theta, \varphi) \quad \boldsymbol{A}_{\delta_{\mathrm{T} 2}}(\theta, \varphi)\right] $

(20)

其中,

$ \begin{array}{c} \left[\boldsymbol{A}_{\delta_{\mathrm{N} 1}}(\theta, \varphi)\right]_{M N K \times K}=\left[\boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{1}, \varphi_{1}^{0}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{M}, \varphi_{1}\right)\quad\cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{M}, \varphi_{2}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{M}, \varphi_{\mathrm{N}}\right)\right]^{\mathrm{T}}\\ \left[A_{\delta_{\mathrm{T} 1}}(\theta, \varphi)\right]_{M N K \times K}=\left[\boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{1}, \varphi_{1}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{M}, \varphi_{1}\right)\quad\cdots \quad \boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{M}, \varphi_{2}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{M}, \varphi_{N}\right)\right]^{\mathrm{T}}\\ \left[A_{\delta_{\mathrm{N} 2}}(\theta, \varphi)\right]_{M N K \times K}=\left[\boldsymbol{a}_{\delta_{\mathrm{N} 2}}\left(\theta_{1}, \varphi_{1}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 2}}\left(\theta_{M}, \varphi_{1}\right)\quad\cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 2}}\left(\theta_{M}, \varphi_{2}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 2}}\left(\theta_{M}, \varphi_{\mathrm{N}}\right)\right]^{\mathrm{T}}\\ \left[A_{\delta_{\mathrm{T} 2}}(\theta, \varphi)\right]_{M N K \times K}=\left[\begin{array}{lll} \boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{1}, \varphi_{1}\right) & \cdots & \boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{M}, \varphi_{1}\right)&\cdots & \boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{M}, \varphi_{2}\right) & \cdots & \boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{M}, \varphi_{N}\right) \end{array}\right]^{\mathrm{T}} \end{array} $

$ \begin{array}{c} \left[\boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{i}, \varphi_{j}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{N} 1}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 1}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right]\\ \left[\boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{i}, \varphi_{j}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{T} 1}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{T} 1}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right]\\ \left[\boldsymbol{a}_{\delta_{\mathrm{N} 2}}\left(\theta_{i}, \varphi_{j}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{N} 2}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 2}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right]\\ \left[\boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{i}, \varphi_{j}\right)\right]_{K \times K}=\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{T} 2}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{T} 2}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right] \end{array} $

$ \left[\boldsymbol{G}^{\prime}{}_{\text {iso }}(\omega)\right]_{M N T \times 4 K}=\boldsymbol{W}^{\prime}(\omega) \boldsymbol{D}\left[\boldsymbol{E} \boldsymbol{A}_{K_{f}}(\theta) \quad \boldsymbol{EA}_{\mu}(\theta) \quad \boldsymbol{E A}_{P e}(\theta) \quad \boldsymbol{E A}_{\rho}(\theta)\right] $

(21)

其中,

$ \begin{array}{c} \left[\begin{array}{l} \boldsymbol{E} \boldsymbol{A}_{K_{f}}(\theta) \end{array}\right]_{M N K \times K}=\left[\begin{array}{llllllll} \boldsymbol{E} \boldsymbol{a}_{K_{f}}\left(\theta_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{K_{f}}\left(\theta_{M}\right) & \boldsymbol{E} \boldsymbol{a}_{K_{f}}\left(\theta_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{K_{f}}\left(\theta_{M}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{K_{f}}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}}\\ \left[\begin{array}{c} \boldsymbol{E} \boldsymbol{A}_{\mu}(\theta) \end{array}\right]_{M N K \times K}=\left[\begin{array}{llllllll} \boldsymbol{E} \boldsymbol{a}_{\mu}\left(\theta_{1}\right) & \cdots & \boldsymbol{E a}_{\mu}\left(\theta_{M}\right) & \boldsymbol{E} \boldsymbol{a}_{\mu}\left(\theta_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\mu}\left(\theta_{M}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\mu}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}}\\ \left[\boldsymbol{E} \boldsymbol{A}_{P e}(\theta)\right]_{M N K \times K}=\left[\begin{array}{llll} \boldsymbol{E} \boldsymbol{a}_{P e}\left(\theta_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{P e}\left(\theta_{M}\right) & \boldsymbol{E} \boldsymbol{a}_{P e}\left(\theta_{1}\right)&\cdots & \boldsymbol{E} \boldsymbol{a}_{P_{e}}\left(\theta_{M}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{P_{e}}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}}\\ \left[\boldsymbol{E} \boldsymbol{A}_{\rho}(\theta)\right]_{M N K \times K}=\left[\begin{array}{llll} \boldsymbol{a}_{\rho}\left(\theta_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\rho}\left(\theta_{M}\right) & \boldsymbol{E} \boldsymbol{a}_{\rho}\left(\theta_{1}\right)&\cdots & \boldsymbol{E} \boldsymbol{a}_{\rho}\left(\theta_{M}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\rho}\left(\theta_{M}\right) \end{array}\right]^{\mathrm{T}} \end{array} $

$ \left[\boldsymbol{E} \boldsymbol{a}_{K_{f}}\left(\theta_{i}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega _1}}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega_T}} } \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{K_{f}}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{K_{f}}^{K}\left(\theta_{i}\right)\right] $

$ \left[\boldsymbol{E} \boldsymbol{a}_{\mu}\left(\theta_{i}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega _1}}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega_T}} } \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{\mu}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{\mu}^{K}\left(\theta_{i}\right)\right] $

$ \left[\boldsymbol{E} \boldsymbol{a}_{Pe}\left(\theta_{i}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega _1}}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega_T}} } \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{Pe}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{Pe}^{K}\left(\theta_{i}\right)\right] $

$ \left[\boldsymbol{E} \boldsymbol{a}_{\rho}\left(\theta_{i}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega _1}}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K^{\omega_T}} } \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{\rho}^{1}\left(\theta_{i}\right) \quad \cdots \quad \boldsymbol{a}_{\rho}^{K}\left(\theta_{i}\right)\right] $

$ \left[\boldsymbol{G}^{\prime}{}_{\text {ani }}(\omega)\right]_{M N T \times 4 K}=\boldsymbol{W}^{\prime}(\omega) \boldsymbol{D}\left[\boldsymbol{E} \boldsymbol{A}_{\delta_{\mathrm{N} 1}}(\theta, \varphi) \quad\boldsymbol{E}_{\delta_{\mathrm{T} 1}}(\theta, \varphi) \quad \boldsymbol{E} \boldsymbol{A}_{\delta_{\mathrm{N} 2}}(\theta, \varphi) \quad \boldsymbol{E} \boldsymbol{A}_{\delta_{\mathrm{T} 2}}(\theta, \varphi)\right] $

(22)

其中,

$ \left[\begin{array}{c} \boldsymbol{E} \boldsymbol{A}_{\delta_{\mathrm{N} 1}}(\theta, \varphi) \end{array}\right]_{M N K \times K}=\left[\begin{array}{lllllll} \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{1}, \varphi_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{M}, \varphi_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{M}, \varphi_{2}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{M}, \varphi_{N}\right) \end{array}\right]^{\mathrm{T}} $

$ \left[\boldsymbol{E} \boldsymbol{A}_{\delta_{\mathrm{T} 1}}(\theta, \varphi)\right]_{M N K \times K}=\left[\begin{array}{llllllll} \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{1}, \varphi_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{M}, \varphi_{1}\right) & \cdots & \boldsymbol{Ea}_{\delta_{\mathrm{T} 1}}\left(\theta_{M}, \varphi_{2}\right) & \cdots & \boldsymbol{Ea}_{\delta_{\mathrm{T} 1}}\left(\theta_{M}, \varphi_{N}\right) \end{array}\right]^{\mathrm{T}} $

$ \left[\boldsymbol{E} \boldsymbol{A}_{\delta_{\mathrm{N} 2}}(\theta, \varphi)\right]_{M N K \times K}=\left[\begin{array}{lllllll} \boldsymbol{E a}_{\delta_{\mathrm{N} 2}}\left(\theta_{1}, \varphi_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N}}}\left(\theta_{M}, \varphi_{1}\right) & \cdots & \boldsymbol{Ea}_{\delta_{\mathrm{N}}}\left(\theta_{M}, \varphi_{2}\right) & \cdots & \boldsymbol{Ea}_{\delta_{\mathrm{N}}}\left(\theta_{M}, \varphi_{N}\right) \end{array}\right]^{\mathrm{T}} $

$ \left[\boldsymbol{E} \boldsymbol{A}_{\delta_{\mathrm{T} 2}}(\theta, \varphi)\right]_{M N K \times K}=\left[\begin{array}{llllllll} \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{1}, \varphi_{1}\right) & \cdots & \boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{M}, \varphi_{1}\right) & \cdots & \boldsymbol{Ea}_{\delta_{\mathrm{T} 2}}\left(\theta_{M}, \varphi_{2}\right) & \cdots & \boldsymbol{Ea}_{\delta_{\mathrm{T} 2}}\left(\theta_{M}, \varphi_{N}\right) \end{array}\right]^{\mathrm{T}} $

$ \left[\boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N} 1}}\left(\theta_{i}, \varphi_{j}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{1}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{T}} \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{N} 1}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 1}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right] $

$ \left[\boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{T} 1}}\left(\theta_{i}, \varphi_{j}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{1}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{T}} \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{T} 1}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{T} 1}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right] $

$ \left[\boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{N} 2}}\left(\theta_{i}, \varphi_{j}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{1}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{T}} \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{N} 2}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{N} 2}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right] $

$ \left[\boldsymbol{E} \boldsymbol{a}_{\delta_{\mathrm{T} 2}}\left(\theta_{i}, \varphi_{j}\right)\right]_{\mathrm{T} \times K}=\left[\begin{array}{ccc} \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{1}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{1}} \\ \vdots & \vdots & \vdots \\ \mathrm{e}^{-\mathrm{i} \tau_{1} \omega_{T}} & \cdots & \mathrm{e}^{-\mathrm{i} \tau_{K} \omega_{T}} \end{array}\right]\operatorname{diag}\left[\boldsymbol{a}_{\delta_{\mathrm{T} 2}}^{1}\left(\theta_{i}, \varphi_{j}\right) \quad \cdots \quad \boldsymbol{a}_{\delta_{\mathrm{T} 2}}^{K}\left(\theta_{i}, \varphi_{j}\right)\right] $

$ \boldsymbol{m}_{\text {iso }}=\left[\begin{array}{lll} \boldsymbol{R}_{K_{f}} \quad \boldsymbol{R}_{\mu} & \boldsymbol{R}_{P{e}} & \boldsymbol{R}_{\rho} \end{array}\right]^{\mathrm{T}} $

$ {\left[\boldsymbol{R}_{K_{f}}\right]_{K \times 1}=\left[\begin{array}{lll} \left(\ln K_{f}\right)^{1} & \cdots & \left(\ln K_{f}\right)^{K} \end{array}\right]^{\mathrm{T}}} $

$ {\left[\boldsymbol{R}_{\mu}\right]_{K \times 1}=\left[\begin{array}{lll} (\ln \mu)^{1} & \cdots & (\ln \mu)^{K} \end{array}\right]^{\mathrm{T}}} $

$ {\left[\boldsymbol{R}_{P e}\right]_{K \times 1}=\left[\begin{array}{lll} (\ln P e)^{1} & \cdots & (\ln P e)^{K} \end{array}\right]^{\mathrm{T}}} $

$ {\left[\boldsymbol{R}_{\rho b}\right]_{K \times 1}=\left[\begin{array}{lll} \left(\ln \rho_{b}\right)^{1} & \cdots & \left(\ln \rho_{b}\right)^{K} \end{array}\right]^{\mathrm{T}}} $

$ \boldsymbol{m}_{\mathrm{ani}}=\left[\begin{array}{llll} \boldsymbol{R}_{\delta_{\mathrm{N} 1}} & \boldsymbol{R}_{\delta_{\mathrm{T} 1}} & \boldsymbol{R}_{\delta_{\mathrm{N} 2}} & R_{\delta_{\mathrm{T} 2}} \end{array}\right]^{\mathrm{T}} $

$ \left[\boldsymbol{R}_{\delta_{\mathrm{N} 1}}\right]_{K \times 1}=\left[\begin{array}{lll} \left(\delta_{\mathrm{N} 1}\right)^{1} & \cdots & \left(\delta_{\mathrm{N} 1}\right)^{K} \end{array}\right]^{\mathrm{T}} $

$ \left[\begin{array}{lll} \boldsymbol{R}_{\delta_{\mathrm{N} 2}} \end{array}\right]_{K \times 1}=\left[\begin{array}{lll} \left(\delta_{\mathrm{N} 2}\right)^{1} & \cdots & \left(\delta_{\mathrm{N} 2}\right)^{K} \end{array}\right]^{\mathrm{T}} $

$ \left[\boldsymbol{R}_{\delta_{\mathrm{T} 1}}\right]_{K \times 1}=\left[\begin{array}{lll} \left(\delta_{\mathrm{T} 1}\right)^{1} & \cdots & \left(\delta_{\mathrm{T} 1}\right)^{K} \end{array}\right]^{\mathrm{T}} $

$ \left[\boldsymbol{R}_{\delta_{\mathrm{T} 2}}\right]_{K \times 1}=\left[\begin{array}{lll} \left(\delta_{\mathrm{T} 2}\right)^{1} & \cdots & \left(\delta_{\mathrm{T} 2}\right)^{K} \end{array}\right]^{\mathrm{T}} $

借助待反演参数模型协方差矩阵C_cov的特征值和特征向量, 对正演算子矩阵及模型参数矩阵进行处理, 以避免因参数尺度或者相关性的原因干扰反演结果, 首先奇异值分解可得矩阵的特征向量U和特征值正定矩阵Σ, 即C_cov=UΣU^T, 相关结果如下:

$ \begin{array}{c} {\left[\begin{array}{cc} \widetilde{\boldsymbol{G}}_{\text {iso }}(t) & \widetilde{\boldsymbol{G}}_{\text {ani }}(t) \\ \widetilde{\boldsymbol{G}}^{\prime}{}_{\text {iso }}(\omega) & \widetilde{\boldsymbol{G}}^{\prime}{}_{\text {ani }}(\omega) \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{G}_{\text {iso }}(t) & \boldsymbol{G}_{\text {ani }}(t) \\ \boldsymbol{G}^{\prime}{ }_{\text {iso }}(\omega) & \boldsymbol{G}^{\prime}{}_{\text {ani }}(\omega) \end{array}\right] \cdot } \\ {\left[\operatorname{kron}\left(\boldsymbol{\varSigma}^{-\frac{1}{2}} U^{\mathrm{T}}, I_{L}\right)\right]^{-1} } \end{array} $

(23)

$ \left[\begin{array}{c} \tilde{\boldsymbol{m}}_{\text {iso }} \\ \tilde{\boldsymbol{m}}_{\text {ani }} \end{array}\right]=\left[\operatorname{kron}\left(\boldsymbol{\varSigma}^{-\frac{1}{2}} \boldsymbol{U}^{\mathrm{T}}, \boldsymbol{I}_{L}\right)\right] \cdot\left[\begin{array}{l} \boldsymbol{m}_{\text {iso }} \\ \boldsymbol{m}_{\text {ani }} \end{array}\right] $

(24)

因此, 地震记录可以写为:

$ \left[\begin{array}{c} \boldsymbol{s}(t) \\ \boldsymbol{S}^{\prime}(\omega) \end{array}\right]=\left[\begin{array}{cc} \tilde{\boldsymbol{G}}_{\mathrm{iso}}(t) & \widetilde{\boldsymbol{G}}_{\mathrm{ani}}(t) \\ \widetilde{\boldsymbol{G}}^{\prime}{}_{\text {iso }}(\omega) & \widetilde{\boldsymbol{G}}^{\prime}{ }_{\text {ani }}(\omega) \end{array}\right] *\left[\begin{array}{c} \tilde{\boldsymbol{m}}_{\text {iso }} \\ \tilde{\boldsymbol{m}}_{\text {ani }} \end{array}\right]+\left[\begin{array}{c} \boldsymbol{n}(t) \\ \boldsymbol{N}^{\prime}(\omega) \end{array}\right] $

(25)

式中: kron(·)表示Kronecker乘积算子, I_L为L阶单位矩阵。构建协方差矩阵的方式有多种, 本文是基于测井数据统计所得, L为井曲线采样点数。

基于时间域正演算子$\mathit{\boldsymbol{\tilde G}}$_iso(t), $\mathit{\boldsymbol{\tilde G}}$_ani(t)以及频率域正演算子$\mathit{\boldsymbol{\tilde G}}$′_iso(ω), $\mathit{\boldsymbol{\tilde G}}$′_ani(ω), 在贝叶斯框架下构建五维地震时频域分步反演目标泛函, 如公式(26)和公式(27):

$ \begin{gathered} F(\tilde{\boldsymbol{m}})=\boldsymbol{J}_{\widetilde{G}}(\tilde{\boldsymbol{m}})+\boldsymbol{J}_{\widetilde{G}^{\prime}}(\tilde{\boldsymbol{m}})+\boldsymbol{J}_{\text {Cauchy }}(\tilde{\boldsymbol{m}})+\boldsymbol{J}_{\mathrm{Smooth}}(\tilde{\boldsymbol{m}}) \\ =(\boldsymbol{s}-\boldsymbol{G} \tilde{\boldsymbol{m}})^{\mathrm{T}}(\boldsymbol{s}-\boldsymbol{G} \boldsymbol{m})+\left(\boldsymbol{S}^{\prime}-\widetilde{\boldsymbol{G}}^{\prime} \tilde{\boldsymbol{m}}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{\prime}-\right. \\ \left.\boldsymbol{G}^{\prime} \tilde{\boldsymbol{m}}\right)+2 \sigma_{n}^{2} \sum\limits_{i=1}^{4} \ln \left(1+\widetilde{\boldsymbol{m}}_{i}^{2} / \sigma_{m}^{2}\right)+\sum\limits_{i=1}^{4} \lambda_{m_{i}}\left(\boldsymbol{\varLambda}_{m_{i}}-\right. \\ \left.\boldsymbol{P}_{\boldsymbol{m}_{i}} \tilde{\boldsymbol{m}}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{\varLambda}_{\boldsymbol{m}_{i}}-\boldsymbol{P}_{m_{i}} \widetilde{\boldsymbol{m}}_{i}\right) \end{gathered} $

(26)

$ \begin{gathered} F\left(\tilde{\boldsymbol{m}}_{\text {ani }}\right)=\boldsymbol{J}_{\tilde{G}}\left(\tilde{\boldsymbol{m}}_{\text {ani }}\right)+\boldsymbol{J}_{\tilde{G}^{\prime}}\left(\tilde{\boldsymbol{m}}_{\text {ani }}\right)+\boldsymbol{J}_{\text {Cauchy }}\left(\tilde{\boldsymbol{m}}_{\text {ani }}\right)+ \\ \boldsymbol{J}_{\mathrm{Smooth}}\left(\tilde{m}_{ {ani }}\right) \\ =\left(\boldsymbol{s}-\boldsymbol{s}_{\text {iso }}-\boldsymbol{G}_{\text {ani }}\right)^{\mathrm{T}}\left(\boldsymbol{s}-\boldsymbol{s}_{\text {iso }}-\boldsymbol{G} \boldsymbol{m}_{\text {ani }}\right)+\left(\boldsymbol{S}^{\prime}-\right. \\ \left.\boldsymbol{S}^{\prime}{}_{\text {iso }}-\widetilde{\boldsymbol{G}}^{\prime} \tilde{\boldsymbol{m}}_{\text {ani }}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{\prime}-\boldsymbol{S}^{\prime}{}_{\text {iso }}-G^{\prime} \tilde{m}_{\text {ani }}\right)+2 \sigma_{n}^{2} \sum\limits_{i=5}^{8} \cdot \\ \ln \left(1+\frac{\tilde{\boldsymbol{m}}_{i}^{2}}{\sigma_{m}^{2}}\right)+\sum\limits_{i=5}^{8} \lambda_{m_{i}}\left(\boldsymbol{\varLambda}_{m_{i}}-\boldsymbol{P}_{m_{i}} \tilde{\boldsymbol{m}}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{\varLambda}_{m_{i}}-\right. \\ \left.\boldsymbol{P}_{\boldsymbol{m}_{i}} \tilde{\boldsymbol{m}}_{i}\right) \end{gathered} $

(27)

式中: λ_mi是模型参数的约束系数; P_mi=∫_t1^t_i·dτ表示积分算子; Λ_{$\mathit{\boldsymbol{\tilde m}}$i}=1/2*ln(R_{$\mathit{\boldsymbol{\tilde m}}$i}/R_{$\mathit{\boldsymbol{\tilde m}}$0}), R_{$\mathit{\boldsymbol{\tilde m}}$0}表示模型参数的初始值, 使用迭代重加权最小二乘算法(iteratively reweighted least-squares, IRLS)对公式(26)和公式(27)进行迭代求解, 首先, 将K_f, μ, P_e, ρ作为第一步的重点优化目标, 然后, 将δ_N1, δ_T1, δ_N2和δ_T2作为第二步的优化参数, 即每一步都是反演4个参数, 最终实现全部待反演模型参数的求取。

2 模型试算及实际资料处理 2.1 模型试算

利用实际裂缝工区中的钻井资料合成方位地震数据, 验证五维地震时频域分步反演有效压力敏感参数、流体体积模量、介质剪切模量、密度、水平裂缝与垂直裂缝法向弱度、切向弱度参数的可行性, 裂缝弱度参数通过岩石物理建模利用井上钻井资料估算得到。首先, 基于五维地震褶积模型合成8个方位: 22.5°, 45°, 67.5°, 90°, 112.5°, 135°, 157.5°和180°的地震道集。在合成地震道集中添加部分随机噪声, 生成不含噪声及信噪比分别为5∶1和2∶1的合成方位道集, 分别如图 10至图 12所示。基于上述合成的8个方位地震道集, 利用五维地震时频域分步反演方法进行方位反演测试。反演结果见图 13至图 18, 图中绿色、蓝色和红色曲线分别表示待反演参数的初始模型、模型参数真实值及模型参数的反演结果。分析不含噪声或含有较强噪声地震记录反演结果可知, 有效压力敏感参数、流体体积模量、介质剪切模量、密度、水平裂缝与垂直裂缝法向弱度、切向弱度参数反演结果与实际测井数据趋势吻合较好, 且数值之间误差较小, 即使在噪声较高的情况下, 同样可实现多参数的直接反演。因此该方法具有较高的准确度和抗噪性, 验证了五维地震时频域分步反演方法直接预测上述8个参数的可行性。

2.2 实际资料处理

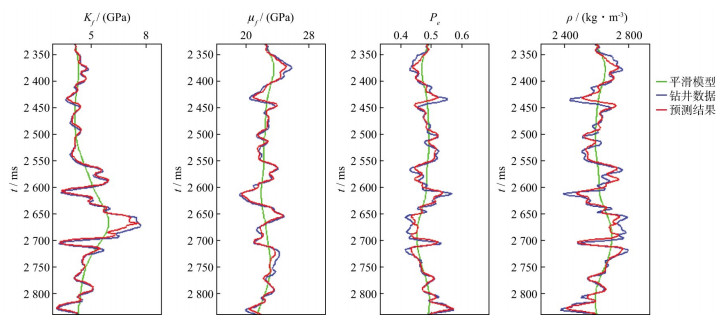
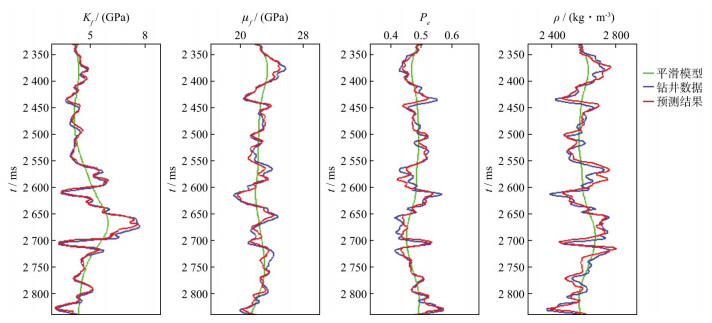
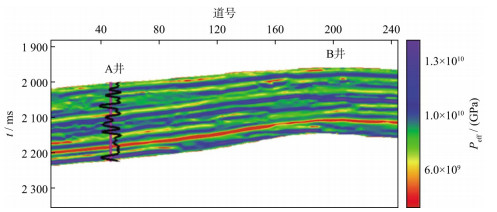
利用我国某地区裂缝型储层的五维地震资料进行处理, 地质资料显示该地区储层横向连续性较好, 且发育大量高角度倾角裂缝, 将该储层裂缝介质等效为正交各向异性介质。选取方位角分别为φ₁=45°, φ₂=75°, φ₃=135°和φ₄=165°的4个方位地震道集, 每个方位地震道集均经过了井控道集优化处理。图 19和图 20是这4个方位的近、中、远部分叠加道集地震二维剖面, 其部分叠加的入射角分别为10°(叠前角度为4°~16°)、22°(叠前角度为16°~28°)及34°(叠前角度为28°~40°)。图 21至图 24是利用井上流体体积模量、介质剪切模量、有效压力敏感参数、密度、水平裂缝与垂直裂缝法向弱度、切向弱度参数插值外推建立的初始模型剖面。图 25至图 28是利用五维地震时频域分步反演方法得到的反演结果剖面。上述参数反演结果整体分辨率较高, 细节特征明显, 趋势变化符合地震资料特征, 与井上数据对比吻合程度较高。由图 26b可以看出, 有效压力敏感参数反演的连井剖面与测井解释保持一致。因此可以在实际资料中实现有效压力敏感参数的直接反演。为更加明确显示流体体积模量反演预测的准确性, 图 29为流体体积模量直接反演结果。图中增加了A井和B井的信息对比, 其中B井为测试井。需要说明的是, 图 29反演结果是利用A井数据建立初始模型反演得到的, 反演过程中没有加入测试井B的任何信息。分析图中红线标识区域可知, 流体体积模量反演剖面中的低值对应该工区流体发育区域, 而且反演结果与测试井上流体解释结果吻合, 验证了反演结果的准确性。为进一步验证该方法的有效性与可靠性, 将井旁道流体体积模量、介质剪切模量、有效压力敏感参数、密度、水平裂缝与垂直裂缝法向弱度、切向弱度反演结果与井上数据进行对比, 如图 30所示, 各参数的反演结果与测井参数吻合程度高, 两者之间的误差较小, 验证了方法的可靠性。图 31是根据有效压力敏感参数计算得到的储层有效压力值, 图中色标红色为低值, 由此可以分析反演中压力低值区为实际生产提供依据。

3 结论

五维地震有效压力参数预测方法旨在从五维地震数据中直接获取裂缝型储层有效压力参数, 以正交各向异性介质为研究对象, 推导有效压力敏感参数直接表征的新的纵波反射系数弱各向异性近似方程, 在此基础上, 创新了贝叶斯框架下五维地震时频域分步反演方法。模型测试结果表明, 即使是在高噪声(信噪比为2∶1)的情况下, 该方法参数反演结果仍与真实模型参数吻合, 针对小贡献度参数(裂缝参数)的反演结果平均误差也较小, 验证了五维地震时频域分步反演方法的可行性与稳定性。利用经过井控道集优化处理的五维地震资料, 实现了裂缝型储层有效压力参数及流体参数和裂缝法向和切向裂缝弱度参数等多参数反演预测。分析可知, 反演结果与实际测井数据吻合良好, 进一步说明了该方法在裂缝型储层有效压力预测中具有广泛的应用前景。需要说明的是, 五维地震有效压力预测应重视地震道集的优化处理, 如果面向品质较差的地震资料, 该方法反演效果会降低, 后续研究可以在该方面做出优化改进。