多次波常见于海洋和陆地地震勘探数据中。在海洋地震勘探中, 存在两个强波阻抗差异界面——海水面和海底面。海水面上层介质为空气, 下层介质为海水。海水层的密度和波速均大于空气的密度与波速, 两者波阻抗差异极大, 故极易产生下行波散射。通常海底面上层介质为海水, 下层介质为沉积物, 两者存在较大的波阻抗差异, 所以地震波容易在水体中发生多次反射[1]。多次波是在海水面至少发生过一次下行反射的波。由于传播深度、路径不同, 海上多次波又可被分为海底多次波、水柱混响和其它多次波。相较于海洋多次波[2], 陆上多次波以层间多次波为主。容易产生层间多次波的页岩、砂岩往往层间距较小, 造成多次波与一次波时差小, 同相轴曲率差异不显著, 直接成像会造成虚假反射。因此, 层间多次波也是陆上地震数据处理的一大难点问题。
地震勘探的目的是使用地震波对地下结构进行探测和成像, 判断其是否存在特殊的构造, 间接反映油气藏存在的可能性。当前使用的地震成像算法多基于一次反射波的波动传播规律, 因此多次波能量聚焦于错误的深度, 引入假界面信息[3]。因此, 对于地震勘探来说, 多次波是一种噪声, 应该从地震数据中识别并压制。
通常使用表面相关多次波衰减法(surface-related multiple elimination, SRME)去除自由表面相关多次波。SRME是被公认为能够有效压制多次波的数据驱动方法, 该方法首先预测多次波, 再将预测的多次波自适应地从地震记录中去除。该方法需要将采集的地震数据排列成数据矩阵, 利用数据矩阵自褶积预测多次波, 因为预测出的多次波能量与实际地震数据的能量不匹配, 所以将预测的多次波从实际地震数据中减去时, 需要用到自适应相减法[4-5]。预测相减过程计算量极大, 易损伤一次波能量。另外, 传统的多次波压制技术通常是将一组地震数据处理参数应用于整个工区数据, 未考虑同一工区中不同位置的差异性, 未实现基于数据驱动的多次波压制, 因此处理精度有待提升。
近年来, 神经网络得到长足发展, 其具有模式识别的特性。利用训练好的网络进行数据处理, 可以极大提升工作效率。因此考虑使用神经网络的方法, 建立合理的数据集, 识别并去除地震记录中的多次波。神经网络问世之初, 由于算力限制, 并未被广泛应用, 直至卷积神经网络问世[6]。卷积神经网络和计算机的发展与进步, 使得深度神经网络可以被训练。自编码器是一类结构对称的前馈神经网络, 其具有压缩感知的特性, 通过将信息先编码后解码, 可以将信息特征稀疏化后并恢复[7]。卷积自编码器使用卷积核连接自编码器的各隐藏层, 首先利用待处理数据建立卷积自编码器输入数据集, 然后通过理想输出数据集建立标签数据集, 再建立卷积自编码器更新网络参数的目标优化函数, 最后即可用迭代的方法训练目标模型。将训练好的模型用于数据处理, 效率可以得到极大提升。江金生等[8-9]将卷积自编码神经网络应用于地震数据的去噪和插值, 取得了良好的应用效果。近年来, 随着深度学习的发展, 各类优化模式被不断提出。WANG等[10]认为卷积网络将图像特征的尺度局限在卷积核大小的范围内, 因此使用空间域自注意力模块建立远距离像素点之间的关联性, 可以进一步提升网络对全局特征的提取能力。本文将已经在地震数据处理中取得良好应用效果的卷积自编码神经网络应用于多次波压制问题, 为了提高该网络对全局特征的感知与提取能力, 引入自注意力机制, 形成了一套行之有效的多次波自动压制神经网络方法。
1 方法技术自编码器作为一种数据维度压缩和特征表达方法, 属于前馈神经网络。自编码器通常由编码器和解码器构成: 编码器可以实现输入数据的稀疏表达, 用于提取输入数据中最有效的信息; 解码器将稀疏表达重构为目标输出。通过设计合理的损失函数, 训练神经网络在编码阶段学习到被关注信号特征的稀疏表达, 在解码阶段尽可能减少损失地将编码输出还原至标签结果[11]。
卷积神经网络由全连接人工神经网络发展而来, 其在网络层间通过具有局部连接和权值共享两大特性的卷积核相连, 从而极大程度地避免了全连接网络的参数爆炸问题。卷积层使得深度网络结构可以被训练, 因此广泛应用于计算机视觉领域。
编码器fθi和解码器gθj可以分别表示为:
| $ \boldsymbol{h}=f_{\theta_{i}}\left(\boldsymbol{W}_{i} \otimes \boldsymbol{x}+b_{i}\right) $ | (1) |
| $ \boldsymbol{y}=g_{\theta_{j}}\left(\boldsymbol{W}_{j} \otimes \boldsymbol{h}+b_{j}\right) $ | (2) |
式中: x为输入的数据张量; h为数据编码后的本征特征; y为重建的数据张量; Wi, Wj, bi, bj分别为编码器和解码器中每个卷积层的权值矩阵与偏置, i, j为编码器中的第i个卷积层和解码器中的第j个卷积层; ⊗为卷积; θ为神经网络结构的超参数, 包括神经网络深度、卷积核个数和初始学习率等。
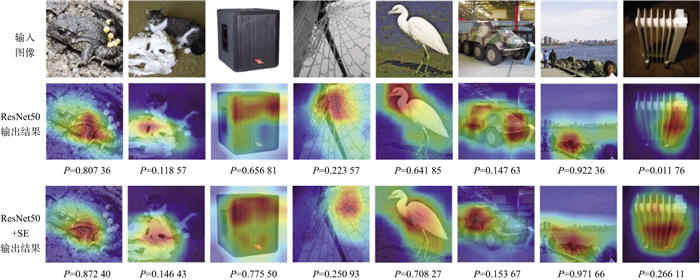
虽然卷积层能够极大地减少神经网络参数量, 但卷积核使得神经网络的关注尺度局限在核大小内, 即更关注局部特征。对于一些特殊视觉任务来说, 目标具有全局特征。自注意力机制可以在一定程度上缓解卷积核带来的局部性, 建立较远距离的地震数据之间的关系, 从而提升神经网络的效果。图 1中, P代表了各输出结果与标签的Softmax得分[13]。例如, 识别第8列输入图像中的物体, 当仅使用残差神经网络时, 网络仅将其部分识别为目标整体, 而加入自注意力模块(SE)后, P值得到明显提升, 对目标体的识别更为精准。增加了自注意力模块的神经网络, 感受野得到拓展, 对目标整体的识别明显增强。
|
图 1 利用添加自注意力模块的残差神经网络进行目标体识别的结果示意[13] |
在计算机视觉问题中, 注意力可表示如下[12]:
| $ \text { Attention }(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{softmax}\left(\frac{\boldsymbol{Q K ^ { \mathrm { T } }}}{\sqrt{d_{k}}}\right) \boldsymbol{V} $ | (3) |
式中: dk为缩放因子, 取值为K的维度, Q, K, V具体表示如下:
| $ \begin{array}{l} \boldsymbol{Q}=\text { flatten }(\boldsymbol{x} * \theta) \\ \boldsymbol{K}=\text { flatten }(\boldsymbol{x} * \varphi) \\ \boldsymbol{V}=\text { flatten }(\boldsymbol{x} * g) \end{array} $ | (4) |
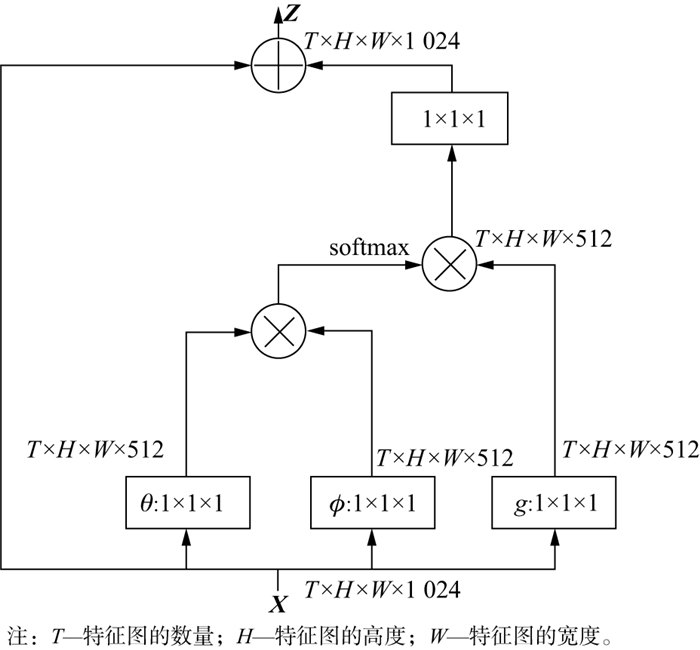
式中: φ, g均为神经网络结构中自注意力模块的超参数。自注意力模块如图 2所示[10], 自注意力机制是通过特征图元素的相关矩阵实现的。
|
图 2 自注意力模块 |
自编码器网络结构对称, 层数不深。层与层之间以卷积核相连接, 构成了卷积自编码器。由此可见, 卷积自编码器是一种轻量化的神经网络结构。对于地震数据中多次波的识别与去除, 由于卷积自编码器具有全局特征, 故在其中可以加入自注意力模块(图 2), 旨在去除多次波的同时, 尽可能地避免对一次波能量造成损伤。
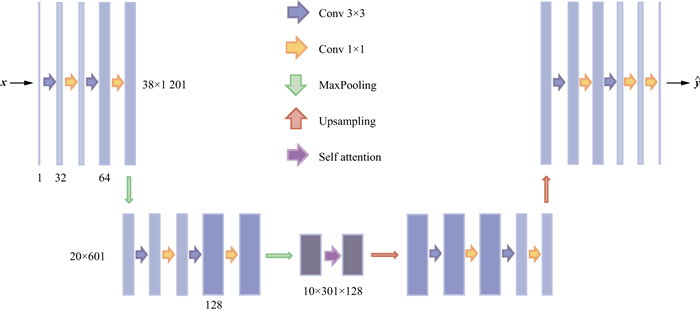
自注意力卷积自编码器的神经结构如图 3所示。在编码阶段依次进行通道数依次倍增的4组卷积计算, 且交替使用3×3和1×1大小的卷积核, 保持特征图尺寸不变。每两组卷积计算后进行一次池化, 池化后特征图的长宽减半。此过程中降维提取输入数据的特征, 得到稀疏化后的特征图。在编码器中加入自注意力模块, 增强特征全局连续性。解码阶段首先对稀疏特征图进行上采样, 使长宽各增加一倍, 同样, 再依次进行通道数依次倍减的4组卷积计算, 每两组卷积计算后进行一次上采样, 直至长宽与输入数据保持一致。最后, 以一次单通道卷积对具有32个通道的特征图进行融合, 此时生成器输出结果的尺寸、维度与输入数据皆保持一致。解码后地震数据特征得以恢复。
|
图 3 自注意力卷积自编码器的神经结构 |
自注意力卷积自编码器网络中将L1范数作为损失函数, 目标函数F可以表示为:
| $ F(\hat{\boldsymbol{y}}, \boldsymbol{y})=\sum\limits_{i=0}^{m}\left|y^{i}-\hat{y}^{i}\right| $ | (5) |
式中:
| $ R(\hat{\boldsymbol{y}}, \boldsymbol{y})=\frac{\sum _{i=0}^{m}\left|y^{i}-\hat{y}^{i}\right|}{m} $ | (6) |
式中: m为$\hat {\boldsymbol{y}}$, y的元素个数; R为残差平均值函数。
选用基于动量法和梯度下降法的Adam优化器, 更新网络的参数。Adam优化算法作为一种基于梯度下降的方法, 既可以利用梯度的一阶矩均值又可以利用梯度的二阶矩均值计算适应性参数学习率, 对于大规模数据的深度学习具有较大优势。Adam优化算法计算过程可以表示如下:
| $ g_{t}=\nabla_{\theta} F_{t}\left(\theta_{t}-1\right) $ | (7a) |
| $ \boldsymbol{m}_{t}=\beta_{1} \cdot \boldsymbol{m}_{t-1}+\left(1-\beta_{1}\right) \cdot g_{t} $ | (7b) |
| $ \boldsymbol{v}_{t}=\beta_{2} \cdot \boldsymbol{v}_{t-1}+\left(1-\beta_{2}\right) \cdot g_{t}^{2} $ | (7c) |
| $ \hat{\boldsymbol{m}}_{t}=\frac{\boldsymbol{m}_{t}}{1-\beta_{1}^{t}} $ | (7d) |
| $ \hat{\boldsymbol{v}}_{t}=\frac{\boldsymbol{v}_{t}}{1-\beta_{2}^{t}} $ | (7e) |
| $ \theta_{t}=\theta_{t-1}-\alpha \cdot \frac{\hat{\boldsymbol{m}}_{t}}{\sqrt{\hat{\boldsymbol{v}}_{t}}+\varepsilon} $ | (7f) |
式中: t为时间步长; gt为优化目标函数Ft在t时间步长的梯度; θt为t时刻的模型参数; α为步长; mt为梯度gt的一阶矩估计; $\hat {\boldsymbol{m}}$t为其相应的网络输出; β1为mt的指数衰减率; vt为梯度gt的二阶矩估计; $\hat {\boldsymbol{v}}$t为其相应的网络输出; β2为vt的指数衰减率, 且β1t, β2t∈[0, 1);令ε=10-8以确保迭代的稳定性。
2 理论地震数据实验神经网络数据集由输入数据集和标签数据集构成。通常进行正式处理前, 会对数据进行预处理, 旨在一定程度上防止过拟合, 预处理的方法有很多, 如数据标准化、数据连续属性离散化等。我们使用数据标准化中的Z-Score标准化, 计算公式如下:
| $ {\boldsymbol{x}}=\frac{{\boldsymbol{x}}_{0}-\mu}{\sigma} $ | (8) |
式中: x0和x分别为标准化前、后的地震数据; μ为数据x0的均值; σ为x0的方差。
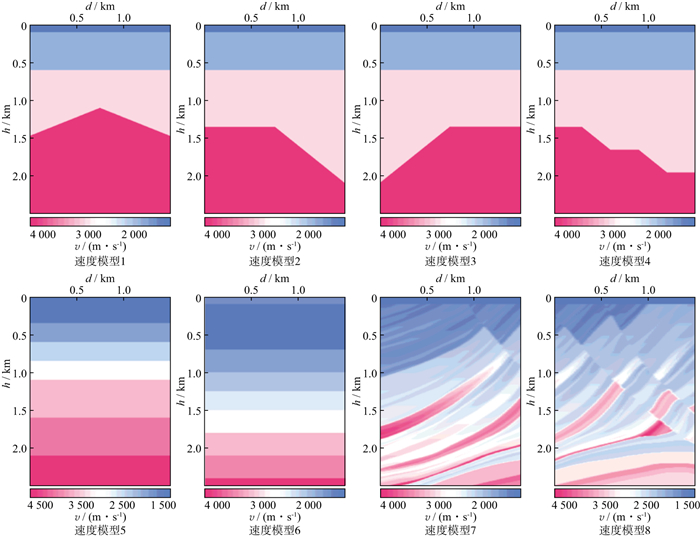
为了验证神经网络的有效性, 我们对模拟地震数据进行测试。由于模拟炮集数据难以仿真层间多次波, 因此通过控制自由地表吸收衰减与否, 来分别模拟带和不带表面相关多次波的地震数据, 利用图 4中的8个速度模型正演生成400炮地震数据训练集(图 5)。图 5a为训练神经网络所使用的带有自由表面多次波的输入数据, 图 5b为不带自由表面多次波的标签数据。
|
图 4 用于生成训练数据集的8个速度模型 |

|
图 5 训练神经网络所使用的带有自由表面多次波的输入数据(a)和不带有自由表面多次波的标签数据(b) |
从图 6可以看出, 多次波成分得到了较好的压制。图 7中网络输出数据与标签数据的残差几乎不可见, 说明网络处理后输出的数据接近标签数据, 残差平均值为0.001 4。图 6与图 7共同说明了本文方法在模拟炮集数据中应用的有效性。在易受多次波干扰的大偏移距处, 有效波与多次波严重相干, 给压制多次波能量带来挑战。
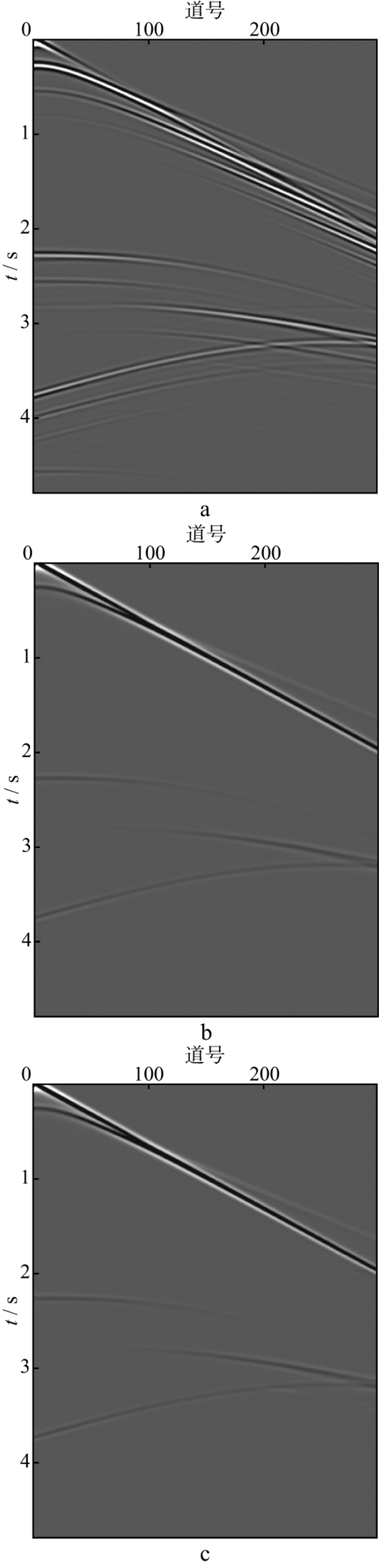
|
图 6 神经网络训练结果 a 网络输入数据; b 标签数据; c 经网络处理后输出的数据 |
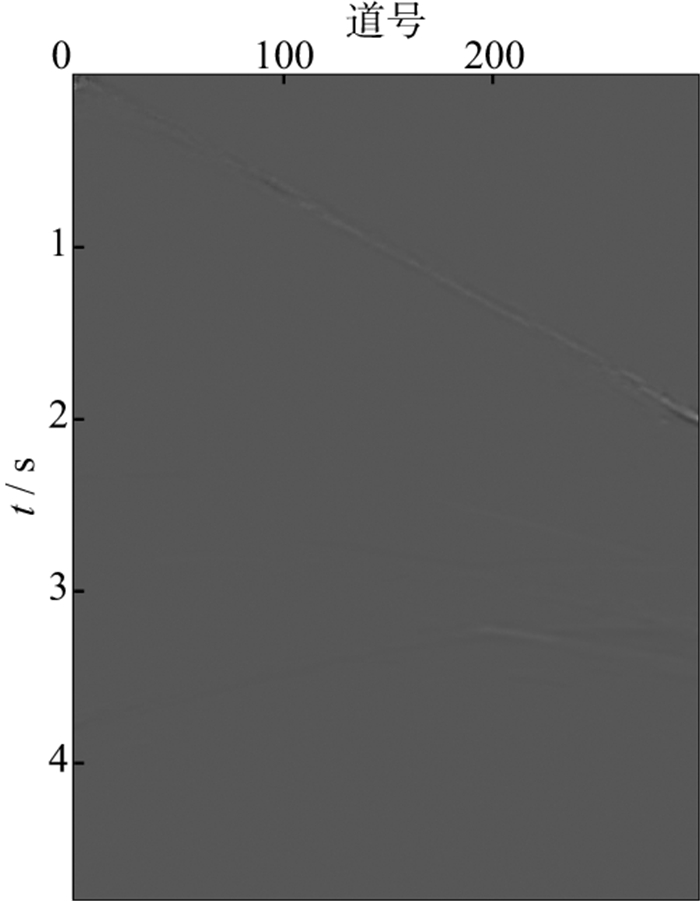
|
图 7 网络输出数据与标签数据的残差图像 |
如图 8所示, 大偏移距处同相轴模糊、扭曲, 而采用增加了自注意力模块的卷积自编码器(convolu-tional auto-encoder, CAE)相较于未增加注意力模块的CAE, 能更好地压制多次波, 恢复有效波能量, 增强一次波同相轴的空间连续性。
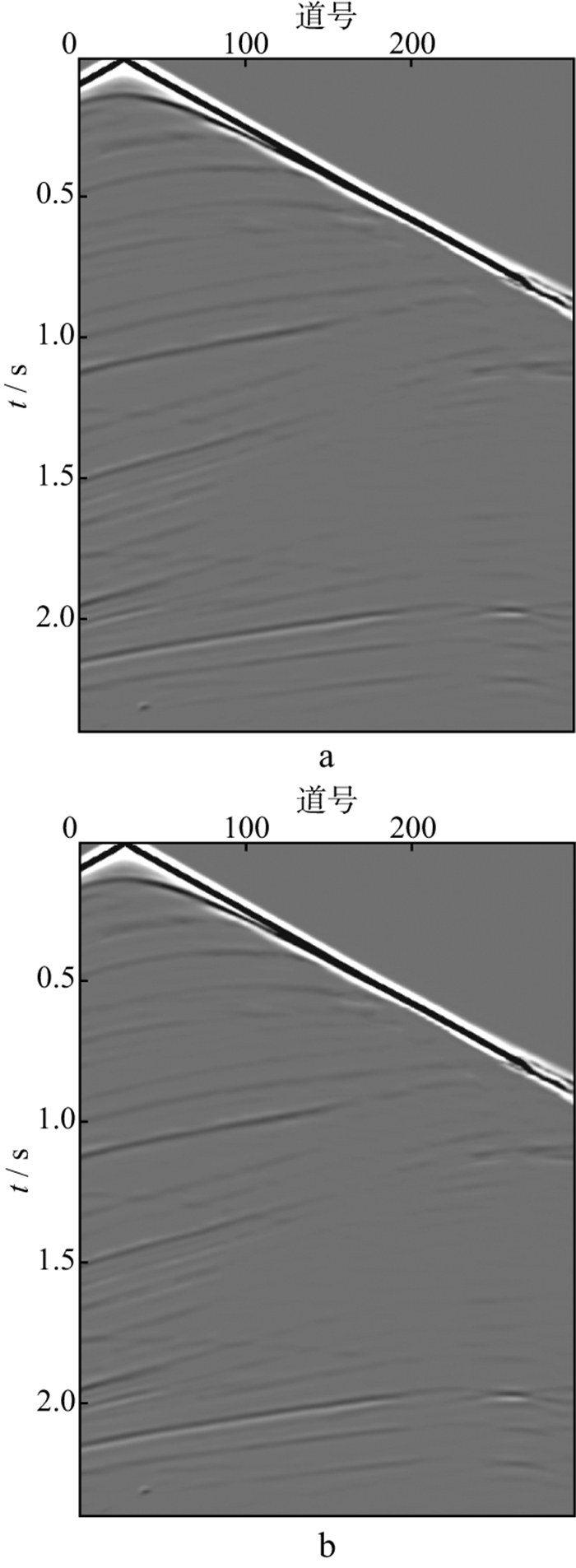
|
图 8 自注意力模块对训练结果的改善示意 a 未增加自注意力模块的CAE压制多次波结果; b 增加了自注意力模块的CAE压制多次波结果 |
传统的多次波压制处理方式如下: 处理员通过交互分析整个工区资料中多次波发育的情况, 综合考虑选择一组参数, 然后将其应用于整个工区进行多次波压制。然而, 实际工区中由于地质条件的不同, 多次波在地震资料中表现形式也不尽相同, 因此, 利用传统多次波压制方法存在局部处理效果不佳的情况。基于人工智能的多次波压制技术实现地震数据驱动的方法, 比人工选择一组固定参数进行整个工区的多次波压制处理, 在理论上具有优势。学习样本由经验丰富的处理员应用商业软件进行处理, 以保证智能算法学习到最优秀处理员的“处理经验”。
为了进一步测试本文所使用的神经网络方法对实测地震数据的有效性, 我们选择某陆上实际地震数据进行测试。与模拟数据不同的是, 我们选取成像后的地震道集进行训练和测试, 这是因为实际地震数据多次波压制的标签和参照对比结果均在商业软件中成像道集上的处理效果更佳。输入数据集由实际地震勘探野外采集并进行预处理得到, 标签数据集是利用商业软件, 人工对输入数据集进行多次波去除后得到的结果。首先, 将具有输入与标签映射关系的数据集以1∶9的比例划分为训练集和测试集。使用小样本对网络进行训练, 并利用训练后的网络对其余样本进行处理, 将网络处理结果与商业软件处理结果进行对比, 证明上述方法可以减少多次波压制过程中繁杂的人工处理流程。
本文使用的基于自注意力的卷集自编码器神经网络, 共迭代训练200 000次, 实际地震数据训练过程中的损失函数收敛曲线如图 9所示, 测试结果的随机抽样样本及其对应的输入、标签数据如图 10至图 12所示。
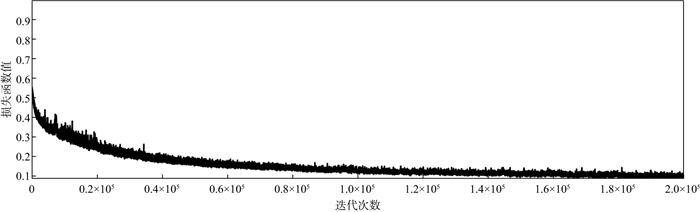
|
图 9 实际地震数据训练过程中的损失函数收敛曲线 |

|
图 10 网络测试地震数据集抽样结果3 a 网络输入数据3; b 网络输出数据3; c 标签数据3 |

|
图 11 网络测试地震数据集抽样结果4及其残差图像(R=0.001 7) a 网络输入数据4; b 网络输出数据4; c 标签数据4; d 网络输入数据4-网络输出数据4; e 网络输入数据4-标签数据4; f 网络输出数据4-标签数据4 |
|
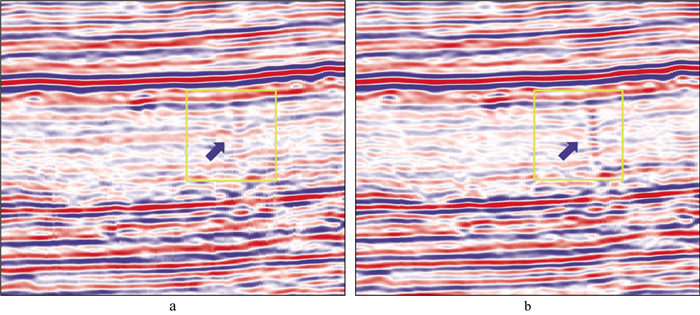
图 12 采用本文方法进行多次波压制前(a)、后(b)的偏移剖面 |
利用本文方法测试地震数据集结果如图 10和图 11所示, 使用小样本训练网络, 可以得到较理想的多次波压制结果。图 10a和图 11a为含有多次波的地震记录, 即网络输入数据, 不难发现, 在成像道集中, 一次波被校平, 速度校正不足的多次波通常表现为倾角随偏移距增大的同相轴。随着旅行时的增加, 一次波与能量更强的多次波互相叠加, 难以辨认一次波信息。经神经网络处理后, 得到图 10b和图 11b, 可见平坦的一次波同相轴被恢复, 与商业软件处理结果一致(图 10c和图 11c)。对比图 11d与图 11e, 可以看出未被校平的多次波能量被有效压制; 网络输出数据与标签数据的残差如图 11f所示, 仍存在不明显的能量泄漏, 平均残差R为0.001 7。
图 12展示了原始偏移剖面和采用本文方法进行多次波压制后的偏移剖面, 与原始剖面相比, 多次波能量被有效压制, 缝洞成像改善。成像效果进一步反映了使用本文方法压制多次波的正确性和有效性。
计算量方面, 利用深度神经网络进行多次波压制的计算量主要在神经网络训练阶段。本次实验处理的10 GB地震成像道集数据中, 利用其中约1 GB的数据进行神经网络训练并且利用带有2张Navidia K40显卡的GPU工作站进行训练, 耗时约5.5 h; 利用训练好的神经网络处理剩余9 GB的数据, 仅需数分钟时间。相较于直接利用传统的商业软件进行人工处理, 自注意力机制的卷积自编码器多次波压制方法的效率得到了显著提升。
4 结论本文提出了一种基于自注意力机制的卷积自编码器神经网络, 用于地震多次波的压制, 并利用正演模拟炮集数据证明了方法的有效性。使用实际地震数据成像道集, 验证了该网络处理方法对实际地震数据的处理能力。自编码器从地震数据集中挖掘数据特征, 调整网络参数, 从而实现智能化且高效率地压制地震数据的多次波, 其包含的自注意力机制进一步提升了网络性能。本文仅使用10%的地震数据对网络进行训练, 训练后的网络有效且高效率地压制了成像道集中的多次波。此过程只需人工处理实际地震数据中的小部分数据, 便可实现大批量数据的多次波压制, 且大幅提高了处理效率。与传统方法的处理结果相比, 基于数据驱动的多次波压制方法在整个工区处理效果均存在一定程度的提升。
| [1] |
VERSCHUUR D J. 地震多次波去除技术的过去、现在和未来[M]. 北京: 石油工业出版社, 2010: 10-158. VERSCHUUR D J. Seismic multiple removal techniques: Past, present and future[M]. Beijing: Petroleum Industry Press, 2010: 10-158. |
| [2] |
王建立, 王真理, 张洪宙, 等. 海上多次波的联合衰减法[J]. 地球物理学进展, 2009, 24(6): 2070-2078. WANG J L, WANG Z L, ZHANG H Z, et al. A joint technique of multiple attenuation for offshore seismic data processings[J]. Progress in Geophysics, 2009, 24(6): 2070-2078. DOI:10.3969/j.issn.1004-2903.2009.06.020 |
| [3] |
李鹏, 刘伊克, 常旭, 等. 多次波问题的研究进展[J]. 地球物理学进展, 2006, 21(3): 888-897. LI P, LIU Y K, CHANG X, et al. Progress on the multiple problems[J]. Progress in Geophysics, 2006, 21(3): 888-897. DOI:10.3969/j.issn.1004-2903.2006.03.029 |
| [4] |
VERSCHUUR D J, BERKHOUT A J, WAPENAAR C, et al. Adaptive surface-related multiple elimination[J]. Geophysics, 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [5] |
NEKUT A G, VERSCHUUR D J. Minimum energy adaptive subtraction in surface-related multiple attenuation[J]. Expanded Abstracts of 58th Annual Internat SEG Mtg, 1998, 1507-1510. |
| [6] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [7] |
MENG L, DING S, XUE Y. Research on denoising sparse autoencoder[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(5): 1719-1729. DOI:10.1007/s13042-016-0550-y |
| [8] |
江金生, 任浩然, 李瀚野. 基于卷积自编码器的地震数据处理[J]. 浙江大学学报(工学版), 2020, 54(5): 978-984. JIANG J S, REN H R, LI H Y. Seismic data processing based on convolutional autoencoder[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(5): 978-984. |
| [9] |
JIANG J S, REN H R, Zhang M. A convolutional autoencoder method for simultaneous seismic data reconstruction and denoising[J]. IEEE Geoscience and Remote Sensing Letters, 2021. DOI:10.1109/LGRS.2021.3073560 |
| [10] |
WANG X, GIRSHICK R, GUPTA A, et al. Non-local neural networks[J]. Proceedings of 2018 IEEE Conference on Computer Vision and Pattern Recognition, 2018, 7794-7803. |
| [11] |
SABATH R, COUTINHO E, SCHULER B. Deep recurrent music writer: Memory-enhanced variational autoencoder-based musical score composition and an objective measure[J]. Proceedings of 2017 International Joint Conference on Neural Networks, 2017, 3467-3474. |
| [12] |
VASWANI A. Attention is all you need[J]. Proceedings of 31st Conference on Neural Information Processing Systems(NIPS), 2017, 30-40. |
| [13] |
WOO S, PARK J, LEE J, et al. CBAM: Convolutional block attention module[J]. Proceedings of 2018 the European Conference on Computer Vision (ECCV), 2018, 3-19. |



