2. 北京华晖盛世能源技术股份有限公司, 北京 101399
2. Beijing Huahui Shengshi Energy Technology Co., Ltd, Beijing 101399, China
传统的裸眼井感应测井是单频激发, 而瞬变电磁过套管测井是大功率瞬变激发, 频谱是连续的且低频幅度大, 这些低频电磁场能够穿透套管进入地层[1-3], 在地层中激发涡流, 在接收线圈产生二次场。连续的各个频率都产生与地层电导率有关的二次场信号, 并且叠加在一起[4-8], 在某个时刻达到极值, 该二次场信号与地层电导率成正比, 从而实现地层电导率的测量[9-12]。瞬变电磁测井的响应由瞬变电磁激发的各个频率的响应叠加而成[13]。每个频率的响应可以用单频的感应测井理论(Doll理论)和几何因子[14]描述。瞬变电磁测井波形每一个时刻的响应值均构成测井曲线, 该曲线也可以用Doll理论和几何因子描述。在套管井内测量, 节箍处的响应幅度最大, 不同源距的响应曲线具有Doll几何因子的形状, 组合在一起完整地刻画了套管井的几何因子形状。因此借助于套管的节箍响应可以获得套管井的几何因子[15]。为有效消除响应中套管射孔和变形等引起的无用信号, 采用相邻两个深度点的测井波形相减的方法[16-18]得到响应差波形。该波形对应于两个相邻的几何因子相减以后形成的差分几何因子, 差分几何因子的形状决定了原始测井曲线的形状:在界面处为峰值, 在地层中间为0。这与通常的电导率曲线差异很大。但是, 这种测井曲线没有丢失地层电导率信息, 只是将测井曲线所包含的地层电导率信息进行了重新组合。如何获取其中的地层电导率信息成了待解决的问题。
为此, 基于文献[15]的研究成果, 本文首先利用Fourier变换给出了瞬变电磁测井的响应; 利用正演模拟分析了差分几何因子和原始测井曲线; 对套管节箍处的响应, 利用纵向拉伸、径向压缩的方法获得套管井的几何因子, 并且采用该几何因子获得套管井的差分几何因子; 然后将套管井的差分几何因子与实际的测井曲线进行反褶积获得套管井地层电导率曲线, 并且与裸眼井的地层电导率曲线进行对比, 验证了套管井测井方法的可行性。
1 瞬变电磁测井的响应波形瞬变电磁测井采取发射线圈电流的导通和关断激发(阶跃信号)瞬变电磁场, 在井内测量瞬变电磁响应的全波波形[11], 其频谱是连续的, 从0开始所有频率都有响应, 包含丰富的地层电导率信息[18-20]。对于单频激发, DOLL[1]利用计算单元环磁通量的方式推导了接收线圈中的总电动势。本文结合瞬变电磁响应, 用Fourier积分获得了整个响应波形Va:
| $ \begin{array}{l} {V_a} = {V_x} + {V_R} = - {\rm{i}}\frac{{\mu {n_T}{n_R}S_0^2}}{{2\pi {L^3}}}\int\limits_{ - \infty }^\infty \omega I(\omega ){{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mu ^2}{n_T}{n_R}S_0^2}}{{4\pi L}}\int\limits_{ - \infty }^\infty {{\omega ^2}} I(\omega ){{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega \int\limits_{ - \infty }^\infty {\int\limits_0^\infty g } \sigma {\rm{d}}r{\rm{d}}z \end{array} $ | (1) |
式中:VR是有用信号, 包含地层电导率σ。
| $ {V_R} = - \frac{{{\mu ^2}{n_T}{n_R}S_0^2}}{{4\pi L}}\int\limits_{ - \infty }^\infty {{\omega ^2}} I(\omega ){{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega \int\limits_{ - \infty }^\infty {\int\limits_0^\infty g } \sigma {\rm{d}}r{\rm{d}}z $ | (2) |
Vx是无用信号, 是接收和发射线圈直接耦合的电动势(一次场):
| $ {V_x} = - {\rm{i}}\frac{{\mu {n_T}{n_R}S_0^2}}{{2\pi {L^3}}}\int\limits_{ - \infty }^\infty \omega I(\omega ){{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega $ | (3) |
(1) 式至(3)式中:nT是发射线圈的圈数; nR是接收线圈的圈数; S0是发射和接收线圈的面积; μ是磁导率; I(ω)是发射电流的幅度谱(与阶跃函数的频谱相似); ω=2πf, f是频率; g是Doll几何因子; L是源距。(2)式中的两个积分各自独立:前面的积分刻画了连续频谱激发时, 各个频率成分响应的叠加, 积分后获得时域波形; 后面的积分表示空间各点地层的电导率对二次场响应的贡献, 这是空间各个位置的涡流不同所引起的。(2)式中两个积分相乘表明:实际测量波形中每一时刻的幅度都与地层的电导率成正比, 均可以构成电导率测井曲线。
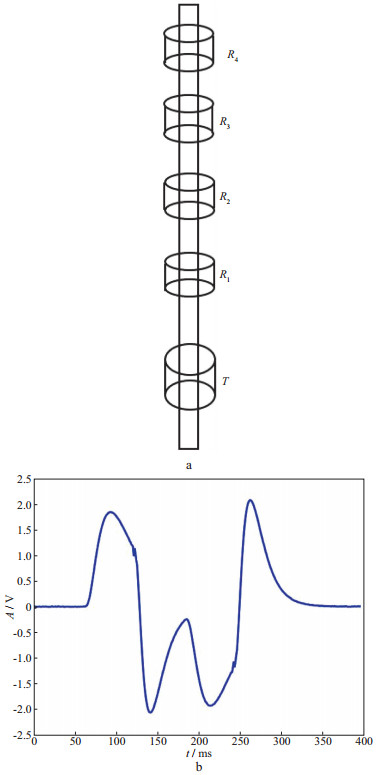
瞬变电磁测井套管井测井的仪器如图 1a所示, T为发射线圈, R1, R2, R3和R4是接收线圈, 本文采用的数据是孤东油田的套管井实际测量数据, 套管内径为139.7mm。实际使用的瞬变电磁套管井测井的接收波形如图 1b所示, 激发周期是400ms, 其中延迟60ms、正向导通60ms、正向关断60ms、反向导通60ms、反向关断60ms, 延迟100ms。由图 1b可以看到有4个峰值时刻分别出现在93, 142, 215, 260ms附近(170ms处的突变是因为波形在衰减时, 受到一个反向导通的激励, 所以再次被激发, 这是瞬变测井波形的一个特点, 一般不称为峰值点)。随着源距的增大, 峰值的到达时间向后移动, 表现出响应的传播特征。
|
图 1 套管井测井仪器示意(a)及套管井瞬变电磁测井实际接收波形(b) |
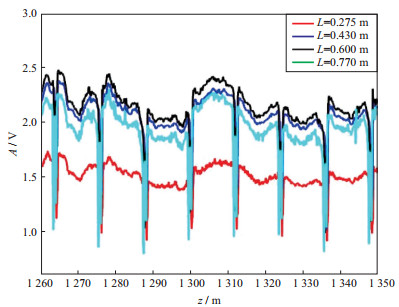
由公式(1)可知, 取接收波形的任何一个时刻的值均构成一条测井曲线, 这是一次场响应Vx和二次场响应VR叠加的结果。图 2表示4个不同源距(L)取图 1b峰值时刻260ms的波形值所得到的曲线。该曲线减去260ms处无用信号, 其形状类似于感应测井曲线。将地层电导率与套管井几何因子进行褶积, 然后减去260ms处的测井波形值得到的曲线, 与感应测井曲线相差一个常数, 该曲线在节箍处幅度很大。
|
图 2 260ms时不同源距的测井曲线 |
套管井条件下, 其有用信号的响应仍然可以用几何因子描述。
2.1 瞬变电磁测井有用信号和几何因子仿照感应测井的仪器常数k[21], 定义瞬变电磁测井任意一时刻响应值所得曲线的仪器常数k(t):
| $ k(t) = - \frac{{{\mu ^2}{n_T}{n_R}S_0^2}}{{4\pi L}}\int\limits_{ - \infty }^\infty {I(\omega ){\omega ^2}{{\rm{e}}^{{\rm{i}}\omega t}}{\rm{d}}\omega } $ | (4) |
则由(2)式可知:
| $ {V_R}(t) = k(t)\int\limits_{ - \infty }^\infty {\int\limits_0^\infty g } \sigma {\rm{d}}r{\rm{d}}z $ | (5) |
通常定义视电导率σa为:
| $ {\sigma _a} = \int\limits_{ - \infty }^\infty {\int\limits_0^\infty g } \sigma {\rm{d}}r{\rm{d}}z $ | (6) |
即:
| $ {V_R}(t) = k(t){\sigma _a} $ | (7) |
将Doll几何因子g对r积分, 求得纵向微分几何因子gz(z):
| $ {g_z}(z) = \int\limits_0^{ + \infty } g (z,r){\rm{d}}r $ | (8) |
显然, 视电导率σa(z)为纵向微分几何因子曲线gz(z)和地层电导率σ(z)的褶积:
| $ {V_R} = k{\sigma _a}(z) = k{g_z}(z) * \sigma (z) $ | (9) |
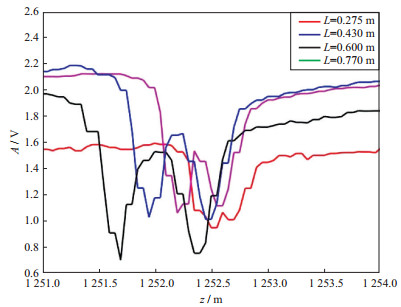
瞬变电磁测井激发的频谱以低频为主, 其集肤深度大, 套管很薄, 容易穿过, 可以将公式(9)推广到套管井, 此时地层的视电导率是地层电导率和纵向微分几何因子的褶积。由于套管的高电导率和磁导率, 套管井瞬变电磁测井的几何因子与Doll几何因子都有一定的区别。图 3是深度1252.5m节箍处实测曲线, 此曲线和Doll几何因子具有很好的相似性[15]。
|
图 3 套管井节箍处响应曲线 |
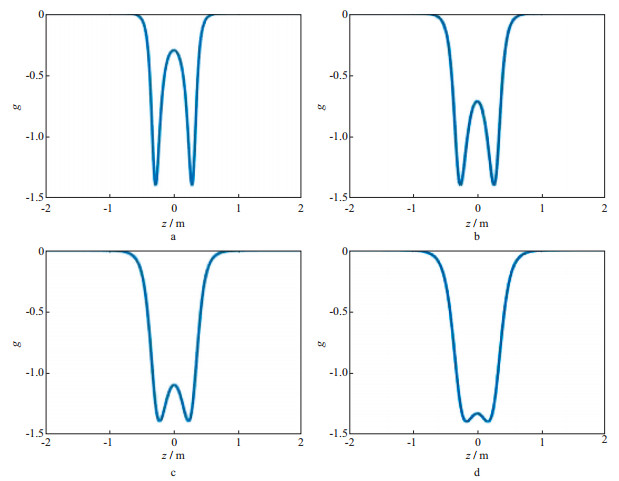
沈建国等[15]发现借助于套管的节箍响应可以获得套管井的几何因子。借鉴其方法和思路, 利用Doll几何因子分析图 3所示节箍处的测井曲线。在Doll几何因子上取不同的r得到随z变化的曲线, 即r不同时的Doll几何因子如图 4所示, 随着径向r的增大, Doll几何因子的中间凸起的峰值逐渐减小, 到r=0.25m时已经几乎消失, 随着r的继续增大, 凸起消失, 几何因子中段曲线变得平滑。
|
图 4 L=0.600m, 半径r不同时Doll几何因子随z变化的曲线 a r=0.10m; b r=0.15m; c r=0.20m; d r=0.25m |
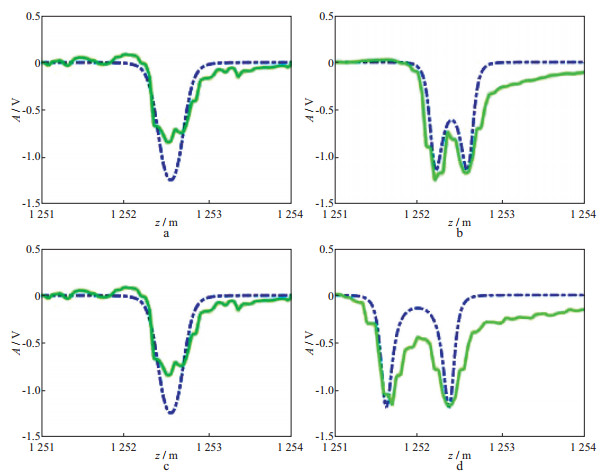
图 5对比了套管井测井曲线和对应源距的Doll几何因子, 反映节箍的响应。由于节箍在径向上很浅, 纵向上很短, 可以视为一个地层电导率的冲击输入, 其响应形状就是一定径向深度的几何因子形状[15, 19-20]。随着源距L的增大, 可以看到中间凸起的峰值越来越明显, 与Doll几何因子中r比较小的情况类似。图中实际测井曲线比同一源距的Doll几何因子长, 这是套管的影响所致:纵向上几何因子被拉长, 径向缩短。根据这个规律拉伸Doll几何因子与实际测井曲线一致即获得套管井的几何因子, 如图 6所示。和文献[15]所述不同, 不同源距的情况压缩和拉伸比例并不一样(表 1), 这是因为选取的节箍在不同井段所造成的, 说明在不同井段的套管井几何因子存在差异, 在不同井段处理测井曲线时需要用对应的几何因子。
|
图 5 不同源距L的套管井测井曲线(绿实线)和对应源距Doll几何因子曲线(蓝虚线)对比 a L=0.275m; b L=0.430m; c L=0.600m; d L=0.770m |

|
图 6 不同源距的Doll几何因子拉伸后曲线(蓝虚线)和实际套管井测井曲线(绿实线)比较 a L=0.275m; b L=0.430m; c L=0.600m; d L=0.770m |
| 表 1 不同源距时Doll几何因子的径纵向压缩比 |
(1) 式中VR是测量的二次响应波形, 当取定时刻t时, 两个深度间隔为Δ的测量波形相减以后的曲线:
| $ \begin{array}{l} {V_a}(z + \Delta ) - {V_a}(z) = - \frac{{{\mu ^2}{n_T}{n_R}S_0^2}}{{4\pi L}}\int\limits_{ - \infty }^\infty I (\omega ){\omega ^2}{{\rm{e}}^{{\rm{i}}\omega t}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{d}}\omega \left\{ {\int\limits_{ - \infty }^\infty {\int\limits_0^\infty {[g(z - \tau + \Delta ,r) - g(z - \tau ,r)]\sigma {\rm{d}}r{\rm{d}}z} } } \right\} \end{array} $ | (10) |
依据(7)式、(9)式和(10)式可写成:
| $ \begin{array}{*{20}{c}} {{V_a}(z + \Delta ) - {V_a}(z) = k[{\sigma _{a2}}(z) - {\sigma _{a1}}(z)] = }\\ {k\sigma (z) * \{ [{g_{z2}}(z) - {g_{z1}}(z)]\} } \end{array} $ | (11) |
从(11)式可以看出:相邻两个深度的曲线相减以后得到的曲线是所测量地层的电导率σ与纵向微分几何因子G(z)=gz2(z)-gz1(z)的褶积。该几何因子是两个相同的Doll几何因子错开深度Δ以后相减得到的。其径向和纵向探测特征与Doll几何因子所刻画的探测特征存在较大的差异, 我们称其为差分几何因子:
| $ {V_a}(z + \Delta ) - {V_a}(z) = k\sigma (z) * G(z) $ | (12) |
从相邻深度点测量波形相减以后的波形中任意取一个时刻的值得到的曲线是差分几何因子与地层电导率的褶积。
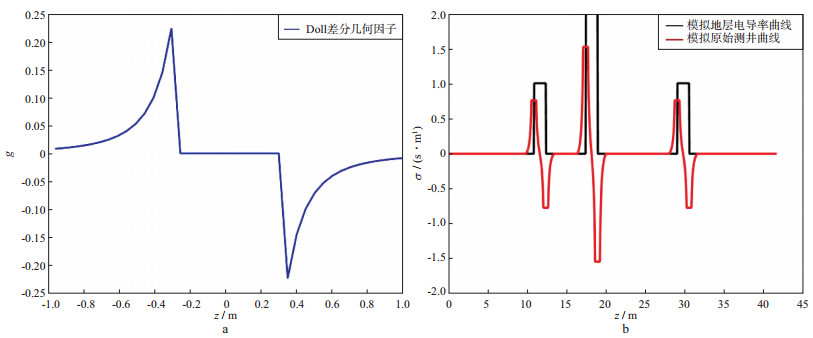
3.2 与原始测井曲线对比分析利用上述方法获得的瞬变电磁测井曲线的形状和普通感应测井曲线形状差异大。本文采用Doll几何因子和模拟地层计算的曲线展现其特征。图 7a是源距为0.600m的Doll差分几何因子, 其形状是上、下有两个峰值, 中间为0。而图 7b中黑线表示模拟地层电导率, 红线表示Doll差分几何因子和地层电导率的褶积, 褶积后的曲线即是由相邻深度点测量波形相减以后的波形所得到的曲线, 即为模拟原始测井曲线。可以看到, 褶积后的曲线在界面处出现峰值。
|
图 7 Doll差分几何因子(源距L=0.600m)(a)及瞬变电磁模拟地层电导率曲线及模拟原始测井曲线(b) |
实际测井波形相邻深度点相减后, 取其中4个峰值时刻的值得到4条曲线(1292.0~1296.0m井段)如图 8所示, 曲线的形状和图 7b中的红线相似。这4条曲线中有明显上、下两个峰值交替的形状, 这是套管井瞬变电磁测井电导率曲线在薄层的响应, 也是其主要特点。

|
图 8 从相邻深度测井波形相减后的波形中取不同时刻的值得到的原始测井曲线 |
对图 6所示套管井几何因子, 利用两个相同的套管井几何因子相隔一个间距相减得到套管井差分几何因子。由3.2节的内容和(12)式可知, 利用实际测量的原始测井曲线和套管井差分几何因子进行反褶积处理, 可以得到过套管地层电导率曲线。对各个井段进行同样的反褶积处理后得到过套管地层电导率曲线。
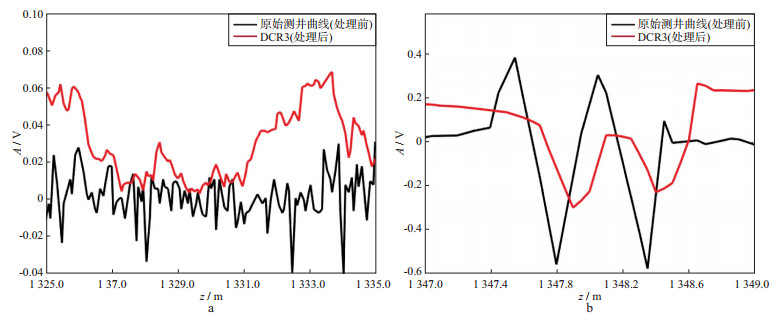
4.1 处理前、后曲线对比图 9对比了不同井段的原始测井曲线和过套管地层电导率曲线, 其中图 9a选取1325.0~1335.0m井段, 黑线是峰值时刻260ms、源距L=0.600m的原始测井曲线, 该曲线与图 8所示曲线相似, 呈现正、负峰交替的形状; 红线是源距L=0.600m的原始测井曲线经反褶积处理后的曲线(用DCR3表示), 也就是过套管地层电导率曲线。图 9b为1347.0~1349.0m井段节箍处的曲线, 由于节箍可以视为一个地层电导率的冲击输入[15], 所以节箍处的原始测井曲线正、负交错的峰很突出, 而处理后的曲线(红色)接近地层电导率的曲线, 反映套管井的几何因子形状特征。
|
图 9 非节箍处原始测井曲线(处理前)和过套管地层电导率曲线(处理后)的对比(源距L=0.600m)(a)及节箍处原始测井曲线(处理前)和过套管地层电导率曲线(处理后)的对比(源距L=0.600m)(b) |
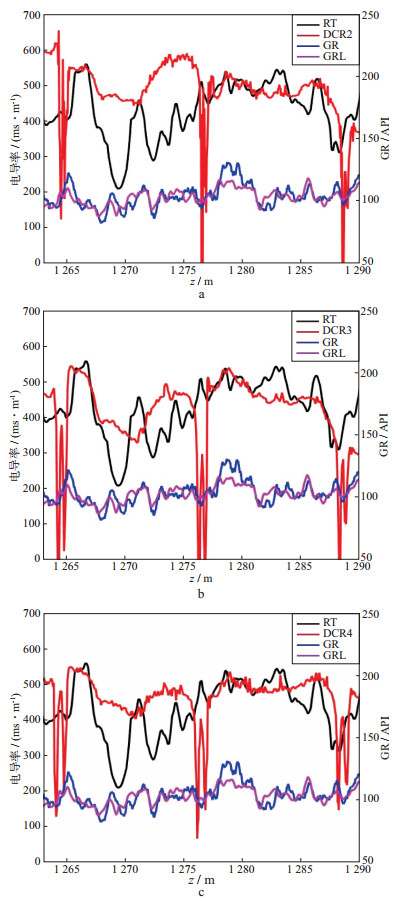
对不同源距的原始测井曲线和套管井差分几何因子进行反褶积处理, 得到的结果如图 10、图 11和图 12所示。图中源距L=0.43m和L=0.77m的原始测井曲线反褶积后得到的曲线, 也就是过套管地层电导率曲线分别用DCR2和DCR4表示, RT表示裸眼井测得的地层电导率曲线, GR表示套管井自然伽马曲线, GRL表示裸眼井的自然伽马曲线。
|
图 10 1263.0~1290.0m井段反褶积处理后的电导率曲线和裸眼井地层电导率曲线的比较 a源距L=0.43m; b源距L=0.6m; c源距L=0.77m |
|
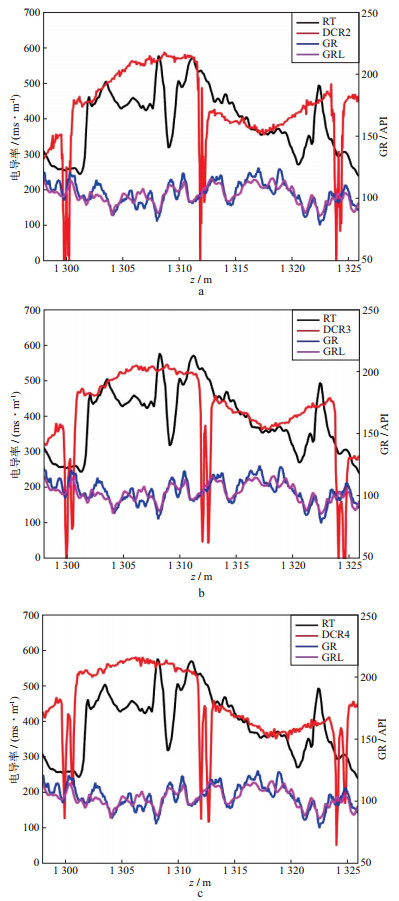
图 11 1298.0~1326.0m井段反褶积后的曲线和裸眼井地层电导率曲线的比较 a源距L=0.43m; b源距L=0.6m; c源距L=0.77m |
|
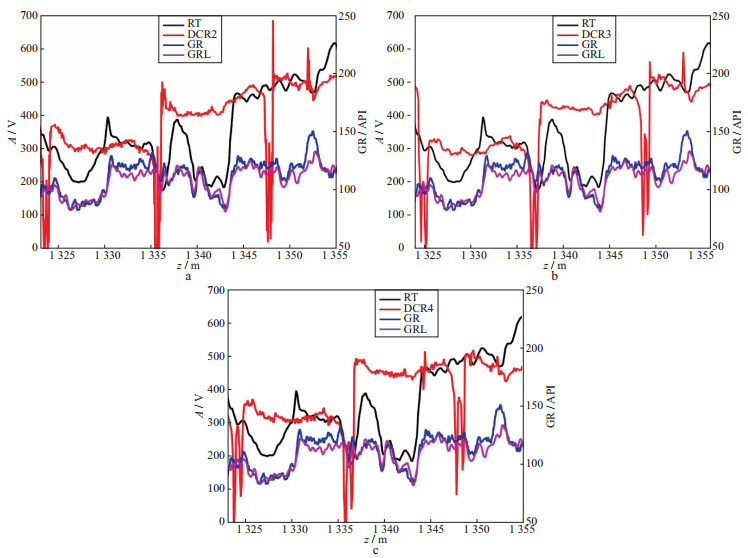
图 12 1323.0~1355.0m井段不同源距反褶积后的曲线和裸眼井地层电导率曲线的比较 a源距L=0.43m; b源距L=0.6m; c源距L=0.77m |
取1298.0~1326.0m两个节箍间的原始测井曲线进行反褶积处理, 得到的曲线如图 11所示。当源距为0.43m时, 只有1316.0~1319.0m处重合较多, 而当源距为0.60m和0.77m时, 1313.0~1319.0m都有较好的重合趋势, 尤其当源距为0.77m时的处理曲线1313.0~1325.0m段重合趋势很明显, 此段的自然伽马也较高。
图 12所示曲线为1323.0~1355.0m井段的相关曲线, 可以看出, 在自然伽马较高的1345.0~1353.0m处, 过套管地层电导率曲线和裸眼井地层电导率曲线的一致性较好。
相较于高伽马地层, 低伽马地层是油层, 开发以后油变成了水, 电导率发生了很大变化, 所以两条曲线不再重合, 而高伽马地层是泥岩, 开发过程中保持不变。如图 12a至图 12c中的1325.0~1330.0m井段和1337.0~1343.0m井段, 过套管地层电导率曲线明显高于裸眼井的电导率曲线, 说明该井段油层中的油已经被采出, 孔隙中的油度换成了水, 或者说被水充填。图 10和图 11中其它井段的低伽马地层也具有同样的特征。
随着源距L的增加, 反褶积处理后的地层电导率曲线在各个井段都不断地向裸眼井的电导率曲线靠近, 和裸眼井的曲线有着更好的一致性, 当L=0.77m时, 两者的一致性最为明显。需要注意的是, 处理各个井段的曲线需要用到对应该井段的套管井几何因子, 从而得到合适的地层电导率曲线。
5 结论为了获取过套管地层电导率曲线, 我们发现:将两个深度间隔为的测量波形相减可去掉无用信号套管变形、射孔和套管腐蚀等影响, 取相减以后的波形上任一个时刻的值均可得到一条原始测井曲线, 运用套管井的差分几何因子和原始测井曲线进行反褶积可以得到过套管地层电导率曲线。从理论上肯定了瞬变电磁测井响应可以用Doll的方法分解为有用信号和无用信号, 套管井响应中的有用信号也可以用几何因子描述。这样便为过套管地层电导率测井提供了一条新途径——瞬变电磁方法。
该方法应用于孤东油田的套管井测量的实际测井数据后发现:瞬变电磁测井能够在套管井获得连续的电导率曲线(现有的过套管电导率测井是点测方式), 在有些井段, 处理得到的地层电导率曲线与裸眼井的电导率曲线形态一致, 重合性较好, 说明这些井段套管特征一致, 地层在开发过程中没有变化。但是在很多井段差异比较明显。说明该井段套管和固井胶结等有变化或者地层有变化, 需要进行套管和水泥环影响校正。
致谢: 感谢中国石油化工股份有限公司胜利石油工程有限公司测井公司朱留方、臧德福、王涛、张付明等的帮助。| [1] |
DOLL H G. Introduction to induction logging and application to logging of wells drilled with oil base mud[J]. Journal of Petroleum Technology, 1949, 1(6): 148-162. DOI:10.2118/949148-G |
| [2] |
王显祥, 底青云, 邓居智. 多通道瞬变电磁法油气藏动态检测[J]. 石油地球物理勘探, 2016, 51(5): 1021-1031. WANG X X, DI Q Y, DENG J Z. Reservoir dynamic detection based on multi-channel transient electromagnetic[J]. Oil Geophysical Prospecting, 2016, 51(5): 1021-1031. |
| [3] |
臧德福, 张福明, 毛彤, 等. 瞬变电磁测井实验研究[J]. 石油管材与仪器, 2015, 1(2): 21-25. ZANG D F, ZHANG F M, MAO T, et al. The experimental study on transient electromagnetic logging[J]. Petroleum Pipes and Instruments, 2015, 1(2): 21-25. DOI:10.3969/j.issn.1004-9134.2015.02.007 |
| [4] |
王杰, 张晓培, 牛建军, 等. 地面瞬变电磁探测系统对比试验[J]. 地球物理学进展, 2017, 32(6): 2670-2676. WANG J, ZHANG X P, NIU J J, et al. Ground transient electromagnetic system contrast test[J]. Progress in Geophysics, 2017, 32(6): 2670-2676. |
| [5] |
PAVLOV D A, ZHDANOV M S. Analysis and interpretation of anomalous conductivity and magnetic permeability effects in time domain electromagnetic data[J]. Journal of Applied Geophysics, 2001, 46(4): 217-233. DOI:10.1016/S0926-9851(01)00040-4 |
| [6] |
唐新功, 胡文宝, 严良俊, 等. 瞬变电磁法油藏动态监测模拟[J]. 石油物探, 2004, 43(2): 192-195. TANG X G, HU W B, YAN L J, et al. Modeling of reservoir dynamic performance by TEM method[J]. Geophysical Prospecting for Petroleum, 2004, 43(2): 192-195. DOI:10.3969/j.issn.1000-1441.2004.02.022 |
| [7] |
AULIA K, POERNOMO B, RICHMOND W, et al. Resistivity behind casing[J]. Oil field Review, 2002, 13(1): 1-94. |
| [8] |
李貅. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社, 2002: 25-26. LI X. Theory and application of transient electronmagnetic sounding[M]. Xi'an: Shaanxi Science and Technology Press, 2002: 25-26. |
| [9] |
周继宏, 王雷, 袁瑞. 套管接箍对过套管电阻率测井的影响分析[J]. 地球物理学进展, 2013, 28(1): 421-426. ZHOU J H, WANG L, YUAN R. Analysis on effect of casing collar on formation resistivity logging through casing[J]. Progress in Geophysics, 2013, 28(1): 421-426. |
| [10] |
谢树棋, 储昭坦, 李克沛, 等. 套管井电阻率测井方法研究[J]. 测井技术, 1999, 23(5): 338-343. XIE S Q, CHU Z T, LI K P, et al. On methodology of resistivity logging through casing[J]. Well Logging Technology, 1999, 23(5): 338-343. DOI:10.3969/j.issn.1004-1338.1999.05.004 |
| [11] |
沈建国, 孟超, 皮光玉. 瞬变电磁测井原理研究——瞬态感应测井[J]. 地球物理学进展, 2016, 31(2): 770-774. SHEN J G, MENG C, PI G Y. Transient electromagnetic logging theory—transient induction logging[J]. Progress in Geophysics, 2016, 31(2): 770-774. |
| [12] |
朱留方, 臧德福, 沈永进, 等. 瞬变电磁测井原理研究Ⅵ:过套管电阻率[J]. 测井技术, 2016, 40(1): 28-32. ZHU L F, ZANG D F, SHEN Y J, et al. Theory of transient electromagnetic logging VI:Through-casing resistivity[J]. Well Logging Technology, 2016, 40(1): 28-32. |
| [13] |
朱留方, 臧德福, 沈永进, 等. 瞬变电磁测井原理研究I:Doll几何因子[J]. 测井技术, 2014, 38(2): 150-157. ZHU L F, ZANG D F, SHEN Y J, et al. The theory studyon transient electromagnetic logging I:Doll geometric factor[J]. Well Logging Technology, 2014, 38(2): 150-157. |
| [14] |
朱留方, 沈建国. 测井曲线几何因子理论[J]. 测井技术, 2013, 37(6): 624-628, 642. ZHU L F, SHEN J G. The geometric factor theory for logging curves[J]. Well Logging Technology, 2013, 37(6): 624-628, 642. DOI:10.3969/j.issn.1004-1338.2013.06.008 |
| [15] |
沈建国, 舒敦利, 沈永进, 等. 套管井瞬变电磁测井在节箍处的响应与几何因子分析[J]. 石油物探, 2019, 58(3): 105-117. SHEN J G, SHU D L, SHEN Y J, et al. Response of casing hoop and geometry factor to transient electromagnetic logging in cased wells[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 105-117. |
| [16] |
KIM H J, LEE K H. Electromagnetic fields in a non-uniform steel-cased borehole[J]. Geophysical Prospecting, 2006, 54(4): 433-439. DOI:10.1111/j.1365-2478.2006.00545.x |
| [17] |
刘宇, 刘国强. 套管非匀质性对过套管电阻率测井影响的数值模拟与分析[J]. 地球物理学报, 2014, 57(4): 1345-1355. LIU Y, LIU G Q. Numerical simulation and analysis on the influence of casing inhomogeneity on through-casing resistivity logging response[J]. Chinese Journal of Geophysics, 2014, 57(4): 1345-1355. |
| [18] |
KAUFMAN A A. The electrical field in a borehole with a casing[J]. Geophysics, 1990, 55(1): 29-38. |
| [19] |
沈建国. 井条件下的几何因子理论[J]. 石油大学学报(自然科学版), 1989, 13(6): 25-34. SHEN J G. Geometric factor for the presence of a well[J]. Journal of the University of Petroleum(Natural Science Edition), 1989, 13(6): 25-34. |
| [20] |
沈建国. 归一化的井条件下的几何因子及其应用[J]. 石油地球物理勘探, 1996, 31(5): 716-723, 750. SHEN J G. Normalized geometric factor in borehole condition and its application[J]. Oil Geophysical Prospecting, 1996, 31(5): 716-723, 750. |
| [21] |
张庚骥. 电法测井(上)[M]. 北京: 石油工业出版社, 1984: 131-148. ZHANG G J. Electric logging(Volume 1)[M]. Beijing: Petroleum Industry Press, 1984: 131-148. |



