2. 北京大学地球与空间科学学院, 北京 100871
2. School of Earth and Space Sciences, Peking University, Beijing 100871, China
目前, 中国西部地区已经成为油气勘探的重点地区之一, 该地区地表条件相对复杂, 如山前带, 戈壁和沙漠, 近地表非成岩低速介质区往往存在近地表高程、厚度和速度的空间变化, 静校正问题突出, 从而影响叠加成像效果以及地表风化层速度异常的检测。
折射类方法在解决静校正问题中发挥了重要作用, 如用于基准面静校正的折射静校正方法[1-2]和层析静校正方法[3-4], 以及基于统计相关实现的剩余静校正方法[5-6]。这些方法的有效性都依赖于初至拾取的准确度, 但复杂地表条件往往伴随着强背景噪声, 降低了初至的信噪比, 导致传统的自动初至拾取的准确度下降, 而手动初至拾取在面对大量地震数据时会产生极大的人力和时间成本。针对这一问题, 有学者提出使用滤波类方法或地震干涉类方法提高初至信噪比, 以保证自动拾取初至的准确性[7-9]。
在地震干涉类方法中, MIKESELL等[10]和ZHANG等[11]使用基于互相关的地震干涉法, 计算两点间的时延, 并使用时延信息进行近地表速度建模, 再基于速度模型计算剩余静校正量。时延估计使用了互相关的方法, 但互相关容易受高斯噪声的影响, 尤其是相干的高斯噪声[12]。为解决这一问题, AN等[8]提出使用高阶累积量替代互相关以提高地震干涉法的抗噪性, 并由此发展了累积量相干积累法用于加强初至波信号。高斯噪声的高阶累积量为0, 可有效提取高斯噪声中的非高斯信号, 更加符合实际地震数据的情况。高阶累积量同时提供信号的幅度和相位信息, 可用于描述信号系统的非线性特征。基于以上特点, 高阶累积量已经被广泛应用于子波特征分析、噪声衰减以及初至拾取等地震数据处理领域[13-15]。
在上述研究的基础上, 本文提出了基于高阶累积量时间延迟估计的自动初至剩余静校正方法, 该方法使用高阶累积量和相干叠加的方法, 估计两点间的初至波时延, 再使用不同时延信息的组合得到炮检点的剩余静校正量。本文方法的优势在于:①互相关使用两道数据进行时延估计, 只能利用二维地震信息, 而高阶累积量使用多道数据, 可以利用三维地震数据信息增强有效信号; ②互相关是基于噪声为高斯分布的假设, 但实际地震数据很可能不满足这一假设, 导致道间时延估计的准确度不高, 而高阶累积量并不要求噪声为高斯分布, 更加符合实际地震数据的情况, 对背景噪声的压制效果更优; ③再结合地震干涉法中相干叠加的思路进一步提高信号的有效叠加次数, 增强信噪比, 保证本文方法获得稳定且可靠的道间时延估计结果; ④本文方法采用完全数据驱动, 相比基于初至拾取的剩余静校正方法, 在面对海量低信噪比地震数据时, 可以有效降低初至拾取所需的高昂时间和人力成本。
1 方法原理本文方法主要包括两个部分:①使用高阶累积量估计两点间的初至波时延, 并使用相干叠加的方法增强信噪比, 保证时延估计的准确性; ②使用时延信息的组合得到炮检点的剩余静校正量。
1.1 高阶累积量时延估计本文方法首先使用高阶累积量估计两点间的时延。二阶统计工具, 如互相关, 常被用于时延估计, 但互相关对高斯噪声敏感, 因而人们开始使用高阶统计工具进行时延估计, 如高阶累积量。在实际问题中, 加性噪声往往具有高斯性, 因此, 使用高阶累积量进行时延估计更加合理, 因为高斯过程的高阶累积量为0[16]。对零均值的平稳随机过程{x0(t), x1(t), …, xk-1(t)}, 其k阶累积量由{x0(t), x1(t+τ1), …, xk-1(t+τk-1)}的联合k阶累积量表示如下[16]:
| $ \begin{array}{*{20}{c}} {{C_k}({\tau _1},{\tau _2}, \cdots ,{\tau _{k - 1}}) = {\rm{Cum }}\{ {x_0}(t),{x_1}(t + {\tau _1}), \cdots ,}\\ {{x_{k - 1}}(t + {\tau _{k - 1}})\} } \end{array} $ | (1) |
其中, Cum{·}是累积量算子, Ck(·)表示k阶累积量函数, τ1, τ2, …, τk-1分别代表x0与x1, x2, …, xk-1之间的时延。常用的二阶、三阶和四阶累积量函数的表达式如下[16]:
| $ {{C_2}(\tau ) = E\{ {x_0}(t),{x_1}(t + \tau )\} } $ | (2) |
| $ {{C_3}({\tau _1},{\tau _2}) = E\{ {x_0}(t),{x_1}(t + {\tau _1}),{x_2}(t + {\tau _2})\} } $ | (3) |
| $ \begin{array}{l} {C_4}({\tau _1},{\tau _2},{\tau _3}) = E\{ {x_0}(t),{x_1}(t + {\tau _1}),{x_2}(t + {\tau _2}),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_3}(t + {\tau _3})\} - {C_2}({\tau _1}){C_2}({\tau _2} - {\tau _3}) - {C_2}({\tau _2}) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_2}({\tau _3} - {\tau _1}) - {C_2}({\tau _3}){C_2}({\tau _1} - {\tau _2}) \end{array} $ | (4) |
其中, E{·}是期望算子。公式(2)表示协方差, 在零均值的假设下等价于互相关。
基于高阶累积量进行两点间初至波时延估计的具体物理过程如下。如图 1所示, 对于炮点S激发, 检波点Rj接收的地震记录Uj(t), 假设它是由初至波Gj(t)和高斯随机噪声w(t)组成的, 其表达式为:
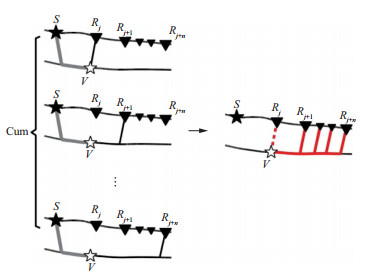
|
图 1 使用高阶累积量估计两点间时延示意 |
| $ {U_j}(t) = {G_j}(t) + w(t) $ | (5) |
使用炮点S在检波点Rj, Rj+1, …, Rj+n接收的n+1道地震记录, 计算其对应的n+1阶累积量的公式如下:
| $ \begin{array}{l} {C_{j;j + 1,j + 2}}, \ldots ,j + n({\tau _1},{\tau _2}, \cdots ,{\tau _n}) = {\rm{Cum}} \{ {U_j}(t),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U_{j + 1}}(t + {\tau _1}), \cdots ,{U_{j + n}}(t + {\tau _n})\} = {\rm{Cum}} \{ {G_j}(t),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_{j + 1}}(t + {\tau _1}), \cdots ,{G_{j + n}}(t + {\tau _n})\} \end{array} $ | (6) |
其中, 在阶数≥3的高阶累积量中, w(t)的响应为0。n+1阶累积量包含n个时延τp(p=1, 2, …, n), τp表示检波点Rj与Rj+p之间的初至波时延。图 1中的V代表虚源位置, 所谓虚源指的是假想的震源, 并非真实存在的震源。S到Rj的旅行时与S到Rj+1的旅行时共用了S到V的旅行时, 对应图 1中的灰色粗线, 共用旅行时在估计时延的过程中被相互抵消, 因此, τp只反映了两个检波点之间的时延, 对应图 1中的红线。高阶累积量方法使用了n+1道信号进行时延估计, 而互相关方法只使用两道进行时延估计, 因此, 高阶累积量方法的抗噪性更好。n+1阶累积量Cj; j+1, j+2, …, j+n(τ1, τ2, …, τn)是n维函数, 理论上可以直接求取n个时延, 但随着n的增大, 存储量和运算量都会显著增加。因此, 本文方法每次只计算一个时延, 实现方式如下:
| $ \begin{array}{*{20}{c}} {{C_{j;j + 1,j, \cdots ,j}}(\tau ,\underbrace {0, \cdots ,0}_{n - 1}) = {\rm{Cum}} \{ {G_j}(t),}\\ {{G_{j + 1}}(t + \tau ),\underbrace {{G_j}(t), \cdots ,{G_j}(t)}_{n - 1}\} } \end{array} $ | (7) |
其中, τ是第j+1个检波点与第j个检波点之间的初至波时延。公式(7)只以两道地震记录为输入, 理论上仍可以得到n阶累积量, 但由于Gj(t)与自身的时延为0, 因此, 不再需要计算累积量中的除τ以外的其它时延, 大大节省了运算量, 并且仍然利用了高阶累积量的抗噪性优势。
1.2 相干叠加为了保证两点间时延估计的准确性, 本文进一步使用相干叠加方法, 增强两点间初至波信噪比, 具体过程如下。如图 2所示, 对炮点S1在检波点R1和R2的初至波记录进行高阶累积量计算, 共用的S1到虚源V的旅行时在时延估计过程中被抵消, 因此, 得到了R1和R2间的初至波响应(图 2b中红线所示), 图中实线表示旅行时为正, 虚线表示旅行时为负。使用其它炮点Si(i=2, 3, …, N)重复上述过程, 炮点Si到V的旅行时仍共用, 在时延估计时被抵消, 因此, 使用不同炮点得到的高阶累积量结果中包含了相同的R1到R2的道间时差(图 2b)。对图 2b中的所有结果进行叠加, 实现了初至波响应的同相位叠加, 而非相干的随机噪声由于具有不同的时延, 不能实现同相位叠加, 叠加能量将小于初至波。至此, 实现了使用相干叠加增强两点间初至波响应的信噪比。
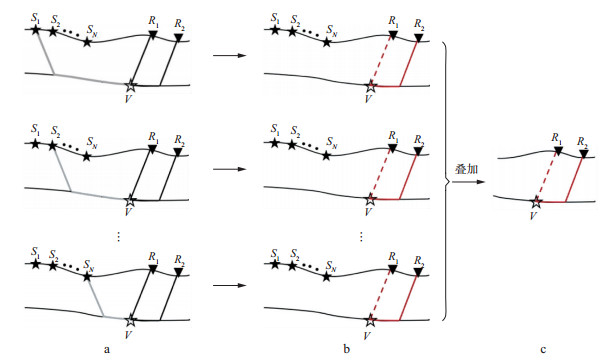
|
图 2 相干叠加示意 a对炮点在检波点R1和R2的初至波记录进行高阶累积量计算; b不同炮点得到的高阶累积量结果; c 图 2b的叠加结果 |
将前文得到的时延信息进行组合, 可以进一步得到炮检点的剩余静校正量, 具体实现过程如下。如图 3a所示, 实际地震资料中记录到的初至波到时包含两部分, 一部分是初至波射线路径所对应的不包含剩余静校正量的旅行时TS, Rj和TS, Rj+1, 即图 3a中从炮点S激发, 经折射层折射, 在检波点Rj和Rj+1接收到的旅行时; 另一部分是炮点剩余静校正量TSstat和检波点剩余静校正量TstatRj和TstatRj+1。因此, 地震资料中记录到的S到Rj和Rj+1的初至到时分别表示为:
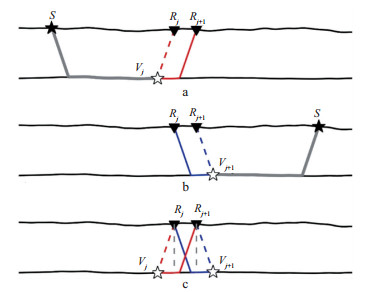
|
图 3 使用时延信息求取剩余静校正量示意 a使用检波点左侧炮点的地震记录进行检波点Rj和Rj+1间的时延估计; b使用检波点右侧炮点的地震记录进行检波点Rj+1和Rj间的时延估计; c使用a和b中得到的时延信息进行相减得到相邻检波点间的相对剩余静校正量 |
| $ {{Y_{S,{R_j}}} = {T_{S,{R_j}}} + T_S^{{\rm{ stat }}} + T_{{R_j}}^{{\rm{ stat }}}} $ | (8) |
| $ {{Y_{S,{R_{j + 1}}}} = {T_{S,{R_{j + 1}}}} + T_S^{{\rm{ stat }}} + T_{{R_{i + 1}}}^{{\rm{ stat }}}} $ | (9) |
使用前文所述方法, 可以得到Rj和Rj+1的地震记录之间的时延Dj, j+1=YS, Rj+1-YS, Rj, 我们将TS, Rj+1-TS, Rj记为ΔTj, j+1, ΔTj, j+1即为Rj和Rj+1之间的真实初至波时延, 其对应的射线路径如图 3a中的红线所示(实线表示旅行时为正, 虚线表示旅行时为负)。同时, 由于使用了相同的炮点S, TSstat在相减过程中被相互抵消, 于是得到:
| $ D_{j,j + 1}^{{\rm{left}}} = {Y_{S,{R_{j + 1}}}} - {Y_{S,{R_j}}} = \Delta {T_{j,j + 1}} + (T_{{R_{j + 1}}}^{{\rm{ stat }}} - T_{{R_j}}^{{\rm{ stat }}}) $ | (10) |
其中, Dj, j+1left的上标left表示该时延估计使用了检波点左侧炮点的地震记录。类似的, 也可以使用检波点右侧炮点的地震记录再次得到Rj和Rj+1地震记录之间的时延(图 3b), 其物理过程与使用左侧炮点地震记录的过程完全一致。
| $ D_{j + 1,j}^{{\rm{right}}} = \Delta {T_{j + 1,j}} + (T_{{R_j}}^{{\rm{ stat }}} - T_{{R_{j + 1}}}^{{\rm{ stat }}}) $ | (11) |
其中, Dj+1, jright的上标right表示该时延估计使用了检波点右侧炮点的地震记录, ΔTj+1, j对应的射线路径如图 3b中的蓝线所示(实线表示旅行时为正, 虚线表示旅行时为负)。
ΔTj, j+1和ΔTj+1, j都包含了传播至Rj和Rj+1的两组上行旅行时和沿高速层顶传播的旅行时。假设地表高程和近地表低速层厚度引起的长波长静校正量已经被消除, 则ΔTj, j+1和ΔTj+1, j包含的上、下行旅行时相同; 同时高速层顶界面的起伏在长波长静校正中被修正, ΔTj, j+1和ΔTj+1, j包含的沿高速层顶的传播距离也近似相等, 由于Rj和Rj+1为相邻检波点, 在相对小的空间范围内, 可以认为高速层顶的速度变化不大, 因此ΔTj, j+1和ΔTj+1, j包含的沿高速层顶传播的旅行时也近似相等, ΔTj, j+1和ΔTj+1, j近似相等, ZHANG等[11]给出过类似的证明。因此, 公式(10)和公式(11)相减得到:
| $ D_{j,j + 1}^{{\rm{ left }}} - D_{j + 1,j}^{{\rm{ right }}} = 2(T_{j + 1}^{{\rm{ stat }}} - T_j^{{\rm{ stat }}}) $ | (12) |
其中, Dj, j+1left和Dj+1, jright可以使用公式(7)和1.2节的“相干叠加”方法得到。因此, 利用公式(12)可以求出Tj+1stat-Tjstat, 即相邻检波点之间的相对剩余静校正量(图 3c)。假定某一个检波点的剩余静校正量为0, 则可以根据相对剩余静校正量逐一求解所有检波点的剩余静校正量, 以上过程实现了检波点剩余静校正量的求取。类似的, 根据炮检点互换原理, 重复上述过程也可以得到炮点的剩余静校正量。
1.4 方法流程本文方法的实现流程如图 4所示。如果数据存在长波长静校正问题, 需要先进行高程静校正或野外静校正; 针对数据可能存在的异常高频噪声, 使用高通滤波进行噪声压制; 使用高阶累积量和相干叠加方法得到两点间的初至时延; 最后, 使用时延信息的组合得到炮检点的剩余静校正量。
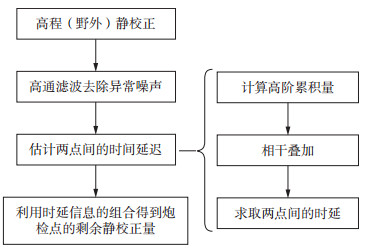
|
图 4 本文方法流程 |
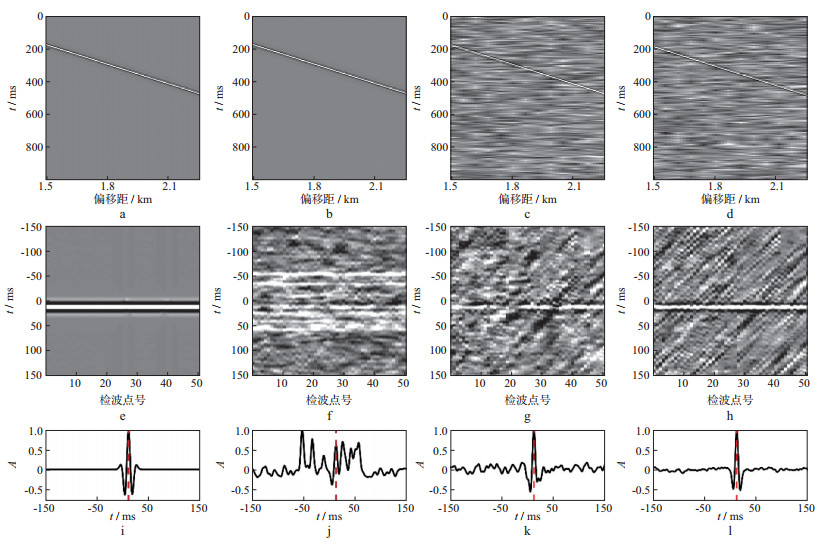
本节通过合成数据实例, 对比了高阶累积量和互相关方法应用于时延估计的抗噪性。图 5a和图 5b展示了仅包含一组折射波信号的两个单炮记录, 折射波视速度为2 500 m/s, 检波点间距为15 m, 两个炮点相距60 m, 雷克子波主频为60 Hz。图 5c和图 5d分别为对图 5a和图 5b加入相干高斯噪声的单炮记录, 其信噪比为-9 dB。图 5a和图 5b的互相关结果如图 5e所示。图 5f、图 5g和图 5h分别为对含噪数据(图 5c和图 5d)使用互相关、三阶累积量和四阶累积量得到的结果。由于互相关对相干噪声敏感, 图 5f的互相关结果中除了包含折射波的响应, 还混入了相干噪声的响应, 信噪比为3 dB, 图 5g和图 5h中的相干噪声被有效压制, 残余噪声也不具有相同的时延, 因此无法实现相干叠加, 其信噪比分别达到了9 dB和15 dB。图 5i、图 5j、图 5k和图 5l分别为对图 5e、图 5f、图 5g和图 5h的结果沿检波点叠加得到的叠加单道。图 5e使用不同检波点得到的折射波响应具有相同的时延, 因此在叠加过程中实现了相干叠加, 叠加结果(图 5i)中的峰值位置与理论时延(红色虚线标示)一致。图 5j中相干噪声响应的峰值大于折射波响应的峰值, 因此难以准确得到折射波响应的时延估计。图 5k和图 5l中包含的折射波响应的峰值位置与理论时延一致。该实例证明了三阶和四阶的高阶累积量方法压制相干白噪声的效果优于互相关方法, 同时, 高阶累积量的阶数越高, 得到的折射波响应的信噪比也越高。
|
图 5 合成数据的测试结果 a, b仅包含一组折射波信号的单炮记录; c, d加入相干高斯噪声的单炮记录; e 图 5a和图 5b的互相关结果; f 图 5c和图 5d的互相关结果; g 图 5c和图 5d的三阶累积量结果; h 图 5c和图 5d的四阶累积量结果; i对图 5e叠加得到的叠加单道; j对图 5f叠加得到的叠加单道; k对图 5g叠加得到的叠加单道; l对图 5h叠加得到的叠加单道 |
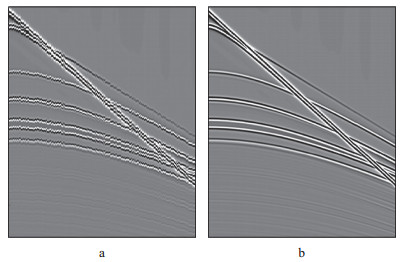
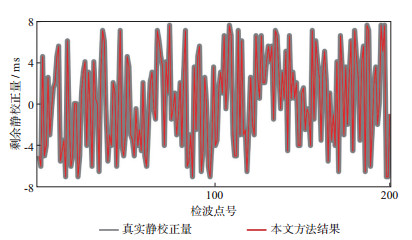
采用声波有限差分正演得到合成数据, 所用模型参数见表 1, 炮距为40 m, 道距为10 m, 炮点数100, 检波点数400。剩余静校正量由随机序列产生, 满足均值为0和标准差为8 ms的正太分布, 正演得到的单炮记录如图 6a所示, 由于剩余静校正量的存在, 图 6a中同相轴的连续性较差。将采用本文方法得到的剩余静校正量应用到单炮记录中, 得到的结果如图 6b所示。由图 6b可见, 单炮记录同相轴的连续性显著提高。图 7给出了对不含噪合成数据采用本文方法得到的剩余静校正量。其中, 灰线表示真实静校正量, 红线表示计算得到的静校正量。由图 7可见, 本文方法计算得到的剩余静校正量与真实值完全吻合。
|
图 6 对不含噪合成数据(a)应用本文方法进行剩余静校正处理后的结果(b) |
|
图 7 对不含噪合成数据应用本文方法得到的剩余静校正量 |
| 表 1 模型参数 |
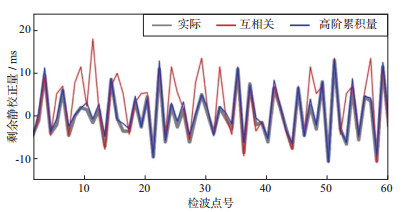
对图 6a数据加入相干高斯噪声, 得到信噪比为-7 dB的含噪数据(图 8a)。将采用本文方法得到的剩余静校正量应用到含噪单炮记录中, 得到如图 8b所示的结果。由图 8b可见, 反射波同相轴连续性明显提高。图 8c和图 8d分别是图 8a和图 8b方框标示区域的局部放大图。图 9展示了对含噪合成数据使用互相关和本文方法得到的剩余静校正量。由图 9可以看出, 本文方法得到的剩余静校正量与真实值基本一致, 互相关方法受相干噪声影响, 其结果偏离真实值较多。该实例验证了本文方法求取剩余静校正量的有效性, 同时, 相比互相关方法, 本文方法不易受相干噪声影响, 抗噪性更好。

|
图 8 对含噪合成数据应用本文方法进行剩余静校正处理后的结果 a未做剩余静校正的单炮记录; b采用本文方法进行剩余静校正处理后的单炮记录; c 图 8a方框区域局部放大结果; d 图 8b方框区域局部放大结果 |
|
图 9 对含噪合成数据使用互相关和本文方法得到的剩余静校正量 |
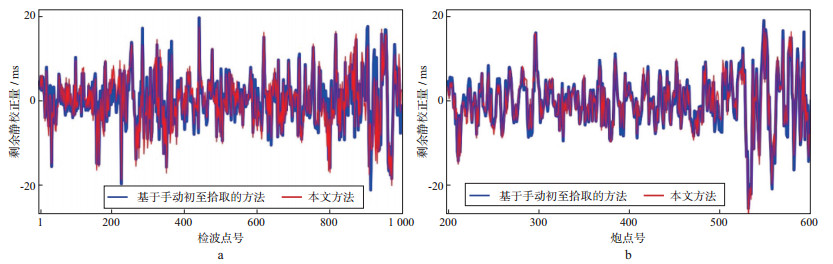
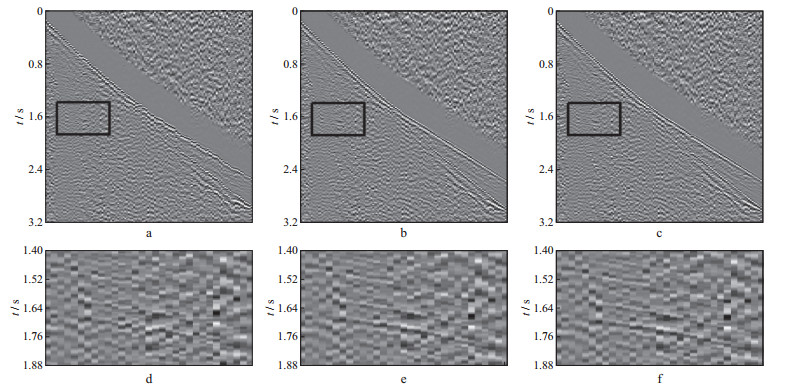
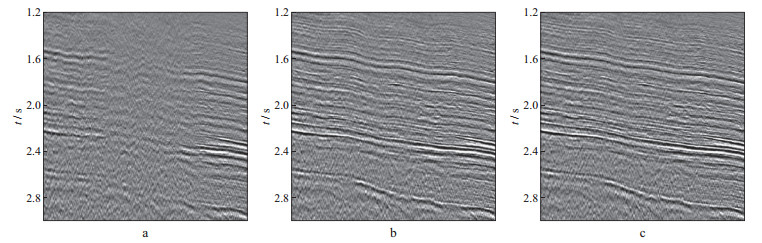
选取中国西部某地区的实际地震资料验证本文方法的有效性。该工区地表存在较强的近地表速度异常, 剩余静校正问题突出。对比了本文方法和某商业软件中的基于初至拾取的初至波剩余静校正模块的结果, 该模块采用的是广义互换的方法。基于初至拾取的剩余静校正方法要求拾取全部道集的初至到时, 但在远偏移距处, 受该工区复杂近地表影响, 初至信噪比极低, 不得不进行耗时耗力的手动初至拾取, 而本文方法可以避免初至拾取的工作量。图 10a和图 10b对比了本文方法和基于手动初至拾取方法得到的检波点和炮点的剩余静校正量, 结果基本吻合, 仅在检波点号为900附近位置存在微弱差异。将剩余静校正量应用到道集数据, 选取剩余静校正问题比较突出的原始单炮(图 11a)进行比较, 该单炮初至波同相轴明显不连续, 图 11b和图 11c分别是应用本文方法和基于初至拾取方法的结果, 两种方法都明显改善了初至波同相轴的连续性, 图 11d至图 11f分别是图 11a至图 11c黑色方框处的局部放大图, 反射波同相轴的连续性也明显改善。图 12对比了本文方法和基于手动初至拾取方法得到的叠加剖面。图 12a为未进行剩余静校正的叠加剖面。由图 12a可见, 该叠加剖面同相轴连续性较差。采用本文方法得到的叠加剖面(图 12b)同相轴的连续性显著改善, 并且与基于手动初至拾取的剩余静校正方法相比, 本文方法避免了手动初至拾取的繁重工作量。
|
图 10 本文方法和基于手动初至拾取方法应用于实际数据得到的剩余静校正量对比 a检波点剩余静校正量对比; b炮点剩余静校正量对比 |
|
图 11 本文方法和基于手动初至拾取方法进行剩余静校正的单炮记录效果对比 a未进行剩余静校正的单炮记录; b采用本文方法进行剩余静校正后的单炮记录; c基于手动初至拾取方法进行剩余静校正后的单炮记录; d 图 11a黑色方框区域的局部放大结果; e 图 11b黑色方框区域的局部放大结果; f 图 11c黑色方框区域的局部放大结果 |
|
图 12 本文方法和基于手动初至拾取方法进行剩余静校正后的叠加剖面效果对比 a未进行剩余静校正的叠加剖面; b采用本文方法进行剩余静校正后的叠加剖面; c基于手动初至拾取方法进行剩余静校正后的叠加剖面 |
本文发展了基于高阶累积量时间延迟估计的自动剩余静校正方法, 采用高阶累积量得到两点间的初至波时延; 使用相干叠加提高信噪比, 保证时延估计的准确性; 再使用时延信息的组合得到炮检点的剩余静校正量。与互相关类方法相比, 使用高阶累积量进行时延估计可有效利用三维地震数据信息增强有效信号, 高阶累积量不再要求噪声为高斯分布, 与实际地震资料的情况更加吻合; 采用相干叠加方法提高信号有效叠加次数和信噪比, 保证本文方法获得稳定且可靠的道间时延估计结果; 本文方法采用完全数据驱动, 与基于初至拾取的剩余静校正方法相比, 可有效避免初至拾取所需的高昂时间和人力成本。模型试验和实际资料的应用结果表明, 本文方法可以明显改善叠加剖面中反射波同相轴的连续性, 为后续地震数据处理提供高品质资料。
本文方法涉及到高阶累积量阶数的选取, 选取的阶数越高, 噪声压制效果越好, 但运算量也同步增加, 本文选取了常用的四阶累积量, 在具体应用于实际地震资料时, 可事先通过参数测试确定适合的累积量阶数, 实现高效稳定的剩余静校正量求取。另外, 本文方法要求观测系统规则化, 以实现两点间初至波响应的相干叠加, 针对不规则观测系统, 可事先使用空间插值技术重构得到规则化道集。本文方法实现了自动剩余静校正, 未来可结合人工智能类方法实现流程参数的自动优化选取, 进一步提高自动化程度以减少人工成本, 更加高效地应用于实际工区的地震资料处理。本文方法可进一步与深度学习结合, 改进传统的基于特征值的时延估计方法, 提高道间时延估计的准确率和对更加复杂噪声环境的适用性, 并同时降低特征提取和筛选的人工成本, 提高计算效率。
| [1] |
HATHERLY P J, UROSEVIC M, LAMBOURNE A, et al. A simple approach to calculating refraction statics corrections[J]. Geophysics, 1994, 59(1): 156-160. |
| [2] |
PALMER D, JONES L. A simple approach to refraction statics with the generalized reciprocal method and the refraction convolution section[J]. Exploration Geophysics, 2005, 36(1): 18-25. |
| [3] |
CHANG X, LIU Y, WANG H, et al. 3-D tomographic static correction[J]. Geophysics, 2002, 67(4): 1275-1285. |
| [4] |
TRYGGVASON A, SCHMELZBACH C, JUHLIN C. Traveltime tomographic inversion with simultaneous static corrections—well worth the effort[J]. Geophysics, 2009, 74(6): WCB25-WCB33. |
| [5] |
GHOLAMI A. Residual statics estimation by sparsity maximization[J]. Geophysics, 2013, 78(1): V11-V19. |
| [6] |
REN X, ZHOU X, QIAN Z, et al. Super-trace residual statics estimation technology[J]. Expanded Abstracts of 86th Annual Internat SEG Mtg, 2016, 2444-2448. |
| [7] |
安圣培, 梁向豪, 彭更新, 等. 低信噪比地震数据折射初至的判别与识别[J]. 石油地球物理勘探, 2015, 50(3): 451-459. AN S P, LIANG X H, PENG G X, et al. Recognization and identify-cation of first-arrival refractions in low SNR prestack seismic data[J]. Oil Geophysical Prospecting, 2015, 50(3): 451-459. |
| [8] |
AN S P, HU T Y, PENG G. 3D cumulant-based coherent integration method to enhance first-break seismic signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(4): 2089-2096. |
| [9] |
梁上林, 胡天跃, 崔栋, 等. 初至拾取中基于超级虚折射干涉的信号加强[J]. 石油物探, 2019, 58(4): 509-516. LIANG S L, HU T Y, CUI D, et al. Signal enhancement based on super-virtual refraction interferometry in first arrival pickup[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 509-516. |
| [10] |
MIKESELL T D, VAN WIJK K, RUIGROK E, et al. A modified delay-time method for statics estimation with the virtual refraction[J]. Geophysics, 2012, 77(6): A29-A33. |
| [11] |
ZHANG C, ZHANG J. 2D seismic residual statics derived from refraction interferometry[J]. Journal of Applied Geophysics, 2016, 130: 145-152. |
| [12] |
AL-HAGAN O, HANAFY S M, SCHUSTER G T. Iterative supervirtual refraction interferometry[J]. Geophysics, 2014, 79(3): Q21-Q30. |
| [13] |
宋维琪, 杨勤勇, 郭全仕, 等. 地面微地震资料弱信号提取方法研究[J]. 石油物探, 2013, 52(2): 131-135. SONG W Q, YANG Q Y, GUO Q S, et al. Weak signal extraction method for surface microseismic monitoring data[J]. Geophysical Prospecting for Petroleum, 2013, 52(2): 131-135. |
| [14] |
盛冠群, 李振春, 王维波, 等. 基于小波分解与高阶统计量的微地震初至拾取方法研究[J]. 石油物探, 2015, 54(4): 388-395. SHENG G Q, LI Z C, WANG W B, et al. A new automatic detection method of microseismic events based on wavelet decomposition and high-order statistics[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 388-395. |
| [15] |
戴永寿, 张漫漫, 张亚南, 等. 基于时频谱模拟的时变混合相位子波提取[J]. 石油地球物理勘探, 2015, 50(5): 830-838. DAI Y S, ZHANG M M, ZHANG Y N, et al. Time-variant mixed-phase seismic wavelet estimation based on spectral modeling in the time-frequency domain[J]. Oil Geophysical Prospecting, 2015, 50(5): 830-838. |
| [16] |
MENDEL J M. Tutorial on higher-order statistics (spectra) in signal processing and system theory:theoretical results and some applications[J]. Proceedings of the IEEE, 1991, 79(3): 278-305. |




