随着地震勘探技术的快速进步, 人们对成像精度的要求也越来越高, 各种叠前去噪方法^[1-2]、振幅补偿方法^[3]、高精度成像方法都得到了长足的发展^[4]。近年来, 人们开始关注叠前处理后得到的共成像点道集对成像结果的影响, 同时叠前道集的优化处理日益受到重视^[5-6]。常规共反射点道集优化处理的目的比较宽泛, 主要包括以提高资料分辨率、信噪比为目的的资料品质改善^[7]和针对振幅、频率和相位信息补偿的岩性预测^[8-9]。在复杂构造情况下, 常规偏移距域或炮域道集存在射线多路径问题, 易引起偏移假象, 并降低成像精度。角度域共成像点道集(angle domain common image gathers, ADCIGs)避免了射线多路径问题, 可以消除偏移剖面上的多波至假象, 并且包含了反射点处所有角度入射的反射波对该点成像值的贡献。XU等^[10]和HOOP等^[11]研究了ADCIGs对射线多路径问题的适应性, 认为采用ADCIGs叠加成像可以有效避免构造假象。ADCIGs本质是利用地震数据中波场传播的方向信息, 并通过ADCIGs的叠加成像, 反映出更为丰富的地层局部信息。但是受地层调谐效应、地下复杂构造及地震数据品质等因素的影响, ADCIGs同样存在一些缺点, 主要表现为在高角度区域, ADCIGs同相轴存在不同程度的波形拉伸与畸变; 在其它数据空间不易区分的噪声干扰, 在角度域更为明显。因此, 在角度域对共成像点道集进行去噪和道集优化处理, 可以消除角度域内的剩余噪声, 进一步提高ADCIGs及其叠加剖面的成像精度。郑忆康等^[12]对ADCIGs应用高分辨率抛物线型Radon变换来压制多次波偏移假象, 有效提高了成像结果的信噪比。赵小龙等^[13]分析了地层调谐效应对叠前道集的影响, 引入了非平稳匹配去调谐的方法, 实现了角度域叠前道集的振幅和波形拉伸校正, 改善了大角度地震数据的品质。姜弢等^[14]提出了一种角度域波形束滤波方法, 较好地改善了弱信噪比地震数据的成像效果。

基于奇异值分解的角度域去噪方法(本文方法)利用地震数据存在相关性这一特点, 将奇异值作为正交基在空间分解信号, 在此基础上利用地震波的相关差异实现波场的分离与去噪^[15], 根据奇异值分解的相关理论, 分解后的奇异值子空间是由水平同相轴组成的, 数据重构后不同能量的水平同相轴叠加, 会出现视觉上弯曲的同相轴。因此奇异值分解更适用于具有线性同相轴的数据, 而利用奇异值分解重构倾斜或弯曲地层理论上会产生较大的误差^[16]。对于偏移速度准确时提取的ADCIGs, 其有效信号为水平同相轴, 各道数据相关性好, 噪声则随机分布于道集内且相关性较差, 这非常适合根据奇异值分解的理论进行信噪分离和去噪。基于ADCIGs具有相关性较好的水平同相轴这一特点, 本文首先对其进行奇异值分解, 然后分析了不同奇异值子空间的映像特征, 并采用累计贡献率的方法确定降噪阶次, 实现角度域地震波场的分离和去噪, 最后利用模型数据和实际资料验证了本文方法的有效性。

对于任意m×n阶矩阵X都可以分解为m×m正交矩阵U、m×n阶对角阵Σ以及n×n阶正交阵V的乘积^[17]:

式中:U由XX^T的特征向量构成; V由X^TX的特征向量构成; Σ由奇异值构成, 即Σ=diag(σ₁, σ₂, …, σ_r)(r≤min{m, n}), 其中σ_i(i=1, 2, …, r)为矩阵X的奇异值, 且按非递增顺序排列。一般定义特征值的平方根为矩阵的奇异值, (1)式也称为矩阵X的奇异值分解。

由(1)式可以导出奇异值分解的另一种表达形式为:

式中:u_i、v_i分别为U、V的第i个特征向量, u_iv_i^T表示第i个奇异值的特征映像。(2)式从左到右可以看做是对X的正交分解, 当矩阵有r个奇异值时, 矩阵X可以分解为r个子空间的代数和。即:

式中:$\boldsymbol{X}_{i}=\sigma_{i} \boldsymbol{u}_{i} \boldsymbol{v}_{i}^{\mathrm{T}}$, i∈[1, r]为第i个奇异值对应的子空间。由于(3)式从左到右是一个分解的过程, 所以从右到左就是一个重构的过程。

地震信号X经过奇异值分解后, 其能量总和可表示为$E_{X}=\sum\limits_{i=1}^{m} \sigma_{i}^{2}$, 说明地震道能量的强弱与σ_i的大小有关, 因此, 奇异值分量越大, 对地震信号的贡献也越大, 当地震道各道都相关时, r=1, 此时E_X=σ₁。因此, 对于地震剖面, 排齐(排列整齐且连续性好)的同相轴对应第一个或前几个奇异值; 未排齐的同相轴对应于一些中间的奇异值; 随机噪声对应于一些后面的小奇异值。图 1为含噪声的ADCIGs及其经过奇异值分解后选取不同奇异值分别重构得到的子空间数据。其中, 图 1a为含噪声的原始ADCIGs, 其在高角度处存在波形拉伸; 图 1b是根据第1个奇异值创建的子空间, 显示了排齐的相干同相轴; 图 1c是根据第2个奇异值创建的子空间, 显示了中断的同相轴; 图 1d和图 1e分别是根据第3和第4个奇异值创建的子空间, 出现了更多的同相轴中断; 图 1f是根据第20个以后的奇异值创建的子空间, 图中只看到噪声。数据重构时选择前k个奇异值对应的子空间, 可得到相关性较好的信号, 如果取最后几个小奇异值重构数据, 则得到的主要是噪声, 因此利用数据重构就可以达到信噪分离和去噪的目的。

图 1(Fig. 1)

图 1 原始ADCIGs及根据其奇异值创建的子空间 a含噪声的原始ADCIGs; b根据σ1创建的子空间; c根据σ2创建的子空间; d根据σ3创建的子空间; e根据σ4创建的子空间; f根据第20个以后的奇异值创建的子空间

由前面分析可知, 奇异值序列中前面较大的k个奇异值由纯信号贡献, 后面较小的奇异值完全由噪声贡献, 因此有效信号的子空间可由前面k个奇异值来重构。定义k₀为降噪阶次, 它是奇异值分解去噪方法的一个重要参数, 一般情况下它的值是难以预知的, 但在实际应用中可以采用单边极大值方法^[18], 伪近邻点法^[19]和累计贡献率法^[20]等方法进行估计。

为了减少弱噪声对降噪阶次估计的影响, 本文首先对奇异值序列进行如下修正:

修正后的奇异值累计贡献率η计算公式如下:

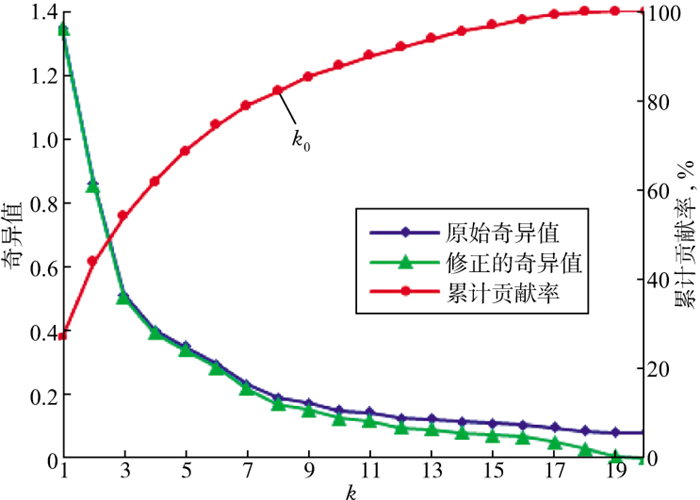
式中:1≤k≤r。这样就可以通过累积贡献率来确定降噪阶次, 统计表明将η达到80%~90%时所对应的k值作为降噪阶次k₀(图 2)时, 可获得较好的去噪效果。

图 2(Fig. 2)

图 2 不同k值下对应的原始奇异值、修正的奇异值及累计贡献率

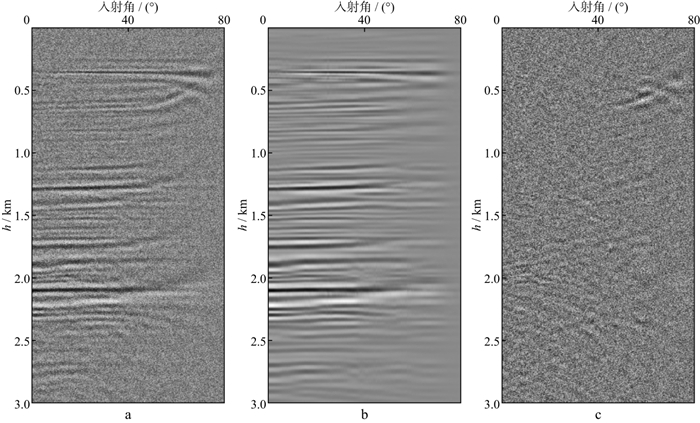
图 3a为对Marmousi模型数据进行角度域偏移并添加随机噪声后的ADCIGs, 可以看到该道集存在较为明显的波形拉伸和随机噪声。去噪时采用累计贡献率法估计降噪阶次, 取前8个奇异值对应的子空间进行数据重建, 去噪结果表明本文方法较好地去除了原始数据中的随机噪声, 高角度的频率拉伸也得到了压制, 剖面的信噪比明显提高(图 3b), 图 3c为去除的噪声, 可以看到噪声数据中不含有具有水平同相轴的信号, 说明去噪后有效信息得到了保护。对采用本文方法去噪后得到的ADCIGs进行叠加(图 4), 可以看到, 原始剖面中的随机干扰得到了压制, 去噪后叠加剖面的信噪比得到了明显改善, ADCIGs高角度处的低频拉伸得到消除, 剖面的分辨率也有所提高。基于奇异值分解的角度域去噪方法应用于ADCIGs时更能发挥其优势, 采用该方法去除角度域内的噪声能有效提高ADCIGs和叠加剖面的质量, 达到了高信噪比的处理效果。

图 3(Fig. 3)

图 3 采用本文方法对模型数据去噪的结果对比 a含噪声的ADCIGs; b去噪后的ADCIGs; c去除的噪声

图 4(Fig. 4)

图 4 采用本文方法对模型数据去噪前(a)、后(b)得到的叠加剖面

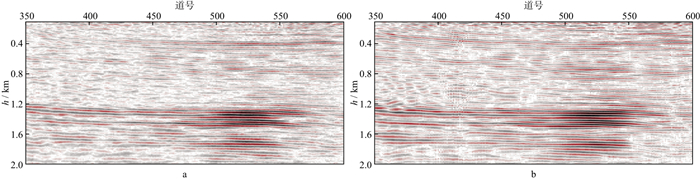
为了验证本文方法的实际应用效果, 本文对宁东探区的部分实际资料进行了试处理。图 5a为叠前局部偏移距成像后利用成像空间的角度映射获得的ADCIGs, 可以看到, 原始ADCIGs上存在较为严重的剩余噪声干扰, 浅层高角度存在波形拉伸, 在上、下边界还存在偏移“画弧”现象, 利用这样的数据进行叠加成像, 势必会降低成像剖面的信噪比, 影响角度域叠加成像效果。因此对ADCIGs进行奇异值分解, 采用奇异值累计贡献率法得出最佳降噪阶次为11, 即主要反射波能量集中在前11个奇异值上; 进而选取前11个奇异值对应的子空间进行数据重构, 实现了角度域内的去噪处理, 结果如图 5b所示。将第12个以后的奇异值对应的子空间进行重构, 获得的数据即为去除的噪声(图 5c)。可以看出, 随机噪声、高角度频率畸变等在去噪后的ADCIGs上得到了有效压制, 其信噪比明显提高; 去除的噪声中主要包含背景随机干扰, 低频波形拉伸和数据边界画弧干扰, 基本不含有效信号; 对高角度波形拉伸的压制改善了大角度地震数据的品质。对该资料应用本文方法前、后得到的叠加剖面如图 6所示, 可以看出, 去噪后的剖面反射波能量增强, 同相轴连续性更好, 剖面信噪比和分辨率均有所提高。特别是在剖面左部浅层和深部区域, 由于去噪后的剖面被压制背景噪声了和高角度的低频干扰, 原始剖面中能量较弱的同相轴在去噪后的剖面中清晰可见, 成像效果得到了明显改善。

图 5(Fig. 5)

图 5 采用本文方法对实际资料进行去噪处理的结果对比 a原始ADCIGs; b去噪后的ADCIGs; c去除的噪声

图 6(Fig. 6)

图 6 采用本文方法对实际资料进行去噪处理前(a)、后(b)得到的叠加剖面

本文实现了基于奇异值分解的角度域去噪, 奇异值分解后的ADCIGs表现为不同中断程度的水平同相轴, 选取不同的子空间数据进行信号重构, 可实现有效信号和噪声完全分离。对奇异值进行修正可以更好地确定有效降噪阶次, 采用累积贡献率法计算降噪阶次快速直观, 具有较好的效果。数值模拟和实际资料的去噪效果表明, 本文方法能有效分离角度域内的随机干扰, 压制高角度处的频率畸变, 改善大角度数据的品质。对ADCIGs进行基于奇异值分解的角度域去噪, 可进一步提高ADCIGs的精度, 进而改善角度域成像剖面的信噪比和分辨率, 也为基于叠前道集的速度分析和叠前反演提供了更为准确的基础数据。