重建缺失的地震数据是一个重要的研究课题, 传统的重建方法有波动方程法[1]、预测滤波法[2]和数学变换法[3]等。波动方程法通常需要先验参数信息, 这限制了它在实际工作中的应用。预测滤波法重建的地震数据一般存在误差较大的问题。数学变换法包括了采用固定基和字典学习两类方法, 固定基重建计算速度较快但是缺乏对不同的地震数据进行自适应稀疏表示的能力[4-6], 字典学习能够对不同的地震数据进行有效的稀疏表示, 但是训练字典较为费时[7-9]。
近十年发展起来的压缩感知理论[10-11]对地震数据的重建工作有着重要的指导意义, 压缩感知理论表明:在信号具有稀疏性的情况下, 采集少量的样本通过非线性重构算法可以重建完整的信号。目前, 压缩感知理论在地震数据处理中已取得了较大进展:HERRMANN等[12]提出了基于压缩感知理论的curvelet变换方法, 成功重建了缺失的地震数据; ZHANG等[13]提出了基于压缩感知的傅里叶变换重建地震数据的方法; LIANG等[14]提出了在压缩感知理论下采用shearlet变换重建缺失地震数据的方法。在压缩感知中, 稀疏基的选择十分重要, 直接影响到地震数据的重建精度[15]。字典学习能够根据不同的地震数据训练出相应的稀疏表示字典, ZHOU等[7]通过字典学习方法实现了混采数据分离, ZHU等[16]将字典学习方法引入地震数据去噪中, 取得了良好的效果。
BOYD等[17]提出了交替方向乘子算法(ADMM), 该方法能够有效地处理稀疏反演问题。STERNFELS等[18]提出了在压缩感知理论下采用ADMM进行奇异值阈值的地震数据去噪方法。HARIKUMAR等[19]提出了采用ADMM更新过完备字典, 并在处理变化幅度大的信号时取得了良好的效果。ZHOU等[20]将采用ADMM更新过完备字典的方法成功地应用于混采数据分离中。
本文在压缩感知理论下提出了一种基于字典学习和ADMM的地震数据重建方法, 首先对缺失的地震记录进行字典学习得到稀疏表示字典, 然后根据炮记录中地震道的缺失情况设计采样矩阵, 接着建立相应的L1范数约束模型, 最后采用ADMM进行求解得到重建的地震数据。用正演模拟数据和实际地震资料验证了本文方法的有效性。
1 基本原理 1.1 压缩感知地震数据的重建问题可以表示为:
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{\varphi y}} $ | (1) |
式中:y∈RM表示原始未缺失的M维地震数据; x∈RN表示N(N < M)维的缺失地震数据; φ∈RM×N表示维度为N×M的采样矩阵。φ是一个对角矩阵, 对角线上的元素与x对应, 当x中地震道数据未缺失时, φ对应对角线上的元素为1, 若x中地震道数据缺失则φ对应对角线上的元素为0。
采用训练得到的过完备字典D(D∈RM×N且M < L)对y进行稀疏表示, 其中a为过完备字典D中维度为L的稀疏系数:
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{\varphi Da}} $ | (2) |
公式(2)是一个欠定问题, 压缩感知理论指出, 当信号的稀疏度为r, 并且φD满足有限等距性质(restricted isometry property, RIP)的常数为νr∈(0, 1)时:
| $ \left( {1-{\nu _{\rm{r}}}} \right)\left\| \mathit{\boldsymbol{a}} \right\|_2^2 \le \left\| {\mathit{\boldsymbol{\varphi Da}}} \right\|_2^2 \le \left( {1 + {\nu _{\rm{r}}}} \right)\left\| \mathit{\boldsymbol{a}} \right\|_2^2 $ | (3) |
公式(2)有唯一解, 但是通常情况下很难通过公式(3)进行严格验证, 而BARANIUK[21]放宽了这一条件, 当φ与D不相关时, φD满足公式(3)中条件的概率很大, φD的相关性定义为:
| $ \boldsymbol{\mu}(\boldsymbol{\varphi} \boldsymbol{D})=\max\limits _{i, j, i \neq j} \frac{\left\langle(\boldsymbol{\varphi} \boldsymbol{D})_{i}^{\mathrm{T}} \cdot(\boldsymbol{\varphi} \boldsymbol{D})_{j}\right\rangle}{\left\|(\boldsymbol{\varphi} \boldsymbol{D})_{i}\right\|_{2} \cdot\left\|(\boldsymbol{\varphi} \boldsymbol{D})_{j}\right\|_{2}} $ | (4) |
式中:i, j分别表示φD中的行和列。GLEICHMAN等[22]验证了过完备字典和0, 1组成的对角矩阵的不相关性, 此时, 公式(2)可以描述为如下数学问题:
| $ \tilde a = {\mathop{\rm argmin}\nolimits} {\left\| \mathit{\boldsymbol{a}} \right\|_0}{\rm{ s}}{\rm{.t}}{\rm{. }}{\left\| {\mathit{\boldsymbol{\varphi Da}}-\mathit{\boldsymbol{y}}} \right\|_2} \le \sigma $ | (5) |
式中:
| $ \tilde a = {\mathop{\rm argmin}\nolimits} \frac{1}{2}\left\| {\mathit{\boldsymbol{\varphi Da}}-\mathit{\boldsymbol{y}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{a}} \right\|_0}, \quad \lambda > 0 $ | (6) |
式中:λ为正则化参数。在满足公式(4)的条件下, 公式(6)可以改写为:
| $ \tilde a = {\mathop{\rm argmin}\nolimits} \frac{1}{2}\left\| {\mathit{\boldsymbol{\varphi Da}}-\mathit{\boldsymbol{x}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{a}} \right\|_1}, \quad \lambda > 0 $ | (7) |
我们采用ADMM求解公式(7), 求得
| $ \mathit{\boldsymbol{\tilde y}} = \mathit{\boldsymbol{D}}\tilde a $ | (8) |
本文采用了K-奇异值分解(K-singular value decomposition, K-SVD)来获取公式(2)中的过完备字典D, K-SVD是一个字典学习的优化方法[23], 它的优化过程可以表示为:
| $ \min\limits _{D, a}\left\{\|\boldsymbol{F}-\boldsymbol{D} \boldsymbol{A}\|_{F}^{2}\right\} \quad \text { s.t. } \quad \forall l, \left\|\boldsymbol{a}^{l}\right\|_{0} \leqslant T $ | (9) |
式中:F∈RM×N表示输入的训练样本; A为样本在字典中的稀疏系数; T表示非零元素个数上限; al为A的第l行。首先需要设定一个初始字典, 本文的初始字典选取了过完备的DCT字典, 如图 1所示。
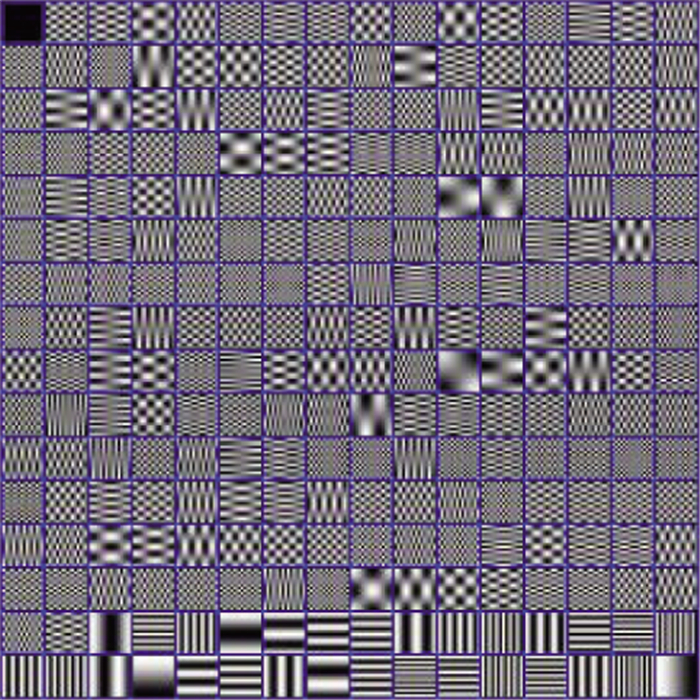
|
图 1 DCT过完备字典 |
然后, 固定初始字典D, 输入训练样本F, 求出稀疏系数al:
| $ {\min\limits _{{a^l}}}\left\{ {\left\| {{f_l}-\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{a}}^l}} \right\|_2^2} \right\}\quad {\rm{ s}}{\rm{.t}}{\rm{. }}\quad \forall l, {\left\| {{a^l}} \right\|_0} \le T $ | (10) |
式中:fl为F的列。在求得稀疏系数al的同时, 固定al, 对字典D进行逐列更新:
| $ \|\boldsymbol{F}-\boldsymbol{D} \boldsymbol{A}\|_{F}^{2}=\left\|\boldsymbol{F}-\sum\limits_{l=1}^{K} \boldsymbol{d}_{l} \boldsymbol{a}^{l}\right\|_{F}^{2}=\\\left\|\left(\boldsymbol{F}-\sum\limits_{l \neq K} \boldsymbol{d}_{l} \boldsymbol{a}^{l}\right)-\boldsymbol{d}_{K} \boldsymbol{a}^{K}\right\|_{F}^{2}=\left\|\boldsymbol{E}_{K}-\boldsymbol{d}_{K} \boldsymbol{a}^{K}\right\|_{F}^{2} $ | (11) |
式中:dl为字典D的列; EK表示抽取dK列后的误差, 可以通过对dKaK进行调整缩小误差。为了保证A的稀疏性, 记下aK中非零元素所在列, 并且除去零元素项得到aK′, EK中仅保留与aK非零元素对应的列, 得到E′K, 对应的字典列记为d′K, 再对E′K进行奇异值分解:
| $ \boldsymbol{E}_{K}^{\prime}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\mathrm{T}} $ | (12) |
式中:E′K为一个m×n阶矩阵; U为m×m阶酉矩阵, Σ为半正定的m×n阶对角矩阵; VT为V的共轭转置, 是n×n阶酉矩阵。用公式(12)中U的第一列替代d′K, Σ的最大奇异值与VT的第一行相乘替代aK′从而完成字典更新。
1.3 交替方向乘子算法与K-SVD采用正交匹配追踪算法求解公式(6)不同, 为了提高计算精度, 通过对L0约束问题向L1约束问题转化, 本文采用ADMM对公式(7)进行求解。
公式(7)是一个凸优化问题, ADMM引入了辅助变量p, h来求解(7)式:
| $ \min f(\boldsymbol{h})+g(\boldsymbol{p}) \quad \text { s.t. } \quad \boldsymbol{h}-\boldsymbol{p}=0 $ | (13) |
式中:f(h)(h∈R)要求为凸函数并且光滑; g(p)(p∈R)要求为凸函数。将公式(7)写成ADMM形式:
| $ \begin{array}{c}{\operatorname{argmin}_{a} \frac{1}{2}\|\boldsymbol{\varphi} \boldsymbol{D} \boldsymbol{a}-\boldsymbol{x}\|_{2}^{2}+\lambda\|\boldsymbol{p}\|_{1}} \\ {\text { s.t. } \quad \boldsymbol{a}-\boldsymbol{p}=0}\end{array} $ | (14) |
其增广目标函数为:
| $ \begin{array}{c}{\arg \min _{\boldsymbol{a, p} }\frac{1}{2}\|\boldsymbol{\varphi} \boldsymbol{D} \boldsymbol{a}-\boldsymbol{x}\|_{2}^{2}+\lambda\|\boldsymbol{p}\|_{1}+} \\ {\frac{\tau}{2}\|\boldsymbol{a}-\boldsymbol{p}\|_{2}^{2} \quad \text { s.t. } \quad \boldsymbol{a}-\boldsymbol{p}=0}\end{array} $ | (15) |
式中:τ为增广拉格朗日参数并且大于0, 它控制着迭代步长。将公式(15)写成增广拉格朗日函数:
| $ \begin{array}{*{20}{c}} {L(\mathit{\boldsymbol{a}}, \mathit{\boldsymbol{p}}, \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}) = \frac{1}{2}\left\| {\mathit{\boldsymbol{\varphi Da}}-\mathit{\boldsymbol{x}}} \right\|_2^2 + \lambda {{\left\| \mathit{\boldsymbol{p}} \right\|}_1} + }\\ {\frac{\tau }{2}\left\| {\mathit{\boldsymbol{a}}-\mathit{\boldsymbol{p}}} \right\|_2^2 + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{T}}}(\mathit{\boldsymbol{a}}-\mathit{\boldsymbol{p}})} \end{array} $ | (16) |
式中:Λ为对偶变量。ADMM的第i次迭代形式为:
| $ \begin{aligned} \boldsymbol{a}^{i+1}=&\left[(\boldsymbol{\varphi} \boldsymbol{D})^{\mathrm{T}} \boldsymbol{\varphi} \boldsymbol{D}+\tau \boldsymbol{I}\right]^{-1}\left[(\boldsymbol{\varphi} \boldsymbol{D})^{\mathrm{T}} \boldsymbol{\varphi} \boldsymbol{D}+{\tau} \boldsymbol{I}\right]^{\mathrm{T}} \boldsymbol{x}+\\ & \tau\left(\boldsymbol{p}^{i}-\boldsymbol{\varLambda}^{i}\right)] \\ \boldsymbol{p}^{i+1} &=\operatorname{soft}\left(\boldsymbol{a}^{i+1}+\boldsymbol{\varLambda}^{i}, \frac{\lambda}{\tau}\right) \\ \boldsymbol{\varLambda}^{i+1} &=\boldsymbol{\varLambda}^{i}+\boldsymbol{a}^{i+1}-\boldsymbol{p}^{i+1} \end{aligned} $ | (17) |
其中, I表示单位矩阵, soft为软阈值函数, 定义:
| $ \operatorname{soft}\left(\boldsymbol{a}^{i+1}+\boldsymbol{\varLambda}^{i}, \frac{\lambda}{\tau}\right)=\\\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}^{i + 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i}-\frac{\lambda }{\tau }}&{{\mathit{\boldsymbol{a}}^{i + 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i} > \frac{\lambda }{\tau }}\\ 0&{-\frac{\lambda }{\tau } \le {\mathit{\boldsymbol{a}}^{i + 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i} \le \frac{\lambda }{\tau }}\\ {{\mathit{\boldsymbol{a}}^{i + 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i} + \frac{\lambda }{\tau }}&{{\mathit{\boldsymbol{a}}^{i + 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i} < \frac{\lambda }{\tau }} \end{array}} \right. $ | (18) |
本文技术流程实现步骤如下。
1) 输入不完整的地震数据作为训练样本, 初始字典选为DCT过完备字典, 采用的字典学习方法为K-SVD, 输出相应的稀疏字典D。
2) 利用D对地震数据进行稀疏表示, 采用ADMM求解基于压缩感知理论建立的数学模型(公式(7))。
3) 求得近似稀疏表示
4) 将上一次迭代得到的地震数据替换为本次迭代得到的地震数据, 重复步骤2)和步骤3), 直到信噪比基本不变为止, 输出迭代后的地震数据
本文采用信噪比(RSN)作为地震数据重建性能的判断标准:
| $ {R_{{\rm{SN}}}} = 10\lg \frac{{\left\| \mathit{\boldsymbol{y}} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{\tilde y}}-\mathit{\boldsymbol{y}}} \right\|_2^2}} $ | (19) |
式中:y表示原始地震数据;
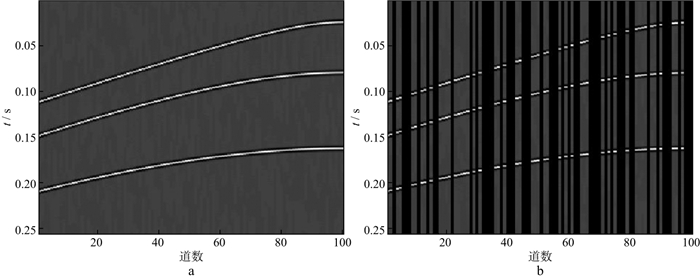
|
图 2 模拟数据(a)和随机缺失50%后的数据(b) |
对图 2b中缺失50%后的模拟数据进行K-SVD训练, 可以得到相应的稀疏字典, 如图 3所示。

|
图 3 模拟数据的K-SVD字典 |
对图 2b中缺失50%的地震数据进行重建。分别采用curvelet稀疏基和OMP、curvelet稀疏基和ADMM、字典学习和OMP、字典学习和ADMM重建模拟数据的结果及对应的重建误差如图 4至图 7所示。这4种重建方法的RSN分别为17.7138, 21.8057, 21.9478, 24.9869dB, 耗时分别为2.56, 4.32, 132.48, 271.09s。从计算效率看, 当需要处理的数据量较大时, 会面临耗时过长的问题, 若数据量较小且需要高精度时, 选取本文方法比较有利。其中, ADMM的正则化参数λ取1, 控制步长的参数τ取1, ADMM中的初始a, p, Λ设为0。
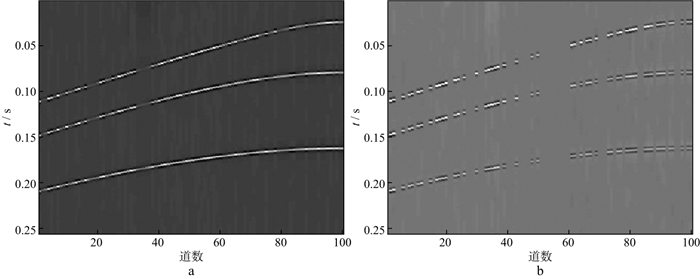
|
图 4 采用curvelet稀疏基和OMP重建模拟数据的结果(a)及重建误差(b) |

|
图 5 采用curvelet稀疏基和ADMM重建模拟数据的结果(a)及重建误差(b) |

|
图 6 采用字典学习和OMP重建模拟数据的结果(a)及重建误差(b) |
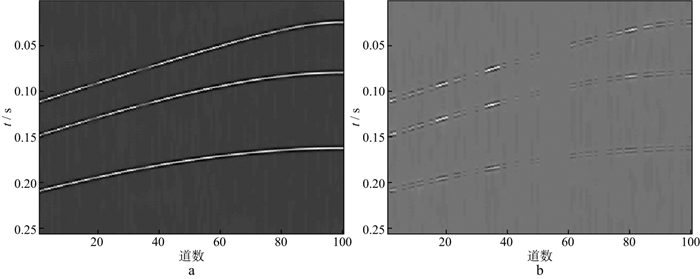
|
图 7 采用字典学习和ADMM重建模拟数据的结果(a)及重建误差(b) |
从图 4至图 7可以看出, 对于正演模拟数据, 基于压缩感知理论的固定基和字典学习方法都可以重建地震数据, 而字典学习重建的性能比固定基重建的性能更好, 重建误差也小。在压缩感知的重建算法中, ADMM重建的性能比OMP重建的性能更优越, 无论是在固定基中还是在字典学习中, ADMM重建的误差均小于OMP重建的误差。图 8是采用4种方法对不同缺失率的地震数据插值后的信噪比曲线, 可以看出, 在缺失10%~50%地震数据的情况下, 采用本文方法重建的效果比采用其它几种方法的效果好, 且有较强的鲁棒性。

|
图 8 采用4种方法对不同缺失率的地震数据插值后的信噪比曲线 |
图 9a为缺失50%的实际数据。选取100道数据, 采样点数为400个, 时间采样率为0.001s, 道间距为10m, 将缺失的实际数据作为训练样本, 得到的稀疏字典如图 9b所示。

|
图 9 实际数据(a)和相应的字典(b) |
分别采用curvelet稀疏基和OMP、curvelet稀疏基和ADMM、字典学习和OMP、字典学习和ADMM 4种方法对图 9a中缺失50%的实际数据进行重建, 其结果及对应的插值部分如图 10至图 13所示。这4种方法的耗时分别为4.15, 7.52, 182.07, 411.30s。其中ADMM中的正则化参数λ取1, 控制步长的参数τ取1, ADMM中的初始a, p, Λ设为0。
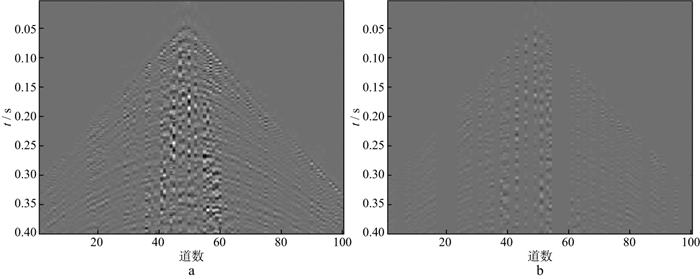
|
图 10 采用curvelet稀疏基和OMP重建实际数据的结果(a)及对应的插值部分(b) |
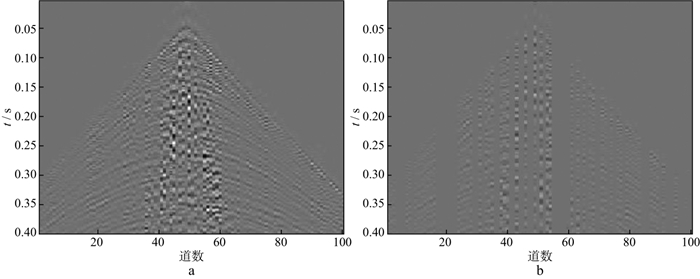
|
图 11 采用curvelet稀疏基和ADMM重建实际数据的结果(a)及对应的插值部分(b) |
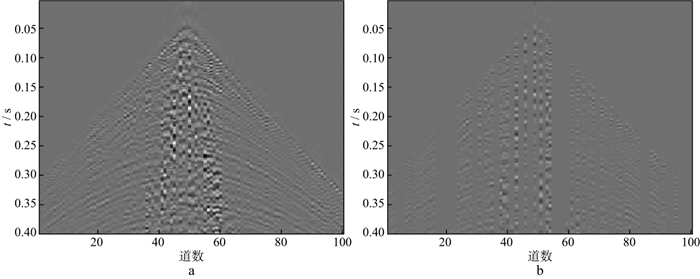
|
图 12 采用字典学习和OMP重建实际数据的结果(a)及对应的插值部分(b) |
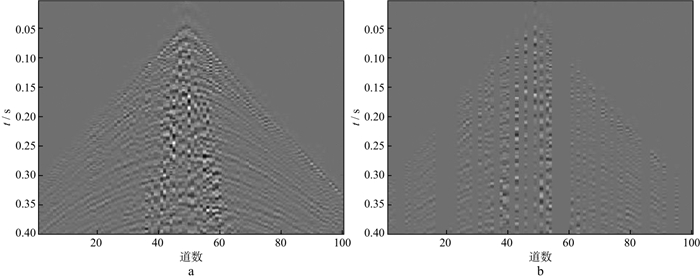
|
图 13 采用字典学习和ADMM重建实际数据的结果(a)及对应的插值部分(b) |
从图 10至图 13可以看出, 压缩感知理论下的固定基和字典学习方法都可以很好地重建实际地震数据, 其中, 采用字典学习比采用固定基的效果更好, 可以对一些细节部分进行较好的重建, 而压缩感知理论下重建算法中的ADMM的重建性能比OMP的重建性能更好, 无论是能量较强的同相轴还是能量较弱的细节部分都可以得到有效重建。
5 结论本文提出了一种压缩感知下基于K-SVD字典学习和ADMM的地震数据重建方法, 并建立了技术实现流程。正演模拟数据和实际地震资料测试结果表明, 本文方法与固定基地震数据插值方法以及字典学习中常用的OMP插值方法相比, 重建精度有很大提高。并且, 在地震数据缺失10%~50%时, 采用本文方法可以较好地对地震数据进行重建, 重建精度较高。但本文方法有耗时过长的缺陷, 当面临较大数据量的插值任务时, 这一缺陷会更大, 如何减少耗时、提高算法的运行效率是下一步的研究方向。
| [1] |
RONEN J. Wave equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984. DOI:10.1190/1.1442366 |
| [2] |
SPITZ S. Seismic trace interpolation in the f-x domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [3] |
ZWARTJES P, GISOLF A. Fourier reconstruction with sparse inversion[J]. Geophysical Prospecting, 2007, 55(2): 199-221. DOI:10.1111/gpr.2007.55.issue-2 |
| [4] |
王本锋, 陆文凯, 陈小宏, 等. 基于3D Curvelet变换的频率域高效地震数据插值方法研究[J]. 石油物探, 2018, 57(1): 65-71. WANG B F, LU W K, CHEN X H, et al. Efficient seismic data interpolation using three-dimensional Curvelet transform in the frequency domain[J]. Geophysical Prospectiong for Petroleum, 2018, 57(1): 65-71. |
| [5] |
周艳辉, 陈文超. 基于稀疏反演的同步震源地震数据分离方法[J]. 石油物探, 2018, 57(1): 33-38. ZHOU Y H, CHEN W C. Separation of simultaneous source data based on sparse inversion[J]. Geophysical Prospectiong for Petroleum, 2018, 57(1): 33-38. |
| [6] |
张良, 韩立国, 刘争光. 基于压缩感知和Contourlet变换的地震数据重建方法[J]. 石油物探, 2017, 56(6): 804-811. ZHANG L, HAN L G, LIU Z G. Seismic data reconstruction based on compressed sensing and Contourlet transform[J]. Geophysical Prospectiong for Petroleum, 2017, 56(6): 804-811. DOI:10.3969/j.issn.1000-1441.2017.06.005 |
| [7] |
ZHOU Y H, CHEN W C, GAO J H, et al. Seismic deblending by sparse inversion over dictionary learning[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg, 2013, 273-278. |
| [8] |
ZHOU Y H, CHEN W C, GAO J H, et al. Separation of seismic blended data by sparse inversion over dictionary learning[J]. Journal of Applied Geophysics, 2014, 106(1): 146-153. |
| [9] |
周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J]. 石油地球物理勘探, 2014, 49(4): 652-662. ZHOU Y T, WANG L L, PU Q S. K-SVD and Dictionary learning of seismic data recovery based on compressed sensing[J]. Oil Geophysical Prospecting, 2014, 49(4): 652-662. |
| [10] |
CANDÈS E J, ROMBERG J, TAO T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [11] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [12] |
HERRMANN F J, HENNENFENT G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. DOI:10.1111/gji.2008.173.issue-1 |
| [13] |
ZHANG H, CHEN X H, WU X M. Seismic data reconstruction based on CS and Fourier theory[J]. Applied Geophysics, 2013, 10(2): 170-180. DOI:10.1007/s11770-013-0375-3 |
| [14] |
LIANG J, MA J, ZHANG X. Seismic data restoration via data-driven tight frame[J]. Geophysics, 2014, 79(3): V65-V74. DOI:10.1190/geo2013-0252.1 |
| [15] |
马继涛, 王建花, 刘国昌. 基于频率域奇异值分解的地震数据插值去噪方法研究[J]. 石油物探, 2016, 55(2): 205-213. MA J T, WANG J H, LIU G C. Seismic data noise attenuation and interpolation using singular value decomposition in frequency domain[J]. Geophysical Prospectiong for Petroleum, 2016, 55(2): 205-213. DOI:10.3969/j.issn.1000-1441.2016.02.006 |
| [16] |
ZHU L, LIU E, MCCLELLAN J H. Seismic data denoising through multiscale and sparsity-promoting dictionary learning[J]. Geophysics, 2015, 80(6): WD45-WD57. DOI:10.1190/geo2015-0047.1 |
| [17] |
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1-122. |
| [18] |
STERNFELS R, VIGUIER G, GONDOIN R, et al. Multidimensional simultaneous random plus erratic noise attenuation and interpolation for seismic data by joint low-rank and sparse inversion[J]. Geophysics, 2015, 80(6): WD129-WD141. DOI:10.1190/geo2015-0066.1 |
| [19] |
HARIKUMAR K, ATHIRA S, NAIR Y C, et al.ADMM based algorithm for spike and smooth signal separation using over-complete dictionary[C]//Communications and Signal Processing (ICCSP).2015 International Conference on Communications and Signal Processing (ICCSP).India: Melmaruvathur, 2015: 1617-1622
|
| [20] |
ZHOU Y, GAO J, CHEN W, et al. Seismic simultaneous source separation via patchwise sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5271-5284. DOI:10.1109/TGRS.2016.2559514 |
| [21] |
BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. DOI:10.1109/MSP.2007.4286571 |
| [22] |
GLEICHMAN S, ELDAR Y C. Blind compressed sensing[J]. IEEE Transactions on Information Theory, 2011, 57(10): 6958-6975. DOI:10.1109/TIT.2011.2165821 |
| [23] |
AHARON M, ELAD M, BRUCKSTEIN A. K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |



