2. 中海油研究总院有限责任公司, 北京 100028
2. CNOOC Research Institute Co.Ltd., Beijing 100028, China
实际地下介质中充满流体、裂缝与裂隙, 会同时表现出各向异性与粘弹性特征, 对地震波的振幅和相位造成影响, 因此, 在进行地震波场数值模拟时, 这种粘滞性特征不能忽视。粘弹各向异性现象在实验室与波场测量中得到了证实[1]。
对于粘弹各向异性介质, 国内外学者进行了大量的研究。CARCIONE[2-3]基于广义标准线性固体(GSLS)模型, 建立了线性粘弹性各向异性本构关系及相应的波动方程, 为后续在粘弹性各向异性介质中的应用进行了大量的研究[4-7]。受制于实际计算和存储能力, 地震数值模拟通常仅能在有限空间进行, 因此, 需要在计算区域周围增加人工边界条件以降低边界反射干扰。完全匹配层(PML)吸收边界条件是一种典型的人工边界条件, 由于其稳健和高效的吸收特性而被广泛使用[8-12]。它由BERENGER[13]于1994年提出, 之后许多学者在其基础上加以改进, 使其变得更加高效。其中最具代表性的是RODEN等[14]提出的卷积完全匹配层(CPML)吸收边界条件, 由于增加了额外的控制参数(α), 其对低频反射与掠射波有较好的吸收效果。随后, 许多学者将CPML吸收边界条件应用到一阶速度-应力方程的数值模拟中, 并取得了较满意的效果[15-18]。LI等[19]在CPML吸收边界条件中引入了辅助记忆变量, 避免了卷积操作并将其成功应用到二阶波动方程数值模拟中。WANG等[20]使用CPML吸收边界条件对分数时间导数的粘声波方程进行了数值模拟。然而, 传统的PML吸收边界条件在大炮检距掠射情况下吸收效果不理想, 对于某些介质存在不稳定性[21], 而CPML吸收边界条件在复杂介质构造情况下, 对低频反射的吸收效果不佳, 干扰了有效波。另一类人工边界条件是随机介质层(RML)边界条件。RML最早由CLAPP[22]提出, 随后有学者将其应用于逆时偏移中[23-24], 方法是在边界区域设置随机介质, 使得波场传播到边界区域时发生不相干散射, 削弱边界反射的能量, 达到减少人工边界反射干扰的目的。
有许多不同的网格被应用于有限差分正演模拟中[25-27]。其中最为经典并应用最广泛的是标准交错网格(stand-staggered-grid, SSG)。SSG由MADARIAGA[28]在研究断层破碎时所提出, 随后被广泛应用于有限差分数值模拟中[29-31]。交错网格是将弹性参数定义在整网格点或半网格点上, 对于包含多参数模型的数值模拟, 在计算某些量的空间导数时, 存在所需模型参数在相应空间节点没有定义的问题, 需要对模型空间进行插值或近似处理。这些模型空间的处理会引入计算误差, 在模型参数变化较为剧烈区域甚至会出现数值计算不稳定现象。为了解决SSG在多参数模型数值模拟中存在的问题, SAENGER等[32-33]提出了旋转交错网格(rotated-staggered-grid, RSG)算法, 因其将弹性参数定义在整网格点或网格中心上, 在计算空间导数时无需进行插值处理, 从而避免了插值处理带来的计算误差, 提高了数值模拟的精度。此外, 由于RSG是利用网格对角线上的信息来求解空间导数, 因此比SSG更加稳定, 得到的数值解更加可靠。由于RSG具有较好的稳定性, 被众多学者应用于各种复杂介质的数值模拟中[34-36]。
本文在前人研究的基础上, 采用基于GSLS模型的粘弹TTI介质波动方程进行数值模拟。在边界处理上, 利用随机边界的散射特点进一步改善CPML吸收边界条件的吸收能力, 提出将CPML吸收边界条件与RML边界条件相结合的策略, 并推导出相应的旋转交错网格有限差分格式, 利用均匀介质模型及复杂介质Hess模型对组合边界条件的正确性及有效性进行了测试及对比分析。
1 理论与方法 1.1 粘弹TTI介质波动方程根据CARCIONE[2-3]基于GSLS模型建立的线性粘弹性各向异性理论, 可得到粘弹TTI介质波动方程。
应力-应变关系:
| $ \mathit{\boldsymbol{\dot \sigma }} = \mathit{\boldsymbol{\psi }} \cdot \mathit{\boldsymbol{\varepsilon }} + {\mathit{\boldsymbol{e}}_0} $ | (1) |
式中:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_0} = \left[ {K{e_{zz}} + 2G{e_{xx}},K{e_{zz}} + 2G{e_{yy}},K{e_{zz}} - } \right.}\\ {{{\left. {2G\left( {{e_{xx}} + {e_{yy}}} \right),{c_{44}}{e_{yz}},{c_{55}}{e_{xz}},{c_{66}}{e_{xy}}} \right]}^{\rm{T}}}} \end{array} $ | (2) |
其中, K为广义非压缩模量, G为广义刚性模量, cij为弹性系数, eij为记忆变量分量。
记忆变量方程为:
| $ \mathit{\boldsymbol{\dot e}} = {\varphi _v}\left( 0 \right) \cdot {\mathit{\boldsymbol{\varepsilon }}_0} - \frac{\mathit{\boldsymbol{e}}}{{\tau _\sigma ^{\left( v \right)}}} $ | (3) |
式中:
| $ \tau _\sigma ^{\left( v \right)} = \frac{1}{{{Q_v}{f_0}}}\left( {\sqrt {Q_v^2 + 1} - 1} \right) $ | (4a) |
| $ \tau _\varepsilon ^{\left( v \right)} = \frac{1}{{{Q_v}{f_0}}}\left( {\sqrt {Q_v^2 + 1} + 1} \right) $ | (4b) |
式中:Qv(v=1, 2)分别为纵、横波品质因子; f0为地震子波主频。
| $ {\mathit{\boldsymbol{\varepsilon }}_0} = {\left( {{\varepsilon _{xx}} - \mathit{\Theta },{\varepsilon _{yy}} - \mathit{\Theta },3\mathit{\Theta },{\gamma _{yz}},{\gamma _{xz}},{\gamma _{xy}}} \right)^{\rm{T}}} $ | (5) |
其中,
| $ \mathit{\Theta } = \left( {{\varepsilon _{xx}} + {\varepsilon _{yy}} + {\varepsilon _{zz}}} \right)/3 $ |
速度与应力关系可用动量守恒方程表示:
| $ \rho \mathit{\boldsymbol{\dot U}} = \mathit{\boldsymbol{L\sigma }} + \rho \mathit{\boldsymbol{F}} $ | (6) |
式中:
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}}&0&0&0&{\frac{\partial }{{\partial z}}}&{\frac{\partial }{{\partial y}}}\\ 0&{\frac{\partial }{{\partial y}}}&0&{\frac{\partial }{{\partial z}}}&0&{\frac{\partial }{{\partial x}}}\\ 0&0&{\frac{\partial }{{\partial z}}}&{\frac{\partial }{{\partial y}}}&{\frac{\partial }{{\partial x}}}&0 \end{array}} \right] $ | (7) |
本文考虑二维情况, 在复数伸展坐标下, (6)式可以写成如下形式[38]:
| $ \left\{ \begin{array}{l} {\rm{i}}\omega \rho {{\tilde v}_x} = \frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial \tilde x}} + \frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial \tilde z}}\\ {\rm{i}}\omega \rho {{\tilde v}_z} = \frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial \tilde x}} + \frac{{\partial {{\tilde \sigma }_{zz}}}}{{\partial \tilde z}} \end{array} \right. $ | (8) |
式中:ω为角频率;
此处, 定义复数坐标
| $ \left\{ \begin{array}{l} \tilde x\left( x \right) = x - \frac{{\rm{i}}}{\omega }\int_0^x {{d_x}\left( s \right){\rm{d}}s} \\ \tilde z\left( z \right) = z - \frac{{\rm{i}}}{\omega }\int_0^z {{d_z}\left( s \right){\rm{d}}s} \end{array} \right. $ | (9) |
式中:x, z和
对(9)式求偏导, 有:
| $ \left\{ \begin{array}{l} {\partial _{\tilde x}} = \frac{{{\rm{i}}\omega }}{{{\rm{i}}\omega + {d_x}}}{\partial _x} = \frac{1}{{{s_x}}}{\partial _x}\\ {\partial _{\tilde z}} = \frac{{{\rm{i}}\omega }}{{{\rm{i}}\omega + {d_z}}}{\partial _z} = \frac{1}{{{s_z}}}{\partial _z} \end{array} \right. $ | (10) |
式中:sx, sz为复频伸展函数。
| $ \left\{ \begin{array}{l} {s_x} = \frac{{{\rm{i}}\omega + {d_x}}}{{{\rm{i}}\omega }} = 1 + \frac{{{d_x}}}{{{\rm{i}}\omega }}\\ {s_z} = \frac{{{\rm{i}}\omega + {d_z}}}{{{\rm{i}}\omega }} = 1 + \frac{{{d_z}}}{{{\rm{i}}\omega }} \end{array} \right. $ | (11) |
将(10)式与(11)式代入(8)式, 并在x, z方向分裂有:
| $ \left\{ \begin{array}{l} {\rm{i}}\omega \rho \tilde v_x^x = \frac{1}{{{s_x}}}\frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial x}} = \frac{{{\rm{i}}\omega }}{{{\rm{i}}\omega + {d_x}}}\frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial x}}\\ {\rm{i}}\omega \rho \tilde v_x^z = \frac{1}{{{s_z}}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial z}} = \frac{{{\rm{i}}\omega }}{{{\rm{i}}\omega + {d_z}}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial z}} \end{array} \right. $ | (12a) |
| $ \left\{ \begin{array}{l} {\rm{i}}\omega \rho \tilde v_z^x = \frac{1}{{{s_x}}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial x}} = \frac{{{\rm{i}}\omega }}{{{\rm{i}}\omega + {d_x}}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial x}}\\ {\rm{i}}\omega \rho \tilde v_z^z = \frac{1}{{{s_z}}}\frac{{\partial {{\tilde \sigma }_{zz}}}}{{\partial z}} = \frac{{{\rm{i}}\omega }}{{{\rm{i}}\omega + {d_z}}}\frac{{\partial {{\tilde \sigma }_{zz}}}}{{\partial z}} \end{array} \right. $ | (12b) |
(12) 式满足
将(12)式变换到时间域便可得到SPML吸收边界条件[18], 即
| $ \left\{ \begin{array}{l} \rho \frac{{\partial v_x^x}}{{\partial t}} + {d_x}v_x^x = \frac{{\partial {\sigma _{xx}}}}{{\partial x}}\\ \rho \frac{{\partial v_x^z}}{{\partial t}} + {d_z}v_x^z = \frac{{\partial {\sigma _{xz}}}}{{\partial z}} \end{array} \right. $ | (13a) |
| $ \left\{ \begin{array}{l} \rho \frac{{\partial v_z^x}}{{\partial t}} + {d_x}v_z^x = \frac{{\partial {\sigma _{xz}}}}{{\partial x}}\\ \rho \frac{{\partial v_z^z}}{{\partial t}} + {d_z}v_z^z = \frac{{\partial {\sigma _{zz}}}}{{\partial z}} \end{array} \right. $ | (13b) |
(13) 式满足
以(6)式为例(忽略外力), 推导出适用于粘弹TTI介质的二维CPML吸收边界条件。对于CPML吸收边界条件, 引入了两个额外的衰减参数κ和α, 使得新的复频伸展函数变为:
| $ \left\{ \begin{array}{l} {s_x} = {\kappa _x} + \frac{{{d_x}}}{{{\alpha _x} + {\rm{i}}\omega }}\\ {s_z} = {\kappa _z} + \frac{{{d_z}}}{{{\alpha _z} + {\rm{i}}\omega }} \end{array} \right. $ | (14) |
式中:κi, αi为辅助衰减系数, 且κi和αi满足κi≥1, αi≥0, i=x, z。
整理(14)式得到:
| $ \left\{ \begin{array}{l} \frac{1}{{{s_x}}} = \frac{1}{{{\kappa _x}}} - \frac{{{d_x}}}{{\kappa _x^2\left[ {{\rm{i}}\omega + \left( {{\alpha _x} + \frac{{{d_x}}}{{{\kappa _x}}}} \right)} \right]}}\\ \frac{1}{{{s_z}}} = \frac{1}{{{\kappa _z}}} - \frac{{{d_z}}}{{\kappa _x^2\left[ {{\rm{i}}\omega + \left( {{\alpha _z} + \frac{{{d_z}}}{{{\kappa _z}}}} \right)} \right]}} \end{array} \right. $ | (15) |
将(10)式与(15)式代入(8)式中的第1个方程(以第1个方程为例, 后面类似)有:
| $ \begin{array}{l} {\rm{i}}\omega \rho {{\tilde v}_x} = \frac{1}{{{\kappa _x}}}\frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial x}} - \frac{{{d_x}}}{{\kappa _x^2\left[ {{\rm{i}}\omega + \left( {{\sigma _x} + \frac{{{d_x}}}{{{\kappa _x}}}} \right)} \right]}}\frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial x}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{\kappa _z}}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial z}} - \frac{{{d_z}}}{{\kappa _z^2\left[ {{\rm{i}}\omega + \left( {{\sigma _z} + \frac{{{d_z}}}{{{\kappa _z}}}} \right)} \right]}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial z}} \end{array} $ | (16) |
令
| $ \left\{ \begin{array}{l} {{\tilde T}_{xx}} = - \frac{{{d_x}}}{{\kappa _x^2\left[ {{\rm{i}}\omega + \left( {{\alpha _x} + \frac{{{d_x}}}{{{\kappa _x}}}} \right)} \right]}}\frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial x}}\\ {{\tilde T}_{xz}} = - \frac{{{d_z}}}{{\kappa _z^2\left[ {{\rm{i}}\omega + \left( {{\alpha _z} + \frac{{{d_z}}}{{{\kappa _z}}}} \right)} \right]}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial z}} \end{array} \right. $ | (17) |
则(16)式可写成:
| $ {\rm{i}}\omega \rho {{\tilde v}_x} = \frac{1}{{{\kappa _x}}}\frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial x}} + {{\tilde T}_{xx}} + \frac{1}{{{\kappa _z}}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial z}} + {{\tilde T}_{xz}} $ | (18) |
整理(17)式得到:
| $ \left\{ \begin{array}{l} {\rm{i}}\omega {{\tilde T}_{xx}} + \left( {{\alpha _x} + \frac{{{d_x}}}{{{\kappa _x}}}} \right){{\tilde T}_{xx}} = - \frac{{{d_x}}}{{\kappa _x^2}}\frac{{\partial {{\tilde \sigma }_{xx}}}}{{\partial x}}\\ {\rm{i}}\omega {{\tilde T}_{xz}} + \left( {{\alpha _z} + \frac{{{d_z}}}{{{\kappa _z}}}} \right){{\tilde T}_{xz}} = - \frac{{{d_z}}}{{\kappa _z^2}}\frac{{\partial {{\tilde \sigma }_{xz}}}}{{\partial z}} \end{array} \right. $ | (19) |
将(19)式变换到时间域, 有:
| $ \left\{ \begin{array}{l} \frac{{\partial {Y_{xx}}}}{{\partial t}} + \left( {{\alpha _x} + \frac{{{d_x}}}{{{\kappa _x}}}} \right){T_{xx}} = - \frac{{{d_x}}}{{\kappa _x^2}}\frac{{\partial {\sigma _{xx}}}}{{\partial x}}\\ \frac{{\partial {Y_{xz}}}}{{\partial t}} + \left( {{\alpha _z} + \frac{{{d_z}}}{{{\kappa _z}}}} \right){T_{xz}} = - \frac{{{d_z}}}{{\kappa _z^2}}\frac{{\partial {\sigma _{xz}}}}{{\partial z}} \end{array} \right. $ | (20) |
不失一般性地, 对于方程
| $ \frac{{\partial f}}{{\partial t}} + Af = B $ | (21) |
其通解为:
| $ f = - \frac{1}{A}{e^{ - At}} + \frac{B}{A} $ | (22) |
(22) 式在时间域离散形式下有:
| $ \left\{ \begin{array}{l} f\left[ {\left( {n + 1} \right)\Delta t} \right] = - \frac{1}{A}{{\rm{e}}^{ - A\left( {n + 1} \right)\Delta t}} + \frac{B}{A}\\ f\left[ {n\Delta t} \right] = - \frac{1}{A}{{\rm{e}}^{ - An\Delta t}} + \frac{B}{A} \end{array} \right. $ | (23) |
即有:
| $ f\left[ {\left( {n + 1} \right)\Delta t} \right] = {{\rm{e}}^{ - A\Delta t}}f\left[ {n\Delta t} \right] + \frac{B}{A}\left( {1 - {{\rm{e}}^{ - A\Delta t}}} \right) $ | (24) |
对比(22)式, (18)式的解为:
| $ \left\{ \begin{array}{l} T_{xx}^{n + 1} = {b_x}T_{xx}^n + {a_x}\frac{{\partial \sigma _{xx}^{n + \frac{1}{2}}}}{{\partial x}}\\ T_{xz}^{n + 1} = {b_z}T_{xz}^n + {a_z}\frac{{\partial \sigma _{xz}^{n + \frac{1}{2}}}}{{\partial z}} \end{array} \right. $ | (25) |
式中:
| $ \begin{array}{l} \left\{ \begin{array}{l} {b_i} = \exp \left[ { - \left( {{\alpha _i} + \frac{{{d_i}}}{{{\kappa _i}}}} \right)\Delta t} \right]\\ {a_i} = \frac{{{d_i}}}{{{\kappa _i}\left( {{d_i} + {\kappa _i}{\alpha _i}} \right)}}\left( {{b_i} - 1} \right) \end{array} \right.\\ \;\;\;i = x,z \end{array} $ | (26) |
则(18)式在时间域的形式为:
| $ \frac{{\partial {v_x}}}{{\partial x}} = \frac{1}{{{\kappa _x}}}\frac{{\partial {\sigma _{xx}}}}{{\partial x}} + {T_{xx}} + \frac{1}{{{\kappa _z}}}\frac{{\partial {\sigma _{xz}}}}{{\partial z}} + {T_{xz}} $ | (27) |
式中:Txx, Txz可采用(25)式迭代求解得到。对比(6)式中vx分量项与(27)式可以发现, 只需将
一般而言, 对于单一随机边界条件, 由于随机边界区域填充的为随机介质, 可被认为由一个个散射点组成, 当波场传播到该区域时, 波场发生随机散射形成非相干能量, 从而达到减少人工边界反射的目的。然而, 由于散射方向是任意的, 因此, 还是有部分较强的能量会被散射到有效物理计算区域, 从而污染了原有的地震波场; 另一方面, 在某些大角度入射的情况下, CPML吸收边界条件对低频反射及掠射波的吸收能力有限, 可采用随机介质将其能量散射。因此, 本文利用随机介质层(RML)边界的散射特点, 提出CPML吸收边界条件与RML边界条件相组合的策略, 进一步提升边界的吸收效果。
图 1为CPML-RML组合边界示意图。其中, 随机边界区域填充的随机介质可采用随机介质建模得到。在具体实施过程中, 根据随机介质建模理论公式, 给定自相关长度(分散程度)、相关半径、方向角度和方差等随机介质建模参数, 然后将计算区域的弹性参数取均值作为随机边界区域弹性参数的背景值, 最后采用随机介质建模程序得到随机弹性参数, 并将其赋值在随机边界区域的每个网格点处, 其中随机边界区域的弹性参数满足其均值为背景值, 方差为给定的方差。因此, 当波场传播到边界时, 首先会进入CPML边界区域进行吸收衰减, 然后会进入随机边界区域, 能量会被散射, 使得最终的人工边界反射被极大地衰减, 从而达到非常好的吸收效果。

|
图 1 CPML-RML组合边界示意图解 |
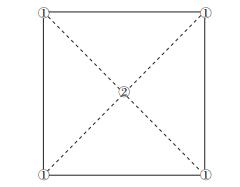
旋转交错网格(RSG)的基本思想是将弹性参数定义在整网格点或网格中心点上, 如图 2所示。
|
图 2 旋转交错网格示意图解 |
在网格点①处存放vi、ρ, 在网格点②处存放σij、eij、cij, 然后在对角线方向上计算相应量的空间导数, 此过程中避免了插值操作, 使得编程实现更简单, 正演模拟的精度和稳定性更高。其计算公式为:
| $ \begin{array}{l} {L_x}\left( {u_{i,j}^n} \right) = \frac{1}{{2\Delta x}}\left\{ {\sum\limits_{m = 1}^N {{c_m}\left[ {u_{i + \left( {2m - 1} \right)/2,j + \left( {2m - 1} \right)/2}^n - } \right.} } \right.\\ \;\;\left. {u_{i - \left( {2m - 1} \right)/2,j - \left( {2m - 1} \right)/2}^n} \right] + \sum\limits_{m = 1}^N {{c_m}\left[ {u_{i + \left( {2m - 1} \right)/2,j - \left( {2m - 1} \right)/2}^n - } \right.} \\ \;\;\left. {\left. {u_{i - \left( {2m - 1} \right)/2,j + \left( {2m - 1} \right)/2}^n} \right]} \right\} \end{array} $ | (28a) |
| $ \begin{array}{l} {L_z}\left( {u_{i,j}^n} \right) = \frac{1}{{2\Delta z}}\left\{ {\sum\limits_{m = 1}^N {{c_m}\left[ {u_{i + \left( {2m - 1} \right)/2,j + \left( {2m - 1} \right)/2}^n - } \right.} } \right.\\ \;\;\left. {u_{i - \left( {2m - 1} \right)/2,j - \left( {2m - 1} \right)/2}^n} \right] + \sum\limits_{m = 1}^N {{c_m}\left[ {u_{i + \left( {2m - 1} \right)/2,j - \left( {2m - 1} \right)/2}^n - } \right.} \\ \;\;\left. {\left. {u_{i - \left( {2m - 1} \right)/2,j + \left( {2m - 1} \right)/2}^n} \right]} \right\} \end{array} $ | (28b) |
式中:i, j, n分别为x, z, t方向样点序号; u为速度波场或应力波场; Lx, Lz分别为x, z方向上的微分算子; Δx, Δz分别为x, z方向上的空间离散步长; N为差分阶数的1/2;m为差分阶数序号; cm为差分系数, 可采用Taylor展开推导得到。
二维情况下的粘弹TTI介质波动方程CPML吸收边界条件旋转交错网格有限差分格式为:
| $ \begin{array}{l} v\left( x \right)_{i,j}^{n + 1} = v\left( x \right)_{i,j}^n + \frac{{\Delta t}}{\rho }\left\{ {\frac{1}{{{\kappa _x}}}{L_x}\left[ {\sigma \left( {xx} \right)_{i,j}^{n + 1/2}} \right] + } \right.\\ \;\;\;\;\;\;\left. {T_{xx}^{n + 1} + \frac{1}{{{\kappa _z}}}{L_z}\left[ {\sigma \left( {xz} \right)_{i,j}^{n + 1/2}} \right] + T_{xz}^{n + 1}} \right\} \end{array} $ | (29a) |
| $ \begin{array}{l} v\left( z \right)_{i,j}^{n + 1} = v\left( z \right)_{i,j}^n + \frac{{\Delta t}}{\rho }\left\{ {\frac{1}{{{\kappa _x}}}{L_x}\left[ {\sigma \left( {xz} \right)_{i,j}^{n + 1/2}} \right] + } \right.\\ \;\;\;\;\;\;\left. {T_{xz}^{n + 1} + \frac{1}{{{\kappa _z}}}{L_z}\left[ {\sigma \left( {zz} \right)_{i,j}^{n + 1/2}} \right] + T_{zz}^{n + 1}} \right\} \end{array} $ | (29b) |
| $ \begin{array}{l} \sigma \left( {xx} \right)_{i + 1/2,j + 1/2}^{n + 1/2} = \sigma \left( {xx} \right)_{i + 1/2,j + 1/2}^{n - 1/2} + \Delta t\left\{ {\frac{{{c_{11}}}}{{{\kappa _x}}}{L_x} \cdot } \right.\\ \;\;\;\;\;\;\;\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + T_{xx}^{n + 1/2} + \frac{{{c_{13}}}}{{{\kappa _z}}}{L_z} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zz}^{n + 1/2} + \frac{{{c_{15}}}}{{{\kappa _z}}}{L_z} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + T_{xz}^{n + 1/2} + \frac{{{c_{15}}}}{{{\kappa _x}}}{L_x} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zx}^{n + 1/2} + k\left[ {e\left( {xx} \right)_{i + 1/2,j + 1/2}^{n + 1/2} + } \right.\\ \;\;\;\;\;\;\;\left. {e\left( {xx} \right)_{i + 1/2,j + 1/2}^{n - 1/2}} \right]/2 + 2{c_{55}}\left[ {e\left( {zz} \right)_{i + 1/2,j + 1/2}^{n + 1/2} + } \right.\\ \left. {\;\;\;\;\;\;\;\left. {e\left( {zz} \right)_{i + 1/2,j + 1/2}^{n - 1/2}} \right]/2} \right\} \end{array} $ | (30a) |
| $ \begin{array}{l} \sigma \left( {zz} \right)_{i + 1/2,j + 1/2}^{n + 1/2} = \sigma \left( {zz} \right)_{i + 1/2,j + 1/2}^{n - 1/2} + \Delta t\left\{ {\frac{{{c_{13}}}}{{{\kappa _x}}}{L_x} \cdot } \right.\\ \;\;\;\;\;\;\;\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + T_{xx}^{n + 1/2} + \frac{{{c_{33}}}}{{{\kappa _z}}}{L_z} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zz}^{n + 1/2} + \frac{{{c_{35}}}}{{{\kappa _z}}}{L_z} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + T_{xz}^{n + 1/2} + \frac{{{c_{35}}}}{{{\kappa _x}}}{L_x} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zx}^{n + 1/2} + k\left[ {e\left( {xx} \right)_{i + 1/2,j + 1/2}^{n + 1/2} + } \right.\\ \;\;\;\;\;\;\;\left. {e\left( {xx} \right)_{i + 1/2,j + 1/2}^{n - 1/2}} \right]/2 - 2{c_{55}}\left[ {e\left( {zz} \right)_{i + 1/2,j + 1/2}^{n + 1/2} + } \right.\\ \left. {\;\;\;\;\;\;\;\left. {e\left( {zz} \right)_{i + 1/2,j + 1/2}^{n - 1/2}} \right]/2} \right\} \end{array} $ | (30b) |
| $ \begin{array}{l} \sigma \left( {xz} \right)_{i + 1/2,j + 1/2}^{n + 1/2} = \sigma \left( {xz} \right)_{i + 1/2,j + 1/2}^{n - 1/2} + \Delta t\left\{ {\frac{{{c_{15}}}}{{{\kappa _x}}}{L_x} \cdot } \right.\\ \;\;\;\;\;\;\;\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + T_{xx}^{n + 1/2} + \frac{{{c_{35}}}}{{{\kappa _z}}}{L_z} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zz}^{n + 1/2} + \frac{{{c_{55}}}}{{{\kappa _z}}}{L_z} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + T_{xz}^{n + 1/2} + \frac{{{c_{55}}}}{{{\kappa _x}}}{L_x} \cdot \\ \;\;\;\;\;\;\;\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zx}^{n + 1/2} + {c_{55}}\left[ {e\left( {xz} \right)_{i + 1/2,j + 1/2}^{n + 1/2} + } \right.\\ \;\;\;\;\;\;\;\left. {\left. {e\left( {xz} \right)_{i + 1/2,j + 1/2}^{n - 1/2}} \right]/2} \right\} \end{array} $ | (30c) |
| $ \begin{array}{l} e\left( {xx} \right)_{i + 1/2,j + 1/2}^{n + 1/2} = \frac{{2\tau _\varepsilon ^{\left( 1 \right)} - \Delta t}}{{2\tau _\varepsilon ^{\left( 1 \right)} + \Delta t}}e\left( {xx} \right)_{i + 1/2,j + 1/2}^{n - 1/2} + \\ \;\;\;\;\;\frac{{2\tau _\varepsilon ^{\left( 1 \right)}}}{{2\tau _\varepsilon ^{\left( 1 \right)} + \Delta t}}\left[ {\frac{{\tau _\varepsilon ^{\left( 1 \right)}}}{{\tau _\sigma ^{\left( 1 \right)}}} - 1} \right]\left\{ {\frac{1}{{{\kappa _x}}}{L_x}\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + } \right.\\ \;\;\;\;\;\left. {T_{xx}^{n + 1/2} + \frac{1}{{{\kappa _z}}}{L_z}\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zz}^{n + 1/2}} \right\} \end{array} $ | (31a) |
| $ \begin{array}{l} e\left( {zz} \right)_{i + 1/2,j + 1/2}^{n + 1/2} = \frac{{2\tau _\varepsilon ^{\left( 2 \right)} - \Delta t}}{{2\tau _\varepsilon ^{\left( 2 \right)} + \Delta t}}e\left( {zz} \right)_{i + 1/2,j + 1/2}^{n - 1/2} + \\ \;\;\;\;\;\frac{{2\tau _\varepsilon ^{\left( 2 \right)}}}{{2\tau _\varepsilon ^{\left( 2 \right)} + \Delta t}}\left[ {\frac{{\tau _\varepsilon ^{\left( 2 \right)}}}{{\tau _\sigma ^{\left( 2 \right)}}} - 1} \right]\left\{ {\frac{1}{{{\kappa _x}}}{L_x}\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + } \right.\\ \;\;\;\;\;\left. {T_{xx}^{n + 1/2} - \frac{1}{{{\kappa _z}}}{L_z}\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] - T_{zz}^{n + 1/2}} \right\} \end{array} $ | (31b) |
| $ \begin{array}{l} e\left( {xz} \right)_{i + 1/2,j + 1/2}^{n + 1/2} = \frac{{2\tau _\varepsilon ^{\left( 2 \right)} - \Delta t}}{{2\tau _\varepsilon ^{\left( 2 \right)} + \Delta t}}e\left( {xz} \right)_{i + 1/2,j + 1/2}^{n - 1/2} + \\ \;\;\;\;\;\frac{{2\tau _\varepsilon ^{\left( 2 \right)}}}{{2\tau _\varepsilon ^{\left( 1 \right)} + \Delta t}}\left[ {\frac{{\tau _\varepsilon ^{\left( 2 \right)}}}{{\tau _\sigma ^{\left( 2 \right)}}} - 1} \right]\left\{ {\frac{1}{{{\kappa _x}}}{L_x}\left[ {v\left( x \right)_{i + 1/2,j + 1/2}^n} \right] + } \right.\\ \;\;\;\;\;\left. {T_{xx}^{n + 1/2} + \frac{1}{{{\kappa _z}}}{L_z}\left[ {v\left( z \right)_{i + 1/2,j + 1/2}^n} \right] + T_{zz}^{n + 1/2}} \right\} \end{array} $ | (31c) |
| $ T_{ij}^{n + 1/2} = {b_j}T_{ij}^{n - 1/2} = {a_j}{L_j}\left[ {{u^n}} \right],\;\;\;\;i,j = x,z $ | (32) |
式中:u为速度波场或应力波场; Δt为时间步长。
2 数值模拟与分析 2.1 二维均匀介质模型为了对比SPML吸收边界条件、CPML吸收边界条件与CPML-RML组合边界条件的吸收效果, 本文设计了一个大小为2500m×500m的均匀介质模型, 网格间距为5m×5m, 时间步长为1ms, 总时间采样点数为2000, 共2s记录长度, 采用30Hz主频的雷克子波, 空间差分阶数为20阶, 边界层厚度为250m(对于组合边界, CPML和RML边界厚度各125m), 震源的位置为(750m, 150m), 接收排列范围为0~2500m, 排列深度为150m, 接收点间距为10m, 共251道接收, 其均匀介质弹性参数见表 1。
| 表 1 粘弹TTI均匀介质弹性参数 |
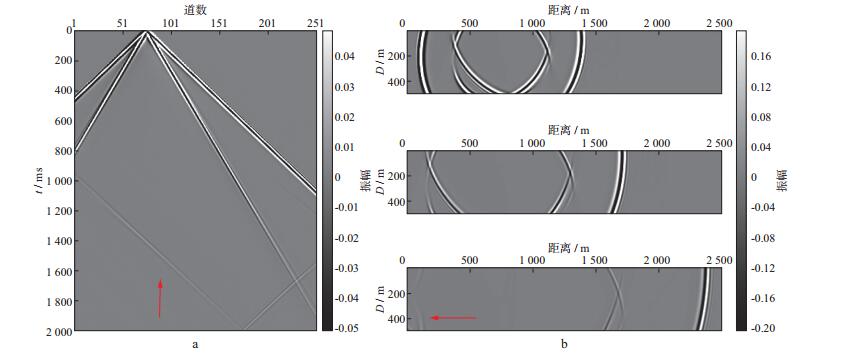
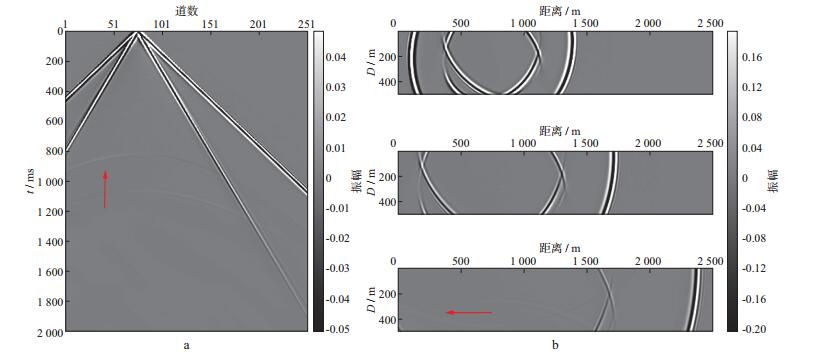
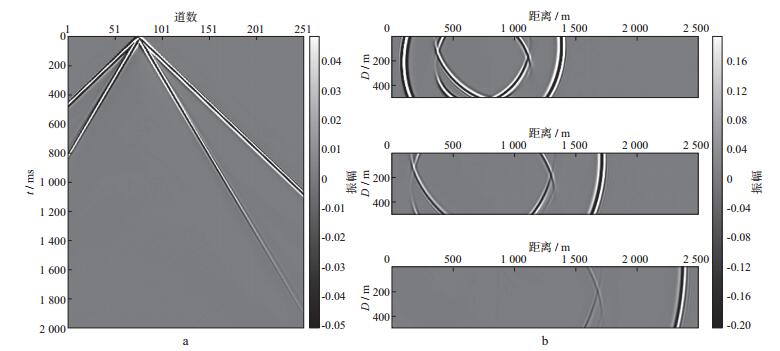
图 3、图 4和图 5分别给出了SPML吸收边界条件、CPML吸收边界条件和CPML-RML组合边界条件的x分量地震记录及波场快照。波场快照从上到下对应的时间依次为0.4s、0.6s和1.0s, 并且为了区分对比, 地震记录及波场快照均做了增益处理, 使其振幅处于同一水平范围, 即在制图过程中, 将所有数据的振幅统一限制在某一更低(相比于原始数据范围)的数值范围内(例如将所有波场快照数据的振幅限制在-0.2~0.2), 这样既能达到增益效果, 又能实现振幅对比。从图 3、图 4和图 5中可以看出, 在0.6s之前, 不论采用哪种边界条件, 其吸收效果均很好, 未看见明显的边界反射, 说明3种吸收边界条件在波场传播的前期均有好的吸收效果。但值得注意的是, 当波场传播到后期(1.0s), 即波场大角度入射到边界时, SPML吸收边界条件会出现如红色箭头所示的边界反射, 即SPML吸收边界条件不能很好地将大角度的边界反射吸收; 而CPML吸收边界条件会出现弱边界反射, 但其效果优于SPML吸收边界条件; CPML-RML组合边界条件从地震记录及波场快照上均未出现边界反射。说明与SPML吸收边界条件和CPML吸收边界条件相比, 本文提出的CPML-RML组合边界条件在吸收人工边界反射方面更加优越。
|
图 3 SPML吸收边界条件的x分量地震记录(a)与波场快照(b) |
|
图 4 CPML吸收边界条件的x分量地震记录(a)与波场快照(b) |
|
图 5 CPML-RML组合边界条件的x分量地震记录(a)与波场快照(b) |
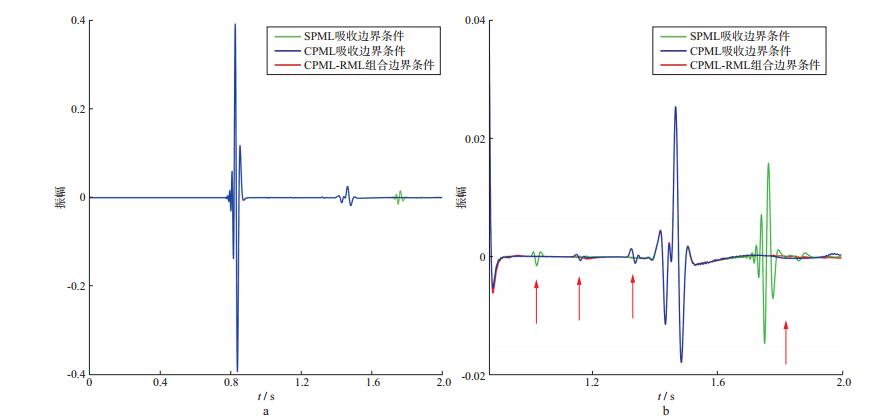
图 6对比了3种边界条件第211道的地震记录, 图 6b为图 6a部分区域的放大结果。从图 6可以看出, SPML吸收边界条件出现了较明显的边界反射, CPML吸收边界条件则出现了弱边界反射, 而CPML-RML组合边界条件未出现边界反射。
|
图 6 3种边界条件第211道地震记录对比 a显示时间范围为0~2.0s; b显示时间范围为0.865~2.000s |
不同边界条件的计算效率如表 2所示。表 2中的计算效率是在Win10系统、i5CPU(2.7GHz)、4G内存以及VS2013+IVF2013编程环境下得出的。从表 2中可以明显地看到, 粘弹TTI介质情形下, 与SPML吸收边界条件相比, CPML-RML组合边界的计算效率高出18.2%, 这是由于SPML吸收边界条件需要将方程进行分裂而导致的, 而CPML吸收边界条件与CPML-RML组合边界条件计算效率相当; 同样地, 由于粘弹性TTI介质方程比弹性TTI介质方程多了记忆变量方程, 因此, 在相同的边界条件下, 弹性TTI介质方程的计算效率比粘弹性TTI介质方程高49.1%, 但粘弹性TTI介质方程更能够反映地下真实介质情况; 另一方面, 各向同性介质的计算效率比弹性TTI介质的计算效率高6.3%。
| 表 2 不同边界条件的计算效率 |
因此, 随着介质复杂程度的提高, 计算效率随之降低, 但更加接近地下真实介质的情况。此外, 由于CPML吸收边界条件不需要对方程进行分裂, 因而其计算效率比SPML吸收边界条件高, 实现简单, 编程方便。由于CPML-RML组合边界条件的吸收效果优于CPML吸收边界条件, 因此更加适用于粘弹性介质方程的数值模拟。
2.2 二维复杂Hess模型为了说明CPML-RML组合边界条件对复杂介质的适应性及正确性, 采用二维Hess粘弹TTI介质模型进行测试。二维Hess模型大小为3000m×2500m, 网格间距为5m×5m, 时间步长为0.2ms, 总时间采样点数为12500, 2.5s记录长度, 采用30Hz主频的雷克子波, 空间差分阶数为20阶, 边界层厚度为300m(对于组合边界, CPML和RML边界厚度各150m), 震源位置为(2000m, 10m), 接收排列范围为0~3000m, 排列深度为0, 接收点间距为10m, 共301道接收。
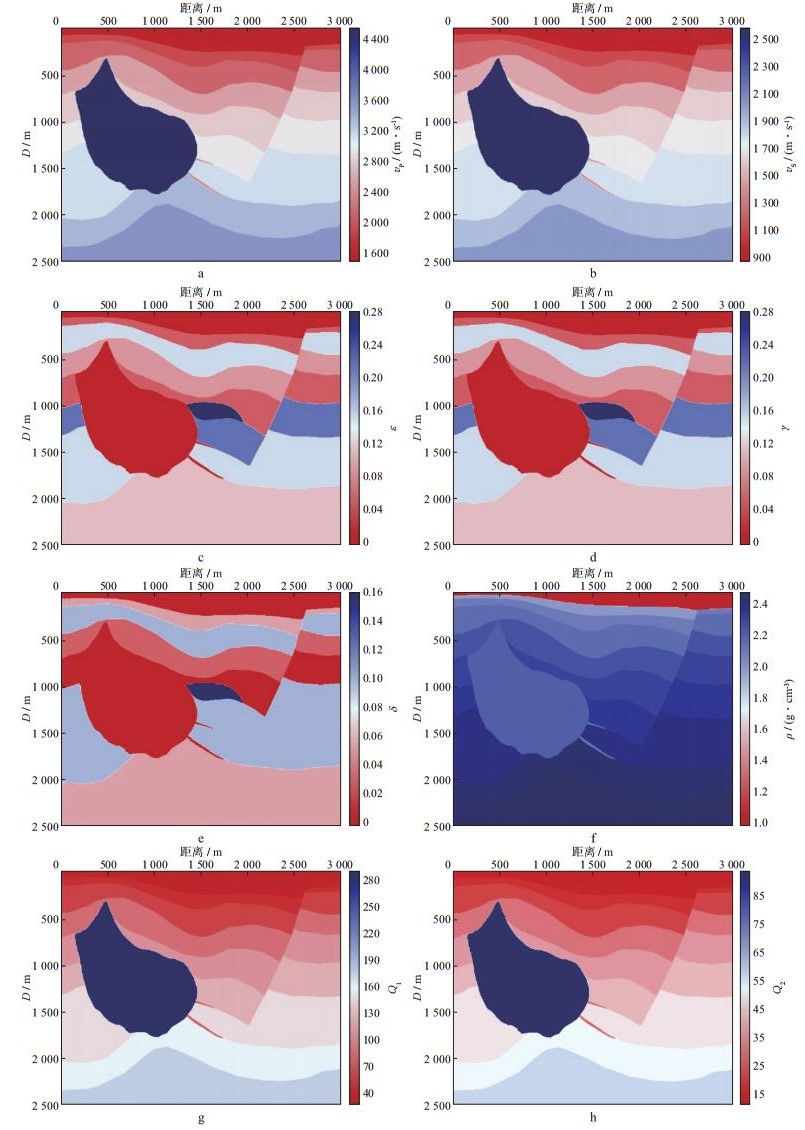
图 7显示的是二维Hess粘弹TTI介质模型参数, 由于SEG公开的二维Hess模型为VTI介质, 即只有vP, ε, δ, ρ, 为得到本文所需的粘弹TTI介质参数, 横波速度由经验公式vS=0.577vP得到, γ=ε, 纵、横波品质因子可由经验公式[39]
|
图 7 二维Hess粘弹TTI介质(θ=0, φ=60°)模型参数 a纵波速度vP; b横波速度vS; c纵波各向异性参数ε; d横波各向异性参数γ; e变异系数δ; f密度ρ; g纵波品质因子Q1; h横波品质因子Q2 |
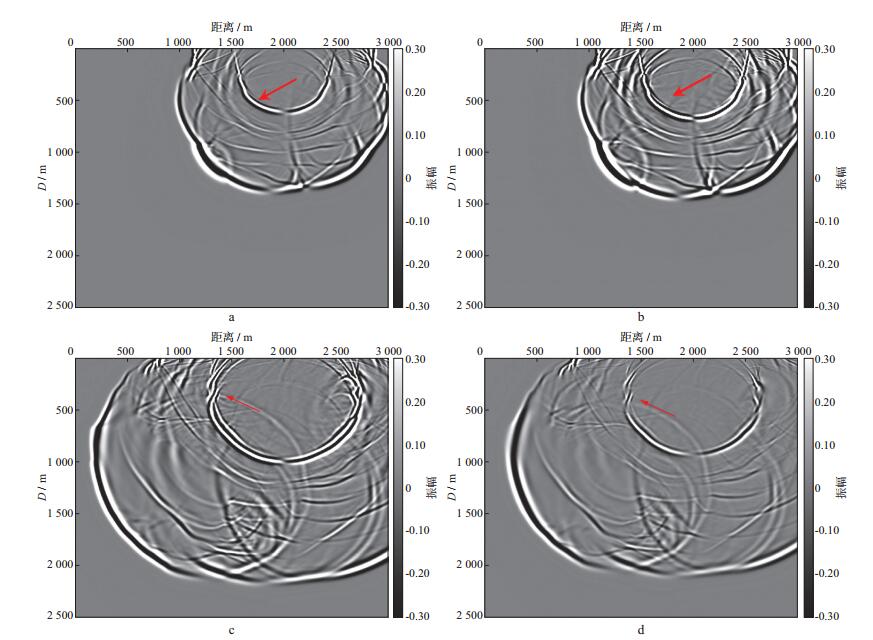
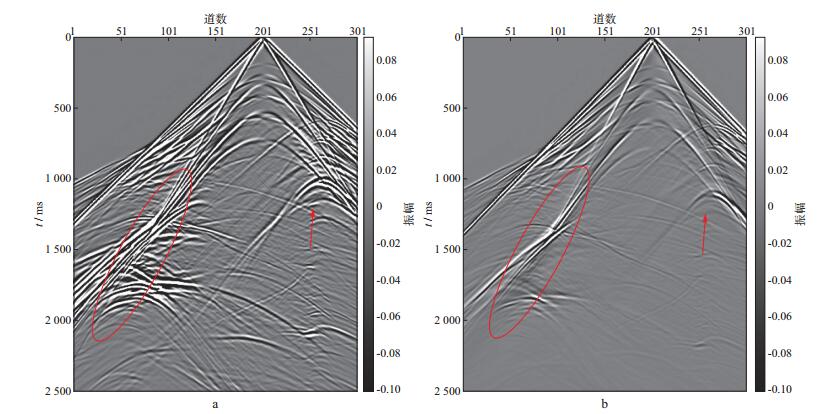
图 8给出了弹性TTI介质与粘弹TTI介质采用组合边界条件在0.6s与0.8s时刻的波场快照。波场快照上未出现边界反射, 说明本文提出的组合边界策略在复杂构造介质中的正确性及有效性; 同时, 也可以从波场快照中明显地看见弹性TTI介质与粘弹TTI介质在能量及旅行时上的差异, 表明粘弹介质存在振幅衰减及相位延迟。图 9给出了弹性TTI介质与粘弹性TTI介质采用组合边界条件得到的地震记录。由图 9也可以看出, 弹性TTI介质与粘弹性TTI介质在能量及相位延迟上的差异, 同时, 在粘弹TTI介质地震记录中, 浅部能量强、深部能量弱, 与实际采集得到的地震记录特征相同, 而弹性TTI介质未表现出该特征, 说明采用粘弹TTI介质进行数值模拟更加符合实际地质情况, 为研究地下波场特征提供了更多的理论依据。
|
图 8 弹性TTI介质与粘弹性TTI介质采用组合边界条件不同时刻波场快照 a弹性TTI介质0.6s时刻波场快照; b粘弹TTI介质0.6s时刻波场快照; c弹性TTI介质0.8s时刻波场快照; d粘弹TTI介质0.8s时刻波场快照 |
|
图 9 弹性TTI介质(a)与粘弹性TTI介质(b)采用组合边界条件得到的地震记录 |
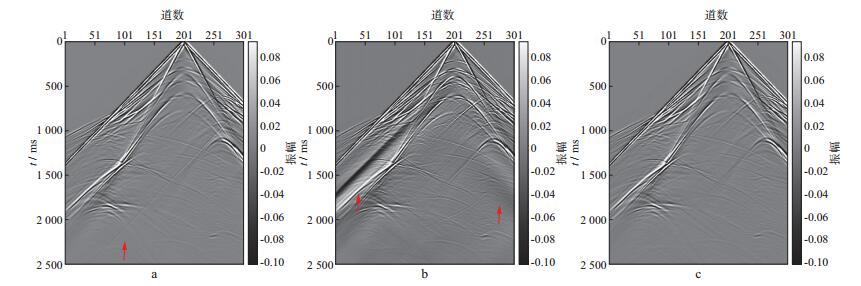
图 10为粘弹TTI介质分别采用SPML吸收边界条件、CPML吸收边界条件与CPML-RML组合边界条件得到的地震记录。对比图 10a、图 10b和图 10c可以看出, 采用SPML吸收边界条件得到的地震记录上出现了边界反射, 采用CPML吸收边界条件得到的地震记录上出现了低频反射, 而采用CPML-RML组合边界条件未出现边界反射, 说明本文提出的组合边界条件吸收效果好。
|
图 10 粘弹性TTI介质采用不同边界条件得到的地震记录 a SPML吸收边界条件; b CPML吸收边界条件; c CPML-RML组合边界条件 |
本文在前人对人工边界条件研究的基础上, 提出了CPML吸收边界条件与RML边界条件相结合的策略, 并将其应用于基于GSLS模型的粘弹TTI介质数值模拟中, 同时给出了适用于粘弹TTI介质的CPML吸收边界条件旋转交错网格有限差分算法, 以提高数值模拟的稳定性及数值解的精确性。采用二维均匀介质模型和复杂Hess模型测试了本文组合边界条件的适应性及正确性, 验证了其吸收效果, 得到以下结论:
1) 与SPML吸收边界条件、CPML吸收边界条件相比, 本文提出的组合边界条件在不增加计算量的情况下具有更好的吸收效果, 能有效减少人工边界反射、提高数值模拟的精度, 获得更好的数值模拟结果, 适合于粘弹TTI介质的数值模拟;
2) 与TTI介质相比, 粘弹TTI介质中的地震波场表现出明显的振幅衰减和相位延迟, 地震记录中浅层能量强、深层能量弱, 较好地表现出了地下真实介质的粘滞性特征。说明本文组合边界条件适用于复杂地下介质。
| [1] |
CHICHININA T, OBOLENTSEVA I, GIK L, et al. Attenuation anisotropy in the linear-slip model:interpretation of physical modeling data[J]. Geophysics, 2009, 74(5): WB165-WB176. DOI:10.1190/1.3173806 |
| [2] |
CARCIONE J M. Wave propagation in anisotropic linear viscoelastic media:theory and simulated wavefield[J]. Geophysical Journal International, 1990, 101(3): 739-750. DOI:10.1111/gji.1990.101.issue-3 |
| [3] |
CARCIONE J M. Constitutive model and wave equations for linear, viscoelastic, anisotropic media[J]. Geophysics, 1995, 60(2): 537-548. DOI:10.1190/1.1443791 |
| [4] |
CARCIONE J M, CAVALLINI F, MAINARDI F, et al. Time-domain seismic modeling of constant-Q seismic wave propagation using fractional derivatives[J]. Pure and Applied Geophysics, 2002, 159(7/8): 1719-1736. |
| [5] |
CARCIONE J M. Effects of pressure and saturating fluid on wave velocity and attenuation of anisotropic rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3): 389-403. DOI:10.1016/S1365-1609(03)00016-9 |
| [6] |
CARCIONE J M. Theory and modeling of constant-Q P-and S-waves using fractional time derivatives[J]. Geophysics, 2009, 74(1): T1-T11. |
| [7] |
CARCIONE J M. A generalization of the Fourier pseudospectral method[J]. Geophysics, 2010, 75(6): A53-A56. |
| [8] |
罗玉钦, 刘财. 近似完全匹配层边界条件吸收效果分析及衰减函数的改进[J]. 石油地球物理勘探, 2018, 53(5): 903-913. LUO Y Q, LIU C. Absorption effects in nearly perfectly matched layers and damping factor improvement[J]. Oil Geophysical Prospecting, 2018, 53(5): 903-913. |
| [9] |
李青阳, 吴国忱, 梁展源. 基于PML边界的时间高阶伪谱法弹性波场模拟[J]. 地球物理学进展, 2018, 33(1): 228-235. LI Q Y, WU G C, LIANG Z Y. Time domain high-order pseudo spectral method based on PML boundary for elastic wavefield simulation[J]. Progress in Geophysics, 2018, 33(1): 228-235. |
| [10] |
谢志南, 章旭斌. 弱形式时域完美匹配层[J]. 地球物理学报, 2017, 60(10): 3823-3831. XIE Z N, ZHANG X B. Weak-form time-domain perfectly matched layer[J]. Chinese Journal of Geophysics, 2017, 60(10): 3823-3831. DOI:10.6038/cjg20171012 |
| [11] |
张衡, 刘洪, 李博, 等. TTI介质声波方程分裂式PML吸收边界条件研究[J]. 石油物探, 2017, 56(3): 349-361. ZHANG H, LIU H, LI B, et al. The research on split PML absorbing boundary conditions of acoustic equation for TTI media[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 39-361. |
| [12] |
马锐, 邹志辉, 芮拥军, 等. 基于SPML和海绵边界的伪谱法弹性波模拟复合吸收边界条件[J]. 石油物探, 2018, 57(1): 94-103. MA R, ZOU Z H, RUI Y J, et al. A composite absorbing boundary based on the SPML and sponge absorbing boundary for pseudo-spectral elastic wave modeling[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 94-103. DOI:10.3969/j.issn.1000-1441.2018.01.013 |
| [13] |
BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. |
| [14] |
RODEN J A, GEDNEY S D. Convolutional PML(CPML):an efficient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave and Optical Technology Letters, 2000, 27(5): 334-339. DOI:10.1002/(ISSN)1098-2760 |
| [15] |
柯璇, 石颖, 宋利伟, 等. 基于褶积完全匹配吸收边界的声波方程数值模拟[J]. 石油物探, 2017, 56(5): 637-643. KE X, SHI Y, SONG L W, et al. Numercial modeling of acoustic wave equations based on convolutional perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 637-643. DOI:10.3969/j.issn.1000-1441.2017.05.003 |
| [16] |
KOMATITSCH D, MARTIN R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 2007, 72(5): SM115-SM167. DOI:10.1190/1.2750424 |
| [17] |
MARTIN R, KOMATITSCH D. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation[J]. Geophysical Journal International, 2009, 179(1): 333-344. DOI:10.1111/gji.2009.179.issue-1 |
| [18] |
冯德山, 王珣. 基于卷积完全匹配层的非规则网格时域有限元探地雷达数值模拟[J]. 地球物理学报, 2017, 60(1): 413-423. FENG D S, WANG X. Convolution perfectly matched layer for the finite-element time-domain method modeling of ground penetrating radar[J]. Chinese Journal of Geophysics, 2017, 60(1): 413-423. |
| [19] |
LI Y F, MATAR O B. Convolutional perfectly matched layer for elastic second-order wave equation[J]. The Journal of the Acoustical Society of America, 2010, 127(3): 1318-1327. DOI:10.1121/1.3290999 |
| [20] |
WANG Y F, ZHOU H, LI Q Q, et al. An unsplit convolutional perfectly matched layer for viso-acoustic wave equation with fractional time derivatives[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 3666-3671. |
| [21] |
FESTA G, VILOTTE J P. The newmark scheme as velocity-stress time-staggering:An efficient PML implementation for spectral-element simulations of elastrodynamics[J]. Geophysical Journal International, 2005, 161(3): 789-812. DOI:10.1111/gji.2005.161.issue-3 |
| [22] |
CLAPP R G. Reverse time migration with random boundaries[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 2809-2813. |
| [23] |
SHEN X K, CLAPP R G. Random boundary condition for memory-efficient waveform inversion gradient computation[J]. Geophysics, 2015, 80(6): R351-R359. DOI:10.1190/geo2014-0542.1 |
| [24] |
秦海旭, 吴国忱. TTI介质弹性波随机边界逆时偏移的实现[J]. 石油物探, 2014, 53(5): 570-578. QIN H X, WU G C. The implementation of ealstic reverse time migration in TTI media based on random boundary[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 570-578. DOI:10.3969/j.issn.1000-1441.2014.05.010 |
| [25] |
孙耀充, 张延腾, 白超英. 二维弹性及粘弹性TTI介质中地震波场数值模拟:四种不同网格高阶有限差分算法研究[J]. 地球物理学进展, 2013, 28(4): 1817-1827. SUN Y C, ZHANG Y T, BAI C Y. Numerical simulation of seismic wavefield in two-dimensional elastic and viscoelastic TTI media:a study of four different grid high-order finite difference algorithms[J]. Progress in Geophysics, 2013, 28(4): 1817-1827. |
| [26] |
刘东洋, 彭苏萍, 师素珍, 等. 基于Lebedev网格的TTI介质二维三分量正演模拟[J]. 石油地球物理勘探, 2018, 53(2): 288-296. LIU D Y, PENG S P, SHI S Z, et al. 2D three-component seismic forward modeling in TTI media based on the Lebedev grid[J]. Oil Geophysical Prospecting, 2018, 53(2): 288-296. |
| [27] |
高静怀, 徐文豪, 吴帮玉, 等. 深度均匀采样梯形网格有限差分地震波场模拟方法[J]. 地球物理学报, 2018, 61(8): 3285-3296. GAO J H, XU W H, WU B Y, et al. Trapezoid grid finite difference seismic wavefield simulation with uniform depth sampling interval[J]. Chinese Journal of Geophysics, 2018, 61(8): 3285-3296. |
| [28] |
MADARIAGA R. Dynamics of an expanding circular fault[J]. Bullentin of the Seismological Society of America, 1976, 66(3): 639-666. |
| [29] |
GRAVES R W. Simulating seismic wave propagation in 3D elastic media using staggered grid finite difference[J]. Bullentin of the Seismological Society of America, 1996, 86(4): 1091-1106. |
| [30] |
LEVANDER A R. 4th-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [31] |
VIRIEUX J. P-SV wave propagation in heterogeneous media:velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901. DOI:10.1190/1.1442147 |
| [32] |
SAENGER E H, GOLD N, SHAPIRO S A. Modeling the propagation of elastic waves using a modified finite-difference grid[J]. Wave Motion, 2000, 31(1): 77-92. DOI:10.1016/S0165-2125(99)00023-2 |
| [33] |
SAENGER E H, BOHLEN T. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid[J]. Geophysics, 2004, 69(2): 583-591. DOI:10.1190/1.1707078 |
| [34] |
姚振岸, 孙成禹, 谢俊法, 等. 黏弹TTI介质旋转交错网格微地震波场模拟[J]. 石油地球物理勘探, 2017, 52(2): 253-263. YAO Z A, SUN C Y, XIE J F, et al. Mocro-seismic forward modeling in viscoelastic TTI media based rotated staggered grid finite-difference method[J]. Oil Geophysical Prospecting, 2017, 52(2): 253-263. |
| [35] |
严红勇, 刘洋. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 2012, 55(4): 1354-1365. YAN H Y, LIU Y. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
| [36] |
李振春, 杨富森, 王小丹. 基于LS-RSGFD方法优化的横向各向异性(TI)介质一阶qP波高精度数值模拟[J]. 地球物理学报, 2016, 59(4): 1477-1490. LI Z C, YANG F S, WANG X D. High-precision numerical simulation of first-order qP-waves in the transversely isotropic (TI) medium optimized by the LS-RSGFD method[J]. Chinese Journal of Geophysics, 2016, 59(4): 1477-1490. |
| [37] |
ZHU J L, DORMAN J. Two-dimensional, three-component wave propagation in a transversely isotropic media with arbitrary-orientation-finite-element modeling[J]. Geophysics, 2000, 65(3): 934-942. DOI:10.1190/1.1444789 |
| [38] |
DROSSAERT F H, GIANNOPOULOS A. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves[J]. Geophysics, 2007, 72(2): T9-T17. DOI:10.1190/1.2424888 |
| [39] |
李庆忠. 走向精确勘探的道路[M]. 北京: 石油工业出版社, 1993: 38-39. LI Q Z. Road to precise exploration[M]. Beijing: Petroleum Industry Press, 1993: 38-39. |




