叠前地震反演技术是解决油气勘探储层岩性、流体预测等问题的重要技术, 在油气勘探开发中越来越受到重视。基于波动方程理论的叠前全波形反演直接利用炮集资料得到地层参数, 但该方法尚未成熟, 同时受制于计算速度和反演精度, 目前还不能在勘探开发生产中大规模推广应用。基于佐普里兹方程及其近似式的叠前地震反演技术利用不同偏移距地震振幅变化信息, 可得到用于精细储层研究的纵、横波速度以及密度、泊松比和流体因子等多种地层参数, 多年来一直是研究的重点。叠前地震反演是复杂的非线性问题, 解决问题的方法主要有两类:一类是将非线性问题局部线性化近似, 通过迭代逼近获得最优解, 方法简单、易行, 但对初始模型依赖性强, 得到的经验是局部最优解, 所以对于实际生产中大规模三维叠前地震数据的反演运算, 还需要研发低成本、高效率的线性化反演方法[1-4]; 另一类是利用非线性反演方法, 主要基于统计数学、物理学和仿生学等, 研究形成的多种非线性反演方法, 如免疫[5]、模拟退火[6]及粒子群[7]算法等, 这些方法可以通过全局搜索获得全局最优解, 但往往存在计算量大的问题, 也难以应用于实际勘探开发生产中。
叠前线性化反演方法的思路是利用泰勒展开式一阶形式, 用初始给定参数模型地震响应和一阶偏导方程矩阵(雅克比矩阵)线性近似表达期望反演参数模型地震响应, 进而构建目标函数和迭代公式, 然后从初始模型出发, 经过迭代更新初始模型, 最后收敛得到最终期望模型, 也就是反演结果。初始模型可以是纵、横波速度、密度等物理意义明确的弹性参数体, 也可以是这些弹性参数对应的反射系数。影响线性化反演精度的因素有以下3个方面:①初始模型的精度, 线性反演属于局部寻优的反演方法, 初始模型越接近实际模型, 越容易反演得到真正的解; ②雅克比矩阵构建精度, 雅克比矩阵由期望反演参数模型地震响应对初始模型参数的偏导求取构建, 目前大多数叠前反演方法中的雅克比矩阵都是基于佐普里兹方程近似式[8-9]构建, 由于佐普里兹方程近似过程中存在小角度入射和弱反射界面的假设, 会影响反演的精度, 因而一些学者尝试直接通过佐普里兹方程来构建雅克比矩阵[10-12], 然后再用于反演迭代, 提高反演精度; ③目标函数和迭代公式的构建, 确定合适的损失函数和正则化参数[13], 确保反演方法的抗噪性和稳定性。
本文面向实际生产的低成本、高效叠前地震反演技术的应用需求, 采用广义线性反演思路, 提出了一种稳定的高精度线性叠前地震反演方法。首先构建目标函数及迭代公式, 确定损失函数, 同时加入正则化约束项来提高反演的稳定性; 其次构建雅克比矩阵, 直接将佐普里兹方程变换为矩阵, 基于矩阵运算进行雅克比矩阵元素的推导和组合; 然后设定正则化参数, 利用地震噪声和反演参数扰动量的高斯统计自动选择正则化参数; 最后将该方法应用于实际资料中, 以验证方法的适用性和有效性。
1 方法原理 1.1 反演目标函数及迭代公式构建模型驱动的高精度叠前地震反演方法是在叠前地震信息和初始纵、横波速度及密度弹性参数约束模型给定的条件下, 基于地震波非垂直入射理论, 同步求解地层三参数(纵、横波速度及密度)的方法。该方法采用逐道反演的方式, 从首道一维初始模型开始正演, 利用模型正演求取地震数据与实际地震数据的差, 再利用差值和迭代公式求取模型参数扰动量, 然后对初始模型迭代更新, 直到残差达到最小, 获得的最终更新模型即为最终反演结果。单道一维叠前地震三参数反演完成后, 依次类推完成整个三维工区的叠前地震参数反演。
反演采用部分角度叠加数据体, 因为需要反演纵、横波速度和密度3个未知量, 因此实际采用的地震数据至少为3个部分角度叠加数据体, 一维地震数据可表示为:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{D}} = }\\ {{{\left[ {\begin{array}{*{20}{l}} {{d_{11}}}& \cdots &{{d_{1n}}}&{{d_{21}}}& \cdots &{{d_{2n}}}&{{d_{31}}}& \cdots &{{d_{3n}}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (1) |
式中:d1n, d2n, d3n分别代表小角度、中角度和大角度叠加地震道中第n个采样点对应的振幅信息。
利用佐普里兹方程关系式进行叠前地震正演, 可得到初始模型对应的3个部分角度叠加地震响应, 表示为:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{S}}({v_{\rm{P}}},{v_{\rm{S}}},\rho ) = }\\ {{{\left[ {\begin{array}{*{20}{c}} {{s_{11}}}& \cdots &{{s_{1n}}}&{{s_{21}}}& \cdots &{{s_{2n}}}&{{s_{31}}}& \cdots &{{s_{3n}}} \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (2) |
| $ \mathit{\boldsymbol{S}}({v_{\rm{P}}},{v_{\rm{S}}},\rho ) = \mathit{\boldsymbol{W}} * \mathit{\boldsymbol{R}}({v_{\rm{P}}},{v_{\rm{S}}},\rho ) $ | (3) |
式中:vP表示模型纵波速度; vS表示模型横波速度; ρ为模型密度; s1n, s2n, s3n分别为小角度、中角度和大角度模型地震正演的第n个采样点振幅信息; R(vP, vS, ρ)为反射系数; W为地震子波。
将期望模型响应S(vP, vS, ρ)Δ在初始模型S(vP, vS, ρ)响应处进行泰勒展开, 并省去二阶及二阶以上的高阶项, 可得包含初始模型响应、雅克比矩阵、模型扰动量的期望模型响应的线性化表达式:
| $ \mathit{\boldsymbol{S}}{({v_{\rm{P}}},{v_{\rm{S}}},\rho )^\Delta } = \mathit{\boldsymbol{S}}({v_{\rm{P}}},{v_{\rm{S}}},\rho ) + \mathit{\boldsymbol{G}}\Delta \mathit{\boldsymbol{M}} $ | (4) |
其中, G是由正演地震响应对纵波速度、横波速度及密度的偏导数组成的雅克比矩阵, 表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{G}} = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {S_{11}}}}{{\partial {v_{{\rm{P1}}}}}}}&{\frac{{\partial {{\rm{S}}_{11}}}}{{\partial {v_{{\rm{S1}}}}}}}&{\frac{{\partial {S_{11}}}}{{\partial {\rho _1}}}}& \cdots &{\frac{{\partial {S_{11}}}}{{\partial {v_{{\rm{P}}n}}}}}&{\frac{{\partial {{\rm{S}}_{11}}}}{{\partial {v_{{\rm{S}}n}}}}}&{\frac{{\partial {{\rm{S}}_{11}}}}{{\partial {\rho _n}}}}\\ \vdots & \vdots & \vdots &{}& \vdots & \vdots & \vdots \\ {\frac{{\partial {S_{1n}}}}{{\partial {v_{{\rm{P1}}}}}}}&{\frac{{\partial {S_{1n}}}}{{\partial {v_{{\rm{S1}}}}}}}&{\frac{{\partial {S_{1n}}}}{{\partial {\rho _1}}}}& \cdots &{\frac{{\partial {S_{1n}}}}{{\partial {v_{{\rm{P}}n}}}}}&{\frac{{\partial {S_{1n}}}}{{\partial {v_{{\rm{S}}n}}}}}&{\frac{{\partial {S_{1n}}}}{{\partial {\rho _n}}}}\\ {\frac{{\partial {S_{21}}}}{{\partial {v_{{\rm{P1}}}}}}}&{\frac{{\partial {S_{21}}}}{{\partial {v_{{\rm{S1}}}}}}}&{\frac{{\partial {S_{21}}}}{{\partial {\rho _1}}}}& \cdots &{\frac{{\partial {S_{21}}}}{{\partial {v_{{\rm{P}}n}}}}}&{\frac{{\partial {S_{21}}}}{{\partial {v_{{\rm{S}}n}}}}}&{\frac{{\partial {S_{21}}}}{{\partial {\rho _n}}}}\\ \vdots & \vdots & \vdots &{}& \vdots & \vdots & \vdots \\ {\frac{{\partial {S_{2n}}}}{{\partial {v_{{\rm{P1}}}}}}}&{\frac{{\partial {S_{2n}}}}{{\partial {v_{{\rm{S1}}}}}}}&{\frac{{\partial {S_{2n}}}}{{\partial {\rho _1}}}}& \cdots &{\frac{{\partial {S_{2n}}}}{{\partial {v_{{\rm{P}}n}}}}}&{\frac{{\partial {S_{2n}}}}{{\partial {v_{{\rm{S}}n}}}}}&{\frac{{\partial {{\rm{S}}_{2n}}}}{{\partial {\rho _n}}}}\\ {\frac{{\partial {S_{31}}}}{{\partial {v_{{\rm{P1}}}}}}}&{\frac{{\partial {S_{31}}}}{{\partial {v_{{\rm{S1}}}}}}}&{\frac{{\partial {S_{31}}}}{{\partial {\rho _1}}}}& \cdots &{\frac{{\partial {S_{31}}}}{{\partial {v_{{\rm{P}}n}}}}}&{\frac{{\partial {S_{31}}}}{{\partial {v_{{\rm{S}}n}}}}}&{\frac{{\partial {S_{31}}}}{{\partial {\rho _n}}}}\\ \vdots & \vdots & \vdots &{}& \vdots & \vdots & \vdots \\ {\frac{{\partial {S_{3n}}}}{{\partial {v_{{\rm{P1}}}}}}}&{\frac{{\partial {S_{3n}}}}{{\partial {v_{{\rm{S1}}}}}}}&{\frac{{\partial {S_{3n}}}}{{\partial {\rho _1}}}}& \cdots &{\frac{{\partial {S_{3n}}}}{{\partial {v_{{\rm{P}}n}}}}}&{\frac{{\partial {S_{3n}}}}{{\partial {v_{{\rm{S}}n}}}}}&{\frac{{\partial {S_{3n}}}}{{\partial {\rho _n}}}} \end{array}} \right] \end{array} $ |
ΔM是由每个采样点纵波速度、横波速度及密度扰动量组成的矩阵, 表示为:
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {\Delta {v_{{\rm{P1}}}}}&{\Delta {v_{{\rm{S1}}}}}&{\Delta {\rho _1}}&{\Delta {v_{{\rm{P2}}}}}&{\Delta {v_{{\rm{S2}}}}}&{\Delta {\rho _2}}& \cdots \end{array}} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left. {\begin{array}{*{20}{c}} {\Delta {v_{{{\rm{P}}_n}}}}&{\Delta {v_{{{\rm{S}}_n}}}}&{\Delta {\rho _n}} \end{array}} \right]^{\rm{T}}} \end{array} $ |
式中:ΔvPn, ΔvSn, Δρn分别为纵波速度、横波速度及密度第n个采样点的扰动量。
反演的目标是单道期望模型正演地震数据与实际地震数据的差值的和最小, 由于每一时间采样点的差值有正有负, 单道差值求和会出现相互抵消情况, 因而采用最小二乘法构建损失函数更为合理, 同时为了增加反演的稳定性, 防止由于模型响应的奇异性造成求取的扰动量过大或过小, 在目标函数中增加了扰动量正则化项, 确保求取的扰动量具有L2范数最小。最终构建的L2正则化最小二乘目标函数由两部分组成, 前一项为残差的平方和, 也就是地震噪声的平方和; 后一项为模型参数扰动量L2范数, 表示为:
| $ \begin{array}{*{20}{l}} {F({v_{\rm{P}}},{v_{\rm{S}}},\rho ) = \frac{1}{2}{{\left\| {\mathit{\boldsymbol{S}}{{({v_{\rm{P}}},{v_{\rm{S}}},\rho )}^\Delta } - \mathit{\boldsymbol{D}}} \right\|}^2} + }\\ {\frac{1}{2}{{\left\| {\Delta \mathit{\boldsymbol{M}}} \right\|}^2} = \frac{1}{2}{{\left\| {\mathit{\boldsymbol{G}}\Delta \mathit{\boldsymbol{M}} - \Delta \mathit{\boldsymbol{D}}} \right\|}^2} + \frac{1}{2}\lambda {{\left\| {\Delta \mathit{\boldsymbol{M}}} \right\|}^2}} \end{array} $ | (5) |
式中:ΔD=D-S(vP, vS, ρ), 表示初始模型响应与实际地震数据的残差; λ为正则化参数。
每次迭代求解目标是寻找最优模型参数扰动量Δ$\hat{\boldsymbol{M}}$, 使目标函数F(vP, vS, ρ)取最小值, 表示为:
| $ \Delta \mathit{\boldsymbol{\hat M}} = {\rm{argmin}}[F({v_{\rm{P}}},{v_{\rm{S}}},\rho )] $ | (6) |
通过对F(vP, vS, ρ)进行微分求极值, 可得扰动量的求解公式:
| $ \Delta \mathit{\boldsymbol{\hat M}} = {({\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}} + \lambda \mathit{\boldsymbol{I}})^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\Delta \mathit{\boldsymbol{D}} $ | (7) |
式中:I为单位矩阵。
在模型扰动量求解的基础上, 进而可以实现模型迭代更新, 迭代公式如下:
| $ {\mathit{\boldsymbol{M}}_{k + 1}} = {\mathit{\boldsymbol{M}}_k} + \Delta \mathit{\boldsymbol{\hat M}} $ | (8) |
式中:k为迭代次数; Mk和Mk+1分别代表第k和k+1次迭代运算时的模型参数, 也就是纵波速度、横波速度及密度。
推导和构建了上述目标函数和迭代公式, 就可以利用地震数据残差求取模型参数扰动量, 进而对模型不断更新迭代, 最终实现单道纵波速度、横波速度及密度的叠前反演, 通过逐道反演就可以得到地下地层三维空间3种弹性参数。由迭代反演方法和过程可以看出, 在初始模型及叠前实际地震数据给定条件下, 雅克比矩阵方程和正则化参数是影响反演精度的主要因素, 因此对这两个因素进行了重点研究。
1.2 高精度雅克比矩阵方程构建叠前地震反演中采用的雅克比矩阵方程基于佐普里兹方程构建, 佐普里兹方程精确表达了地震反射系数和透射系数与地震波入射角度、地层弹性参数之间的关系, 是叠前弹性参数反演的重要理论基础。传统雅克比矩阵的构建基于佐普里兹方程近似解析式, 构建简单但精度低。本文采用佐普里兹方程变换为矩阵后直接通过矩阵运算构建雅克比矩阵方式, 不做任何小入射角及弱反射界面的假设, 直接从佐普里兹方程求取反射系数对弹性参数的偏导表达式, 构建高精度雅克比矩阵方程, 并应用到反演迭代求解中。
佐普里兹方程精确表达式如下:
| $ \left[ {\begin{array}{*{20}{c}} {{\rm{sin}}\alpha }&{{\rm{cos}}\beta }&{ - {\rm{sin}}{\alpha ^\prime }}&{{\rm{cos}}{\beta ^\prime }}\\ {{\rm{cos}}\alpha }&{ - {\rm{sin}}\beta }&{{\rm{cos}}{\alpha ^\prime }}&{{\rm{sin}}{\beta ^\prime }}\\ {{\rm{cos}}2\beta }&{ - \frac{{{v_{{\rm{S1}}}}}}{{{v_{{\rm{P1}}}}}}{\rm{sin}}2\beta }&{ - \frac{{{\rho _2}{v_{{\rm{P2}}}}}}{{{\rho _1}{v_{{\rm{P1}}}}}}{\rm{cos}}2{\beta ^\prime }}&{ - \frac{{{\rho _2}{v_{{\rm{S2}}}}}}{{{\rho _1}{v_{{\rm{P1}}}}}}{\rm{sin}}2{\beta ^\prime }}\\ {\frac{{v_{{\rm{S1}}}^2}}{{{v_{{\rm{P1}}}}}}{\rm{sin}}2\alpha }&{{v_{{\rm{S1}}}}{\rm{cos}}2\beta }&{\frac{{{\rho _2}v_{{\rm{S2}}}^2}}{{{\rho _1}{v_{{\rm{P2}}}}}}{\rm{sin}}2{\alpha ^\prime }}&{ - \frac{{{\rho _2}v_{{\rm{S2}}}^2}}{{{\rho _1}}}{\rm{cos}}2{\beta ^\prime }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{R_{{\rm{PP}}}}}\\ {{R_{{\rm{PS}}}}}\\ {{T_{{\rm{PP}}}}}\\ {{T_{{\rm{PS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {\rm{sin}}\alpha }\\ {{\rm{cos}}\alpha }\\ { - {\rm{cos}}2\beta }\\ {\frac{{v_{{\rm{S1}}}^2}}{{{v_{{\rm{P1}}}}}}{\rm{sin}}2\alpha } \end{array}} \right] $ | (9) |
式中:RPP, RPS, TPP和TPS分别为纵波、转换横波、透射纵波、透射横波的反射系数; α为纵波反射角; β转换横波反射角; α′透射纵波折射角; β′透射横波折射角; vP1, vS1, ρ1, vP2, vS2, ρ2分别为地层上、下介质纵、横波速度以及密度。
根据斯奈尔定律, 用纵波反射角分别替换佐普里兹方程中横波反射角、透射纵波折射角及透射横波折射角, 同时将(9)式用矩阵形式表示:
| $ \mathit{\boldsymbol{AR}} = \mathit{\boldsymbol{B}} $ | (10) |
式中:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\rm{sin}}{\alpha _1}}&{\sqrt {1 - \frac{{v_{{\rm{S1}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}} }&{ - \frac{{{v_{{\rm{P2}}}}{\rm{sin}}{\alpha _1}}}{{{v_{{\rm{P1}}}}}}}&{\sqrt {1 - \frac{{v_{{\rm{S2}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}} }\\ {{\rm{cos}}{\alpha _1}}&{ - \frac{{{v_{{\rm{S1}}}}}}{{{v_{{\rm{P1}}}}}}{\rm{sin}}{\alpha _1}}&{\sqrt {1 - \frac{{v_{{\rm{P2}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}} }&{\frac{{{v_{{\rm{S2}}}}{\rm{sin}}{\alpha _1}}}{{{v_{{\rm{P1}}}}}}}\\ {1 - 2\frac{{v_{{\rm{S1}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}}&{ - 2\frac{{v_{{\rm{S1}}}^2}}{{v_{{\rm{P1}}}^2}}\sqrt {{\rm{si}}{{\rm{n}}^2}{\alpha _1} - \frac{{v_{{\rm{S1}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^4}{\alpha _1}} }&{ - \frac{{{\rho _2}}}{{{\rho _1}}}\frac{{{v_{{\rm{P2}}}}}}{{{v_{{\rm{P1}}}}}}\left( {1 - 2\frac{{v_{{\rm{S2}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}} \right)}&{ - 2\frac{{{\rho _2}}}{{{\rho _1}}}\frac{{v_{{\rm{S2}}}^2}}{{v_{{\rm{P1}}}^2}}\sqrt {{\rm{si}}{{\rm{n}}^2}{\alpha _1} - \frac{{v_{{\rm{S2}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^4}{\alpha _1}} }\\ {{\rm{sin}}2{\alpha _1}}&{\frac{{{v_{{\rm{P1}}}}}}{{{v_{{\rm{S1}}}}}} - 2\frac{{{v_{{\rm{S1}}}}}}{{{v_{{\rm{P1}}}}}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}}&{2\frac{{{\rho _2}}}{{{\rho _1}}}\frac{{v_{{\rm{S2}}}^2}}{{v_{{\rm{S1}}}^2}}\sqrt {{\rm{si}}{{\rm{n}}^2}{\alpha _1} - \frac{{v_{{\rm{P2}}}^2}}{{v_{{\rm{S1}}}^2}}{\rm{si}}{{\rm{n}}^4}{\alpha _1}} }&{ - \frac{{{\rho _2}}}{{{\rho _1}}}\frac{{{v_{{\rm{P1}}}}{v_{{\rm{S2}}}}}}{{v_{{\rm{S1}}}^2}}\left( {1 - 2\frac{{v_{{\rm{S2}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}} \right)} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{R}} = {{\left[ {\begin{array}{*{20}{l}} {{R_{{\rm{PP}}}}}&{{R_{{\rm{PS}}}}}&{{T_{{\rm{PP}}}}}&{{T_{{\rm{PS}}}}} \end{array}} \right]}^{\rm{T}}}} $ |
| $ {\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - {\rm{sin}}{\alpha _1}}\\ {{\rm{cos}}{\alpha _1}}\\ { - 1 + 2\frac{{v_{{\rm{S1}}}^2}}{{v_{{\rm{P1}}}^2}}{\rm{si}}{{\rm{n}}^2}{\alpha _1}}\\ {{\rm{sin}}2{\alpha _1}} \end{array}} \right]} $ |
公式(10)两边分别对地层上、下界面纵、横波速度以及密度6个地层弹性参数求偏导, 可得反射系数及透射系数对地层弹性参数的偏导方程:
| $ \frac{{\partial \mathit{\boldsymbol{R}}}}{{\partial \mathit{\boldsymbol{m}}}} = - {\mathit{\boldsymbol{A}}^{ - 1}}\frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial \mathit{\boldsymbol{m}}}}{\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{A}}^{ - 1}}\frac{{\partial \mathit{\boldsymbol{B}}}}{{\partial \mathit{\boldsymbol{m}}}} $ | (11) |
式中:m=(vPi, vSi, vPi+1, vSi+1, ρi, ρi+1), 代表第i个采样点及其下一个相邻采样点的纵波速度、横波速度及密度参数。
1.3 正则化参数设定叠前反演目标函数((5)式)正则化项就是对损失函数加上约束, 等价于对反演参数引入先验分布, 一方面解决了反演的不适定性, 保证产生的解存在且唯一, 另一方面解决了反演过拟合问题, 使反演结果稳定而平滑。由于叠前地震反演目标函数中损失函数取值往往明显小于正则化项, 因此正则化参数λ还起到平衡目标函数两部分影响能力的作用。当初始模型、雅克比矩阵、地震记录都给定时, 模型参数的扰动量求解与正则化参数λ大小密切相关。若正则化参数过大, 那么正则化项对目标函数的影响能力强, 而地震残差影响能力小, 导致最终求解的扰动量很小, 初始模型难以迭代更新; 若正则化参数过小, 那么正则化项对目标函数影响能力弱, 而地震残差对目标函数的影响能力强, 导致最终求解的扰动量很大, 反演结果容易发散。
常用的正则化参数选取方式有固定不变、线性修正和自适应修正三种方式。本文重点研究了自适应修正正则化参数的选取方式, 目标函数中的地震残差项和扰动量项, 都符合高斯统计分布, 因此可分别表示为ΔD~(0, σn2)和ΔM~(0, σΔm2), 基于高斯分布的贝叶斯理论, 推导出高斯自适应修正正则化参数的表达式:
| $ \lambda = \frac{{\sigma _n^2}}{{\sigma _{\Delta m}^2}} $ | (12) |
式中:σn2为噪声的方差; σΔm2为反演参数扰动量的方差。
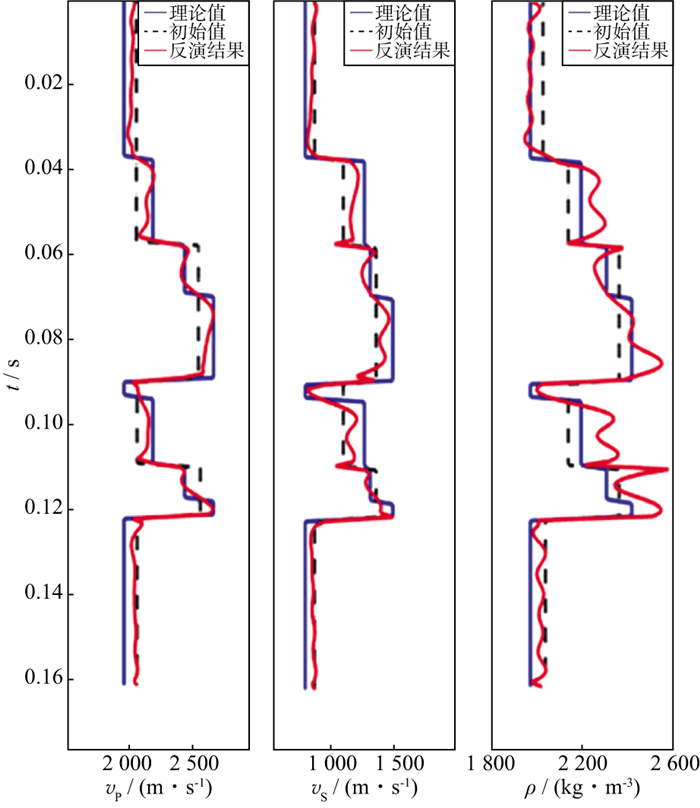
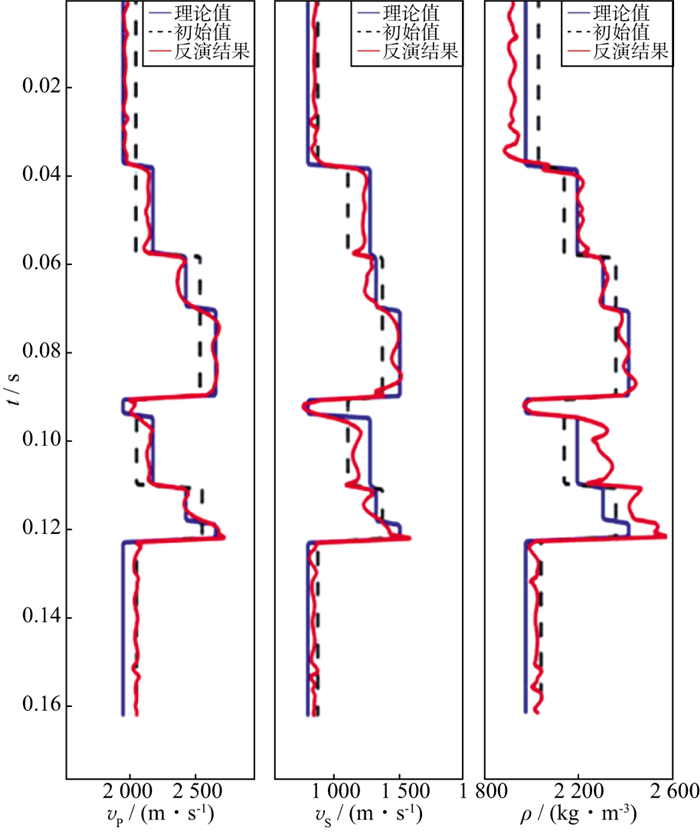
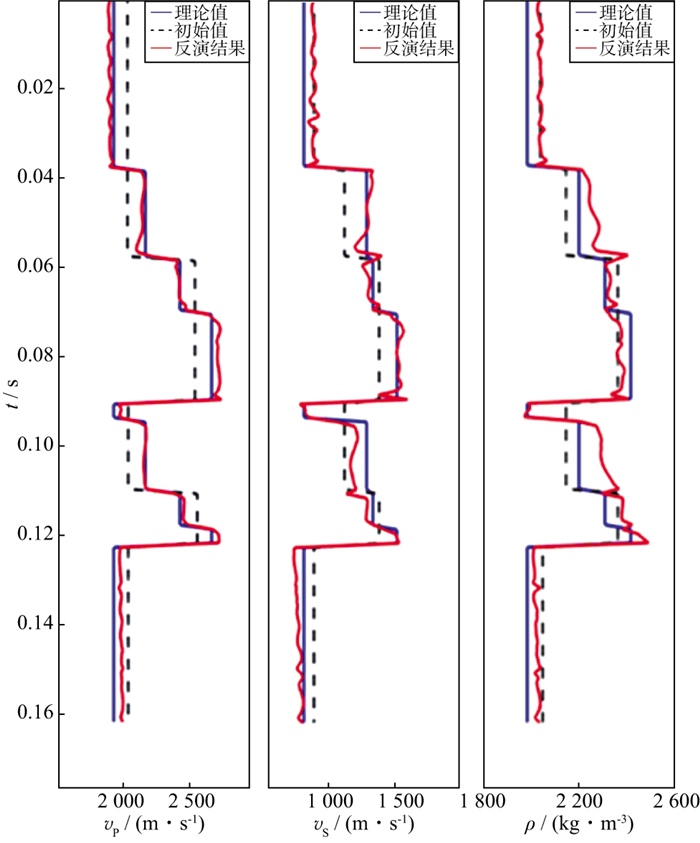
通过实验, 对比测试了固定不变、线性修正以及高斯自适应修正正则化参数λ对反演结果的影响。从图 1、图 2及图 3可知, 高斯自适应选择的正则化参数, 减少了人工正则化参数测试工作, 智能化选择正则化参数, 反演结果稳定, 且具有较高的反演精度。
|
图 1 采用固定不变λ的反演结果 |
|
图 2 采用线性修正λ的反演结果 |
|
图 3 采用高斯自适应修正λ的反演结果 |
垦东北地区位于垦东凸起北部斜坡带, 北靠桩东凹陷, 断裂疏导体系发育, 该地区处在油气运移的有利指向带上, 油气成藏条件好, 是油气富集地区。垦东北新近系浅层馆陶组河流相储层是胜利油田重要勘探开发层系, 馆陶组上段为曲流河沉积, 岩性主要为灰色细砂岩、粉砂岩、粗砂岩、砾岩与灰绿色泥岩等; 馆陶组下段为辫状河沉积, 岩性主要为灰色块状含砾砂岩、块状砂岩、粗砂岩夹灰色泥岩。该区地质构造沉积演化背景复杂, 断裂系统发育, 地层岩性和油藏类型多, 砂岩储层纵横向变化快, 利用地震振幅和叠后波阻抗预测储层岩性和流体时多解性强。
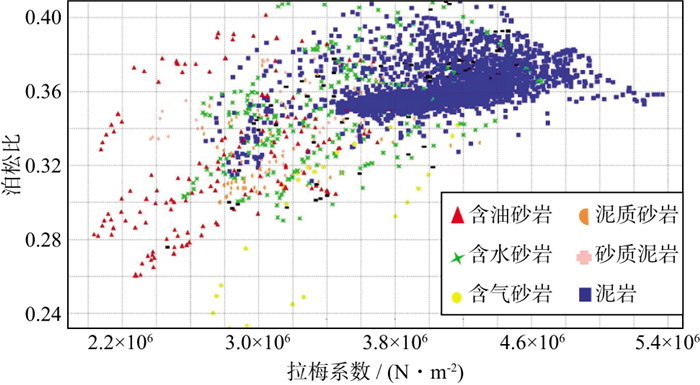
在目标层岩性分析基础上, 采用了针对砂泥岩碎屑地层岩石物理横波估算方法[14], 得到了横波速度、纵横波速度比、拉梅系数及泊松比等多种参数, 对储层岩性及流体弹性参数进行了敏感性分析[15]。浅层河道砂岩具有高孔隙、低纵波阻抗和低泊松比特征, 含油气后, 纵波阻抗和泊松比变低; 纯泥岩由于粘土矿物成分多, 具有低阻抗、高泊松比特征; 砂质泥岩和泥质砂岩具有高阻抗、中高泊松比特征。综合分析认为, 砂岩与围岩纵波阻抗差异小, 因此利用叠后地震振幅和反演属性预测砂岩储层多解性强, 而砂岩低泊松比和低拉梅系数特征明显(图 4)。解决该储层岩性和流体预测问题, 需要应用叠前反演储层预测技术, 采用本文方法获取纵波速度、横波速度及密度参数, 进一步利用弹性参数的物理关系构建泊松比及拉梅系数并进行储层预测。
|
图 4 岩石物理敏感弹性参数分析 |
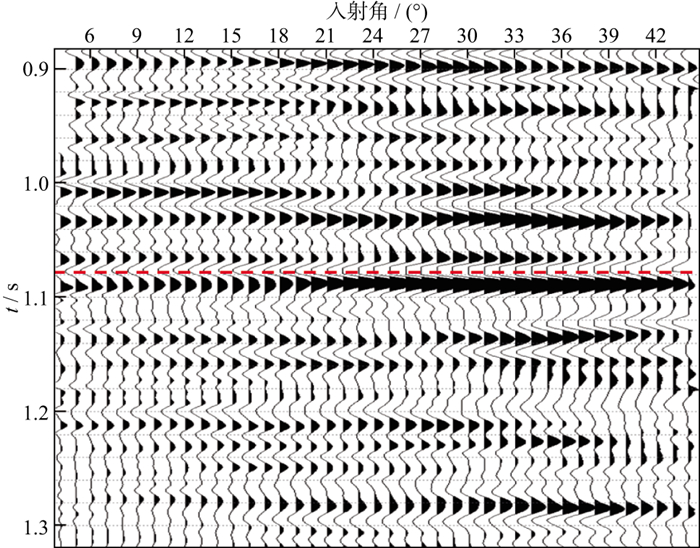
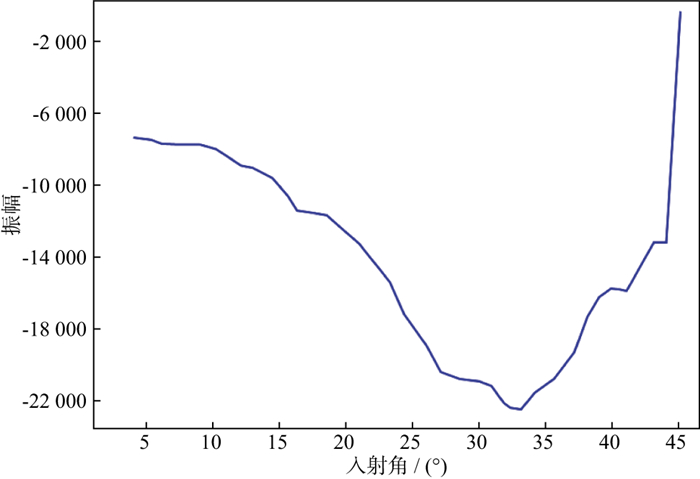
叠前地震反演是一项综合性强的储层预测技术, 叠前反演方法、叠前地震资料品质、初始模型和子波都是影响反演结果的重要因素。首先开展了叠前地震保幅优化处理及角度道集提取, 并对道集进行了分析。图 5为KD403井旁叠前角度道集, 红线代表高阻抗砂质泥岩与10m厚油层的分界面。图 6展示了该界面振幅随角度的(AVA)变化。该岩性组合在入射角度小于33°时表现为Ⅲ类AVO特征, 也就是振幅绝对值随角度的增加而增加, 且变化梯度较大, 但当入射角度大于33°后地震振幅和波形发生较大改变, 应用大于入射角度33°信息会影响叠前反演效果, 同时考虑小角度地震缺失, 叠前道集应用角度范围为3°~33°。然后在道集优化选取基础上, 开展了反演子波的提取, 分析地震资料频带可知优势频带为6~65Hz, 主频32Hz左右, 结合地震频带分析, 利用井震标定确定性子波提取方法, 获得与实际地震匹配的反演子波。最后构建反演初始约束模型, 初始纵波速度由地震动校偏移速度转换为层速度得到, 利用测井岩石物理统计关系, 构建横波速度和密度模型。
|
图 5 KD403井旁叠前角度道集 |
|
图 6 叠前AVA特征分析 |
利用约束稀疏脉冲叠前反演方法和本文方法分别进行了反演处理, 得到了纵、横波速度和密度参数数据体, 再利用岩石物理弹性参数关系, 进一步得到了纵横波速度比、泊松比及拉梅系数等敏感弹性参数。
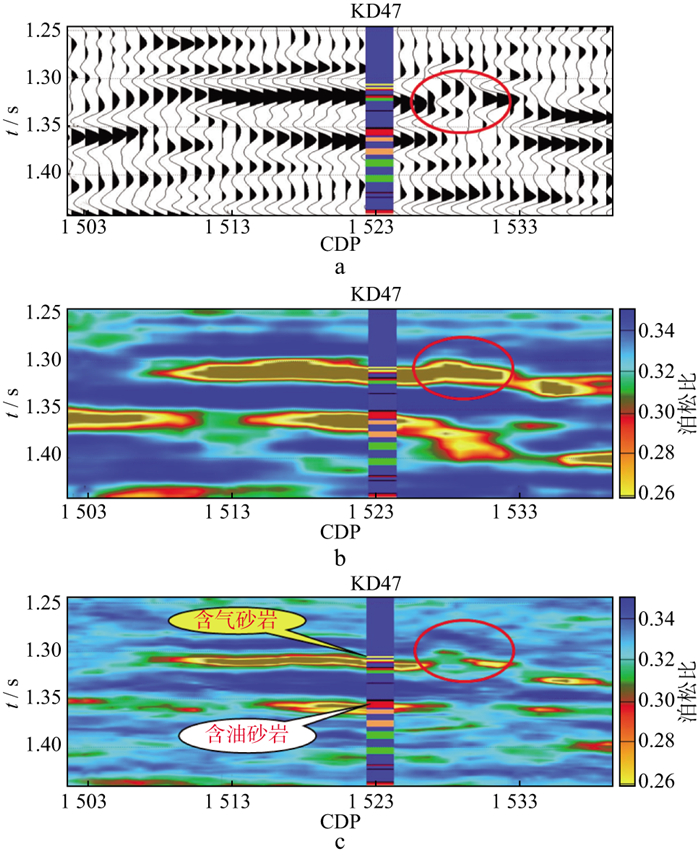
图 7为过KD47井的叠后地震剖面、约束稀疏脉冲叠前反演泊松比剖面及本文方法反演泊松比剖面, 对比发现, 河道砂岩的顶为强阻抗到弱阻抗变化界面, 为强波谷反射, 两种反演方法得到的结果中, 低泊松比均位于地震强波谷和波峰之间, KD47井钻遇的含气、含油砂岩, 低泊松比特征都非常明显, 均很好地体现了叠前地震变化特征。由图 7a红圈位置可见, 地震振幅和波形存在细微的差别; 对比图 7b和图 7c可看出, 与约束稀疏脉冲叠前反演泊松比相比, 本文方法反演结果更能体现地震细微变化特征, 对储层厚度和尖灭点变化表现清楚。
|
图 7 过KD47井的叠后地震剖面(a)、约束稀疏脉冲叠前反演泊松比剖面(b)及本文方法反演泊松比剖面(c) |
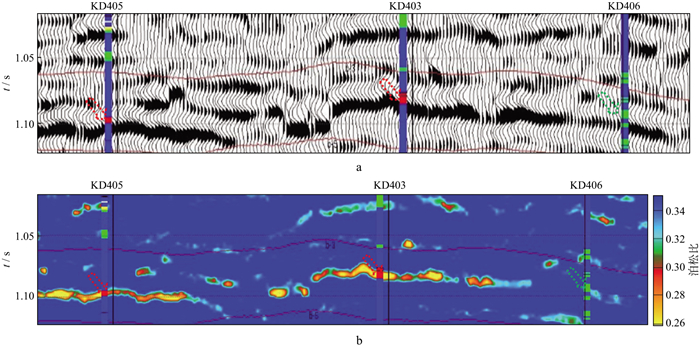
利用由本文方法得到的泊松比资料进行了储层预测。图 8为过KD405井、KD403井和KD406井叠后地震剖面和泊松比反演剖面, 在馆上4砂组3口井都钻遇砂岩储层, 与图 7中KD47井钻遇储层地震反射特征相同, 储层相比围岩为低阻抗, 储层顶对应波谷, 而储层底对应波峰, 钻井证实KD405井和KD403井都钻遇含油砂岩, KD406井钻遇含水砂岩, KD403井和KD406井砂岩储层厚度相近, 均为10m左右。KD403井和KD405井储层含油气, 而KD406井储层含水, 含油气会引起纵波速度和纵波阻抗的降低, 地震振幅略微增强, 地震振幅体现流体变化特征, 但叠前反演泊松比对流体变化更敏感, 且反演消除了子波干涉效应, 很好的反映了地质体厚度变化, 更有利于储层含油气识别。
|
图 8 叠后地震剖面(a)和本文方法反演泊松比剖面(b) |
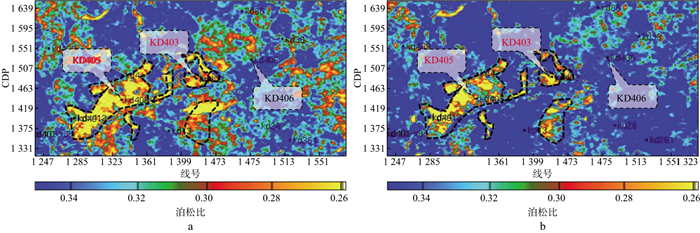
钻井资料表明, 在研究区域馆上4砂组仅有KD405井、KD403井及其附近井钻遇较好的油层, 周边部署井均未发现油层。图 9a和图 9b分别为利用叠后地震数据提取的和利用本文方法反演的馆上4砂组泊松比剖面。在叠后地震振幅属性平面图(图 9a)中, 含油储层和含水储层振幅差异小, 储层含流体难以区分, 有利储层边界描述不清楚。而在本文方法反演得到的高精度泊松比属性平面图(图 9b)中, 低泊松比代表的含油有利储层主要分布在KD405井和KD403井附近, 在砂岩储层不发育和含油气差的区域中高泊松比特征明显, 叠前泊松比含油气预测结果与钻井结果吻合好。应用本文方法既降低了油气预测的多解性, 更准确地刻画了砂体边界, 为储层预测和井位部署提供了更准确的地层弹性参数, 降低了油气勘探开发风险。
|
图 9 利用叠后地震数据提取的(a)和利用本文方法反演的(b)馆上4砂组泊松比剖面 |
本文从目标函数、迭代公式、雅克比矩阵构建及正则化参数设定等多个方面对线性化叠前地震反演方法进行了研究, 形成了模型驱动的高精度叠前地震反演方法。叠前反演目标函数构建中增加了正则化约束项, 确保了反演的稳定性, 采用直接基于佐普里兹方程矩阵形式构建精确雅克比矩阵, 确保了反演精度和复杂地震地质资料的适应性, 高斯自适应正则化参数选取提高了正则化参数选取的智能化和反演精度。实际工区资料应用结果表明, 本文方法对实际地震资料适应性好, 反演精度高, 在复杂岩性流体预测方面具有广阔应用前景。
叠前地震反演是一综合性方法技术, 影响反演结果的因素较多, 本文主要对叠前反演技术核心方法开展了研究, 结果表明, 初始模型和子波对反演影响作用同样大, 下一步应该加强初始模型构建和反演子波提取及应用方面的研究。另外, 研究形成的自适应正则化参数选取方法, 没有考虑纵波速度、横波速度及密度扰动量的差异, 正则化参数选取不够精细, 需要进一步加强研究。
| [1] |
张丰麒, 魏福吉, 王彦春, 等. 基于精确Zoeppritz方程三变量柯西分布先验约束的广义线性AVO反演[J]. 地球物理学报, 2013, 56(6): 2098-2115. ZHANG F Q, WEI F J, WANG Y C, et al. Generalized linear AVO inversion with the priori constraint of trivariate cauchy distribution based on Zoeppritz equation[J]. Chinese Journal of Geophysics, 2013, 56(6): 2098-2115. |
| [2] |
代荣获, 张繁昌, 刘汉卿. 叠前地震资料AVA变参数反演方法[J]. 地球物理学进展, 2015, 30(1): 261-266. DAI R H, ZHANG F C, LIU H Q. AVA inversion using replacing parameters method for pre-stack seismic data[J]. Progress in Geophysics, 2015, 30(1): 261-266. |
| [3] |
刘晓晶, 印兴耀, 吴国忱, 等. 基于基追踪弹性阻抗反演的深部储层流体识别方法[J]. 地球物理学报, 2016, 59(1): 277-286. LIU X J, YIN X Y, WU G C, et al. Identification of deep reservoir fuids based on basis pursuit inversion for elastic impedance.Chinese[J]. Chinese Journal of Geophysics, 2016, 59(1): 277-286. |
| [4] |
张丰麒, 金之钧, 盛秀杰, 等. 基于基追踪-BI_Zoeppritiz方程广义线性脆性指数直接反演方法[J]. 地球物理学报, 2017, 60(10): 3954-3968. ZHANG F Q, JIN Z J, SHENG X J. A direct inversion for brittleness indes based on GLI with basic-pursuit decomposition[J]. Chinese Journal of Geophysics, 2017, 60(10): 3954-3968. |
| [5] |
张海燕, 刘怀山, 童思友, 等. 基于免疫遗传算法的弹性参数变化率多阶段叠前反演[J]. 石油地球物理勘探, 2009, 44(6): 690-694. ZHANG H Y, LIU H S, TONG S Y, et al. Elastic parameter change rate multi-stage pre-stack inversion based on immune genetic algorithm[J]. Oil Geophysical Prospecting, 2009, 44(6): 690-694. |
| [6] |
王彦超, 沈云发, 黄捍东. 基于快速模拟退火算法的叠前三参数同步反演[J]. 工程地球物理学报, 2012, 9(2): 221-226. WANG Y C, SHEN Y F, HUANG H D. Pre-stack simultaneous three-parameter inversion based on fast simulated annealing algorithm[J]. Chinese Journal of Engineering Geophysics, 2012, 9(2): 221-226. |
| [7] |
张进, 陈晓琦, 邢磊, 等. 基于改进粒子群算法的叠前弹性阻抗反演[J]. 物探化探计算技术, 2016, 38(3): 353-360. ZHANG J, CHEN X Q, XING L, et al. Application of particle swarm optimization in prestack elastic im pedance inversion[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2016, 38(3): 353-360. |
| [8] |
印兴耀, 王慧欣, 曹丹平, 等. 利用三参数AVO近似方程的深层叠前地震反演[J]. 石油地球物理勘探, 2018, 53(1): 129-135. YIN X Y, WANG H X, CAO D P, et al. Three term AVO approximation of Kf-fm-ρ and prestack seismic inversion for deep reservoirs[J]. Oil Geophysical Prospecting, 2018, 53(1): 129-135. |
| [9] |
张瑞, 文晓涛, 杨吉鑫, 等. 杨氏模量和泊松比反射系数近似方程及地震叠前反演[J]. 石油地球物理勘探, 2019, 54(1): 145-153. ZHANG R, WEN X T, YANG J X, et al. Two-term reflection coefficient equation with Young's modulus and Poisson ratio and its prestack seismic inversion[J]. Oil Geophysical Prospecting, 2019, 54(1): 145-153. |
| [10] |
刘福平, 孟宪军. 反演纵横波速度的Jacobian矩阵及精确计算方法[J]. 中国科学:地球科学, 2010, 40(11): 1608-1616. LIU F P, MENG X J. Jacobian matrix for the inversion of P- and S-wave velocities and its accurate computation method[J]. Scientia Sinica(Terrae), 2010, 40(11): 1608-1616. |
| [11] |
黄捍东, 王彦超, 郭飞, 等. 基于佐普里兹方程的高精度叠前反演方法[J]. 石油地球物理勘探, 2013, 48(5): 740-749. HUANG H D, WANG Y C, GUO F, et al. High precision prestack inversion algorithm based on Zoeppritz equations[J]. Oil Geophysical Prospecting, 2013, 48(5): 740-749. |
| [12] |
王振涛, 王玉梅, 王希萍. 基于精确偏导计算的高精度叠前反演方法[J]. 科学技术与工程, 2014, 14(20): 26-30. WANG Z T, WANG Y M, WANG X P. High accurate prestack inversion method based on the accurate partial derivative calculation[J]. Science Technology and Engineering, 2014, 14(20): 26-30. |
| [13] |
张繁昌, 李栋, 代荣获. 基于边缘保持平滑正则化的地震反演方法[J]. 中国矿业大学学报, 2015, 44(2): 255-261. ZHANG F C, LI D, DAI R H. Seismic inversion based on edge preserving smooth regularization[J]. Journal of China University of Mining & Technology, 2015, 44(2): 255-261. |
| [14] |
张元中, 周开金, 赵建斌, 等. 砂泥岩地层横波测井曲线预测方法研究[J]. 石油物探, 2012, 51(5): 508-514. ZHANG Y Z, ZHOU K J, ZHAO J B, et al. Shear-wave logging curve prediction method for shaly sand formation[J]. Geophysical Prospecting for Petroleum, 2012, 51(5): 508-514. |
| [15] |
王振涛, 董月昌, 王玉梅. 孤南地区浅层稠油弹性参数敏感性分析及应用[J]. 石油物探, 2014, 53(3): 360-366. WANG Z T, DONG Y C, WANG Y M. Sensitivity analysis of elastic parameter for heavy oil reservoir and its application in Gu'nan area[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 360-366. |



