2. 三峡大学, 湖北宜昌 443002
2. China Three Gorges University, YiChang 443002, China
常规的偏移算法主要记录由连续反射层或主要不连续点(大断层)定义的“高能事件”, 它是地震解释人员通常使用的地震信息, 常被称作“镜像”能量。随着油气勘探开发研究的深入, 勘探目标逐步转向断层、裂缝、河道、粗糙岩丘边缘等地下小尺度不连续地质体[1], 这些小尺度地质体的地震响应通常表现为能量较弱的绕射波。
20世纪50年代, KREY[2]首先利用绕射波信息来研究地下地质异常体如断层、断点等。KLEM-MUSATOV等[3]指出, 绕射波振幅通常比反射波振幅弱一到两个数量级, 且在常规处理流程中多以反射波作为有效信号, 而那些高分辨率、低能量的绕射波信号常被破坏或压制。为了充分利用地震记录中的绕射波信息来刻画地下非均质地质体, 需要在全波场记录中将绕射波场分离并单独成像[4]。基于反射波和绕射波在运动学和动力学方面的特征差异[5-6], 国内外学者提出了许多不同的绕射波分离成像方法。按照绕射波分离成像的方法原理以及处理手段的差异可将现有方法分为:叠加、滤波、平面波解构滤波、聚焦-反聚焦、Radon变换-反Radon变换等。
1) 叠加方法:LANDA等[7]、KANASEWICH等[8]、TSINGAS等[9]提出在共偏移距道集和共断层点道集上使用绕射波走时曲线来描述绕射波相干的总和。LANDA等[10]利用在共绕射点剖面上叠加来自绕射点处的地震信号识别局部非均质地质体。
2) 滤波方法:KOZLOV等[11]进一步修改Kirchhoff偏移算子中的锥形权函数使其更好地压制反射能量, 对地震响应中的弱绕射波信息进行准确成像; BANSAL等[12]讨论了多种分离反射和绕射波场的方法, 主要包括共偏移距倾角滤波、正常时差校正倾角滤波、正常时差-倾角时差校正倾角滤波、特征向量滤波、Radon滤波等, 并由合成记录阐述了不同分离方法的优缺点; MOSER等[13]在Kirchhoff偏移积分公式中通过修改加权函数来实现反稳相绕射波提取; KOREN等[14]提出一种绕射波成像新方法, 即利用方向角分解设计加权叠加滤波器实现各向同性/各向异性介质中绕射波和反射波的分离, 同时提高连续构造和小尺度地质体的成像分辨率; 李晓峰等[15]在传统的Kirchhoff偏移算子中引入反稳相滤波器来压制反射波能量, 凸显绕射波能量, 并在成像过程中引入校正极性算子实现绕射波准确成像; 刘培君等[16]借助相关分析以及高斯束偏移的射线追踪构建反稳相滤波算子, 采用反稳相偏移得到绕射波成像剖面。
3) 平面波解构滤波方法:CLAERBOUT[17]最先提出平面波解构滤波器的概念, 并于1994年[18]进一步完善了该滤波器方法; FOMEL[19]改进了平面波解构滤波器, 使所需唯一参数为局部平面波场的斜率; TANER等[20]模拟了平面波剖面和平面波分解滤波器, 并依据反射波和绕射波在平面波地震记录上的同相轴连续性差异在叠前道集中进行绕射波分离成像; 黄建平等[21]对平面波分解(PWD)解构滤波器使用方法及其在叠前、叠后道集上分离成像绕射波进行了系统总结; 孔雪等[22]和刘玉金等[23]证实平面波剖面本质上具有区分绕射波和反射波特性, 并利用平面波解构滤波技术压制反射波来获得绕射波; 朱生旺等[24]利用局部倾角滤波技术和预测反演技术修正绕射波场分离时低倾角信息估计不足对平面波分解滤波器的影响, 从而提高绕射波成像结果的横向分辨率; DECKER等[25]在叠前偏移倾角道集上对每个固定倾角的成像剖面应用PWD解构滤波技术并叠加绕射波场获得单独的绕射波成像剖面。
4) 聚焦-反聚焦方法:KHAIDUKOV等[26]在叠前共炮点道集将反射波聚焦于镜像虚震源点, 而绕射波仍保持发散的状态, 利用聚焦切除-反聚焦方法成功提取断层、断点等小尺度地质体, 并对其成像; MOSER等[13]提出两种绕射波分离成像的方法, 一种方法是在叠前深度域利用聚焦滤除反射波实现绕射波分离与成像, 另一种方法是修改偏移算法的核函数, 采用反稳相偏移压制反射能量; BERKOVITCH等[27]利用绕射多次聚焦叠加的方法将选取的绕射波最优同相轴叠加从而得到主要包含绕射波的叠加剖面; RESHEF等[28]利用角道集上的绕射能量进行高分辨率速度分析。
5) Radon变换-反Radon变换方法:KLOKOV等[29]根据反射波同相轴在倾角域CIGs中表现为开口向上的“笑脸”状, 利用混合域Radon变换识别反射波顶点并消除反射能量, 增强绕射信号; KLOKOV等[30]推导了偏移倾角域反射波和绕射波的解析表达式, 并利用混合域Radon变换实现绕射波场和反射波场分离。该方法计算成本低, 但是利用常规分辨率Radon变换分离的绕射波场中会存在大量残余反射波, 国内外学者致力于提高Radon变换的分辨率来改善波场分离效果。
Radon变换(Radon Transform, RT)首先由奥地利著名数学家J.RADON在1917年提出。20世纪70年代, 美国斯坦福大学以CLAERBOUT为代表的地球物理小组首次将Radon变换应用于地震勘探中, 并对线性Radon变换(τ-p变换)进行了重点研究。THORSON等[31]提出的随机反演方法提高了时间域Radon变换的分辨率; HAMPSON[32]提出频率域最小平方抛物线Radon变换, 该方法因其高效的计算效率迅速成为当时工业界的标准; SCALES等[33]将迭代重加权最小二乘算法与预条件共轭梯度法相结合, 有效求解了线性方程组中的大型稀疏矩阵; SACCHI等[34]提出高精度Radon变换, 即以有效信号的稀疏性作为约束条件利用迭代高分辨率算法求解; CARY[35]指出时间域Radon变换结果具有更强的稀疏性而频率域Radon变换能更准确地刻画有效信号的频率特征; HERRMANN[36]提出去假频高分辨率抛物线Radon变换(DHR), 该方法利用低频数据的无假频模型解构造加权算子来压制高频数据Radon空间的假频能量, 获得了较高的信噪比和分辨率。
在国内, 同样有许多学者致力于Radon变换研究。吴律[37]全面分析讨论了 τ-p变换的原理和应用; 牛滨华等[38]首次提出多项式Radon变换。许多国内学者[39-44]在提高Radon变换分辨率方面做了大量系统深入的研究工作。
为了解决Radon变换能量团泄漏, 绕射波场分离不彻底的问题, 本文在时间-频率混合域, 引入预条件算子并构建了新的时变稀疏模型权, 在倾角域CIGs上发展了一种基于预条件共轭梯度(PCG)算法的混合域高分辨率Radon变换绕射波分离成像方法。文中对比分析了本文方法与常规分辨率Radon变换、频率域高分辨率Radon变换在绕射波分离中的应用效果。
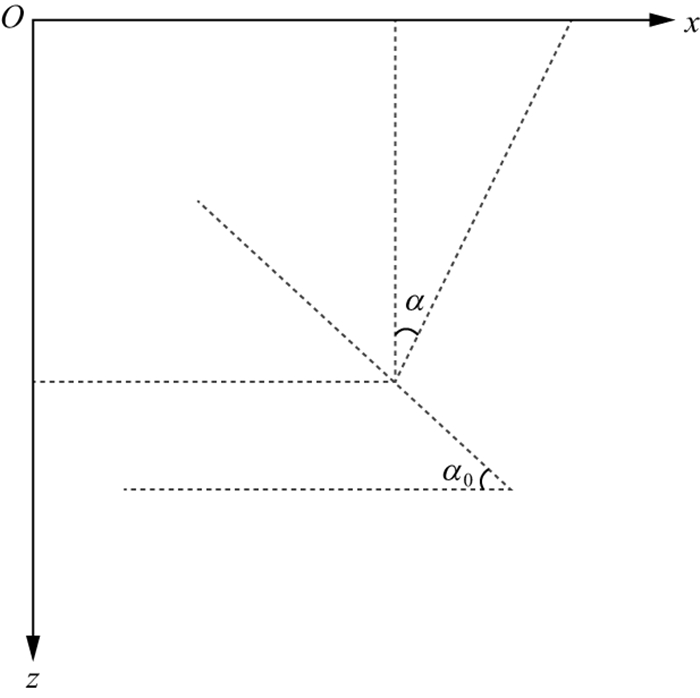
1 方法原理 1.1 倾角域共成像点道集波场特征分析常速介质叠后偏移反射面的深度z(x)可以表示为(图 1)[30]:
| $ z(x) = {z_0} + x{\kern 1pt} {\kern 1pt} {\rm{tan}}{\alpha _0} $ | (1) |
|
图 1 零偏移距反射示意 |
式中:z0表示倾斜反射界面与z轴交点的深度; α0为反射界面的倾角。在地表y处的自激自收地震响应可表示为:
| $ t(y) = \frac{{2({z_0}{\rm{cos}}{\alpha _0} + y{\rm{sin}}{\alpha _0})}}{v} $ | (2) |
式中:v表示介质速度, t为旅行时间。
由模型坐标{x, z}和数据坐标{y, t}之间的映射关系可以得到偏移公式:
| $ {x = y - \frac{{{v_{\rm{m}}}t}}{2}{\rm{sin}}\alpha } $ | (3) |
| $ {z = \frac{{{v_{\rm{m}}}t}}{2}{\rm{cos}}\alpha } $ | (4) |
式中:vm是偏移速度; α为偏移倾角。将公式(2)代入公式(3)和公式(4), 并消去y得到倾斜反射界面在倾角域的成像表达式:
| $ {z_\alpha }(x,\alpha ) = \frac{{({z_0}{\rm{cos}}{\alpha _0} + x{\rm{sin}}{\alpha _0}){v_{\rm{m}}}{\rm{cos}}\alpha }}{{v - {v_{\rm{m}}}{\rm{sin}}{\alpha _0}{\rm{sin}}\alpha }} $ | (5) |
对(5)式求偏导可以得到:
| $ \frac{{\partial {z_\alpha }(x,\alpha )}}{{\partial \alpha }} = \frac{{({z_0}{\rm{cos}}{\alpha _0} + x{\rm{sin}}{\alpha _0})({v_{\rm{m}}}{\rm{sin}}{\alpha _0} - v{\kern 1pt} {\rm{sin}}\alpha )}}{{{{(v - {v_{\rm{m}}}{\rm{sin}}{\alpha _0}{\rm{sin}}\alpha )}^2}}} $ | (6) |
从公式(6)可以看出, 当偏移速度准确时, 即vm=v且α=α0时, (6)式的偏导数值为0, 即α0为(5)式的一个极小值点。因此, 对于准确的偏移速度, 在倾角域CIGs上, 反射响应是一个具有稳相顶点的“笑脸”状曲线, 且稳相顶点的位置与地层倾角相对应。
类似地, 可以得到地下绕射点(x0, z0)处的倾角域响应表达式:
| $ {z_\alpha }(x,\alpha ) = \frac{{{v_{\rm{m}}}{\rm{cos}}\alpha [(x - {x_0}){v_{\rm{m}}}{\rm{sin}}\alpha + D]}}{{{v^2} - v_{\rm{m}}^2{\rm{si}}{{\rm{n}}^2}\alpha }} $ | (7) |
其中,
| $ {z_\alpha }(\alpha ) = {z_0} $ | (8) |
由(8)式可以看出绕射响应为一水平直线。
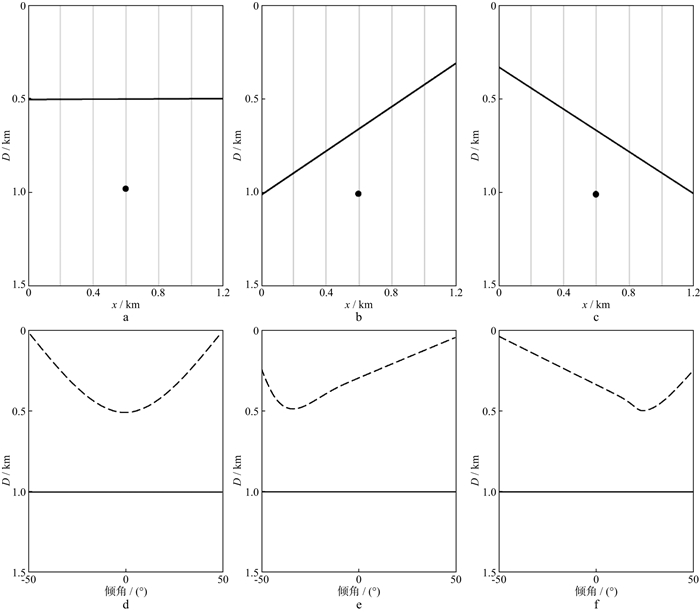
下面用3个理论模型来直观阐明倾角域道集曲线的特点, 并进一步分析反射波和绕射波的差异。图 2a至图 2c显示了3个理论模型, 均包含一个反射界面和一个绕射体, 绕射体位于地下1km处。图 2a中水平反射界面位于地下0.5km处, 图 2b和图 2c中反射界面分别向左倾斜和向右倾斜。我们从理论模型0.6km位置处(绕射点正上方)提取倾角域CIGs(图 2d至图 2f), 图 2d至图 2f中虚线表示反射界面(水平和30°倾斜反射界面); 实线表示绕射点处的倾角域响应曲线。
|
图 2 理论模型及偏移速度正确时的倾角域共成像点道集示意 a, b, c 包含一个反射界面和一个绕射点的理论模型; d a在0.6km处的倾角域CIGs; e b在0.6km处的倾角域CIGs; f c在0.6km处的倾角域CIGs |
从图 2d至图 2f可以看出, 对于反射界面来说, 不论界面是否倾斜, 在倾角域道集中响应曲线总是保持“微笑”的形状(如图中虚线所示), 且曲线的稳相顶点刚好指示界面的倾角; 而在绕射点位置处的绕射响应为水平直线(如图中实线所示)。
综上可知, 在倾角域CIGs中, 反射与绕射响应曲线存在明显的几何形态差异, 其中反射响应为具有稳相顶点的凹形曲线, 绕射响应为水平直线。我们可以利用两者之间形状差异将绕射波同相轴单独分离。下面以此原理我们采用抛物线Radon变换来分离倾角域CIGs中反射波和绕射波。
1.2 Radon变换原理二维Radon变换的定义式为:
| $ d(t,x) = \int\limits_{ - \infty }^{ + \infty } m (\tau = t - q{x^2},q){\rm{d}}q $ | (9) |
式中:d(t, x)为时间域地震数据; m(τ, q)为Radon域数据; t, τ分别为时空域的时间和Radon域的截距时间; q表示曲率参数; x为炮检距。将(9)式进行离散傅里叶变换, 转换到频率域, 可得:
| $ \mathit{\boldsymbol{D}}(\omega ,{x_k}) = \sum\limits_{i = 0}^{n - 1} \mathit{\boldsymbol{M}} (\omega ,{q_i}){{\rm{e}}^{ - {\rm{i}}\omega {q_i}x_k^2}} $ | (10) |
式中:D(ω, x)和M(ω, q)分别为d(t, x)和m(τ, q)的傅里叶变换结果; ω为频率; n为Radon域的曲率个数。由(10)式可知, 对于某一频率ω, Radon变换可以表示为一个线性方程组的求解问题:
| $ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{LM}} $ | (11) |
式中:L是Radon变换算子, 由地震数据道的相对空间位置x0, x1, …, xm-1和Radon变换参数q0, q1, …, qn-1来确定, 可表示为:
| $ \mathit{\boldsymbol{L}}(\omega ) = {\left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{i}}\omega {q_0}x_0^2}}}&{{{\rm{e}}^{{\rm{i}}\omega {q_1}x_0^2}}}& \cdots &{{{\rm{e}}^{{\rm{i}}\omega {q_{n-1}} }}x_0^2}\\ {{{\rm{e}}^{{\rm{i}}\omega {q_0}x_1^2}}}&{{{\rm{e}}^{{\rm{i}}\omega {q_1}x_1^2}}}& \cdots &{{{\rm{e}}^{{\rm{i}}\omega {q_{n - 1}}x_1^2}}}\\ \vdots & \vdots &{}& \vdots \\ {{{\rm{e}}^{{\rm{i}}\omega {q_0}x_{m - 1}^2}}}&{{{\rm{e}}^{{\rm{i}}\omega {q_1}x_{m - 1}^2}}}& \cdots &{{{\rm{e}}^{{\rm{i}}\omega {q_{n - 1}}x_{m - 1}^2}}} \end{array}} \right]_{m \times n}} $ | (12) |
| $ \mathit{\boldsymbol{D}} = {\left[ {\begin{array}{*{20}{c}} {d[0][\omega ]}\\ {d[1][\omega ]}\\ \vdots \\ {d[m - 1][\omega ]} \end{array}} \right]_{m \times 1}} $ | (13) |
| $ \mathit{\boldsymbol{M}} = {\left[ {\begin{array}{*{20}{c}} {m[0][\omega ]}\\ {m[1][\omega ]}\\ \vdots \\ {m[n - 1][\omega ]} \end{array}} \right]_{n \times 1}} $ | (14) |
常规Radon变换采用最小二乘反演计算, 定义目标函数:
| $ J = \left\| {\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{LM}}} \right\|_2^2 + \beta \left\| \mathit{\boldsymbol{M}} \right\|_2^2 $ | (15) |
对上述目标函数求极小值, 可以得到M的常规最小二乘解, 即:
| $ \mathit{\boldsymbol{M}} = {({\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}} + \beta \mathit{\boldsymbol{I}})^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{D}} $ | (16) |
其中, β为正则化参数, 用于调节观测数据误差‖D-LM‖的L2范数与约束项‖M‖22之间的权重, I表示单位矩阵。由(16)式可以看出, 在传统最小二乘意义下进行Radon变换计算时, 对所有频率均采用相同的β值, 其目的是为了提高矩阵运算的稳定性, 但该因子同时也对Radon域的数据进行了平滑, 降低了Radon变换的分辨率, 不能有效压制离散Radon变换产生的截断效应。此外, 在野外实际地震资料采集时由于采集孔径有限以及地震道的缺失, 基于最小二乘的常规分辨率Radon变换对能量团泄漏引起的剪刀状拖尾效应压制不够。
1.3 基于预条件共轭梯度(PCG)迭代的混合域高分辨率Radon变换为了提高Radon变换的分辨率, 在模型中引入稀疏约束条件, 将目标函数改写为:
| $ {J^\prime } = \left\| {\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{LM}}} \right\|_2^2 + \beta R(\mathit{\boldsymbol{M}}) $ | (17) |
式中:R(M)表示稀疏约束项。考虑到模型空间的噪声对Radon变换分辨率的影响比实际地震数据中的非线性噪声影响更为严重, 因此仅引入模型加权矩阵Wm来提高模型的拟合度, 如分辨率和平滑度。求解方程
| $ (\lambda \mathit{\boldsymbol{W}}_{\rm{m}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{\rm{m}}} + {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}})\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{D}} $ | (18) |
将Wm与抛物线型Radon变换算子L整合为新的核函数LWm-1, 并在计算矩阵与向量乘积时采用傅里叶变换(FFT)转换到频率域, 利用频率域Radon变换算子与频率域计算的解耦特性减少计算量, 然后再采用反FFT转换到时间域进行PCG迭代。因此, 优化方程(18)应改写为:
| $ (\lambda \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{W}}_{\rm{m}}^{ - {\rm{T}}}{F^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}F\mathit{\boldsymbol{W}}_{\rm{m}}^{ - 1})\mathit{\boldsymbol{\tilde M}} = \mathit{\boldsymbol{W}}_{\rm{m}}^{ - {\rm{T}}}{F^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}F\mathit{\boldsymbol{D}} $ | (19) |
其中,
| $ \mathit{\boldsymbol{W}}_{\rm{m}}^{ - {\rm{T}}}{F^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{LFW}}_{\rm{m}}^{ - 1}\mathit{\boldsymbol{\widetilde M}} = \mathit{\boldsymbol{W}}_{\rm{m}}^{ - {\rm{T}}}{F^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}F\mathit{\boldsymbol{D}} $ | (20) |
令A=F-1LTLF, b=F-1LTFD, 则方程(20)可以写为:
| $ \mathit{\boldsymbol{W}}_{\rm{m}}^{ - {\rm{T}}}\mathit{\boldsymbol{AM}} = \mathit{\boldsymbol{W}}_{\rm{m}}^{ - {\rm{T}}}b $ | (21) |
可得残差量表达式为:
| $ z = \mathit{\boldsymbol{W}}_{\rm{m}}^{ - {\rm{T}}}(b - \mathit{\boldsymbol{AM}}) $ | (22) |
常规Radon变换采用共轭梯度(CG)算法求解, 高分辨率Radon变换采用PCG反演方法, 本文基于PCG算法的高分辨率Radon变换处理步骤如下。
1) 由方程(11)计算得到频率域常规分辨率解, 经傅里叶变换由频率域变换到时间域, 作为PCG高分辨率迭代的初始解m0。
2) 外循环迭代计算模型矩阵Wm。Radon域数据元素为n×s(s表示加权矩阵在时间域τ方向的元素个数)个, 仅当模型加权矩阵是一个(n×s)×(n×s)的二维矩阵时, 其对角线元素个数才能是n×s个。由于该稀疏矩阵仅主对角线元素不为0, 且在使用共轭梯度法计算时不涉及该矩阵的求逆, 所以我们采用紧凑的模型权矩阵, 即与模型大小相同的加权矩阵进行隐式计算。其中,
3) 内循环迭代。用PCG法[45]迭代求解方程(20), 其中关键求解步骤如下。
① 计算初始残差值。r0:=b-Am0, z0:=Wm-1r0, p0:=z0。
② 求解迭代步长。αj:=(rj, zj)/(Apj, pj), 其中, j=0, 1, …, nmax为内部迭代次数, nmax表示设置的最大迭代次数。
③ 计算新的迭代解。mj+1:=mj+αjpj。
④ 计算更新残差。rj+1:=rj-αjApj。
⑤ 计算预条件残差值。zj+1:=Wm-1rj+1。
⑥ 求解共轭方向的搜索步长。βj:=(rj+1, zj+1)/(rj, zj)。
⑦ 计算下一次迭代的共轭向量。pj+1:=zj+1+βjpj。
当多次迭代后达到事先设置好的误差极限时, 即可得到(τ, q)的解。
4) 继续进行外部迭代, 求取满意的高分辨率解。利用步骤3)中的(τ, q)解, 重新计算稀疏约束矩阵, 重复步骤2)和步骤3), 继续迭代。外部迭代的主要作用是更新稀疏权, 增加(τ, q)解的稀疏性。
5) 进行Radon反变换, 完成反射波切除, 得到绕射波分离结果。
2 数据测试应用的技术流程主要包括:对倾角域CIGs进行Radon变换, 在Radon域将开口向上的反射波聚焦于曲率小于0的位置, 而绕射波的曲率在零值附近。在进行反射波切除时, 选择的Radon域切除的q值在0值附近, 以减少反射波能量的干扰并尽可能完整地保留绕射波信号。最后采用反Radon变换将分离出的绕射波同相轴恢复为时空域数据, 即从全波场中分离出绕射波。
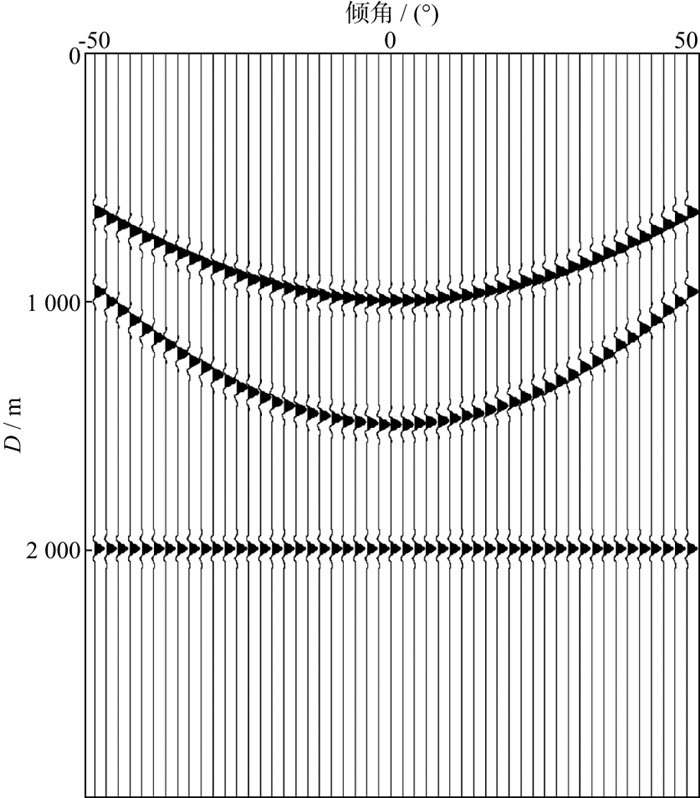
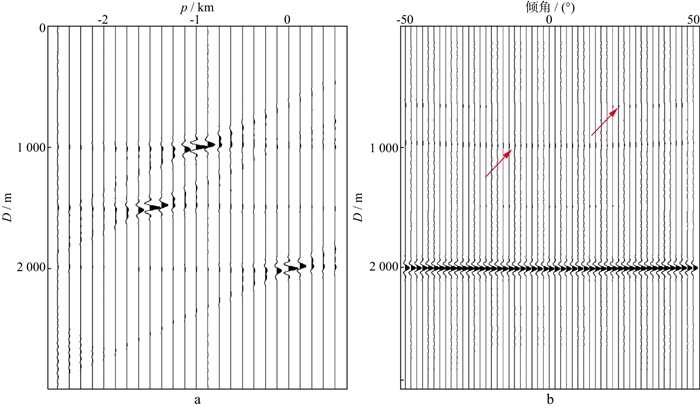
2.1 模拟数据测试在模拟的倾角域CIGs中, 包含两个反射波和一个绕射波响应曲线, 反射波顶点分别位于1000m、1500m, 绕射波则处于地下2000m, 如图 3所示。我们对比分析了最小二乘Radon变换方法、频率域高分辨率Radon变换方法和本文方法在Radon域中对绕射波的分离效果。采用最小二乘Radon变换对倾角域CIGs进行绕射波分离, 其Radon变换结果以及绕射波分离后的结果如图 4所示, 基于该方法所得到的Radon域结果具有明显的剪刀状发散, 这些有限孔径产生的端点假象严重影响了Radon变换的信噪比, 进而导致在绕射波分离结果中存在大量残余的反射能量(图 4b中红色箭头所示)。
|
图 3 模拟数据的CIGs记录 |
|
图 4 最小二乘Radon变换对绕射波的分离结果 a Radon域结果; b 绕射波分离后的结果 |
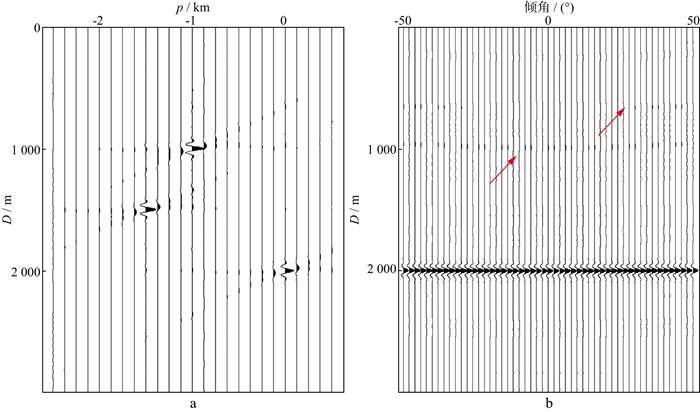
采用频率域高分辨率Radon变换对模拟CIGs记录进行绕射波分离, 其结果如图 5所示。从图 5可以看出, 频率域高分辨率Radon变换结果相较于最小二乘Radon变换结果, 剪刀状发散能量减弱, 分辨率有了明显提高, 但在绕射波上方的假象仍然存在。我们将内循环迭代次数分别选取为10次、20次、40次, 谱白化因子分别选取为0.01、0.05、0.10, 该假象依然存在。该方法得到的绕射波分离后的结果中同样存在反射波的残余。
|
图 5 频率域高分辨率Radon变换对绕射波的分离结果 a Radon域结果; b 绕射波分离后的结果 |
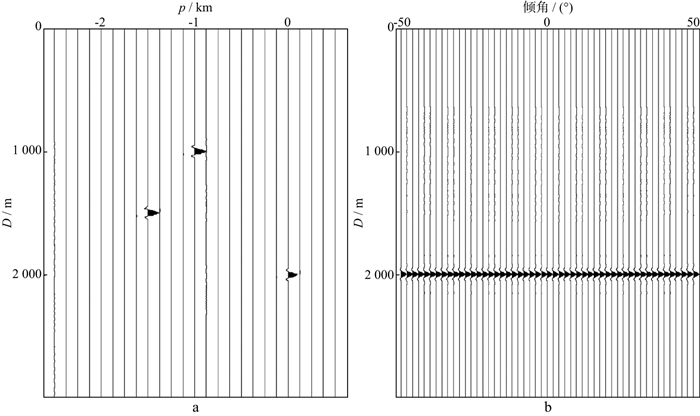
采用本文方法对该模拟数据进行绕射波分离, 结果如图 6所示。从图 6可以看出, 基于混合域高分辨率Radon变换的子波幅度无损失且分辨率很高, 绕射波分离后的结果也优于其它两种方法。
|
图 6 混合域高分辨率Radon变换对绕射波的分离结果 a Radon域结果; b 绕射波分离后的结果 |
绕射波场分离效果的好坏直接影响绕射波成像效果, 对比3种方法的分离结果可见, 基于混合域高分辨率Radon变换的绕射目标成像方法相较于其它两种方法得到的结果分辨率更高, 子波保持得更好, 这将有利于后续小尺度地质异常体的准确识别和定位。
2.2 实际资料测试选取中国西部M地区实际地震资料进行测试, 该地区溶蚀孔洞和裂缝储层十分发育, 利用传统的成像处理流程难以对储层内的多种绕射目标体如速度异常体、河道、断层、生物礁等进行精确成像。首先利用本文方法对某一CDP点下Kirchhoff叠前深度偏移(PSDM)中产生的倾角域CIGs进行反射波和绕射波分离。
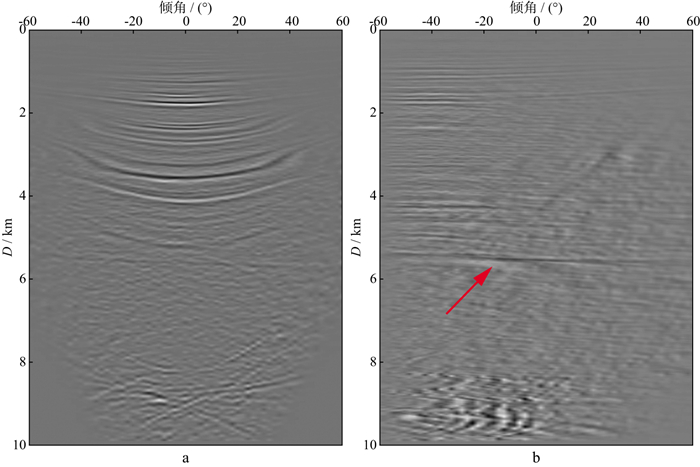
图 7a和图 7b分别为实际地震数据的倾角域CIGs和采用本文方法分离后的绕射波数据。从图 7可以看出, 原始道集中的强反射能量被明显压制, 由于大部分反射能量被去除, 淹没在全波场中的弱绕射能量凸显出来, 位于地下约5.5km处的绕射波同相轴能量明显加强, 如图中红色箭头所指部位。
|
图 7 基于混合域高分辨率Radon变换的倾角域CIGs波场分离结果 a 实际地震数据的全波场CIGs; b 波场分离后的绕射波CIGs |
进一步将本文方法应用于该地区某条测线的倾角域CIGs, 其波场分离前的PSDM剖面如图 8a所示, 由于强反射能量的干扰, 绕射点、断层点的位置难以识别。采用本文方法分离后的绕射波成像剖面如图 8b所示, 岩丘边界刻画更加清晰, 并且强反射同相轴被滤除, 淹没的绕射点、断层点位置凸显出来, 如图中红色箭头所指之处。图 8a和图 8b中蓝色方框部分的局部放大结果如图 8c和图 8d所示。从图 8d中能明显区分出绕射点, 如红色椭圆标示, 地下小型绕射体也被凸显出来。因此, 经过混合域高分辨率Radon变换滤波后得到的绕射波成像剖面可以联合反射波成像剖面进行准确、高确定性的地震解释。
3 结论本文通过对倾角域CIGs中的波场特征进行分析得到波场分离的依据, 进一步利用模拟数据对比分析了常规最小二乘Radon变换、频率域高分辨率Radon变换和混合域高分辨率Radon变换方法在波场分离中的效果, 并结合实际地震资料的应用, 得到以下结论。
1) 在倾角域CIGs中, 反射波地震响应曲线总是呈现出开口向上的“笑脸”状曲线, 绕射波同相轴则表现为拟线性。两者曲线形态的显著差异可以实现波场分离。
2) 与最小二乘Radon变换、频率域高分辨率Radon变换的倾角域绕射波波场分离方法相比, 混合域高分辨率Radon变换方法不仅可以有效保留子波的幅度, 而且在提高分辨率方面均优于其它两种方法, 在生产中具有更好的应用价值。
3) 本文绕射波分离成像技术完整保留了地下高分辨率、超高分辨率的绕射波信息, 分离的绕射波能够揭示地下小规模断裂构造、缝洞储层, 并与反映地下连续反射层或主要不连续点(大断层等)的反射能量联合解释, 可有效提高地震解释的精度。
| [1] |
LAUBACH S, MARRETT R, OlSON J. New directions in fracture characterization[J]. The Leading Edge, 2000, 19(7): 87-97. |
| [2] |
KREY T. The significance of diffraction in the investigation of faults[J]. Geophysical Prospecting, 1961, 9(S2): 77-92. DOI:10.1111/j.1365-2478.1961.tb01691.x |
| [3] |
KLEM-MUSATOV K, KOVALEVSKY G. On the intensity of waves diffracted on the edge[J]. Geology and Geophysics, 1972, 5(2): 82-92. |
| [4] |
HARLAN W S, CLAERBOUT J F, ROCCA F. Signal/noise separation and velocity estimation[J]. Geophysics, 1984, 49(4): 1869-1880. |
| [5] |
BAZELAIRE E D. Normal moveout revisited:inhomogeneous media and curved interfaces[J]. SEG Technical Program Expanded Abstracts, 1986, 5(1): 403. |
| [6] |
TROREY A W. A simple theory for seismic diffractions[J]. Geophysics, 1970, 35(5): 762-784. DOI:10.1190/1.1440129 |
| [7] |
LANDA E, SHTIVELMAN V, GELCHINSKY B. A method for detection of diffracted waves on common-offset sections[J]. Geophysical Prospecting, 1987, 35(4): 359-373. DOI:10.1111/j.1365-2478.1987.tb00823.x |
| [8] |
KANASEWICH E R, PHADKE S M. Imaging discontinuities on seismic sections[J]. Geophysics, 1988, 53(3): 334-345. DOI:10.1190/1.1442467 |
| [9] |
TSINGAS C, MARHFOUI B E, SATTI S, et al. Diffraction imaging as an interpretation tool[J]. First Break, 2011, 29(1): 57-61. |
| [10] |
LANDA E, KEYDAR S. Seismic monitoring of diffraction images for detection of local heterogeneities[J]. Geophysics, 1998, 63(3): 1093-1100. DOI:10.1190/1.1444387 |
| [11] |
KOZLOV E, BARASKY N, KOROLEV E. Imaging scattering objects masked by specular reflections[J]. Expanded Abstracts of 74th Annual Internat SEG Mtg, 2004, 1131-1134. |
| [12] |
BANSAL R, IMHOF M G. Diffraction enhancement in prestack seismic data[J]. Geophysics, 2005, 70(3): V73-V79. DOI:10.1190/1.1926577 |
| [13] |
MOSER T J, HOWARD C B. Diffraction imaging in depth[J]. Geophysical Prospecting, 2008, 56(5): 627-641. DOI:10.1111/j.1365-2478.2007.00718.x |
| [14] |
KOREN Z, RAVVE I. Specular/diffraction imaging by full azimuth subsurface angle domain decomposition[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg, 2010, 3268-3272. |
| [15] |
李晓峰, 黄建平, 李振春, 等. 基于反稳相滤波的边缘绕射成像方法研究[J]. 地球物理学进展, 2015, 30(3): 1205-1213. LI X F, HUANG J P, LI Z C, et al. Based on the steady phase filter edge diffraction imaging method research[J]. Progress in Geophysics, 2015, 30(3): 1205-1213. |
| [16] |
刘培君, 黄建平, 李振春, 等. 一种基于反稳相的深度域绕射波分离成像方法[J]. 石油地球物理勘探, 2017, 52(5): 967-973. LIU P J, HUANG J P, LI Z C, et al. A deep filed diffraction method based on anti-stationary phase[J]. Oil Geophysical Prospecting, 2017, 52(5): 967-973. |
| [17] |
CLAERBOUT JON F. Earth soundings analysis:Processing versus inversion[M]. London: Blackwell Scientific Publications, Inc, 1992: 1-334.
|
| [18] |
CLAERBOUT J F. Applications of two- and three-dimensional filtering[J]. Expanded Abstracts of 64th Annual Internat SEG Mtg, 1994, 1572-1575. |
| [19] |
FOMEL S. Applications of plane-wave destructor filters[J]. Geophysics, 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [20] |
TANER M T, FOMEL S, LANDA E. Separation and imaging of seismic diffractions using plane-wave decomposition[J]. Expanded Abstracts of 76th Annual Internat SEG Mtg, 2006, 2401-2405. |
| [21] |
黄建平, 李振春, 孔雪, 等. 基于PWD的绕射波波场分离成像方法综述[J]. 地球物理学进展, 2012, 27(6): 2499-2510. HUANG J P, LI Z C, KONG X, et al. The review of the wave filed separation method about reflection and diffraction based on the PWD[J]. Progress in Geophysics, 2012, 27(6): 2499-2510. |
| [22] |
孔雪, 李振春, 黄建平, 等. 基于平面波记录的绕射目标成像方法研究[J]. 石油地球物理勘探, 2012, 47(4): 674-681. KONG X, LI Z C, HUANG J P, et al. Research of diffraction imaging based on plane-wave record[J]. Oil Geophysical Prospecting, 2012, 47(4): 674-681. |
| [23] |
刘玉金, 李振春, 黄建平, 等. 绕射波叠前时间偏移速度分析及成像[J]. 地球物理学进展, 2013, 28(6): 3022-3029. LIU Y J, LI Z C, HUANG J P, et al. Time migration velocity analysis and imaging before diffraction wave stack[J]. Progress in Geophysics, 2013, 28(6): 3022-3029. |
| [24] |
朱生旺, 李佩, 宁俊瑞. 局部倾角滤波和预测反演联合分离绕射波[J]. 地球物理学报, 2013, 56(1): 280-288. ZHU S W, LI P, NING J R. Local dip filtering and predictive inversion combined with a separate diffraction wave[J]. Chinese Journal of Geophysics, 2013, 56(1): 280-288. |
| [25] |
DECKER L, KLOKOV A. Diffraction extraction by plane-wave destruction of partial images[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014, 3862-3867. |
| [26] |
KHAIDUKOV V, LANDA E, MOSER T J. Diffraction imaging by focusing-defocusing: An outlook on seismic superresolution[J]. Geophysics, 2004, 69(6): 1478-1490. DOI:10.1190/1.1836821 |
| [27] |
BERKOVITCH A, BELFER I, HASSIN Y, et al. Diffraction imaging by multifocusing[J]. Geophysics, 2009, 74(6): WCA75-WCA81. DOI:10.1190/1.3198210 |
| [28] |
RESHEF M, LIPZER N, LANDA E. Interval velocity analysis in complex areas-azimuth considerations[J]. Expanded Abstracts of 71st EAGE Conference and Exhibition, 2009, U010. |
| [29] |
KLOKOV A, BAINA R, LANDA E, et al. Diffraction imaging for fracture detection:Synthetic case study[J]. Expanded Abstracts of 80th Annual Internat SEG Mtg, 2010, 3354-3358. |
| [30] |
KLOKOV A, FOMEL S. Separation and imaging of seismic diffractions using migrated dip-angle gathers[J]. Geophysics, 2012, 77(6): S131-S143. DOI:10.1190/geo2012-0017.1 |
| [31] |
THORSON J R, CLAREBOUT J F. Velocity-stack and slant-stack stochastic inversion[J]. Geophysics, 1985, 50(12): 2727-2741. DOI:10.1190/1.1441893 |
| [32] |
HAMPSON D. Inverse velocity stacking for multiple elimination[J]. Expanded Abstracts of 56th Annual Internat SEG Mtg, 1986, 422-424. |
| [33] |
SCALES J A, GERSZTENKORN A, TREITE S. Fast Ip solution of large, sparse, linear systems: Application to seismic travel time tomography[J]. Journal of Computational Physics, 1988, 75(2): 314-333. DOI:10.1016/0021-9991(88)90115-5 |
| [34] |
SACCHI M D, ULRYCH T J. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 1995, 60(4): 1169-1177. DOI:10.1190/1.1443845 |
| [35] |
CARY P W. The simplest discrete Radon transform[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1998, 1999-2002. |
| [36] |
HERRMANN P. De-aliased, high-resolution radon transforms[J]. Expanded Abstracts of 70th Annual Internat SEG Mtg, 2000, 1953-1956. |
| [37] |
吴律. τ-ρ变换及应用[M]. 北京: 石油工业出版社, 1993: 9-11. WU L. τ-ρ transform and it's application[M]. Beijing: Petroleum Industry Press, 1993: 9-11. |
| [38] |
牛滨华, 孙春岩, 张中杰, 等. 多项式Radon变换[J]. 地球物理学报, 2001, 44(2): 263-271. NIU B H, SUN C Y, ZHANG Z J, et al. Polynomial radon transform[J]. Chinese Journal of Geophysics, 2001, 44(2): 263-271. |
| [39] |
朱生旺, 魏修成, 李锋, 等. 用抛物线Radon变换稀疏解分离和压制多次波[J]. 石油地球物理勘探, 2002, 37(2): 110-115. ZHU S W, WEI X C, LI F, et al. Separating and suppressing multiples by sparse solution of parabolic Radon transform[J]. Oil Geophysical Prospecting, 2002, 37(2): 110-115. |
| [40] |
刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15. LIU X W, LIU H, LI Y M. High resolution radon transform and its application in seismic signal processing[J]. Progress in Geophysics, 2004, 19(1): 8-15. |
| [41] |
霍志周, 熊登, 张剑锋. 预条件共轭梯度法在地震数据重建方法中的应用[J]. 地球物理学报, 2013, 56(4): 1321-1330. HUO Z Z, XIONG D, ZHANG J F. Application of the preconditioned conjugate gradient method to reconstruction of seismic data[J]. Chinese Journal of Geophysics, 2013, 56(4): 1321-1330. |
| [42] |
巩向博, 韩立国, 王升超. 混合域高分辨率双曲Radon变换及其在多次波压制中的应用[J]. 石油物探, 2016, 55(5): 711-718. GONG X B, HAN L G, WANG S C. High-resolution hyperbolic Radon transform and its application in multiple suppression[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 711-718. |
| [43] |
邱新明, 汪超, 苑益军, 等. Radon变换及其在地震矢量数据处理中的应用研究现状[J]. 石油物探, 2017, 56(6): 905-914. QIU X M, WANG C, YUAN Y J, et al. Research status of the application of Radon transform in seismic vector field processing[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 905-914. |
| [44] |
薛亚茹, 王敏, 陈小宏. 基于SL0的高分辨率Radon变换及数据重建[J]. 石油地球物理勘探, 2018, 53(1): 1-7. XUE Y R, WANG M, CHEN X H. High resolution Radon transform based on SL0 and its application in data reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 1-7. |
| [45] |
SAAD Y. Iterative methods for sparse linear systems, second edition[J]. IEEE Computational Science & Engineering, 1996, 3(4): 88. |