2. 东华理工大学地球物理与测控技术学院, 江西南昌 330013
2. School of Geophysics and Measurement Control Technology, East China University of Science and Technology, Nanchang 330013, China
地震旅行时层析成像技术可用于预测地下地质体的分布情况, 该技术已广泛应用于石油勘探、矿产勘查和工程勘探等领域[1-6]。旅行时正演模拟是地震旅行时层析成像技术的重要组成部分, 正演模拟的精度和计算效率影响着最终的反演效果[7]。射线追踪类方法、程函方程的有限元解法和有限差分解法是常见的3类地震旅行时正演模拟方法[8-13], 其中有限差分法相对有限元法更易于实现, 且能计算出目标区域内所有网格节点的旅行时, 不存在射线追踪类方法无法到达的阴影区域, 因此该方法在地震波旅行时计算中得到广泛应用。
1988年VIDALE[14]提出了盒式扩展法, 利用有限差分的盒式扩展形式计算程函方程的数值解, 首次快速高效地计算了复杂速度模型的地震波旅行时场, 但这种方法的扩展规律不符合程函方程的因果关系条件, 因此稳定性较差。1991年VAN等[15]改进了盒式扩展法的有限差分格式, 并结合迎风差分格式提高了地震波旅行时计算方法的稳定性。1992年QIN等[16]以波前面的波前点作为扩展要素, 提出了波前扩展方法, 该方法的求解方式存在缺陷, 计算复杂速度模型时稳定性较差。后经不断改进, 有限差分计算方法求解程函方程的结果稳定性有了明显改善。1996年SETHIAN[17]结合迎风有限差分方法和窄带技术提出了快速推进算法, 2004年ZHAO[18]综合利用程函方程的因果关系条件和Gauss-Seidel迭代法提出了快速扫描算法。上述两种有限差分旅行时计算方法都具有计算精度高、计算速度快且无条件稳定的特点, 是现今较为成熟的旅行时计算方法[19-21]。
快速推进算法在考虑因果关系条件的前提下, 采用了窄带技术[22], 该技术的思路是将计算区域内的网格节点分为接受点(旅行时已知的网格点)、窄带点(旅行时等待计算的网格点)和远离点(旅行时尚未计算的网格点)。窄带技术先将远离点逐步转化为窄带点, 再进一步转换为接受点, 最终使未知点全部转换为已知点。在转换过程中, 需要频繁查找窄带点中的最小旅行时点, 并将其代入后续的迭代运算。
高效的排序方法能极大地提高快速推进算法的计算效率, 但相关的研究成果并不多见。常规的快速推进算法一般采用计算机技术中排序能力强的方法对窄带点进行排序。堆排序方法如二叉树和三叉树排序方法是快速推进算法中常用的排序方法, 能有效提高算法的计算效率[23-24]。但堆排序方法仍然存在一定的不足:堆排序法属于非稳定类排序方法, 计算精度不如稳定类排序方法; 堆排序法的实现步骤较为繁琐, 需要额外的运算成本。针对上述问题, YATZIV等[25]提出了一种基于非严格优先列队的快速推进算法, 以提高旅行时算法的稳定性。在此基础上, 杨昊[26]对该算法进行了改进, 提出了分段最小排序的思路, 进一步提升了排序方法的稳定性。虽然这两种改进后的排序方法都属于稳定类排序法, 但二者只在排序层面讨论了算法的可行性, 未深入发掘旅行时场本身所隐含的有序性。本文通过分析程函方程的因果关系条件, 从原理上论证了旅行时场的有序性, 并以此为基础, 设计了适用于快速推进算法的插入排序方法。
本文首先介绍了利用有限差分格式求解程函方程的基本过程; 然后从程函方程的因果关系条件出发, 论证了旅行时场的有序性; 接着介绍了窄带技术的具体实现过程, 设计了相应的插入排序方法对窄带点进行排序, 进而实现了插入排序快速推进算法的应用; 然后将本文提出的插入排序快速推进算法与常规的三叉树堆排序快速推进算法以及作为稳定对照组的常规快速扫描方法分别进行测试并比较, 展示了插入排序快速推进算法的优势和不足; 最后, 详细分析和讨论了影响插入排序快速推进算法计算效率的因素, 以及算法计算效率与旅行时场的有序程度之间的相关性, 拓展了插入排序方法的适用领域。
1 方法原理 1.1 程函方程| $ {\left( {\frac{{\partial T}}{{\partial x}}} \right)^2} + {\left( {\frac{{\partial T}}{{\partial y}}} \right)^2} = {S^2}(x,y) $ | (1) |
式中:S为慢度; (x, y)为计算区域内任意一点的空间坐标; T为地震波旅行时。
利用迎风有限差分格式将程函方程离散, 可以得到网格节点(i, j)的旅行时计算公式:
当|Txmin-Tymin|≥Sh时:
| $ {T_{i,j}} = {\rm{min}}({T_{x{\rm{min}}}},{T_{y{\rm{min}}}}) + Sh $ | (2) |
当|Txmin-Tymin| < Sh时:
| $ {T_{i,j}} = \frac{{{T_{x{\rm{min}}}} + {T_{y{\rm{min}}}}\sqrt {2{S^2}{h^2} - ({T_{x{\rm{min}}}} - {T_{y{\rm{min}}}})} }}{2} $ | (3) |
式中:下标i和j分别对应x和y轴方向上的网格节点序号; h代表网格间距(假设网格为等间距网格); Txmin=min(Ti+1, j, Ti-1, j), Tymin=min(Ti, j+1, Ti, j-1), min表示取括号中两个值的较小值。
1.2 因果条件程函方程属于哈密顿-雅克比方程(Hamilton-Jacobi equation), 二维哈密顿-雅克比方程因果关系条件为[27]:
| $ \frac{{\partial H}}{{\partial {p_x}}} \ge 0\quad \frac{{\partial H}}{{\partial {p_y}}} \ge 0 $ | (4) |
式中:H为哈密顿算子; px, py分别为x轴和y轴的广义坐标。
二维地震波程函方程对应的哈密顿算子可以表示为:
| $ H(x,y) = {\left( {\frac{{\partial T}}{{\partial x}}} \right)^2} + {\left( {\frac{{\partial T}}{{\partial y}}} \right)^2} - {S^2}(x,y) $ | (5) |
其对应的因果条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {2\frac{{\partial T}}{{\partial x}} \ge 0}\\ {2\frac{{\partial T}}{{\partial y}} \ge 0} \end{array}} \right. $ | (6) |
离散形式表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_{i,j}} - {T_{x{\rm{min}}}} \ge 0}\\ {{T_{i,j}} - {T_{y{\rm{min}}}} \ge 0} \end{array}} \right. $ | (7) |
式中:Ti, j由(2)式、(3)式计算得到。(7)式的物理意义如图 1所示, 图中波前面(虚线)与波场传播方向垂直, 波前面到达每个网格节点的先后顺序决定了该点的旅行时。
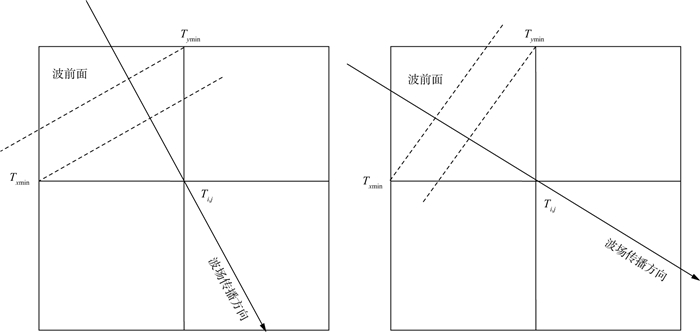
|
图 1 不同的波场传播方向和波前面示意 |
图 1展示了旅行时计算的局部规律, 由程函方程因果关系条件可知, 随着计算的进行, 旅行时有逐渐增大的趋势。均匀速度模型(速度为1km/s)的旅行时场展示了旅行时场的有序性。其整体规律表现为:网格节点上的旅行时值随网格节点位置与源点间的距离增大而增大(图 2)。
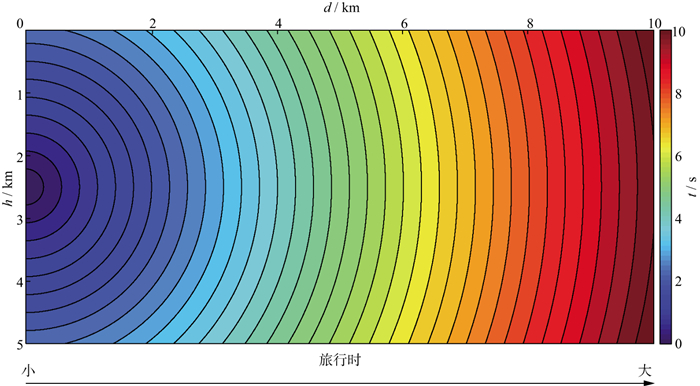
|
图 2 均匀速度模型的旅行时场(速度为1km/s) |
选取快速推进算法的排序方法时, 应当考虑以下3个方面的因素:①排序方法的排序能力强弱; ②实现排序方法所需的运算成本大小; ③排序目标是否存在特殊规律, 可否简化排序过程。
常规快速推进算法主要考虑排序方法的排序能力强弱, 因此认为“堆排序方法”的排序效果较好[23-24]。实际上, 虽然堆排序方法的排序能力强, 但其运算成本高。因果关系条件表明, 作为排序对象的旅行时场存在由小到大的分布规律。根据这一规律, 本文采用运算成本较小的插入排序方法替换堆排序方法, 以取得更好的计算效果。
对比插入排序方法和堆排序方法的时间和空间复杂度[24, 27], 结果见表 1, O为不同数值方法的复杂度函数, n代表模型网格节点的数量。插入排序方法在时间复杂度(最佳)上优于堆排序方法。这说明在适当的条件下, 插入排序方法的效率高于堆排序方法。
| 表 1 排序算法的时间和空间复杂度 |
快速推进算法采用窄带技术将计算区域内的所有网格节点分为接受点、窄带点和远离点(图 3)。接受点代表计算完成的已知旅行时点, 在后续计算过程中不再变化。远离点代表尚未计算的网格节点, 等待转换为窄带点接受计算。窄带点处于接受点与远离点之间, 是准备接受计算的点, 类似于地震波传播过程中的波前面。地震波场的传播方向由上风区向下风区扩散传播。在这一传播过程中, 首先将窄带点转化为接受点, 再将与窄带点相邻的远离点转化为窄带点, 使地震波场逐渐向外扩展, 从而达到将远离点全部转换为接受点的目的。
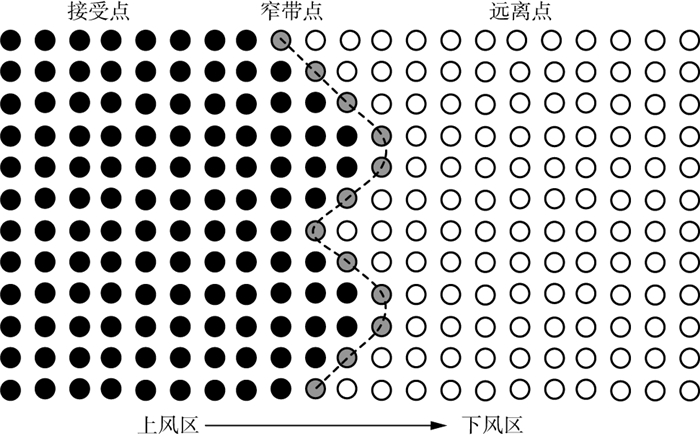
|
图 3 窄带技术示意 |
在快速推进算法的迭代过程中, 需要频繁地查找窄带点中的最小旅行时点并将其代入迭代计算中。常规快速推进算法通常采用堆排序的方法, 将窄带点中的数据按二叉树或三叉树形式进行排序。当排序的数据量较大时, 该方法能有效提升排序效率。
堆排序方法属于非稳定排序方法。非稳定排序方法定义如下:若序列中存在数据点a=b, 且原序列中a排列在b之前, 那么排序之后a可能会出现在b之后[27]。这种非稳定性对排序结果造成了一定程度的不利影响。插入排序法属于稳定的排序方法, 作为线性类型的排序方法, 其实现过程简单稳定。考虑到旅行时场具有有序性, 理论上需要排序的窄带点数组的数据量不会太大, 本文设计并实现了插入排序快速推进算法。
插入排序快速推进算法的具体流程如下。
1) 初始化
首先令源点处的旅行时T0=0, 并将其设置为接受点; 然后计算出源点的相邻点旅行时, 并将相邻点设为窄带点; 再将窄带点数组中的元素按旅行时值由小到大排序; 最后将其它网格节点设置为某个大于全局可能旅行时值的较大值, 将其属性设为远离点。
2) 迭代
在迭代过程中, 若窄带点数组(T1, T2, …, Tk, …, Tn)中共有n个元素, 则以k=1, 2, 3, …, n的顺序从窄带点数组中选取Tk点代入循环。此时窄带点数组中的元素由小到大排列, 因此每次选取的Tk点必定为窄带点数组中的最小值点。
选定Tk点后, 利用(2)式和(3)式更新Tk点的旅行时值, 并将Tk点属性从窄带点转换为接受点, 更新与Tk点相邻的远离点的旅行时值得到Tnew, 将这些点的属性转换为窄带点, 并将其插入窄带点数组中。其它与Tk点相邻的非远离点不作处理。
将更新得到的旅行时Tnew插入至窄带点数组的方法为:首先从数组末尾向前, 查找数组中刚好小于旅行时Tnew的点, 在数组的第m点处, 若Tm>Tnew, 则将窄带点数组中的Tm点向后移动一位, 即Tm+1=Tm; 接着令m=m-1, 对比下一个点的Tm值, 直到m点的旅行时值满足Tm < Tnew; 最后将新计算的点插入至Tm点的后一位, 即Tm+1=Tnew。完成以上插入流程后, 窄带点数组将保持由小到大的排列规律不变。
当所有与Tk相邻的远离点都完成了插入操作后, 令k=k+1, 选取窄带点数组中的下一个最小值点Tk代入循环, 直到满足迭代终止条件。
3) 截止条件
随着波前面的扩展和推进, 当计算区域内的所有网格节点都变为接受点时, 算法终止迭代。
3 数值模拟本文选用3种有限差分旅行时算法(插入排序快速推进算法(insert-sorting fast marching method, 简称FMM 1)、三叉树堆排序快速推进算法(ternary tree fast marching method, 简称FMM 2)和常规快速扫描算法(fast sweeping method, FSM))参与测试。因常规快速扫描算法经多次迭代扫描可以保证结果达到稳定收敛状态, 故将其作为一个稳定的参考解。将快速扫描算法的迭代终止的阈值设置为δ=10-9, 即相邻两次迭代间的旅行时场误差小于10-9时, 终止迭代。
测试的3个速度模型分别为:光滑非均匀速度模型、盐丘速度模型和Marmousi速度模型。其中光滑非均匀速度模型具有解析解, 可直接用于测试算法的精度; 其它两个复杂速度模型可用于测试算法的稳定性。
为对比3种有限差分算法的计算效率, 我们将每个速度模型都采样成6种网格离散模型, 网格节点数分别为:201×201, 401×401, 801×801, 1601×1601, 3201×3201, 6401×6401。对不同网格的模型测试3种算法, 每种算法测试5次, 并统计CPU时间, 取CPU时间的均值作为最终的运行时间。
3.1 光滑非均匀速度模型参考等梯度速度模型, 令模型速度值随计算点与源点之间的距离呈等梯度变化, 得到光滑非均匀速度模型[28]。该速度模型S(x)可表示为:
| $ \frac{1}{{\mathit{\boldsymbol{S}}(\mathit{\boldsymbol{x}})}} = \frac{1}{{{\mathit{\boldsymbol{S}}_0}}} + {\mathit{\boldsymbol{G}}_0}(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_0}) $ | (8) |
式中:S0为初始源点的慢度; G0为梯度向量; x表示计算点的空间位置; x0表示震源点的空间位置。
该速度模型的解析解为:
| $ {T_{{\rm{ ana }}}} = \frac{1}{{|{\mathit{\boldsymbol{G}}_0}|}}{\rm{ arccosh }}\left[ {1 + \frac{{\mathit{\boldsymbol{S}}(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{G}}_0^2{{(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_0})}^2}}}{2}} \right] $ | (9) |
| $ {\rm{arccosh}}(a) = {\rm{ln}}(a + \sqrt {{a^2} - 1} ) $ | (10) |
式中:a代表任意输入变量。
令S0=1, G0=(0.2, 0.2), 计算区域为10km×10km, 震源点为(5km, 0), 图 4为网格节点数为401×401时光滑非均匀速度模型的旅行时场。
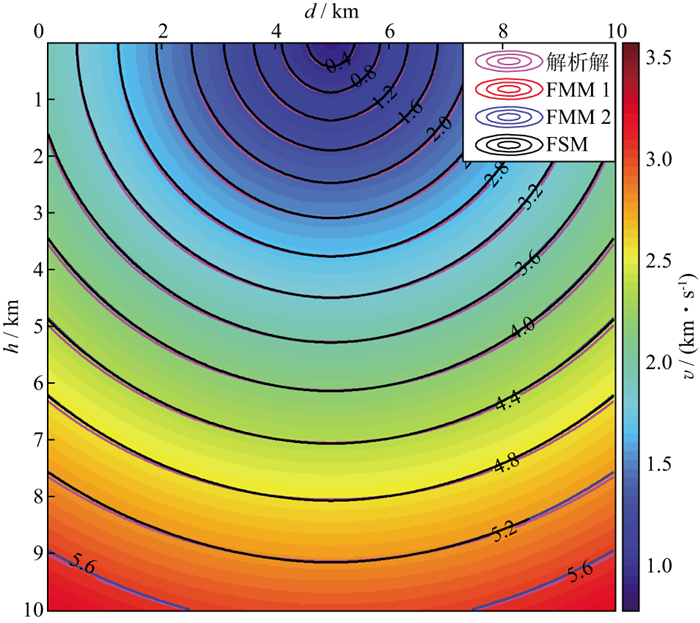
|
图 4 光滑非均匀速度模型的旅行时场(网格节点数为401×401) |
图 4中红色、蓝色和黑色等值线分别代表插入排序快速推进算法(FMM 1)、三叉树堆排序快速推进算法(FMM 2)和常规快速扫描算法(FSM)计算得到的旅行时, 紫色等值线代表(9)式的解析解。图 4中4种颜色的等值线几乎完全重合, 难以分辨采用3种不同算法计算得到的旅行时场之间的差别。
为了更详细地分析3种算法的计算精度, 根据如下公式:
| $ E = |{T_{{\rm{ ana }}}} - {T_{{\rm{ num }}}}| $ | (11) |
计算解析解Tana和数值解Tnum之间的误差E。
为方便比较, 将图 5中的色标(数值)范围固定为0~0.04s, 经逐点验证可知, 采用FMM 1和FSM得到的数值解与解析解的旅行时误差计算结果完全一致, 因此图 5a可同时表示FMM 1、FSM的数值解与解析解之间的旅行时误差。由于直角坐标系下的常规有限差分旅行时算法存在源点奇异性问题, 因此算法的计算误差较大, 且误差区域主要分布在假设波前与实际波前不匹配的区域(相对源点的倾斜方向上)[29]。对比图 5a和图 5b可以看出, 图 5a的旅行时误差明显更小, 且分布更为规律和平滑; 图 5b的旅行时误差分布一定程度上呈现锯齿状且较为散乱, 这证明采用FMM 2得到的旅行时计算结果收敛程度不够。
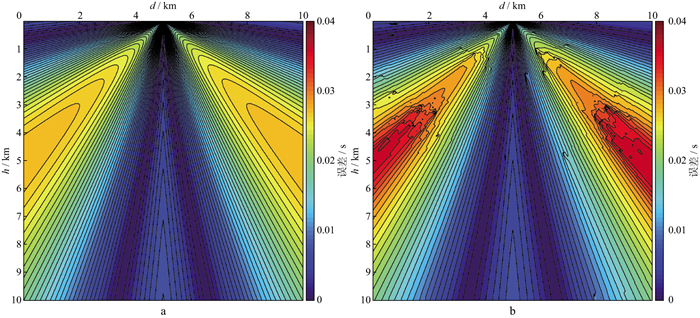
|
图 5 光滑非均匀速度模型中采用不同算法得到的数值解与解析解的旅行时误差 a FMM 1、FSM的数值解与解析解的旅行时误差; b FMM 2的数值解与解析解的旅行时误差 |
固定计算区域不变, 测试不同网格大小的光滑非均匀速度模型下各个算法的L2误差和CPU时间。图 6a展示了FMM 1和FMM 2的L2误差(均方差)统计结果[28]。可以看出整体上采用FMM 1得到的L2误差明显低于采用FMM 2得到的L2误差, 并且随着网格节点数的增加, 采用FMM 1得到的L2误差曲线下降更快。
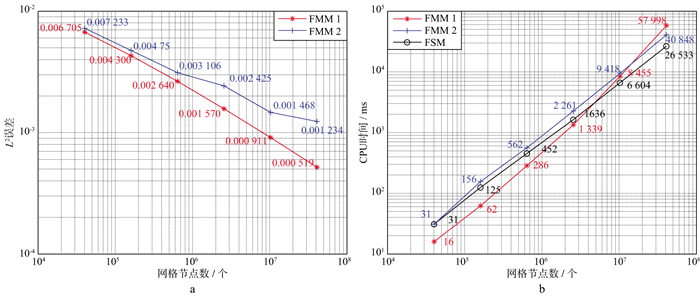
|
图 6 不同网格大小的光滑非均匀速度模型下各个算法的L2误差和CPU时间 a FMM 1和FMM 2的L2误差; b 3种算法的CPU时间 |
比较图 6b中3种算法的CPU时间可知, 在网格节点数小于801×801的情况下, 采用FMM 1所需的CPU时间约为其它两种方法耗时的一半, 说明在相同条件下FMM 1的运算效率明显更高。随着网格节点数的增加, FMM 1的运算效率逐渐降低。这是由于常规旅行时计算方法存在源点奇异性问题, 网格点数增加导致波前窄带点的数量增多且无序性增强。
3.2 盐丘速度模型通过增加盐丘速度模型的复杂度, 来测试复杂模型下插入排序快速推进算法的稳定性和计算效率。盐丘速度模型的计算区域为6.50km×4.99km, 震源点位置为(3.25km, 0), 图 7a为盐丘速度模型网格节点数为651×500时的测试结果。
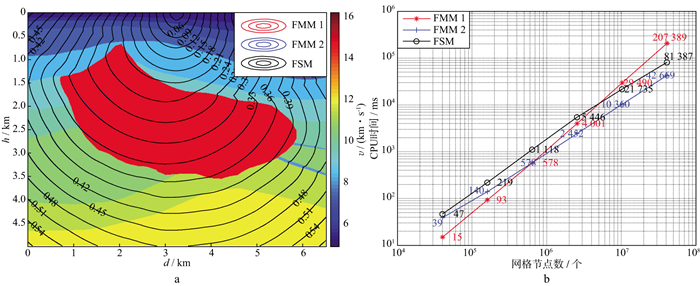
|
图 7 盐丘速度模型的测试结果 a 3种算法的旅行时场; b 3种算法的CPU时间 |
盐丘速度模型的旅行时场如图 7a所示, 采用FMM 1、FMM 2和FSM计算得到的旅行时一致性良好(三者的等值线几乎完全重合), 在一定程度上证明插入排序快速推进算法可在复杂模型中保持良好的稳定性。
由于模型的复杂度增加, 采用FSM时, 需要进行6次迭代才能满足迭代终止条件, 这一方面保证了旅行时计算结果足够稳定和精确, 另一方面也导致在该模型下采用FSM所需的CPU时间比采用FMM 2所需的CPU时间更长(图 7b)。此外, 相较于简单模型, 复杂模型中FMM 1的运算时间随模型网格节点数的增加上升得更快。
3.3 Marmousi速度模型Marmousi速度模型的计算区域为7.36km×7.49km, 源点位置为(3.68km, 0), 图 8a展示了该模型下网格节点数为737×750时的测试结果。
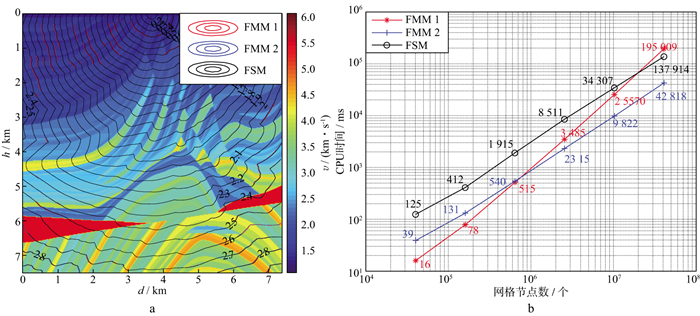
|
图 8 Marmousi速度模型的测试结果 a 3种算法的旅行时场; b 3种算法的CPU时间 |
如图 8a所示, Marmousi速度模型中, 采用3种算法所计算的旅行时结果整体匹配良好, 这进一步证明了FMM 1算法的稳定性。由于Marmousi速度模型的复杂度高于盐丘模型, 因此采用FSM需要9次迭代才能满足迭代终止的条件。如图 8b所示, 采用FSM所需的CPU时间明显大于采用FMM 2所需的CPU时间。结合图 6b、图 7b和图 8b, 进一步证明了模型的复杂度影响了FMM 1的运算效率。随着模型复杂度的增加, FMM 1的CPU时间随网格节点数增加而增长的趋势愈发强烈。
4 讨论与分析从上述的数值模拟结果不难发现, 模型网格节点数增多后, 插入排序快速推进算法的计算效率有所下降。为了进一步分析影响插入排序方法计算效率的因素, 我们统计了模型网格节点数均为401×401时, 各个模型中每个点在插入排序过程中向前移动的次数, 统计结果如图 9所示。图中某一点的移动次数越多, 则该点在运算过程中所需的排序时间越长。

|
图 9 各模型中各计算点在插入排序过程中向前移动的次数 a 光滑非均匀速度模型(未固定色标范围); b 光滑非均匀速度模型(固定色标范围); c 盐丘速度模型(固定色标范围); d Marmousi速度模型(固定色标范围) |
为了更好地判断旅行时场的有序程度与计算效率之间的关系, 我们对不同模型中旅行时的有序程度进行量化, 并定义其计算公式为:
| $ \mu = \frac{{\sum\nolimits_{i = 1}^n {{\tau _i}} }}{n} $ | (12) |
式中:μ为有序程度量, μ越小则表明旅行时场越有序, 反之则越无序; τi为i点在排序过程中向前移动的次数; n为模型的总网格节点数。
图 9a的色标范围为0~140次, 图 9b, 图 9c和图 9d的色标范围为0~700次。对比图 9a和图 5, 可以发现向前移动次数较多的点集中在因源点奇异性导致的误差较大的区域(图 9a中相对源点呈45°方向的明亮区域)。图 9c和图 9d分别与图 7a和图 8a存在相似的分布规律, 这证明源点奇异性不仅会影响插入排序快速推进算法的计算精度, 还会影响其计算效率。图 9中3个模型的有序程度量分别为18.902, 122.310, 133.302。根据有序程度量的定义可知, 图 9c和图 9d的两个速度模型的旅行时场比光滑非均匀速度模型的旅行时场更无序。回顾之前的CPU时间统计结果可知, 相较于简单模型(图 6b), 复杂模型(图 7b和图 8b)中采用FMM 1所需的CPU时间曲线随模型网格节点数的增加上升得更快, 证明了旅行时场越无序, 插入排序快速推进算法的效率越低。
图 9中排序次数较多的区域明显集中在由源点奇异性导致的误差较大的区域, 证明了源点奇异性与排序次数之间存在相关性。由于极坐标网格形态与点源地震波场的形态相似, 因此当震源点位于极坐标原点时, 源点奇异性问题可以被很好地压制[28]。为了排除源点奇异性对计算结果的影响, 从而更好地分析排序方法与计算效率之间的关系, 我们在极坐标系下对插入排序快速推进算法展开了测试。除了极坐标插入排序快速推进算法之外, 其它能压制源点奇异性问题的方法还包括在震源点周围局部网格加密和因式分解方法等[22, 29-31]。
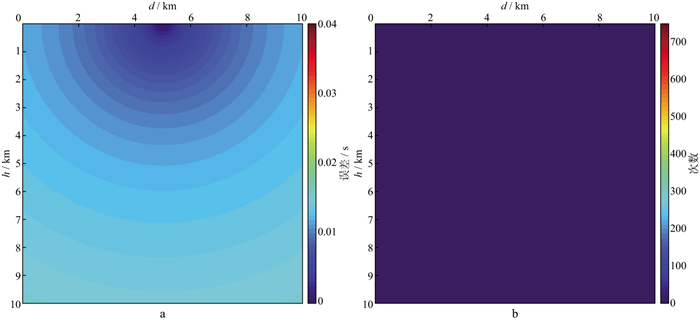
利用光滑非均匀速度模型测试极坐标插入排序快速推进算法。计算区域设置为半径7.1km的半圆, 本文只展示10km×10km的矩形计算区域, 模型网格节点数为401×401, 源点位于极坐标原点(5.0km, 0)处, 模型的速度分布情况与图 4一致, 测试结果如图 10所示。
|
图 10 光滑非均匀速度模型下极坐标插入排序快速推进算法的测试结果 a 解析解与数值解之间的误差; b 插入排序过程中全部计算点向前移动的次数 |
图 10a中的色标范围为0~0.04s(与图 5一致), 对比图 5和图 10a可知, 采用极坐标插入排序快速推进算法得到的误差远小于直角坐标插入排序快速推进算法得到的误差。前者得到的数值解与解析解之间的误差主要由模型网格化过程中导致的截断误差组成, 误差分布光滑, 极大地压制了由源点奇异性引起的误差。因此, 采用极坐标插入排序快速推进算法得到的旅行时计算结果更接近理论结果。图 10b中, 窄带点数组中的全部计算点向前移动的次数全部为0, 即有序程度量为0, 理论上旅行时场处于高度有序状态。
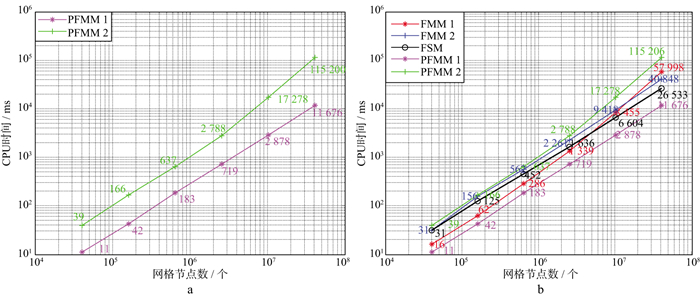
我们又统计了光滑非均匀速度模型在不同网格点数条件下, 采用极坐标插入排序快速推进算法(PFMM 1)和极坐标三叉树堆排序快速推进算法(PFMM 2)所需的CPU时间, 并将统计结果与之前的统计结果进行了比较, 结果分别如图 11a和图 11b所示。
|
图 11 光滑非均匀速度模型下各个快速推进算法的CPU时间统计结果 a PFMM 1和PFMM 2的CPU时间; b 5种算法的CPU时间 |
根据图 11的统计结果进一步分析快速推进方法的适用范围。该算法的运算成本可以粗略地拆分为:
| $ K = {K_{\rm{a}}} + {K_{\rm{b}}} + {K_{\rm{c}}} $ | (13) |
式中:K表示实现快速推进算法所需的总运算成本, Ka表示实现排序方法所需的运算成本; Kb表示不同排序方法对窄带点排序所需的运算成本; Kc表示计算旅行时所需的运算成本。
设插入排序快速推进算法的总运算成本为K1, 且分别由Ka1(实现插入排序方法所需的运算成本), Kb1(插入排序方法对窄带点排序所需的运算成本)和Kc1(插入排序快速推进算法计算旅行时所需的运算成本)组成。设堆排序快速推进算法的总运算成本为K2, 分别由Ka2(实现堆排序方法所需的运算成本), Kb2(堆排序方法对窄带点排序所需的运算成本)和Kc2(堆排序快速推进算法计算旅行时所需的运算成本)组成。由于插入排序方法的实现过程比堆排序方法的更简单(方法实现的运算成本更少), 因此Ka1 < Ka2; 由于堆排序方法的排序能力更强(同样数量的排序任务, 堆排序方法对窄带点排序所需的运算成本更少), 因此Kb1>Kb2; 由于旅行时计算方法完全一样, 这两种算法计算旅行时所需的时间相差无几, 因此Kc1≈Kc2。
综上所述, 分析各测试模型的CPU时间统计结果, 可以发现影响算法计算效率的关键因素是Ka和Kb在总运算成本K中所占比重。对于常规的直角坐标快速推进算法, 由于源点奇异性问题的存在, 造成窄带点数组的有序程度低, 因此增加模型网格节点数量会增加Kb在运算成本中所占的比重, 且由于Kb1>Kb2, 最终导致随着网格节点数增加插入排序方法所需的运算成本显著增加。在极坐标系下, 快速推进算法克服了源点奇异性问题, Kb在总运算成本中所占的比重小, 故受网格点数变化的影响也小, 且由于Ka1 < Ka2, 因此图 11a中PFMM 1整体的运算效率要远高于PFMM 2。
对比图 11b中5种算法的CPU时间可知, PFMM 1的计算效率明显优于其它方法, 说明在克服了源点奇异性问题的情况下, 快速推进算法无需采用复杂的排序方法对窄带点数组进行排序, 即可通过简单的插入排序方法可取得最佳的计算效果。
5 结论本文对程函方程的因果条件进行分析, 探讨了旅行时场隐含的有序性。在此基础上利用插入排序方法传统的堆排序方法对窄带点排序, 实现了基于插入排序方法的快速推进算法。采用数值模拟方法对插入排序快速推进算法、三叉树堆排序快速推进算法和快速扫描算法进行测试, 统计和比较3种算法的精度和效率, 结果表明:插入排序快速推进算法的计算精度要高于常规的三叉树堆排序快速推进算法, 计算结果与作为稳定参考组的快速扫描算法计算结果完全相同, 达到高度收敛状态, 三叉树堆排序快速推进算法存在计算结果不够收敛的问题。在计算效率的研究中, 分析插入排序快速推进算法的运算效率与旅行时场的有序性之间的关系可知, 对于一般(未解决源点奇异性问题)的直角坐标快速推进算法, 源点奇异性问题会导致旅行时场无序, 从而导致插入排序快速推进算法的计算效率不能达到理想状态, 此时插入排序快速推进算法的运算效率只在模型网格点数较少的情况下具有优势。但在压制了源点奇异性问题后, 旅行时场的有序性接近理论状态, 此时极坐标插入排序快速推进算法的计算效率全面优于常规的堆排序快速推进算法。
同样的技术应用于不同领域时, 应当考虑不同领域自身的特殊性。在选取快速推进算法的排序方法时, 应当考虑到旅行时场潜在的规律性, 而不应仅考虑排序方法的排序能力强弱。虽然对于存在源点奇异性问题的快速推进算法而言, 随着模型网格点数的增加, 堆排序方法的计算效率优于插入排序方法, 但造成这一现象的原因并不只是堆排序方法的排序能力优于插入排序方法, 其基本前提还包括了旅行时场受源点奇异性影响导致其有序性被破坏。随着旅行时算法的不断发展, 源点奇异性问题被解决, 因此采用插入排序方法替换原算法中的堆排序方法将是更好的选择。
| [1] |
ENGQUIST B, RUNBORG O. Computational high frequency wave propagation[J]. Acta Numerica, 2003, 12: 181-266. DOI:10.1017/S0962492902000119 |
| [2] |
RAWLINSON N, SAMBRIDGE M. The fast marching method:an effective tool for tomographic imaging and tracking multiple phases in complex layered media[J]. Exploration Geophysics, 2005, 36(4): 341-350. DOI:10.1071/EG05341 |
| [3] |
HUANG G, ZHOU B, LI H, et al. Seismic traveltime inversion based on tomographic equation without integral terms[J]. Computers & Geosciences, 2017, 104: 29-34. |
| [4] |
黄光南, 刘洋, TRYGGVASON A, 等. 变网格间距速度层析成像方法[J]. 石油地球物理勘探, 2013, 48(3): 379-389. HUANG G N, LIU Y, TRYGGVASON A, et al. Variable grid spacing velocity tomography[J]. Oil Geophysical Prospecting, 2013, 48(3): 379-389. |
| [5] |
黄国娇, 孙江兵, 白超英, 等. 三维TI介质中多波走时层析成像[J]. 石油地球物理勘探, 2018, 53(1): 63-72. HUANG G J, SUN J B, BAI C Y, et al. Seismic multi-wave traveltime tomography in 3D TI media[J]. Oil Geophysical Prospecting, 2018, 53(1): 63-72. |
| [6] |
黄光南, 邓居智, 李红星, 等. P-SV波和P-SH波非线性旅行时层析成像[J]. 石油地球物理勘探, 2015, 50(6): 1127-1133. HUANG G N, DENG J Z, LI H X, et al. Nonlinear traveltime tomography of P-SV and P-SH waves variable grid spacing velocity tomography[J]. Oil Geophysical Prospecting, 2015, 50(6): 1127-1133. |
| [7] |
张宇. 从成像到反演:叠前深度偏移的理论、实践与发展[J]. 石油物探, 2018, 57(1): 1-23. ZHANG Y. From imaging to inversion:Theory, practice, and technological evolution of prestack depth migration[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 1-23. |
| [8] |
赵烽帆, 马婷, 徐涛. 地震波初至走时的计算方法综述[J]. 地球物理学进展, 2014, 29(3): 1102-1113. ZHAO F F, MA T, XU T. A review of the travel-time calculation methods of seismic first break[J]. Progress in Geophysics, 2014, 29(3): 1102-1113. |
| [9] |
吴彦, 马玥, 刘玉金, 等. 全走时反演及其应用[J]. 石油物探, 2017, 56(1): 50-56. WU Y, MA Y, LIU Y J, et al. Full-traveltime inversion and its application[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 50-56. |
| [10] |
黄光南, 邓居智, 李红星, 等. 非均匀节点网格TI介质反射波射线追踪研究[J]. 石油物探, 2016, 55(1): 25-32. HUANG G N, DENG J Z, LI H X, et al. Reflected wave ray tracing in TI medium based on the nonuniform node meshes[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 25-32. |
| [11] |
黄兴国, 孙建国, 孙章庆, 等. 基于复程函方程和改进的快速推进法的复旅行时计算方法[J]. 石油地球物理勘探, 2016, 51(6): 1109-1118. HUANG X G, SUN J G, SUN Z Q, et al. A method for complex traveltime calculation based on the complex eikonal equation and the modified fast marching[J]. Oil Geophysical Prospecting, 2016, 51(6): 1109-1118. |
| [12] |
罗飞, 王华忠, 冯波, 等. 透射波旅行时Beam层析成像方法[J]. 石油物探, 2019, 58(3): 356-370. LUO F, WANG H Z, FENG B, et al. Beam tomography based on transmission traveltime[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 356-370. |
| [13] |
冯波, 吴成梁, 王华忠. 反射波层析反演速度建模方法[J]. 石油物探, 2019, 58(3): 371-380. FENG B, WU C L, WANG H Z. Velocity model building using reflection tomography[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 371-380. |
| [14] |
VIDALE J. Finite-difference calculation of travel times[J]. Bulletin of the Seismological Society of America, 1988, 53(5): 521-526. |
| [15] |
VAN T J, SYMES W W. Upwind finite-difference calculation of traveltimes[J]. Geophysics, 1991, 56(6): 812-821. DOI:10.1190/1.1443099 |
| [16] |
QIN F, LUO Y, OLSEN K B, et al. Finite-difference solution of the eikonal equation along expanding wavefronts[J]. Geophysics, 1992, 57(3): 478-487. DOI:10.1190/1.1443263 |
| [17] |
SETHIAN J. A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the National Academy of Sciences, 1996, 93(4): 1591-1595. DOI:10.1073/pnas.93.4.1591 |
| [18] |
ZHAO H K. A fast sweeping method for Eikonal equations[J]. Mathematics of Computation, 2004, 74(250): 603-628. DOI:10.1090/S0025-5718-04-01678-3 |
| [19] |
ZHANG Y T, ZHAO H K, QIAN J. High order fast sweeping methods for static Hamilton-Jacobi equations[J]. Journal of Scientific Computing, 2006, 29(1): 25-56. |
| [20] |
QIAN J, ZHANG Y T, ZHAO H K. A fast sweeping method for static convex Hamilton-Jacobi equations[J]. Journal of Scientific Computing, 2007, 30(1/2): 237-271. |
| [21] |
兰海强, 张智, 徐涛, 等. 地震波走时场模拟的快速推进法和快速扫描法比较研究[J]. 地球物理学进展, 2012, 27(5): 1863-1870. LAN H Q, ZANG Z, XU T, et al. A comparative study on fast marching and fast sweeping methods in the calculation of first-arrival traveltime field[J]. Progress in Geophysics, 2012, 27(5): 1863-1870. |
| [22] |
RAWLINSON N, SAMBRIDGE M. The fast marching method:an effective tool for tomographic imaging and tracking multiple phases in complex layered media[J]. Exploration Geophysics, 2005, 36(4): 341-350. DOI:10.1071/EG05341 |
| [23] |
孙章庆.复杂地表条件下地震波走时计算方法研究[D].长春: 吉林大学, 2008 SUN Z Q.Study on the computation method of seismic traveltimes including surface topography[D]. Changchun: Jilin University, 2008 |
| [24] |
杨昊, 孙建国, 韩复兴, 等. 基于完全三叉树堆排序的波前扩展有限差分地震波走时快速算法[J]. 吉林大学学报:地球科学版, 2010, 40(1): 188-194. YANG H, SUN J G, HAN F X, et al. Fast algorithm of the expanding wavefronts finite-difference traveltime calculation based on the three branch tree structure heap sorts[J]. Journal of Jilin University(Earth Science Edition), 2010, 40(1): 188-194. |
| [25] |
YATZIV L, BARTESAG A, SAPIRO G, et al. Short note:On implementation of the fast marching algorithm[J]. Journal of Computational Physics, 2006, 212(2): 393-399. DOI:10.1016/j.jcp.2005.08.005 |
| [26] |
杨昊.有限差分法地震波走时计算的快速算法研究[D].长春: 吉林大学, 2007 YANG H.Study on the fast computation technique of seismic traveltimes with finite-difference method[D]. Changchun: Jilin University, 2007 |
| [27] |
王立柱. C/C++与数据结构[M]. 第四版. 北京: 清华大学出版社, 2002: 30-31. WANG L Z. C/C++ and data structure[M]. Fourth Edition. Beijing: Tsinghua University Press, 2002: 30-31. |
| [28] |
ALKHALIFAH T, FOMEL S. Implementing the fast marching eikonal solver:Spherical versus Cartesian coordinates[J]. Geophysical Prospecting, 2001, 49(2): 165-178. DOI:10.1046/j.1365-2478.2001.00245.x |
| [29] |
FOMEL S, LUO S, ZHAO H. Fast sweeping method for the factored eikonal equation[J]. Journal of Computational Physics, 2009, 228(17): 6440-6455. DOI:10.1016/j.jcp.2009.05.029 |
| [30] |
BOUTEILLER P L, BWNJEMAA M, METIVIER L, et al. An accurate discontinuous Galerkin method for solving point-source Eikonal equation in 2-D heterogeneous anisotropic media[J]. Geophysical Journal International, 2018, 212(3): 1498-1522. DOI:10.1093/gji/ggx463 |
| [31] |
HUANG G, LUO S, ARI T, et al. First-arrival tomography with fast sweeping method solving the factored eikonal equation[J]. Exploration Geophysics, 2019, 50(2): 144-158. DOI:10.1080/08123985.2019.1577110 |




