2. 中国石油化工股份有限公司西北油田分公司, 新疆乌鲁木齐 830011
2. Northwest Oilfield Branch of Sinopec, Urumchi 830011, China
当前陆上油气地震勘探往往投入大量人力、物力、财力, 开展超过数百平方千米的高精度三维地震数据采集。期望通过时间采样间隔1ms, 道间距15m, 超过100次覆盖, 千道接收, 24位数字记录, 井中小药量激发, 检波器深埋、紧埋, 小组距小面积组合, 降低地面干扰背景等多种措施, 得到地下构造的高分辨率精细图像。地震数据处理时, 常以“提升高频、展宽频带”作为高分辨率处理技术的思路, 如多种子波处理及反褶积, 精细静校正、精细速度分析以及Q补偿等技术。通过这些努力, 所得到的目的层反射波数据的优势频率多保持在20~30Hz, 高截频通常不超过40Hz, 个别能达到50~60Hz, 这与高精度地震数据采集的目的相悖。
这一结果似乎与数字地震仪中存在“高频死亡线”的论断相符合, 地震反射信号高频成分的采集是否止步于此, 陆上地震勘探的分辨率是否局限于此, 本文对此进行讨论。
高频死亡线[1]是以数字地震仪中的分频记录和数字占位为基础, 判断强弱不同的高、低频成分能够同时记录下来的极限。在地震数据采集记录过程中, 如果高频成分振幅弱于低频成分振幅1000倍以上(60dB), 那么此类高频成分因难以在后续的处理中被恢复真实波形而死亡。反褶积处理和谱白化处理中的白噪系数使高频振幅不可提升, 频率泄漏无助于减小低频和高频振幅之间的差距, 也不能使高频成分振幅与强低频成分振幅之差小于1000倍, 因此地震数据处理无益于恢复弱高频率成分。以上皆为高频死亡线成立的理由。
根据李庆忠[1]提出的“仪器中存在60dB高频死亡线”的论断, 可以得出以下的推论。①对陆上的石油地震勘探而言, 现在的主要问题是风吹草动引起的高频微震干扰太强, 远超中、深层反射波的高频信号电平, 因此强度仅占总强度1/1000的高频信号难以被准确地分离, 并被恢复真实波形[1], 此时追求优质的24位A/D地震仪或优质的高频检波器已经失去了实际意义[2]。②依据60dB高频死亡线, 可推算出不同地区的死亡频率, 如新疆沙漠地区, 反射时间为1.09s的T2层, 死亡频率为50Hz; 反射时间为2.09s的T3层, 死亡频率为43Hz, 反射时间为3.09s的T4层, 死亡频率为40Hz[3]。
在数字地震仪中是否存在限制高频信号记录的高频死亡线?高频信号是如何被记录下来的?本文围绕上述问题进行讨论。
1 地震仪对高频信号的可记录范围 1.1 高频死亡线的提出李庆忠[1]的专著《走向精确勘探的道路——高分辨率地震勘探系统工程剖析》在“地震仪对高频信号的可记录范围”一章中, 讨论了高、低频信号能够同时记录的极限, 并提出“仪器动态范围是指地震仪可以分别接收由浅到深、强弱相差110dB的信号”, “现在我们要讨论的问题不是深、浅层信号强弱变化的范围, 而是在同一时刻, 弱高频信号与强低频信号同时进来的情况下, 高频弱信号能否以足够的精度被记录下来”, “假设高频弱信号在记录中至少用4个二进位数(15个值)、加符号位才能初步记录下它的波形, 使该波形在数字处理中得以恢复其大致面貌”, “如此, 强低频信号与弱高频信号的振幅相对差为210=1024倍(即60dB), 我认为这就是高、低频信号能同时被记录下来的极限”, “我称这种高频信息不能被地震仪器记录下来的60dB限制为高频的‘死亡线’”等观点。
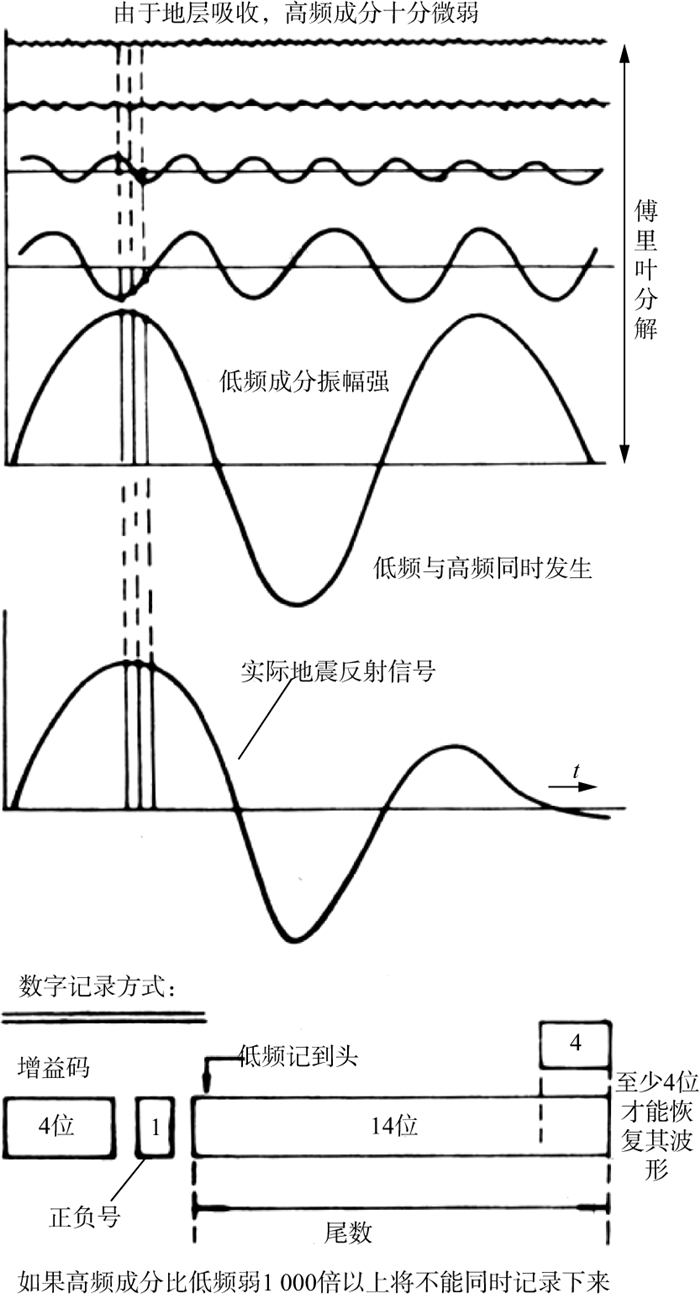
文献[1]的图34展示了地震信号数字记录的过程, 也是高频死亡线提出的依据(图 1):①地震信号进入仪器后, 经傅里叶变换被分解为不同频率、不同振幅的多个谐波, 其中, 低频谐波振幅强, 高频谐波振幅弱; ②对这些谐波进行离散采样, 同一时刻可以得到多个不同频率的、不同强弱的振幅值, 它们将被记录在同一个存储单元中; ③对不同频率谐波的振幅值, 依据数值的大小, 分别占据同一个存储单元尾数的不同数位(bit), 其中振幅数值小的弱高频成分, 如果最多只能占到尾数的最后4位有效位, 而强低频振幅占到尾数的14位时, 此时弱高频振幅比强低频振幅弱1000倍以上(60dB), 那么高频信号因难以在后续的处理中恢复其真实波形而死亡。李庆忠[1]还指出“如果野外记录上存在强面波, 则面波的振幅往往比低频有效波强10~20倍, 此类情况下, 高频有效波可以被记录下来的瞬时动态范围就不到40dB了”。由此可见, 弱高频成分死亡的根本原因是在数字记录过程中存在信号的“分频”和数据的“占位”。
|
图 1 地震信号数字记录的过程[1] |
所谓“分频”, 是指地震信号进入地震仪之后, 经傅里叶变换分解为不同频率、不同振幅值的谐波, 这些谐波的振幅值在同一时刻被离散采样得到多个振幅值。所谓“占位”, 是指同一时刻的多个强弱不同的低频和高频振幅值被存入同一个存储单元, 它们依据其各自振幅的强弱, 占据这个存储单元尾数中的不同数位。
1.2 叠前数据滤波扫描证实陆上原始数据缺失高频成分在地震信号数据记录过程中, 弱高频信号会死亡, 文献[1-2]均介绍了判断地震采集数据中是否存在有效高频成分的分频扫描方法—倍频程带通滤波扫描, 用于判断在实际数据中是否存在上述情况。
倍频程带通滤波扫描是检查信噪比谱的最佳方法, 可直观地判断信号与噪声在全频谱上的分布特点(存在同相轴影子, 即信噪比大于1)。该方法采用大约一个倍频程的带通滤波器, 从低频档一直扫描到高频档, 分析信号与噪声在不同频档的表现。实际应用时发现, 对于陆上野外地震数据往往扫描到60~120Hz就呈现一片混乱, 扫描结果似乎佐证着高频死亡线的存在。因此, 李庆忠在文献[1]中指出, “由此可以看出80Hz以上的高频信号在野外就没有以足够的信噪比记录下来, 可惜我们野外采集人员往往看不到这种分频扫描的结果。”这似乎在告诉地震数据采集专家, 野外采集技术措施存在问题, 需要加以改进, 以记录更高的频率成分; 同时也似乎在告诉地震数据处理和应用专家, 目前采集到的地震数据中高频成分到此为止, 如果试图通过地震数据处理得到更高的频率成分, 可能是在做“无米之炊”。
2 地震信号记录的真实过程 2.1 无分频过程的数字地震仪地震波被激发后, 检波器将接收到的地面振动转换为电信号, 传送到数字地震仪。在仪器中, 电信号历经模拟放大、滤波、多路编排、模/数转换, 最后以数字形式被记录于磁介质, 如早期16位数字地震仪的九轨磁带。
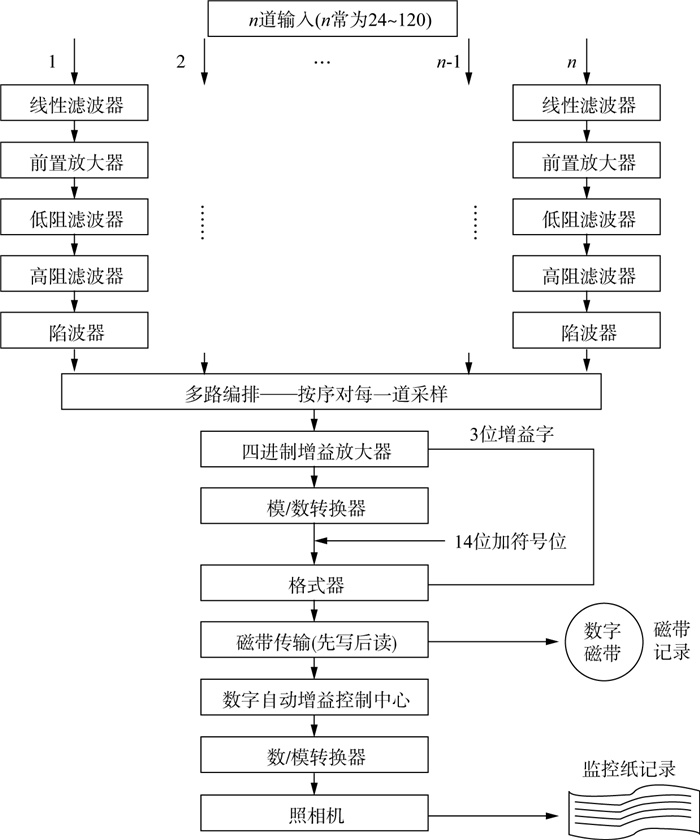
上世纪70年代起, 我国开始使用数字地震仪, 主要包括DFS-V和SN338(SN348)。关于这一代数字地震仪的基本工作过程, R.E.谢利夫在文献[4]中通过图A-8地震放大器的两个框图进行了说明, 图 2为其中的瞬时浮点数字记录系统框图。可以看出, 瞬时浮点数字记录系统由如下4个组成部分。
|
图 2 瞬时浮点数字记录系统框图[4] |
第1部分, 在多路转换开关之前每道均存在多个功能的部件, 各部件的功能分别为:①线性滤波器压制由检波器电缆感应进来的静态射频; ②前置放大器使信号水平增加某个固定常数值; ③如果阻抗匹配, 低阻滤波器可用于补充被地震检波器消除的极低频地震波, 为防止假频出现, 高阻滤波器的斜率一般为72dB/倍频程; ④陷波器压制50Hz或60Hz的电力线干扰[4]。需要指出的是, 仪器中各种滤波均实施于模拟电信号, 故不会出现数字化数据处理过程中存在的频率泄漏现象[1]。
第2部分, 多路编排到模/数转换。多路编排[4-5]通常是对不同的输入道以规则间隔的方式展开有序取样, 并将样点馈入单一的输出道, 数字地震磁带多以这种方式进行多路编排。模/数转换器用于测量信号振幅, 第1位输出的是振幅极性, 后14位输出的是振幅大小。
第3部分, 磁带记录。将经多路编排及模/数转换后的数据直接写入磁带。
第4部分, 回放。先读磁带中的记录, 然后在数字自动增益控制中心放大输出数据, 再在数/模转换器中将其转换为模拟量, 最后采用照相方法将模拟量记录在监控纸带上。
可见不包括照相机的野外数字记录系统由3个部件和两个连接电缆组成。3个部件分别为模拟部件、控制部件和磁带机部件。其中, 模拟部件接收地震检波器信号, 提供模拟电信号的放大器并模拟滤波, 在多路编排和模/数转换等处理之后, 对信号进行离散数字形式[6]的采样。
之后发展了24位遥测和有线遥测数字地震仪, 如SN388[7], 其地震数据采集由脉冲编码系统完成, 该系统包括前置放大、采样、浮点放大等部分。整个仪器记录的核心部分为通过模/数转换器将地震数据转换为二进制数码序列。
上述引用和论述旨在说明数字地震仪中无傅里叶分解的部件, 在整个地震信号记录过程中, 不存在以傅里叶变换为基础的频率分解, 因而在某一时刻采样的振幅值不可能变换为多个不同频率的谐波振幅值。
2.2 一个存储单元中只能存放一个振幅值一个16位的存储单元由数符(符号位)、阶符+阶码(增益码)和尾数组成。在数据存储时, 某个采样时刻的一个振幅值, 存入某一个存储单元, 享有这个单元的16位数位。其中, 14个数位的尾数表示其有效值, 符号位表示其正、负极性, 增益码和尾数共同表示数值大小。不论数值正负, 大小, 该数值只能存放于某一个存储单元, 尾数的14个数位以“1”或“0”的形式表示有效值。尾数全为“1”表示其为最大绝对值, 尾数全为“0”表示其为零值。每个采样时刻的振幅值都是一个具有独立作用的数值, 在波形的恢复中起着不可或缺的作用, 振幅值既不会死亡, 也不能死亡, 如果缺少了某些时刻的振幅值, 恢复的波形就会产生畸变。
由于仪器中没有频率分解单元, 同一时刻进入存储单元的数值只有一个振幅值, 因此不存在多个数值抢占同一个尾数的14个数位的问题, 也不存在强振幅占的数位多, 弱振幅占的数位少的问题。显然, 文献[1]所设想的多个大小不同的数值在同一存储单元中同一个尾数各自占有不同数位的情况, 物理不可实现。
2.3 白噪系数有助于反褶积算法稳定且有利于提升高频成分的振幅李庆忠[2]认为由于反褶积模块中常用的白噪系数为0.1%~1.0%, 因此低于低频分量振幅1000倍的高频频率成分不能再提升。于是白噪系数成为高频死亡线存在的3个理由之一。
白噪系数是反褶积模块中的一个参数。最小平方反褶积算法中的白噪系数被称作为稳定常数[8]。白噪系数只用于反滤波器的设计, 并未将其加入最终的数据。加入白噪声的做法是在时间域叠加一个脉冲, 或者使频率域的振幅频率曲线移位[4]。振幅频率曲线移位即在振幅谱各个频率的振幅上加一个常数值, 即所谓白噪声值。加入白噪声的目的在于保证求取反子波的算法稳定收敛。
大量数据反褶积处理的实践表明, 相较低频振幅数据, 采用反褶积处理后高频成分的振幅得到明显提升, 并且频带也被拓宽。采用的白噪系数值越小(如0.001), 高频振幅的提升幅度越大。李庆忠[2]所谓“低于低频分量1000倍的高频成分就不能再提升”, 与地震数据反褶积处理的结果不符。反褶积处理后, 虽然噪声可能有所增大, 但因得益于数据处理系统包含多种噪声压制技术, 所以白噪声在后续处理中可以被压制。
总之, 反褶积处理有利于提升高频振幅, 白噪系数有利于保持反褶积算法的稳定性。
2.4 频率泄漏是一种可以预防和抑制的现象高频死亡线存在的另一个理由是频率泄漏。李庆忠[2]认为, 由于各种滤波算子始终存在“频率泄漏”, 即在通放带之外, 还存在千分之几的泄漏, 所以当把占总强度1/1000的高频弱信号放大1000倍时, 低频强信号也会同时放大若干倍, 后者依然具有压倒性优势。这似乎意味着频率泄漏使高频振幅与低频振幅的差异无法改变。另外, 当出现振幅较强的高频成分时, 我们往往考虑这是否为频率泄漏所致。
频率泄漏是地震数据处理中客观存在的一种现象, 包括时间域和频率域两种类型的泄漏。无限长时间域连续信号的离散采样和截断会产生低频和高频的频率泄漏; 频率域截断(有限频带宽度)导致的吉布斯效应在幅频曲线上产生的波纹现象, 在时间域脉冲信号上产生的伴生振荡现象, 也是一种频率泄漏。
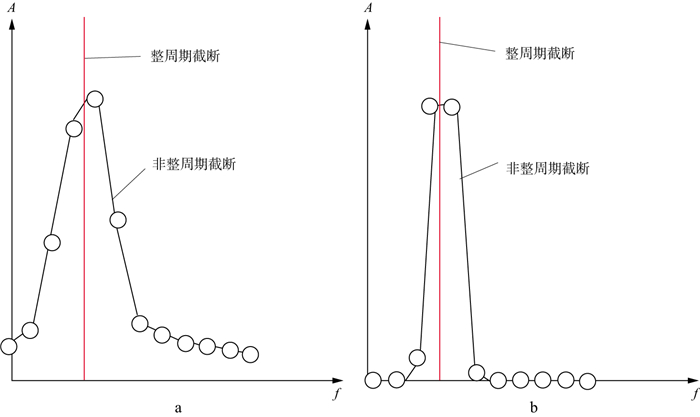
2.4.1 时间域离散采样和截断产生的频率泄漏地震数据处理时需要对长度无限的连续时间函数进行离散采样和截断, 进而得到用于数字分析的长度有限的离散时间序列。利用离散时间序列进行频谱分析, 会出现如下两种频率泄漏现象。①非周期截断造成的频率泄漏:时间域信号的非周期截断造成信号频谱出现“展宽”和“拖尾”现象, 使频谱向低频和高频延展, 产生低频和高频成分的泄漏。由图 3a中未加汉宁窗的余弦函数振幅谱可知, 余弦函数整周期性截断不产生频率泄漏(图 3a中红色谱线); 而非整周期截断则产生频率泄漏(图 3a中黑色谱线)。脉冲地震信号由无限多个不同频率、不同振幅的谐波组成, 在时间域被截断时, 这些谐波部分被整周期截断, 其余则被非整周期截断, 因此时间域截断产生的频率泄漏不可避免[9]。②连续时间序列在离散采样时, 振幅谱上会出现周期性重复的多个“伪门”, 伪门即为频率泄漏的产物[4, 9]。
|
图 3 未加汉宁窗(a)和加汉宁窗后(b)非整周期截断和整周期截断的余弦函数振幅谱 |
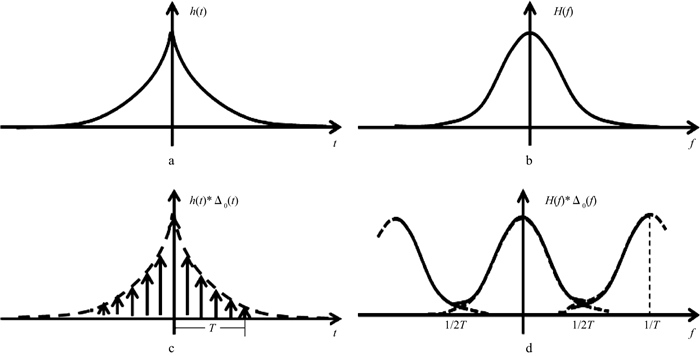
上述频率泄漏现象可以抑制和避免。如图 3b所示, 由时间域截断产生的频率泄漏可通过在数据截断时加汉宁窗、高斯函数等方法予以抑制。图 3b中黑色谱线是加了汉宁窗的非周期截断的余弦函数振幅谱, 该振幅谱频率范围既接近余弦函数真实频率范围, 又压制了频率泄漏产生的低频成分和高频成分[9]。时间域离散采样造成的伪门可利用仪器中的去假频滤波加以压制。伪门中心频率是时间采样率的倒数, 如图 4所示, 当采样间隔T为2ms时, 伪门中心频率1/T为512Hz, 振幅谱重叠部分的频率为256Hz。将地震电信号输入仪器后, 可利用压制混叠频率的低通滤波(去假频滤波)器压制伪门的频率成分。早期的数字地震仪通常采用2ms的采样率, 其伪门出现在512Hz处, 去假频滤波器的高截频为128Hz, 高边频斜率为72dB/倍频程[4], 此时, 256Hz处信号振幅降低72dB, 为原振幅的1/3981, 512Hz处信号振幅降低144dB, 为原振幅的1/15848932, 伪门得到足够的抑制, 这为128~256Hz的高频成分预留了充足的频段。当采样间隔为1ms时, 伪门出现在1024Hz附近, 去假频滤波器截止频率为256Hz, 在512Hz处信号振幅降为原振幅的1/3981, 1024Hz处信号振幅降为原振幅的1/15848932, 这为256~512Hz的高频成分预留下了充足的频段。由于模拟电信号滤波不会产生频率泄漏[1], 因此滤波之后再离散采样, 可避免出现伪门导致的频率泄漏。仪器中的去假频滤波器可以有效抑制伪门, 减小伪门产生的频率泄漏[4, 9]。
|
图 4 时间域连续函数离散采样导致振幅谱出现伪门的过程[9] a时间域连续函数h(t); b连续函数的振幅谱; c采样间隔为T的时间域离散函数; d离散函数的振幅谱 |
吉布斯效应是一种在频率域截断后频谱产生的波纹现象以及波形产生的振荡现象。当滤波因子的幅频特性曲线为不连续函数(存在间断点), 且滤波因子取有限项时(频率域截断), 会产生吉布斯效应, 理想门式滤波器即为这样的滤波因子[8], 其幅频曲线上的波纹现象使不同频率的振幅产生畸变, 波纹最大幅度畸变约为9%。对应的时间域波形出现的振荡效应使脉冲波波形畸变, 在地震剖面上产生多个频率较高的同相轴, 可能被误认为高频信息。此外, 在分频滤波中观测到一种由吉布斯效应导致的低频成分泄漏现象。当采用理想数字滤波器或算子长度较小时, 由于频谱截断的突跳(间断点)会产生吉布斯现象, 使主频段内的能量泄漏, 从而造成高频段的滤波档出现低频段的信号, 并且伴有相位上的改变[10]。图 5为高通滤波扫描时出现低频泄漏的实例, 在低截频为80Hz和100Hz的高通滤波档出现了低于40Hz的低频反射波。

|
图 5 高通滤波扫描时出现低频泄漏的实例 |
设计滤波算子或反褶积算子时, 不可避免地需要在频率域进行频率截断, 这是否会导致严重的吉布斯现象, 取决于滤波算子是否存在间断点(阶跃函数)。前人研究了多种滤波器的设计方案以抑制吉布斯效应的产生, 减小和压制可能出现的频率泄漏, 包括:①窗函数法; ②镶边法, 在原来不连续的理想频率响应的两边镶上两个连续变化的边; ③改变滤波因子截断长度, 增加截断长度抑制泄漏效应; ④数据翻转法, 在输入信号未进入滤波器之前展开变换以尽可能削弱吉布斯现象[4, 8, 10-11]。实际数据处理软件中的多种滤波器[4]由于采取了诸如优选滤波算子、加镶边函数等措施, 因此滤波器两边并未出现具有间断点的阶跃函数, 反而呈现平缓的连续函数, 其幅频特性曲线也不存在波纹现象。滤波器的这种幅频特性曲线在数据处理中以滤波参数的形式出现。如带通滤波器参数“14/18-56/36”, 其含义是, 振幅下降3dB(70%)的低截频为14Hz, 斜率为18dB/倍频程; 振幅下降3dB的高截频为56Hz, 斜率为36dB/倍频程。与具有间断点的理想门式滤波算子相比, 此类滤波算子所表征的无波纹现象的幅频曲线对应的时间域算子(脉冲波形)不会发生畸变。实际应用中, 无论是滤波算子或反褶积算子, 均不会采用理想门式算子, 因此利用理想门式算子讨论频率泄漏或其对高频成分振幅的影响, 均不能反映地震数据处理的真实情况。
无论是时间域的离散采样或截断产生的频率泄漏, 还是频率域截断引起的吉布斯效应导致的频率泄漏, 其危害均可减小和避免。在地震数据处理系统中, 采用了多种技术措施抑制和避免频率泄漏产生的影响(图 3b、图 4d)。有关滤波(反滤波)算子的软件设计时已采用多种算法压制和减小此类影响。此外, 不管是时间域数据截断和离散采样, 还是滤波算子因频率域截断而产生的频率泄漏, 均呈现高频泄漏和低频泄漏相伴出现的现象, 并且泄漏的低频成分振幅往往强于高频成分, 低频泄漏成为频率泄漏的显著标志(图 5)。
2.5 数字地震仪中无高频死亡线上述分析表明, 在地震仪中不存在信号傅里叶分解的分频记录, 也不存在多个高频振幅和低频振幅分别在同一存储单元的14位尾数中各自占有不同数位(占位)的可能, 因此由文献[1]中地震仪对高频信号的可记录范围的分析, 推测出占不到尾数的最后4位的弱振幅信号就会死亡的论断, 与实际地震数据记录过程不符合, 60dB高频死亡线是一种不符合仪器记录实际过程的推断, 数字地震仪器中不存在高频死亡线。在数据处理中, 由于计算机存储单元的位数更多, 数值变化范围将会更大, 将1/1000的振幅差异用于衡量高频成分是否会死亡, 与实际数据处理更加不相符。在反褶积处理中利用小的白噪系数可提升高频成分的振幅。白噪声虽然降低了地震数据信噪比, 但是经过适当的随机噪声压制处理, 完全可以消除白噪声的影响。频率泄漏是地震数据处理中有损数据品质的问题, 目前有多种方法和算法可以抑制频率泄漏所产生的影响。因此所谓“高频成分振幅如果小于强低频振幅的1/1000, 白噪系数和频率泄漏无法使高频成分振幅提升”的讨论并无依据, 高频死亡线所依据的3个理由均不能成立[1]。
3 地震信号高频成分的记录因为数字地震仪中不存在分频记录, 所以本文将讨论如何记录高频成分以及可记录的低频和高频成分振幅的数值范围。
3.1 动态范围地震波激发后, 地面的振动至少包括地下反射波、各种规则干扰波和随机噪声等3类, 它们相互叠加, 被检波器接收, 进而转换为持续一定时段、振幅变化的电信号, 即一个连续时间序列的复合波。进入仪器的复合波电信号经模拟放大、滤波、离散采样, 转变为具有一定时间间隔的振幅值, 各个时刻采样的振幅值, 即反射波、干扰波和噪声在该时刻振幅的复合值。因此, 仪器记录的是复合波在各个时刻的、唯一的复合振幅值。
仪器能够记录下来的地震信号的振幅范围, 公认的衡量标准是“动态范围”。文献[4]对动态范围进行了如下的说明:“①最大读数对最小读数(常常是噪声水平)的比, 它可以被记录并不需改变比例直接从仪器上读数。②系统记录很大很小振幅信号的能力, 然后还能恢复它们。能够恢复的小信号常常被认为是系统的噪声水平。而动态范围是用在小于固定畸变量(1%~3%)记录的最大信号与均方根噪声的比……。③然而, 有时即使信号被掩盖于噪声之中也能被提取。定义又是考虑整个信号提取过程而不仅仅是记录仪器。”R·E·谢里夫[4]给出的动态范围定义, 不仅包括了仪器记录过程的动态范围, 还包括了数据处理中整个信号提取过程的动态范围。
文献[1]中给出的16位数字地震仪的动态范围为最大输入信号电压与换算至入口处的仪器噪声之比, 在该动态范围内地震仪可以接收由浅到深、振幅相差110dB的信号。进入地震仪的信号, 如果振幅在0~110dB动态范围内变化, 均可被记录。由于单个时刻的振幅值是有效信号、干扰、噪声3类信号在该时刻的复合振幅值, 如果复合振幅值刚好达到动态范围的最小可记录门槛, 那么组成复合振幅值的有效反射波弱振幅信号也可被记录。这就是文献[4]中“掩盖于噪声之中的弱信号”, 亦即不在仪器动态范围内的弱信号。此类弱信号经数据处理之后有可能被提取。因此仪器记录数据经处理后的动态范围有可能大于仪器本身的动态范围。出于习惯, 我们往往以仪器的动态范围来衡量强弱信号可记录的范围, 但是要注意掩盖于噪声中的弱信号经数据处理后有可能被提取出来, 因此“仪器记录+数据处理”的动态范围更大, 可以记录和提取更弱的信号。
3.2 地震信号中高频成分记录的形式既然记录在存储单元中的数值是反射波、干扰和噪声的一个复合振幅值, 那么高频成分是以怎样的形式被记录下来的?为此需要了解高频成分以什么样的形态赋存于时间域脉冲波中, 或者高频成分是如何影响时间域脉冲波特征的, 在此通过一个简单的试验说明这一问题。
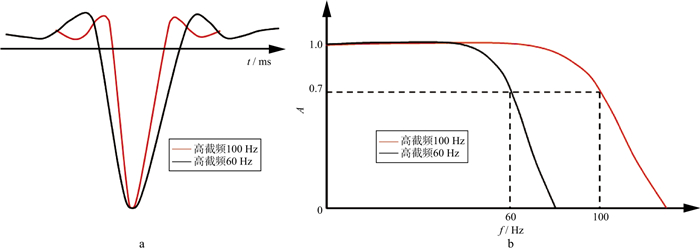
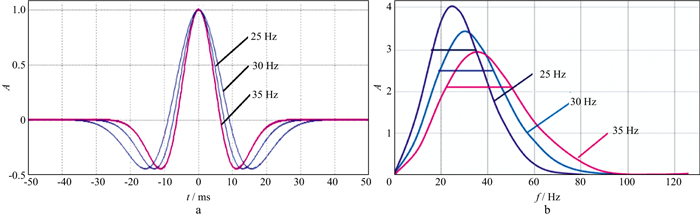
图 6为两个不同频带宽度和高截频的子波波形及其对应的振幅谱, 它们的最低频率均为0, 仅高截频变化, 分别为60Hz和100Hz。图中用黑线和红线分别表示高截频为60Hz和100Hz的振幅谱和相应的脉冲子波。结果表明, 高截频为100Hz的子波波形偏“瘦”, 高截频为60Hz的子波波形偏“胖”。这一现象说明, 脉冲波的“瘦”和“胖”可以表征其高频成分的多少。图 7为不同主频和频带宽度的雷克子波及其对应的振幅谱, 随着主频升高, 频带展宽。波形的“瘦”和“胖”与高频成分的振幅大小直接相关。提升主频、展宽频带, 提升高频振幅, 都会使脉冲波变“瘦”。这说明只要真实地记录地震脉冲波的波形和振幅, 就能真实地记录时间域脉冲波中应有的高频成分。在地震数据记录时, 提高地震数据记录的采样率, 或提高地震仪器存储单元的数位(如从16位增加至24位), 就能以更高的精度记录脉冲波形及振幅的变化, 更有效地记录脉冲波中应有的高频成分。在地震数据采集时, 相较于16位数字地震仪和2ms时间采样间隔, 采用24位数字地震仪和1ms时间采样间隔更有利于真实地记录地震波形和振幅变化, 从而有利于高频成分的保护和记录。
|
图 6 不同频带宽度和高截频的子波波形(a)及其对应的振幅谱(b) |
|
图 7 不同主频和频带宽度的雷克子波(a)及其对应的振幅谱(b) |
总之, 真实记录脉冲波的波形和振幅, 就能够记录脉冲波中应有的高频成分, 不必担心弱高频成分振幅值因占不到尾数的后4位而死亡。
3.3 可记录的反射波高频成分的估计文献[1]根据地层地质模型制作典型地层吸收衰减模型, 并估算该地区可能记录到的高频成分。在华北平原区, 按照60dB高频死亡线估算出反射时间t0为3.0s的反射波可记录的高频成分的上限为60Hz, 如果按照仪器动态范围上限110dB, 可记录的高频成分上限将达到120Hz。在松辽和内蒙地区, 根据60dB的高频死亡线, 估算出t0为3.0s的反射波高频成分的上限为100Hz, 如果按仪器的动态范围110dB, 可记录的高频成分上限为180Hz。
需要注意的是, 上述仪器动态范围是针对有效波、规则干扰和随机噪声的复合波均方根振幅而言的。当这类复合波经过数据处理, 分解出规则干扰和随机噪声并加以压制, 可能提取出均方根振幅更小的反射波有效信号。换言之, 数据处理后, 可提取的有效信号振幅范围将会更大, 相应地, 更微弱的高频信号也能被提取。
由此可知, 按照仪器动态范围110dB确定的高频信号可记录范围几乎是高频死亡线60dB的两倍, 足以提振对高频信号观测记录的信心。
4 高频死亡线推算的死亡频率与实际数据频率成分不符合根据新疆沙漠地区某地层速度模型计算得到吸收衰减模型参数, 并推算出该区的死亡频率, 反射时间(t0)与对应的死亡频率分别为:1.09s对应50Hz; 2.09s对应43Hz; 3.09s对应41Hz(表 1)[1, 3]。
根据塔河油田某工区的地层速度模型制作了吸收衰减模型。该区表层低速带和降速带的总厚度约为10m, 层速度分别为360m/s和600m/s, 其下的潜水层层速度为1600m/s。根据该区的地层速度模型采用文献[1]中的方法得到吸收衰减模型并推算死亡频率, 反射时间(t0)与对应的死亡频率分别是:1.000s对应89Hz, 2.000s对应70Hz, 3.000s对应61Hz, 4.000s对应55Hz(表 2)。
| 表 2 塔河油田某工区吸收衰减模型参数及推算的60dB死亡频率[1] |
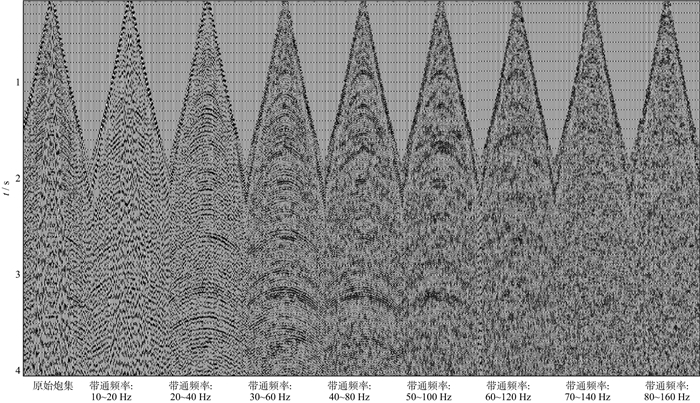
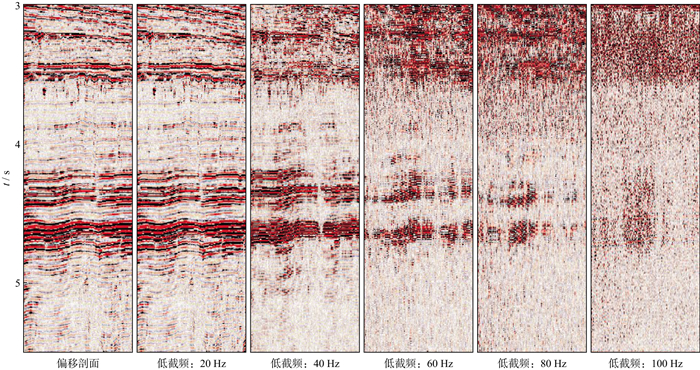
图 8所示是该工区的原始炮集及其带通滤波扫描结果, 图 9所示是该工区叠前时间偏移剖面及其高通滤波扫描结果。可以看出, 原始炮集在2s以下的层位存在50Hz的高频成分, 高于文献[3]给出的死亡频率(表 1), 与表 2所列的死亡频率大体相当; 但当叠前时间偏移数据在3~5s的时窗时, 其频率为80~100Hz, 高于表 2所列的死亡频率, 更高于表 1所列的死亡频率。按照文献[1]的推论可知, 在地震数据记录过程中死亡的频率成分无法通过数据处理恢复出来, 显然这一推论与图 8和图 9中展示的扫描结果不符合。对比图 8和图 9可知, 在原始炮集数据中被噪声淹没的深层高频数据经过数据处理也能够被恢复, 这与文献[4]中动态范围的定义“有时即使信号被掩盖于噪声中也能被提取”相符合, 该定义考虑了整个信号提取过程。由此可见, 动态范围的定义既应包括仪器记录过程的动态范围, 还应包括数据处理中信号提取过程的动态范围。该定义符合地震数据采集和处理的实际情况, 有利于在地震数据采集和处理过程中采用合理的方法技术, 实现提升高频, 展宽频带, 提高分辨率的目标。
|
图 8 塔河油田某工区原始炮集及其带通滤波扫描结果 |
|
图 9 塔河油田某工区叠前时间偏移剖面及其高通滤波扫描结果 |
依据60dB高频死亡线估算可记录的高频成分上限, 低于实际地震数据中记录的高频成分, 故高频死亡线不能正确反映实际地震数据采集与处理过程中频率成分的分布特征。
5 几点认识利用地震反射波的有效高频成分进行地下探测, 是我国薄互层碎屑岩中薄砂层油气区[12-15]探测的重要方向之一。获取过高的频率成分目前不一定能实现, 但是突破思想认识上的桎梏, 对已采集的地震数据中频率成分形成正确的认知, 利用数据处理将已经记录的高频成分尽可能地提取出来, 是目前可以完成的工作, 也是有益于薄互层中薄储集层(体)预测的重要举措之一。
对地震数据采集中的高频成分进行了简要分析后, 获得了以下认识。
1) 在地震数据采集、记录的过程中, 输入数字地震仪的地震信号至少由地震反射波、各类干扰波和噪声等3类信号叠加复合为一体的连续时间域波动电信号组成, 经过一系列变换转换为数字信号。由于数字地震仪中不存在进行傅里叶分解的部件, 故波动信号不可能经历傅里叶变换的分频过程。因此, 复合波的振幅不可能被分解为多个不同频率、振幅的谐波, 不存在多个不同频率、大小的振幅值需要在同一个存储单元尾数的14位数位中同时记录的情况, 也不会出现低频和高频成分的振幅值各自占有同一个尾数不同数位的情况, 更不会出现强低频成分振幅占据了尾数的14个数位, 导致弱高频成分振幅在尾数中占不到4个数位而死亡的问题。此外, 多个振幅值在同一个存储单元中尾数的14个数位上分别占有不同数位也是物理不可实现的。因此, 基于分频记录和分频数值占位的60dB的“高频死亡线”推论也就失去了依据, 更重要的是, 实际数据的频率成分分析表明, 依据“高频死亡线”不可能正确估计一个地区高频成分可记录的范围。
2) 白噪系数有利于反褶积算法的稳定性, 可确保反褶积能够有效提升高频成分的振幅。连续波形离散采样使频谱出现“伪门”, 数据截断使频谱向低频和高频端展宽, 产生两种类型的频率泄漏; 使用理想门式滤波(反滤波)算子对频率成分截断, 可能使滤波(反滤波)后的波形出现变异, 造成时间域波形尾随相位增加, 从而降低地震数据品质, 甚至产生低频泄漏。上述问题均可采用一定的技术方案加以抑制和消除, 以保护和提升地震信号中的高频成分。
3) 对某个特定地区, 根据吸收衰减模型与仪器动态范围, 可以较好地估算出该地区的高频成分可记录的范围。但需要注意的是, 真实的动态范围应该是仪器的动态范围+数据处理的动态范围。
4) 反射波的高频成分寓于地震波形之中, 波形的“瘦”或“胖”表征高频成分的多或少。因此, 在地震数据采集中, 采用24位数字地震仪和1ms时间采样间隔能够更真实地记录地震波形和振幅变化, 有利于高频成分的保护和记录。充分运用数据处理技术有效提升高频成分, 可为地震数据处理提供更高分辨率的地震数据。
5) 倍频程带通滤波扫描可用于调查地震数据在不同滤波档范围内的信噪比分布。原始炮集数据由于信噪比低, 对其进行滤波扫描后得到的结果不能用于判断地震反射波的高频成分范围, 也不能据此确定数据处理过程中应保留的频带范围, 更不能在处理过程中采用压制高频的措施压制那些“看不见”的高频成分。因此, 调查地震数据是否存在高频信号, 应针对处理后的地震数据, 特别是对经过多重保护提升高频成分处理后得到的地震数据进行滤波扫描, 才可以正确地判断数据的频率分布。在滤波器扫描地震数据时, 注意依据低频和高频成分振幅的差异, 选择振幅范围, 以保证微弱地震信号能够正常显示。
6) 地震数据处理时, 对复合为一体的反射波、干扰波和噪声的时间域脉冲信号进行分解, 压制其中的干扰和噪声, 保留真实反射波, 进一步提升高频成分振幅值[16], 是获得主频高、频带宽的地震数据的关键环节。压制干扰和噪声、反褶积、子波处理、高频补偿、提高动静校正的精度等均为提升高频成分振幅的重要措施。然而一些伤害高频信息的处理思路和措施却容易被忽视, 使得陆地地震高精度采集得到的数据在处理后停留在主频为20~30Hz、高截频不超过40~50Hz的水平上。在厘清高频死亡线的有关问题后, 需要对上述数据处理的问题另文展开讨论。
6 结论分析表明, 在数字地震仪记录地震数据的过程中, 傅里叶分解既不是现实, 也不可能实现; 在同一个存储单元的尾数中多个振幅值各自占据不同数位更是物理不可实现。因此, 在地震数据记录过程中不存在60dB高频死亡线。地震数据中的高频成分是否被记录, 需要结合地震地质条件, 并根据仪器的动态范围和数据处理提高信噪比和提升高频展宽频带的能力展开综合分析。
上述对地震数据采集中反射波高频成分的认识, 期望引起重视, 更希望对此开展试验, 以验证认识的真伪。
| [1] |
李庆忠. 走向精确勘探的道路—高分辨率地震勘探系统工程剖析[M]. 北京: 石油工业出版社, 1994: 35-44, 45-46, 67-68. LI Q Z. The way to obtain a better resolution in seismic prospecting: A systematical analysis of high resolution seismic exploration[M]. Beijing: Petroleum Industry Press, 1994: 35-44, 45-46, 67-68. |
| [2] |
李庆忠. 地震高分辨率勘探中的误区与对策[J]. 石油地球物理勘探, 1997, 32(6): 751-783. LI Q Z. Some mistaken concepts in high-resolution seismic exploration and corresponding countermeasures[J]. Oil Geophysical Prospecting, 1997, 32(6): 751-783. |
| [3] |
李庆忠, 魏继东. 高密度地震采集中组合效应对高频截止频率的影响[J]. 石油地球物理勘探, 2007, 42(4): 363-369. LI Q Z, WEI J D. Influence of array effect on cutoff frequency of high density frequency in high seismic acquisition[J]. Oil Geophysical Prospecting, 2007, 42(4): 363-369. |
| [4] |
谢里夫 R.E.. 勘探地球物理百科词典[M]. 南京: 南京大学出版社, 1994: 8-9, 107-108, 133-134, 227. SHERIFF R E. Encyclopedic dictionary of exploration geophysics[M]. Nanjing: Nanjing University Press, 1994: 8-9, 107-108, 133-134, 227. |
| [5] |
《Dictionary of Prospecting Geophysics》Writing Group. Dictionary of prospecting geophysics[M]. Beijing: Science Press, 1976: 45.
|
| [6] |
本刊编辑部. DFS-V数字地震仪性能介绍[J]. 石油物探, 1977, 16(4): 108-135. Editorial Department of Geophysical Prospecting for Petroleum. Performance introduction of DFS-V digital seismograph[J]. Geophysical Prospecting for Petroleum, 1977, 16(4): 108-135. |
| [7] |
龚大伟. SN388有线遥测数字地震仪直流漂移的产生和抑制[J]. 石油仪器, 2001, 15(3): 57-59. GONG D W. An effect on DC-shift and its restrain of SN388 cable telemetering digital seismograph[J]. Petroleum Instruments, 2001, 15(3): 57-59. |
| [8] |
牟永光. 地震勘探资料数字处理方法[M]. 北京: 石油工业出版社, 1981: 44-45, 65-73. MOU Y G. Digital processing method for data of Seismic exploration[M]. Beijing: Petroleum Industry Press, 1981: 44-45, 65-73. |
| [9] |
布赖姆 E.O. 快速富里叶变换[M]. 上海: 上海科学技术出版社, 1979: 155-162. BRIGHAM E O. The fast fourier transform[M]. Shanghai: Shanghai Science and Technology Press, 1979: 155-162. |
| [10] |
武喜尊. 试论数字滤波中吉布斯现象的产生与消除[J]. 中国煤田地质, 1996, 8(4): 68-70, 75. WU X Z. On the generation and elimination of Gibbs phenomenon in digital filtering[J]. Coal Geology of China, 1996, 8(4): 68-70, 75. |
| [11] |
王秀芳, 张光华, 陈雪松. 消除数字滤波器中Gibbs现象的研究[J]. 信号处理, 2003, 19(增刊1): 13-16. WANG X F, ZHANG G H, CHEN X S. A studying of eliminating Gibbs phenomenon in digital filter[J]. Journal of Signal Processing, 2003, 19(S1): 13-16. |
| [12] |
梁锋, 袁淑琴. 储层反演技术在埕北断阶区岩性油气藏评价中的应用[J]. 石油地球物理勘探, 2008, 43(1): 53-58. LIANG F, YUAN S Q. Application of reservoir inversion to evaluate lithological oil/gas reservoir in Chengbei Fault Terrace area[J]. Oil Geophysical Prospecting, 2008, 43(1): 53-58. |
| [13] |
苑书金. 鄂尔多斯盆地大牛地气田下石盒子组地震储层预测技术的研究和应用[J]. 石油地球物理勘探, 2008, 43(1): 48-52. YUAN S J. Study on Technique of Lower Shihezhi Formation reservoir prediction in Daniudi gas-field of Ordos Basin by seismic and application[J]. Oil Geophysical Prospecting, 2008, 43(1): 48-52. |
| [14] |
边树涛, 狄帮让, 董艳蕾, 等. 地质统计反演在东濮凹陷白庙气田沙三段储层预测中的应用[J]. 石油地球物理勘探, 2010, 45(3): 398-405. BIAN S T, DI B R, DONG Y L, et al. Application of geostatistical inversion in reservoir prediction in the third member of Shahejie Formation, Baimiao gas-field, Dongpu Depression[J]. Oil Geophysical Prospecting, 2010, 45(3): 398-405. |
| [15] |
钱勇先, 傅旦丹.反射波地震资料的信息分辨率[C]//中国地球物理学会.中国地球物理学会第十一届论文集.北京: 科学出版社, 1995: 59-65 QIAN Y X, FU D D.The information resolution of reflection seismic data[C]//Chinese Geophysical Society.Proceedings of 11th Chinese Geophysical Society.Beijing: Science Press, 1995: 59-65 |
| [16] |
杨汝超, 王晓华, 周彤, 等. 如何制定高分辨率地震勘探中的技术指标[J]. 石油物探, 2001, 40(1): 121-126. YANG R C, WANG X H, ZHOU T, et al. How to make the technical index for the high resolution seismic exploration[J]. Geophysical Prospecting for Petroleum, 2001, 40(1): 121-126. |



