2. 中国石油化工股份有限公司胜利油田分公司, 山东东营 257001
2. Shengli Oilfield, SINOPEC, Dongying 257001, China
时频分析[1]在地球物理勘探中的应用十分广泛。目前比较常用的时频分析方法主要有短时傅里叶变换[2]、小波变换[3]、S变换[4]、希尔伯特-黄变换[5]、二次型时频分布[6]和匹配追踪分解[7]等。短时傅里叶变换相当于地震道在一个固定的时间窗上与正弦基的互相关, 一旦窗函数选定, 时频分辨率便可确定下来, 这使得短时傅里叶变换对非平稳地震信号的分析存在局限性; 小波变换是地震道与小波字典的互相关, 是对短时傅里叶变换的改进, 小波变换受测不准原理的影响, 需要在时间分辨率和频率分辨率之间进行权衡, 因此很难满足精细储层预测的要求; S变换是短时傅里叶变换和小波变换的继承和发展, S变换具有良好的时频特性, 在时频分辨率上有所改进; 希尔伯特-黄变换将信号分解为有限的几个固有模态函数, 进而得到信号的时频谱, 其不足是对噪声较敏感; 二次型时频分布在时频平面存在非常严重的交叉项, 导致其在地震勘探中的应用并不广泛; 匹配追踪分解是将地震信号看作由许多被称作为原子信号的加权总和, 将每个原子信号的频谱进行叠加就可得到地震道的时频谱。
最小二乘法在地震勘探中的应用十分广泛, 约束最小二乘地震反演[8]使用最小二乘方法构建目标函数, 极大提髙了解的收敛速度, 其优点是反演过程稳定、计算效率高; 最小二乘偏移[9-10]是一种基于线性化反演理论的真振幅成像方法, 它将成像问题当作一个反问题来处理, 以寻求更接近于真实的地下反射系数; 罗水亮等[11]提出了一种基于变形Pride模型和Lee模型(P-L模型)的矩阵方程迭代精细横波预测方法, 其核心是通过最小二乘将横波估计目标函数的最优化问题转化为求解线性矩阵方程组问题, 从而极大地提高了横波估计的效率和稳定性。
VANÍČEK[12]有效地将频谱分析和最小二乘相结合, 提出了基于最小二乘拟合的谱分析方法, 绕过傅里叶变换, 在窗口内使用最小二乘分析直接求解信号的频谱; PURYEAR等[13]提出了约束最小二乘时频分析方法, 有效地提高了时频分析的分辨率; 李海英等[14]在上述研究的基础上, 基于整形正则化方法, 改进了最小二乘时频分析方法, 取得了较好的应用效果。
本文在前人研究成果[12-16]的基础上, 提出了改进的约束最小二乘时频分析方法(improved constrained least squares time frequency analysis, ICLS)。基于反演的思路将频谱分析转换成一个求解反问题的过程, 通过正则化约束最小二乘方法求解该问题, 进而得到地震信号的时频分析结果, 理论模型和实际应用验证了本文方法的有效性。
1 方法原理定义如下由待求的频谱和不同频率的三角函数计算信号的正演过程:
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Sh}} $ | (1) |
式中:d表示待分析的信号, 在实际应用中, d往往是实数, 为了提高时频估计结果的稳定性和分辨率, 可以通过Hilbert变换将d转换成复数的形式; S表示不同频率的三角函数构成的矩阵; h表示待求的频谱向量。已知信号d和矩阵S求频谱h, 这是一个典型的反问题, 这里用正则化最小二乘的思路进行求解。
S的具体形式如下:
| $ \begin{array}{l} \mathit{\boldsymbol{S}} = \\ \left[ {\begin{array}{*{20}{c}} {\cos (2\pi \Delta \Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \Delta t\Delta f)}&{\cos (2\pi \Delta t \cdot 2\Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \Delta \cdot 2\Delta f)}& \cdots &{\cos (2\pi \Delta t \cdot \alpha \Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \Delta \cdot \alpha \Delta f)}\\ {\cos (2\pi \cdot 2\Delta \Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \cdot 2\Delta t\Delta f)}&{\cos (2\pi \cdot 2\Delta t \cdot 2\Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \cdot 2\Delta \cdot 2\Delta f)}& \cdots &{\cos (2\pi \cdot 2\Delta t \cdot \alpha \Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \cdot 2\Delta t \cdot a\Delta f)}\\ \vdots & \vdots &{}& \vdots \\ {\cos (2\pi \cdot \beta \Delta \Delta f) + \sin (2\pi \cdot \beta \Delta \Delta f)}&{\cos (2\pi \cdot \beta \Delta \cdot 2\Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \cdot \beta \Delta \cdot 2\Delta f)}& \cdots &{\cos (2\pi \cdot \beta \Delta t \cdot \alpha \Delta f) + {\mathop{\rm isin}\nolimits} (2\pi \cdot \beta \Delta \cdot a\Delta f)} \end{array}} \right] \end{array} $ | (2) |
式中:Δt表示时间采样间隔; β表示时间采样点数; Δf表示频率采样间隔; α表示频率采样点数。
对于精确的数据, 待求的频谱向量为:
| $ \mathit{\boldsymbol{h}} = {\mathit{\boldsymbol{S}}^{ - 1}}\mathit{\boldsymbol{d}} $ | (3) |
但在实际计算过程中, 正演方程((1)式)往往是超定的或是欠定的, 所以没有精确解, 即:
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{s}}{\mathit{\boldsymbol{h}}_e} + \mathit{\boldsymbol{e}} $ | (4) |
式中:he为计算的频谱结果; e表示实际数据中存在的误差。
通过普通最小二乘法即可以得到he的解:
| $ {\mathit{\boldsymbol{h}}_e} = {\left( {\mathit{\boldsymbol{S'S}}} \right)^{ - 1}}\mathit{\boldsymbol{S'd}} $ | (5) |
式中:S′表示S的共轭转置矩阵。
进一步, 为了得到信号的时频谱, 需要以待分析点为参考, 对待分析信号加窗函数, 目的是提取待分析点处前后的若干点, 当待分析的信号加上窗函数后, 矩阵S的元素变得相关, 因此, 为了获得稳定的解, 需要加约束, 引入对角矩阵Z:
| $ \begin{array}{*{20}{l}} {\;{\kern 1pt} \begin{array}{*{20}{l}} {{\bf{Z}} = \frac{1}{2}{\mathop{\rm Diag}\nolimits} \left[ {1 + \cos ( - \pi ), \cdots , 1 + \cos \left( {\frac{{ - 3\pi }}{{{N_w}}}} \right), } \right.}\\ {1 + \cos \left( {\frac{{ - 2\pi }}{{{N_w}}}} \right), 1 + \cos \left( {\frac{{ - \pi }}{{{N_w}}}} \right), 0, 1 + \cos \left( {\frac{\pi }{{{N_w}}}} \right), }\\ {\left. {1 + \cos \left( {\frac{{2\pi }}{{{N_w}}}} \right), 1 + \cos \left( {\frac{{3\pi }}{{{N_w}}}} \right), \cdots , 1 + \cos \pi } \right]} \end{array}} \end{array} $ | (6) |
式中:Nw=ceil(β/2), ceil表示将实数向无穷远的方向舍入到最接近的整数; Diag表示求对角矩阵。此时, (1)式可以进一步写成:
| $ {\mathit{\boldsymbol{d}}_w} = {\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{h}} $ | (7) |
式中:dw=Zd; Sw=ZS。
利用最小二乘法求解(7)式。为了进一步提高求解的稳定性和唯一性, 需要对求解过程加约束[17], 由于L2范数正则化可以有解析形式的解, 更易于求解, 因此选用L2范数正则化约束最小二乘法(附录A), 最终可以得到ICLS时频分析结果:
| $ {\mathit{\boldsymbol{h}}_e} = \mathit{\boldsymbol{S}}_w^\prime {\left( {{\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{S}}_w^\prime + \mu \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)^{ - 1}}{\mathit{\boldsymbol{d}}_w} $ | (8) |
式中:Ω表示约束对角矩阵[13]; μ为权重系数, 用于调节约束的大小, 实际求解过程中, 可不断调节μ的大小, 直到获得一个时间分辨率和频率分辨率折中的时频分析结果。加入μΩ约束分量后, 对于信噪比较低、时间段较短的信号的频谱分析会有更好的效果, 可以有效地提高频谱分析过程的稳定性。逐点加窗计算(8)式即可得到待求信号段的时频谱。
进一步, 可以通过公式(9)方便地实现ICLS反变换:
| $ {\mathit{\boldsymbol{d}}_{{\rm{inv}}}} = \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{h}}_e} $ | (9) |
式中:dinv为经过反变换后重构的信号。
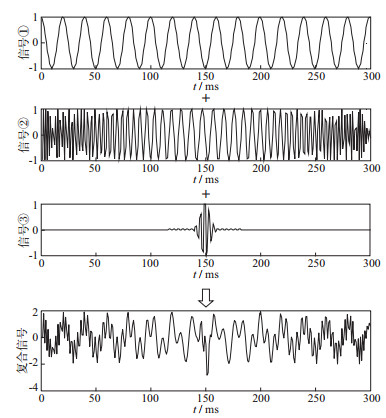
2 模型试算设计一个由3个信号叠加而成的复合信号, 如图 1所示, 3个信号分别为平稳单频信号①、频率随时间变化的信号②和加高斯窗函数的单频高频信号③。
|
图 1 复合信号 |
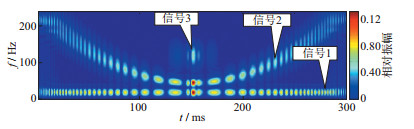
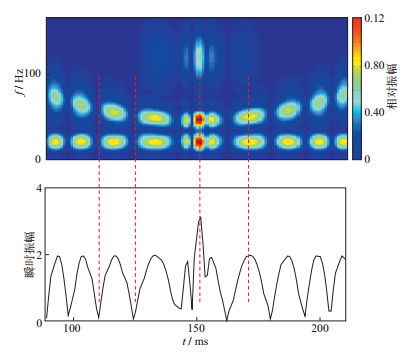
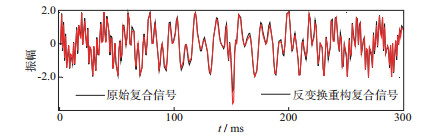
采用本文方法(ICLS)对该复合信号进行时频分析, 如图 2所示, 从图 2中可以看出, 时频分析结果客观、准确地描述了该复合信号频率成分的变化, 分辨率高。图 3为复合信号的瞬时振幅及本文方法时频谱的局部放大显示, 可以看出, 时频谱为零的地方对应着复合信号瞬时振幅零点的位置, 时频谱非零值对应着复合信号的瞬时振幅非零值的位置, 也就是说, 本文方法时频谱不仅可以描述频谱随时间的变化, 同时也描述了原始信号瞬时振幅的大小。图 4为本文方法反变换复合信号重构结果, 可以看出, 重构后复合信号与原始复合信号几乎重合, 说明了本文方法的准确性。
|
图 2 复合信号的ICLS时频谱 |
|
图 3 复合信号瞬时振幅及其ICLS时频谱 |
|
图 4 ICLS反变换 |
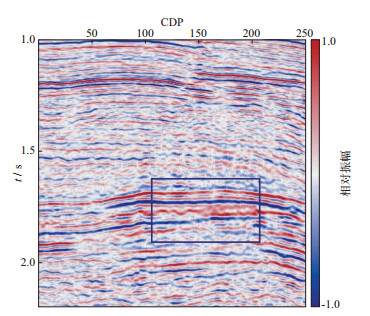
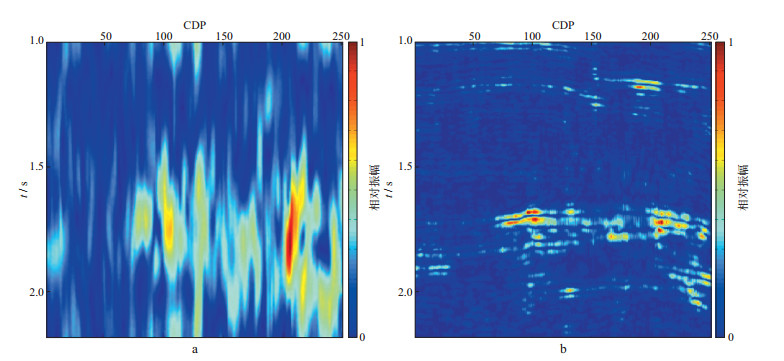
实际资料来自胜利油田某工区, 原始剖面如图 5所示, 在1.7s左右、CDP100~CDP200处有一背斜油气藏。分别采用本文方法(ICLS)和广义S变换(STFT)[18]对该剖面进行时频分析, 结果如图 6至图 8所示。从图 6至图 8可以看出, ICLS和STFT的时频分析结果具有较好的一致性, STFT的时频分析结果在频率较高的频谱分量上分辨率也较高, 但在低频的频谱分量上分辨率较低, 这已经无法满足目前隐蔽油气藏精细勘探的要求, 相比而言, ICLS时频分析结果的分辨率更高、准确性更好, 如对10Hz频谱分量依然具有很好的聚焦能力。
|
图 5 原始地震剖面 |
|
图 6 STFT和ICLS的时频谱分析结果(10Hz) a STFT; b ICLS |
|
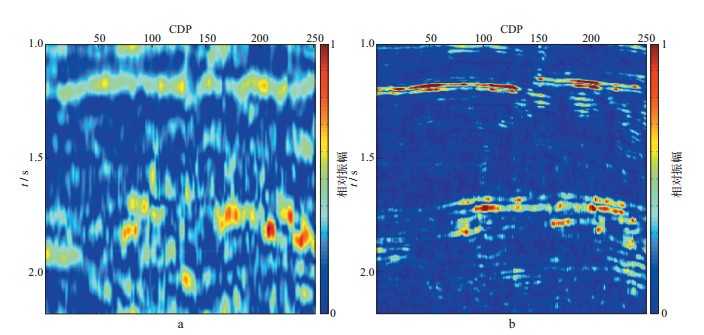
图 7 STFT和ICLS的时频谱分析结果(30Hz) a STFT; b ICLS |
|
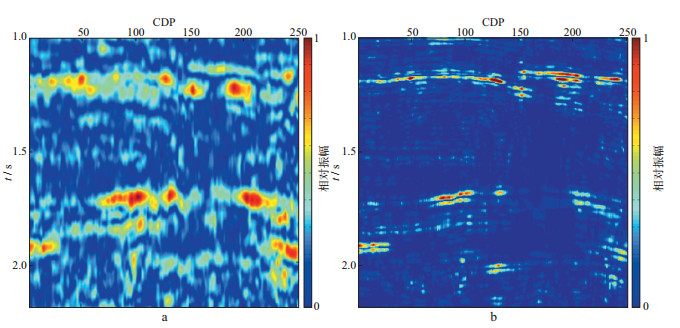
图 8 STFT和ICLS的时频谱分析结果(50Hz) a STFT; b ICLS |
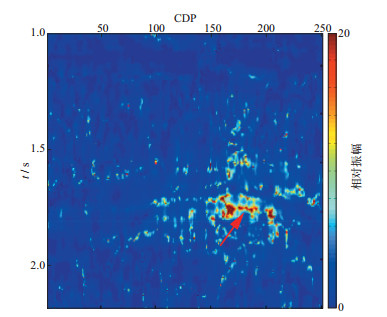
图 9为ICLS时频分析结果的10Hz频谱分量除以50Hz频谱分量的频谱比剖面, 箭头处数值较大, 可以明显看出该背斜存在低频增加、高频衰减的现象, 指示了一套气藏的存在。
|
图 9 频谱比剖面(10Hz/50Hz) |
基于正则化约束最小二乘估计的思路, 提出了一种改进的最小二乘时频分析方法。模型试算结果表明, 采用本文方法可以得到准确的、高分辨率的时频分析结果; 实际应用结果表明, 本文方法对于地震信号的高中低频部分都有很高的分辨率和稳定性, 可以有效地提高储层预测的准确度和可靠性, 在隐蔽油气藏精细勘探中具有广阔的应用前景。
附录A正则化约束在线性代数理论中, 不适定问题通常是由一组线性代数方程定义的, 而且这组方程组通常来源于有着很大的条件数的不适定反问题。当线性方程式解不存在或者解不唯一时, 就是所谓的病态问题。很多时候, 需要对病态问题求解, 对于解不存在的情况, 解决办法是增加一些条件找一个近似解; 而对于解不唯一的情况, 解决办法是增加一些限制缩小解的范围, 这种通过增加条件或限制要求求解病态问题的方法就是正则化方法。
1.1 线性拟合问题首先考虑m维线性拟合问题, 假设有n个观测数据对, 每对数据满足关系式:
| $ {y_i} = \sum\limits_{j = 0}^m {{x_{ij}}} {w_j} + {\varepsilon _i} $ | (A1) |
式中:xij表示自变量; yi表示因变量; εi为第i个数据与回归结果间的垂直距离, 称为不吻合量或预测误差。则最小二乘估计的损失函数定义为:
| $ \sum\limits_{i = 1}^n {\varepsilon _i^2} = \sum\limits_{i = 1}^n {{{\left( {{y_i} - \sum\limits_{j = 0}^m {{x_{ij}}} {w_j}} \right)}^2}} \Rightarrow \min $ | (A2) |
将(A2)式写成矩阵的形式:
| $ \left\| {\mathit{\boldsymbol{XW}} - \mathit{\boldsymbol{Y}}} \right\|_2^2 \Rightarrow \min $ | (A3) |
这个最小化形成了一个连续可微的无约束凸优化问题, 利用(A3)式对wj求偏导, 再除以2, 令其等于0, 可得:
| $ {\mathit{\boldsymbol{X}}^{\rm{T}}}(\mathit{\boldsymbol{XW}} - \mathit{\boldsymbol{Y}}) = 0 $ | (A4) |
进而可得到如下求解W的正态方程:
| $ \mathit{\boldsymbol{W}} = {\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ | (A5) |
(A5) 式即为线性拟合的最小二乘解。然而, 实际应用中海森矩阵(Hessian Matrix)XTX往往是奇异或是近似奇异的, 导致求逆困难, 此时可以通过迭代或是求伪逆来得到其近似解, 更一般的思路是通过各种正则化的方法来得到约束下的精确解。
1.2 L2范数正则化Tikhonov正则化处理矩阵求逆的数值不稳定性问题, 在海森矩阵的对角线上加一个正常数, 目的是使奇异矩阵变得非奇异[19], 则W的解析解的形式变为:
| $ \mathit{\boldsymbol{W}} = {\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ | (A6) |
式中:I为对角矩阵; λ为常数。(A6)式对应下面的最优化问题:
| $ \sum\limits_{i = 1}^n {{{\left( {{y_i} - \sum\limits_{j = 0}^m {{x_{ij}}} {w_j}} \right)}^2}} + \lambda \sum\limits_{j = 0}^m {w_j^2} \Rightarrow \min $ | (A7) |
可以看出, 这也是一个无约束连续可微凸优化问题, 它是带有与w的平方值成比例的惩罚项的损失函数, 即为L2范数正则化, 矩阵形式如下所示:
| $ \left\| {\mathit{\boldsymbol{XW}} - \mathit{\boldsymbol{Y}}} \right\|_2^2 + \lambda \left\| \mathit{\boldsymbol{W}} \right\|_2^2 \Rightarrow \min $ | (A8) |
式中:
L2范数正则化是实现数值稳定性和提高预测性能的有效手段, 但是, 估计结果的简约性和系数值的可解释性有待提高, L2范数上不会产生稀疏性的估计结果, 并且生成的模型通常具有与所有系数相关的非零值[20]。相对于L2范数, L1范数具有两个特点:①L1范数可以生成更容易解释的、稀疏的估计结果; ②在观测数据信噪比较低的情况下, L1范数估计结果会更加稳定。
用L1范数替换(A8)式中的L2范数, 得到以下表达式:
| $ \left\| {\mathit{\boldsymbol{XW}} - \mathit{\boldsymbol{Y}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{W}} \right\|_1} \Rightarrow \min $ | (A9) |
除了L1、L2范数之外, 还会用到L0范数, L0范数是指向量中非0的元素的个数, 用L0范数来规则化参数矩阵W, 就是希望W的大部分元素都是0, L0范数可以实现稀疏解, 但是实际中会使用L1取代L0, 因为L0范数很难优化求解, L1范数是L0范数的最优凸近似, 它比L0范数要容易优化求解。L2范数的作用是改善过拟合, 可以使得W的每个元素都很小, 都接近于0, 越小的参数说明模型越简单, 越简单的模型则越不容易产生过拟合现象。
| [1] |
PARTYKA G, GRIDLEY J, LOPEZ J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360. |
| [2] |
严海滔, 周怀来, 牛聪, 等. 同步挤压改进短时傅里叶变换分频相干技术在断裂识别中的应用[J]. 石油地球物理勘探, 2019, 54(4): 860-866. YAN H T, ZHOU H L, NIU C, et al. Fault identification with short-time Fourier transform frequency-decomposed coherence improved by synchronous extrusion[J]. Oil Geophysical Prospecting, 2019, 54(4): 860-866. |
| [3] |
蔡剑华, 熊锐. 基于频率切片小波变换的时频分析与MT信号去噪[J]. 石油物探, 2016, 55(6): 904-912. CAI J H, XIONG R. Magnetotelluric data denosing based on time-frequency analysis of the frequency slice wavelet transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 904-912. |
| [4] |
PINNEGAR C R, MANSINBA L. The S-transform with windows of arbitrary and varying shape[J]. Geophysics, 2003, 68(1): 381-385. |
| [5] |
尚平萍, 李鹏, 杨安琪, 等. 基于CEEMDAN的地震信号高分辨率时频分析方法[J]. 石油物探, 2019, 58(4): 547-554. SHANG P P, LI P, YANG A Q, et al. Seismic high-resolution time-frequency analysis based on CEEMDAN[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 547-554. |
| [6] |
亓雪静, 董立生, 邵卓娜. 二次型时频分析技术的开发与应用[J]. 油气地质与采收率, 2007, 14(3): 67-69. QI X J, DONG L S, SHAO Z N. Development and application of quadratic form time-frequency analysis technology[J]. Petroleum Geology and Recovery Efficiency, 2007, 14(3): 67-69. |
| [7] |
PURYEAR C I, TAI S, CASTAGNA J P, et al. Comparison of frequency attributes from CWT and MPD spectral decompositions of a complex turbidite channel model[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008, 393-397. |
| [8] |
林恬, 孟小红, 张致付. 基于约束最小二乘与信赖域的储层参数反演方法[J]. 地球物理学报, 2017, 60(10): 3969-3983. LIN T, MENG X H, ZHANG Z F. The petrophysical parameter inversion method based on constrained least squares and trust region approach[J]. Chinese Journal of Geophysics, 2017, 60(10): 3969-3983. |
| [9] |
AOKI N, SCHUSTER G T. Fast least squares migration with a deblurring filter[J]. Geophysics, 2009, 74(6): WCA83-WCA93. DOI:10.1190/1.3155162 |
| [10] |
刘定进, 张永升, 段心标, 等. 三维数据域最小二乘逆时偏移技术研究[J]. 石油物探, 2019, 58(6): 890-897. LIU D J, ZHANG Y S, DUAN X B, et al. Three-dimenstional data domain least-squares reverse timemigration[J]. Geophysical Prospecting for Petroleum, 2019, 58(6): 890-897. |
| [11] |
罗水亮, 杨培杰, 胡光明, 等. 基于变形P-L模型的矩阵方程迭代精细横波预测[J]. 地球物理学报, 2016, 59(5): 1839-1848. LUO S L, YANG P J, HU G M, et al. S-wave velocity prediction based on the modified P-L model and matrix equation iteration[J]. Chinese Journal of Geophysics, 2016, 59(5): 1839-1848. |
| [12] |
VANÍČEK P. Approximate spectral analysis by least-squares fit[J]. Astrophysics and Space Science, 1969, 4: 387-391. DOI:10.1007/BF00651344 |
| [13] |
PURYEAR C I, TAI S, CASTAGNA J P, et al. Constrained least-squares spectral analysis:Application to seismic data[J]. Geophysics, 2012, 77(5): V143-V167. DOI:10.1190/geo2011-0210.1 |
| [14] |
李海英, 武国宁, 陈小民. 最小二乘约束下的频谱分析技术及其应用[J]. 地球物理学进展, 2014, 29(6): 2685-2698. LI H Y, WU G N, CHEN X M. Least square constrained time frequency method and its applications[J]. Progress in Geophysics, 2014, 29(6): 2685-2698. |
| [15] |
PORTNIAGUINE O, CASTAGNA J P. Inverse spectral decomposition[J]. Expanded Abstracts of 74th Annual Internat SEG Mtg, 2004, 1786-1789. |
| [16] |
CASTAGNA J, OYEM A, PORTNIAGUINE O, et al. Phase decomposition[J]. Interpretation, 2016, 4(3): SN1-SN10. |
| [17] |
杨培杰.地震子波盲提取与非线性反演[D].东营: 中国石油大学, 2008 YANG P J.Seismic wavelet blind extraction and non-linear inversion[D].Dongying: China University of Petroleum, 2008 |
| [18] |
王长江, 杨培杰, 罗红梅, 等. 基于广义S变换的时变分频技术[J]. 石油物探, 2013, 52(5): 489-494. WANG C J, YANG P J, LUO H M. Time varying frequency division based on generalized S transform[J]. Geophysical Prospecting for Petroleum, 2013, 52(5): 489-494. |
| [19] |
STEPHEN B, VANDENBERGHE L. Convex optimization[M]. New York: Cambridge University Press, 2004: 1-727.
|
| [20] |
TIBSHIRANI R.Regression shrinkage and selection via the lasso[D].Toronto: University of Toronto, 1994
|



