2. 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
2. Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
陆上地震勘探受地形、障碍物、禁采区等采集环境以及采集成本、采集设备等的影响, 采集到的地震数据常常出现道间距过大、坏道、部分偏移距数据缺失等问题, 使得数据连续性变差, 用这种不连续的地震数据进行成像处理时往往会产生空间假频或虚假绕射, 从而降低了地震剖面的分辨率[1]。海上拖缆和海底地震勘探受成本、设备与洋流等影响, 采集到的数据也常常出现空间方向的不规则、道距稀疏等现象, 不规则的稀疏数据同样会在偏移剖面中产生空间假频、绕射噪声或虚假同相轴等问题[2], 造成这些问题的原因在于现有的许多处理技术都假设采集到的数据是完整连续的, 当实际输入数据不满足这一假设条件时必然会产生误差, 因此需要在成像处理之前采用合适的技术对这种缺道地震数据进行重构, 使其满足后续成像处理所需的假设条件。
地震数据插值重构方法的研究始于20世纪80年代, LARNER等[3]基于同相轴倾角一致的假设, 给出了一种地震数据分时窗倾角扫描并内插的方法。之后业界先后发展出一系列地震数据插值技术, 主要分为以下4类, 第一类为基于预测滤波的方法, 如SPITZ[4]提出的f-x域缺失地震数据插值恢复方法, 该方法能够一定程度上克服空间假频, 但只对规则采样且当地震记录的同相轴为线性时的数据有用。国九英等[5]在f-x域预测滤波的基础上将其拓展到f-k域, 提高了插值计算效率。随后GULUNAY等[6]提出抗假频f-k域缺失地震道插值方法, 并对该方法进行扩展, 提出适用性更广泛的广义f-k域缺失地震道插值方法[7]。基于预测滤波的重构方法可以加密空间采样率, 防止空间假频, 但要求输入数据必须规则采样。第二类为基于稀疏变换的方法, 如傅里叶变换[2]、Radon变换[8]、曲波变换[9-10]等, 这类方法对于非规则缺失数据插值效果较好, 但该类方法大都需要人为设定阈值, 插值效果依赖于处理人员的经验。第三类为矩阵降秩的方法[11], 该类方法将高维数据通过低秩矩阵进行表示然后重建, 计算简单快速, 并发展到了五维地震数据重构[12], 但该方法的计算量会随着地震数据维度的增加而成倍地增长, 对硬件要求很高。第四类为基于波动方程的方法, FOMEL[13]基于有限差分法进行波动方程缺失数据重构, LIU等[14]基于快速傅里叶变换的共轭梯度并结合快速矢量矩阵乘法的数值算法进行了空间带限信号的波场重建。这类方法需要速度信息, 并且计算量大, 因而没有得到广泛应用, 而且该类方法主要是对满足传统Nyquist采样定律的地震数据进行插值加密处理, 对于不满足传统Nyquist采样定理的地震数据插值效果不甚理想。
压缩感知理论的提出, 给信号恢复和重构带来新的思路, 地球物理学者将其引入地震数据恢复领域[15-17]。该理论以信号的稀疏性为前提, 可以对远低于Nyquist标准的欠采样数据进行准确恢复, 打破了Nyquist采样定理的约束。FOMEL等[18]和LIU等[19]基于该理论提出了适用于地震数据的Seislet变换, 实现了地震数据插值重构。此外基于压缩感知的Bregman迭代[20]、迭代阈值法[21]等地震数据重构方法得到不断研究和应用。
由于采集环境等因素的影响, 野外地震数据往往存在随机噪声干扰, 这种噪声使得缺失数据得不到充分重建, 或重构精度较低, 因此在重构过程中需要对随机噪声进行适当压制[22-23]。ZHANG等[24]利用二维曲波变换对地震数据同时进行重构和去噪, 取得了较好的效果。本文基于压缩感知理论, 提出双重Bregman迭代算法, 即将分裂Bregman迭代作为内部迭代用于压制随机噪声, 将线性Bregman迭代作为外部迭代用于数据重构, 更高效地实现含噪缺失地震数据的同步重构与去噪。
1 地震数据重构与去噪的数学反问题地震数据重建可以归纳为一类线性估计问题:假设需重建的地震数据为m, 实际观测到的数据为d, 则d和m之间的关系可表示为:
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Lm}} $ | (1) |
式中:L为空间采样算子。由观测到的已知信号d求解需重建数据m的过程就是地震数据重构过程。
FOMEL[25]指出:对缺失地震数据进行重构, 可设置一个掩膜矩阵K代替空间采样算子L, 则公式(1)可表示为:
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Km}} $ | (2) |
掩膜矩阵K为对角矩阵, K中待重构位置处的元素为0, 其它位置处的元素为1。
本文目标是利用压缩感知理论由已知的观测数据d求取未知的完整数据m。由于压缩感知理论假设信号m具有稀疏特性, 因此设计一个稀疏基Φ对m进行稀疏表示:
| $ \mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\mathit{\boldsymbol{x}} $ | (3) |
式中:x为m的变换域系数。将公式(3)代入公式(2)可得:
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\mathit{\boldsymbol{x}} = \mathit{\boldsymbol{Ax}} $ | (4) |
式中:A=KΦ-1为感知矩阵, 掩膜矩阵K与稀疏矩阵Φ满足等距约束性准则[26]。
由此, 求解完整数据m的过程转换为求解稀疏信号x的过程, 根据压缩感知理论, 将公式(4)转化成L0范数问题进行求解:
| $ \mathop {{\rm{min}}}\limits_x {\left\| \mathit{\boldsymbol{x}} \right\|_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{d}} $ | (5) |
式中:‖·‖0为L0范数。
L0范数的求解较困难, 利用L1范数代替L0范数, 将L0范数最优化问题转化为L1范数的凸优化问题:
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} {\left\| \mathit{\boldsymbol{x}} \right\|_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{d}} $ | (6) |
其中:
构造惩罚函数将公式(6)统一转化成下列形式:
| $ \mathit{\boldsymbol{x}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} \mu {\left\| \mathit{\boldsymbol{x}} \right\|_1} + \frac{1}{2}\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{d}}} \right\|_2^2 $ | (7) |
或
| $ \mathit{\boldsymbol{x}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} {\left\| \mathit{\boldsymbol{x}} \right\|_1} + \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{d}}} \right\|_2^2 $ | (8) |
式中:μ和λ为罚参数, 用于平衡正则项和保真项。
对(7)式或(8)式进行求解可获得稀疏信号x, 进而通过公式(3)得到完整地震数据m。如果利用单位矩阵E代替掩膜矩阵K, 则地震数据重构问题便转换成了地震数据去噪问题。问题的关键是如何准确求解公式(7)或公式(8)。
2 基于双重Bregman迭代的地震数据重构与去噪 2.1 Bregman迭代重构算法对于公式(7)或公式(8)的求解, YIN等[27]以Bregman迭代正则化算法为基础, 结合不动点延续(fixed-point continuation, FPC)算法形成了一种新的Bregman迭代框架, 即:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{b}}^0} = 0}\\ {{\mathit{\boldsymbol{x}}^{k + 1}} = \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} {{\left\| \mathit{\boldsymbol{x}} \right\|}_1}{\kern 1pt} + \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Ax - }}{\mathit{\boldsymbol{b}}^k}} \right\|_2^2}\\ {{\mathit{\boldsymbol{b}}^{k + 1}} = {\mathit{\boldsymbol{b}}^k} + (\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^{k + 1}})} \end{array}} \right. $ | (9) |
式中:k=0, 1, …, 表示迭代次数; bk为计算xk所需的中间变量。公式(9)的关键问题在于求解
FPC算法是基于算子的向前、向后分裂, 结合不动点迭代和连续算法形成的不动点延续算法。为书写方便, 令
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}^{k + 1}} = \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} {{\left\| \mathit{\boldsymbol{x}} \right\|}_1} + \frac{\lambda }{{2{\delta ^k}}}\left\| {\mathit{\boldsymbol{x}} - [{\mathit{\boldsymbol{x}}^k} - } \right.}\\ {\left. {{\delta ^k}\nabla H({\mathit{\boldsymbol{x}}^k})]} \right\|_2^2} \end{array} $ | (10) |
式中:δk为正数, 表示第k次迭代的迭代步长; ▽H(xk)表示xk的梯度。公式(10)中的未知变量x可分解为n个分量xi, i=1, 2, …, n, 每一个xi能够通过阈值算子独立获得, 公式为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_i^{k + 1} = {\rm{shrink}} [{{({\mathit{\boldsymbol{x}}^k} - {\delta ^k}\nabla H({\mathit{\boldsymbol{x}}^k})]}_i},\frac{{{\delta ^k}}}{\lambda })}\\ {i = 1, \cdots ,n} \end{array} $ | (11) |
其中, 阈值算子shrink的定义为:设实数空间R中, y∈R, α∈R+, 则
| $ \begin{array}{*{20}{l}} {{\rm{shrink}}(y,\alpha ) = {\rm{ sgn}} (y){\rm{max}}\{ |y| - \alpha ,0\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left\{ {\begin{array}{*{20}{c}} {y - \alpha }&{y \in (\alpha ,\infty )}\\ 0&{y \in [ - \alpha ,\alpha ]}\\ {y + \alpha }&{y \in ( - \infty , - \alpha )} \end{array}} \right.} \end{array} $ | (12) |
为提高公式(10)的求解效率, 使用FPC方法求解。根据文献[28]可知, FPC算法具体迭代流程如表 1所示。
| 表 1 FPC算法实现步骤 |
YIN等[27]的研究结果表明, 由公式(9)迭代算法重构出的数据更精确, 图像对比度更高, 且由于使用了FPC算法, 计算速度更快, 因此本文采用公式(9)进行缺失地震数据插值处理。
表 1迭代过程中, 迭代次数k是决定能否得到最优值的关键参数, k过小无法收敛到最优解, k过大则会降低计算效率, 因此需要通过设定迭代停止准则来控制迭代次数, 本文采用的迭代停止准则为:
| $ \frac{{\left\| {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^k} - \mathit{\boldsymbol{d}}} \right\|_2^2}}{{\left\| \mathit{\boldsymbol{d}} \right\|_2^2}} < {10^{ - 5}} $ | (13) |
分裂Bregman迭代算法由GOLDSTEIN等[29]提出, 本文基于Rudin-Osher-Fatemi(ROF)模型[29]推导分裂Bregman迭代去噪框架。ROF模型利用数据的全变分将图像降噪问题转化为求解最优化问题, 对于高斯噪声, 具体的ROF模型表示形式为:
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} {\left\| {\nabla \mathit{\boldsymbol{x}}} \right\|_1} + \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{d}}} \right\|_2^2 $ | (14) |
式中:矩阵A在这里单纯用于去噪, 为单位矩阵; ▽x表示数据的梯度; ‖▽x‖1为L1范数部分, 表示数据x的全变分, 作为正则项, 用于实现噪声平滑, 去除噪声;
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} {\left\| \mathit{\boldsymbol{D}} \right\|_1} + \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{d}}} \right\|_2^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ s}}{\rm{.t}}{\rm{. }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{D}} = \nabla \mathit{\boldsymbol{x}} $ | (15) |
参照公式(8)加入罚函数λ1, 可得:
| $ \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{D}}} {\left\| \mathit{\boldsymbol{D}} \right\|_1} + \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{d}}} \right\|_2^2 + \frac{{{\lambda _1}}}{2}\left\| {\mathit{\boldsymbol{D}} - \nabla \mathit{\boldsymbol{x}}} \right\|_2^2 $ | (16) |
令
| $ \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{D}}} E(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{D}}) + \frac{{{\lambda _1}}}{2}\left\| {\mathit{\boldsymbol{D}} - \nabla \mathit{\boldsymbol{x}}} \right\|_2^2 $ | (17) |
可以看出公式(17)与公式(8)形式相同。参照上述Bregman的迭代步骤, 利用公式(9)即可将公式(16)转化为以下多变量的Bregman迭代形式:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{b}}^0} = {\mathit{\boldsymbol{x}}^0} = {\mathit{\boldsymbol{D}}^0} = 0}\\ {({\mathit{\boldsymbol{x}}^{k + 1}},{\mathit{\boldsymbol{D}}^{k + 1}}) = \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{D}},\mathit{\boldsymbol{x}}} {{\left\| \mathit{\boldsymbol{D}} \right\|}_1} + \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Ax}} - } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. \mathit{\boldsymbol{d}} \right\|_2^2 + \frac{{{\lambda _1}}}{2}\left\| \mathit{\boldsymbol{D}} \right\|_2^2}\\ {{\mathit{\boldsymbol{b}}^{k + 1}} = {\mathit{\boldsymbol{b}}^k} + (\nabla {\mathit{\boldsymbol{x}}^{k + 1}} - {\mathit{\boldsymbol{D}}^{k + 1}})} \end{array}} \right. $ | (18) |
上述公式含有两个变量x, D, 根据文献[29], 为获得公式(18)的最优解, 解耦公式(18)中的L1部分和L2部分, 分别对D和x进行迭代最小化, 迭代过程如下。
第一步:固定Dk, 更新xk。公式为:
| $ {\mathit{\boldsymbol{x}}^{k + 1}} = \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{d}}} \right\|_2^2 + \frac{{{\lambda _1}}}{2}\left\| {{\mathit{\boldsymbol{D}}^k} - \nabla \mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{b}}^k}} \right\|_2^2 $ | (19) |
第二步:固定xk, 更新Dk。公式为:
| $ {\mathit{\boldsymbol{D}}^{k + 1}} = \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{D}} {\left\| \mathit{\boldsymbol{D}} \right\|_1} + \frac{{{\lambda _1}}}{2}\left\| {\mathit{\boldsymbol{D}} - \nabla {\mathit{\boldsymbol{x}}^{k + 1}} - {\mathit{\boldsymbol{b}}^k}} \right\|_2^2 $ | (20) |
第三步:更新bk。公式为:
| $ {\mathit{\boldsymbol{b}}^{k + 1}} = {\mathit{\boldsymbol{b}}^k} + (\nabla {\mathit{\boldsymbol{x}}^{k + 1}} - {\mathit{\boldsymbol{D}}^{k + 1}}) $ | (21) |
公式(19)具体可用Gauss-Seidel方法进行求解, 写为xik+1=Gik的分量形式:
| $ \begin{array}{l} G_i^k = \frac{{{\lambda _1}}}{{\lambda + 4{\lambda _1}}}(x_{i + 1}^k + x_{i - 1}^k + D_{i - 1}^k - D_i^k - b_{i - 1}^k + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b_i^k) + \frac{\lambda }{{\lambda + 4{\lambda _1}}}{{\rm{d}}_i} \end{array} $ | (22) |
D可通过Dk+1=shrink(▽xk+1+bk, 1/λ1)获得。
分裂Bregman迭代的迭代停止准则为:
| $ \frac{{\left\| {{\mathit{\boldsymbol{x}}^k} - {\mathit{\boldsymbol{x}}^{k - 1}}} \right\|_2^2}}{{\left\| {{\mathit{\boldsymbol{x}}^k}} \right\|_2^2}} < 5 \times {10^{ - 3}} $ | (23) |
本文采用傅里叶变换对地震数据进行稀疏表示, 采用掩膜算子作为观测矩阵, 以YIN等[27]提出的Bregman迭代作为外部迭代, GOLDSTEIN等[29]提出的分裂Bregman迭代作为内部迭代, 形成双重Bregman迭代, 在满足迭代停止准则的条件下完成对含噪声的缺失地震记录进行重构和去噪。具体实现流程见图 1。
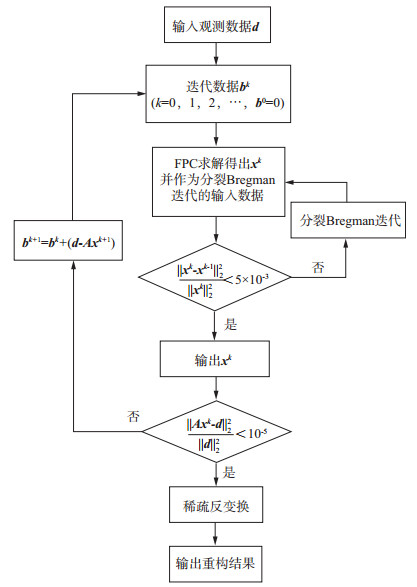
|
图 1 双重Bregman迭代流程 |
为验证双重Bregman算法的迭代效果, 选择Marmousi部分模型(图 2)正演数据的纵波分量进行算法测试。正演记录由弹性波方程有限差分模拟得到, 模拟所用的参数如下:地表激发和接收, 激发震源为主频30Hz的Ricker子波, 接收道为601道, 道间距为5m, 采样间隔为0.35ms, 记录长度为2100ms。图 3a为模拟单炮记录, 图 3b为加入信噪比为3.46dB的高斯随机噪声后的单炮记录, 随机抽取30%的地震道充零(图 3c), 对充零后的地震记录进行双重Bregman迭代。根据迭代准则(13)式和(23)式, 设置内部迭代允许最大迭代误差为10-3, 外部迭代允许最大误差为10-5; 为避免出现程序无限迭代不能正常退出的情况, 经多次试验, 同时限定了内部和外部迭代的最大迭代次数为20次。计算得到的重构结果如图 3d所示, 图 3e所示为算法误差剖面, 是图 3a和图 3d相减后的结果。结合图 3d和图 3e可以看出, 对含随机噪声的缺失地震数据, 采用本文算法实现了地震数据的重构与去噪同步进行, 可以有效压制随机噪声, 并同时获得完整的重构数据, 提高了信噪比。
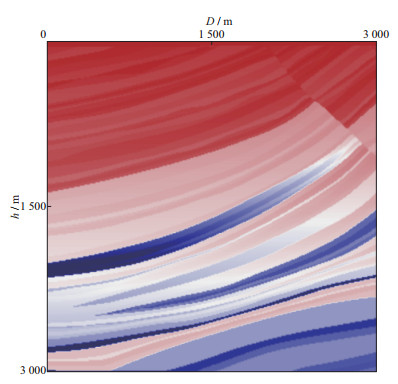
|
图 2 Marmousi部分模型 |
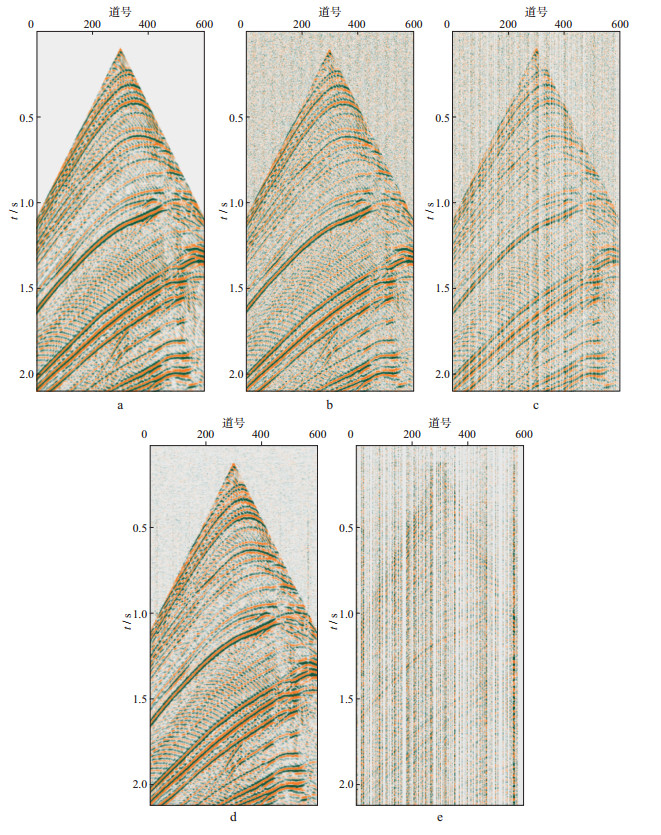
|
图 3 Marmousi模型含噪声的缺失地震记录重构与去噪 a不含噪声的模拟单炮记录; b加入信噪比为3.46dB高斯随机噪声后的单炮记录; c对含噪声的地震记录随机抽取30%地震道充零后的单炮记录; d对抽样后的含噪声地震记录进行双重Bregman迭代后的单炮记录; e双重Bregman迭代误差剖面 |
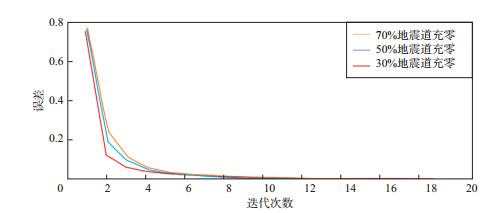
利用本文方法对不同缺失程度下地震数据的重构与去噪效果以及该方法计算误差剖面如图 4所示。其中, 图 4a和图 4d分别为对信噪比为3.46dB的Marmousi地震数据进行50%地震道充零和70%地震道充零, 然后进行与30%地震道充零相同的双重Bregman迭代重构与去噪处理, 分别得到如图 4b和图 4e所示的重构与去噪结果, 以及图 4c和图 4f的误差剖面。图 5为3种情况下的误差曲线。另外, 为对比本文方法与线性Bregman迭代的重构效果与计算效率, 对上述3种地震数据同时进行了线性Bregman迭代计算。计算环境参数为:CPU 2.60GHz, RAM 4.0GB, 64位Windows 7系统。重构和去噪时间以及处理后的信噪比量化评价结果见表 2。综合图 3、图 4、图 5以及表 2, 可得如下结论:当欠采样数据为完整数据的70%时, 利用本文方法能够得到相对完整的重构数据, 处理后的信噪比为8.73, 得到了大幅度提升; 当欠采样数据为完整数据的50%时, 本文方法基本上实现了对缺失数据的重构, 并且重构与处理后的信噪比由原来的3.46提升到4.46;当欠采样数据为完整数据的30%时, 本文方法能够较完整地重建出缺失数据, 但仍有部分数据未能得到准确重构, 而且可能由于缺失程度较大、迭代过程中引入重构噪声等因素, 迭代处理后的数据信噪比有所降低。经测试发现, 当欠采样数据为完整数据的一半及以上时, 能够利用本文方法得到相对完整的重构与去噪成果, 并且数据缺失越少, 重构和去噪所需计算时间越少, 误差曲线下降越快, 信噪比提升也越高; 在不同缺失程度下, 双重Bregman迭代与线性Bregman迭代的运行时间相差不大。这是因为分裂Bregman迭代的速度相当快。GOLDSTEIN等[29]曾指出, 分裂Bregman迭代速度很快的主要原因是由其计算方法决定的, 分裂Bregman迭代是将L1和L2部分进行解耦, 然后分别用快速收敛的Gauss-Seidel方法和阈值算子方法求解, 这种算法加快了分裂Bregman迭代的速度; 另外, 分裂Bregman的迭代速度与参数选择有很大关系, 参数选择得当, 该算法非常快速。综上, 双重Bregman迭代不仅有效去除了随机噪声, 其结果的信噪比明显高于线性Bregman迭代结果, 而且运算时间并没有大量增加, 因此, 对于含有随机噪声的地震数据, 本文方法优于线性Bregman迭代方法, 具有一定的研究意义及应用价值。
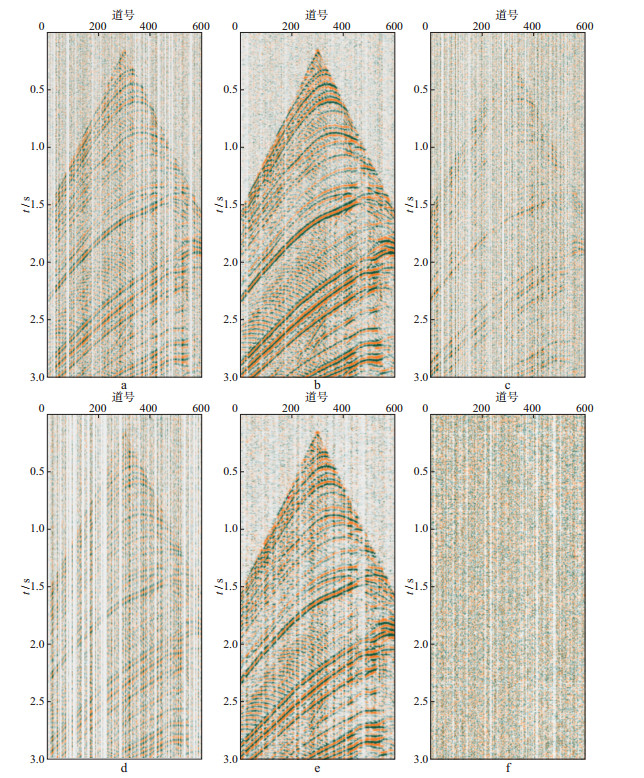
|
图 4 不同缺失程度下双重Bregman迭代对含噪声地震数据的重构与去噪结果和误差剖面 a随机抽取50%地震道充零; b 50%地震道充零后基于双重Bregman迭代的重构与去噪结果; c 50%地震道充零后基于双重Bregman迭代的重构与去噪误差剖面; d随机抽取70%地震道充零; e 70%地震道充零后基于双重Bregman迭代的重构与去噪结果; f 70%地震道充零后基于双重Bregman迭代的重构与去噪误差剖面 |
| 表 2 双重Bregman迭代和线性Bregman迭代在不同缺失程度下的重构和去噪时间及信噪比 |
|
图 5 不同缺失程度下含噪声地震数据的重构与去噪误差曲线 |
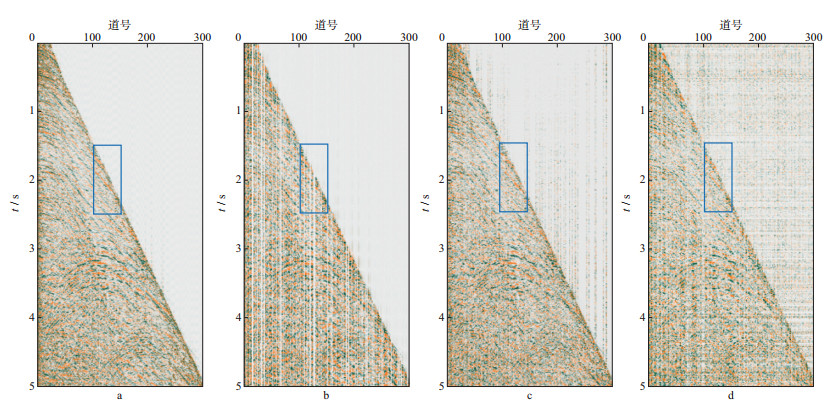
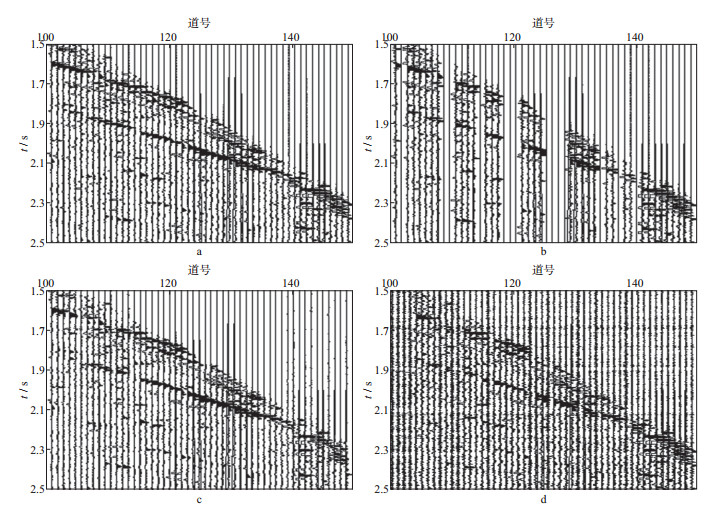
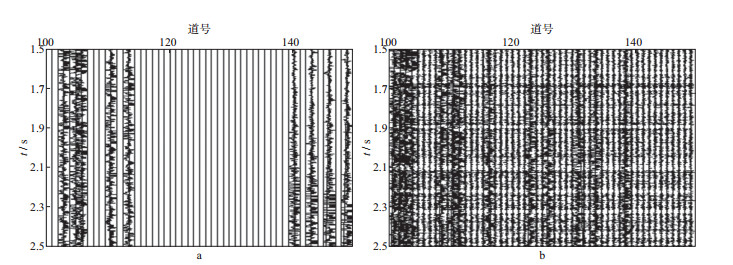
利用海上某工区实际地震数据进行测试, 原始地震数据共301道, 每道10001个采样点, 重构工作在CDP道集(图 6a)上进行, 对该数据随机抽取30%的地震道充零后的结果如图 6b, 对抽稀后的地震数据进行双重Bregman迭代, 迭代停止准则采用公式(13)和公式(23), 经多次试验, 同时设置内部迭代允许最大迭代次数为50次, 外部迭代允许最大迭代次数为100次, 得到的结果如图 6c。为说明本文算法的重构与去噪效果, 对图 6b进行线性Bregman迭代计算, 迭代停止准则为公式(13), 允许最大迭代次数为100次, 迭代结果如图 6d。结合图 6中蓝色方框对应的局部放大波形显示(图 7)可以看出, 两种迭代算法都能够对缺失数据进行较好恢复, 但本文迭代算法与原始数据的重合度更高。将两种算法迭代后的地震数据与原始地震数据求差, 其中1.5~2.5s时间段第100~150道(即蓝色方框对应范围)的误差如图 8所示, 整体地震数据的重构误差如图 9所示, 对比可以看出, 双重Bregman算法迭代误差远远小于线性Bregman迭代, 进一步显现出本文迭代算法的优越性。
|
图 6 实测地震记录的重构与去噪 a原始CDP道集; b对原始数据随机抽取30%的地震道充零后的道集; c对抽样后的地震道集进行双重Bregman迭代后的结果; d对抽样后的地震道集进行线性Bregman迭代的结果 |
|
图 7 图 6蓝色方框的放大显示 a原始CDP道集; b对原始数据随机抽取30%的地震道充零后的道集; c对抽样后的地震道集进行双重Bregman迭代后的结果; d对抽样后的地震道集进行线性Bregman迭代的结果 |
|
图 8 两种Bregman迭代局部结果的精度比较 a双重Bregman迭代误差; b线性Bregman迭代误差 |
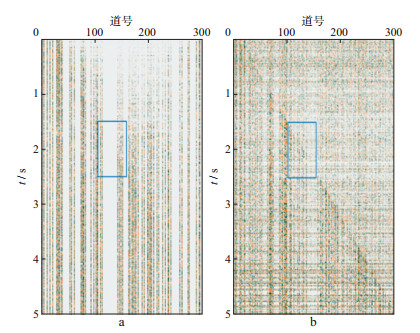
|
图 9 两种Bregman迭代整体结果的精度比较 a双重Bregman迭代误差; b线性Bregman迭代误差 |
本文结合Bregman迭代重构算法与分裂Bregman迭代去噪算法, 提出了一种基于双重Bregman迭代的地震数据重构与去噪方法。Marmousi模型数值模拟实验和实际数据应用结果表明:本文算法没有因两种独立算法的结合而减弱对数据的处理效果, 且只需较少次数的迭代就能高效实现含噪声缺道地震数据的同时重构与去噪, 为地震数据恢复提供了一种新的缺失地震数据处理方法。
基于压缩感知的地震数据处理方法需要先将地震数据通过数学变换进行稀疏表示, 本文采用了最常用的傅里叶稀疏表示方法, 而该方法只适用于同相轴近似线性或者平稳变化的地震数据, 因此本文进一步的工作是寻找复杂地质构造下地震数据的最佳稀疏表示方法, 结合双重Bregman迭代, 进一步研究复杂地质构造下含噪声缺失地震数据的高精度重构与去噪方法。
| [1] |
陈可洋, 范兴才, 吴清岭, 等. 提高逆时偏移成像精度的叠前插值处理研究与应用[J]. 石油物探, 2013, 52(4): 409-416. CHEN K Y, FAN X C, WU Q L, et al. Seismic wave pre-stack interpolation processing for improving the precision of reverse-time migration and its application[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 409-416. |
| [2] |
高建军, 陈小宏, 李景叶, 等. 基于非均匀Fourier变换的地震数据重建方法研究[J]. 地球物理学进展, 2009, 24(5): 1741-1747. GAO J J, CHEN X H, LI J Y, et al. Study on reconstruction of seismic data based on nonuniform Fourier transform[J]. Progress in Geophysics, 2009, 24(5): 1741-1747. |
| [3] |
LARNER K, GIBSON B, ROTHMAN D. Trace interpolation and the design of seismic surveys[J]. Geophysics, 1981, 46(4): 407-409. |
| [4] |
SPITZ S. Seismic trace interpolation in the f-x domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [5] |
国九英, 周兴元. f-k域等道距道内插[J]. 石油地球物理勘探, 1996, 31(2): 211-218. GUO J Y, ZHOU X Y. Iso-interval trace interpolation in f-k domain[J]. Oil Geophysical Prospecting, 1996, 31(2): 211-218. |
| [6] |
GULUNAY N, CHAMBERS R E. Unaliased f-k domain trace interpolation (UFKI)[J]. Expanded Abstracts of 66th Annual Internat SEG Mtg, 1996, 1461-1464. |
| [7] |
GULUANY N. Seismic trace interpolation in the Fourier transform domain[J]. Geophysics, 2003, 68(1): 355-369. |
| [8] |
王升超, 韩立国, 巩向博. 基于各向异性Radon变换的叠前地震数据重建[J]. 石油物探, 2016, 55(6): 808-815,839. WANG S C, HAN L G, GONG X B. Prestack seismic data reconstruction based on anisotropic Radon transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 808-815,839. |
| [9] |
王本锋, 陆文凯, 陈小宏, 等. 基于3D Curvelet变换的频率域高效地震数据插值方法研究[J]. 石油物探, 2018, 57(1): 65-71. WANG B F, LU W K, CHEN X H, et al. Efficient seismic data interpolation using three-dimensional Curvelet transform in the frequency domain[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 65-71. |
| [10] |
李欣, 杨婷, 孙文博, 等. 一种基于光滑L1范数的地震数据插值方法[J]. 石油地球物理勘探, 2018, 53(2): 251-256. LI X, YANG T, SUN W B, et al. A gradient projection method for smooth L1 norm regularization based seismic data sparse interpolation[J]. Oil Geophysical Prospecting, 2018, 53(2): 251-256. |
| [11] |
GAO J J, SACCHI M D, CHEN X H. A fast reduced-rank interpolation method for prestack seismic volumes that depend on four spatial dimensions[J]. Geophysics, 2013, 78(1): V21-V30. |
| [12] |
CHEN Y, DONG Z, JIN Z, et al. Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method[J]. Geophysical Journal International, 2016, 206(3): 1695-1717. DOI:10.1093/gji/ggw230 |
| [13] |
FOMEL S. Seismic reflection data interpolation with differential offset and shot continuation[J]. Geophysics, 2003, 68(2): 733-744. |
| [14] |
LIU B, SACCHI M D. Minimum weighted norm interpolation of seismic records[J]. Geophysics, 2004, 69(6): 1560-1568. DOI:10.1190/1.1836829 |
| [15] |
刘争光, 韩立国, 张良, 等. 压缩感知理论下基于快速不动点连续算法的地震数据重建[J]. 石油物探, 2018, 57(1): 50-57,71. LIU Z G, HAN L G, ZHANG L, et al. Seismic data reconstruction using FFPC algorithm based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 50-57,71. |
| [16] |
陈祖斌, 王丽芝, 宋杨, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重构[J]. 石油地球物理勘探, 2018, 53(4): 674-681,693. CHEN Z B, WANG L Z, SONG Y, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674-681,693. |
| [17] |
马坚伟. 压缩感知走进地球物理勘探[J]. 石油物探, 2018, 57(1): 24-27. MA J W. Compressed sensing in geophysical exploration[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 24-27. |
| [18] |
FOMEL S, LIU Y. Seislet transform and seislet frame[J]. Geophysics, 2010, 75(3): V25-V38. DOI:10.1190/1.3380591 |
| [19] |
LIU Y, FOMEL S. OC-seislet:Seislet transform construction with differential offset continuation[J]. Geophysics, 2010, 75(6): WB235-WB245. DOI:10.1190/1.3479554 |
| [20] |
刘洋, 张鹏, 刘财, 等. 地震数据Bregman整形迭代插值方法[J]. 地球物理学报, 2018, 61(4): 1400-1412. LIU Y, ZHANG P, LIU C, et al. Seismic data interpolation based on Bregman shaping iteration[J]. Chinese Journal of Geophysics, 2018, 61(4): 1400-1412. |
| [21] |
LIU C, LI P, LIU Y, et al. Anti-aliasing iterative data interpolation method based on seislet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1619-1627. |
| [22] |
LIU W, CAO S, LI G. Reconstruction of seismic data with missing traces based on local random sampling and curvelet transform[J]. Journal of Applied Geophysics, 2015, 115(6): 129-139. |
| [23] |
CHEN Y K, MA J W, FOMEL S. Double-sparsity dictionary for seismic noise attenuation[J]. Geophysics, 2016, 81(2): V17-V30. |
| [24] |
ZHANG H, CHEN X H, ZHANG L Y. 3D simultaneous seismic data reconstruction and noise suppression based on the curvelet transform[J]. Applied Geophysics, 2017, 14(1): 87-95,190. DOI:10.1007/s11770-017-0607-z |
| [25] |
FOMEL S.Three-dimensional seismic data regularization[D].Palo Alto: Stanford University, 2001
|
| [26] |
CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [27] |
YIN W, OSHER S, GOLDFARB D, et al. Bregman iterative algorithms for L1-minimization with applications to compressed sensing[J]. SIAM Journal on Imaging Sciences, 2008, 1(1): 143-168. DOI:10.1137/070703983 |
| [28] |
HALE E T, YIN W T, ZHANG Y. Fixed-point continuation applied to compressed sensing:Implementation and numerical experiments[J]. Journal of Computational Mathematics, 2010, 28(2): 170-194. DOI:10.4208/jcm.2009.10-m1007 |
| [29] |
GOLDSTEIN T, OSHER S. The Split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. DOI:10.1137/080725891 |




