2. 中国科学技术大学地球和空间科学学院, 安徽合肥 230026
2. School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China
在地震勘探及地震学领域, 初至层析反演是近地表速度建模的常用手段, 现已在区域和全球地震学[1-4]、油气勘探[5-7]、浅表地球物理勘探[8-9]等领域得到了广泛应用。初至波旅行时拾取的精度直接影响了层析反演的效果。地表条件复杂的情况下, 地震资料信噪比低, 初至变化大, 干扰严重, 难以使用常用的商业软件或方法进行自动拾取, 海量的初至需要人工拾取, 因此使得处理效率大大降低。
经过40多年的研究, 众多学者提出了多种初至拾取方法。但对于近地表条件复杂的西南山区低信噪比地震数据, 目前还没有一种方法能取得良好的效果。1972年PERALDI等[10]提出了相关法拾取初至, 其精度受限于子波的选取。1985年COPPENS[11]提出了滑动时窗的能量比法拾取初至, 该方法能很好避开续至波的干扰, 但是容易误判初至前的强干扰, 且时窗长度的选取会随工区条件发生变化。徐钰等[12]在此基础上提出了多时窗能量比法, 考虑能量比的次极值, 利用相位域起跳点及奇异值检测技术来质控, 提高了拾取精度。许银坡等[13]先用能量比法确定初至波大致位置并评价其可信度, 然后再拾取可信度高的初至, 该方法降低了人工标注的时间, 但对于地形复杂下的初至拾取效果改善不大。BP神经网络算法考虑了相邻道之间的关系, 易于实现, 王金峰等[14]提出改进的BP神经网络算法来拾取初至, 取得较好效果, 但该方法需要人工提取特征, 且随着地形变化及数据量不断增加, 人工经验提取特征局限性越来越大, 因而该方法的应用效果有限。曾富英等[15]根据分形原理, 用时窗的变化来反映地震道曲线的局部形态特征, 提出了一种初至拾取方法, 精度较高, 但拾取效果取决于小圆半径的选取。李辉峰等[16]使用数字图像处理技术拾取初至, 取得较好效果, 但初至与背景噪声边界模糊时效果不佳。
深度学习[17]作为机器学习的一个分支, 在地震勘探领域得到了广泛应用, 例如基于地震图像先验模型构建的全波形反演[18]、基于卷积神经网络的地震数据去噪[19]、基于卷积神经网络的速度拾取[20]及深度学习层析成像[21]等方法。在初至拾取方面, 刘佳楠等[22]利用全卷积神经网络(FCN)[23]自动拾取地震初至, 在高噪声地震数据处理中取得了较好的结果, 但依赖大量数据且收敛速度慢。蔡振宇等[24]利用卷积神经网络(CNN)对汶川地震余震P波进行自动拾取, 当信噪比较低时仍能准确拾取初至, 但该方法只是针对天然地震数据, 未进一步测试勘探地震数据。生成对抗网络(GAN)是一种通过对抗网络来估计生成模型的新的深度学习框架[25], 在此基础上加入卷积神经网络, 结合二者优点, 发展成为深度卷积生成对抗网络(DCGAN)[26], 具有分辨率更高、生成样本特征更明显等特点。
本文构建了一种适用于地震数据初至拾取的DCGAN, 并将之用于地震数据初至拾取。在对地震数据进行能量均衡等预处理后, 选取初至时刻后含波峰的半波长数据作为初至特征加入训练。首先初始化DCGAN, 然后分别将预处理后的地震数据与初至数据用于生成器与判别器的训练, 直到得到网络结构的最优参数。初至拾取的过程为:将地震数据输入训练完成的网络, 在生成器中生成一个初至数据, 再对其每道求取峰值时间, 即为每道的初至时间。最后, 用山地地震数据进行初至拾取实验, 并与现有初至拾取方法(如长短时窗比(STA/LTA)法和峰度赤池信息量准则(AIC)法)进行对比, 验证了本文方法的可行性和有效性。
1 DCGAN基本原理GAN的基本思想源自于博弈论中的纳什均衡理论, 可以将GAN网络中的生成网络模型(Generator, 即生成器)和判别网络模型(Discriminator, 即判别器)看作是参与博弈游戏的双方。生成器学习真实数据分布特征, 以生成与真实数据相似的生成数据, 其最终目的是使生成数据能欺骗判别器; 而判别器的最终目的是通过学习能正确判断输入数据是真实数据还是生成数据; 双方为取得胜利, 必须不断学习优化, 提高自身的生成能力和判别能力, 最终达到二者之间的纳什均衡。
在地震初至拾取中, 生成器和判别器可分别表示为G和D, 其输入数据分别为地震数据z及真实初至x。对于判别器D, 当生成器G固定时, 训练的目标函数可表示为:
| $ \begin{array}{*{20}{c}} {{\rm{ob}}{{\rm{j}}^{\rm{D}}}\left( {{\theta ^{\rm{D}}},{\theta ^{\rm{G}}}} \right) = - \frac{1}{2}{E_{x\~{P_{{\rm{data}}}}(x)}}[\log D(x)] - }\\ {\frac{1}{2}{E_{z\~{P_z}(z)}}\{ \log [1 - D(G(z))]\} } \end{array} $ | (1) |
式中:θD和θG分别表示判别器和生成器的待优化参数; Pdata(x)为真实初至分布; Pz(z)为地震数据分布; x~Pdata(x)为服从真实初至分布下的采样; z~Pz(z)为服从地震数据分布下的采样; Ex~Pdata(x)(·)表示在x~Pdata(x)条件下计算期望值; Ez~Pz(z)(·)表示在z~Pz(z)条件下计算期望值; D(x)表示x为真实初至的概率; G(z)表示输入为z时的生成器生成数据。在实际训练时, 判别器的训练数据集来源于两部分:真实初至集Pdata(x)(标注为1)和生成器的数据集PG(x)(标注为0)。
当输入数据来自真实初至集x时, D的目标是使输出的D(x)趋近1, 反之当输入数据来自生成数据集G(z)时, D的目标是使输出的D(G(z))趋近0, 与此同时G的目标是使之趋近1。因此, 生成对抗网络训练的过程是一个极小-极大化问题, 其目标函数可以描述为:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_G \;\;\mathop {\max }\limits_D V(D, G) = {E_{x\~{P_{{\rm{data }}}}(x)}}[\log D(x)] + }\\ {{E_{z\~{P_z}(z)}}\{ \log [1 - D(G(z))]\} } \end{array} $ | (2) |
总而言之, 生成对抗网络训练学习的过程, 不仅要训练判别器D来最大化判别数据来源的准确率, 同时也要训练生成器G来最小化log[1-D(G(z))]。求解目标函数(2)可以采用交替优化的方法:先固定G, 优化D, 使D的判别准确率最大; 然后固定D, 优化G, 使D的判别准确率最小; 最后的结果是当且仅当Pdata=PG时达到全局最优解。在训练的同一轮参数更新中, 一般对D的参数更新多次后再对G的参数更新一次。
DCGAN首次将卷积网络引入到GAN, 利用卷积层强大的特征提取能力来提高GAN的效果。为提高收敛速度和样本质量, DCGAN对G和D的卷积神经网络做如下改变:
1) 取消池化层, G中使用反卷积进行上采样, D中用步幅卷积层(strided convolutions)替代池化层;
2) G和D中数据均进行批量归一化处理, 解决初始化差的问题;
3) G中移除全连接层, 变为全卷积网络(FCN);
4) G网络中激活函数用ReLU函数, 最后一层用Tanh函数;
5) D网络中所有层激活函数用LeakyReLU函数。
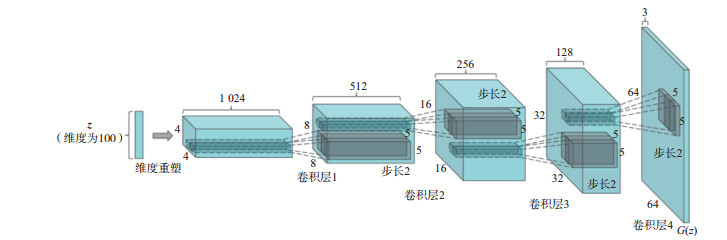
图 1为一个典型DCGAN生成器结构图, 主要由4个卷积层构成。将一个维度为100的向量z重塑后作为输入, 不断进行反卷积, 每个卷积层都是一个步长为2的转置卷积运算, 输出数据的维度是输入层的两倍, 最后输出一个64×64×3的数据。
|
图 1 典型的DCGAN生成器结构 |
对于炮集记录, 初至只是时间信息, 转化成数据信息比较单一, 因此本文将初至时刻后包含波峰的第一个半波长数据作为初至数据, 并从参与训练的地震数据中提取出来, 作为真实初至数据。
由于不同道间、炮间的地震数据能量差别很大, 有时会相差几个量级, 这时如果直接参与训练会使训练过程不稳定或不收敛。因此本文首先对每个炮集记录做道间均衡处理:
| $ x_i^\prime = \frac{{\bar X}}{{{{\bar x}_i}}} \cdot {x_i} $ | (3) |
式中:x'i为第i道做完道间均衡后的数据; X为整个炮集数据取绝对值后的平均值; xi为第i道数据取绝对值后的平均值; xi为第i道地震数据。用于DCGAN训练的数据必须做归一化处理, 有:
| $ {x''_{i,j}} = \frac{{{{x'}_{i,j}} - {{X'}_{\min }}}}{{{{X'}_{\max }} - {{X'}_{\min }}}} $ | (4) |
式中:x″i, j表示归一化后第i道第j个采样点的值; x′i, j为道间均衡后第i道第j个采样点的值; X′min和X′max分别表示整个道间均衡后道集的最小值和最大值。
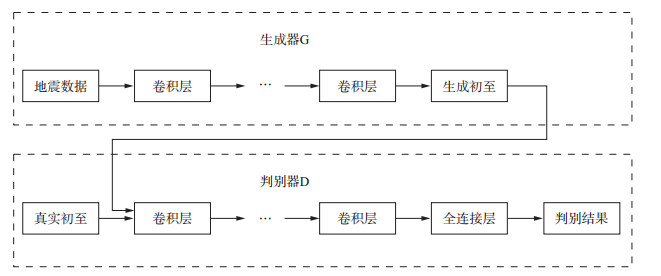
2.2 DCGAN初至拾取拓扑结构本文提出的用于初至拾取的DCGAN结构如图 2所示。训练网络分为生成器和判别器两部分, 生成器由多个卷积层(conv)构成, 每层卷积核大小均为3×3;判别器由多个卷积层和最后一个全连接层(FC)构成, 每层卷积核大小也是3×3。在生成器中, 除最后一层外, 每个卷积层的卷积核个数设置为64个, 即做完卷积操作后得到64个特征映射; 判别器中, 每个卷积层的卷积核个数设置为128个, 即做完卷积后得到128个特征映射。本文输入的地震数据可看作一个250×90×1的向量, 在生成器中经过第一个卷积层后生成一个250×90×64的向量, 此后经每个卷积层都输出一个250×90×64的向量, 经过最后一层卷积层输出为250×90×1的向量。判别器的输入为代表真实初至的250×90×1向量, 经每层卷积层都输出一个250×90×128的向量, 最后经全连接层输出一个0~1的实数。
|
图 2 用于初至拾取的DCGAN结构示意 |
网络的训练过程为:将地震数据输入到生成器, 经过一系列卷积层的卷积操作, 最后生成一个初至数据, 再与所对应地震数据的真实初至同时作为输入进行判别器训练, 判别器将两个初至的相似程度反馈给生成器, 就实现了生成器与判别器的相互迭代优化。
2.3 地震数据初至拾取DCGAN的特点针对地震数据的特殊属性, 本文DCGAN具有如下特点。
1) 数据体优化:在卷积层进行卷积操作前对输入的特征数据进行扩展边界处理, 补零值至与输入数据相同大小, 保证了输出数据大小与输入数据一致。
2) 优化算法:生成器与判别器中除最后一层外均使用批量归一化(Batch Normalization)优化算法以及丢弃正则化层(dropout)。批量归一化优化算法可以归一化每一层的输入, 使它们的均值为0、方差为1, 使数据更集中而不用担心数据太小或者太大, 有助于处理初始化不良导致的训练问题, 提升网络的稳定性; 丢弃正则化层可以在每个卷积层输出后随机丢弃一些特征, 避免整个网络偏向某一特征, 一定程度上避免了过拟合问题。
3) 卷积层数:生成器与判别器均由卷积神经网络构成, 卷积层数直接影响到整个网络的性能。卷积层数较少时, 提取到的样本特征比较简单, 可能导致网络训练不完全, 网络模型精度低。卷积层数的增加使得网络能提取到更深层的特征、网络模型精度更高, 但增加到一定程度后, 随着层数的增加可能产生过拟合问题, 即网络模型在训练集上表现很好, 但是在测试集中表现不好。因此本文通过改变生成器和判别器的卷积层数来进行测试, 选取最优网络。
3 实验分析本文选用西南某探区的山地地震资料进行测试, 选取300炮地震数据作为样本训练DCGAN, 其中每炮选取90道, 每道250个采样点(采样间隔为4ms, 总时长为1000ms)。
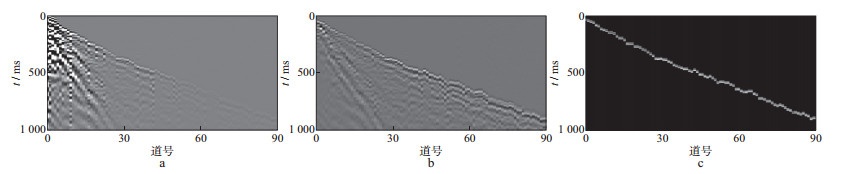
首先对全部地震样本数据进行预处理, 图 3对比了其中某单炮样本数据预处理前后的结果。从图 3a可以看出, 原始地震单炮能量不均衡, 近道能量是远道能量的几十甚至上百倍, 此时如果直接用于训练会使整个训练过程无法收敛甚至崩溃, 因此须做能量均衡和归一化处理。图 3b为预处理后的单炮样本数据。图 3c为选取人工拾取初至后的半波长数据, 作为真实初至参与判别器训练。
|
图 3 地震样本数据预处理 a原始地震单炮数据; b预处理后的地震单炮样本数据; c预处理后的真实初至数据 |
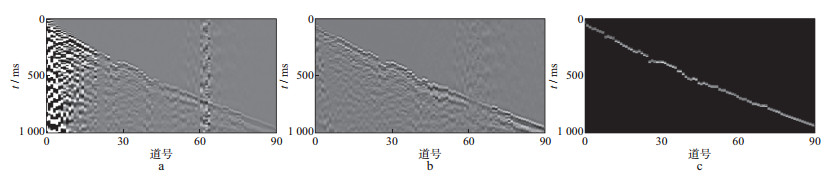
在深度学习中, 不同的网络结构会影响网络的性能和精度, 最优网络结构问题是深度学习领域的一个研究热点, 到目前为止仍没有一个确切的方法来选择一个最优的网络结构。为确定生成器与判别器的最佳卷积层数, 本文参考前人对深度学习参数选取的研究[27-29]以及生成对抗网络在图像处理中的成功经验[30-31], 使用5种不同方案的网络结构来训练DCGAN, 如表 1所示, 每种方案均经过100历元(epoch), 1个epoch等于使用训练集中的全部样本训练一次。另外随机选取工区内的某一炮地震数据作为试验炮进行效果测试, 如图 4所示。对试验炮先进行人工初至拾取以及预处理, 为比较拾取效果, 取人工拾取初至时刻后的半波长数据作为真实初至数据。
|
图 4 地震试验数据预处理 a原始地震单炮数据; b预处理后的地震单炮数据; c预处理后的真实初至数据 |
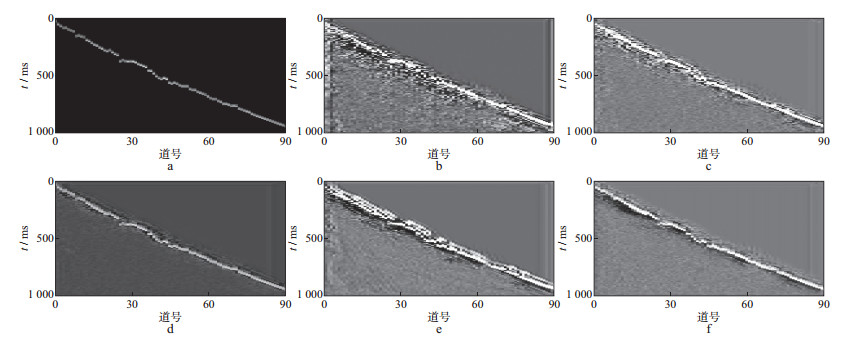
分别用表 1中5种不同方案训练的DCGAN进行初至拾取, 结果如图 5所示。由图 5可以看出, 在网络卷积层数不够时(方案一、方案二), 由于训练不完全, 更深层特征没有得到训练, 因此拾取结果很模糊, 初至特征不明显, 很难辨认初至波; 而在网络卷积层数过多时(方案四、方案五), 可能产生过拟合问题, 最终导致拾取结果不理想。最终测试结果表明只有当生成器与判别器卷积层数都选取合适时, 才能得到最优的网络结构, 使初至特征得到体现, 达到最佳拾取初至的效果。
| 表 1 DCGAN参数 |
|
图 5 不同网络结构初至拾取结果 a人工拾取真实初至; b方案一; c方案二; d方案三; e方案四; f方案五 |
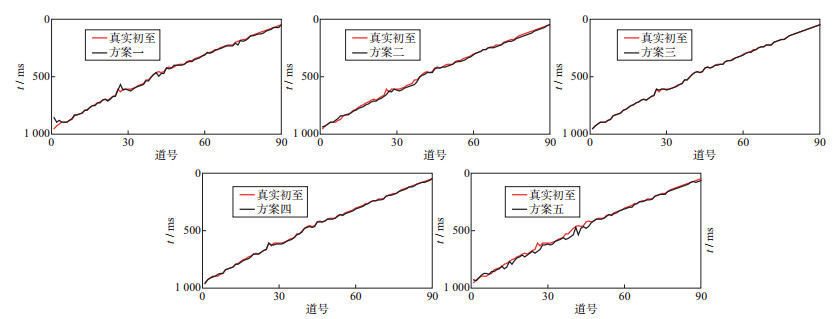
经过本文方法得到的初至数据是初至时间后包含波峰的半波长数据, 因此还需对拾取结果的每一道计算峰值, 得到真实初至波峰时刻的时间值, 5种不同方案拾取的初至时间结果如图 6所示。
|
图 6 不同方案结果与真实初至对比 |
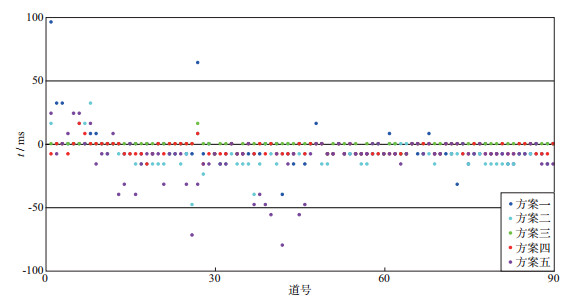
为了直观显示每种方案初至(波峰)拾取的最终结果, 对每一道定义误差E=TG-TR, 其中TG为本文方法拾取的初至, TR为人工拾取的初至, 可认为是真实初至。计算5种不同方案在每道上拾取的误差, 结果如图 7所示, 可以看出, 方案三拾取效果最佳, 结果最接近真实初至, 只有少量几道存在误差, 且都在4个采样点以内, 因此可认为方案三拾取结果能达到实际生产需要。
|
图 7 不同方案的拾取误差 |
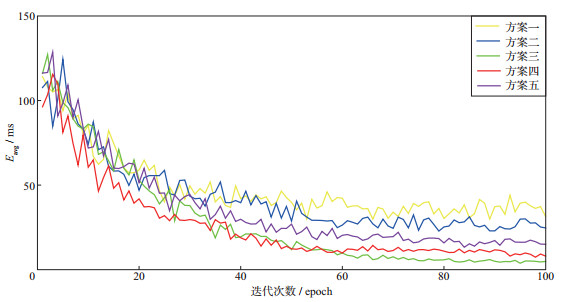
为分析不同网络模型的训练过程和拾取效果, 选取最优网络, 本文定义拾取的平均误差
|
图 8 不同方案平均误差随迭代次数变化的曲线 |
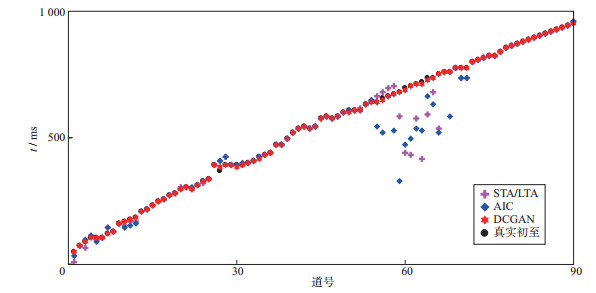
长短时窗比(STA/LTA)法和峰度赤池信息量准则(AIC)法都是目前比较常用的初至拾取方法, 为有效说明本文方法的拾取效果, 分别用STA/LTA法和AIC法拾取初至, 将拾取结果与本文方法的拾取结果进行对比, 人工拾取初至视为真实初至, 最终结果如图 9所示。
|
图 9 本文方法与常用方法拾取结果对比 |
由图 9可看出, STA/LTA法和AIC法在含噪声的55~65道附近拾取效果不佳, 而本文方法拾取精度较高, 在图中可以看出误差只在1~2个采样点。对于近道和初至时间变化较大的相邻道, STA/LTA法和AIC法的拾取结果也不如本文方法的拾取结果, 因此可认为本文方法在拾取精度方面优于STA/LTA法和AIC法, 能满足生产需要。
4 结论深度学习技术在地震勘探领域的应用研究处于起步阶段, 虽然在地震数据去噪、断层识别、储层预测等方面已经有一些研究, 但还没有在图像处理或语音识别等领域的应用那么成功。深度卷积生成对抗网络是近年来提出的深度学习方法, 在图像处理领域的应用已经取得巨大成功, 本文将该方法引入到地震勘探领域, 作为一种新的地震数据初至拾取方法进行了探索性研究。
地震初至拾取算法的关键在于构建一个适合的DCGAN, 该网络分为生成器和判别器两部分, 且都由卷积神经网络构成。卷积层中分别加入ReLU、Tanh、LeakyReLU等激活函数, 使用批量归一化优化算法, 再加上丢弃正则化层防止过拟合, 使DCGAN训练在保证较高分辨率和精度的情况下, 保留更多原始数据细节, 从而使得训练过程更稳定。初至拾取实验表明:在选取最优DCGAN网络的情况下, 本文方法具有一定可行性, 拾取的初至仍能保证较高的精度, 与现有方法(如STA/LTA法、AIC法)相比, 拾取结果较好, 能满足生产需要。
本文通过对不同网络深度结构进行测试, 得到了一个最优的DCGAN网络模型。下一步工作是对更多参数进行测试, 如每个卷积层的激活函数及卷积核个数、大小、步长等。另一方面, 当前得到的模型由同一个工区的部分数据训练得到, 面对更多类型的复杂数据可能很难取得效果, 因此还需对更多类型地震数据进行训练, 提高模型泛化能力。
| [1] |
臧绍先, 宁杰远. 西太平洋俯冲带的研究及其动力学意义[J]. 地球物理学报, 1996, 39(2): 188-202. ZANG S X, NING J Y. Study on the Western Pacific Subduction Belt and its dynamic significance[J]. Chinese Journal of Geophysics, 1996, 39(2): 188-202. |
| [2] |
朱介寿, 曹家敏, 蔡学林, 等. 东亚及西太平洋边缘海高分辨率面波层析成像[J]. 地球物理学报, 2002, 45(5): 646-664. ZHU J S, CAO J M, CAI X L, et al. High resolution surface wave tomography in East Asia and West Pacific marginal seas[J]. Chinese Journal of Geophysics, 2002, 45(5): 646-664. |
| [3] |
滕吉文, 王夫运, 赵文智, 等. 鄂尔多斯盆地上地壳速度分布与沉积建造和结晶基底起伏的构造研究[J]. 地球物理学报, 2008, 51(6): 1753-1766. TENG J W, WANG F Y, ZHAO W Z, et al. Velocity distribution of upper crust, undulation of sedimentary formation and crystalline basement beneath the Ordos basin in North China[J]. Chinese Journal of Geophysics, 2008, 51(6): 1753-1766. |
| [4] |
谭俊敏, 杨国权, 王永刚, 等. 潍北凹陷砂砾岩体的地球物理特征研究[J]. 石油物探, 2004, 43(4): 341-344. TAN J M, YANG G Q, WANG Y G, et al. Geophysical characters of glutenite unit in Weibei depression[J]. Geophysical Prospecting for Petroleum, 2004, 43(4): 341-344. |
| [5] |
郭恺, 杨林. 一种新的TTI介质多参数联合层析反演方法[J]. 石油物探, 2019, 58(3): 412-418. GUO K, YANG L. A new multi-parameter joint tomography inversion method for TTI medium[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 412-418. |
| [6] |
蔡杰雄. 高斯束偏移与高斯束层析反演速度建模[J]. 石油物探, 2018, 57(2): 262-273. CAI J X. Gaussian beam operator-based migration and tomography[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 262-273. |
| [7] |
胡光辉, 李熙盛, 郭丽, 等. 构造约束全波形反演及其海上资料应用[J]. 石油物探, 2018, 57(4): 592-596. HU G H, LI X S, GUO L, et al. Structure-constrained full waveform inversion and its application in marine seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 592-596. |
| [8] |
胡平, 刘保金, 白立新, 等. 奥林匹克公园地区隐伏断裂综合探测[J]. 地球物理学报, 2010, 53(6): 1486-1494. HU P, LIU B J, BAI L X, et al. Synthetic exploration of the buried faults in Olympic park area[J]. Chinese Journal of Geophysics, 2010, 53(6): 1486-1494. |
| [9] |
刘江平, 王莹莹, 刘震, 等. 近地表反射和折射法的进展及应用[J]. 地球物理学报, 2015, 58(9): 3286-3305. LIU J P, WANG Y Y, LIU Z, et al. Progress and application of near-surface reflection and refraction method[J]. Chinese Journal of Geophysics, 2015, 58(9): 3286-3305. |
| [10] |
PERALDI R, CLEMENT A. Digital processing of refraction data:Study of first arrivals[J]. Geophysical Prospecting, 1972, 20(3): 529-548. DOI:10.1111/j.1365-2478.1972.tb00653.x |
| [11] |
COPPENS F. First arrival picking on common-offset trace collections for automatic estimation of static corrections[J]. Geophysical Prospecting, 1985, 33(8): 1212-1231. DOI:10.1111/j.1365-2478.1985.tb01360.x |
| [12] |
徐钰, 曾维辉, 宋建国, 等. 浅层折射波勘探中初至自动拾取新算法[J]. 石油地球物理勘探, 2012, 47(2): 218-224. XU Y, ZENG W H, SONG J G, et al. A new method for first-break picking in refraction explortion[J]. Oil Geophysical Prospecting, 2012, 47(2): 218-224. |
| [13] |
许银坡, 杨海申, 杨剑, 等. 初至波能量比迭代拾取方法[J]. 地球物理学进展, 2016, 31(2): 845-850. XU Y P, YANG H S, YANG J, et al. Iteration picking method of first break using energy ratio[J]. Progress in Geophysics, 2016, 31(2): 845-850. |
| [14] |
王金峰, 罗省贤. BP神经网络的改进及其在初至波拾取中的应用[J]. 物探化探计算技术, 2006, 28(1): 14-17. WANG J F, LUO X X. The improved BP neural network and its application in seismic first breaks picking[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2006, 28(1): 14-17. |
| [15] |
曾富英, 李敏锋, 申维. 地震波初至拾取的分形研究[J]. 现代地质, 2002, 16(2): 209-213. ZENG F Y, LI M F, SHEN W. The fractal study on detecting arrival time of the first break[J]. Geoscience, 2002, 16(2): 209-213. |
| [16] |
李辉峰, 邹强, 金文昱. 基于边缘检测的初至波自动拾取方法[J]. 石油地球物理勘探, 2006, 41(2): 150-155. LI H F, ZOU Q, JIN W Y. Method of automatic first breaks pick-up based on edge detection[J]. Oil Geophysical Prospecting, 2006, 41(2): 150-155. |
| [17] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [18] |
LEWIS W, VIGH D. Deep learning prior models from seismic images for full-waveform inversion[J]. Expanded Abstracts of 87th Annual Internat SEG Mtg, 2017, 1512-1517. |
| [19] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN W X, ZHOU Y T, CHI Y. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. |
| [20] |
MA Y, JI X, FEI T W, et al. Automatic velocity picking with convolutional neural networks[J]. Expanded Abstracts of 88th Annual Internat SEG Mtg, 2018, 2066-2070. |
| [21] |
ARAYA P M, JENNINGS J, ADLER A, et al. Deep-learning tomography[J]. The Leading Edge, 2018, 37(1): 58-66. |
| [22] |
刘佳楠, 武杰. 基于全卷积神经网络的地震初至波拾取[J]. 信息技术与网络安全, 2018, 37(11): 62-67. LIU J N, WU J. Seismic first arrival picking based on fully convolutional networks[J]. Information Technology and Network Security, 2018, 37(11): 62-67. |
| [23] |
LONG J, SHELHAMER E, DARRELL T. Fully convolutional networks for semantic segmentation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014, 39(4): 640-651. |
| [24] |
蔡振宇, 盖增喜. 人工智能在拾取地震P波初至中的应用——以汶川地震余震序列为例[J]. 北京大学学报(自然科学版), 2019, 55(3): 451-460. CAI Z Y, GE Z X. Using artificial intelligence to pick P-wave first-arrival of the microseisms:taking the aftershock sequence of wenchuan earthquake as an example[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2019, 55(3): 451-460. |
| [25] |
GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[J]. Advances in Neural Information Processing Systems, 2014, 2672-2680. |
| [26] |
RADFORD A, METZ L, CHINTALA S.Unsupervised representation learning with deep convolutional generative adversarial networks[EB/OL].[2019-10-28].https://arxiv.org/abs/1511.06434v2
|
| [27] |
GURCAN M N, CHAN H P, SAHINER B, et al. Optimal neural network architecture selection:improvement in computerized detection of microcalcifications[J]. Academic Radiology, 2002, 9(4): 420-429. DOI:10.1016/S1076-6332(03)80187-3 |
| [28] |
ALBELWI S, MAHMOOD A.Automated optimal architecture of deep convolutional neural networks for image recognition[C]//2016 15th IEEE International Conference on Machine Learning and Applications(ICMLA).[s.l.]: IEEE, 2016: 53-60
|
| [29] |
GURCAN M N, SAHINER B, CHAN H P, et al.Optimal selection of neural network architecture for CAD using simulated annealing[C]//Proceedings of the 22nd Annual International Conference of the IEEE Engineering in Medicine and Biology Society(Cat.No.00CH37143).[s.l.]: IEEE, 2000: 3052-3055
|
| [30] |
王鑫磊.基于深度卷积生成对抗网络的图像修复研究与应用[D].重庆: 重庆大学, 2018 WANG X L.Research and application of image inpainting based on deep convolutional Generative Adversarial Network[D].Chongqing: Chongqing University, 2018 |
| [31] |
唐贤伦, 杜一铭, 刘雨薇, 等. 基于条件深度卷积生成对抗网络的图像识别方法[J]. 自动化学报, 2018, 44(5): 855-864. TANG X L, DU Y M, LIU Y W, et al. Image recognition with conditional deep convolutional generative adversarial networks[J]. Acta Automatica Sinica, 2018, 44(5): 855-864. |



