2. 酒泉卫星发射中心, 甘肃酒泉 732750;
3. 西安交通大学电子与信息学部, 陕西西安 710049;
4. 中国石油新疆油田勘探开发研究院地球物理研究所, 新疆乌鲁木齐 830013
2. Jiuquan Satellite Launch Center, Jiuquan 732750, China;
3. School of Information and Communication Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
4. Institute of Geophysics, Research Institute of Petroleum Exploration & Development of Xinjiang Oilfield Company, PetroChina Co Ltd., Urumqi 830013, China
传统的炸药震源对环境破坏大且可控性差。可控震源是不同于炸药震源的另一种形式的激发源。可控震源激发方式具有安全环保、组织灵活、激发信号人为可控等优点, 同时能够满足宽方位、高密度、点激发等高精度地震勘探的需求, 在国内外得到越来越广泛的关注和应用[1-3]。目前, 滑动扫描是可控震源用于地震勘探的一种常见的高效采集方式, 该方法压缩了相邻两次信号扫描的间隔时间, 极大地提高了野外采集效率[4-7]。
可控震源滑动扫描采集技术日趋成熟, 采用该方法能够得到高密度炮点、高覆盖次数的地震数据, 但其最大问题是谐波畸变[8]。李振春等[9]研究了可控震源产生的两种谐波形成机理与特征, 认为采用可控震源滑动扫描采集的地震数据产生谐波噪声的主要原因有两个:一是机械系统的畸变导致产生谐波, 二是表层的介质畸变导致产生谐波。根据谐波干扰产生原因, 李振春等[9]将这两类谐波分别称为机械系统谐波与表层响应谐波, 同时, 还归纳总结了两种谐波噪声的几个重要特征:①机械系统谐波频率为基波频率整数倍, 表层响应谐波频率集中在一段狭窄的频率范围内; ②当使用线性升频信号作为扫描信号时, 机械系统谐波出现在负时间轴, 表层响应谐波主要出现在正时间轴; ③机械系统谐波噪声在整个剖面出现, 表层响应谐波主要出现在本炮近偏移距附近, 两种谐波噪声出现位置都具有一定的随机性, 难以预测。
针对滑动扫描采集方式产生的谐波干扰, 国内外学者提出了不同的解决思路与方案, 主要有改善可控震源构造、相关前谐波噪声压制和相关后谐波噪声压制3类方法。SERIFF[10]分析了可控震源的基板和地面耦合导致高阶谐波这一现象。张宏乐[11]提出了通过减小可控震源的驱动幅度、增大系统阻尼系数、采用变相位的扫描信号3种改善可控震源的方式来减小可控震源谐波畸变。针对相关前的地震记录谐波噪声压制, 近年来许多学者提出了多种思路与方案。LI等[12]提出了一种利用纯相移方法压制滑动扫描地震数据中谐波干扰的方法, 该方法比较简单而且容易实现, 可以有效压制近场和远场谐波噪声。黄建平等[13]、周学锋[14]、李凤磊[15]设计了纯相移滤波器来滤除谐波, 该方法比较稳定且容易实现。ZHANG等[16]提出反相关法, 依次压制二次谐波、三次谐波以及更高阶次的谐波噪声, 该方法只需先对相关后的数据做反相关处理且省时、高效, 可以处理相关前的地震数据, 也可以处理相关后的地震数据。针对可控震源基板与地面的谐波畸变, XIA等[17]提出了利用时频域奇异值分解(Singular Value Decomposition, SVD)压制谐波噪声的方法, 可以达到压制谐波噪声的目的, 但该方法针对的是可控震源基板与地面耦合产生的谐波畸变, 无法压制可控震源自身产生的谐波干扰。相关前地震数据谐波噪声的压制方法可以有效压制谐波噪声, 但相关前的地震数据量大, 计算效率相对低, 需要的数据存储空间更大, 因此, 为满足需求, 研究人员将大量精力集中在压制相关后地震数据谐波噪声方面。YU等[18]提出了分频异常振幅压制方法, 该方法相当于在时频域进行滤波处理, 能够压制一部分谐波与面波, 但会明显损伤有效信号。SHARMA等[19]提出使用模拟退火法压制谐波噪声, 该方法能够压制一定的谐波噪声, 但算法效率较低。SICKING等[20]提出地面力信号滤波法, 此方法需要相关后数据、地面力信号和每一炮数据初至时间。WANG等[21]基于震源力信号设计谐波预测算子, 求取相关后记录中的谐波干扰, 然后根据求得的谐波干扰, 在被干扰区域中剔除谐波噪声, 以达到压制地震数据中谐波干扰的目的, 但该方法需要震源力信号, 且需要在上一炮数据中减掉本炮对上一炮的谐波干扰, 因此必须从没有受到谐波干扰的最后一炮数据开始处理, 所以该算法无法进行单炮数据处理。LI等[22]和罗勇等[23]利用时频域稀疏优化方法压制相关后地震记录数据中的谐波噪声, 该方法在确保有效信号保真性的同时, 不需要震源力信号就能够直接有效压制谐波噪声, 且可以进行单炮处理, 降低了采集成本。
由于可控震源与检波器距离远近及地表介质结构的差异, 导致地震数据中谐波噪声位置分布与各道数据中谐波噪声强弱难以预测。在利用时频域稀疏优化方法对谐波干扰噪声进行压制时, 如果不考虑谐波噪声强弱, 往往会导致对某些道的谐波噪声压制不彻底或损伤有效信号的问题。因此需要考虑地震数据所含谐波噪声的强弱, 针对性地选择算法参数。如果只凭直觉和经验判断谐波噪声强弱, 不仅效率很低, 而且也不够科学和精确。因此, 迫切需要一种能够自动衡量可控震源滑动扫描采集地震数据中谐波噪声强弱的方法。为此, 本文提出了一种衡量自动相关后地震资料中谐波噪声能量的振幅谱比值方法, 并应用于谐波噪声的自适应压制。
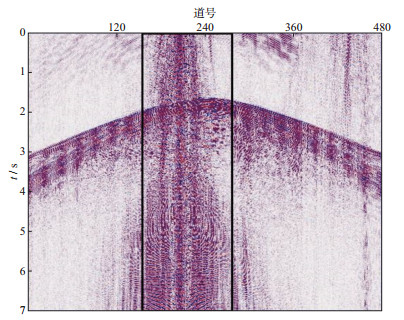
1 谐波噪声振幅谱比值衡量方法 1.1 谐波噪声分析在可控震源滑动扫描施工中, 采集到的地震数据往往受谐波噪声的干扰。图 1为西部某油田可控震源滑动扫描采集的相关后炮集记录, 每条测线480道, 记录长度为7.0s, 采样间隔为2ms。从图 1中可以看到, 谐波噪声的影响较为严重, 尤其在黑框区域, 谐波噪声掩盖了部分同相轴, 降低了数据信噪比, 严重影响地震数据后续的分析与处理。
|
图 1 可控震源滑动扫描实际地震数据 |
可控震源地震勘探使用的线性扫描信号频率是随时间线性变化的, 如下式所示:
| $ s(t) = a(t)\sin \left[ {2{\rm{ \mathsf{ π} }}\left( {{f_1} + \frac{{qt}}{2}} \right)t} \right]\;\;\;0 \le t \le T $ | (1) |
式中:f1为扫描信号起始频率; q为扫描信号频率变化率, 其中, q>0表示s(t)为线性升频扫描信号, q < 0表示s(t)为线性降频扫描信号, 本文选择q>0;T为扫描信号持续时间, 即扫描长度; a(t)为扫描信号的窗函数。a(t)可表示为:
| $ \begin{array}{l} a\left( t \right)=\\ \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2}\left[ {1 + \cos \left( {{\rm{ \mathsf{ π} }}\frac{{t + {T_1}}}{{{T_1}}}} \right)} \right]}&{0 \le t \le {T_1}}\\ 1&{{T_1} < t \le T - {T_1}}\\ {\frac{1}{2}\left[ {1 - \cos \left( {{\rm{ \mathsf{ π} }}\frac{{T - t}}{{{T_1}}}} \right)} \right]}&{T - {T_1} < t \le T} \end{array}} \right. \end{array} $ | (2) |
式中:T1为该窗函数在扫描信号两端增加的一个逐渐变化的过渡带的长度。
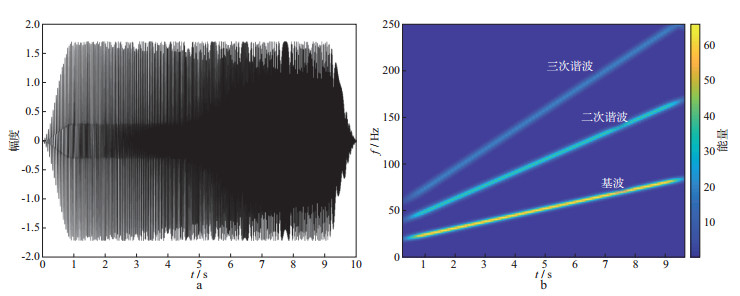
谐波畸变扫描信号的波形与时频谱如图 2所示。谐波畸变扫描信号可以定义为:
| $ s(t) = \sum\limits_{n = 1}^N {{a_n}} (t)\sin \left[ {2{\rm{ \mathsf{ π} }}n\left( {{f_1} + \frac{{qt}}{2}} \right)t} \right] $ | (3) |
|
图 2 谐波畸变信号波形(a)及其时频谱(b) |
式中:fs(t)表示基波以及各次谐波的振幅包络(n=1表示参考扫描信号, n=2表示二阶谐波, n=3表示三阶谐波)。一般从地面力信号能够分析得到谐波畸变阶数, 由于更高阶的谐波噪声经过地层衰减后残留能量很低, 因此本文只考虑二阶、三阶的谐波噪声。
可控震源勘探施工包括采集和相关两个过程。所谓相关, 是指将检波器上原始采集的地震记录数据与参考扫描信号进行互相关, 使得相关后的谐波噪声分布在负的时间轴上(对于线性升频扫描信号)。假设x(t)为检波器记录的信号, s(t)为参考扫描信号, 两者做互相关处理后, 获得相关后的数据s1(t):
| $ {s_1}(t) = \int_{ - \infty }^\infty x (\tau )s(\tau - t){\rm{d}}\tau $ | (4) |
式中:τ为信号的时间。
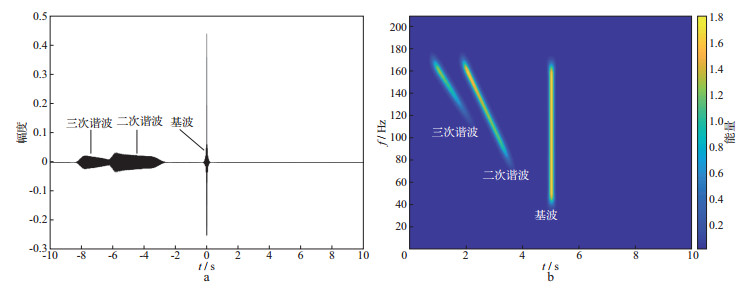
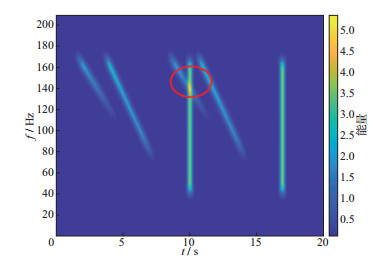
根据滑动扫描采集理论, 为了提高采集效率, 本炮尚未接收完毕就可开始进行下一炮的激发。图 3为相关后的时域波形及其时频谱(以升频扫描信号为例), 可见, 相关后的谐波噪声出现在负的时间轴上。图 4为相关后的模拟地震记录时频谱, 图中红圈处参考扫描信号与下一炮谐波噪声有交叉重叠部分, 也就是本炮数据主要受到下一炮谐波噪声干扰。
|
图 3 相关后模拟地震信号(单炮数据)波形(a)及其时频谱(b) |
|
图 4 相关后模拟地震信号(两炮数据)时频谱 |
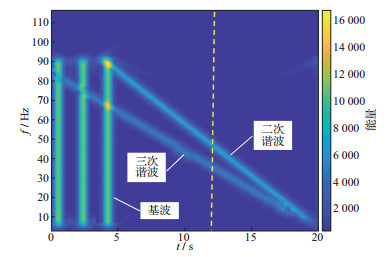
图 5展示了起始频率为5Hz, 终止频率为90Hz的模拟数据滑动扫描相关后的时频谱, 可以清晰地看到有效信号(基波)及噪声干扰(二次谐波), 也可清晰观察到二次谐波起始频率为10Hz, 三次谐波起始频率为20Hz, 与理论推导结果一致。在实际勘探中, 为了节省存储及计算时间, 一般根据最深目标层确定相关后数据长度, 会将完整的相关后数据截短, 如图 5中黄色虚线所示。此时, 截取后的数据, 主要保留了谐波噪声的高频能量部分, 即谐波干扰的起始频率将抬高, 不再是原来的10Hz及20Hz。
|
图 5 单道信号的时频谱 |
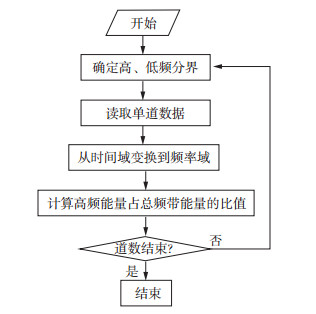
自动衡量可控震源滑动扫描采集地震记录中谐波噪声强弱的振幅谱比值方法的计算流程如图 6所示, 主要步骤如下。
|
图 6 振幅谱比值方法的计算流程 |
1) 假设x[n]表示单道地震数据, X[k]为x[n]的离散傅里叶变换(DFT):
| $ X[k] = {\mathop{\rm DFT}\nolimits} (x[n]) $ | (5) |
假设单道地震数据x[n]的采样点个数为N, 则通过DFT得到的频谱离散采样点个数也为N; 本文记采样频率为fs, 由于DFT算法得到的频谱以尼奎斯特(Nyquist)频率对称, 因此最多只需考虑前N/2个离散点的频谱。
2) 假设基于震源力信号起始低频值及相关后数据长度确定的高、低频分界点的频率为fs, 可以确定地震记录高频能量计算起始点p的频率为fs/fs, 即谐波噪声在DFT域主要能量分布起始位置, 计算总频带能量及分界点以上的高频带能量。
| $ {{E_{fh}} = \sum\limits_{k = \rho }^M {{\mathop{\rm abs}\nolimits} } (X[k])} $ | (6) |
| $ {E_f} = \sum\limits_{k = 0}^M {\rm{a}} {\rm{bs}}(X[k]) $ | (7) |
式中:Efh为地震记录高频能量; Ef为地震数据总频带能量; 假设谐波噪声频带范围上限为fmax, 则M可
由Nfmax/fs确定。
3) 计算分界点高频带能量与总频带能量的比值, 即为振幅谱比值α:
| $ \alpha = {E_{fh}}/{E_f} $ | (8) |
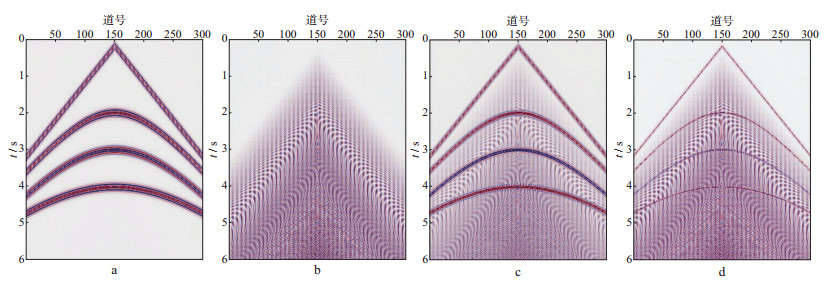
用简单的层状介质模型数据进行测试。图 7a、图 7b分别为合成的有效信号和谐波噪声模型数据, 共300道, 记录长度为6.0s, 采样间隔为2ms。从图 7b中可以看到, 近偏移距的谐波噪声强于远偏移距。将图 7a的有效信号与图 7b的谐波噪声相加, 得到图 7c所示的含噪模型数据, 信噪比为23.86。将图 7a的有效信号加上10倍的图 7b的谐波噪声, 得到图 7d的含噪模型数据, 信噪比为-22.19。很明显, 图 7d合成数据的谐波噪声要强于图 7c合成数据的谐波噪声。
|
图 7 模型数据 a有效信号; b谐波噪声; c含弱噪数据; d含强噪数据 |
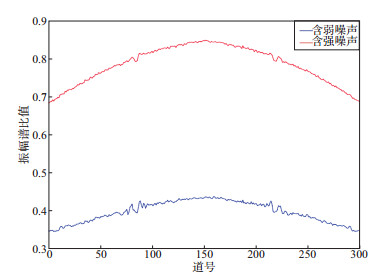
分别计算这两种含噪合成数据各道的振幅谱比值。基于震源力信号起始低频值及相关后数据长度确定高、低频的分界点的频率fs为40Hz, 即40~100Hz作为高频带, 0~100Hz作为全频带。计算的振幅谱比值如图 8所示。从图 8可以看到, 含强谐波噪声合成数据每一道的振幅谱比值高于同一道的含弱谐波噪声数据, 说明单道地震数据谐波噪声越强, 其振幅谱比值越大; 此外, 无论是图 7c的弱噪模型数据还是图 7d的强噪模型数据, 其振幅谱比值曲线都是先增大后减小, 与含噪模型数据的谐波噪声在近偏移距要强于远偏移距的特点一致。分别抽取图 7c与图 7d所示数据的第50道、第150道、第200道, 计算其振幅谱比值, 对比结果如表 1所示, 可以看到, 谐波噪声越强, 振幅谱比值越大。
|
图 8 不同信噪比合成数据的振幅谱比值 |
| 表 1 单道合成数据的振幅谱比值 |
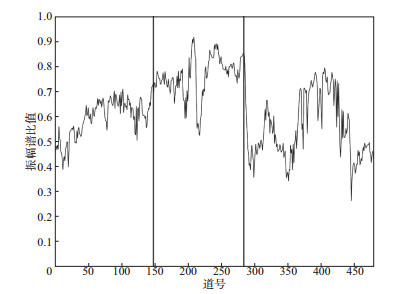
计算图 1所示的实际地震数据的振幅谱比值。基于震源力信号起始低频值及相关后数据长度, 我们选择50Hz作为高、低频带的分界频率, 即选择50~100Hz作为高频带, 0~100Hz作为全频带, 计算振幅谱比值, 结果如图 9所示。从图 9可以看到, 在黑框内对应的区域振幅谱比值较大, 其它区域振幅谱比值较小, 也就是说, 谐波噪声越强的区域, 振幅谱比值越大。
|
图 9 实际地震数据的振幅谱比值 |
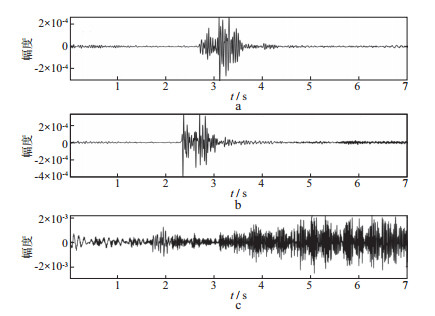
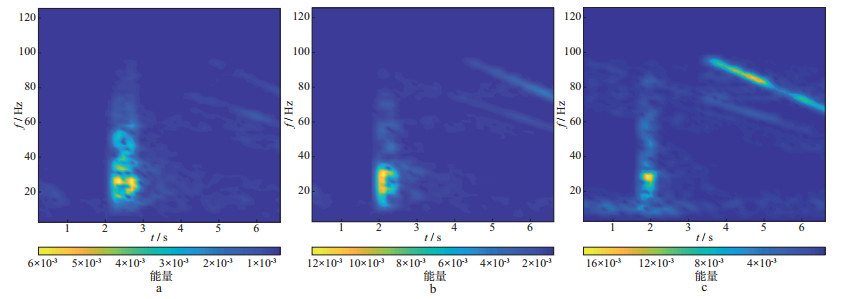
为了进一步验证振幅谱比值方法, 我们从图 1所示的实际地震资料中抽取第50道、第100道和第210道数据进行分析, 其波形和时频谱分别如图 10和图 11所示。可以看出, 第50道含有较弱谐波噪声, 第100道含有中等强度谐波噪声, 第210道含有较强谐波噪声。采用本文方法计算振幅谱比值, 第50道数据振幅谱比值为0.6095, 第100道数据振幅谱比值为0.6947, 第210道数据振幅谱比值为0.8912, 反映出单道数据的谐波噪声越强, 其振幅谱比值越大。因此, 采用本文方法可以自动衡量滑动扫描地震数据的谐波噪声强弱。
|
图 10 第50道(a)、第100道(b)及第210道(c)数据波形 |
|
图 11 第50道(a)、第100道(b)及第210道(c)数据时频谱 |
自动衡量谐波噪声强弱的振幅谱比值方法是一种高效算法, 采用该方法处理10×104道(每道3500个采样点)地震数据仅耗时62.7s(单核处理)。
从模型数据与实际数据的实验结果可以看出, 谐波噪声越弱, 振幅谱比值越小, 反之, 谐波噪声越强, 振幅谱比值越强。因此, 使用振幅谱比值可以对三维工区地震数据的每一道数据中谐波噪声能量的强弱进行自动估计, 并且可以根据谐波噪声强弱自动调节谐波噪声压制算法中的一些关键参数。例如, 在使用基于稀疏优化压制谐波噪声算法中, 当谐波噪声能量较强时, 则可调小稀疏表示谐波噪声字典的阈值系数参数, 反之则调大阈值系数, 以实现谐波噪声的自适应压制。
图 12为可控震源滑动扫描采集的实际叠后地震数据, 共有420道, 采样长度为6.0s, 采样间隔为2ms, 可见, 该地震数据受到较强谐波噪声的干扰。

|
图 12 实际地震数据 |
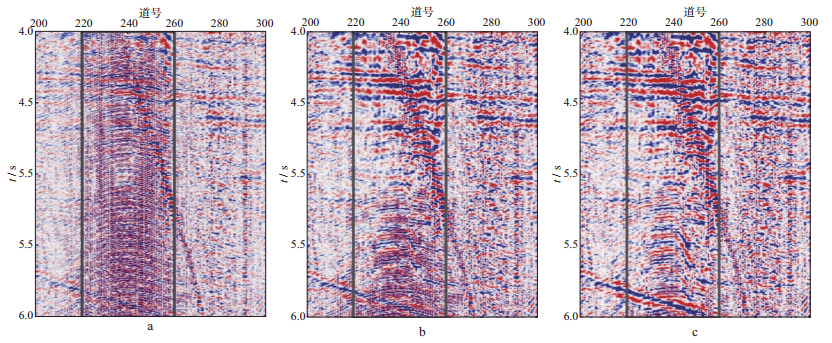
图 13a为该数据中局部区域(201~300道, 4.0~6.0s)的放大显示。首先采用固定参数的稀疏优化方法(即处理各道数据时参数相同, 通过多次实验得到最佳的固定参数)对该地震数据进行去噪处理, 并选择201~300道, 4.0~6.0s的时窗区域进行放大观察, 结果如图 13b所示。采用本文的振幅谱比值方法衡量每道数据的谐波噪声强弱, 然后根据噪声强弱自适应地选择压噪算法的参数, 并同样选择201~300道, 4.0~6.0s的时窗区域进行观察, 去噪结果如图 13c所示。可以看到, 两种方法都能够压制5s以内的浅层区域谐波噪声, 但是观察图 13中黑框区域可知, 采用固定参数方法进行去噪处理后具有明显的谐波噪声残留, 而采用自适应压噪方法对谐波噪声的压制效果则更加彻底, 几乎没有谐波噪声残留。为了进一步验证此结论, 抽取第240道数据分析其时频谱, 结果如图 14所示, 同样可以看到, 采用固定参数的稀疏优化方法残留谐波噪声比较明显, 采用自适应压噪方法能够更加彻底压制谐波噪声。因此, 基于振幅谱比值的谐波噪声自适应压噪方法有效解决了固定参数的稀疏优化方法可能带来的谐波噪声压制不彻底的问题, 具有很强的自适应性。
|
图 13 采用不同方法压制谐波噪声的结果 a局部原始地震数据; b固定参数方法压制噪声的结果; c自适应方法压制噪声的结果 |
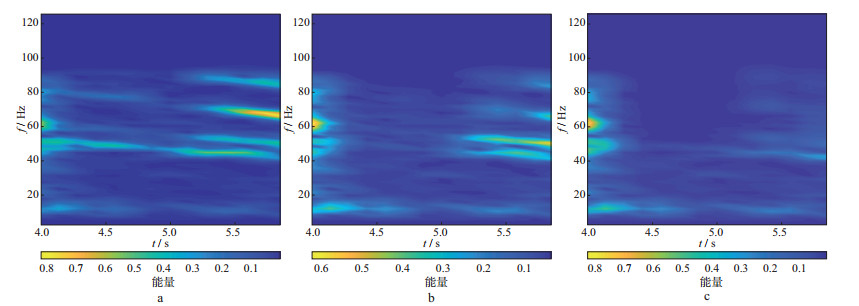
|
图 14 采用不同方法压制谐波噪声的时频谱 a原始地震数据; b固定参数方法压制噪声后的数据; c自适应方法压制噪声后的数据 |
单道地震数据从时域变换到频率域, 基于震源力信号起始低频值及相关后数据长度确定高、低频分界点, 计算高频能量占总频带能量的比值, 作为衡量谐波噪声强弱的指标。模型数据与实际数据实验结果表明, 谐波噪声能量越强, 振幅谱比值越大。振幅谱比值能够自动估计可控震源滑动扫描地震记录中谐波噪声能量的强弱。根据振幅谱比值自动选择谐波噪声压制算法中的参数, 可以实现谐波噪声的自适应压制。
| [1] |
凌云, 高军, 孙德胜, 等. 可控震源在地震勘探中的应用前景与问题分析[J]. 石油物探, 2008, 47(5): 425-438. LING Y, GAO J, SUN D S, et al. Analysis of vibroseis in seismic exploration and its application[J]. Geophysical Prospection for Petroleum, 2008, 47(5): 425-438. |
| [2] |
柴书常. 采集与相关[J]. 石油仪器, 2002, 16(3): 1-6. CHAI S C. Acquisition and correlation[J]. Petroleum Instruments, 2002, 16(3): 1-6. |
| [3] |
槐永军, 武永生. 可控震源的相关技术[J]. 物探装备, 2009, 19(1): 30-32. HUAI Y J, WU Y S. Correlation technique of vibroseis[J]. Equipment for Geophysical Prospecting, 2009, 19(1): 30-32. |
| [4] |
魏铁, 张慕刚, 汪长辉. 可控震源高效采集技术及在国际项目中的应用[J]. 石油科技论坛, 2012, 31(2): 7-10. WEI T, ZHANG M G, WANG C H. High-productivity vibroseis techniques and their application in international seismic projects[J]. Oil Forum, 2012, 31(2): 7-10. |
| [5] |
魏国伟, 张慕刚, 魏铁, 等. 可控震源滑动扫描采集方法及应用[J]. 石油地球物理勘探, 2008, 43(增刊2): 67-69. WEI G W, ZHANG M G, WEI T, et al. Slide-sweeping acquisition method of vibroseis and application[J]. Oil Geophysical Prospecting, 2008, 43(S2): 67-69. |
| [6] |
丁伟, 胡立新, 何京国, 等. 可控震源高效地震采集技术研究及应用[J]. 石油物探, 2014, 53(3): 338-343. DING W, HU L X, HE J G, et al. The research on vibrator high efficient simulation technology and its application[J]. Geophysical Prospection for Petroleum, 2014, 53(3): 338-343. |
| [7] |
骆飞, 石双虎, 邓志文, 等. 可控震源分频同时扫描采集方法实现与应用[J]. 石油物探, 2018, 57(1): 28-32. LUO F, SHI S H, DENG Z W, et al. Implementation and application of vibroseis acquisition using frequency-separated simultaneous sweep technology[J]. Geophysical Prospection for Petroleum, 2018, 57(1): 28-32. |
| [8] |
李明亮, 谢伟, 王强. 可控震源谐波干扰的分析讨论[J]. 中国设备工程, 2019, 417(6): 177-178. LI M L, XIE W, WANG Q. Analysis of harmonic of vibroseis[J]. Research and Exploration, 2019, 417(6): 177-178. |
| [9] |
李振春, 曲英铭, 韩文功, 等. 可控震源两种谐波产生机理与特征研究[J]. 石油物探, 2016, 55(2): 159-172. LI Z C, QU Y M, HANG W G, et al. Generation mechanism and characteristics of two kinds of harmonic waves for vibroseis[J]. Geophysical Prospection for Petroleum, 2016, 55(2): 159-172. |
| [10] |
SERIFF A J. The effect of harmonic distortion in the use of vibratory surface sources[J]. Geophysics, 1970, 35(2): 234-246. DOI:10.1190/1.1440087 |
| [11] |
张宏乐. 可控震源信号中的谐波畸变影响及消除[J]. 物探装备, 2003, 13(4): 223-230. ZHANG H L. Influence of distorted harmonics in vibroseis signal and how to remove it[J]. Equipment for Geophysical Prospecting, 2003, 13(4): 223-230. |
| [12] |
LI X P, SOELLNER W, HUBRAL P. Elimination of harmonic distortion in vibroseis data[J]. Geophysics, 1995, 60(2): 503-516. DOI:10.1190/1.1443787 |
| [13] |
黄建平, 周学锋, 郭军, 等. 滑动扫描记录中压制谐波干扰方法[J]. 中国石油大学学报(自然科学版), 2012, 36(2): 81-85. HUANG J P, ZHOU X F, GUO J, et al. Method of harmonic noise elimination in slip sweep data[J]. Journal of China University of Petroleum(Edition of Natural Science), 2012, 36(2): 81-85. |
| [14] |
周学锋.基于预测滤波的谐波干扰压制方法研究[D].青岛: 中国石油大学, 2011 ZHOU X F.Method of harmonic noise elimination based on its estimation[D].Qingdao: China University of Petroleum, 2011 |
| [15] |
李凤磊.可控震源滑动扫描谐波干扰压制方法研究[D].青岛: 中国石油大学, 2011 LI F L.The research of harmonic noise rejection based on slip-sweep acquisition method[D].Qingdao: China University of Petroleum, 2011 |
| [16] |
ZHANG H J, ZHOU H, ABD E K A E, et al. The anti-correlation method for removing harmonic distortion in vibro seis slip-sweep data[J]. Applied Geophysics, 2012, 9(2): 159-167. DOI:10.1007/s11770-012-0325-5 |
| [17] |
XIA J, JIE Y, YONG G, et al. Suppressing harmonics based on singular value decomposition in time frequency domain[J]. SEG Technical Program Expanded, 1949, 1-5. |
| [18] |
YU Z, GAROSSINO P. High-energy noise attenuation of seismic data in the wavelet-transform domain[J]. Integrated Computer Aided Engineering, 2005, 12(1): 57-67. DOI:10.3233/ICA-2005-12105 |
| [19] |
SHARMA S P, TILDY P, IRANPOUR K, et al. Attenuation of harmonic noise in vibroseis data using Simulated Annealing[J]. EGU General Assembly 2009, 2009, EGU2009-8693. |
| [20] |
SICKING C, FLEURE T, NELAN S, et al. Slip sweep harmonic noise rejection on correlated shot data[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 36-40. |
| [21] |
WANG B, LI H, BO Z, et al. Cross-harmonic noise removal on slip-sweep vibroseis data[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012, 59-64. |
| [22] |
LI X F, CHEN W C, WANG W, et al. Harmonic noise removal in united time-frequency domain via sparse promotion[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 4725-4729. |
| [23] |
罗勇, 刘宏杰, 毛海波, 等. 时频域稀疏优化谐波噪声压制方法及其在准噶尔盆地高密度地震勘探中的应用[J]. 石油物探, 2018, 57(1): 79-85. LUO Y, LIU H J, MAO H B, et al. Harmonic noise suppression in the time-frequency domain via sparse optimization and application to high-density seismic exploration in Junggar Basin[J]. Geophysical Prospection for Petroleum, 2018, 57(1): 79-85. |



