2. 中国石油集团东方地球物理勘探有限责任公司研究院, 新疆乌鲁木齐 830002;
3. 中国石油集团东方地球物理勘探有限责任公司新疆物探处, 新疆乌鲁木齐 830002;
4. 西安交通大学电子与信息工程学院, 陕西西安 710049
2. Research Institute of BGP INC., China National Petroleum Corporation, Urumqi 830002, China;
3. Xinjiang Geophysical Exploration Company, BGP Inc., China National Petroleum Corporation, Urumqi 830002, China;
4. School of Information and Communication Engineering, Xi'an Jiaotong University, Xi'an 710049, China
在地震勘探中, 传统的炸药震源激发方式对环境具有不可逆转的污染, 且可控性差。与炸药震源相比, 可控震源不仅安全环保、施工效率高、成本低, 而且组织灵活, 可按照特定的深层地质目标和工区地表条件人为地调整所激发的信号, 提升能量利用率。基于可控震源的上述优点, 目前它已经成为陆上地震勘探的主要激发方式之一, 在国内外得到了大规模的应用[1]。
可控震源滑动扫描采集方式极大地提高了地震数据采集效率, 覆盖次数较炸药震源提高几倍乃至几十倍, 但是因滑动扫描方式采集的地震数据在不同炮记录时间上部分重叠在一起, 在相关处理后本炮数据会受到后一炮数据的谐波干扰。滑动扫描的滑动时间越短, 采集到的地震记录受谐波干扰就越严重。谐波噪声降低了地震资料的信噪比和分辨率, 对有效信号造成了干扰, 进而会影响震资料的成像与解释。因此, 高效的谐波噪声压制方法必然会受到关注。对于海量地震数据, 高效的谐波噪声压制技术也是其工业化应用的前提。
按照地震数据的不同, 可控震源地震记录谐波噪声压制方法主要分为相关前和相关后两大类。针对相关前的地震数据谐波噪声压制问题, LI等[2]对扫频信号进行分析得到纯相移滤波算子, 再对单道地震数据进行纯相移滤波处理压制谐波噪声; 黄建平等[3]通过统计分析获得统一的地面力信号, 然后设计各谐波分量对应的相移滤波器, 该方法可以对多炮数据进行处理, 但是它只对相关前地震数据的高次谐波具有较好的压制效果。由于相关前地震数据量较大, 计算速度较慢, 难以满足实际生产需求, 相关后的地震数据谐波噪声压制问题是目前主要的研究方向。YU等[4]提出了分频异常振幅压制方法, 根据谐波噪声与有效信号小波系数的差异, 对地震数据有效信号的小波系数进行阈值处理, 进而达到压制谐波噪声的目的, 这种方法处理速度较快, 但是当有效信号与谐波噪声的小波系数差异不明显时, 有效信号成分不能有效还原, 从而造成较大损伤。SICKING等[5]提出地面力信号滤波法, 该方法首先使用地面力信号分解得到基波和谐波, 然后利用傅里叶变换将基波和谐波变换到频率域, 最后将谐波频谱与基波频谱的比值作为滤波器的系数来设计谐波噪声滤波器。钟飞等[6]将单道地震信号进行Hilbert-Huang变换, 在变换域设置阈值滤除谐波。WANG等[7]设计了一种谐波预测算子, 在干扰区域成功将谐波噪声剔除。然而, 与常规方法相同, 该方法必须从最后一炮地震记录开始处理, 无法进行单炮处理。韩文功等[8]认为谐波噪声是谐波畸变信号与反射系数的褶积, 谐波噪声能够由精确的反射系数和地面力信号估算出来。曲英铭等[9]首先采用谐波压制滤波器基于最小二乘法对预测的谐波干扰进行修正, 以实现对力信号内含谐波的准确压制, 然后分频滤波压制谐波噪声。罗勇等[10]将时频域稀疏优化谐波噪声压制方法应用于准噶尔盆地玛湖地区三维典型单炮记录谐波噪声压制, 该方法具有良好的保真性。LI等[11]将时频域稀疏优化方法引入到谐波噪声压制问题中, 该方法按照有效信号与谐波噪声在时频域的形态特征差异, 通过分析选择连续小波变换对有效信号进行稀疏表示, 选择Chirplet变换对谐波噪声进行稀疏表示, 组成可以用分块坐标松弛算法求解的超完备字典, 进而迭代求解得到有效信号和谐波噪声。陈建友等[12]在LI等[11]提出的时频域稀疏优化方法的基础上, 应用振幅谱比值衡量谐波噪声强弱, 可以自适应地选择参数压制不同强度的谐波噪声。时频域稀疏优化谐波噪声压制方法在实际应用中取得了良好的效果, 但考虑到地震资料的复杂性, 采用固定字典的稀疏优化方法, 在有些区域仍然存在谐波噪声压制效果不理想及有效信号损伤的问题。同时, 与传统的固定字典稀疏表示方法相比, 自适应学习字典方法能更好地适应复杂数据[13-14], 进而取得更好的谐波噪声压制效果。为此, 本文提出了基于自适应学习字典的谐波噪声压制方法, 该方法直接从相关后地震炮集记录中学习稀疏表示字典, 根据谐波噪声与有效信号的波形形态差异, 将学习得到的字典原子分类为谐波噪声子字典与有效信号子字典, 分别稀疏表示谐波噪声和有效信号。然后应用分块坐标下降算法, 利用分类得到的子字典分别重构谐波噪声与有效信号, 实现自适应地分离谐波噪声的目的。
1 方法原理 1.1 建立模型假设地震单道信号s为有效信号sr、谐波噪声sh和随机噪声sn的线性叠加:
| $ \mathit{\boldsymbol{s}} = {\mathit{\boldsymbol{s}}_{\rm{r}}} + {\mathit{\boldsymbol{s}}_{\rm{h}}} + {\mathit{\boldsymbol{s}}_{\rm{n}}} $ | (1) |
其中, 随机噪声sn可使得该模型具有更加普遍的适用性。有效信号sr与谐波噪声sh的分离需要解决如下优化问题:
| $ \begin{array}{*{20}{c}} {\mathop {{\mathop{\rm argmin}\nolimits} }\limits_{{\rm{\{ }}{x_r}, {x_{\rm{h}}}\} } {{\left\| {{\mathit{\boldsymbol{x}}_{\rm{r}}}} \right\|}_1} + {{\left\| {{\mathit{\boldsymbol{x}}_{\rm{h}}}} \right\|}_1}\quad {\rm{ s}}{\rm{.t}}{\rm{. }}}\\ {{{\left\| {\mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{D}}_{\rm{r}}}{\mathit{\boldsymbol{x}}_{\rm{r}}} - {\mathit{\boldsymbol{D}}_{\rm{h}}}{\mathit{\boldsymbol{x}}_{\rm{h}}}} \right\|}^2} \le \varepsilon } \end{array} $ | (2) |
式中: xr为有效信号字典Dr对应的有效信号稀疏表示系数向量; xh为谐波噪声字典Dh对应的谐波噪声稀疏表示系数向量; ε是误差门限, 目的是使该优化问题在随机噪声或者其它干扰下保持稳定。
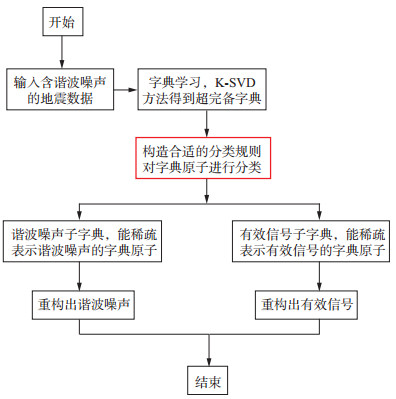
公式(2)的求解关键是得到可以分别稀疏表示有效信号与谐波噪声的字典, 本文根据两种信号的时间域波形特征差异, 首先利用K-SVD得到超完备字典, 然后对超完备字典进行分类。由于谐波噪声的能量呈现高频端集中的特点, 为了最大程度地逼近谐波噪声的波形特征, 将谐波噪声原子选择为学习得到的超完备字典中能量集中在高频端的原子。高、低频分界点可以通过计算振幅谱比确定, 设置振幅谱比的阈值将超完备字典分类为有效噪声的子字典Dr与谐波信号的子字典Dh。最后, 利用分类所得的两个子字典分别稀疏重构谐波噪声与有效信号, 实现分离谐波噪声的目的, 其技术流程如图 1所示。
|
图 1 本文算法流程 |
傅里叶变换[15]、小波变换[16]、Ridgelet变换[17]、Curvelet变换[18]、Shearlet变换[19]等使用固定的波形字典, 因此无法完全匹配地震信号的复杂特征。与固定字典相比, 学习字典可以自适应地学习信号特征以匹配复杂信号的特征。ENGAN等[20]提出的最优方向字典学习算法(MOD)需要计算矩阵的伪逆, 导致算法具有很高的复杂度, 实用性不强。AHARON等[21]提出的K-SVD字典学习算法逐列更新字典原子, 克服了MOD算法需要计算矩阵伪逆的缺陷, 有效地提高了字典学习的效率。
K-SVD算法通过逐列更新字典的方法来更新字典A, 其目标方程可以表示为:
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{X}}} \left\{ {\parallel \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}\parallel _F^2} \right\}\quad {\rm{ s}}{\rm{.t}}{\rm{. }}\quad \forall i, {\left\| {{x_i}} \right\|_0} \le {T_0} $ | (3) |
式中: A ∈ Rn×K表示超完备字典, R表示实数集; y ={yi}i=1N为N个待表示信号的集合; x ={xi}i=1N为y的稀疏系数矩阵; T0表示系数中非零元素最大值。
求解公式(3), 首先利用初始固定字典A求得信号的稀疏表示系数矩阵x, 然后再根据系数矩阵x通过逐列更新字典原子获得最终的字典A。
首先, 使用正交匹配追踪算法(OMP)[22]求解稀疏系数。MALLAT等[23]提出匹配追踪算法(MP)求解信号的稀疏表示, 但是MP算法是纯贪婪算法, 计算复杂度大, 无法保证每次迭代的投影是正交投影, 最终求解结果可能并不稀疏。PATI等[22]提出的OMP算法, 在MP算法基础上每次迭代后进行正交化处理, 克服了MP算法的缺点。信号y经过l次分解后如下式:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}} = \sum\limits_{i = 1}^l {{\mathit{\boldsymbol{a}}_i}} {x_i} + {\mathit{\boldsymbol{R}}_l}\mathit{\boldsymbol{y}}\quad {\rm{ s}}{\rm{.t}}{\rm{. }}}\\ {\left\langle {{\mathit{\boldsymbol{R}}_l}\mathit{\boldsymbol{y}}, {\mathit{\boldsymbol{a}}_i}} \right\rangle = 0\quad i = 1, 2, \cdots , k} \end{array} $ | (4) |
式中: ai为第i次分解的原子; xi为第i次分解时的系数; Rly为l次分解后的残差。
为了满足正交条件, OMP算法需要由重建原子集合中利用最小二乘算法得到第l次分解的稀疏表示系数:
| $ \mathit{\boldsymbol{x}}_l^\prime = {\mathop{\rm argmin}\nolimits} \left\| {\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{A}}_l}\mathit{\boldsymbol{x}}} \right\| $ | (5) |
然后更新残差:
| $ {\mathit{\boldsymbol{R}}_l}\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}_l^\prime \quad l = l + 1 $ | (6) |
使得OMP算法残差逐渐减小, 直到算法收敛。
字典更新时首先固定系数矩阵x和字典A, 更新字典的第k列ak时, 令x中字典原子ak对应第k行为xk, 则字典学习的目标函数可改写为:
| $ \begin{array}{l} \left\| {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{Ax}}} \right\|_F^2 = \left\| {\mathit{\boldsymbol{Y}} - \sum\limits_{j = 1}^K {{\mathit{\boldsymbol{a}}_j}} {\mathit{\boldsymbol{x}}_j}} \right\|_F^2 = \parallel (\mathit{\boldsymbol{Y}}-\\ \sum\limits_{j \ne k}^K {{\mathit{\boldsymbol{a}}_j}} {\mathit{\boldsymbol{x}}_j}) - {\mathit{\boldsymbol{a}}_k}{\mathit{\boldsymbol{x}}_k}\parallel _F^2 = \left\| {{\mathit{\boldsymbol{E}}_k} - {\mathit{\boldsymbol{a}}_k}{\mathit{\boldsymbol{x}}_k}} \right\|_F^2 \end{array} $ | (7) |
式中: Ek为去掉原子ak影响的误差。将Ax分解成L个秩为1的矩阵的和。逐列更新字典的第k列原子时, 固定其它的L-1列。
利用奇异值分解(SVD)方法处理字典矩阵A以更新ak和xk, 但是经过SVD之后, xk将会满向量, 即SVD得到的xk中非零值的数量和位置会和原xk不同, al将不能满足稀疏表示的条件。
因此仅保留xk中非零值(去掉xk中所有的零值), 再应用SVD更新al和xk, (7)式转化为下式:
| $ \left\| {{\mathit{\boldsymbol{E}}_l}{\mathit{\Omega }_l} - {\mathit{\boldsymbol{a}}_l}x_k^l{\mathit{\Omega }_l}} \right\|_F^2 = \left\| {\mathit{\boldsymbol{E}}_R^l - {\mathit{\boldsymbol{a}}_l}x_R^l} \right\|_F^2 $ | (8) |
式中:ωl={i|1≤i≤N, xkl(i)≠0}为xkl(i)≠0的点的索引值; Ωl=N×|ωl|, 在[ωl(i), i]处的值都为1, 其它点为0;xRl=xklΩl为xkl去掉零输入后得到的非零系数, 长度为|ωl|; ERl= ElΩl为El只保留xkl对应的非零元素项, 其为n×|ωl|矩阵。
1.3 字典分类本文通过计算每个超完备字典原子振幅谱比, 选定一个高、低频分界点阈值, 将字典原子分类为谐波噪声子字典与有效信号子字典, 用于分别稀疏表示谐波噪声与有效信号。高、低频分界点的阈值选择是一个经验值, 主要评估信噪分离后有效信号的保真程度及压制掉的噪声强度。如果这个阈值选择过小, 压制的噪声能量大, 有可能会损伤一定的有效信号; 如果选择过大, 则有效信号保真度高, 但是噪声残余多。
字典原子振幅谱比计算步骤如下。
1) 确定高、低频的分界点p, 计算分界点以上的高频带能量与总频带能量, 地震信号的频率一般不会超过100 Hz, 所以计算能量时将100 Hz以上的能量舍弃以减少运算量, 算式如下。
| $ {E_{fh}} = \sum\limits_{k = kp}^{k100} {{{\left\| {{D^\prime }[k]} \right\|}^2}} $ | (9) |
| $ {E_f} = \sum\limits_{k = 0}^{k100} {{{\left\| {{D^\prime }[k]} \right\|}^2}} $ | (10) |
式中:D′[k]为字典原子Fourier振幅谱; Efh为高频能量; Ef为总频带能量。
2) 计算振幅谱比值α, 即分界点p以上的高频带能量与总频带能量的比值:
| $ \alpha = {E_{fh}}/{E_f} $ | (11) |
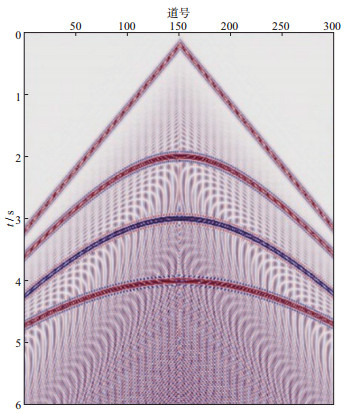
图 2为合成地震数据, 由有效信号与谐波噪声叠加得到。该数据包含3个反射层, 利用卷积模型生成, 所用扫描信号为线性升频扫描信号:
| $ s(t) = a(t)\sin \left[ {2{\rm{ \mathit{ π} }}\left( {{f_1} + \frac{{qt}}{2}} \right)t} \right]\quad 0 \le t \le T $ | (12) |
|
图 2 含谐波噪声合成地震数据 |
扫描信号的最低频率为3 Hz, 最高频率为90 Hz, 谐波噪声包含二次谐波和三次谐波。该合成地震数据共有300道, 采样点为3 000, 采样间隔为2 ms。
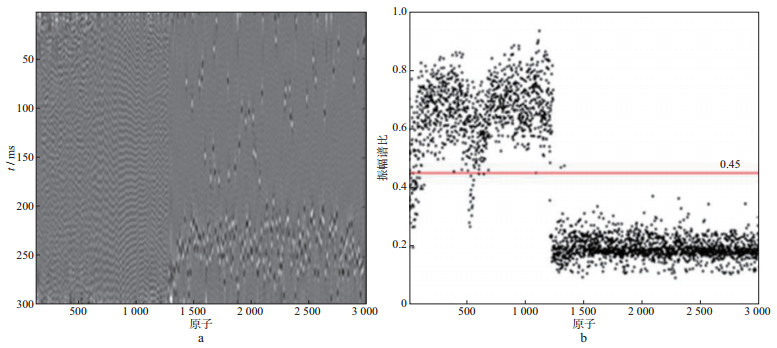
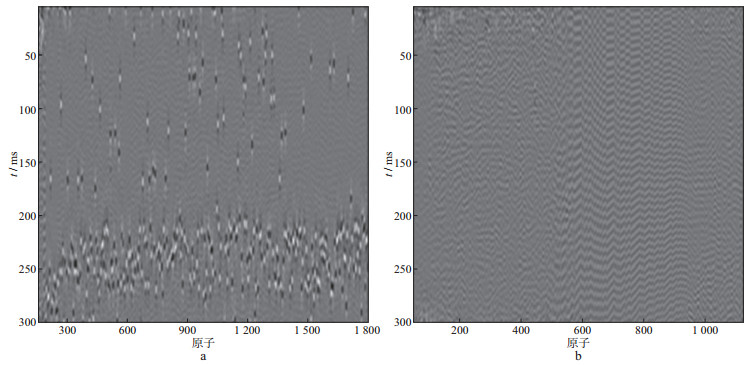
首先应用K-SVD字典学习方法在样本集上进行字典学习, 得到超完备字典如图 3a所示, 然后计算字典原子的振幅谱比, 选择40 Hz作为计算高低频能量的分界频率点, 即利用40~100 Hz频率范围计算高频带能量, 0~100 Hz频率范围计算总频带能量。图 3b为超完备字典原子振幅谱比计算结果, 其中红线值为0.45, 是设置的阈值, 字典原子振幅谱比值高于阈值的为谐波噪声字典原子, 低于阈值的为有效信号字典原子, 分类得到的有效信号字典和谐波噪声字典如图 4所示。
|
图 3 合成数据字典训练(a)与K-SVD训练得到的超完备字典的字典原子振幅谱比(b) |
|
图 4 合成数据有效信号字典(a)与谐波噪声字典(b) |
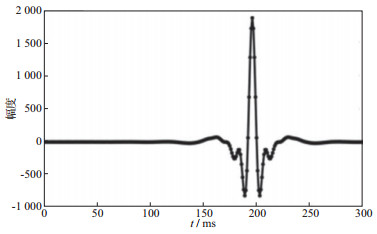
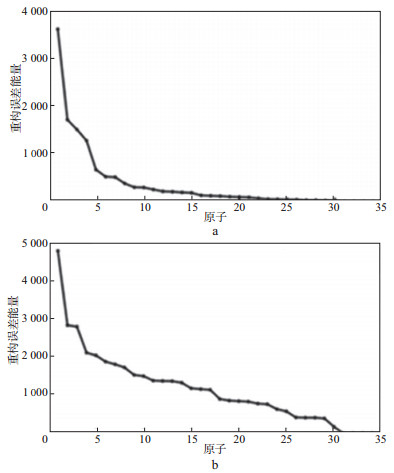
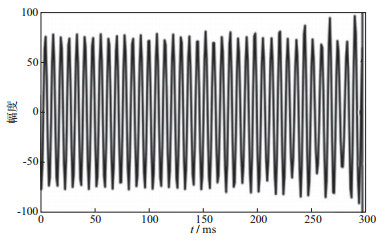
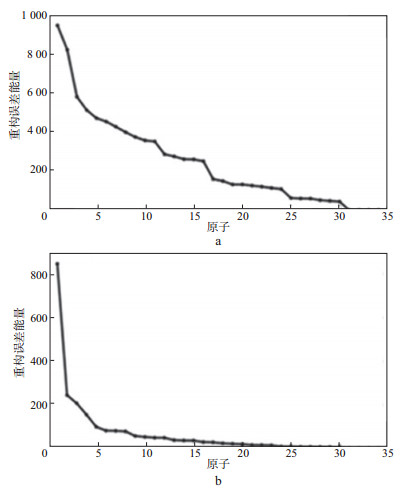
为了验证本文方法分类得到的有效信号子字典与谐波噪声子字典对有效信号与谐波噪声表示的稀疏性, 随机提取一段用于构建图 2合成数据的有效信号(如图 5), 计算图 4中有效信号子字典与谐波噪声子字典对图 5所示有效信号的表示系数, 结果见图 6。对比可得, 本文分类得到的有效信号子字典相比于谐波噪声子字典对原始有效信号的表示更稀疏, 仅用5个有效信号的原子即可实现对有效信号的表示, 而采用谐波噪声子字典对有效信号进行表示时需要大约30个原子。进一步随机提取一段用于构建图 2合成数据的谐波噪声(图 7), 计算图 4中有效信号子字典与谐波噪声子字典对其的表示系数, 结果如图 8所示。对比可得, 本文分类得到的谐波噪声子字典相比于有效信号子字典对谐波噪声的表示更稀疏。上述结果说明了本文提出的分类方法得到的有效信号子字典与谐波噪声子字典都更能够稀疏表示各自的信号, 而对另一种信号的表示更不稀疏, 满足了信号分离的条件。
|
图 5 选取的有效信号 |
|
图 6 有效信号字典(a)和谐波噪声字典(b)分别对有效信号的稀疏表示系数 |
|
图 7 谐波噪声 |
|
图 8 有效信号字典(a)和谐波噪声字典(b)分别对谐波噪声的稀疏表示系数 |
应用分类得到的子字典分别重构合成信号的有效信号与谐波噪声如图 9所示。对比图 2a合成的有效信号与图 9a使用本文方法压制谐波噪声得到的有效信号可见, 本文方法能够高保真地恢复合成的有效信号, 并且有效压制谐波噪声。图 9b为本文方法得到的谐波噪声剖面, 可以看到, 噪声剖面几乎没有反射波的损伤, 只对直达波有少许损伤。因此, 本文方法成功地压制了谐波噪声。

|
图 9 合成地震数据处理结果 a 本文方法得到的有效信号; b 本文方法得到的谐波噪声 |
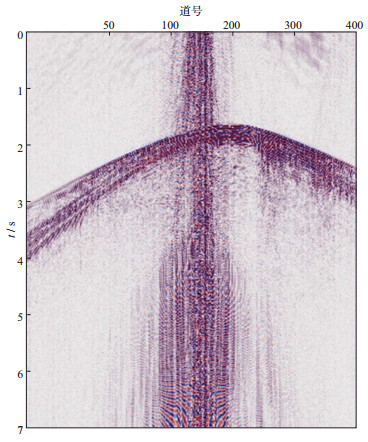
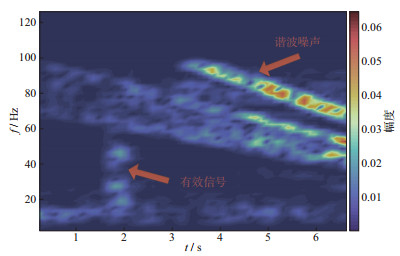
含有谐波噪声的实际地震数据如图 10所示, 每炮数据共400道, 采样间隔为2 ms, 采样点为3 501, 记录长度为7 s。图 11是实际地震数据第210道信号的时频图, 图中谐波噪声与有效信号相比, 主要表现为高频, 有效信号相对于谐波噪声主要表现为低频。
|
图 10 原始地震数据 |
|
图 11 实际地震数据第210道数据时频图 |
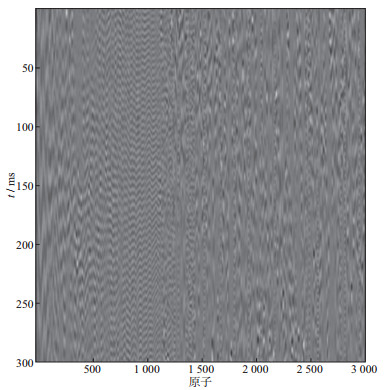
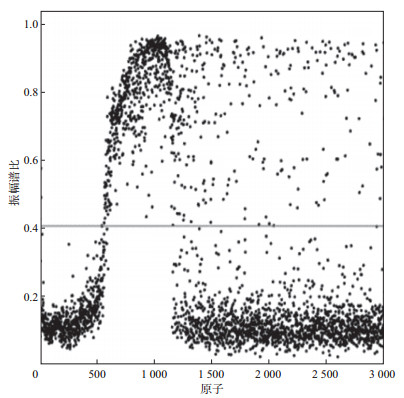
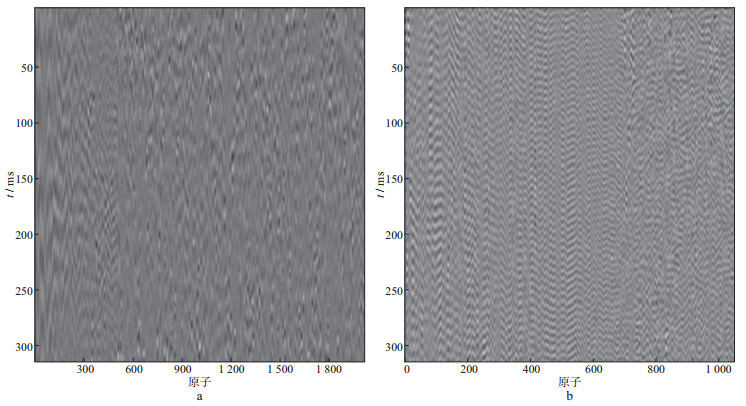
首先进行单道循环滑动截取组成样本数据集, 截取长度为300采样点, 每隔10个采样点截取一个样本。应用K-SVD算法在样本集上训练, 初始字典选择离散余弦变换(DCT), 迭代次数为50, 字典原子为300采样点, 冗余度为10, 得到的超完备字典如图 12所示。然后计算字典原子的振幅谱比, 选择40 Hz作为计算高频能量的分界频率点, 即使用40~100 Hz频率范围计算高频带能量, 0~100 Hz频率范围计算总频带能量。图 13为振幅谱比计算结果, 其中灰色直线值为0.40是设置的阈值, 字典原子振幅谱比值高于阈值的为谐波噪声字典原子, 低于阈值的为有效信号字典原子, 将超完备字典分类为有效信号字典(图 14a)与谐波噪声字典(图 14b)。需要指出的是, 这里的阈值0.40是一个经验值, 在其附近都可以实现谐波噪声压制。本文选择阈值0.40主要用于评估信噪分离后有效信号的保真程度及压制掉的噪声强度。
|
图 12 实际地震数据训练得到的超完备字典 |
|
图 13 实际地震数据训练得到的字典原子振幅谱比 |
|
图 14 实际地震数据训练得到的有效信号字典(a)和谐波噪声字典(b) |
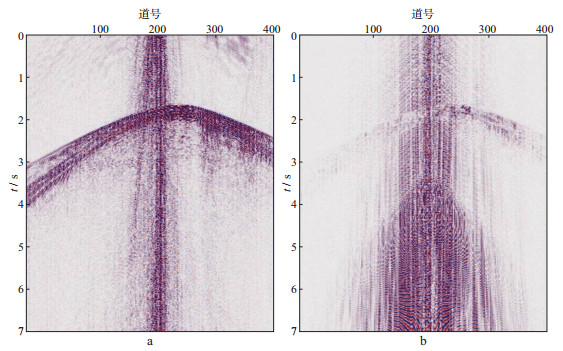
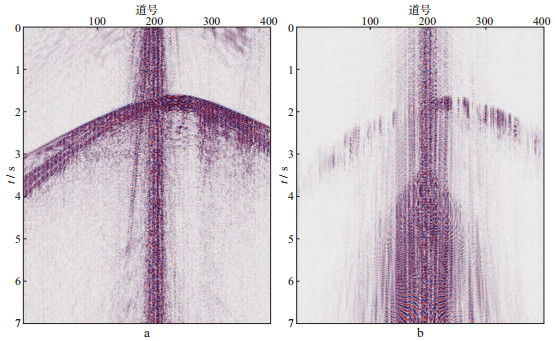
采用本文方法重构得到的有效信号与谐波噪声分别如图 15a、图 15b所示。对比图 10原始地震资料与采用本文方法得到的有效信号图 15a可见, 原始地震资料中的谐波噪声得到了有效压制, 且对有效信号的损伤较小, 结果验证了本文方法压制谐波噪声的有效性。同样, 采用自适应稀疏优化方法[12]对图 10数据进行处理, 得到的结果如图 16所示, 其中, 图 16a为有效信号, 图 16b为谐波噪声。对比图 15b与图 16b可知, 本文方法对近炮点数据有些许损伤, 对远炮点数据几乎没有损伤, 而自适应稀疏优化方法几乎对整炮数据均有损伤。
|
图 15 采用本文方法得到的有效信号(a)和谐波噪声(b) |
|
图 16 采用自适应稀疏优化法得到的有效信号(a)和谐波噪声(b) |
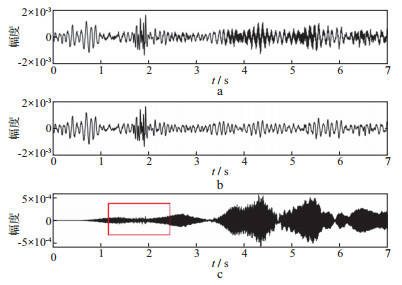
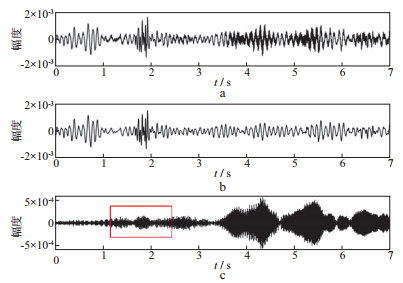
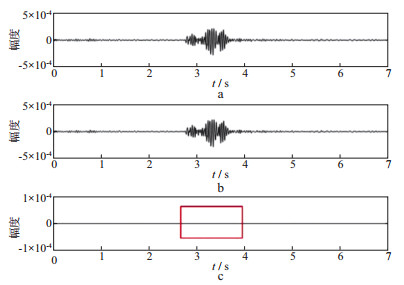
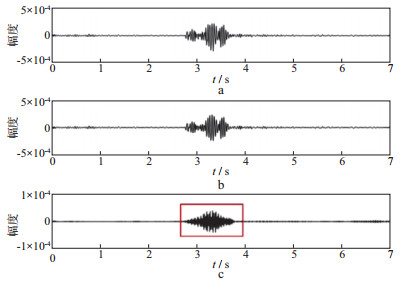
为了进一步观察, 我们提取近炮点强噪声区域第220道数据与远炮点几乎无噪声的第60道数据进行分析。图 17和图 18分别为近炮点第220道地震数据本文方法和稀疏优化方法处理对应的原始数据、有效信号、谐波噪声。图 19和图 20分别为远炮点第60道地震数据本文方法和稀疏优化方法处理对应的原始数据、有效信号、谐波噪声。对比图 17与图 18谐波噪声(红色方框区域有效信号损伤)可见, 在近炮点强噪声区域, 本文方法对有效信号损伤比自适应稀疏优化方法小。对比图 19与图 20谐波噪声(红色方框区域有效信号损伤)可见, 在远炮点区域本文方法对有效信号几乎没有损伤, 而自适应稀疏优化方法对有效信号的损伤很大。综合分析认为本文方法虽然在强噪声区域浅层有少量噪声残留, 但对整个剖面而言, 对有效信号损伤较小。因此, 本文方法有效地压制了谐波噪声。
|
图 17 近炮点地震道(第220道)本文方法结果 a 原始数据; b 有效信号; c 谐波噪声 |
|
图 18 近炮点地震道(第220道)自适应稀疏优化方法结果 a 原始数据; b 有效信号; c 谐波噪声 |
|
图 19 远炮点地震道(第60道)本文方法结果 a 原始数据; b 有效信号; c 谐波噪声 |
|
图 20 远炮点地震道(第60道)自适应稀疏优化方法结果 a 原始数据; b 有效信号; c 谐波噪声 |
本文提出了一种基于自适应学习字典的谐波噪声压制方法。基于有效信号能量主要集中于低频端与谐波噪声能量主要集中于高频端的频率特征, 提出了应用字典原子振幅谱比将K-SVD方法学习得到的超完备字典分类为有效信号稀疏表示子字典和谐波噪声稀疏表示子字典, 最后利用两个子字典分别重构有效信号与谐波噪声以达到压制谐波噪声的目的。合成地震数据及实际数据的应用结果验证了本文方法的可行性。对比本文方法与自适应稀疏优化方法的应用结果, 表明本文方法压制了绝大部分的噪声, 同时无论在近炮点还是远炮点对有效信号的损伤都小于自适应稀疏优化方法, 说明了本文方法的有效性。
同时, 本文方法还有进一步提升的空间。首先, 字典分类方法是本文方法的核心, 本文仅使用振幅谱比单一指标作为字典分类的依据, 阈值的选择会影响字典分类的准确性, 尤其是对选定阈值附近的字典很难准确区分。而通过多个指标综合决定字典的分类, 会提升字典分类的准确性, 进而提升谐波噪声压制的效果, 提出多个字典分类方法, 并综合应用于字典分类是本文方法未来的一个研究方向; 其次, K-SVD方法获得的字典原子没有明确的物理含义, 若能加上一些人为约束, 使得获得的字典原子具有明确的物理含义, 这会提升对字典的理解, 字典分类的准确性会有较大提升, 这也是本文方法未来的研究方向。
| [1] |
倪宇东, 王井富, 马涛, 等. 可控震源地震采集技术的进展[J]. 石油地球物理勘探, 2011, 46(3): 349-356. NI Y D, WANG J F, MA T, et al. Advances in vibroseis acquisition[J]. Oil Geophysical Prospecting, 2011, 46(3): 349-356. |
| [2] |
LI X P, SOELLNER W, HUBRAL P. Elimination of harmonic distortion in vibroseis data[J]. Geophysics, 1995, 60(2): 503-516. |
| [3] |
黄建平, 周学锋, 郭军, 等. 滑动扫描记录中压制谐波干扰方法[J]. 中国石油大学学报(自然科学版), 2012, 36(2): 81-85. HUANG J P, ZHOU X F, GUO J, et al. Method of harmonic noise elimination in slip sweep data[J]. Journal of China University of Petroleum(Edition of Natural Science), 2012, 36(2): 81-85. |
| [4] |
YU Z, GAROSSINO P G A. High-energy noise attenuation of seismic data in the wavelet-transform domain[J]. Integrated Computer Aided Engineering, 2005, 12(1): 57-67. DOI:10.3233/ICA-2005-12105 |
| [5] |
SICKING C, FLEURE T, NELAN S, et al. Slip sweep harmonic noise rejection on correlated shot data[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 36-40. |
| [6] |
钟飞, 张伟, 钟约先. Hilbert-Huang变换去除可控震源谐波畸变[J]. 清华大学学报:自然科学版, 2011, 51(6): 862-867. ZHONG F, ZHANG W, ZHONG Y X. Removal of harmonic distortions in vibroseis data using Hilbert-Huang transformation[J]. Journal of Tsinghua University(Science and Technology), 2011, 51(6): 862-867. |
| [7] |
WANG B B, LI H Q, ZHAO B, et al. Cross-harmonic noise removal on slip-sweep vibroseis data[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012, seg2012-0059. |
| [8] |
韩文功, 曲英铭, 胡立新, 等. 基于反射系数和地面力信号的谐波干扰消除法[J]. 地球物理学进展, 2015, 30(6): 2647-2659. HAN W G, QU Y M, HU L X, et al. Method of suppressing harmonic noise based on reflection coefficient and ground force signal[J]. Progress in Geophysics, 2015, 30(6): 2647-2659. |
| [9] |
曲英铭, 李金丽, 李振春, 等. 可控震源相关数据谐波干扰联合压制方法[J]. 石油物探, 2018, 57(2): 237-247. QU Y M, LI J L, LI Z C, et al. Joint suppression of two types vibroseis harmonic noise of correlation data[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 237-247. |
| [10] |
罗勇, 刘宏杰, 毛海波, 等. 时频域稀疏优化谐波噪声压制方法及其在准噶尔盆地高密度地震勘探中的应用[J]. 石油物探, 2018, 57(1): 79-85. LUO Y, LIU H J, MAO H B, et al. Harmonic noise suppression in the time-frequency domain via sparse optimization and application to high-density seismic exploration in Junggar Basin, China[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 79-85. |
| [11] |
LI X F, CHEN W C, WANG W, et al. Harmonic noise removal in united time-frequency domain via sparse promotion[J]. Expanded Abstracts of 85th Annual Internat SEG Mtg, 2015, 4725-4729. |
| [12] |
陈建友.基于稀疏优化的谐波噪声及光缆耦合噪声自适应压制方法研究[D].西安: 西安交通大学, 2017 CHEN J Y.The harmonic noise and fiber cable coupled noise self-adapting suppression research based on sparse optimization[D].Xi'an : Xi'an Jiaotong University, 2017 |
| [13] |
乐友喜, 杨涛, 曾贤德. CEEMD与KSVD字典训练相结合的去噪方法[J]. 石油地球物理勘探, 2019, 54(4): 729-736. YUE Y X, YANG T, ZENG X D. Seismic denoising with CEEMD and KSVD dictionary combined training[J]. Oil Geophysical Prospecting, 2019, 54(4): 729-736. |
| [14] |
李慧, 韩立国, 张良, 等. 基于字典学习和ADMM的地震数据重建[J]. 石油物探, 2019, 58(3): 419-426. LI H, HAN L G, ZHANG L, et al. Seismic data reconstruction using dictionary learning and the alternating direction method of multipliers[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 419-426. |
| [15] |
GRIFFIN D, LIM J S. Signal estimation from modified short-time Fourier transform[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1984, 32(2): 236-243. |
| [16] |
DAUBECHIES I. The wavelet transform, time-frequency localization and signal analysis[J]. IEEE Transactions on Information Theory, 1990, 36(5): 961-1005. DOI:10.1109/18.57199 |
| [17] |
CANDÈS E J.Ridgelets: Theory and applications[D].Palo Alto: Stanford University, 1998
|
| [18] |
CANDÈS E J, DEMANET L, DONOHO D, et al. Fast discrete curvelet transforms[J]. Multiscale Modeling & Simulation, 2006, 5(3): 861-899. |
| [19] |
EASLEY G, LABATE D, LIM W Q. Sparse directional image representations using the discrete shearlet transform[J]. Applied & Computational Harmonic Analysis, 2008, 25(1): 25-46. |
| [20] |
ENGAN K, AASE S O, HUSOY J H. Method of optimal directions for frame design[J]. IEEE International Conference on Acoustics, Speech, and Signal Processing, 1999, 2443-2446. |
| [21] |
AHARON M, ELAD M, BRUCKSTEIN A. K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [22] |
PATI Y C, REZAⅡFAR R, KRISHNAPRASAD P S. Orthogonal matching pursuit:Recursive function approximation with applications to wavelet decomposition[J]. Proceedings of 27th IEEE Asilomar Conference on Signals, Systems and Computers, 1993, 40-44. |
| [23] |
MALLAT S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |



